1. Durante la temporada de invierno se sitúa en una playa un dispositivo para medir la altura de ola. Se muestrean al azar 133 olas que arrojan una altura media de 2.54 metros con desviación típica 0.26

  1. ¿Muestran estos datos evidencia suficiente de que la altura media de ola en este playa durante el invierno es mayor que 2.2 metros?

  2. De las 133 olas, 74 superaron los 2.5 metros. ¿Es ésta evidencia suficiente de que más de la mitad de las olas de esta playa en invierno superan los 2.5 metros?


  1. Se desea determinar si la altura media de ola es diferente entre la mañana y la noche. Con este fin se elige un día al azar y se muestrean 58 olas por la mañana y otras 58 por la noche. Los muestreos se realizan en el mismo lugar de la playa. Los valores medios y desviaciones típicas observados en las alturas de ola respectivas son:
n media Desv. Típica
Mañana 58 2.2231 0.2215
Noche 58 2.1216 0.3627

Se muestra a continuación el resultado de analizar los datos utilizando R. Se han realizado los contrastes de normalidad de Shapiro-Wilk y los contrastes de la t de Student y de la W de Wilcoxon (estos dos últimos contrastes suponiendo las muestras tanto independientes como emparejadas).

Con la información obtenida,

  1. ¿se puede asegurar que la altura media de ola difiere significativamente en función del momento del dia? Justifica tu respuesta explicando qué contrastes has elegido y por qué.
shapiro.test(muestra1)
## 
##  Shapiro-Wilk normality test
## 
## data:  muestra1
## W = 0.95631, p-value = 0.03573
shapiro.test(muestra2) 
## 
##  Shapiro-Wilk normality test
## 
## data:  muestra2
## W = 0.9633, p-value = 0.07671
t.test(muestra1,muestra2)
## 
##  Welch Two Sample t-test
## 
## data:  muestra1 and muestra2
## t = 1.8186, df = 94.342, p-value = 0.07215
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -0.009310694  0.212268724
## sample estimates:
## mean of x mean of y 
##  2.223051  2.121572
t.test(muestra1,muestra2,paired=TRUE)
## 
##  Paired t-test
## 
## data:  muestra1 and muestra2
## t = 1.7558, df = 57, p-value = 0.0845
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -0.01425841  0.21721644
## sample estimates:
## mean of the differences 
##                0.101479
wilcox.test(muestra1,muestra2) 
## 
##  Wilcoxon rank sum test with continuity correction
## 
## data:  muestra1 and muestra2
## W = 2079, p-value = 0.02857
## alternative hypothesis: true location shift is not equal to 0
wilcox.test(muestra1,muestra2,paired=TRUE) 
## 
##  Wilcoxon signed rank test with continuity correction
## 
## data:  muestra1 and muestra2
## V = 1091, p-value = 0.06884
## alternative hypothesis: true location shift is not equal to 0
  1. Estima un intervalo de confianza al 95% para la diferencia en las alturas medias de ola entre ambos momentos del día.


  1. Se ha colocado una boya a 2 km de la playa. Esta boya mide velocidad del viento y altura de ola a intervalos de 30 minutos. La siguiente figura muestra la representación gráfica de un registro de 80 medidas de ambas variables :

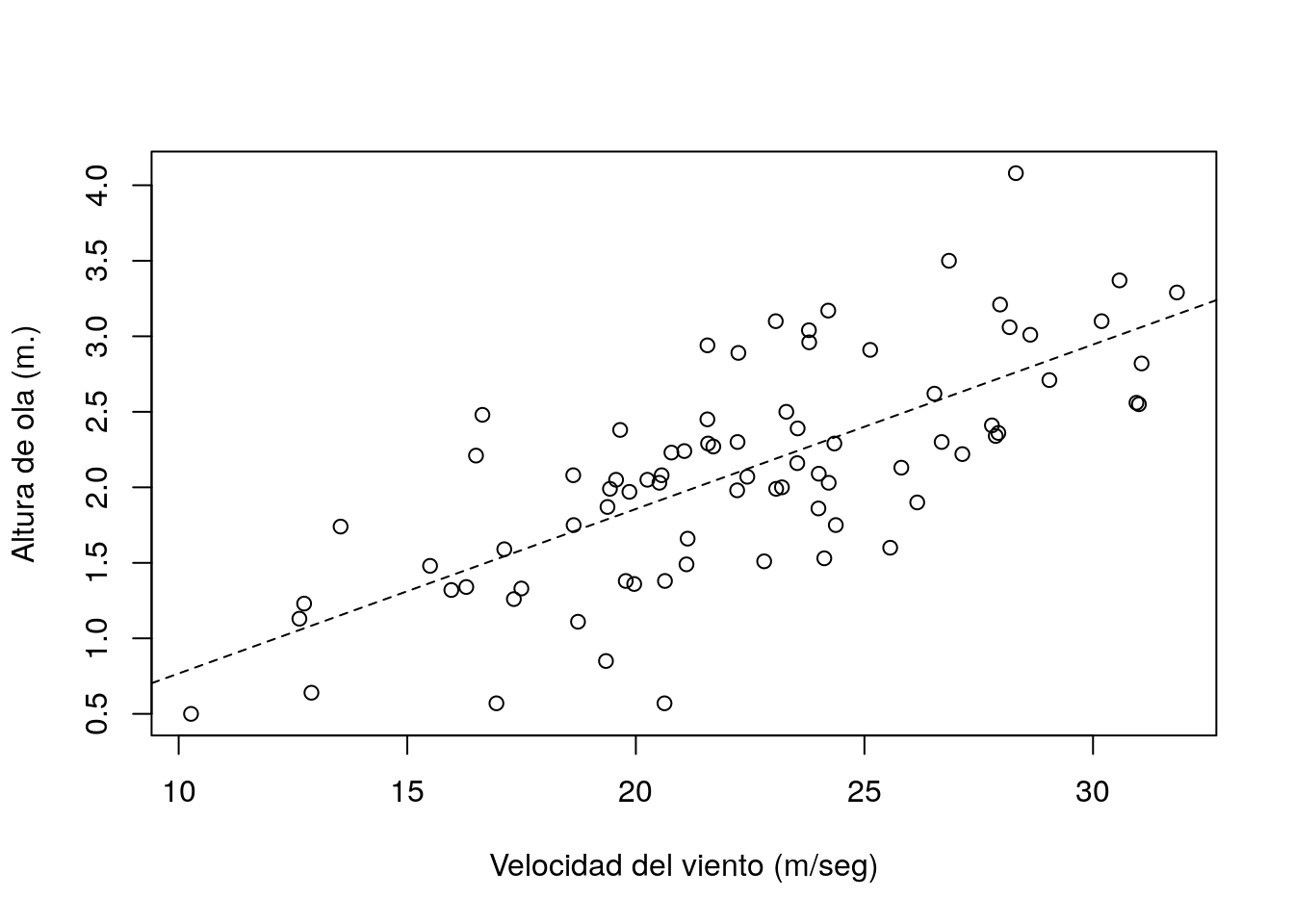
La siguiente tabla muestra un estudio descriptivo de los datos de esta muestra, así como el ajuste de la recta de regresión para predecir la altura de ola en función de la velocidad del viento:

media Desviación Típica Correlación
Velocidad Viento (m/s) 22.35 4.77 0.72
Altura de ola (m) 2.11 0.73

Recta de Regresión \[alt.Ola=-0.32+ 0.11\,vel.V\]

\(\hat{\sigma_\epsilon}=0.51\)

Con esta información:

Puede apreciarse que la pendiente de esta recta de regresión toma un valor bajo. ¿Puede concluirse que en la población dicho valor es nulo, o existe evidencia suficiente de que es positivo?


  1. Se desea determinar si la talla media de las capturas de L. pealeii ha disminuido durante los últimos años. Con este fin se recuperan datos de un estudio realizado en el periodo 1977-1980. En dicho estudio se realizó un muestreo de 840 ejemplares durante la temporada de primavera-verano, elegidos al azar entre los disponibles en los mercados de la zona. Asimismo se utilizan los datos de otro muestreo, también de 840 ejemplares, durante la misma temporada y en los mismos mercados, pero durante el periodo 2015-18. Como medida de talla se utilizó la Longitud Dorsal del Manto (en mm) del calamar. Los valores medios y desviaciones típicas observados durante cada periodo fueron:
n media Desv. Típica
1977-1980 840 174.1481 39.4769
2015-2018 840 170.6182 41.2194

Se muestra a continuación el resultado de analizar los datos utilizando R. Se han realizado los contrastes de normalidad de Shapiro-Wilk y los contrastes de la t de Student y de la W de Wilcoxon (estos dos últimos contrastes suponiendo las muestras tanto independientes como emparejadas).

Con esta información,

  1. ¿existe evidencia suficiente de que se ha producido una disminución en la talla media de esta especie desde 1977 hasta la actualidad? Justifica tu respuesta explicando qué contrastes has elegido y por qué.
shapiro.test(muestra1)
## 
##  Shapiro-Wilk normality test
## 
## data:  muestra1
## W = 0.99892, p-value = 0.9107
shapiro.test(muestra2)
## 
##  Shapiro-Wilk normality test
## 
## data:  muestra2
## W = 0.99781, p-value = 0.3443
t.test(muestra1,muestra2,alternative="greater")
## 
##  Welch Two Sample t-test
## 
## data:  muestra1 and muestra2
## t = 1.7925, df = 1674.9, p-value = 0.03662
## alternative hypothesis: true difference in means is greater than 0
## 95 percent confidence interval:
##  0.2889137       Inf
## sample estimates:
## mean of x mean of y 
##  174.1481  170.6182
t.test(muestra1,muestra2,alternative="greater",paired = TRUE)
## 
##  Paired t-test
## 
## data:  muestra1 and muestra2
## t = 1.8024, df = 839, p-value = 0.03592
## alternative hypothesis: true difference in means is greater than 0
## 95 percent confidence interval:
##  0.3050459       Inf
## sample estimates:
## mean of the differences 
##                3.529829
wilcox.test(muestra1,muestra2,alternative = "greater")
## 
##  Wilcoxon rank sum test with continuity correction
## 
## data:  muestra1 and muestra2
## W = 372759, p-value = 0.02235
## alternative hypothesis: true location shift is greater than 0
wilcox.test(muestra1,muestra2,alternative = "greater",paired = TRUE)
## 
##  Wilcoxon signed rank test with continuity correction
## 
## data:  muestra1 and muestra2
## V = 189200, p-value = 0.03675
## alternative hypothesis: true location shift is greater than 0
  1. Estima un intervalo de confianza al 95% para la diferencia entre la talla media de L. pealeii antes y ahora.


  1. A partir de la muestra de 840 calamares del periodo 2015-18 se evalúa la recta de regresión que relaciona el peso del calamar (Y) con la longitud dorsal del manto (X)

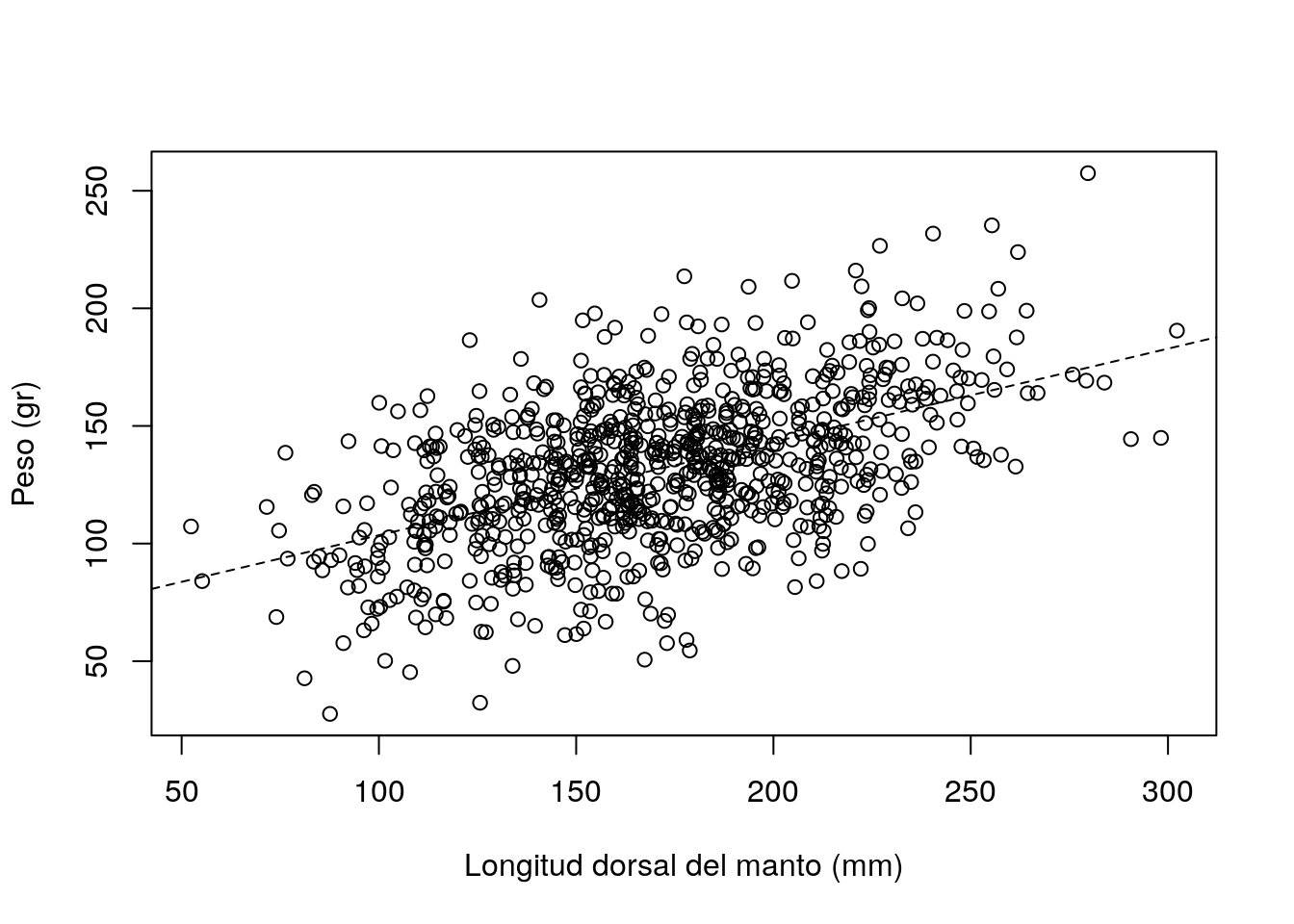
La siguiente tabla muestra un estudio descriptivo de los datos de esta muestra, así como el ajuste de la recta de regresión para predecir el peso del calamar en función de la longitud dorsal del manto:

media Desviación Típica Correlación
Longitud dorsal del manto (mm) 170.62 41.22 0.51
Peso (gr) 131.55 32.08

Recta de Regresión \[Peso=63.89+ 0.4\,Long\]

\(\hat{\sigma_\epsilon}=27.62\)

Con esta información:

  1. Construye un intervalo de confianza al 95% para la pendiente de la recta de regresión. A partir de dicho intervalo, ¿puede aceptarse la hipótesis de que por cada mm adicional de LDM el peso del calamar se incrementa en 0.5 gr?

  2. Calcula el peso que cabe esperar en un calamar cuya LDM es de 200 mm, así como un intervalo de confianza al 95% para dicho valor

 





© 2016 Angelo Santana, Carmen N. Hernández, Departamento de Matemáticas   ULPGC