Gráficos en R: Histogramas
Angelo Santana & Carmen Nieves Hernández,
Departamento de Matemáticas, ULPGC
Un histograma es una representación gráfica de la distribución de frecuencias de una variable continua. Consiste en una sucesión de rectángulos levantados sobre un eje que representa los valores de la variable. Cada rectángulo tiene un área proporcional a la frecuencia de valores observada en el intervalo sobre el que se levanta. En esta sección aprenderemos a construir un histograma con R, a superponerle una distribución de probabilidad teórica y otra estimada no paramétricamente, a insertar títulos, etiquetas, etc.
Datos.
Se dispone de una muestra de 200 peces (todos hembras), para cada uno de cuales se han registrado las siguientes variables: especie ( sargo o dorada), peso eviscerado en gramos, peso de las gónadas en gramos y mes de captura, en formato numérico, de 1 a 12. Podemos leer el archivo de datos desde la dirección de internet en que se encuentra, simplemente mediante:
peces=read.csv2("https://estadistica-dma.ulpgc.es/cursoR4ULPGC/datos/datosGrafica.csv")
str(peces)
head(peces)## 'data.frame': 200 obs. of 4 variables:
## $ especie : Factor w/ 2 levels "Dorada","Sargo": 2 1 1 1 2 1 1 2 1 2 ...
## $ mes : int 7 7 7 9 10 11 9 4 12 6 ...
## $ pesoEvis: int 1061 1062 1207 1057 1303 1219 1494 1266 1178 1054 ...
## $ gonada : int 53 79 43 32 63 38 12 169 78 70 ...## especie mes pesoEvis gonada
## 1 Sargo 7 1061 53
## 2 Dorada 7 1062 79
## 3 Dorada 7 1207 43
## 4 Dorada 9 1057 32
## 5 Sargo 10 1303 63
## 6 Dorada 11 1219 38Nuestro objetivo será construir el siguiente histograma con la variable peso eviscerado:
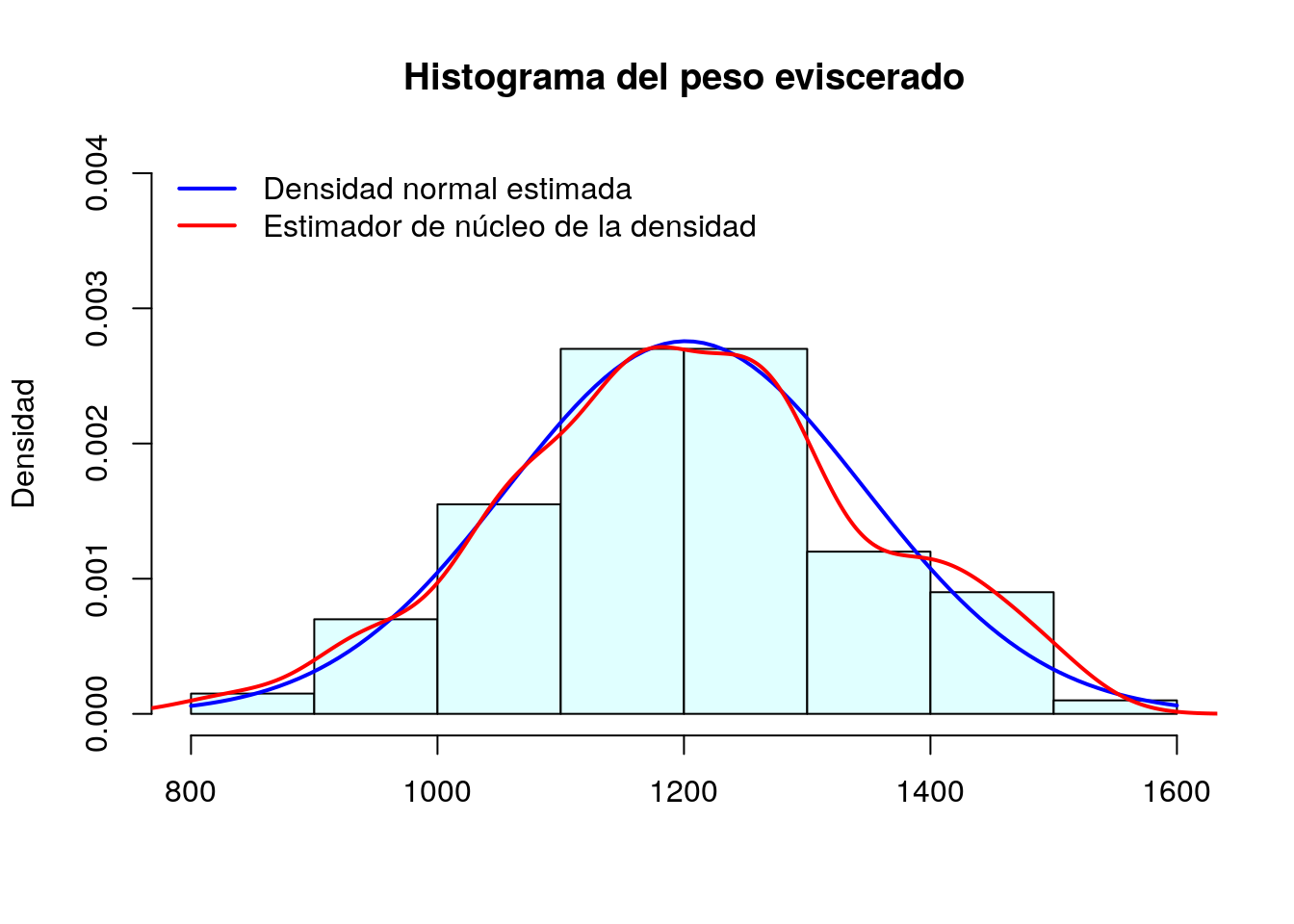
Construcción del histograma básico
Consultar la ayuda: help(hist). Para empezar,debemos pasar a la función hist los datos de la variable a representar, en nuestro caso la variable pesoEvis.
hist(peces$pesoEvis)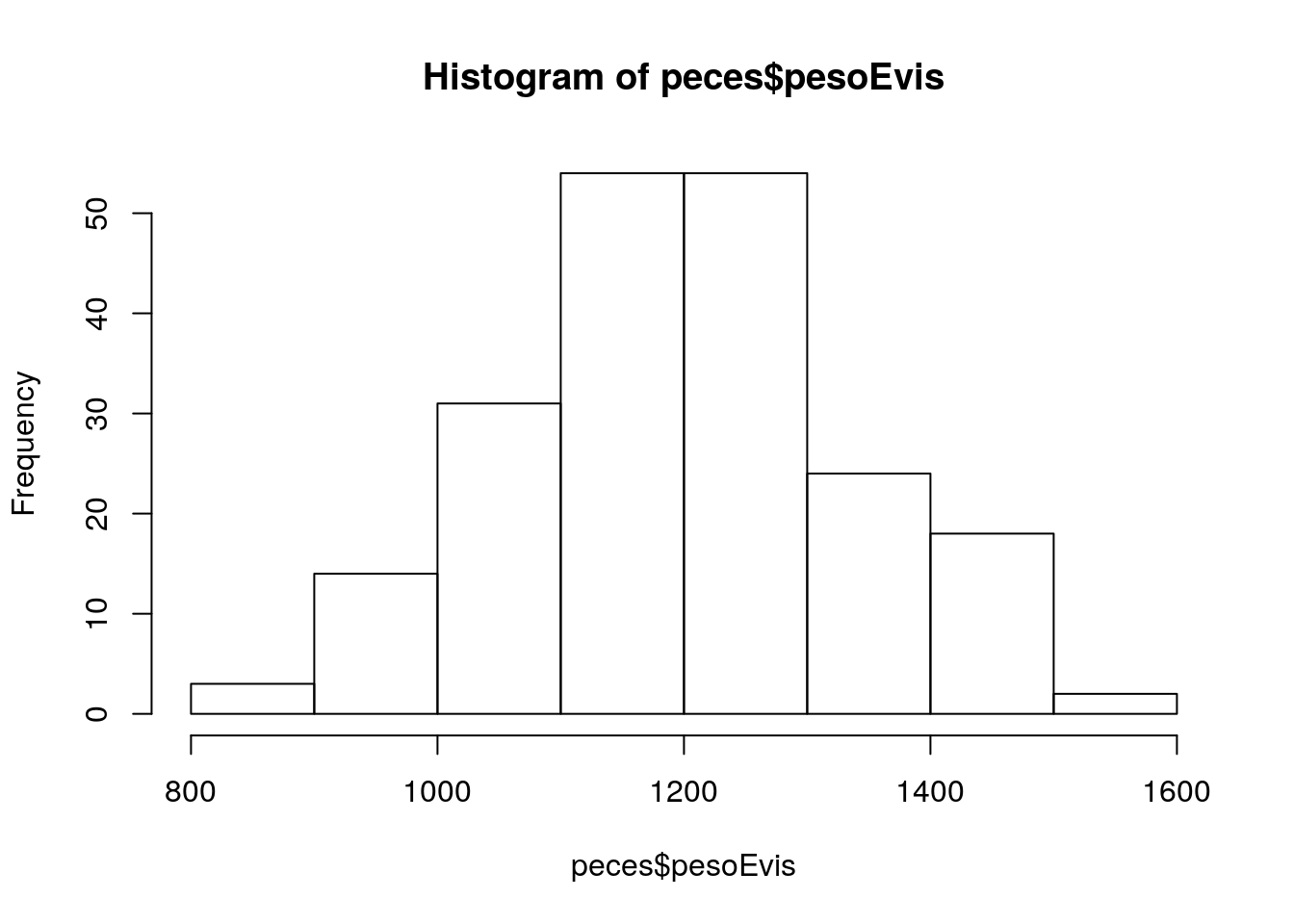
Definición del eje de ordenadas en frecuencias relativas y color del histograma
El eje de ordenadas muestra por defecto frecuencias absolutas; el gráfico que queremos construir es con frecuencias relativas en este eje. Para ello utilizamos la opción freq=FALSE; además le damos color al histograma mediante col="lightcyan"
hist(peces$pesoEvis,freq=FALSE,col="lightcyan")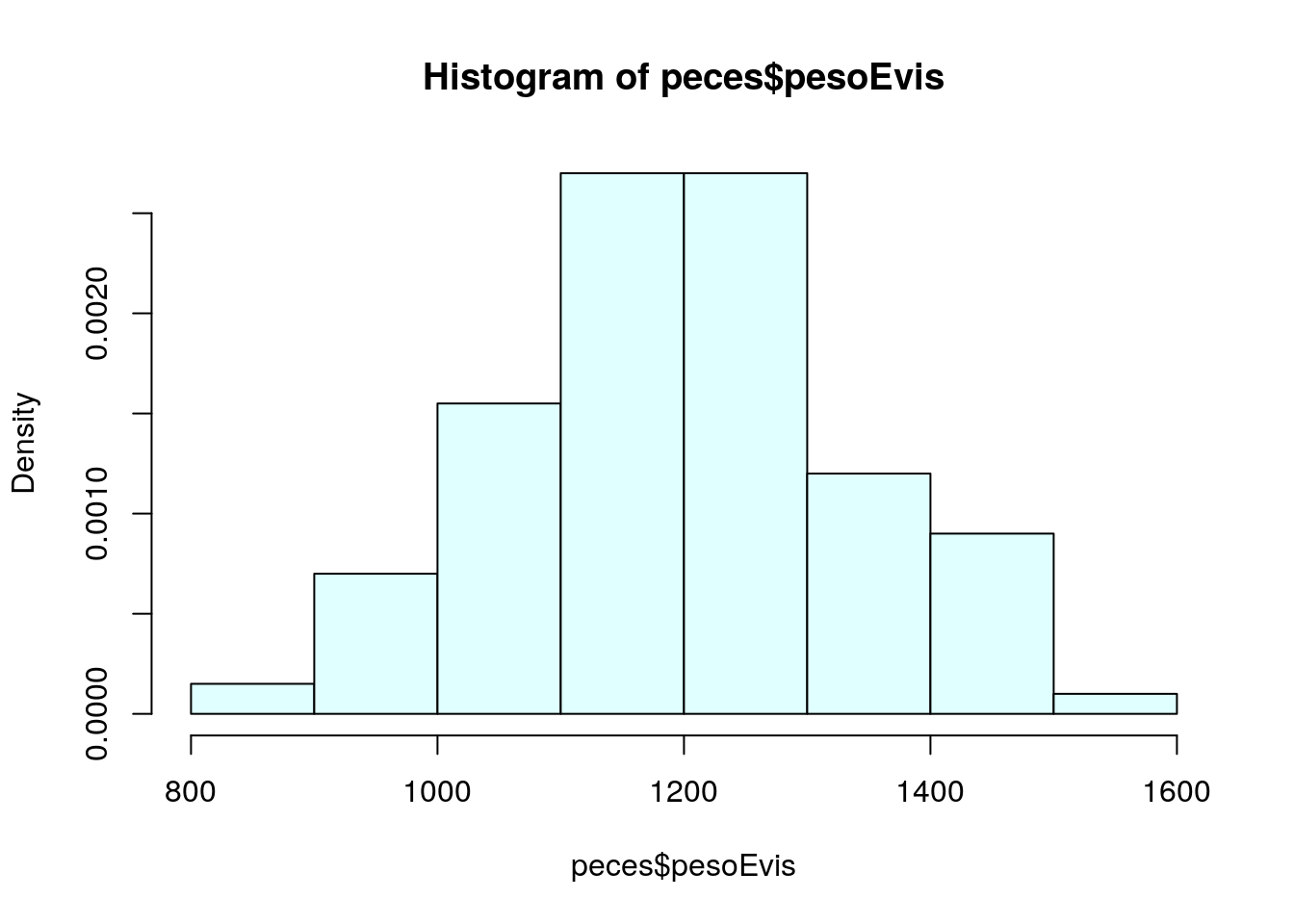
Incremento de la longitud del eje de ordenadas
Para que en la gráfica haya espacio para la leyenda, alargamos el eje de ordenadas mediante la opción ylim:
hist(peces$pesoEvis,freq=FALSE, col="lightcyan", ylim=c(0,0.004))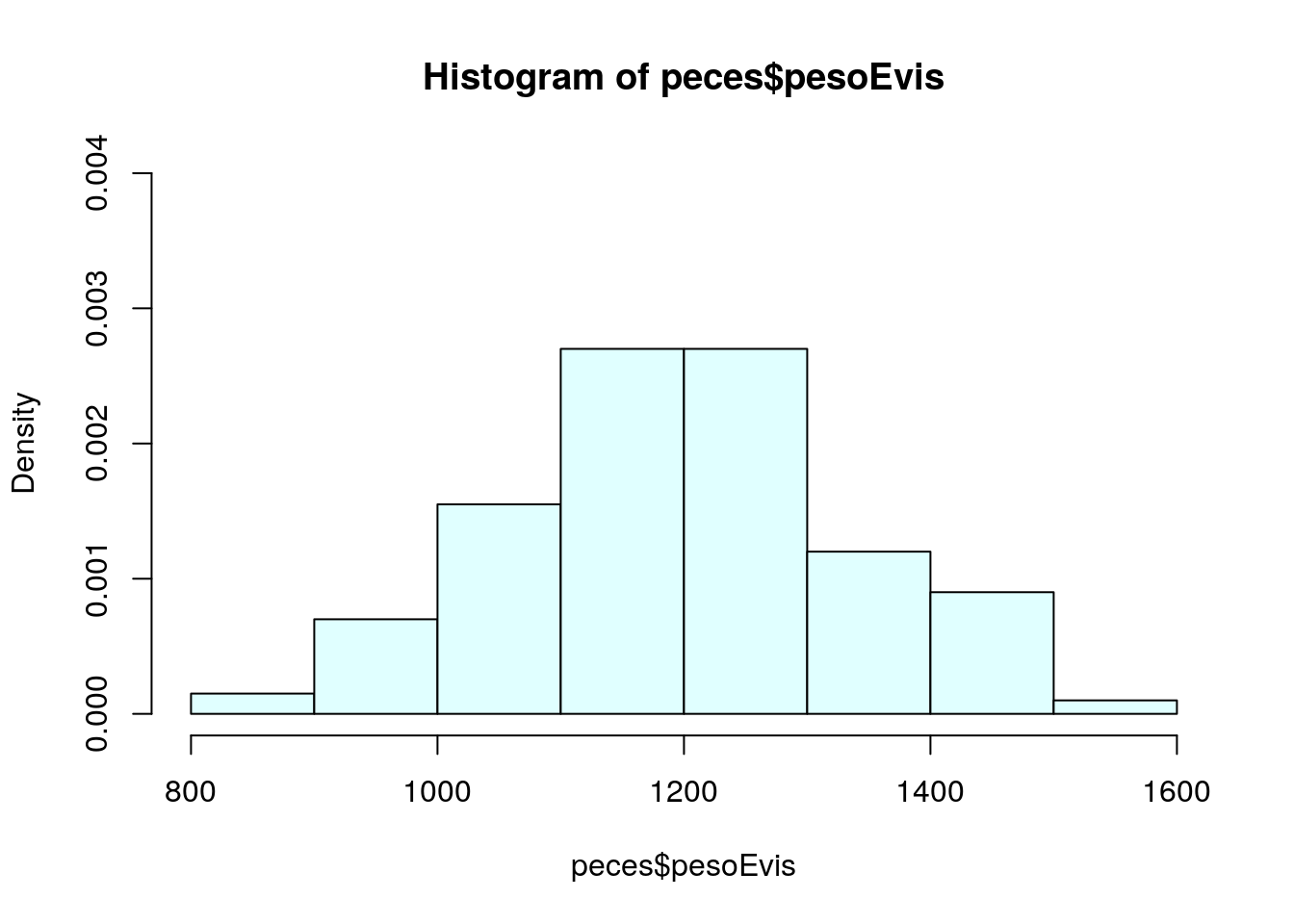
Inserción de un título
Para ello utilizamos el argumento main:
hist(peces$pesoEvis,freq=FALSE, col="lightcyan",ylim=c(0,0.004), main="Histograma del peso eviscerado")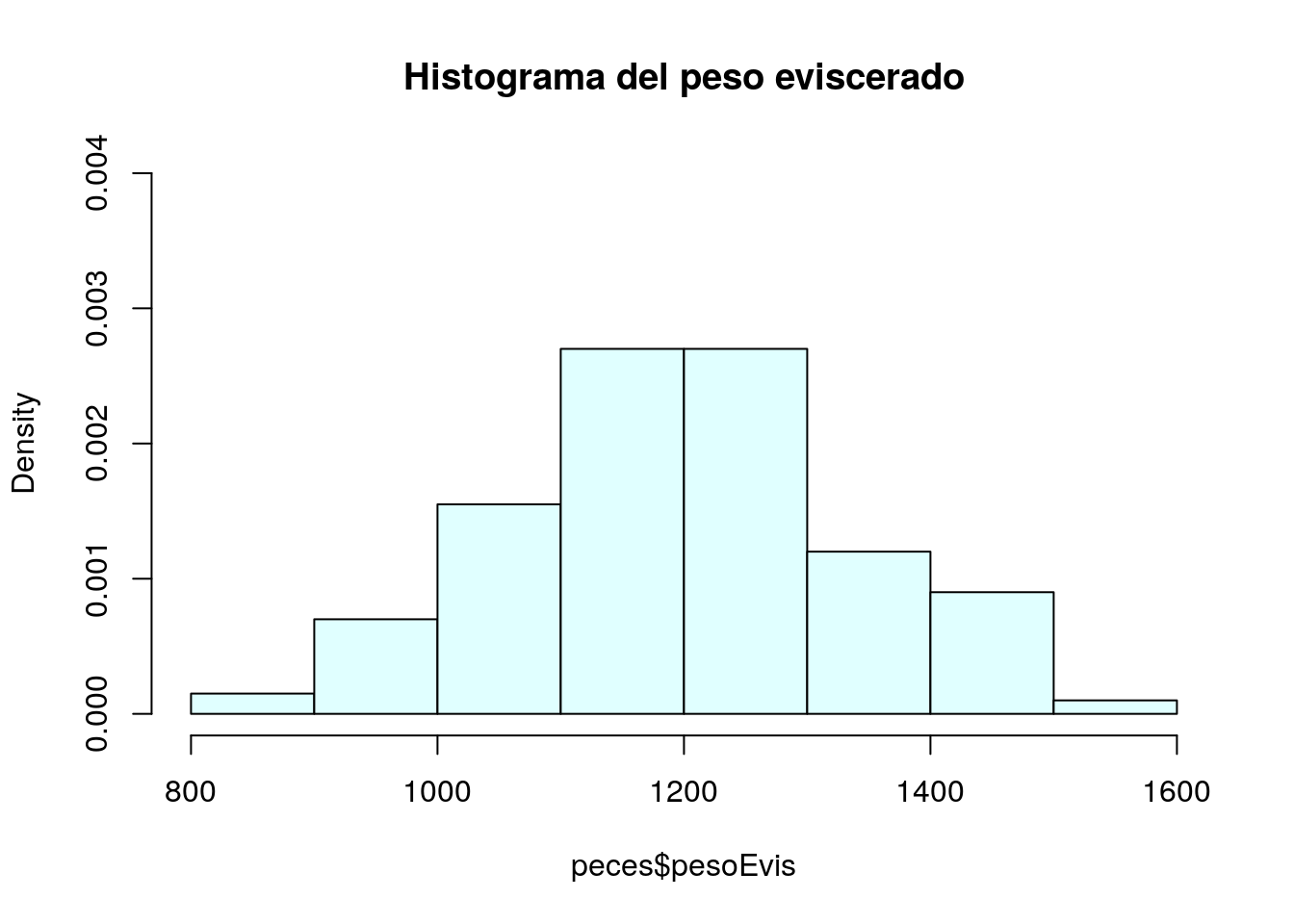
Eliminación de la etiqueta del eje X
Mediante la opción xlab="" especificamos que el eje X no lleva etiqueta.
hist(peces$pesoEvis,freq=FALSE,col="lightcyan", ylim=c(0,0.004),main="Histograma del peso eviscerado",xlab="")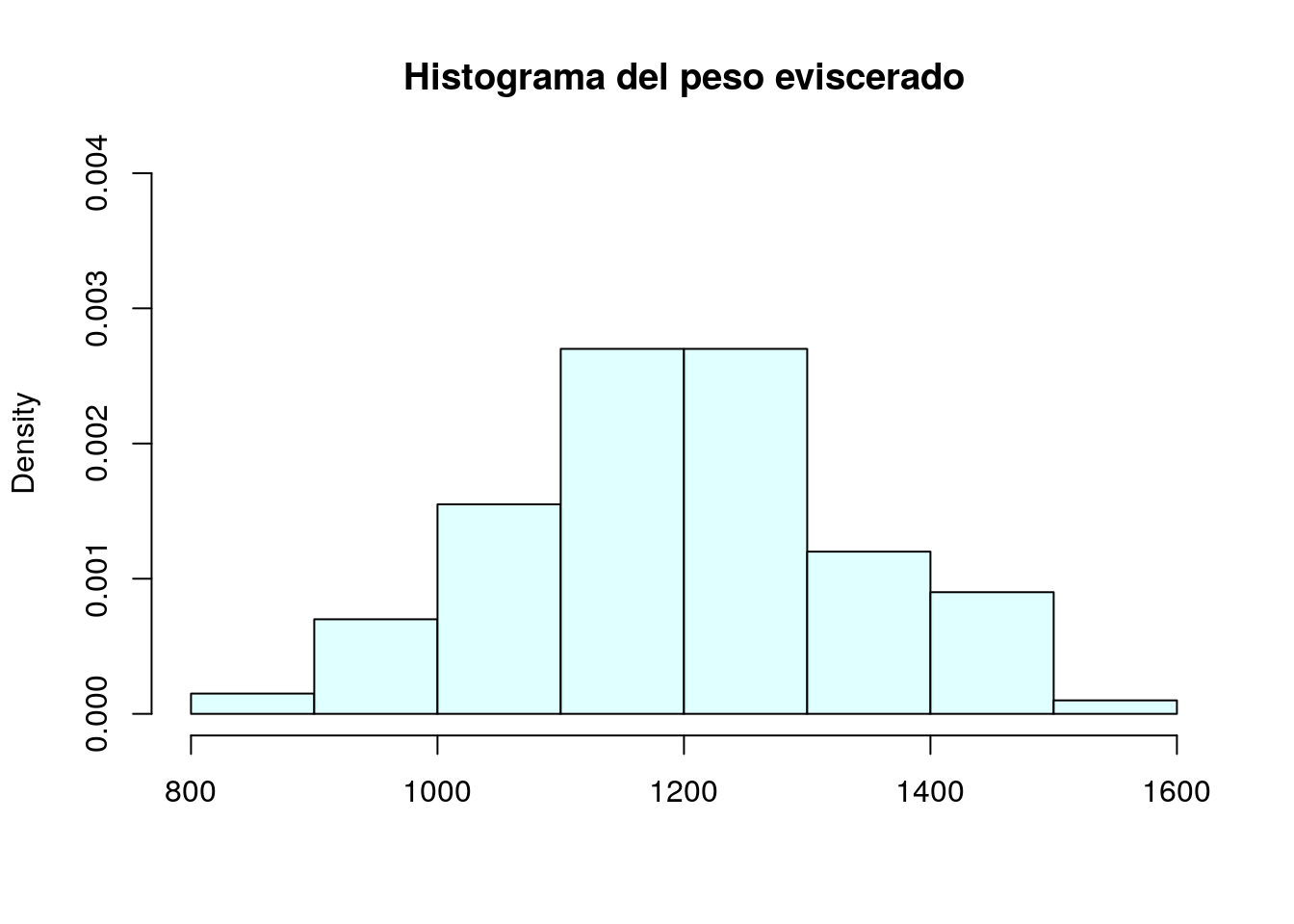
Asignación de etiqueta del eje Y
Etiquetamos el eje Y como Densidad. Para ello utilizamos el argumento ylab:
hist(peces$pesoEvis,freq=FALSE, col="lightcyan",ylim=c(0,0.004),
main="Histograma del peso eviscerado",xlab="",ylab="Densidad")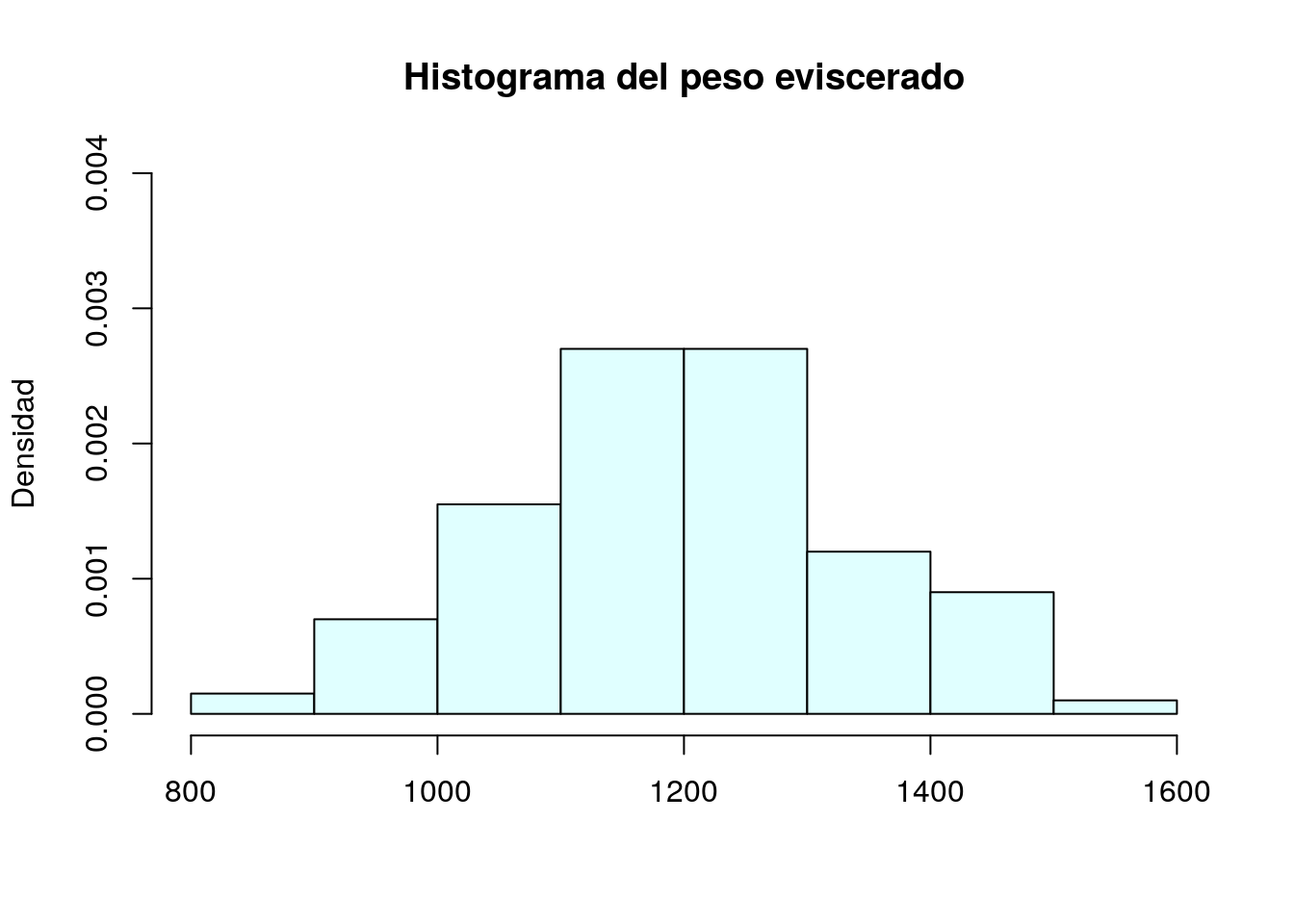
Estimación de la función de densidad de la variable mediante un estimador de nucleo
El estimador de núcleo de la función de densidad del peso eviscerado se calcula mediante density(peces$pesoEvis). Para superponer esta función al histograma utilizaremos la función de bajo nivel lines; además dibujamos la línea con grosor lwd=2 y de color rojo:
lines(density(peces$pesoEvis),col="red",lwd=2)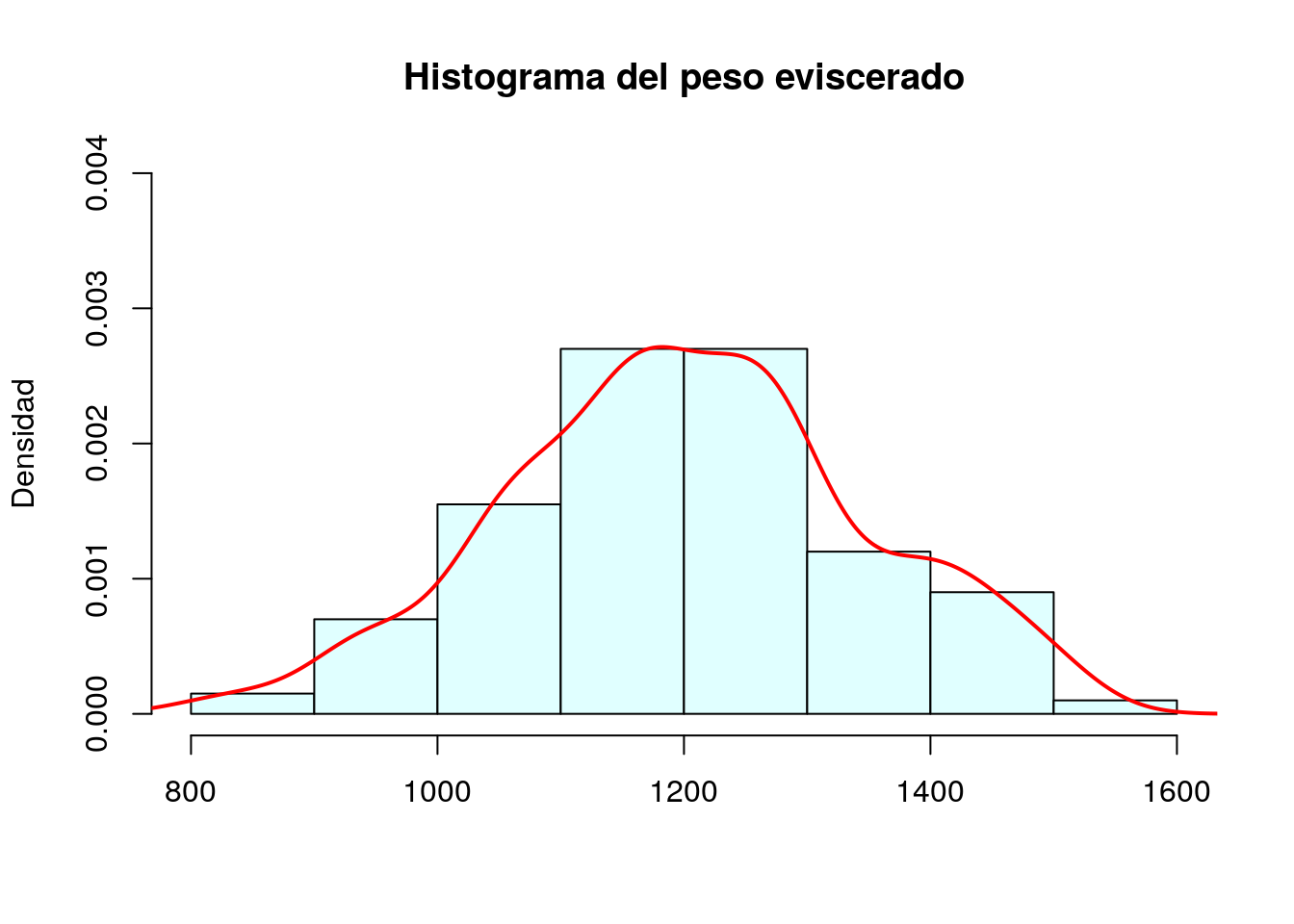
Ajuste de una función de densidad normal con media y desviación estándar estimadas a partir de los datos
Ajustamos también a nuestros datos una función de densidad normal con media igual a la media estimada del peso eviscerado (1201.485) y desviación típica también igual a la observada en la muestra (144.696771)
curve(dnorm(x,mean=mean(peces$pesoEvis),sd=sd(peces$pesoEvis)), from=800,to=1600,
add=TRUE, col="blue", lwd=2)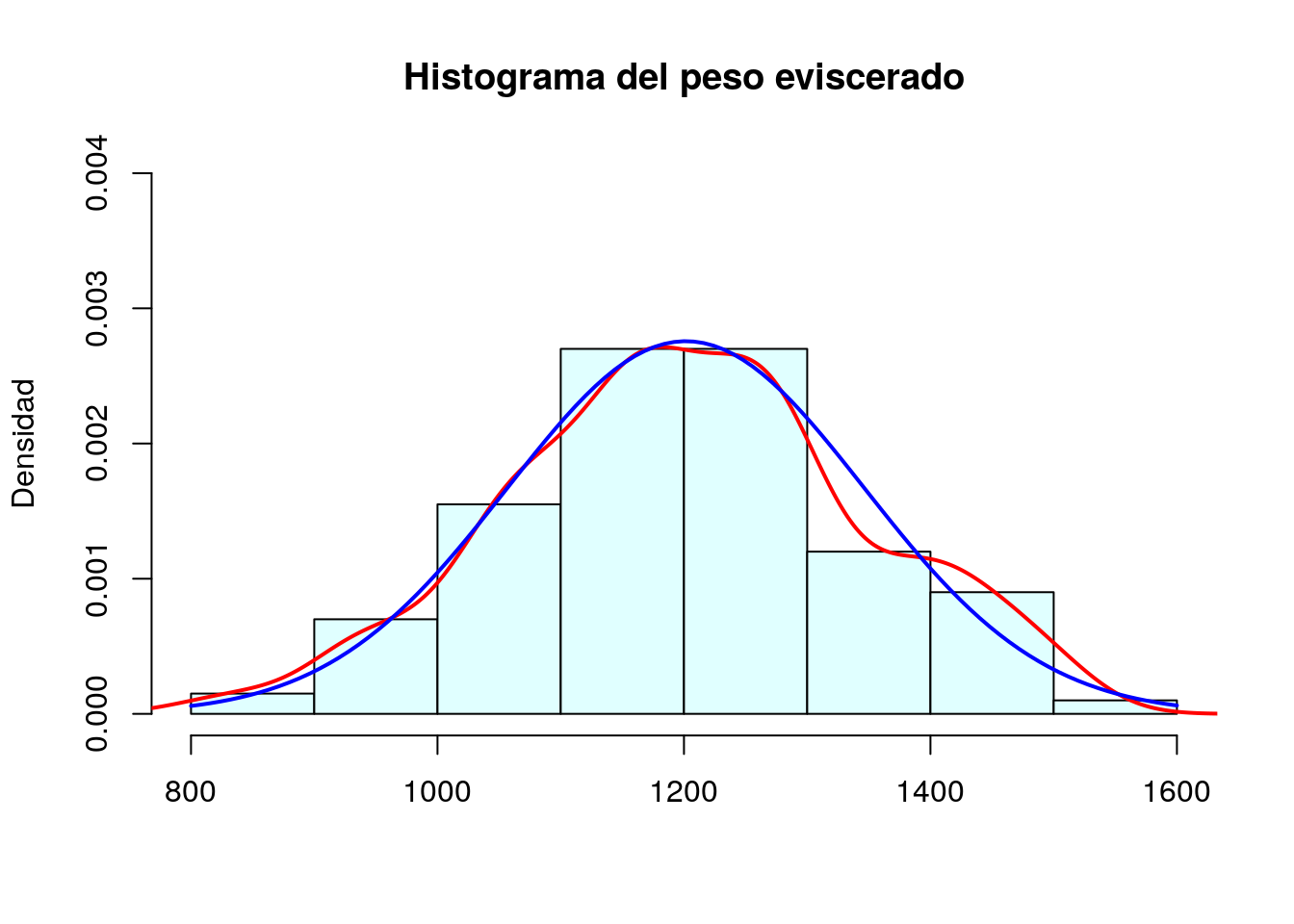
Leyenda
Por último añadimos una leyenda explicando qué representa cada curva:
legend("topleft",col=c("blue","red"),legend =c("Densidad normal estimada","Estimador de núcleo de la densidad"),lwd=2, bty = "n")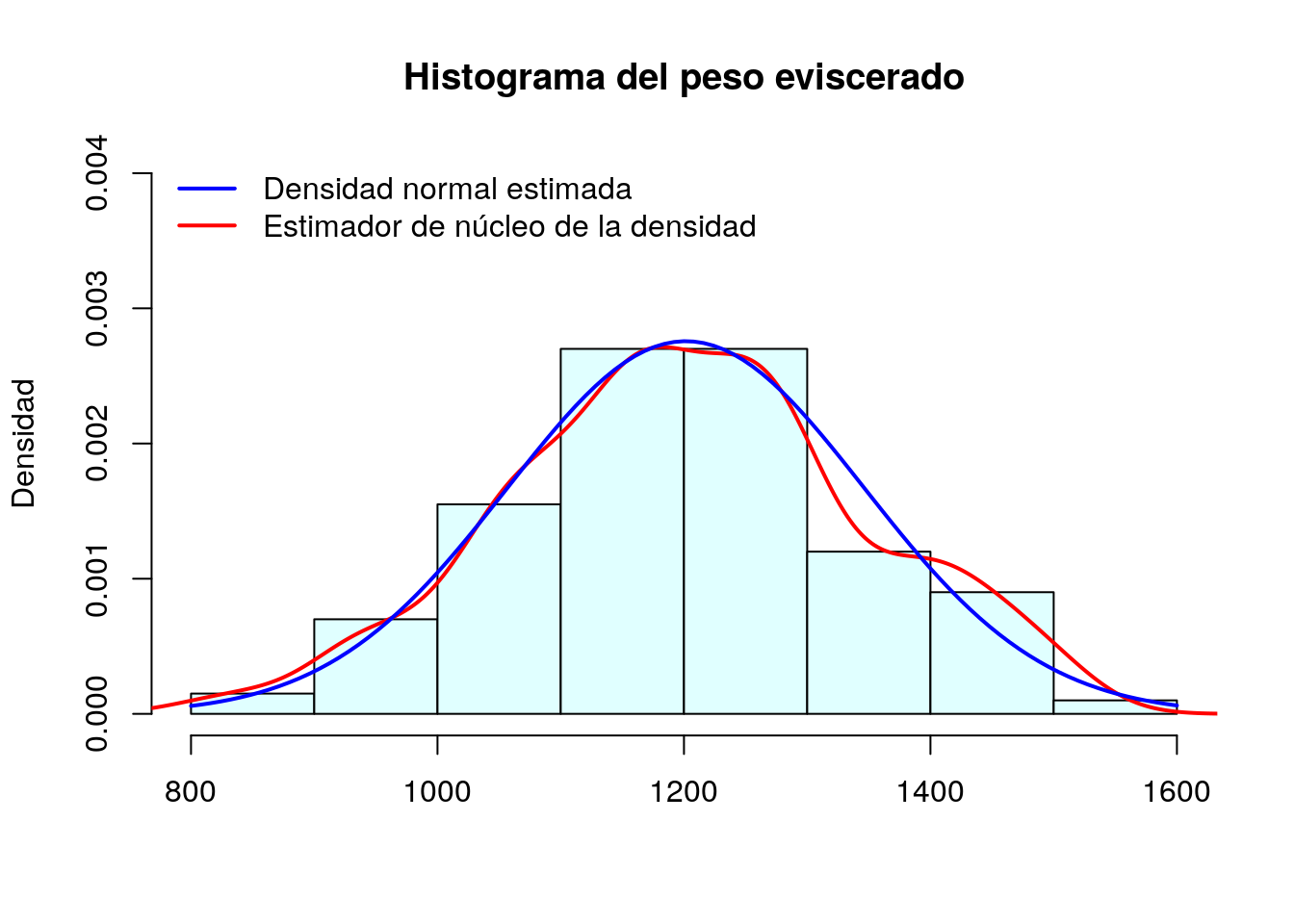
© 2016 Angelo Santana, Carmen N. Hernández, Departamento de Matemáticas ULPGC