Objetos en R: Series temporales

La clase ts

R cuenta con numerosas funciones para el análisis de series temporales. El uso de tales funciones requiere que los objetos a los que se aplican sean de la clase ts (time series). La función ts() convierte un objeto a serie temporal.

IMPORTANTE: La construcción de objetos de la clase ts requiere que los datos de partida estén distribuidos regularmente en la escala temporal utilizada; por ejemplo, que haya siempre un dato por día, o dos datos por mes o un dato cada dos años. En caso de que la serie temporal a tratar esté constituida por valores irregularmente distribuidos en el tiempo deberemos utilizar objetos de la clase zoo.

Ejemplo 1

El archivo liga2013-14.csv contiene los resultados de todos los partidos de fútbol de la liga española de primera división de la temporada 2013-14. Cada fila de este archivo corresponde a un partido, y las variables gLoc y gVis indican el número de goles marcados, respectivamente, por el equipo local y por el equipo visitante en cada partido:

library(RCurl)
ligaCsv=getURL("http://www.dma.ulpgc.es/profesores/personal/stat/datos/liga2013-14.csv")
liga1314=read.csv2(textConnection(ligaCsv),encoding="UTF-8",stringsAsFactors=FALSE)
head(liga1314)

##   jornada      fecha         local  visitante gLoc gVis
## 1       1 18-08-2013     Barcelona    Levante    7    0
## 2       1 18-08-2013      Valencia    MÃ¡laga    1    0
## 3       1 18-08-2013   Real Madrid      Betis    2    1
## 4       1 18-08-2013       Sevilla At. Madrid    1    3
## 5       1 18-08-2013 Real Sociedad     Getafe    2    0
## 6       1 18-08-2013    Valladolid At. Bilbao    1    2

La siguiente función construye un dataframe que contiene el total de goles marcados en cada jornada de esta liga:

nMedioGoles=with(liga1314,tapply(gLoc+gVis,jornada,sum))
nMedioGoles

##  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 
## 35 25 29 33 27 29 17 30 19 32 33 23 33 42 27 27 37 26 28 24 38 26 30 20 23 
## 26 27 28 29 30 31 32 33 34 35 36 37 38 
## 22 27 28 28 21 24 29 24 28 29 24 24 24

Podemos convertir la sucesión de goles marcados por jornada en una serie temporal simplemente mediante:

goles=ts(nMedioGoles)
goles

## Time Series:
## Start = 1 
## End = 38 
## Frequency = 1 
##  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 
## 35 25 29 33 27 29 17 30 19 32 33 23 33 42 27 27 37 26 28 24 38 26 30 20 23 
## 26 27 28 29 30 31 32 33 34 35 36 37 38 
## 22 27 28 28 21 24 29 24 28 29 24 24 24

El objeto que hemos creado, goles, es un objeto de clase Time Series con inicio en 1, final en 38 y frecuencia 1; en resumen, es una simple sucesión ordenada de valores. La función plot() muestra gráficamente la secuencia temporal de observaciones de esta variable.

plot(goles,main="Goles marcados durante la liga 2013-14",xlab="Jornada",ylab="Número de goles")
grid()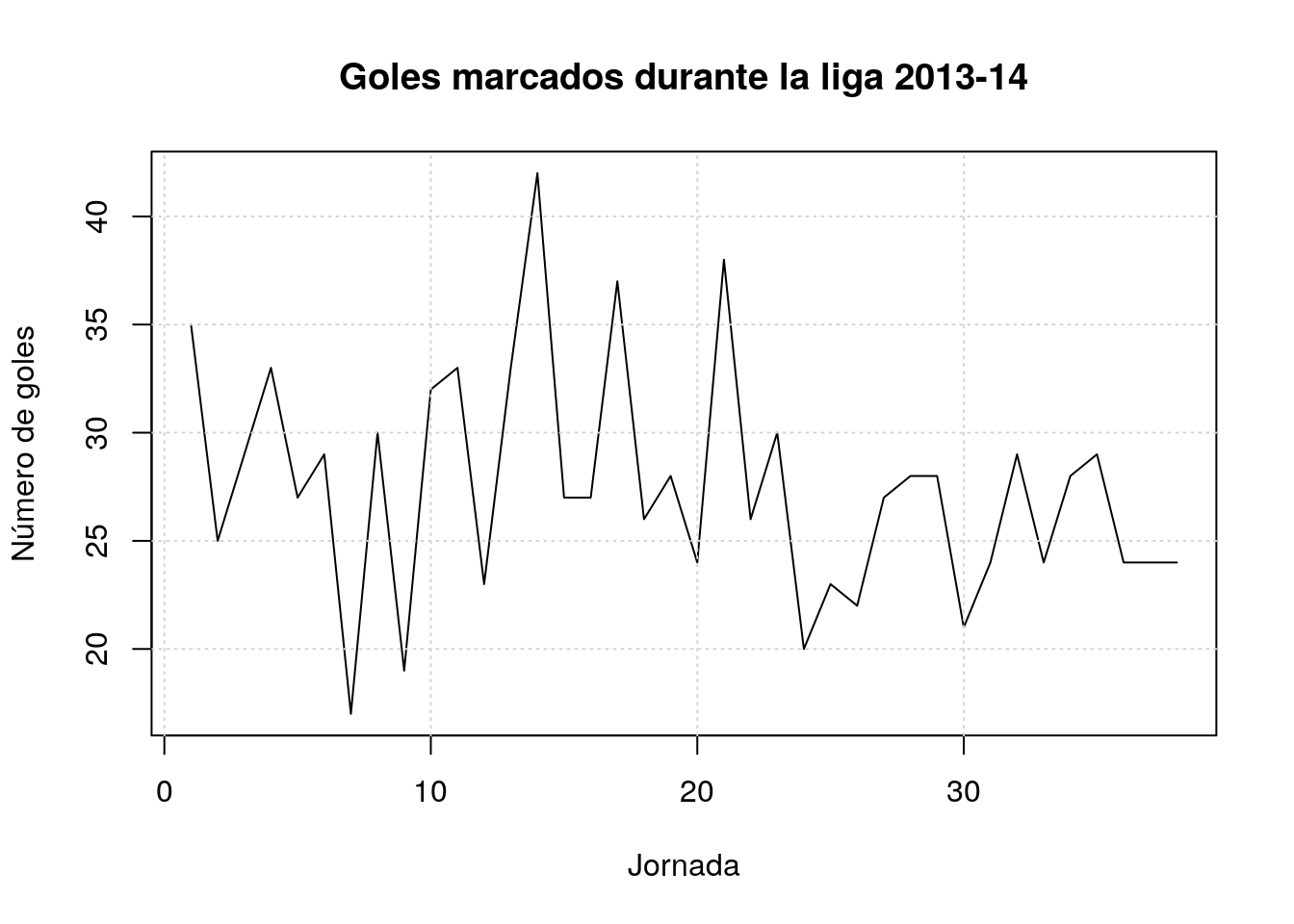

Nótese que en la construcción de esta serie temporal no hemos utilizado la fecha de celebración de cada jornada; por defecto, la función ts() cuando no se especifica ninguna opción, asume que los datos se proporcionan en una secuencia regular; en este caso es simplemente la secuencia de valores de 1 a 38 (que corresponden precisamente a las jornadas de liga). No se ha tenido en cuenta que a veces se celebran dos jornadas en la misma semana, o que la última semana de diciembre no hay jornada de fútbol.

Ejemplo 2: observaciones con frecuencia mensual

El archivo tempMediaGando.csv contiene las temperaturas medias mensuales en el aeropuerto de Gran Canaria (Gando) desde enero de 1981 hasta diciembre de 2013. Podemos leer este archivo mediante:

gandoCsv=getURL("http://www.dma.ulpgc.es/profesores/personal/stat/datos/tempMediaGando.csv")
gando=read.csv2(textConnection(gandoCsv))
str(gando)

## 'data.frame':    396 obs. of  1 variable:
##  $ temp: num  16.8 16.1 18.5 17.7 18.9 21.4 22.1 22.8 22.9 21.7 ...

Como podemos observar, el dataframe gando contiene una única variable temp (no hay ninguna variable de fecha). Podemos convertir esta variable a una serie temporal mediante:

tempGando=ts(gando$temp,freq=12,start=c(1981,1))

En este caso hemos especificado freq=12, lo que indica que a cada unidad temporal le corresponden 12 observaciones; R asume entonces que la unidad temporal a considerar es el año. Además la opción start=c(1981,1) indica que la primera observación corresponde a enero de 1981. Si pedimos a R que nos muestre la estructura de la variable tempGando obtenemos:

str(tempGando)

##  Time-Series [1:396] from 1981 to 2014: 16.8 16.1 18.5 17.7 18.9 21.4 22.1 22.8 22.9 21.7 ...

y si le pedimos que nos presente la variable:

tempGando

##       Jan  Feb  Mar  Apr  May  Jun  Jul  Aug  Sep  Oct  Nov  Dec
## 1981 16.8 16.1 18.5 17.7 18.9 21.4 22.1 22.8 22.9 21.7 21.3 18.9
## 1982 17.7 17.3 17.6 18.0 19.5 21.0 23.1 22.9 22.7 21.9 20.0 17.4
## 1983 16.9 17.0 18.3 18.7 18.9 21.9 22.5 22.9 24.4 23.9 21.0 18.9
## 1984 17.6 17.2 17.7 19.1 19.2 20.6 23.7 22.9 23.1 22.3 19.9 18.1
## 1985 16.8 17.3 17.8 18.7 18.9 22.1 22.8 24.3 24.0 22.8 20.8 18.4
## 1986 17.3 16.9 17.2 17.5 19.8 20.3 21.8 23.2 23.8 21.9 19.7 18.0
## 1987 17.5 17.8 19.2 19.8 20.4 22.3 22.9 24.2 25.8 22.3 21.3 19.3
## 1988 17.7 17.4 18.4 18.8 20.1 21.7 23.6 24.3 23.7 22.4 20.8 18.9
## 1989 17.6 18.0 18.9 18.2 20.0 22.4 24.3 25.4 24.5 23.9 20.7 19.6
## 1990 17.7 19.7 20.5 18.7 20.7 22.1 23.7 26.2 24.3 23.1 21.2 19.2
## 1991 17.6 17.0 17.9 17.9 18.9 21.0 22.7 23.3 24.3 21.6 20.2 18.5
## 1992 17.4 17.4 18.0 18.8 19.6 20.8 22.6 23.4 22.8 21.6 20.0 17.8
## 1993 16.8 16.9 17.4 17.9 19.0 20.9 22.3 22.9 22.6 21.3 18.8 18.1
## 1994 16.8 17.0 17.4 18.5 19.6 21.7 23.6 23.9 23.2 22.1 21.2 19.7
## 1995 18.1 18.5 18.8 19.5 21.2 22.3 24.3 24.3 23.8 23.5 21.8 19.4
## 1996 18.7 17.6 17.9 19.2 21.4 22.0 23.2 23.8 23.5 23.0 21.1 19.1
## 1997 18.2 19.6 20.0 20.0 20.9 22.7 23.2 23.8 23.9 23.3 22.3 20.2
## 1998 19.3 20.6 20.8 19.7 20.1 22.2 23.2 24.5 24.6 23.4 22.5 19.4
## 1999 18.1 18.0 18.7 20.1 20.9 22.2 24.1 25.6 24.6 23.0 21.2 18.6
## 2000 17.2 18.6 19.5 19.2 20.3 21.9 23.4 24.3 24.2 22.6 20.6 19.8
## 2001 18.9 18.7 20.0 19.6 20.5 22.3 23.4 24.4 24.2 23.7 20.8 20.1
## 2002 18.8 18.8 19.4 20.0 20.1 21.8 22.2 23.0 23.7 24.4 21.7 19.9
## 2003 17.7 17.3 18.5 19.0 20.8 22.2 23.6 24.4 23.9 22.3 20.0 18.7
## 2004 17.6 18.4 18.2 18.4 19.3 22.4 24.3 25.8 24.4 23.4 21.1 18.3
## 2005 16.9 16.1 18.2 19.1 20.4 21.9 23.3 24.1 24.6 23.0 20.4 18.5
## 2006 16.9 17.2 17.9 19.2 20.2 21.8 23.4 24.2 24.7 22.9 21.9 18.4
## 2007 17.8 17.7 17.8 18.8 20.7 22.0 24.1 23.3 22.9 22.6 20.8 18.8
## 2008 18.5 18.6 18.8 21.2 21.0 22.2 23.5 23.9 23.3 21.8 19.3 17.7
## 2009 16.9 16.8 18.5 18.7 20.0 22.4 25.0 24.8 23.7 23.9 22.0 20.9
## 2010 18.9 20.1 20.1 20.7 21.0 22.3 23.7 25.1 24.4 23.0 21.5 20.4
## 2011 18.4 17.8 17.7 19.2 20.9 23.1 23.4 23.8 24.0 23.5 20.7 19.4
## 2012 18.0 16.8 18.5 18.5 21.8 23.6 24.2 25.6 24.7 23.5 21.6 19.4
## 2013 18.5 18.3 19.6 20.6 20.6 21.8 23.5 25.8 24.3 23.6 21.4 19.6

Vemos, pues, que R organiza automáticamente la variable en meses y años. La representación gráfica tiene en cuenta esta secuencia temporal:

plot(tempGando,main="Temperatura media mensual en el aeropuerto de Gran Canaria", xlab="Año", ylab="Temperatura")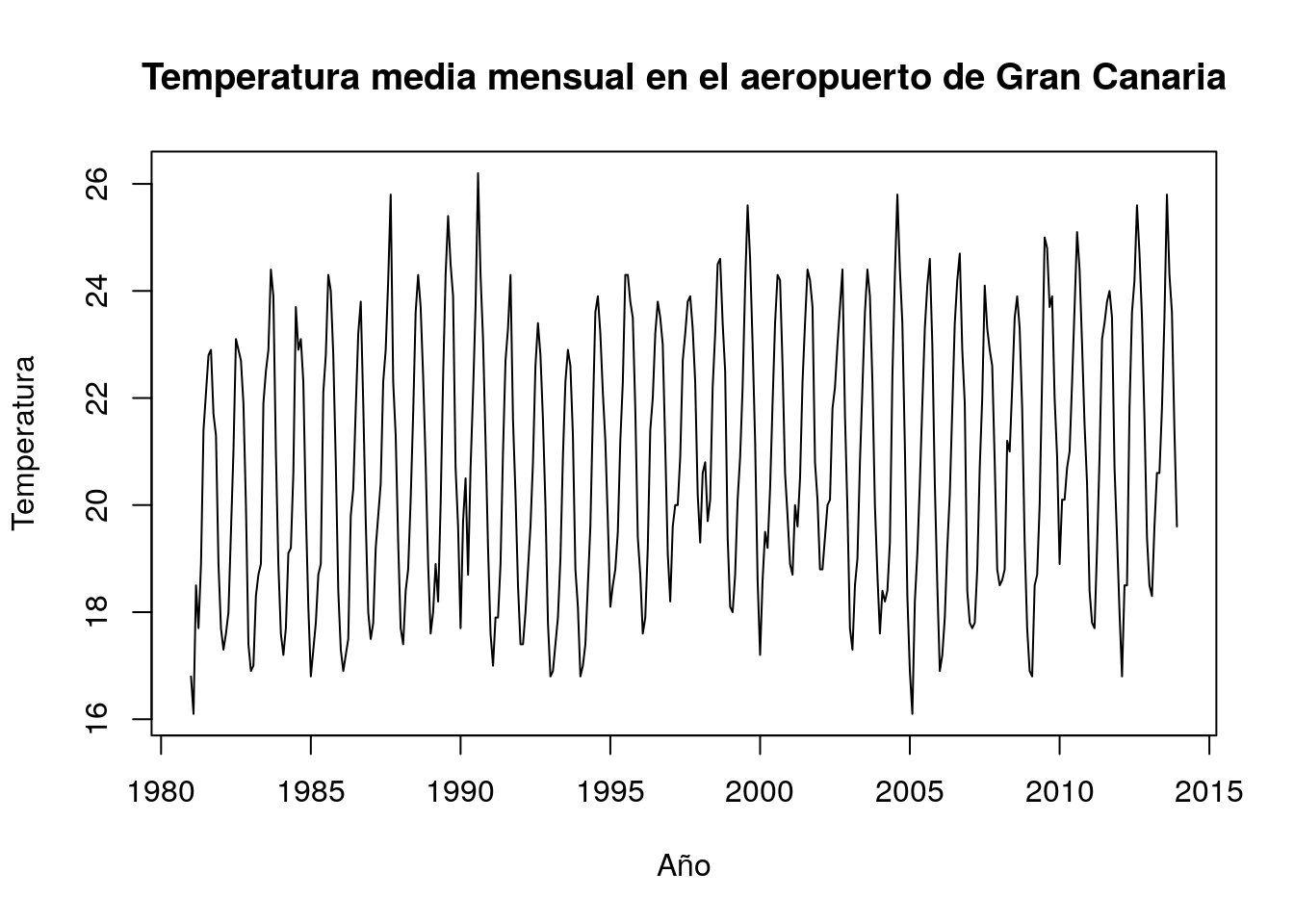

Ejemplo 3: serie temporal multivariante

La función ts() puede aplicarse también a un dataframe que contenga varias variables; en tal caso, cada variable se convierte a serie temporal, y el dataframe adquiere la clase mts (multivariate time series). El archivo tempVientoGando.csv contiene los valores mínimo, máximo y medio mensuales de temperaturas y velocidades de viento registrados en el aeropuerto de Gran Canaria desde enero de 1981:

gandoCsv=getURL("http://www.dma.ulpgc.es/profesores/personal/stat/datos/tempVientoGando.csv")
gando2=read.csv2(textConnection(gandoCsv))
head(gando2)

##   TEMP.min TEMP.max TEMP.media WIND.min WIND.max WIND.media
## 1       13       24       16.8        0     16.4        4.7
## 2       10       23       16.1        0     12.8        5.1
## 3       13       30       18.5        0     12.8        4.8
## 4       13       23       17.7        0     13.8        5.8
## 5       15       24       18.9        0     15.4        7.3
## 6       17       26       21.4        0     14.4        7.7

Podemos convertirlo a serie temporal multivariante mediante:

vtGando=ts(gando2,freq=12,start=c(1981,1))
str(vtGando)

##  Time-Series [1:403, 1:6] from 1981 to 2014: 13 10 13 13 15 17 19 18 19 18 ...
##  - attr(*, "dimnames")=List of 2
##   ..$ : NULL
##   ..$ : chr [1:6] "TEMP.min" "TEMP.max" "TEMP.media" "WIND.min" ...

vtGando

##          TEMP.min TEMP.max TEMP.media WIND.min WIND.max WIND.media
## Jan 1981       13       24       16.8      0.0     16.4        4.7
## Feb 1981       10       23       16.1      0.0     12.8        5.1
## Mar 1981       13       30       18.5      0.0     12.8        4.8
## Apr 1981       13       23       17.7      0.0     13.8        5.8
## May 1981       15       24       18.9      0.0     15.4        7.3
## Jun 1981       17       26       21.4      0.0     14.4        7.7
## Jul 1981       19       31       22.1      5.1     16.9       10.1
## Aug 1981       18       32       22.8      0.0     16.9        8.5
## Sep 1981       19       28       22.9      0.0     13.8        8.1
## Oct 1981       18       25       21.7      0.0     12.3        5.6
## Nov 1981       16       28       21.3      0.0     11.8        2.9
## Dec 1981       14       24       18.9      0.0     14.4        4.7

En este caso, el comando plot() representa gráficamente todas las series del dataframe:

plot(vtGando,main="Temperatura y Viento en el aeropuerto de Gran Canaria")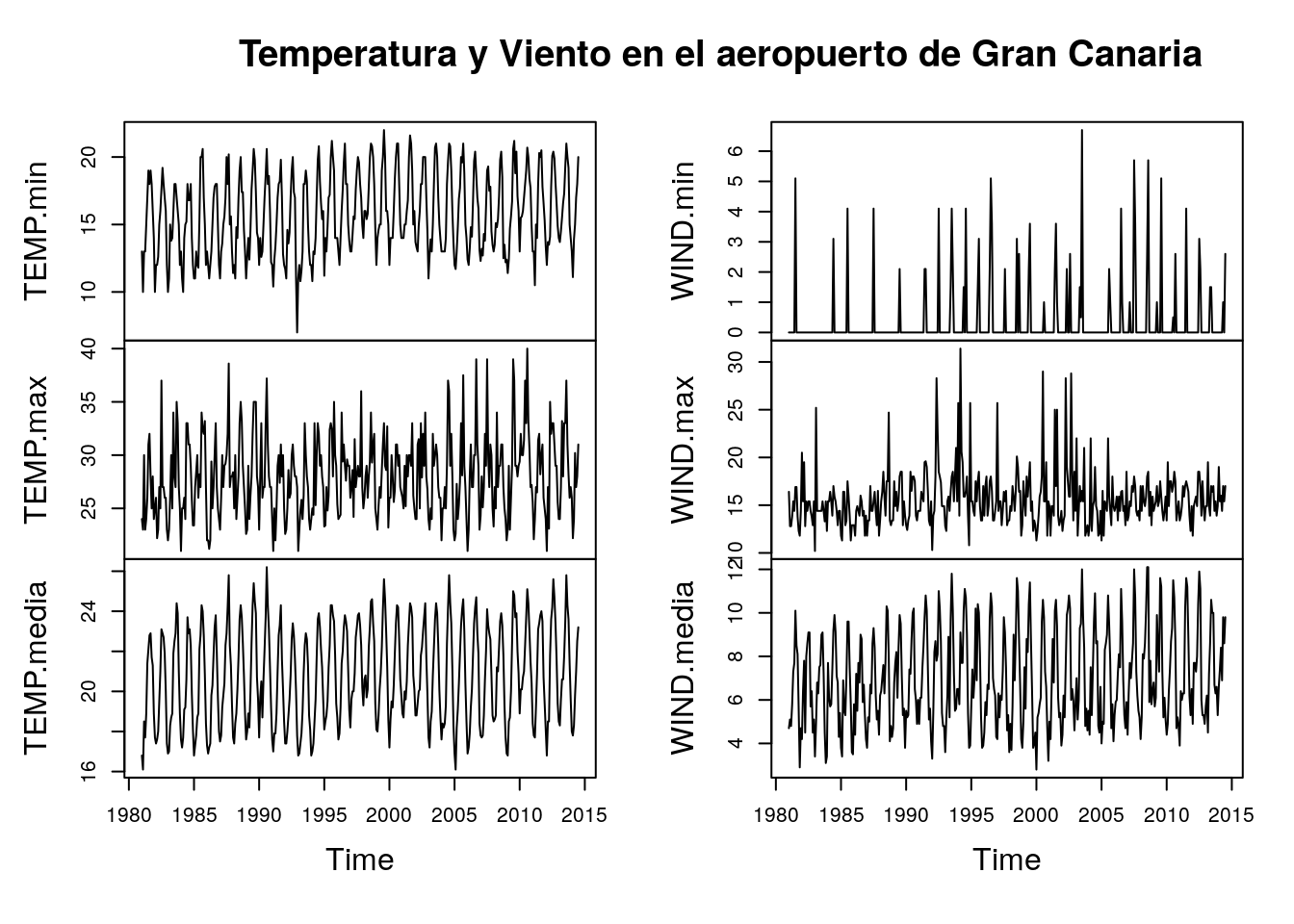

Funciones que operan sobre series temporales

Combinación de series temporales

Dadas dos series temporales $X_t$ e $Y_t$, observadas con la misma frecuencia, si queremos combinarlas en una única serie temporal multivariante (con dos columnas, una para la $X_t$ y otra para la $Y_t$) podemos utilizar las funciones:

ts.union(): junta las dos series, rellenando con NA los periodos en que una serie sea más larga que la otra.
intersect.ts(): junta ambas series, pero sólo con los datos correspondientes al periodo común a ambas.

Ejemplo:

serie1=ts(1:20, freq=12, start=c(1981,3))
serie2=ts(1:15, freq=12, start=c(1980,9))
serie1

##      Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec
## 1981           1   2   3   4   5   6   7   8   9  10
## 1982  11  12  13  14  15  16  17  18  19  20

serie2

##      Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec
## 1980                                   1   2   3   4
## 1981   5   6   7   8   9  10  11  12  13  14  15

ts.union(serie1,serie2)

##          serie1 serie2
## Sep 1980     NA      1
## Oct 1980     NA      2
## Nov 1980     NA      3
## Dec 1980     NA      4
## Jan 1981     NA      5
## Feb 1981     NA      6
## Mar 1981      1      7
## Apr 1981      2      8
## May 1981      3      9
## Jun 1981      4     10
## Jul 1981      5     11
## Aug 1981      6     12
## Sep 1981      7     13
## Oct 1981      8     14
## Nov 1981      9     15
## Dec 1981     10     NA
## Jan 1982     11     NA
## Feb 1982     12     NA
## Mar 1982     13     NA
## Apr 1982     14     NA
## May 1982     15     NA
## Jun 1982     16     NA
## Jul 1982     17     NA
## Aug 1982     18     NA
## Sep 1982     19     NA
## Oct 1982     20     NA

ts.intersect(serie1,serie2)

##          serie1 serie2
## Mar 1981      1      7
## Apr 1981      2      8
## May 1981      3      9
## Jun 1981      4     10
## Jul 1981      5     11
## Aug 1981      6     12
## Sep 1981      7     13
## Oct 1981      8     14
## Nov 1981      9     15

start(), end()

Las funciones start() y end() muestran, respectivamente, los instantes correspondientes a la observaciones inicial y final de una serie temporal:

start(tempGando)

## [1] 1981    1

end(tempGando)

## [1] 2013   12

window()

La función window() extrae los valores de la serie temporal comprendidos entre una fecha de inicio y otra final. Podemos especificar sólo el año:

window(tempGando,start=1982,end=1985)

##       Jan  Feb  Mar  Apr  May  Jun  Jul  Aug  Sep  Oct  Nov  Dec
## 1982 17.7 17.3 17.6 18.0 19.5 21.0 23.1 22.9 22.7 21.9 20.0 17.4
## 1983 16.9 17.0 18.3 18.7 18.9 21.9 22.5 22.9 24.4 23.9 21.0 18.9
## 1984 17.6 17.2 17.7 19.1 19.2 20.6 23.7 22.9 23.1 22.3 19.9 18.1
## 1985 16.8

O también año y mes:

window(tempGando,start=c(1982,1),end=c(1985,12))

##       Jan  Feb  Mar  Apr  May  Jun  Jul  Aug  Sep  Oct  Nov  Dec
## 1982 17.7 17.3 17.6 18.0 19.5 21.0 23.1 22.9 22.7 21.9 20.0 17.4
## 1983 16.9 17.0 18.3 18.7 18.9 21.9 22.5 22.9 24.4 23.9 21.0 18.9
## 1984 17.6 17.2 17.7 19.1 19.2 20.6 23.7 22.9 23.1 22.3 19.9 18.1
## 1985 16.8 17.3 17.8 18.7 18.9 22.1 22.8 24.3 24.0 22.8 20.8 18.4

time()

La función time() crea un objeto de clase ts con los instantes en que ha sido muestreada una serie temporal (en escala decimal).

time(tempGando)

##          Jan     Feb     Mar     Apr     May     Jun     Jul     Aug
## 1981 1981.00 1981.08 1981.17 1981.25 1981.33 1981.42 1981.50 1981.58
## 1982 1982.00 1982.08 1982.17 1982.25 1982.33 1982.42 1982.50 1982.58
## 1983 1983.00 1983.08 1983.17 1983.25 1983.33 1983.42 1983.50 1983.58
##          Sep     Oct     Nov     Dec
## 1981 1981.67 1981.75 1981.83 1981.92
## 1982 1982.67 1982.75 1982.83 1982.92
## 1983 1983.67 1983.75 1983.83 1983.92

deltat() y frequency()

Estas funciones nos muestran el tiempo entre observaciones (deltat()) y número de observaciones por unidad de tiempo (frequency()) de una serie temporal. Así, para las temperaturas del aeropuerto de Gran Canaria, donde la unidad de tiempo es el año:

deltat(tempGando)

## [1] 0.0833333

frequency(tempGando)

## [1] 12

lag()

La función lag() construye una versión desfasada de la serie temporal, retardando (o adelantando) los valores de la serie en la magnitud del desfase especificado. Concretamente:

\[\mathsf{lag(}X_{t},k\mathsf{)}=X_{t+k}\]

Si no se especifica, el valor del desfase $k$ por defecto es 1.

A modo de ejemplo, mostramos seguidamente el efecto de desfasar en uno y dos meses (hacia delante y hacia atrás) la serie de temperaturas medias mensuales en el aeropuerto de Gran Canaria:

head(cbind(lag(tempGando,-2),lag(tempGando,-1), tempGando,lag(tempGando),lag(tempGando,2)))

##      lag(tempGando, -2) lag(tempGando, -1) tempGando lag(tempGando) lag(tempGando, 2)
## [1,]                 NA                 NA        NA             NA              16.8
## [2,]                 NA                 NA        NA           16.8              16.1
## [3,]                 NA                 NA      16.8           16.1              18.5
## [4,]                 NA               16.8      16.1           18.5              17.7
## [5,]               16.8               16.1      18.5           17.7              18.9
## [6,]               16.1               18.5      17.7           18.9              21.4

En la siguiente figura representamos gráficamente los valores de la serie desfasada una unidad ($X_{t+k}$), frente a los valores originales $X_t$. Puede apreciarse una clara relación lineal:

plot(tempGando,lag(tempGando),xlab="temp.Gando(t)",ylab="temp.Gando(t+1)")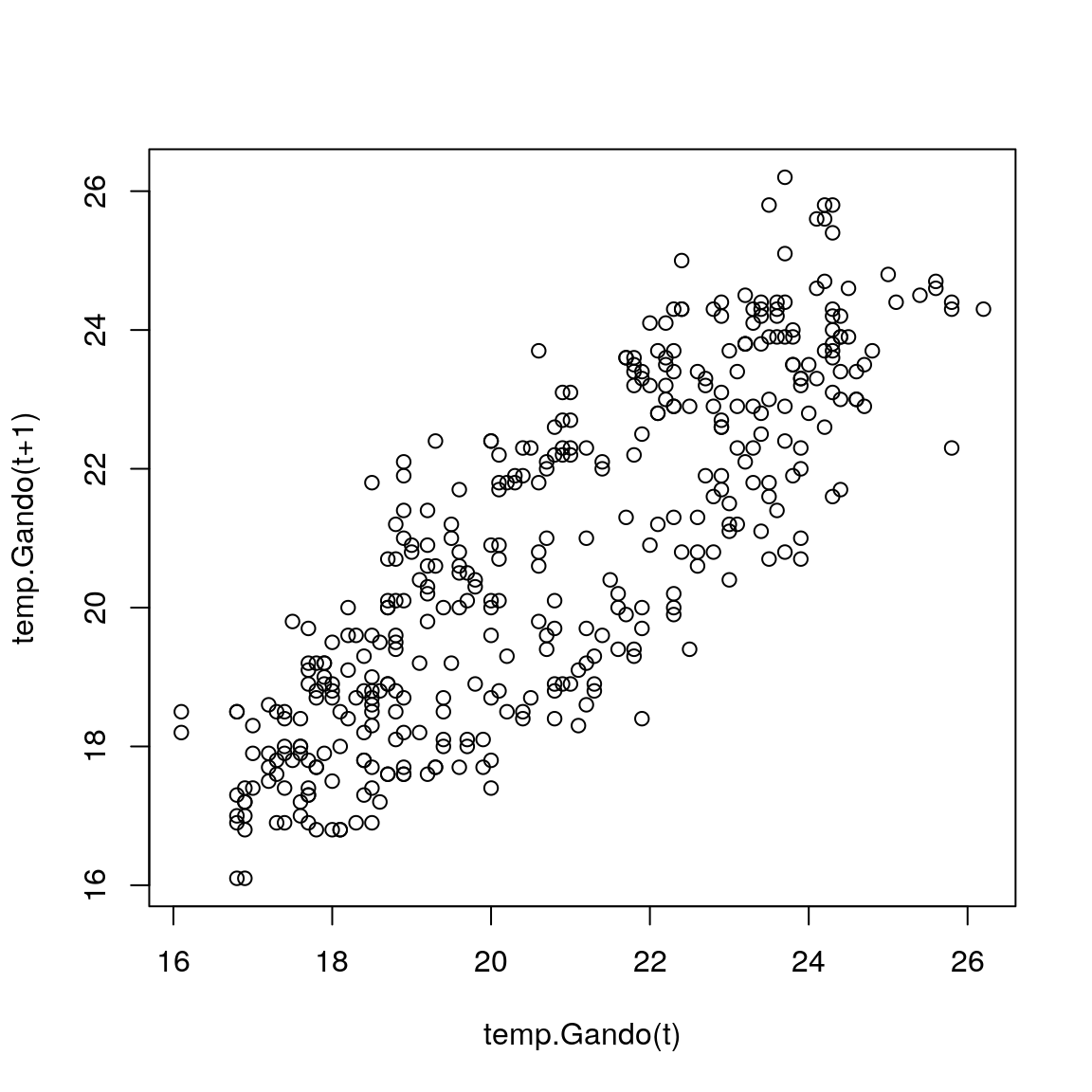

lag.plot()

Esta función representa la serie observada frente a una versión suya desfasada lags unidades de tiempo, por lo que permite visualizar la “autodependencia” de la serie. Concretamente, lag.plot(x,lags=k) es equivalente a plot(lag(x,k),x). No obstante, la función lag.plot() presenta algunas ventajas, como por ejemplo hacer una representación simultánea para varios desfases:

lag.plot(tempGando, main="Temperatura media mensual en el aeropuerto de Gran Canaria")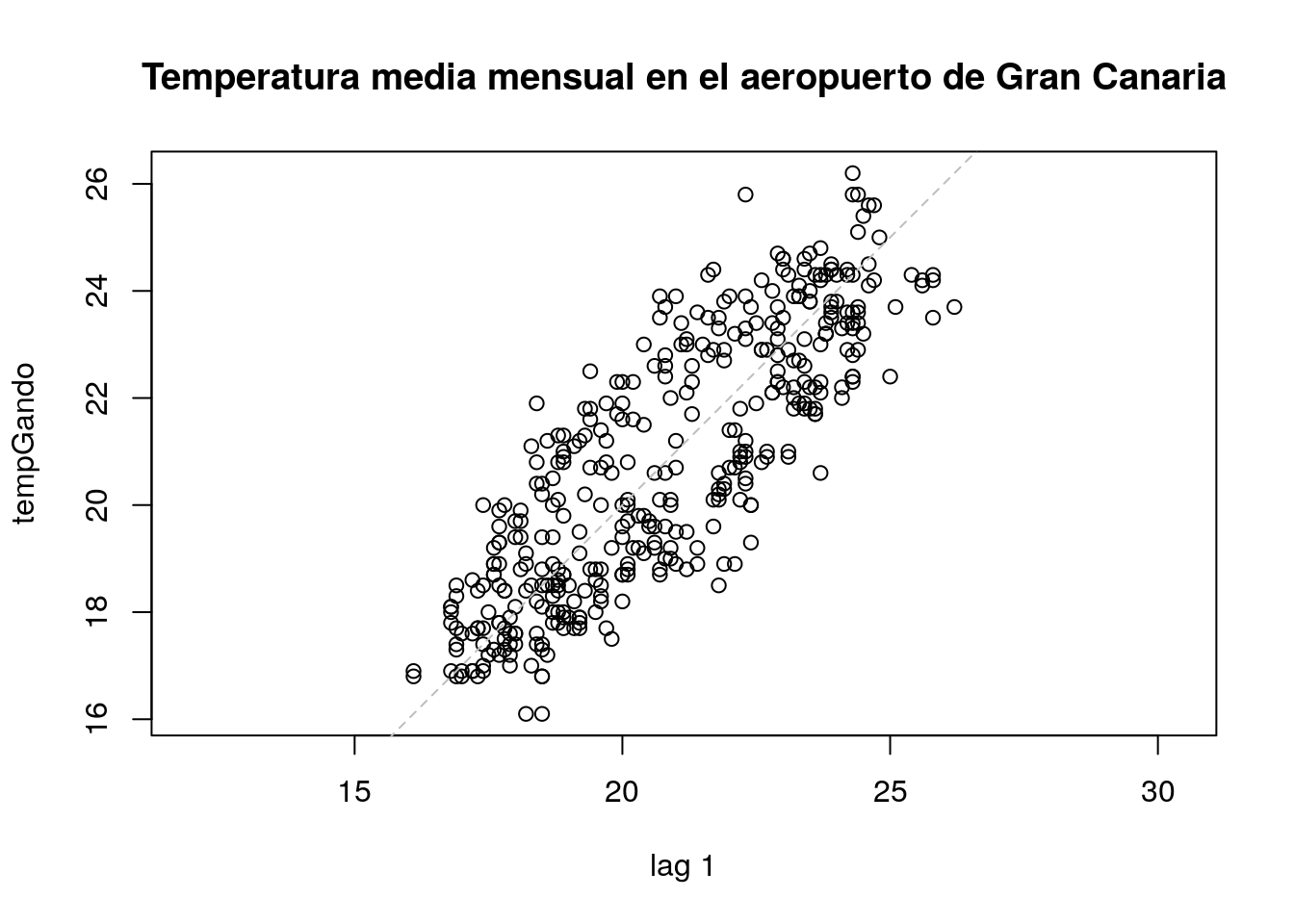

lag.plot(tempGando,lags=4,layout=c(2,2))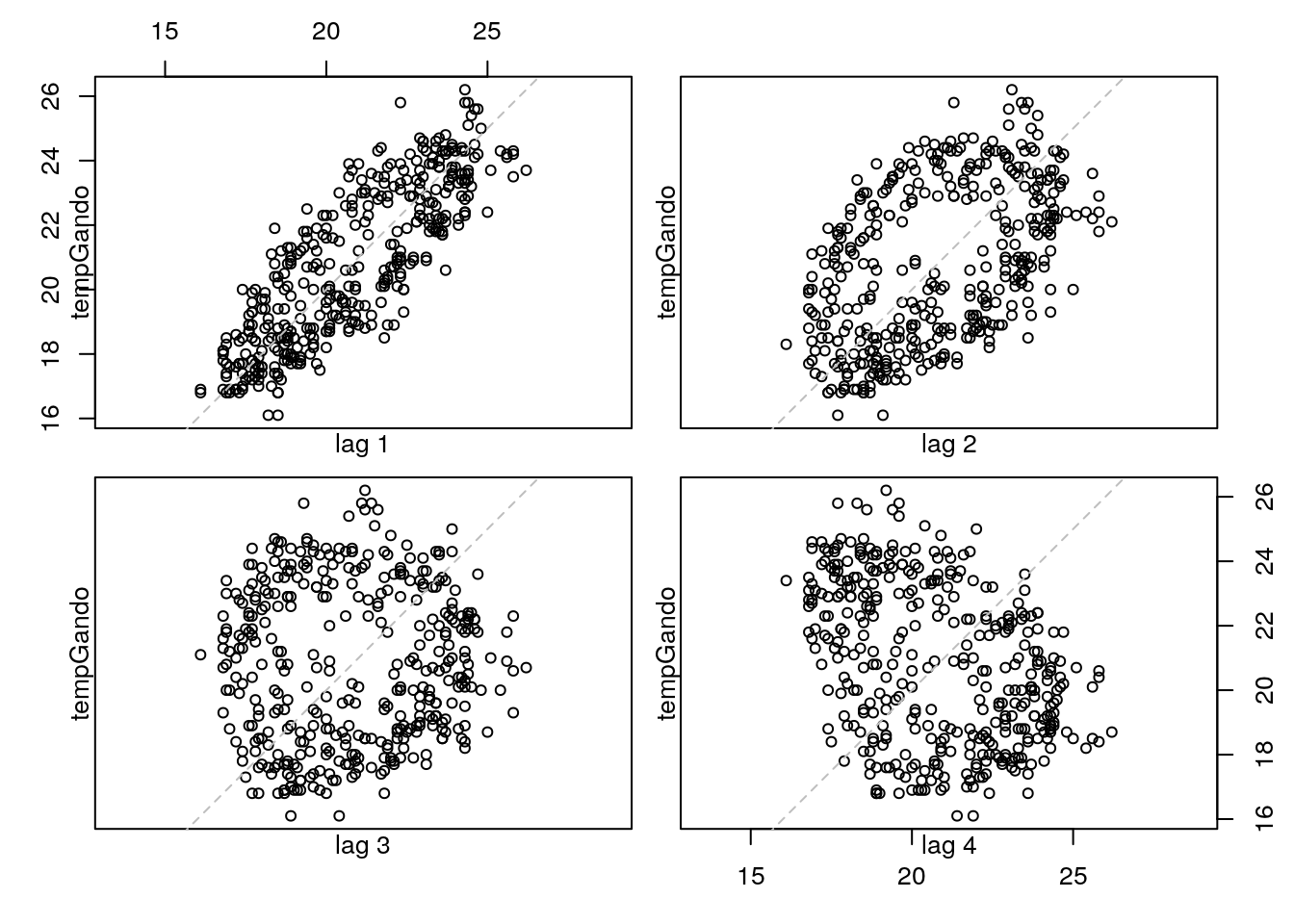

Diferenciación

Diferenciar una serie temporal $X_t$ en tiempo discreto, consiste en transformar $X_t$ en una nueva serie $D_{t}^{\left(1\right)}$ definida como: \[D_{t}^{\left(1\right)}=D\left(X_{t}\right)=X_{t}-X_{t-1}\]

El procedimiento de diferenciación puede volver a aplicarse sobre una serie previamente diferenciada; obtenemos así las diferencias de segundo orden: \[D_{t}^{\left(2\right)}=D\left(D_{t}^{\left(1\right)}\right)=D_{t}^{\left(1\right)}-D_{t-\text{1}}^{\left(1\right)}\]

En general, la diferencia de orden $m$ se obtiene como: \[D_{t}^{\left(m\right)}=D\left(D_{t}^{\left(m-1\right)}\right)=D_{t}^{\left(m-1\right)}-D_{t-\text{1}}^{\left(m-1\right)}\]

En general la diferenciación es una técnica utilizada habitualmente para eliminar la tendencia en una serie temporal.

Las diferencias pueden calcularse también sobre valores de la serie separados un desfase $k$: \[D_{t,k}^{\left(1\right)}=D\left(X_{t}\right)=X_{t}-X_{t-k}\] y, en general: \[D_{t,k}^{\left(m\right)}=D_{t}^{\left(m-1\right)}-D_{t-\text{k}}^{\left(m-1\right)}\] En series temporales mensuales la diferenciación con desfase $k=12$ suele recibir el nombre de diferenciación estacional.

En R, la función diff() permite diferenciar una o más veces una serie temporal. Concretamente: \[D_{t,k}^{\left(m\right)}=\mathsf{diff(}X_{t},\mathsf{lag=}k,\mathsf{order}=m\mathsf{)}\]

Por ejemplo:

Diferencia de primer orden y desfase 1:

dtg=diff(tempGando)
head(dtg,12)

##  [1] -0.7  2.4 -0.8  1.2  2.5  0.7  0.7  0.1 -1.2 -0.4 -2.4 -1.2

plot(dtg)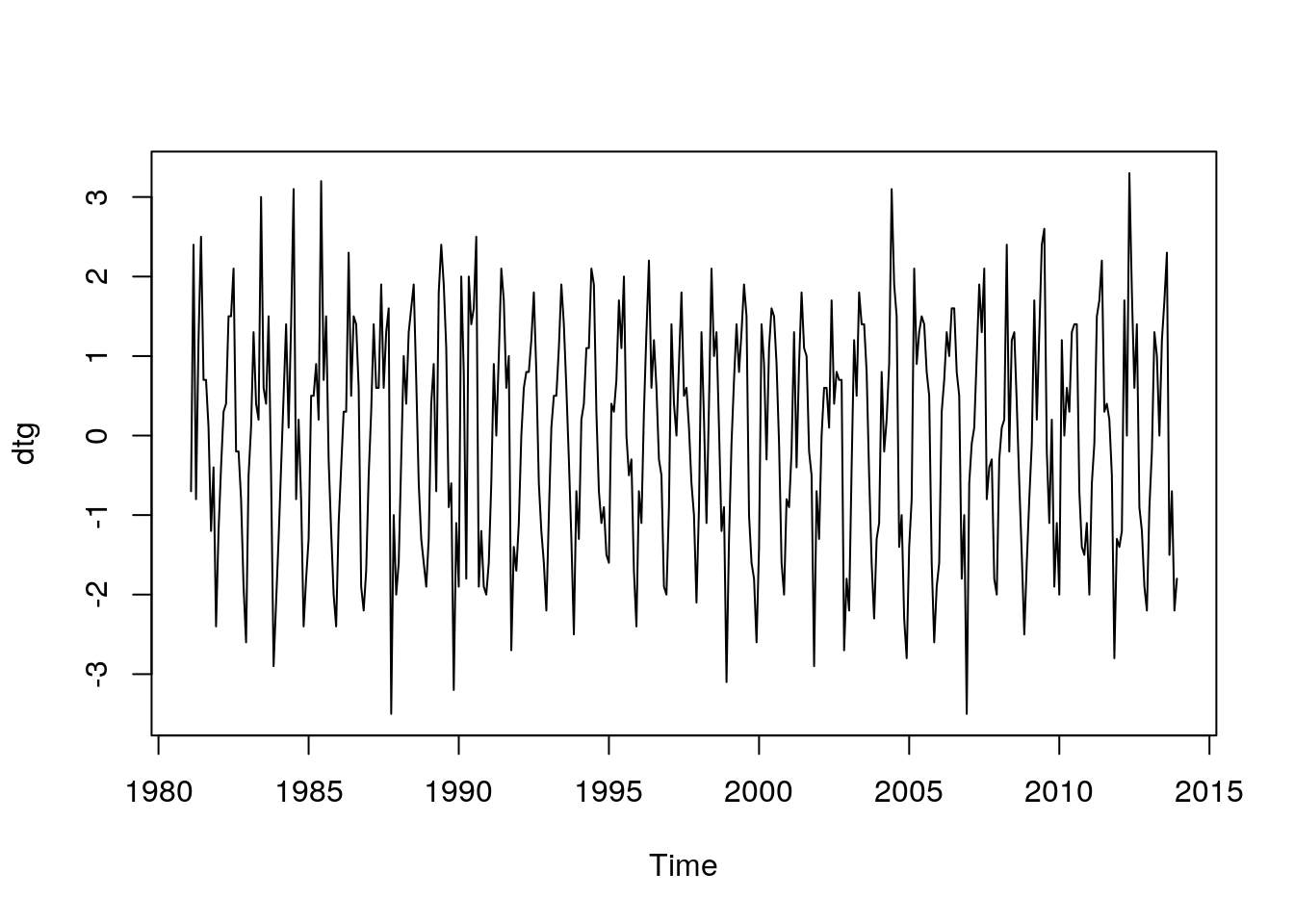

Diferencia de segundo orden y desfase 1:

dtg2=diff(tempGando,differences=2)
head(dtg2,12)

##  [1]  3.10000e+00 -3.20000e+00  2.00000e+00  1.30000e+00 -1.80000e+00 -3.55271e-15
##  [7] -6.00000e-01 -1.30000e+00  8.00000e-01 -2.00000e+00  1.20000e+00  8.00000e-01

plot(dtg2)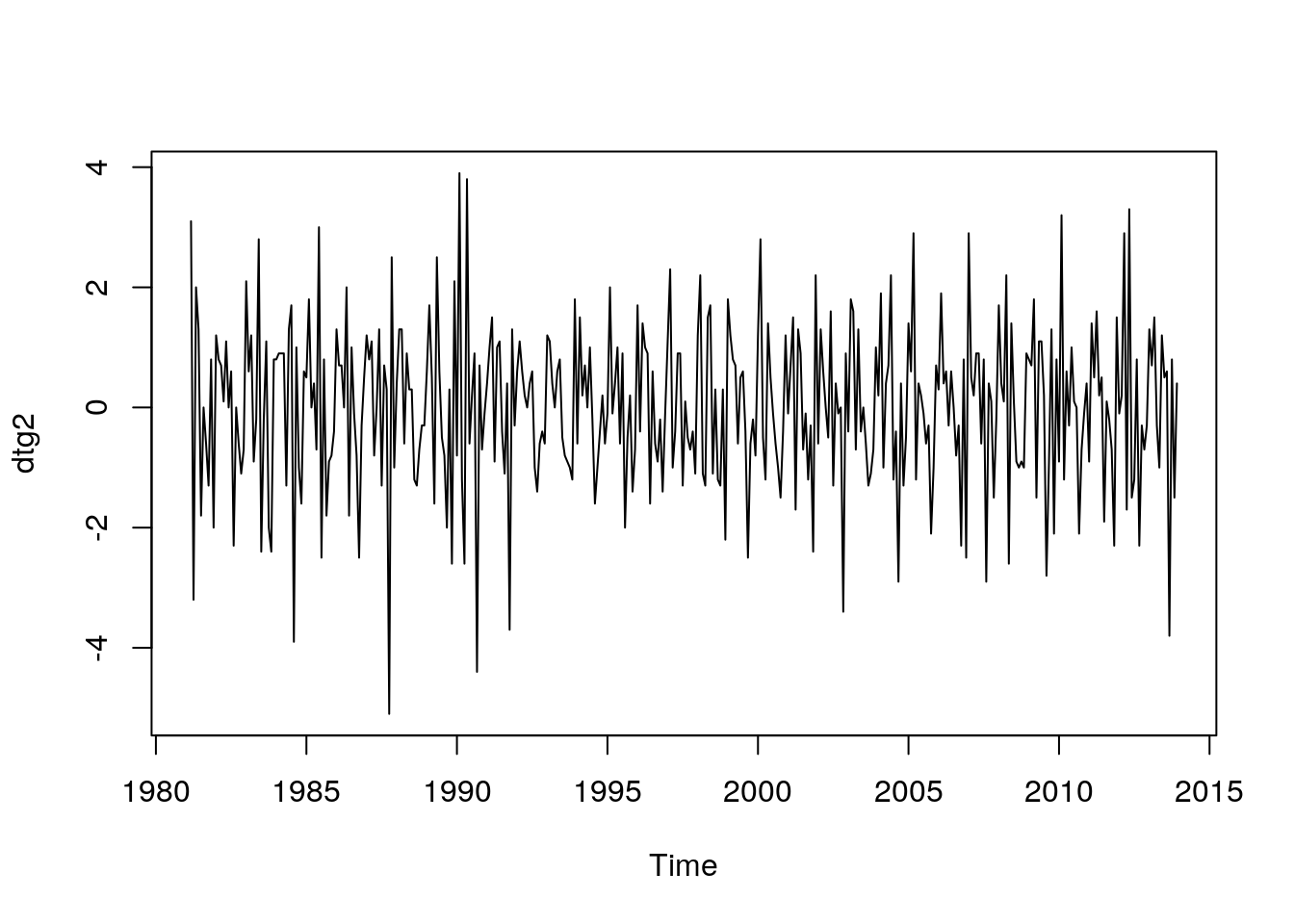

Diferencia estacional de primer orden:

difest=diff(tempGando,lag=12)
head(difest,12)

##  [1]  0.9  1.2 -0.9  0.3  0.6 -0.4  1.0  0.1 -0.2  0.2 -1.3 -1.5

plot(difest,main="Temperaturas Medias en el aeropuerto con una diferencia estacional")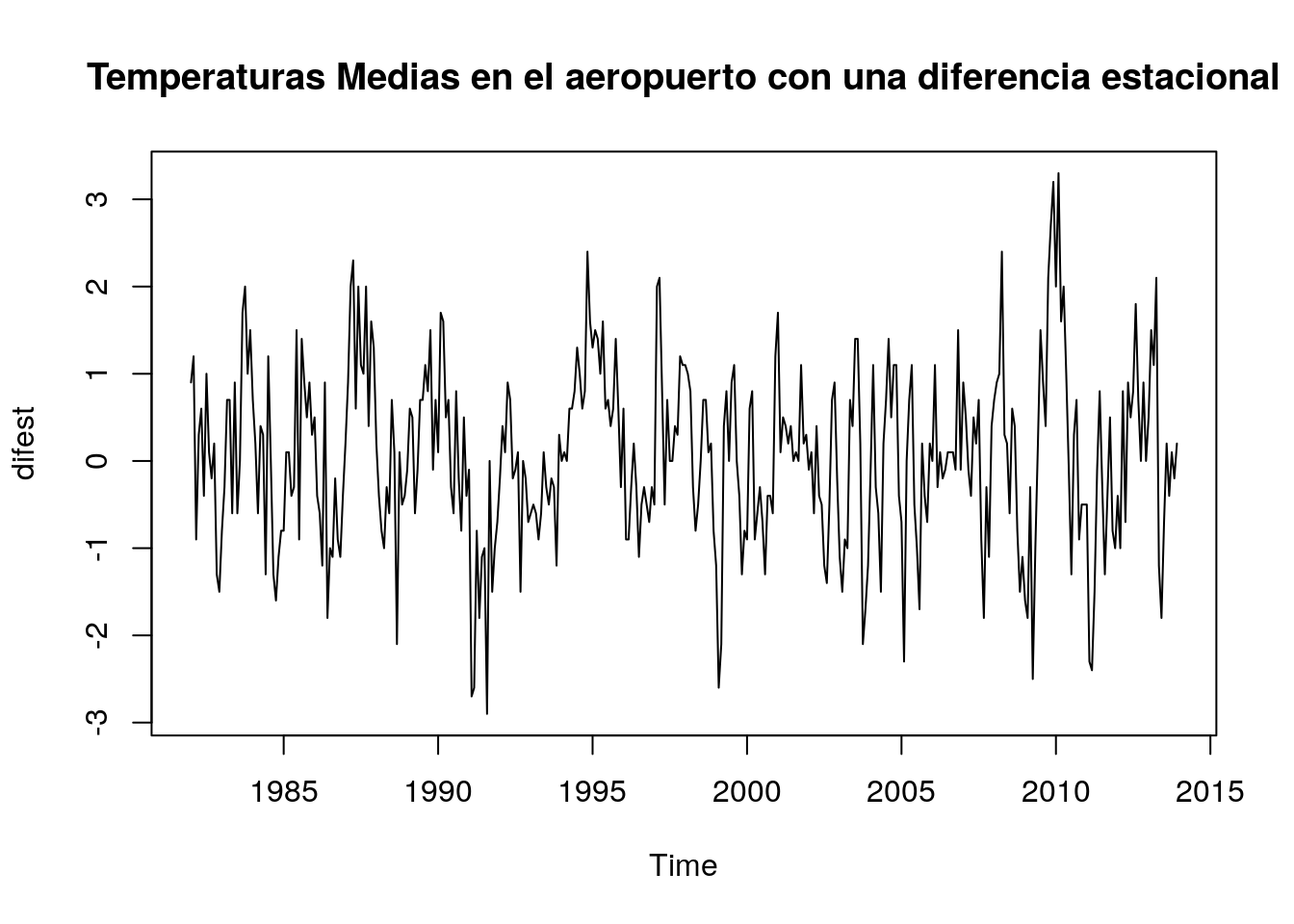

Diferencia estacional de segundo orden:

difest2=diff(tempGando,lag=12, differences=2)
head(difest2,12)

##  [1] -1.7 -1.5  1.6  0.4 -1.2  1.3 -1.6 -0.1  1.9  1.8  2.3  3.0

plot(difest2,main="Temperaturas Medias en el aeropuerto \ncon una diferencia estacional de segundo orden")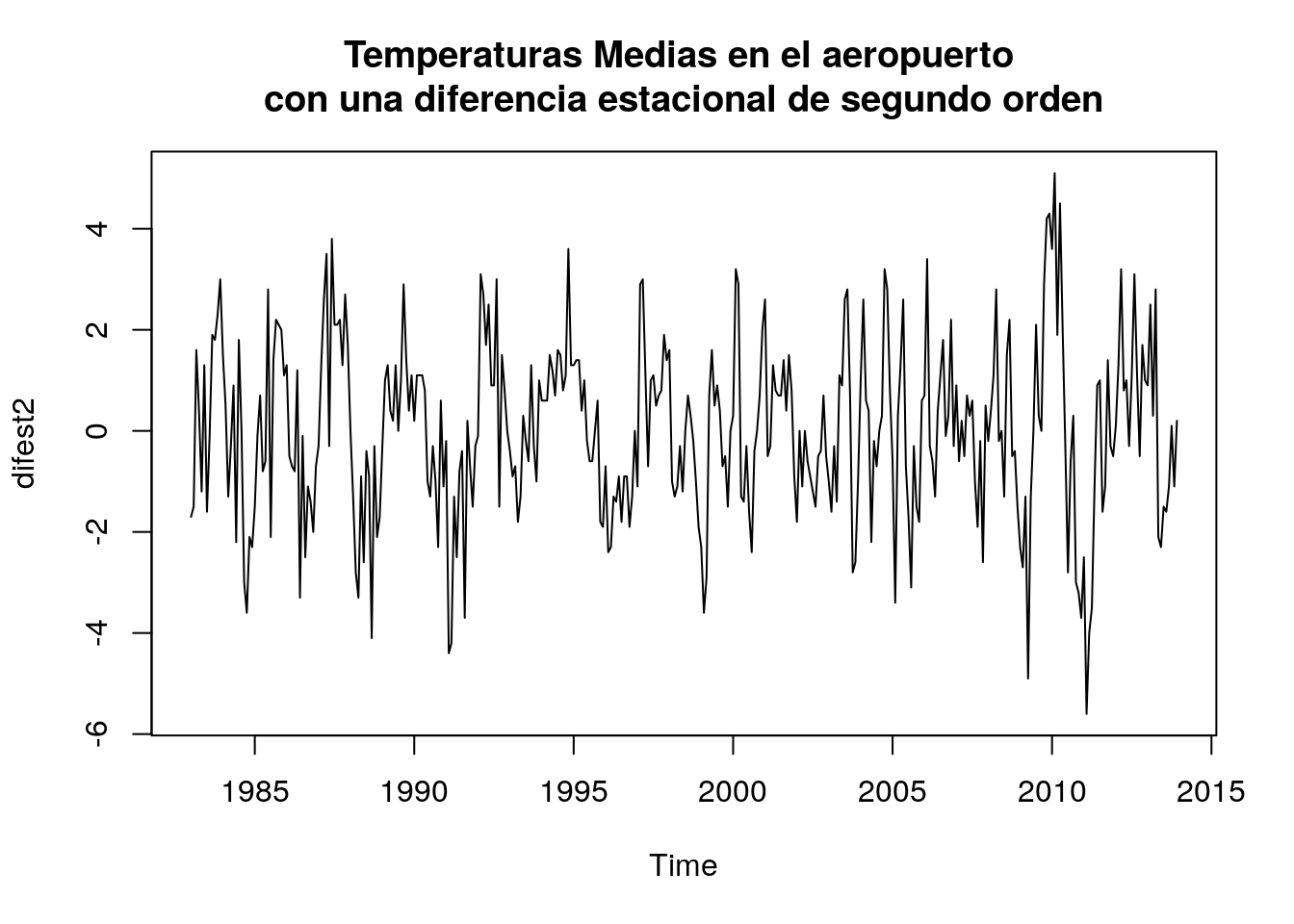

Funciones de autocorrelación

acf() calcula la función de autocorrelación simple de una serie temporal, y pacf() la función de autocorrelación parcial. En ambos casos, por defecto se muestra el gráfico con bandas de confianza al 95%.

acf(tempGando)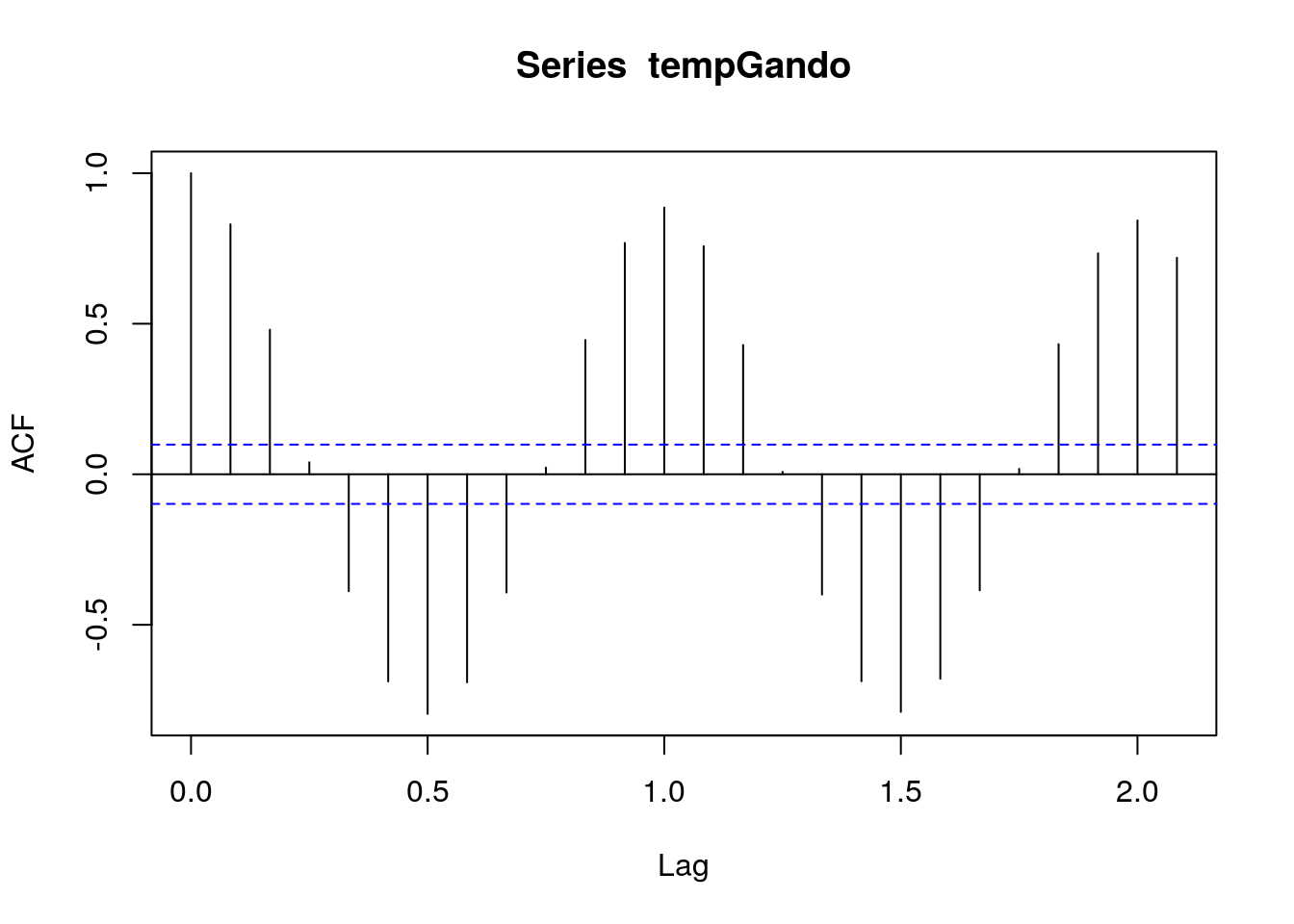

pacf(tempGando)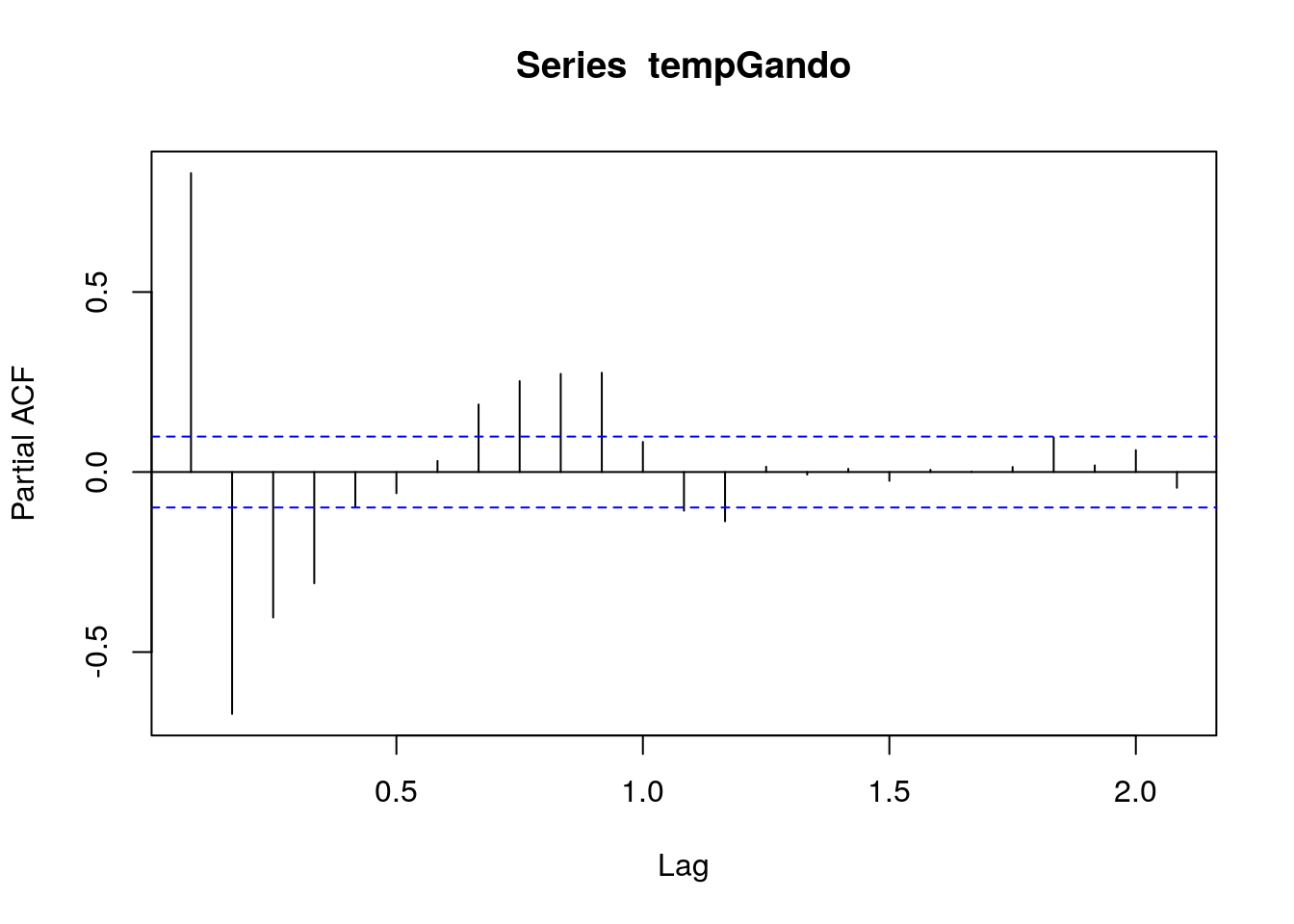

En caso de que deseáramos extraer los valores numéricos de las autocorrelaciones, simplemente asignamos el resultado de la función a una variable y la mostramos:

acfTemp=acf(tempGando, plot=FALSE)
acfTemp

## 
## Autocorrelations of series 'tempGando', by lag
## 
## 0.0000 0.0833 0.1667 0.2500 0.3333 0.4167 0.5000 0.5833 0.6667 0.7500 0.8333 0.9167 
##  1.000  0.830  0.480  0.040 -0.388 -0.688 -0.796 -0.691 -0.393  0.022  0.446  0.768 
## 1.0000 1.0833 1.1667 1.2500 1.3333 1.4167 1.5000 1.5833 1.6667 1.7500 1.8333 1.9167 
##  0.886  0.758  0.429  0.008 -0.400 -0.688 -0.789 -0.679 -0.385  0.018  0.432  0.734 
## 2.0000 2.0833 
##  0.843  0.719

Correlación cruzada

La función ccf() calcula la correlación cruzada entre dos series temporales. En particular el valor del retardo k devuelto por ccf(X,Y) corresponde a la correlación entre $X_{t+k}$ e $Y_t$.

ccf(vtGando[,"TEMP.min"],vtGando[,"TEMP.max"])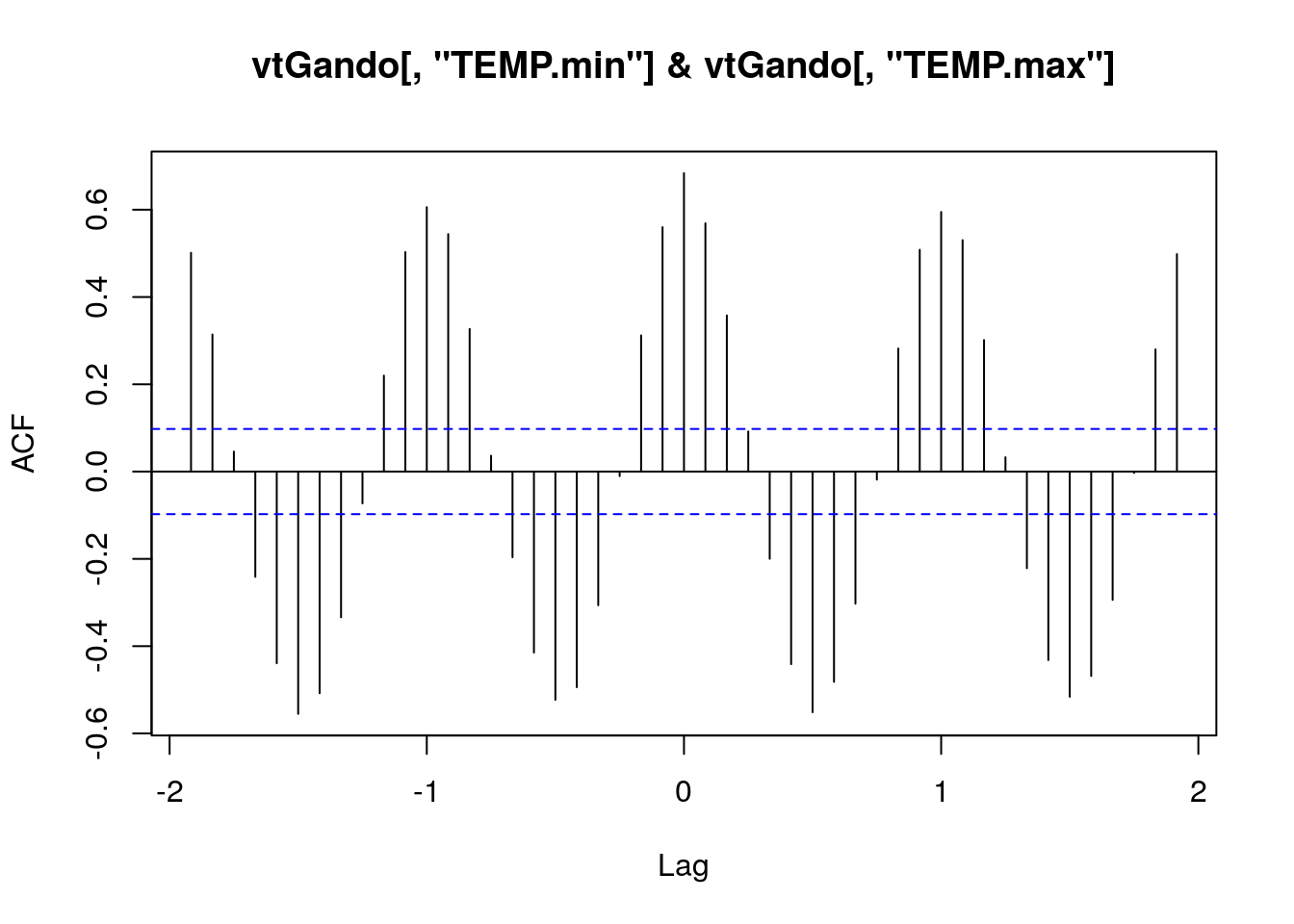

Podemos extraer los valores numéricos de las correlaciones cruzadas del mismo modo que hicimos para acf():

ccfTemp=ccf(vtGando[,"TEMP.min"],vtGando[,"TEMP.max"],plot=FALSE)
ccfTemp

## 
## Autocorrelations of series 'X', by lag
## 
## -1.9167 -1.8333 -1.7500 -1.6667 -1.5833 -1.5000 -1.4167 -1.3333 -1.2500 -1.1667 -1.0833 
##   0.501   0.314   0.046  -0.241  -0.439  -0.555  -0.508  -0.334  -0.073   0.220   0.503 
## -1.0000 -0.9167 -0.8333 -0.7500 -0.6667 -0.5833 -0.5000 -0.4167 -0.3333 -0.2500 -0.1667 
##   0.606   0.544   0.327   0.036  -0.196  -0.415  -0.523  -0.494  -0.306  -0.010   0.312 
## -0.0833  0.0000  0.0833  0.1667  0.2500  0.3333  0.4167  0.5000  0.5833  0.6667  0.7500 
##   0.560   0.684   0.569   0.358   0.092  -0.200  -0.441  -0.551  -0.482  -0.303  -0.018 
##  0.8333  0.9167  1.0000  1.0833  1.1667  1.2500  1.3333  1.4167  1.5000  1.5833  1.6667 
##   0.282   0.508   0.595   0.530   0.301   0.033  -0.221  -0.432  -0.516  -0.468  -0.294 
##  1.7500  1.8333  1.9167 
##  -0.003   0.280   0.498

Espectro

La función spectrum() permite estimar el espectro de una serie temporal. De no especificarse ninguna opción se obtiene el periodograma “crudo” de la serie:

spectrum(tempGando)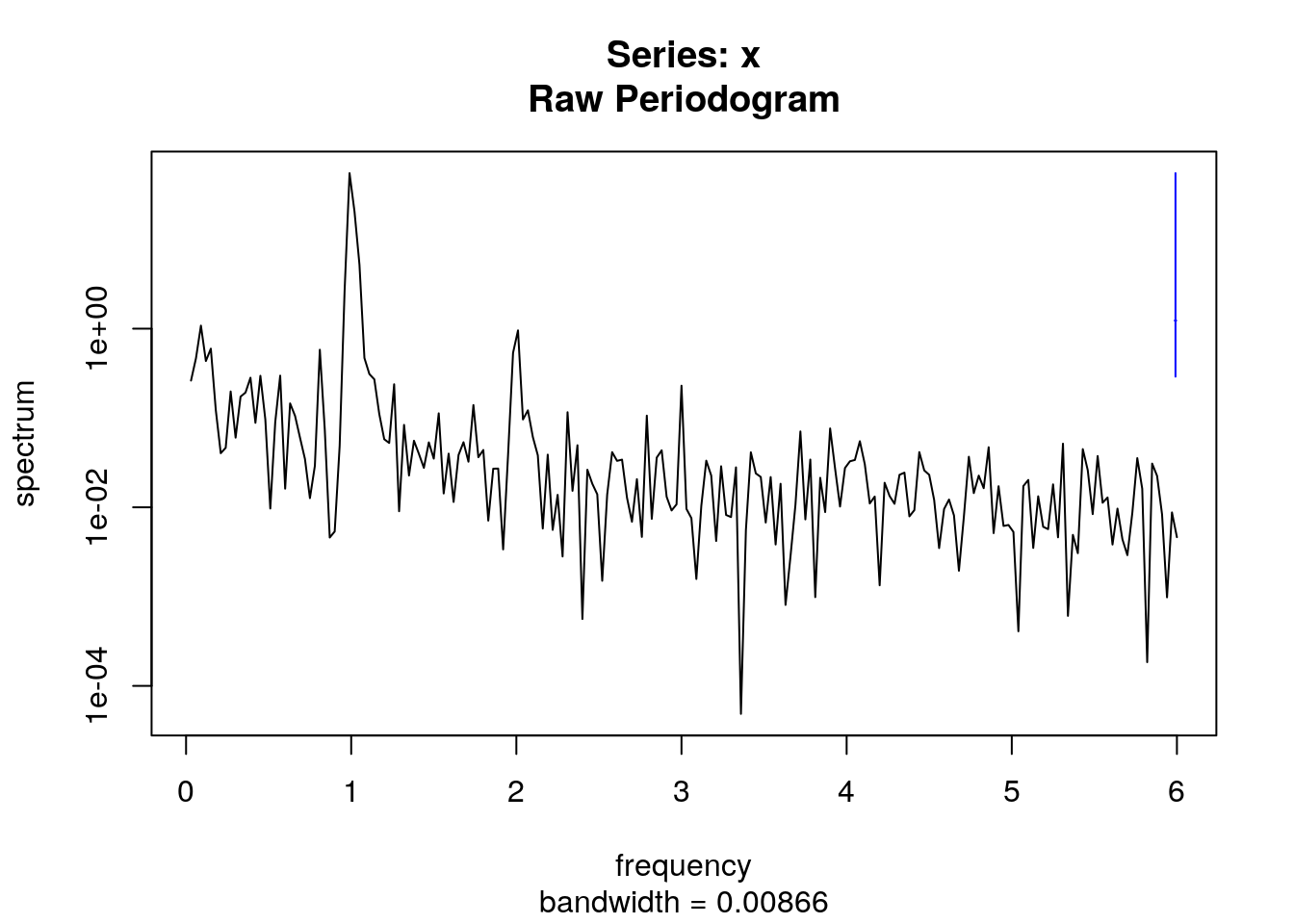

La opción spans permite suavizar el periodograma:

spectrum(tempGando,spans=c(5,5))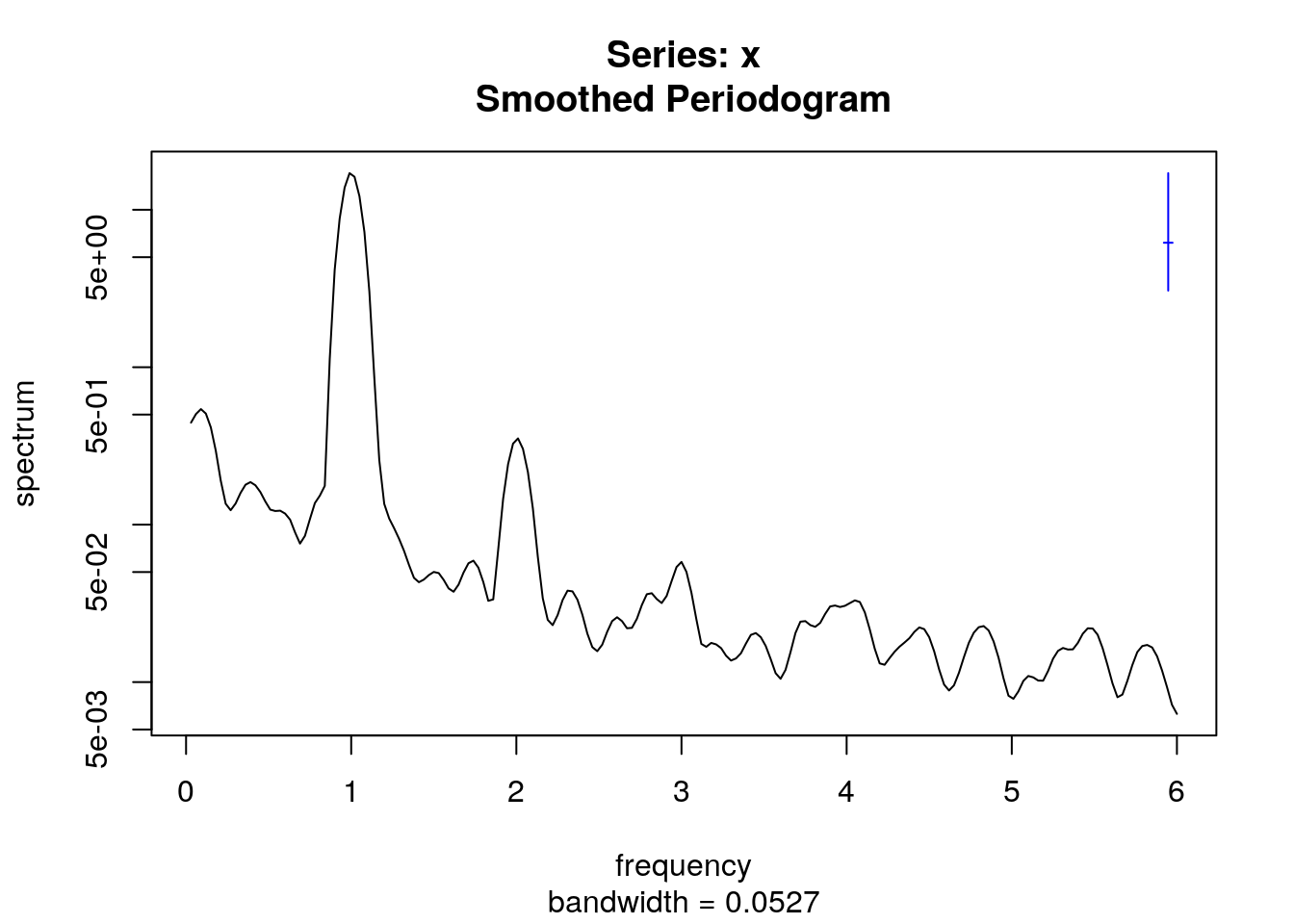

Descomposición de una serie temporal

Las funciones decompose() y stl() permiten descomponer una serie temporal en sus componentes estacional, de tendencia y de ruido. En el caso de decompose() la descomposición se lleva a cabo mediante un ajuste de medias móviles, mientras que stl() realiza la descomposición mediante una ajuste polinómico local.

Descomposición utilizando decompose():

descomp1=decompose(tempGando)
str(descomp1)

## List of 6
##  $ x       : Time-Series [1:396] from 1981 to 2014: 16.8 16.1 18.5 17.7 18.9 21.4 22.1 22.8 22.9 21.7 ...
##  $ seasonal: Time-Series [1:396] from 1981 to 2014: -3.022 -2.915 -2.208 -1.709 -0.606 ...
##  $ trend   : Time-Series [1:396] from 1981 to 2014: NA NA NA NA NA ...
##  $ random  : Time-Series [1:396] from 1981 to 2014: NA NA NA NA NA ...
##  $ figure  : num [1:12] -3.022 -2.915 -2.208 -1.709 -0.606 ...
##  $ type    : chr "additive"
##  - attr(*, "class")= chr "decomposed.ts"

plot(descomp1)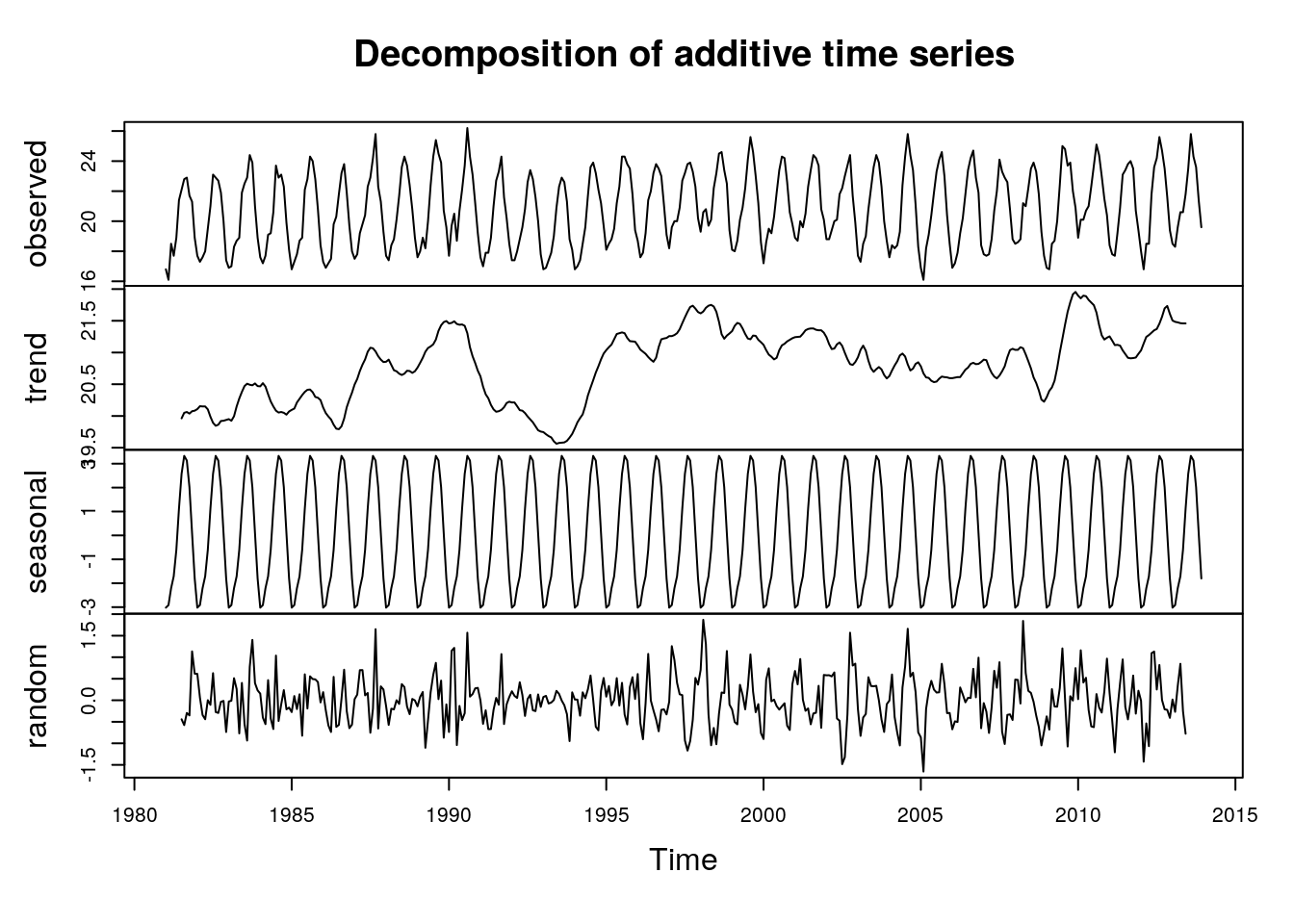

Si queremos “eliminar” la componente estacional de nuestra serie temporal, y dejar solamente la componente de tendencia y el ruido, basta con restar a la serie original la parte estacional (descomp1$seasonal) que acabamos de calcular:

tempGandoDes=tempGando-descomp1$seasonal
plot(tempGandoDes,main="Temperaturas medias mensuales desestacionalizadas \nAeropuerto de Gran Canaria 1981-2013")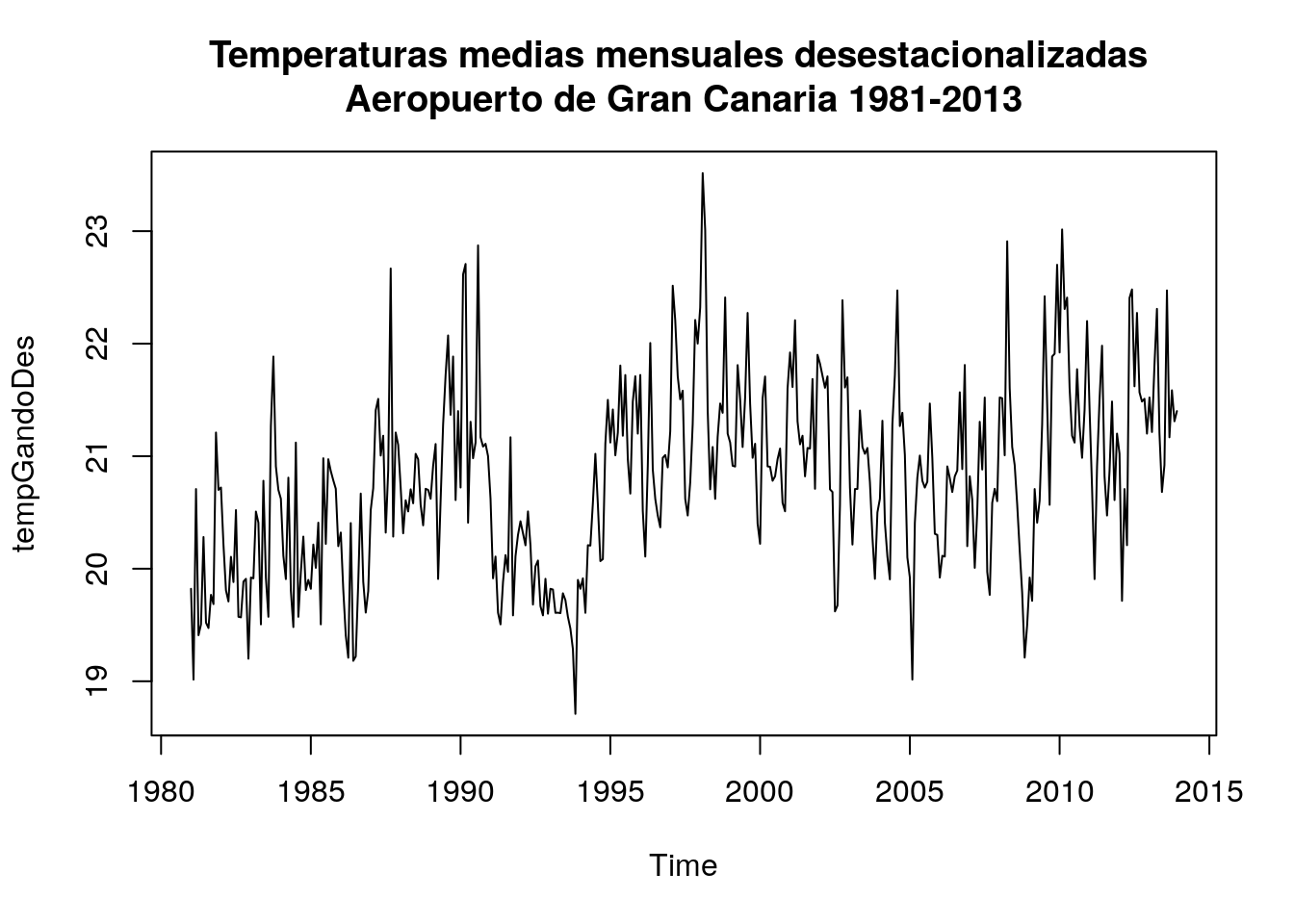

Descomposición utilizando stl():

descomp2=stl(tempGando,s.window="periodic")
str(descomp2)

## List of 8
##  $ time.series: Time-Series [1:396, 1:3] from 1981 to 2014: -3.018 -2.937 -2.18 -1.722 -0.618 ...
##   ..- attr(*, "dimnames")=List of 2
##   .. ..$ : NULL
##   .. ..$ : chr [1:3] "seasonal" "trend" "remainder"
##  $ weights    : num [1:396] 1 1 1 1 1 1 1 1 1 1 ...
##  $ call       : language stl(x = tempGando, s.window = "periodic")
##  $ win        : Named num [1:3] 3961 19 13
##   ..- attr(*, "names")= chr [1:3] "s" "t" "l"
##  $ deg        : Named int [1:3] 0 1 1
##   ..- attr(*, "names")= chr [1:3] "s" "t" "l"
##  $ jump       : Named num [1:3] 397 2 2
##   ..- attr(*, "names")= chr [1:3] "s" "t" "l"
##  $ inner      : int 2
##  $ outer      : int 0
##  - attr(*, "class")= chr "stl"

plot(descomp2)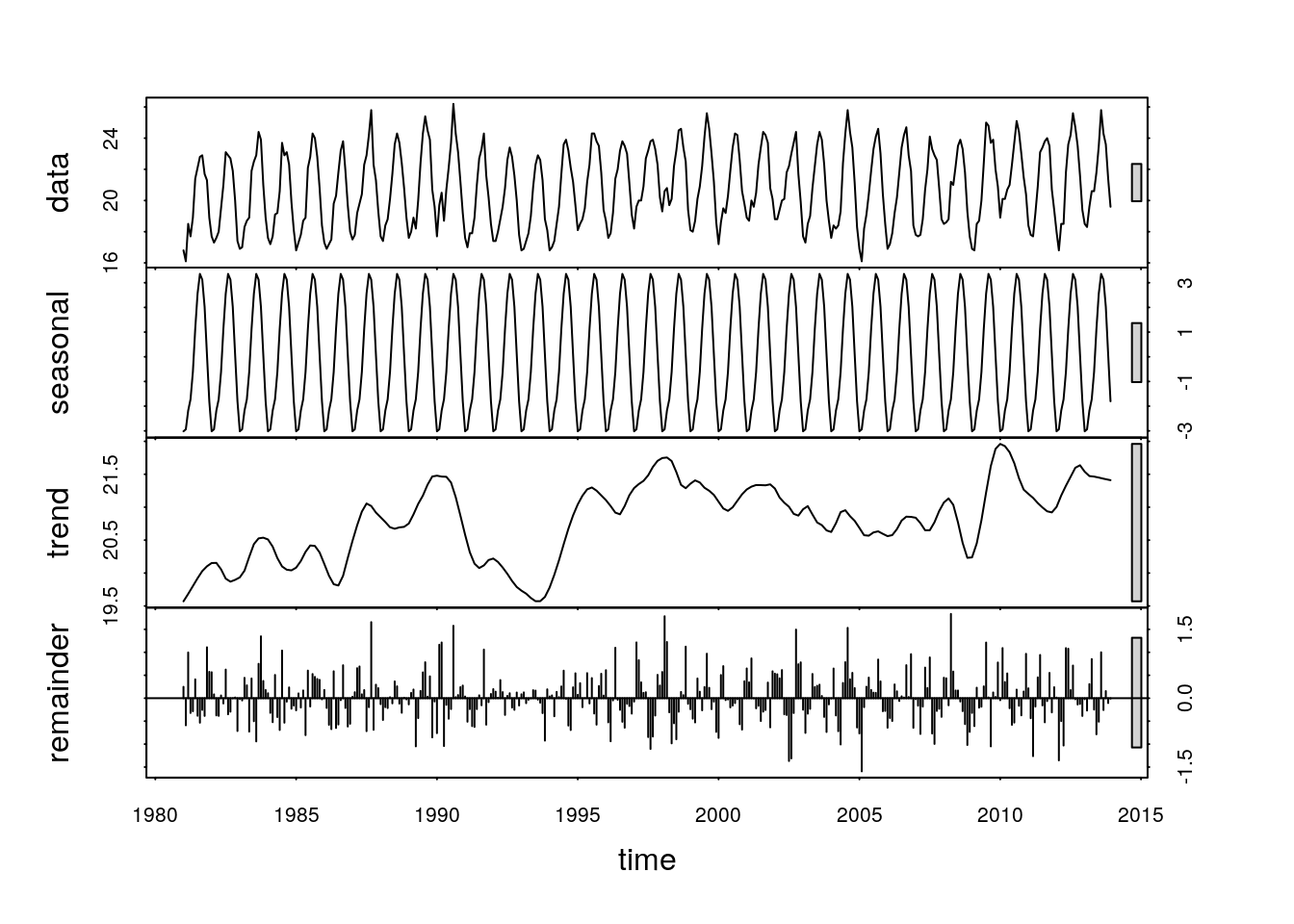

Modelos ARIMA.

Existe una amplia literatura sobre la aplicación de modelos ARIMA en series temporales. R cuenta con numerosos procedimientos para la estimación, validación y predicción con estos modelos:

El uso adecuado de algunas funciones que ya hemos visto (acf(), pacf() y diff()) permite al usuario identificar posibles modelos candidatos para representar una serie temporal estacionaria.
Estos modelos pueden estimarse fácilmente en R mediante la función arima().
El paquete forecast incluye la función auto.arima() que realiza un ajuste automático de un modelo ARIMA a una serie temporal dada.
La diagnosis del modelo estimado puede llevarse a cabo mediante la función ts.diag().
Se pueden realizar predicciones mediante predict() o forecast() (esta última función en el paquete homónimo, forecast).
Por último, señalemos que la función arima.sim() permite simular una serie temporal de acuerdo con el modelo ARIMA especificado por el usuario.

Un ejemplo.

Simulamos una serie temporal de acuerdo con un modelo ARIMA(1,1,1):

miSerie = arima.sim(list(order = c(1,1,1), ar=0.5, ma=0.6), sd=1.55, n = 730)
plot(miSerie)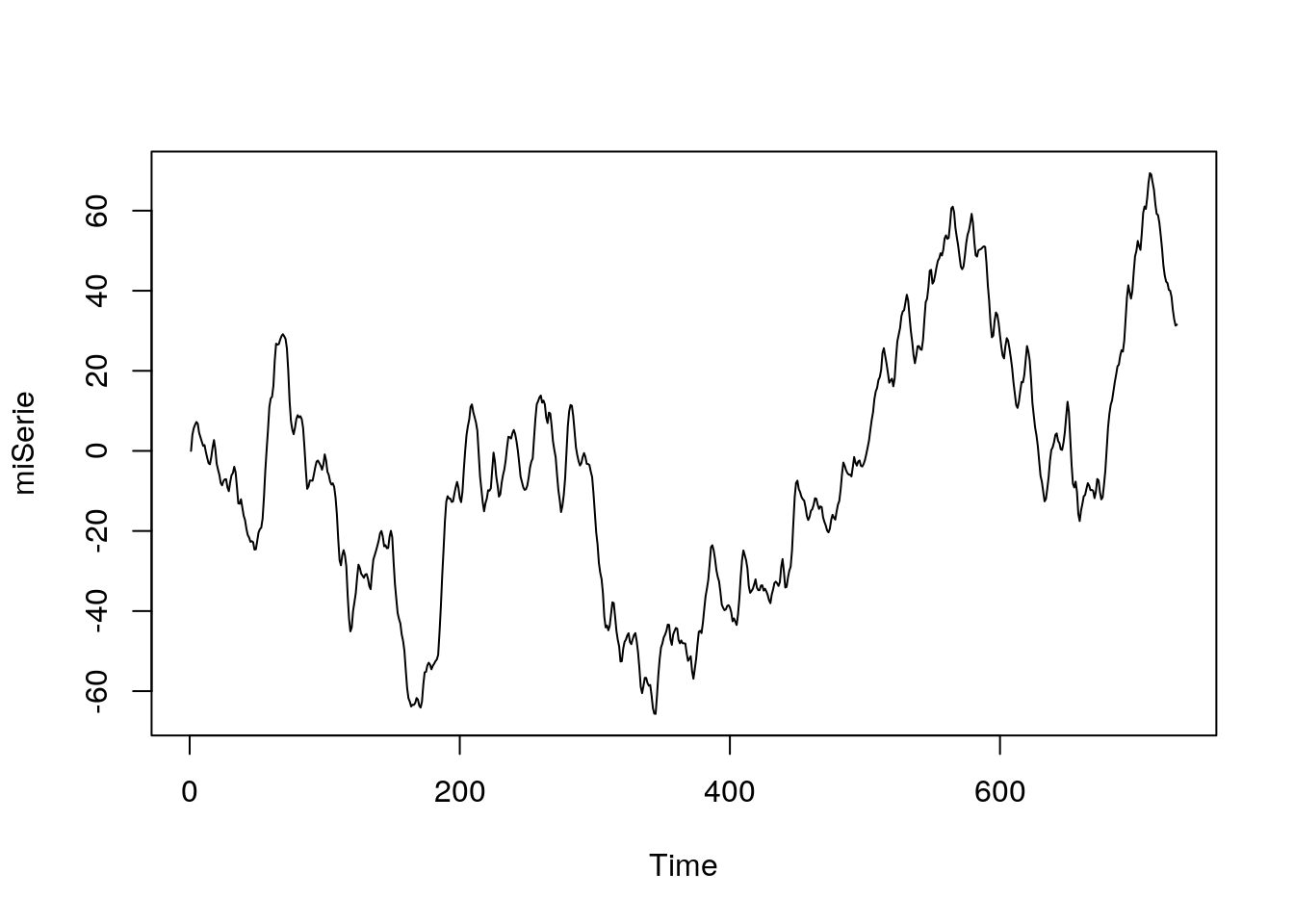

Veamos ahora como podemos utilizar R para estimar un modelo ARIMA para esta serie:
La serie es obviamente no estacionaria. Sin embargo, la serie diferenciada es razonablemente estacionaria:

dms=diff(miSerie)
plot(dms)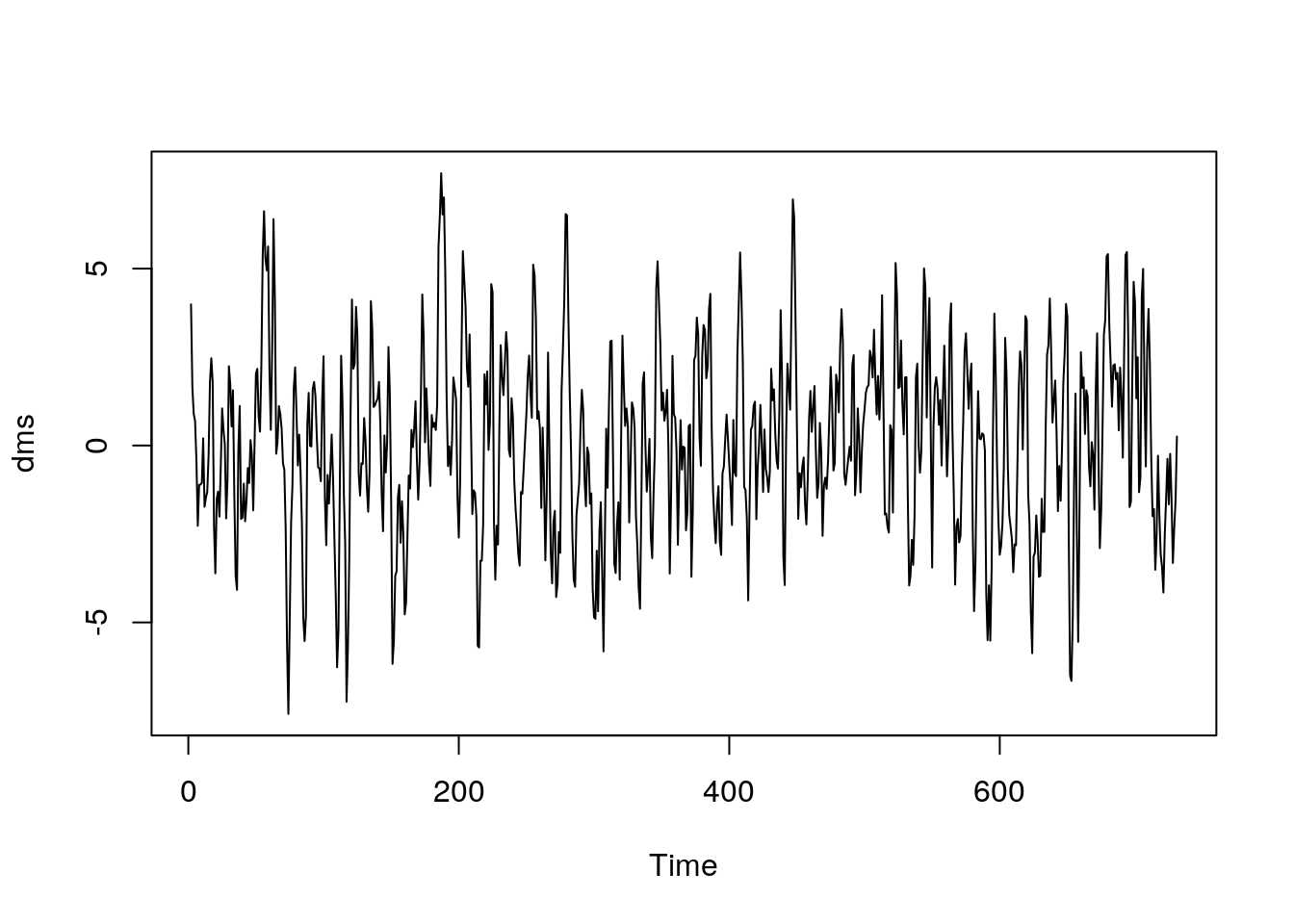

Los correlogramas sugieren un modelo ARMA(1,1) para la serie diferenciada:

par(mfrow=c(1,2))
acf(dms)
pacf(dms)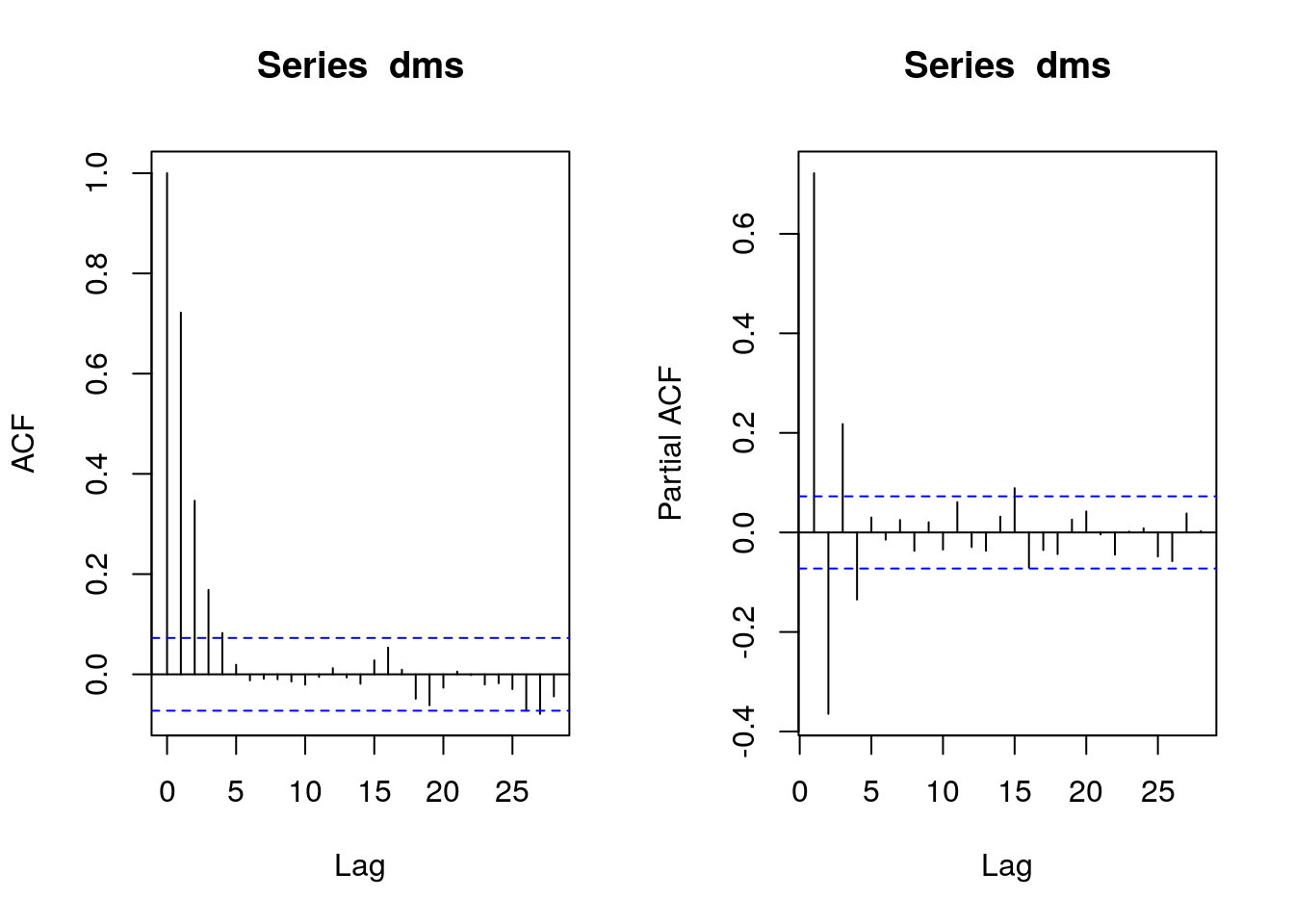

Este modelo puede estimarse a partir de los datos mediante:

ajuste=arima(miSerie,order=c(1,1,1))
ajuste

## 
## Call:
## arima(x = miSerie, order = c(1, 1, 1))
## 
## Coefficients:
##         ar1    ma1
##       0.488  0.620
## s.e.  0.038  0.035
## 
## sigma^2 estimated as 2.51:  log likelihood = -1373.08,  aic = 2752.17

La función tsdiag() muestra que no queda estructura de autocorrelación en los residuos del ajuste:

tsdiag(ajuste)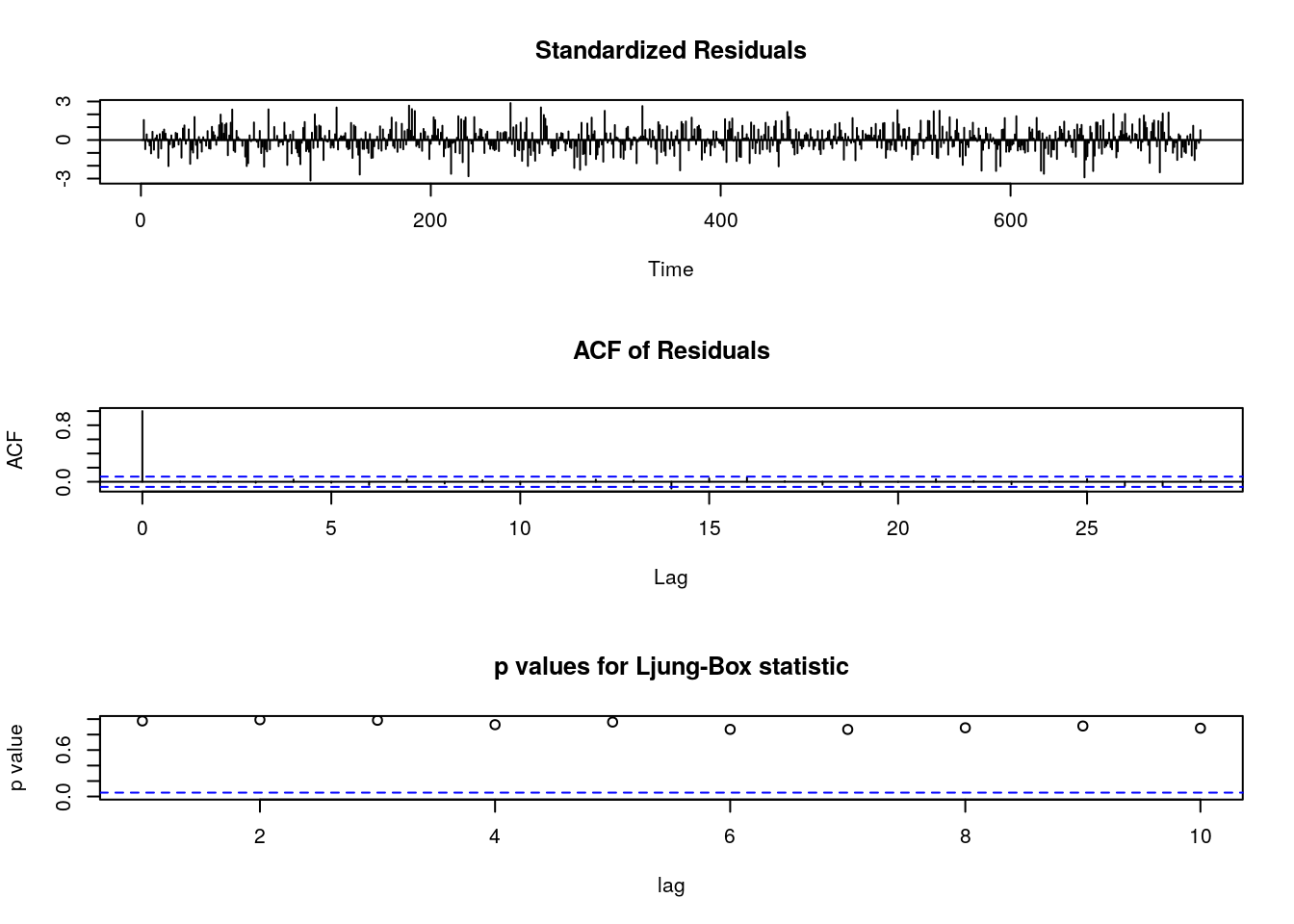

Si utilizamos la función auto.arima() obtenemos el mismo modelo:

library(forecast)
ajuste2=auto.arima(miSerie)
ajuste2

## Series: miSerie 
## ARIMA(1,1,1) 
## 
## Coefficients:
##         ar1    ma1
##       0.488  0.620
## s.e.  0.038  0.035
## 
## sigma^2 estimated as 2.52:  log likelihood=-1373.08
## AIC=2752.17   AICc=2752.2   BIC=2765.94

Podemos hacer predicciones con este modelo utilizando predict():

predict(ajuste,n.ahead=12)

## $pred
## Time Series:
## Start = 732 
## End = 743 
## Frequency = 1 
##  [1] 32.4211 32.8502 33.0595 33.1615 33.2112 33.2355 33.2473 33.2530 33.2558 33.2572
## [11] 33.2579 33.2582
## 
## $se
## Time Series:
## Start = 732 
## End = 743 
## Frequency = 1 
##  [1]  1.58584  3.70002  5.59702  7.25571  8.71125 10.00466 11.17047 12.23521 13.21879
## [10] 14.13607 14.99827 15.81395

o también forecast():

forecast(ajuste)

##     Point Forecast   Lo 80   Hi 80    Lo 95   Hi 95
## 732        32.4211 30.3888 34.4534 29.31290 35.5293
## 733        32.8502 28.1085 37.5920 25.59834 40.1021
## 734        33.0595 25.8866 40.2323 22.08951 44.0294
## 735        33.1615 23.8629 42.4600 18.94054 47.3824
## 736        33.2112 22.0473 44.3751 16.13747 50.2849
## 737        33.2355 20.4140 46.0569 13.62667 52.8442
## 738        33.2473 18.9317 47.5628 11.35356 55.1410
## 739        33.2530 17.5730 48.9331  9.27246 57.2336
## 740        33.2558 16.3153 50.1964  7.34749 59.1642
## 741        33.2572 15.1411 51.3733  5.55102 60.9634

plot(forecast(ajuste))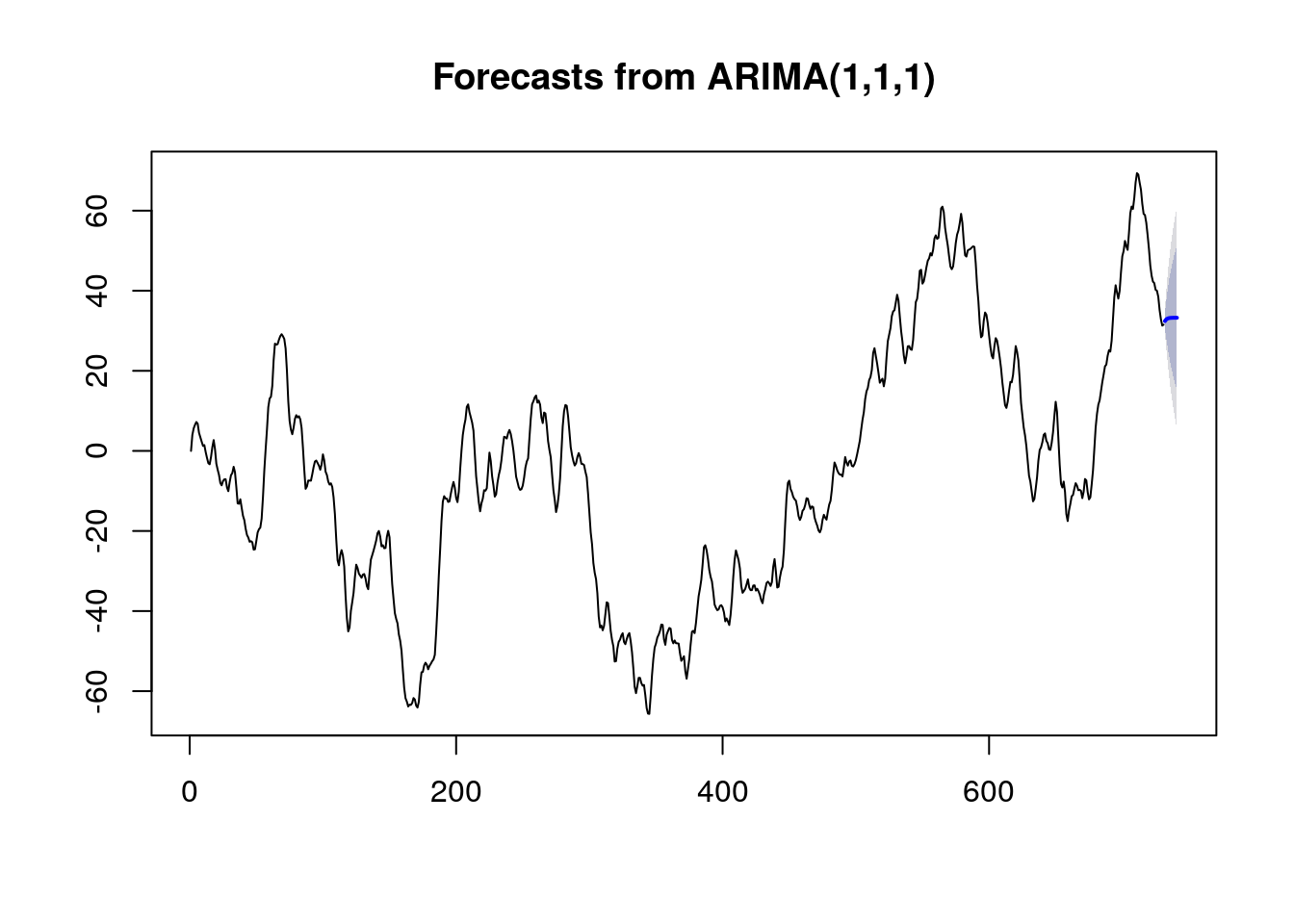

Series temporales irregularmente espaciadas: la clase zoo

Como hemos señalado más arriba, la creación de objetos de clase ts() requiere que las observaciones estén distribuidas de modo regular a lo largo del tiempo. En caso de que no sea así, podemos utilizar objetos de la clase zoo (el nombre de la clase deriva del apellido del autor del paquete, Zeilies Ordered Observations). Los objetos de esta clase se crean mediante la función zoo().

Ejemplo

Supongamos que en nuestro primer ejemplo (partidos de la liga de fútbol española durante la temporada 2013-14) quisiéramos disponer de la sucesión del número medio de goles marcados por los equipos locales en cada jornada con su fecha concreta de celebración. Para ello:

Extraemos la sucesión de fechas en que se celebró cada jornada mediante:

fechasLiga=with(liga1314,tapply(fecha,jornada,unique))
fechasLiga=as.Date(fechasLiga,format="%d-%m-%Y")

Calculamos el número medio de goles por partido marcados por los equipos locales en cada jornada:

nMedioGolesLocal=with(liga1314,tapply(gLoc,jornada,mean))

Creamos un objeto de clase zoo, especificando la variable fechasLiga como variable de ordenación:

library(zoo)
equipoLocal=zoo(nMedioGolesLocal, order.by=fechasLiga)
str(equipoLocal)

## 'zoo' series from 2013-08-18 to 2014-05-18
##   Data: Named num [1:38] 2.2 1.6 1.3 2.2 1.4 2 0.7 2 0.9 1.9 ...
##  - attr(*, "names")= chr [1:38] "1" "2" "3" "4" ...
##   Index:  Date[1:38], format: "2013-08-18" "2013-08-25" "2013-09-01" "2013-09-15" "2013-09-22" "2013-09-25" ...

Gráficamente:

plot(equipoLocal, main="Número medio de goles por partido marcados por el equipo local\nLiga 2013-14",
     ylab="Goles",xlab="Mes")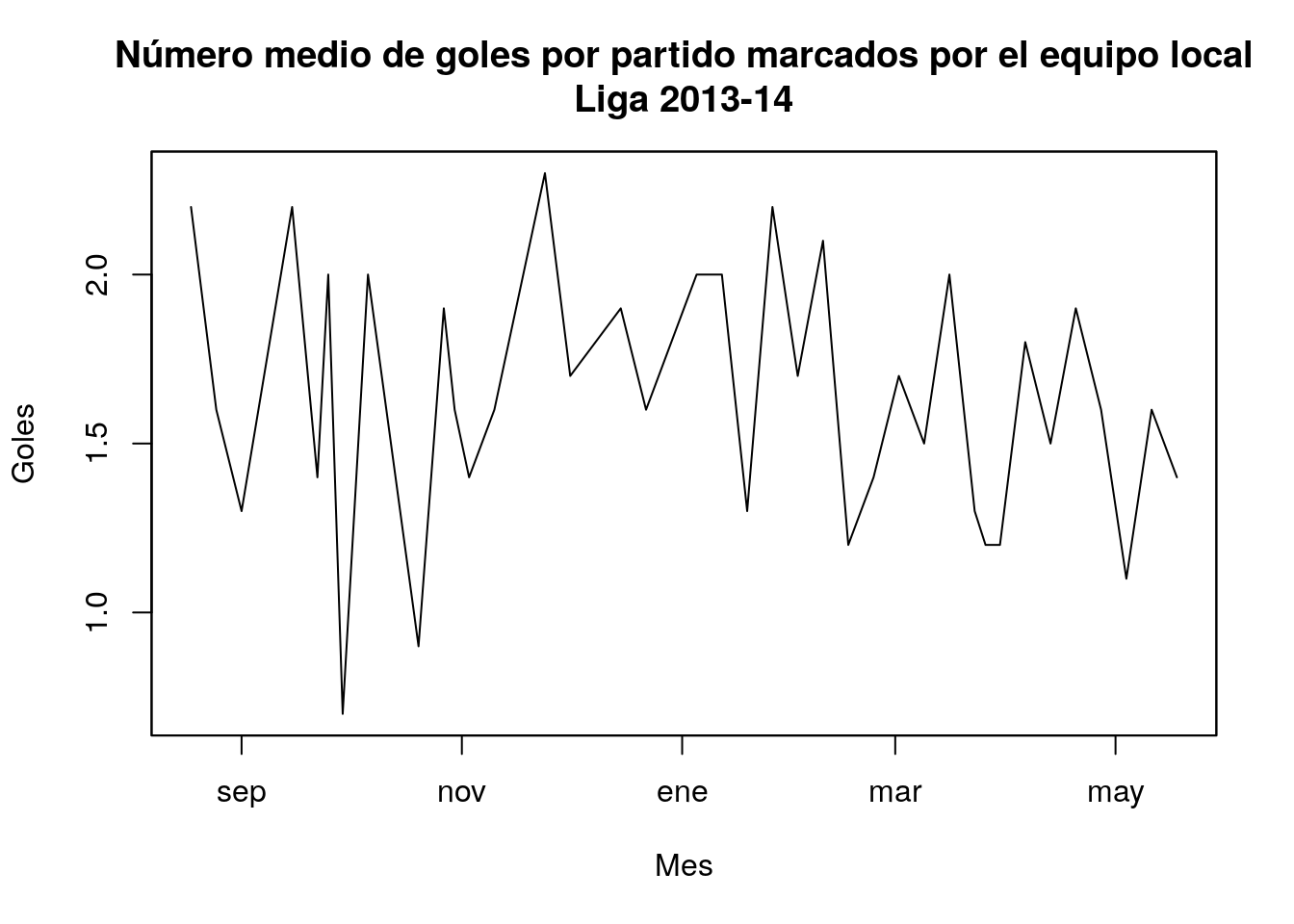

La función index()

Una vez que se ha definido un objeto de clase zoo la función index() aplicada a dicho objeto devuelve los valores de tiempo en que la serie se ha observado:

index(equipoLocal)

##  [1] "2013-08-18" "2013-08-25" "2013-09-01" "2013-09-15" "2013-09-22" "2013-09-25"
##  [7] "2013-09-29" "2013-10-06" "2013-10-20" "2013-10-27" "2013-10-30" "2013-11-03"
## [13] "2013-11-10" "2013-11-24" "2013-12-01" "2013-12-15" "2013-12-22" "2014-01-05"
## [19] "2014-01-12" "2014-01-19" "2014-01-26" "2014-02-02" "2014-02-09" "2014-02-16"
## [25] "2014-02-23" "2014-03-02" "2014-03-09" "2014-03-16" "2014-03-23" "2014-03-26"
## [31] "2014-03-30" "2014-04-06" "2014-04-13" "2014-04-20" "2014-04-27" "2014-05-04"
## [37] "2014-05-11" "2014-05-18"

Combinación de objetos de clase zoo

Para combinar objetos de clase zoo no se pueden usar ts.intersect() o ts.union() que solo funcionan con objetos de clase ts(). En su lugar deberemos utilizar merge().

A modo de ejemplo, podemos proceder como antes para construir el número medio de goles por partido marcados ahora por los equipos visitantes en cada jornada:

nMedioGolesVisit=with(liga1314,tapply(gVis,jornada,mean))
equipoVisitante=zoo(nMedioGolesVisit, order.by=fechasLiga)

Para combinar los números medios de goles por partido marcados por los equipos locales y los visitantes en un único objeto de clase zoo utilizamos merge:

goles1314=merge(equipoLocal,equipoVisitante)

Podemos representar ambas series gráficamente. Por defecto se genera una gráfica para cada serie:

plot(goles1314, main="Número medio de goles por partido durante la liga 2013-14",xlab="Mes")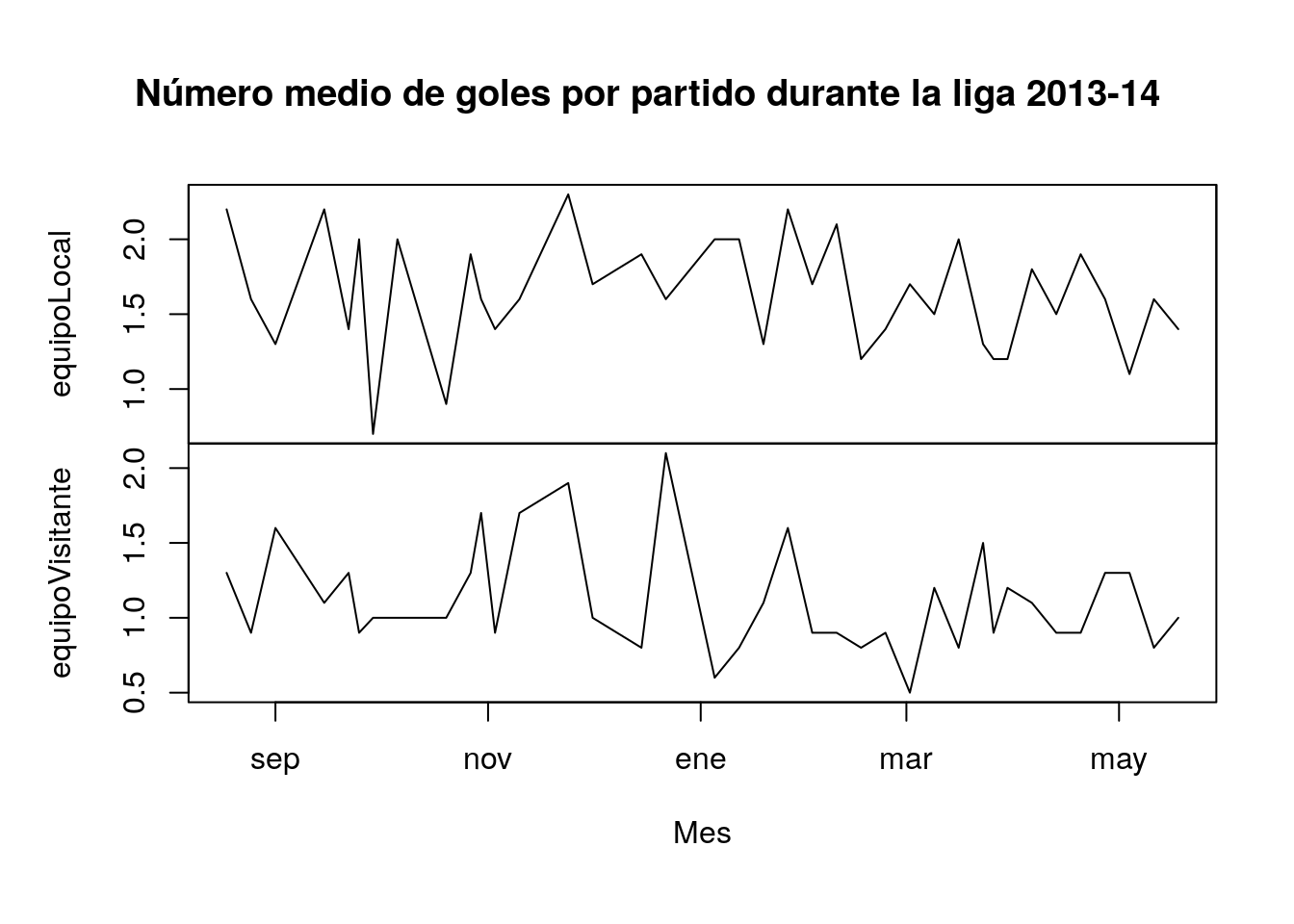

Si deseamos una representación conjunta en un único gráfico (que en este caso permite visualizar mejor el comportamiento conjunto de ambas series) utilizamos la opción plot.type='single':

plot(goles1314, main="Número medio de goles por partido durante la liga 2013-14",xlab="Mes",
     ylab="Numero de goles", plot.type="single", col=c("red","blue"),lty=c(1,2))
legend("topright",title="Equipos:",legend=c("Locales","Visitantes"),col=c("red","blue"),lty=c(1,2))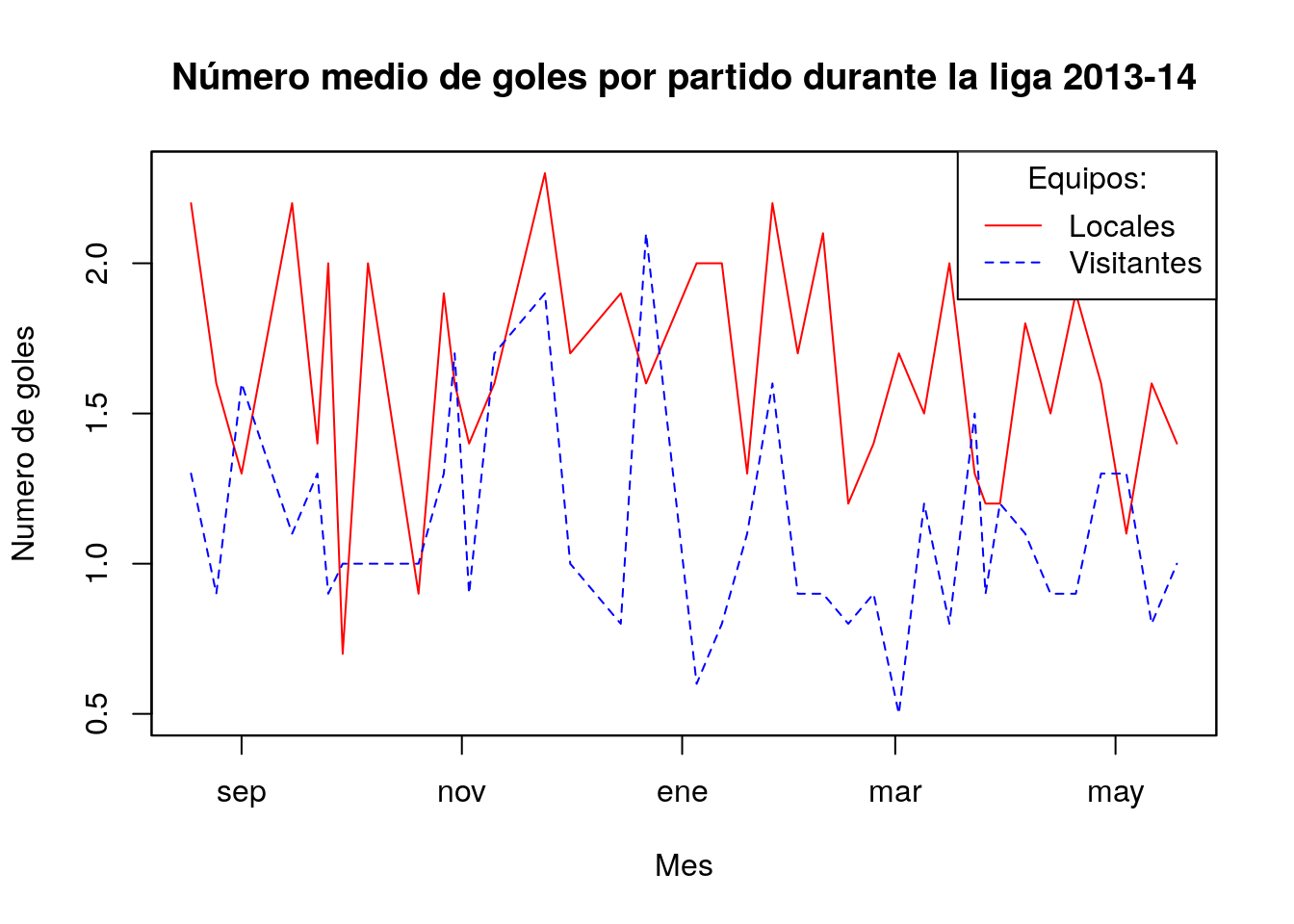

Como puede apreciarse en la gráfica, en general marcan más goles los equipos locales que los visitantes.

Imputación de valores perdidos

El paquete zoo cuenta con algunas herramientas para rellenar valores perdidos en una serie temporal. Para conocer su funcionamiento consideraremos los datos del siguiente archivo, que contiene los valores medios diarios de presión atmosférica en el aeropuerto de Gran Canaria durante el mes de junio de 2014:

PAcsv=getURL("http://www.dma.ulpgc.es/profesores/personal/stat/datos/PAtmJun14.csv")
PAjun14=read.csv2(textConnection(PAcsv),encoding="UTF-8",stringsAsFactors=FALSE)
PAjun14

##         fecha presAtm
## 1  2014-06-01 1018.73
## 2  2014-06-02 1019.08
## 3  2014-06-03 1019.44
## 4  2014-06-04 1018.15
## 5  2014-06-05      NA
## 6  2014-06-06 1016.53
## 7  2014-06-07 1018.29
## 8  2014-06-08 1020.27
## 9  2014-06-09      NA
## 10 2014-06-10 1019.40
## 11 2014-06-11 1017.65
## 12 2014-06-12 1016.83
## 13 2014-06-13 1015.46
## 14 2014-06-14      NA
## 15 2014-06-15 1016.10
## 16 2014-06-16 1017.14
## 17 2014-06-17 1017.59
## 18 2014-06-18 1019.30
## 19 2014-06-19      NA
## 20 2014-06-20 1019.46
## 21 2014-06-21 1020.32
## 22 2014-06-22 1021.46
## 23 2014-06-23 1022.33
## 24 2014-06-24      NA
## 25 2014-06-25 1021.33
## 26 2014-06-26 1018.97
## 27 2014-06-27 1019.11
## 28 2014-06-28      NA
## 29 2014-06-29 1018.63
## 30 2014-06-30 1016.80

En primer lugar convertimos la presión atmosférica en un objeto de clase zoo:

presAtm=zoo(PAjun14$presAtm,order.by=as.Date(PAjun14$fecha,format="%Y-%m-%d"))
presAtm

## 2014-06-01 2014-06-02 2014-06-03 2014-06-04 2014-06-05 2014-06-06 2014-06-07 2014-06-08 
##    1018.73    1019.08    1019.44    1018.15         NA    1016.53    1018.29    1020.27 
## 2014-06-09 2014-06-10 2014-06-11 2014-06-12 2014-06-13 2014-06-14 2014-06-15 2014-06-16 
##         NA    1019.40    1017.65    1016.83    1015.46         NA    1016.10    1017.14 
## 2014-06-17 2014-06-18 2014-06-19 2014-06-20 2014-06-21 2014-06-22 2014-06-23 2014-06-24 
##    1017.59    1019.30         NA    1019.46    1020.32    1021.46    1022.33         NA 
## 2014-06-25 2014-06-26 2014-06-27 2014-06-28 2014-06-29 2014-06-30 
##    1021.33    1018.97    1019.11         NA    1018.63    1016.80

Podemos observar que faltan algunos días (concretamente los días 5, 9, 14, 19, 24 y 28). Existen tres métodos para que zoo impute los valores perdidos:

na.approx(): reemplaza los valores perdidos por una interpolación lineal calculada a partir de los valores adyacentes:

na.approx(presAtm)

## 2014-06-01 2014-06-02 2014-06-03 2014-06-04 2014-06-05 2014-06-06 2014-06-07 2014-06-08 
##    1018.73    1019.08    1019.44    1018.15    1017.34    1016.53    1018.29    1020.27 
## 2014-06-09 2014-06-10 2014-06-11 2014-06-12 2014-06-13 2014-06-14 2014-06-15 2014-06-16 
##    1019.84    1019.40    1017.65    1016.83    1015.46    1015.78    1016.10    1017.14 
## 2014-06-17 2014-06-18 2014-06-19 2014-06-20 2014-06-21 2014-06-22 2014-06-23 2014-06-24 
##    1017.59    1019.30    1019.38    1019.46    1020.32    1021.46    1022.33    1021.83 
## 2014-06-25 2014-06-26 2014-06-27 2014-06-28 2014-06-29 2014-06-30 
##    1021.33    1018.97    1019.11    1018.87    1018.63    1016.80

Si se especifica la opción maxgap=n las secuencias de NA sucesivos de longitud mayor que n se quedan como están y no se imputan.

na.locf(): remplaza cada valor perdido por el valor no perdido anterior más reciente; en caso de que el primer valor de la serie sea un valor perdido, dicho valor se elimina. En nuestro ejemplo:

na.locf(presAtm)

## 2014-06-01 2014-06-02 2014-06-03 2014-06-04 2014-06-05 2014-06-06 2014-06-07 2014-06-08 
##    1018.73    1019.08    1019.44    1018.15    1018.15    1016.53    1018.29    1020.27 
## 2014-06-09 2014-06-10 2014-06-11 2014-06-12 2014-06-13 2014-06-14 2014-06-15 2014-06-16 
##    1020.27    1019.40    1017.65    1016.83    1015.46    1015.46    1016.10    1017.14 
## 2014-06-17 2014-06-18 2014-06-19 2014-06-20 2014-06-21 2014-06-22 2014-06-23 2014-06-24 
##    1017.59    1019.30    1019.30    1019.46    1020.32    1021.46    1022.33    1022.33 
## 2014-06-25 2014-06-26 2014-06-27 2014-06-28 2014-06-29 2014-06-30 
##    1021.33    1018.97    1019.11    1019.11    1018.63    1016.80

Si se utiliza la opción fromLast=TRUE, cada valor perdido se sustituye por el inmediato valor no perdido posterior. Al igual que con na.approx() Se puede especificar también un valor maxgap si se desea que secuencias de NA de longitud mayor que dicho valor no sean imputadas.

na.spline(): reemplaza los valores perdidos a partir de un spline cúbico ajustado a los datos:

na.spline(presAtm)

## 2014-06-01 2014-06-02 2014-06-03 2014-06-04 2014-06-05 2014-06-06 2014-06-07 2014-06-08 
##    1018.73    1019.08    1019.44    1018.15    1016.70    1016.53    1018.29    1020.27 
## 2014-06-09 2014-06-10 2014-06-11 2014-06-12 2014-06-13 2014-06-14 2014-06-15 2014-06-16 
##    1020.61    1019.40    1017.65    1016.83    1015.46    1015.22    1016.10    1017.14 
## 2014-06-17 2014-06-18 2014-06-19 2014-06-20 2014-06-21 2014-06-22 2014-06-23 2014-06-24 
##    1017.59    1019.30    1019.64    1019.46    1020.32    1021.46    1022.33    1022.57 
## 2014-06-25 2014-06-26 2014-06-27 2014-06-28 2014-06-29 2014-06-30 
##    1021.33    1018.97    1019.11    1019.33    1018.63    1016.80

Objetos en R: Series temporales

Angelo Santana & Carmen Nieves Hernández,
Departamento de Matemáticas, ULPGC

La clase ts

Ejemplo 1

Ejemplo 2: observaciones con frecuencia mensual

Ejemplo 3: serie temporal multivariante

Funciones que operan sobre series temporales

Combinación de series temporales

start(), end()

window()

time()

deltat() y frequency()

lag()

lag.plot()

Diferenciación

Funciones de autocorrelación

Correlación cruzada

Espectro

Descomposición de una serie temporal

Modelos ARIMA.

Un ejemplo.

Series temporales irregularmente espaciadas: la clase zoo

Ejemplo

La función index()

Combinación de objetos de clase zoo

Imputación de valores perdidos

Más información

Objetos en R: Series temporales

Angelo Santana & Carmen Nieves Hernández, Departamento de Matemáticas, ULPGC

La clase ts

Ejemplo 1

Ejemplo 2: observaciones con frecuencia mensual

Ejemplo 3: serie temporal multivariante

Funciones que operan sobre series temporales

Combinación de series temporales

start(), end()

window()

time()

deltat() y frequency()

lag()

lag.plot()

Diferenciación

Funciones de autocorrelación

Correlación cruzada

Espectro

Descomposición de una serie temporal

Modelos ARIMA.

Un ejemplo.

Series temporales irregularmente espaciadas: la clase zoo

Ejemplo

La función index()

Combinación de objetos de clase zoo

Imputación de valores perdidos

Más información

Angelo Santana & Carmen Nieves Hernández,
Departamento de Matemáticas, ULPGC