Lenguajes de programación.

El lenguaje natural de los ordenadores es el código binario. Cada tipo de microprocesador particular entiende además sólo su particular conjunto de instrucciones, escritas en este código. Esta colección de instrucciones, específica de cada procesador, se denomina lenguaje máquina. Obviamente escribir instrucciones en binario resulta harto difícil, por lo que desde los inicios de la informática se empezaron a utilizar lenguajes ensambladores, que consistían básicamente en conjuntos de etiquetas (palabras simples) que sustituían a las instrucciones binarias. Ambos tipos de lenguaje reciben el nombre de lenguajes de bajo nivel. Estos lenguajes no sólo resultan complejos, sino que al ser específicos de cada tipo de procesador particular, obligan a que distintos procesadores requieran distintos códigos para resolver un mismo problema.

Por ello a partir de los lenguajes ensambladores fueron desarrollándose los lenguajes de alto nivel, que son lenguajes más próximos al lenguaje humano y que añaden una capa de abstracción que evita que el programador deba preocuparse por los detalles técnicos específicos de cada máquina; así, por ejemplo, si deseamos guardar el número 5 en una posición de memoria llamada ‘a’, en un lenguaje de alto nivel bastaría con escribir algo como:

a=5

mientras que en lenguaje ensamblador habría que definir exactamente donde se encuentra la posición de memoria ‘a’ (en binario) y detallar los pasos que debe realizar el procesador para archivar el número 5 en esa posición. Existen numerosos lenguajes de programación de alto nivel (C, Fortran, Java, Python, el propio R, Matlab, …) y el uso de uno u otro depende de su adecuación al contexto o problema para el que se desarrolla el programa.

Puesto que el procesador sólo entiende instrucciones en código máquina, los programas escritos en lenguajes de alto nivel deberán ser traducidos para que el procesador pueda ejecutarlos. Hay dos clases de programas que realizan esta traducción, los compiladores y los intérpretes:

  • Un compilador cbuilding function with rstudioonvierte el programa de alto nivel en código máquina directamente ejecutable por el procesador a través del sistema operativo que gestiona su funcionamiento. Por ello los programas compilados son específicos de sistemas operativos concretos, y un programa compilado para Linux no se ejecuta en Windows, por ejemplo.

  • Un intérprete, en cambio, analiza el código de alto nivel y lo va ejecutando línea por linea, sin convertir el programa globalmente en código máquina. Por ello los programas interpretados pueden ejecutarse en cualquier sistema operativo que disponga del intérprete correspondiente.

Un programa compilado es similar a un libro traducido; aunque el libro original esté escrito en otro idioma, una vez traducido al español cualquier hablante de esta lengua será capaz de leer sin ayuda el libro traducido. En cambio un programa interpretado es equivalente a dejar el libro en su lengua original; cada vez que un hablante español quiera leerlo habrá de contar con los servicios de un intérprete que se lo vaya traduciendo frase a frase.

Los programas compilados tienen la ventaja de que, al estar ya “traducidos”, se ejecutan directamente sobre el procesador en su propio código máquina, por lo que son muy rápidos. Los programas interpretados son más lentos porque deben “traducirse” cada vez que se ejecutan; pero a cambio tienen la ventaja de funcionar en todas las máquinas para las que se disponga de intérprete. En particular, R es un lenguaje interpretado, que puede ejecutarse en Linux, Mac y Windows porque existen intérpretes disponibles en estos sistemas operativos. En cualquier caso, al ser un lenguaje interpretado siempre será más lento que un lenguaje compilado. Si se busca velocidad de cómputo en problemas complejos, R no es el programa adecuado. Sin embargo, si se busca un compromiso entre sencillez de manejo y velocidad de ejecución razonable en el análisis de conjuntos de datos, R puede ser la herramienta perfecta.

En este sentido, debe señalarse que aunque muchas funciones de R están programadas en el propio código R, pero muchas otras están programadas en C o en Fortran, con lo que su ejecución es muy rápida. En muchas ocasiones (posiblemente la mayoría), el usuario de R no necesita conocer las complejidades del programa (en C o en Fortran) que se encuentra detrás del alguna función, y le basta simplemente con que dicha función pueda integrarse cómodamente con el resto de su proceso de datos.

Algoritmos.

Un algoritmo es la secuencia (finita) de instrucciones que deben llevarse a cabo para resolver un problema. Cuando el problema se plantea en términos matemáticos, el algoritmo especifica la sucesión de asignaciones y operaciones que conduce a la solución del problema.

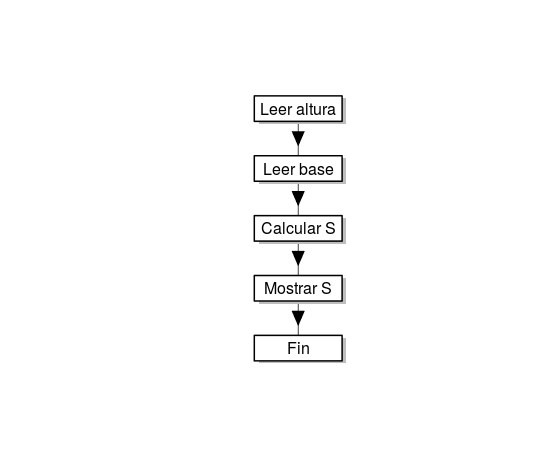
Ejemplo: Un algoritmo para calcular la superficie de un rectángulo dadas las longitudes de su base y altura podría ser el siguiente:

  1. Leer la longitud de la base a.

  2. Leer la longitud de la altura b.

  3. Calcular \(S=a\cdot b\)

  4. Devolver el valor de S

Los algoritmos suelen representarse mediante diagramas de flujo. Un diagrama de flujo es un gráfico que contiene los distintos pasos del algoritmo, utilizando distintos símbolos según el tipo de acción que se realice en cada paso.

diagrama de flujo



Programas.

Un programa es la implementación de un algoritmo en un lenguaje de programación concreto. Como metodología general para desarrollar un programa orientado a resolver un problema, resulta conveniente seguir el siguiente esquema:

  1. Analizar el problema. ¿Es el ordenador la herramienta adecuada para su resolución?

  2. Determinar los posibles métodos de resolución del problema y elegir el más adecuado.

  3. Desarrollar un algoritmo, lo más claro y conciso posible, que concrete los pasos a seguir de acuerdo con el método elegido para resolver el problema. En usuarios que están iniciándose en la programación resulta de gran ayuda utilizar diagramas de flujo, por muy tentador que resulte lanzarse a escribir directamente el programa. Un algoritmo bien pensado y estructurado puede ahorrar mucho trabajo de programación.

  4. Realización del programa.

  5. Probar y depurar el programa, optimizando los recursos que utiliza.

  6. Documentar el programa, insertando lineas de comentario que expliquen qué hace cada fragmento del mismo. En programas complejos resulta conveniente redactar menús de ayuda o manuales de instrucciones. La documentación es útil no sólo para que el programa lo utilicen otras personas, sino incluso para el propio autor; una vez transcurridos unos meses es más que probable que no sea capaz de recordar como funciona el programa o qué hace cada parte del mismo.



Creando el programa

Las siguientes líneas de código, que podemos escribir en un archivo script de R y ejecutar seguidamente, calcula la superficie de un rectángulo de base 3 y altura 4:

b=3
h=4
S=b*h
S
## [1] 12

En las dos primeras lineas hemos asignado el valor 3 a la base y el valor 4 a la altura del rectángulo; a continuación hemos calculado la superficie \(S\) como el producto de la base por la altura, y por último hemos mostrado el valor de \(S\) en la consola, en este caso es 12. El término “[1]” que aparece antes del valor de \(S\) indica simplemente que la salida ocupa sólo una línea. Esta sucesión de instrucciones ejecutadas en la consola no es propiamente un programa, ya que el valor de \(S\) no se recalcula al cambiar los valores de la base y la altura; en efecto, podemos comprobarlo ejecutando ahora:

b=5
h=4
S
## [1] 12

Como vemos, el valor de \(S\) no se ha actualizado, sino que continúa siendo el de la asignación original 12. Resulta sencillo transformar las lineas anteriores en un verdadero programa. Para ello utilizamos la siguiente sintaxis

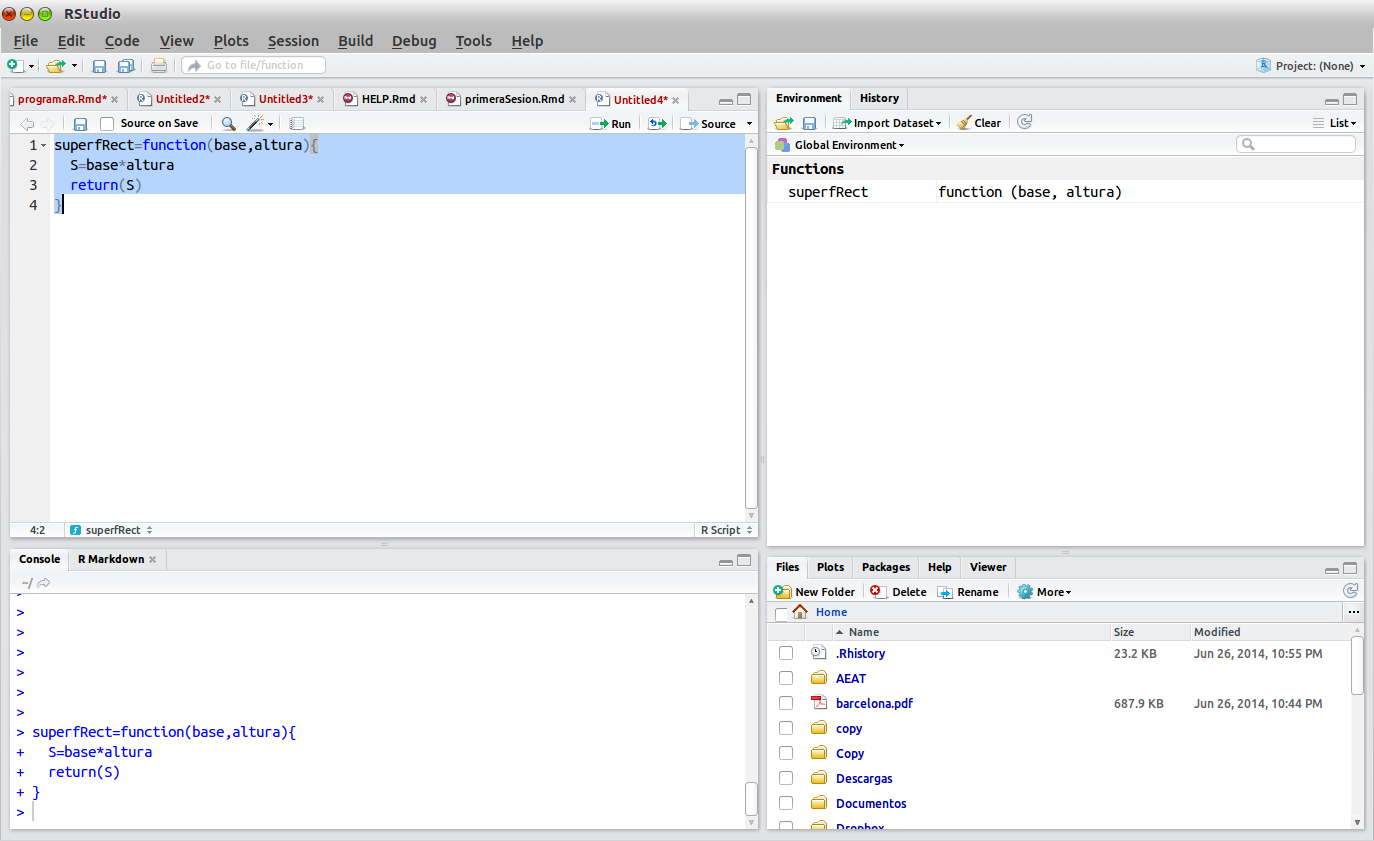
superfRect=function(base,altura){
                      S=base*altura
                      return(S)
                     }

En estas líneas hemos definido una función, superfRect(), que recibe como argumentos los valores de la base y la altura del rectángulo, y devuelve como resultado el valor de su superficie.

Para que R sea capaz de ejecutar esta función, primero debemos hacer que el intérprete de R la lea y compruebe que la sintaxis es correcta. Para ello, utilizando el ratón, marcamos las líneas anteriores y pinchamos en el icono iconoRun, en la parte superior de la ventana de edición en Rstudio. Si no hemos cometido errores de sintaxis, nuestra función se debe reproducir en la consola (ventana inferior izquierda). En la ventana superior derecha aparece el nombre de la función en el espacio de memoria actual, tal como se ve en la figura siguiente:

Memoria Función



Ahora ya estamos en condiciones de ejecutar nuestra función con algunos valores concretos. Para ello debemos invocarla mediante su nombre, añadiendo entre paréntesis los valores de sus argumentos (en este caso, base y altura) tal como se han especificado en la definición de la función. Podemos probar a ejecutarla varias veces y comprobar como, cada vez que cambiemos los valores de la base y la altura, obtenemos la superficie correcta:

superfRect(2,3)
## [1] 6
superfRect(5,6)
## [1] 30

De manera equivalente podemos llamar a la función especificando también los nombres de sus argumentos (que, lógicamente, deben coincidir con los nombres especificados en la definición de la función). Cuando se especifican los nombres de los argumentos, éstos pueden colocarse en cualquier orden, no necesariamente el que se utilizó en la definición de la función):

superfRect(base=3,altura=8)
## [1] 24
superfRect(altura=5,base=6)
## [1] 30

Así pues, nuestro programa para el cálculo de la superficie de un rectángulo se reduce simplemente a la función que acabamos de definir. Podemos guardar este programa para volver a utilizarlo más adelante, indicando a continuación el nombre del archivo donde queremos guardar el programa. Resulta recomendable que los archivos que contienen código R tengan la extensión .R, de tal forma que podamos identificarlos fácilmente en los directorios de nuestro ordenador. Antes de guardar el programa coloquemos lineas de comentario que nos aclaren lo que hace la función:

superfRect=function(base,altura){ 
  # Esta función calcula la superficie de un rectangulo dadas su base y altura
                      S=base*altura
                      return(S)
                     }



Estructura básica de una función en R.

A modo de resumen de lo que hemos visto en la sección anterior, podemos sintetizar la estructura de una función en R en el siguiente cuadro:

Nombre_función = function(argumentos){

        Cuerpo de la función

        return(salida)

  }

Observamos aquí la presencia de dos palabras reservadas (palabras propias del lenguaje R), function y return. Como vemos, para definir una función, primero ha de especificarse su nombre seguido del signo “=” (puede utilizarse también el símbolo “<–”), la palabra function, y a continuación entre paréntesis los argumentos que recibe la función; el cuerpo de la función (secuencia de instrucciones que debe realizar) se escribe seguidamente entre llaves {}, y normalmente termina con el comando return() que incluye entre paréntesis el objeto que debe devolver como salida la función una vez ejecutada.



Un programa con entrada/salida más elaborada.

En ocasiones es necesario escribir programas que soliciten explícitamente al usuario la introducción de algunos valores. Supongamos, por ejemplo, que en nuestro programa para el cálculo de la superficie del rectángulo no queremos llamar a la función con unos valores concretos de base y altura, sino que nos interesa que sea la propia función la que los pida al usuario. Podemos conseguir este objetivo definiendo la función de la forma siguiente:

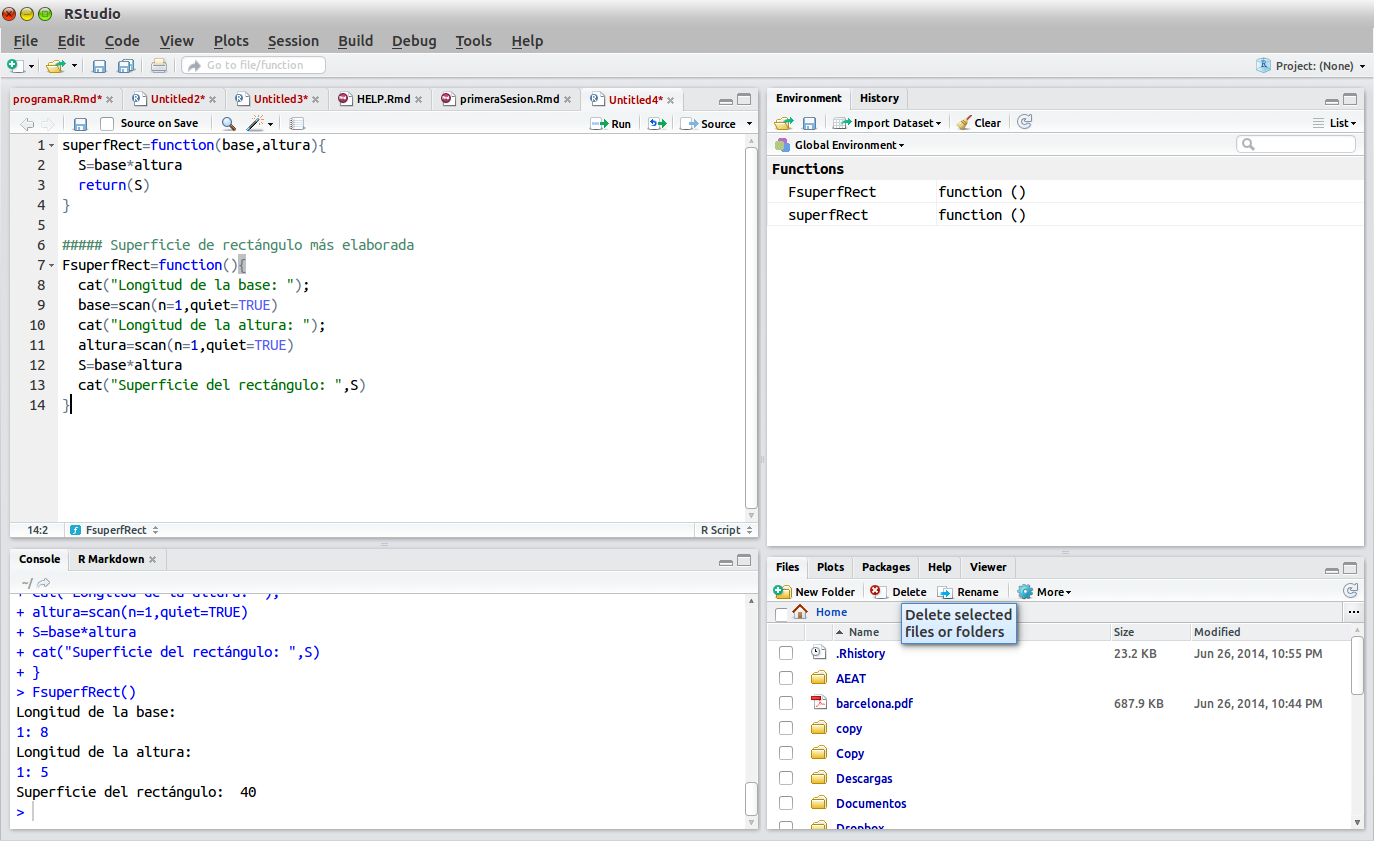
FsuperfRect=function(){
  cat("Longitud de la base: ");   
    base=scan(n=1,quiet=TRUE) 
    cat("Longitud de la altura: "); 
    altura=scan(n=1,quiet=TRUE) 
    S=base*altura 
    cat("Superficie del rectángulo: ",S) 
  }

Observemos que ahora la función no recibe argumentos, por lo que los paréntesis tras la palabra function deben quedar en blanco, (). A continuación hemos utilizado dos nuevos comandos:

  • El comando cat() que, de manera muy simple, nos permite presentar texto en la consola.

  • El comando scan(), que permite leer valores desde el teclado y asignarlos, respectivamente, a las variables base y altura; con este comando hemos utilizado además las opciones n=1, que indica que se va a leer un único valor, y quiet=TRUE que indica a scan que, una vez leído ese valor, no informe por pantalla de cuántos valores ha leído (ese sería su comportamiento por defecto y no nos interesa en este caso).

Nuevamente, tras introducir esta función en la ventana de edición marcarla con el ratón, y pinchar en el icono , si no hay errores de sintaxis la función se reproduce en la consola. Para ejecutarla, la invocamos en la consola mediante:

FsuperfRect()

Si queremos calcular la superficie de un rectángulo de base 8 y altura 5, introduciríamos dichos valores a medida que el programa los solicite, obteniendo finalmente el resultado.

Memoria Función



Ejecución condicional de comandos: if - else

El comando if permite la ejecución de un comando condicionado al valor de una variable. Así, por ejemplo, la siguiente función permite determinar el menor de dos números:

menor=function(a,b){
  if (a<b) menor=a else menor=b
    return(menor)
}

En esta función la condición es muy sencilla, por lo que la instrucción condicional if ocupa una sola línea. En general, la sintaxis del comando if es la siguiente:

if (condición){
  expresión
  }
  else {
    expresión alternativa
    }

El comando else puede omitirse si no se realiza ninguna acción alternativa; asimismo pueden encadenarse varios comandos else if, como en el siguiente ejemplo:

dimVector=function(x){
  if (length(x)==1) print("El vector es de dimensión 1")
    else if (length(x)==2) print("El vector es de dimensión 2")
    else print("El vector es de dimensión mayor que 2") 
}

obsérvese en este código que:

  • length(x) nos devuelve la dimensión del vector.

  • La comparación se realiza con el doble signo ==

  • else if se escribe separado.

Cuando hay un encadenamiento de alternativas else if puede resultar más conveniente utilizar la función switch (ver ?switch).



Bucles.

En R hay varios comandos que permiten implementar bucles: for, while y repeat. En esencia, un bucle es una secuencia de comandos que se repite hasta que se cumple determinada condición.


For.

El bucle más sencillo es el bucle for. Así, por ejemplo, para calcular la suma de los cuadrados de los números enteros de 1 a n podríamos utilizar la siguiente función:

sumaCuadrados=function(n){
          suma=0
            for (i in 1:n){
            suma=suma+i^2
    }
    return(suma)
}

En general, la sintaxis de un bucle for es la siguiente:

for (variable in secuencia){
              expresión
            }



While.

Otra forma de realizar la misma tarea es mediante la utilización de un bucle while: mientras se cumpla la condición que se especifica, se va repitiendo le ejecución del contenido del bucle:

otraSumaCuadrados=function(n){
  suma=0
    i=1
    while (i<=n){
        suma=suma+i^2
        i=i+1
    }
    return(suma)
}

La sintaxis del bucle while es de la forma:

while (condición){
              expresión
            }



Repeat

Por último, R también dispone del comando repeat que repite una expresión indefinidamente hasta que encuentra el comando break. Así, nuestro ejemplo de la suma de cuadrados podría implementarse también del siguiente modo:

otraSumaCuadradosMas=function(n){
  suma=0
    i=0
    repeat {
        i=i+1
        suma=suma+i^2
        if (i==n) break
    }       
    return(suma)
}

La sintaxis de un bucle repeat es, pues, de la forma:

repeat {
    expresión
    if (condición) break
    }

Dependiendo del problema a resolver será más sencilla la implementación de uno u otro tipo de bucle.

En cualquiera de los bucles anteriores es posible introducir el comando next, que produce un salto inmediato a la siguiente iteración. Asimismo, en los bucles for y while es posible utilizar break para producir la salida inmediata del bucle.




Vectorización de los cálculos.

Al ser un programa interpretado, la ejecución de bucles en R suele ser muy lenta. Por ello conviene evitar los bucles tanto como sea posible.

Una manera muy simple de evitar bucles es aprovechar la aritmética vectorial de R. La aritmética vectorial significa que las operaciones básicas y las funciones elementales están preparadas para operar directamente sobre vectores, y devolver su resultado también en forma vectorial. Por ejemplo, si:

x=1:10

podríamos calcular un vector y cuyos elementos sean los cuadrados de los elementos de x utilizando un bucle for:

y=integer(10) # Definimos 'y' como un vector de enteros de longitud 10, inicialmente vacío 
              # y que nos servirá para acumular los cuadrados de x
for (i in 1:10) y[i]=x[i]^2
y
##  [1]   1   4   9  16  25  36  49  64  81 100

pero si aprovechamos la aritmética vectorial de R, es mucho más eficiente definir directamente:

y=x^2
y
##  [1]   1   4   9  16  25  36  49  64  81 100

ya que la operación x^2 funciona de manera vectorial. En ambos casos hemos obtenido, obviamente, el mismo resultado. Podemos comprobar cuánto tiempo emplea R en calcular el vector y de ambas formas; para ello utilizamos la función system.time() que computa el tiempo que tarda en ejecutarse una instrucción o conjunto de instrucciones. Para apreciar mejor la diferencia, definimos x como un vector que contiene los valores de 1 a un millón:

n=1000000
x=1:n
tiempo1=system.time({y=integer(n)
             for (i in 1:n) y[i]=x[i]^2
             })
tiempo1
##    user  system elapsed 
##   0.073   0.004   0.076
tiempo2=system.time({y=x^2})
tiempo2
##    user  system elapsed 
##   0.000   0.004   0.004

Como vemos, el segundo método es ¡¡¡nada menos que 19 veces más rápido que el primero!!!. La función más eficiente para calcular la suma de cuadrados de los números de 1 a n es, pues:

sumaCuadradosDefinitiva=function(n){
  sum((1:n)^2)
}




La familia de funciones apply

Las funciones apply(), sapply(), lapply() y tapply() resultan extremadamente útiles también para evitar bucles. Su objetivo fundamental es aplicar (de ahí el nombre) una función a todos los elementos de un objeto. En realidad son funciones que de alguna manera ejecutan un bucle, pero este bucle se ejecuta en código compilado lo que hace que sea más rápido que utilizar los comandos for, repeat o ```while````que siempre deben ser interpretados. No siempre será posible sustituir un bucle por una función de la familia apply, pero cuando lo sea, su utilización es muy ventajosa.

Concretamente:

  • apply(M,i,fun): si i vale 1, aplica la función fun a todas las filas de la matriz M; si i vale 2, la aplica a las columnas.

Por ejemplo, supongamos que queremos calcular la suma de los cuadrados de cada fila y de cada columna de una matriz de términos aleatorios:

A = matrix(runif(50),nrow=10) # Matriz de dimensión 10x10 cuyos elementos son valores
                               # aleatorios con distribución uniforme en (0,1)
A
##            [,1]      [,2]      [,3]     [,4]      [,5]
##  [1,] 0.9558914 0.9802538 0.3069206 0.369409 0.8513814
##  [2,] 0.4412640 0.3204837 0.3023765 0.491005 0.6534177
##  [3,] 0.9908249 0.5219432 0.2546336 0.238091 0.6300302
##  [4,] 0.1024441 0.4941257 0.6350941 0.679205 0.6901290
##  [5,] 0.1910438 0.9137953 0.9564185 0.149533 0.0694580
##  [6,] 0.0148326 0.9900607 0.0132147 0.433943 0.6632850
##  [7,] 0.2090850 0.8120726 0.0462860 0.671916 0.3862261
##  [8,] 0.8620731 0.2057444 0.2149388 0.316434 0.9266473
##  [9,] 0.5610298 0.0134554 0.8438138 0.435034 0.0656376
## [10,] 0.6941297 0.4770955 0.3835432 0.738051 0.8306575
sumCuadrados=function(x){sum(x^2)}  # Función que calcula la suma de cuadrados de 
                                    # los términos de un vector x
apply(A,1,sumCuadrados)  # Devuelve la suma de cuadrados de cada fila de A
##  [1] 2.83014 1.05690 1.77262 1.59560 1.81344 1.60887 1.30596 1.79051
##  [9] 1.22052 2.09125
apply(A,2,sumCuadrados)  # Devuelve la suma de cuadrados de cada columna de A
## [1] 3.72085 4.32503 2.47619 2.39180 4.17194




  • lapply(L,fun): aplica la función fun a todos los elementos de la lista L. El resultado se devuelve también en una lista.

Por ejemplo, supongamos que tenemos una lista con las edades de los alumnos de 5 aulas (el número de alumnos en cada aula es distinto):

edades=list(aula1=c(12,11,14,11,12,11,12,11,14,12,13,12,11),
            aula2=c(11,12,12,11,13,13,13,14,12,12,11),
            aula3=c(10,9,9,9,9,8,8,7,7,9,9,10,10,9,8,7,8,8),
            aula4=c(14,16,14,14,15,14,14,16),
            aula5=c(17,17,18,17,16,16,16))

Queremos determinar el número de alumnos en cada aula, así como la media de edad. Usando lapply():

lapply(edades,length) # Número de alumnos en cada aula
## $aula1
## [1] 13
## 
## $aula2
## [1] 11
## 
## $aula3
## [1] 18
## 
## $aula4
## [1] 8
## 
## $aula5
## [1] 7
lapply(edades,mean)   # Valor medio de edad en cada aula
## $aula1
## [1] 12
## 
## $aula2
## [1] 12.1818
## 
## $aula3
## [1] 8.55556
## 
## $aula4
## [1] 14.625
## 
## $aula5
## [1] 16.7143




  • sapply(L,fun): al igual que lapply(), aplica la función fun a todos los elementos de la lista L, pero devuelve el resultado en forma de vector o matriz:
sapply(edades,length) # Número de alumnos en cada aula
## aula1 aula2 aula3 aula4 aula5 
##    13    11    18     8     7
sapply(edades,mean)   # Valor medio de edad en cada aula
##    aula1    aula2    aula3    aula4    aula5 
## 12.00000 12.18182  8.55556 14.62500 16.71429




  • tapply(variable,factor,fun): aplica la función fun a cada uno de los grupos de datos de variable definidos por los niveles de factor.

Por ejemplo, tenemos las edades de un grupo de chicos y chicas:

grupo=data.frame(edad=c(12,13,12,11,13,14,15,11),sexo=c("H","M","H","H","M","H","M","H"))

Podemos calcular la edad media para cada sexo mediante:

tapply(grupo$edad,grupo$sexo,mean)
##       H       M 
## 12.0000 13.6667




ifelse

ifelse() es una versión vectorial de los condicionales if - else. Su sintaxis es:

  • ifelse(condicion, valor_si_TRUE, valor_si_FALSE)

Por ejemplo, supongamos que a partir de la matriz A que vimos más arriba:

A
##            [,1]      [,2]      [,3]     [,4]      [,5]
##  [1,] 0.9558914 0.9802538 0.3069206 0.369409 0.8513814
##  [2,] 0.4412640 0.3204837 0.3023765 0.491005 0.6534177
##  [3,] 0.9908249 0.5219432 0.2546336 0.238091 0.6300302
##  [4,] 0.1024441 0.4941257 0.6350941 0.679205 0.6901290
##  [5,] 0.1910438 0.9137953 0.9564185 0.149533 0.0694580
##  [6,] 0.0148326 0.9900607 0.0132147 0.433943 0.6632850
##  [7,] 0.2090850 0.8120726 0.0462860 0.671916 0.3862261
##  [8,] 0.8620731 0.2057444 0.2149388 0.316434 0.9266473
##  [9,] 0.5610298 0.0134554 0.8438138 0.435034 0.0656376
## [10,] 0.6941297 0.4770955 0.3835432 0.738051 0.8306575

queremos construir una matriz B que tenga un 0 en aquellas posiciones en que el valor correspondiente de A sea menor que 0.5 y un 1 en caso contrario. Podríamos conseguirlo mediante:

B=ifelse(A<0.5,0,1)
B
##       [,1] [,2] [,3] [,4] [,5]
##  [1,]    1    1    0    0    1
##  [2,]    0    0    0    0    1
##  [3,]    1    1    0    0    1
##  [4,]    0    0    1    1    1
##  [5,]    0    1    1    0    0
##  [6,]    0    1    0    0    1
##  [7,]    0    1    0    1    0
##  [8,]    1    0    0    0    1
##  [9,]    1    0    1    0    0
## [10,]    1    0    0    1    1








© 2016 Angelo Santana, Carmen N. Hernández, Departamento de Matemáticas   ULPGC