El modelo de regresión lineal
Angelo Santana & Carmen Nieves Hernández,
Departamento de Matemáticas, ULPGC
Definición
Un vector de variables aleatorias \(\mathbf{Y}= \left(y_1,y_2,\dots, y_n\right)\) sigue un modelo de regresión lineal si:
\[\mathbf{Y} \cong \mathbf{N_n} \left(\mathbf{X} \beta, \mathbf{I_n} \right)\]
donde:
\(\mathbf{X}\) es una matriz de dimensión \(n\times p\).
\(\beta\) es un vector de parámetros \(p\)-dimensional.
\(\mathbf{I_{n}}\) es la matriz identidad de orden \(n\).
En este documento mostraremos como es posible utilizar R para estimar el modelo de regresión (coeficientes, matrices de covarianzas, errores estándar, coeficiente de determinación, etc.) utilizando álgebra matricial y aplicando directamente las expresiones algebraicas que pueden deducirse de la estimación por mínimos cuadrados. Veremos además que dicha estimación puede realizarse directamente mediante el uso de la función lm().
Ejemplos
Utilizaremos los siguientes archivos de datos para ilustrar los modelos de regresión con R:
Veamos el contenido de estos ficheros:
Ejemplo 1 (Regresión simple)
A continuación se muestra un conjunto de datos correspondientes a un estudio experimental cuyo objetivo fue evaluar el efecto que tiene la velocidad de mezclado (\(x\)) sobre el porcentaje de impurezas (\(y\)) en una pintura producida mediante un proceso químico.
ejemplo1## velocidad impurezas
## 1 20 8.4
## 2 22 9.5
## 3 24 11.8
## 4 26 10.4
## 5 28 13.3
## 6 30 14.8
## 7 32 13.2
## 8 34 14.7
## 9 36 16.4
## 10 38 16.5
## 11 40 18.9
## 12 42 18.5plot(ejemplo1)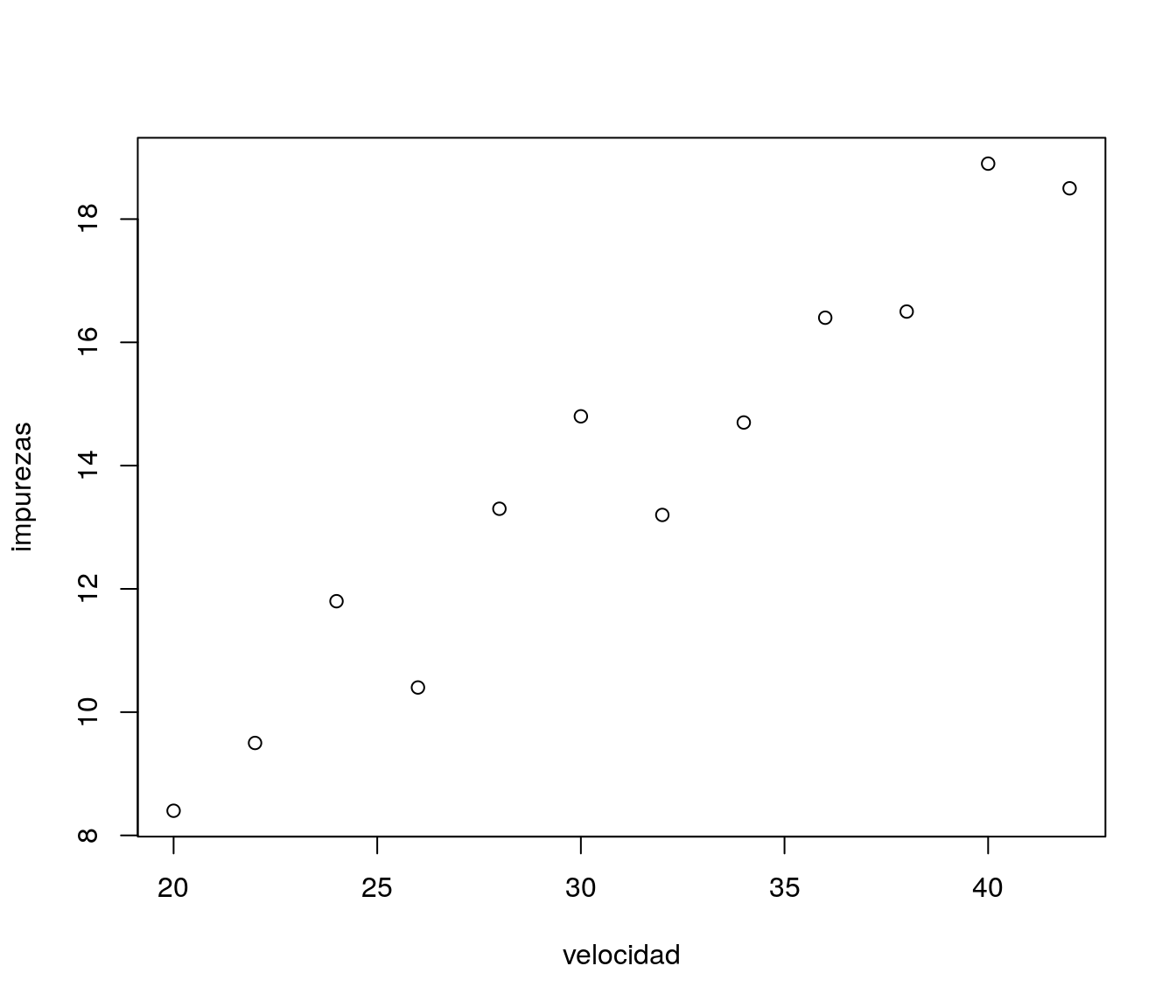
Ejemplo 2 (Regresión múltiple)
En este caso se estudia la eficiencia térmica de un reactor químico (en %) como función de la tasa de flujo en lb/h de dos gases (fluidizante y flotante), apertura de la boquilla (en mm) y temperatura de entrada del gas flotante (en ºF). Mostramos a continuación los 10 primeros casos del archivo:
head(ejemplo7,10)## eficienciaTermica tasaFlujoGas1 tasaFlujoGas2 aperturaBoq tempGas
## 1 47.83 124.17 134.07 23.32 210.11
## 2 59.51 149.46 142.21 41.82 229.67
## 3 50.38 131.65 146.62 21.14 231.10
## 4 53.24 139.49 136.16 45.79 206.03
## 5 47.26 113.03 125.41 41.51 222.67
## 6 50.52 134.57 165.84 32.42 219.59
## 7 50.78 140.92 128.17 27.95 223.25
## 8 54.59 172.06 139.52 34.27 211.76
## 9 59.80 151.36 152.54 57.09 235.86
## 10 48.90 136.56 91.19 34.42 216.78plot(ejemplo7)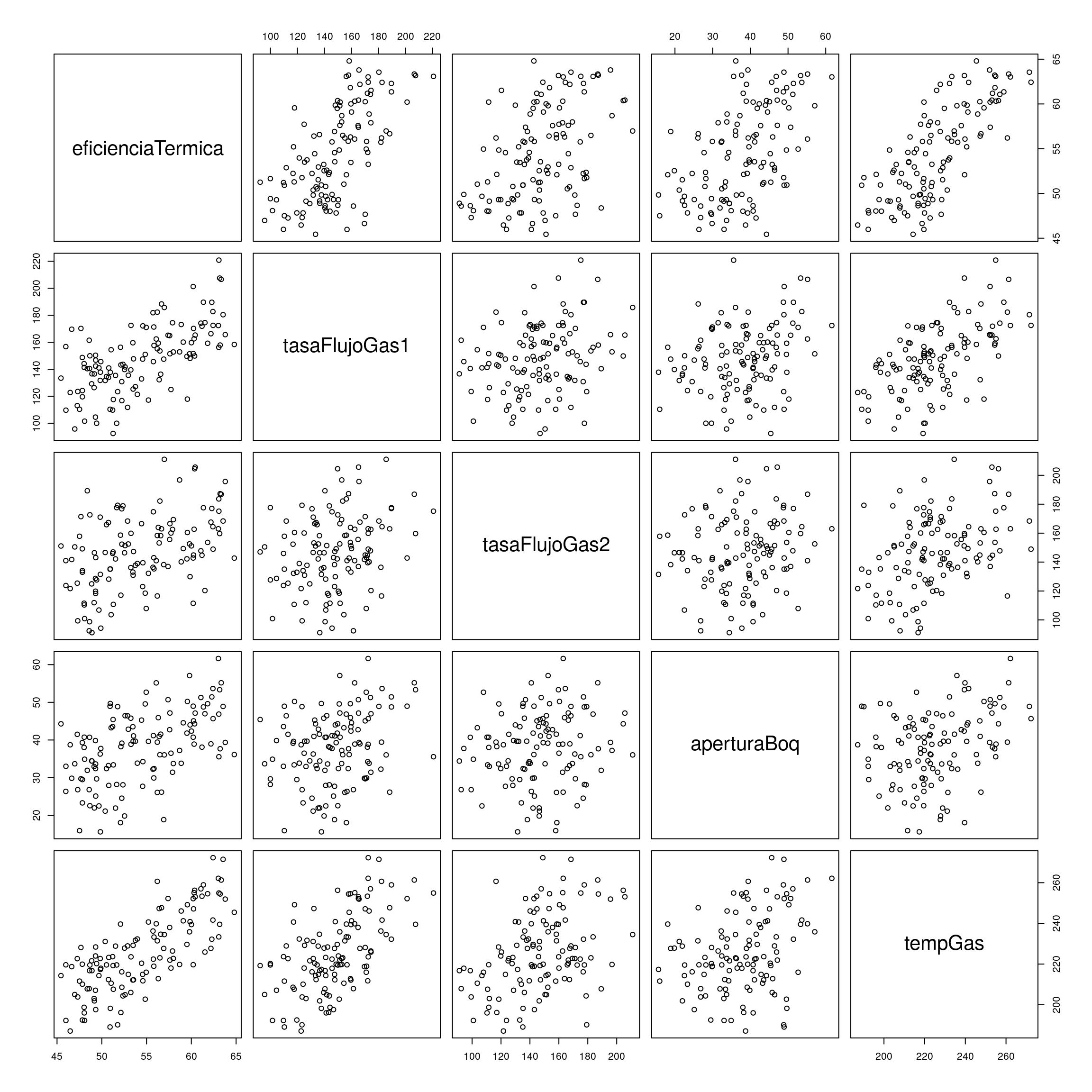
Modelo de regresión simple: ejemplo 1
Estimación:
Construimos las matrices X e Y:
Y= ejemplo1$impurezas
X= cbind(1,ejemplo1$velocidad)
Y## [1] 8.4 9.5 11.8 10.4 13.3 14.8 13.2 14.7 16.4 16.5 18.9 18.5X## [,1] [,2]
## [1,] 1 20
## [2,] 1 22
## [3,] 1 24
## [4,] 1 26
## [5,] 1 28
## [6,] 1 30
## [7,] 1 32
## [8,] 1 34
## [9,] 1 36
## [10,] 1 38
## [11,] 1 40
## [12,] 1 42Calculamos el estimador de \(\beta\) utilizando directamente el cálculo matricial:
\[ \hat{\beta} = \left(X^{t}X\right)^{-1}X^{t}Y\]
(la inversa de una matriz A en R se calcula mediante solve(A), la traspuesta mediante t(A), y el producto de dos matrices mediante el operador %*%)
solve(t(X)%*%X)%*%t(X)%*%Y## [,1]
## [1,] -0.28928
## [2,] 0.45664En R la función lm() permite obtener directamente de manera muy simple el estimador de \(\beta\). Podemos comprobar que se obtiene el mismo resultado:
lm(impurezas~velocidad,data=ejemplo1)##
## Call:
## lm(formula = impurezas ~ velocidad, data = ejemplo1)
##
## Coefficients:
## (Intercept) velocidad
## -0.289 0.457Podemos dibujar la recta de regresión mediante el comando abline():
recta=lm(impurezas~velocidad,data=ejemplo1)
plot(ejemplo1)
abline(recta,col="red",lwd=2)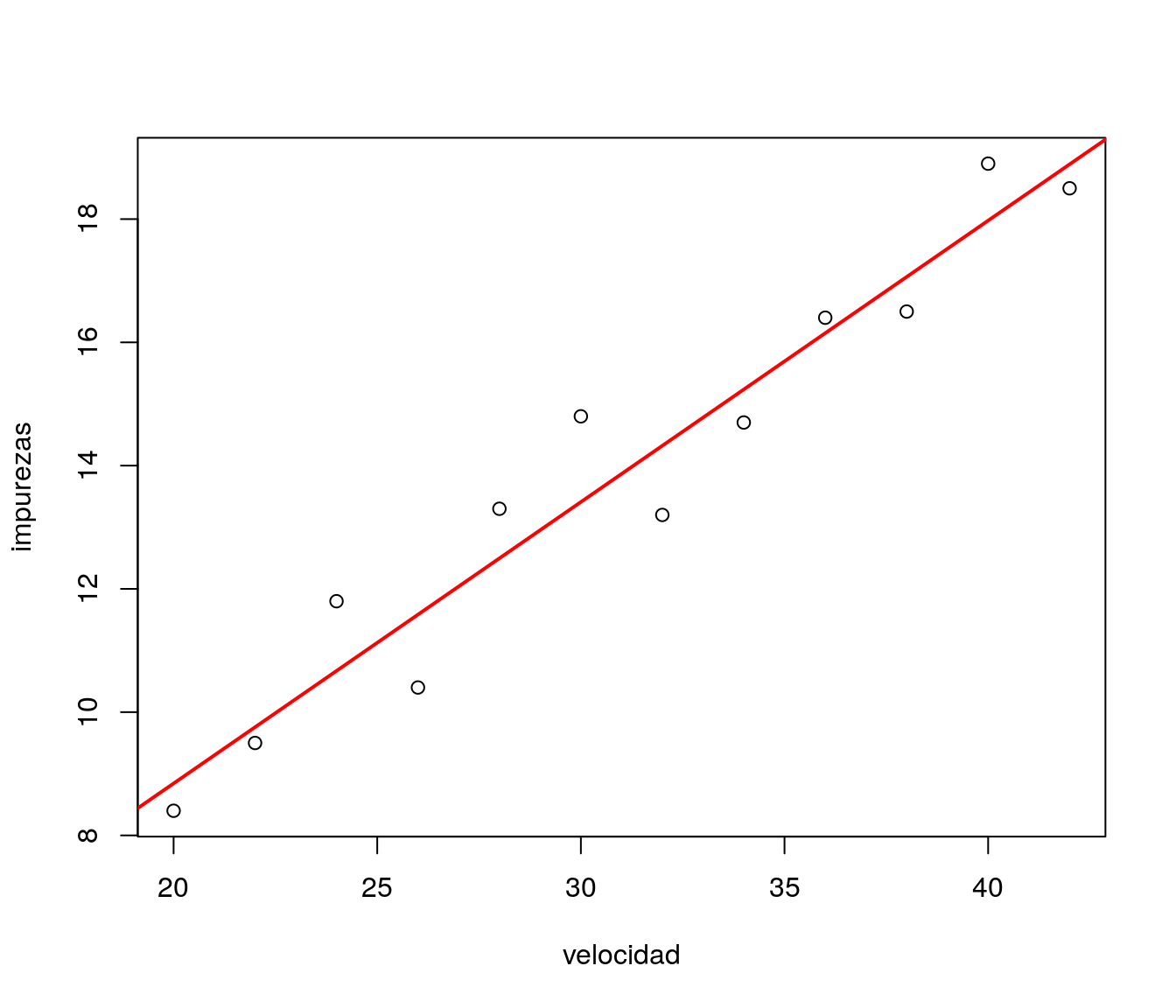
Varianza residual.
La varianza residual se estima del modo que se muestra a continuación, donde el término \(X_i\) se refiere a la fila \(i\)-ésima de la matriz \(\mathbf{X}\):
\[\hat{\sigma}^{2}=\frac{1}{n-p}\sum_{i=1}^{n}\left(y_{i}-\hat{y_{i}}\right)^{2}=\frac{1}{n-p}\sum_{i=1}^{n}\left(y_{i}-X_{i}\hat{\beta}\right)^{2}=\frac{1}{n-p}\left(\mathbf{Y-X}\hat{\beta}\right)^{t}\left(\mathbf{Y-X}\hat{\beta}\right)\]
En esta ecuación el valor de \(p\) corresponde al número de parámetros del modelo. En el caso de la regresión lineal simple se tiene que \(p=2\) (hay dos parámetros, \(\beta_0\) y \(\beta_1\)).
Determinamos en primer lugar los valores de \(n\), \(p\) y \(b=\hat{\beta}\):
b=solve(t(X)%*%X)%*%t(X)%*%Y
n=length(Y)
p=length(b)R nos permite ahora hacer el cálculo de \(\hat{\sigma}^2\) de las dos formas:
- Mediante cálculo matricial:
(S2=t(Y-X%*%b)%*%(Y-X%*%b)/(n-p))## [,1]
## [1,] 0.84514- Mediante la suma de las diferencias al cuadrado entre observaciones y predicciones:
(S2=sum((Y-X%*%b)^2)/(n-p))## [1] 0.84514Obviamente obtenemos el mismo valor.
Error estándar residual.
Es la desviación típica residual (raíz cuadrada de la varianza residual): \(\hat{\sigma}=\sqrt{\hat{\sigma}^2}\)
(Se=sqrt(S2))## [1] 0.91932Matriz de covarianzas de los estimadores de los parámetros.
Esta matriz es de la forma:
\[\textrm{Var}\left(\hat{\beta}\right)=\hat{\sigma}^{2}\left(X^{t}X\right)^{-1}\]
y puede calcularse mediante:
(V_b=S2*solve(t(X)%*%X))## [,1] [,2]
## [1,] 1.490326 -0.0458032
## [2,] -0.045803 0.0014775Error estándar de los estimadores de los parámetros.
Es la raiz cuadrada de la diagonal de la matriz anterior:
sqrt(diag(V_b))## [1] 1.220789 0.038439Bondad de Ajuste: coeficiente \(R^2\)
En un modelo de regresión, la variabilidad total (VT) presente en la variable Y puede descomponerse en la variabilidad explicada (VE) por el modelo de regresión y la variabilidad no explicada o residual (VR):
\[\underset{(VT)}{\sum_{i=1}^{n}\left(y_{i}-\overline{y}\right)^{2}}=\underset{\left(VE\right)}{\sum_{i=1}^{n}\left(\hat{y}_{i}-\overline{y}\right)^{2}}+\underset{\left(VR\right)}{\sum_{i=1}^{n}\left(y_{i}-\hat{y}_{i}\right)^{2}}\]
siendo los \(\hat{y}_{i}\) los valores predichos por el modelo. Matricialmente:
\[\sum_{i=1}^{n}\left(y_{i}-\overline{y}\right)^{2}= ||\mathbf{Y-1}\overline{Y}||^{2}\]
\[\sum_{i=1}^{n}\left(\hat{y}_{i}-\overline{y}\right)^{2}= ||\mathbf{X}\hat{\beta}-\mathbf{1}\overline{Y}||^{2} \]
\[\sum_{i=1}^{n}\left(y_{i}-\hat{y}_{i}\right)^{2}= ||\mathbf{Y-}\mathbf{X}\hat{\beta}||^{2} \]
Estos términos pueden calcularse sin dificultad con R.
Variabilidad total:
\[||\mathbf{Y-1}\overline{Y}||^{2}=\left(\mathbf{Y-1}{\overline{Y}}\right)^{t}\left(\mathbf{Y-1}\overline{Y}\right)\]
(VT=t(Y-mean(Y))%*%(Y-mean(Y)))## [,1]
## [1,] 127.73Variabilidad explicada por (o atribuible a) el modelo:
\[||\mathbf{X}\hat{\beta}-\mathbf{1}\overline{Y}||^{2}=\left(\mathbf{X}\hat{\beta}-\mathbf{1}\overline{Y}\right)^{t}\left(\mathbf{X}\hat{\beta}-\mathbf{1}\overline{Y}\right)\]
(VE=t(X%*%b-mean(Y))%*%(X%*%b-mean(Y)))## [,1]
## [1,] 119.28Variabilidad residual:
\[||\mathbf{Y-}\mathbf{X}\hat{\beta}||^{2}=\left(\mathbf{Y-}\mathbf{X}\hat{\beta}\right)^{t}\left(\mathbf{Y-}\mathbf{X}\hat{\beta}\right)\]
(VR=t(Y-X%*%b)%*%(Y-X%*%b))## [,1]
## [1,] 8.4514Coeficiente de determinación:
El coeficiente de determinación se define como la proporción de la variabilidad total que es explicada por el modelo de regresión:
\[R^2=\frac{VE}{VT}\]
Puede obtenerse fácilmente a partir de las expresiones calculadas anteriormente:
(R2=VE/VT)## [,1]
## [1,] 0.93383Coeficiente de determinación corregido (o ajustado)
El coeficiente de determinación \(R^2\) puede expresarse como: \[R^{2}=\frac{VE}{VT}=1-\frac{VR}{VT}\] El coeficiente de determinación corregido se define de manera similar mediante: \[\tilde{R}^{2}=1-\frac{VR/\left(n-p\right)}{VT/\left(n-1\right)}=1-\frac{n-1}{n-p}\frac{VR}{VT}=1-\frac{n-1}{n-p}\left(1-R^{2}\right)=\frac{n-1}{n-p}\left(R^{2}-\frac{p-1}{n-p}\right)\]
(R2.corregido=1-(1-R2)*(n-1)/(n-p))## [,1]
## [1,] 0.92722Contraste de la regresión
Es el contraste de hipótesis de la forma:
\[H_0:\beta_1=0\]
que de forma matricial puede expresarse como:
\[H_0:\left(\begin{array}{cc} 0 & 1\end{array}\right)\left(\begin{array}{c} \beta_{0}\\ \beta_{1} \end{array}\right)=0\]
Este es un contraste lineal de la forma:
\[H_0:\mathbf{A\beta}=0\]
Cuando \(H_0\) es cierta el test estadístico:
\[F=\frac{1}{q\hat{\sigma}^{2}}\hat{\beta}^{t}\mathbf{A}^{t}\left(\mathbf{A}\left(\mathbf{X}^{t}\mathbf{X}\right)^{-1}\mathbf{A}^{t}\right)^{-1}\mathbf{A\hat{\beta}}\]
(siendo \(q\) el número de filas de la matriz \(\mathbf{A}\)) sigue una distribución \(F\) de Fisher-Snedecor con \(q\) y \(n-p\) grados de libertad. El p-valor del contraste es
\[p-valor=P\left(F_{q,n-q}>F_{obs}\right)=1-P\left(F_{q,n-q} \le F_{obs}\right)\]
siendo \(F_{obs}\) el valor observado del test estadístico \(F\).
A=matrix(c(0,1),byrow=TRUE,nrow=1)
q=nrow(A)
F.obs=(1/(q*S2))*t(b)%*%t(A)%*%solve(A%*%solve(t(X)%*%X)%*%t(A))%*%A%*%b
F.obs## [,1]
## [1,] 141.13p.valor=1-pf(F.obs,q,n-p)
p.valor## [,1]
## [1,] 3.2112e-07Nota: el valor del test estadístico \(F_{obs}\) para el contraste de la regresión puede obtenerse también como:
\[F_{obs}=\frac{VE/(p-1)}{VR/(n-p)}\]
En efecto:
(VE/(p-1))/(VR/(n-p))## [,1]
## [1,] 141.13Estimación del modelo de regresión con R
R nos permite obtener todos los resultados anteriores de una manera más sencilla aplicando la función summary() al ajuste conseguido mediante lm():
summary(recta)##
## Call:
## lm(formula = impurezas ~ velocidad, data = ejemplo1)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.183 -0.543 -0.323 0.833 1.390
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.2893 1.2208 -0.24 0.82
## velocidad 0.4566 0.0384 11.88 3.2e-07 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.919 on 10 degrees of freedom
## Multiple R-squared: 0.934, Adjusted R-squared: 0.927
## F-statistic: 141 on 1 and 10 DF, p-value: 3.21e-07La función anova() presenta el análisis de la varianza con la descomposición de la variabilidad total en sus fuentes de variación:
anova(recta)## Analysis of Variance Table
##
## Response: impurezas
## Df Sum Sq Mean Sq F value Pr(>F)
## velocidad 1 119.3 119.3 141 3.2e-07 ***
## Residuals 10 8.5 0.8
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Asimismo, la función confint() permite obtener de manera muy simple intervalos de confianza para los parámetros de la regresión:
confint(recta)## 2.5 % 97.5 %
## (Intercept) -3.0094 2.43081
## velocidad 0.3710 0.54229Regresión múltiple con R.
Estimación:
Construimos las matrices X e Y a partir de los datos del dataframe ejemplo7
Y= ejemplo7[,1]
X= as.matrix(cbind(b0=1,ejemplo7[,2:5]))
head(Y)## [1] 47.83 59.51 50.38 53.24 47.26 50.52head(X)## b0 tasaFlujoGas1 tasaFlujoGas2 aperturaBoq tempGas
## [1,] 1 124.17 134.07 23.32 210.11
## [2,] 1 149.46 142.21 41.82 229.67
## [3,] 1 131.65 146.62 21.14 231.10
## [4,] 1 139.49 136.16 45.79 206.03
## [5,] 1 113.03 125.41 41.51 222.67
## [6,] 1 134.57 165.84 32.42 219.59Calculamos el estimador de \(\beta\) utilizando directamente cálculo matricial:
solve(t(X)%*%X)%*%t(X)%*%Y## [,1]
## b0 7.522869
## tasaFlujoGas1 0.052898
## tasaFlujoGas2 0.034512
## aperturaBoq 0.153457
## tempGas 0.124906Calculamos el estimador de \(\beta\) utilizando la función lm() de R:
lm(eficienciaTermica~tasaFlujoGas1+tasaFlujoGas2+aperturaBoq+tempGas,data=ejemplo7)##
## Call:
## lm(formula = eficienciaTermica ~ tasaFlujoGas1 + tasaFlujoGas2 +
## aperturaBoq + tempGas, data = ejemplo7)
##
## Coefficients:
## (Intercept) tasaFlujoGas1 tasaFlujoGas2 aperturaBoq tempGas
## 7.5229 0.0529 0.0345 0.1535 0.1249Podemos representar gráficamente el plano de regresión de la variable respuesta frente a dos variables explicativas:
library(scatterplot3d)
attach(ejemplo7)
s3d <-scatterplot3d(tasaFlujoGas1,tasaFlujoGas2,eficienciaTermica, pch=16, highlight.3d=TRUE,
type="h", main="3D Scatterplot")
fit <- lm(eficienciaTermica ~ tasaFlujoGas1+tasaFlujoGas2)
s3d$plane3d(fit)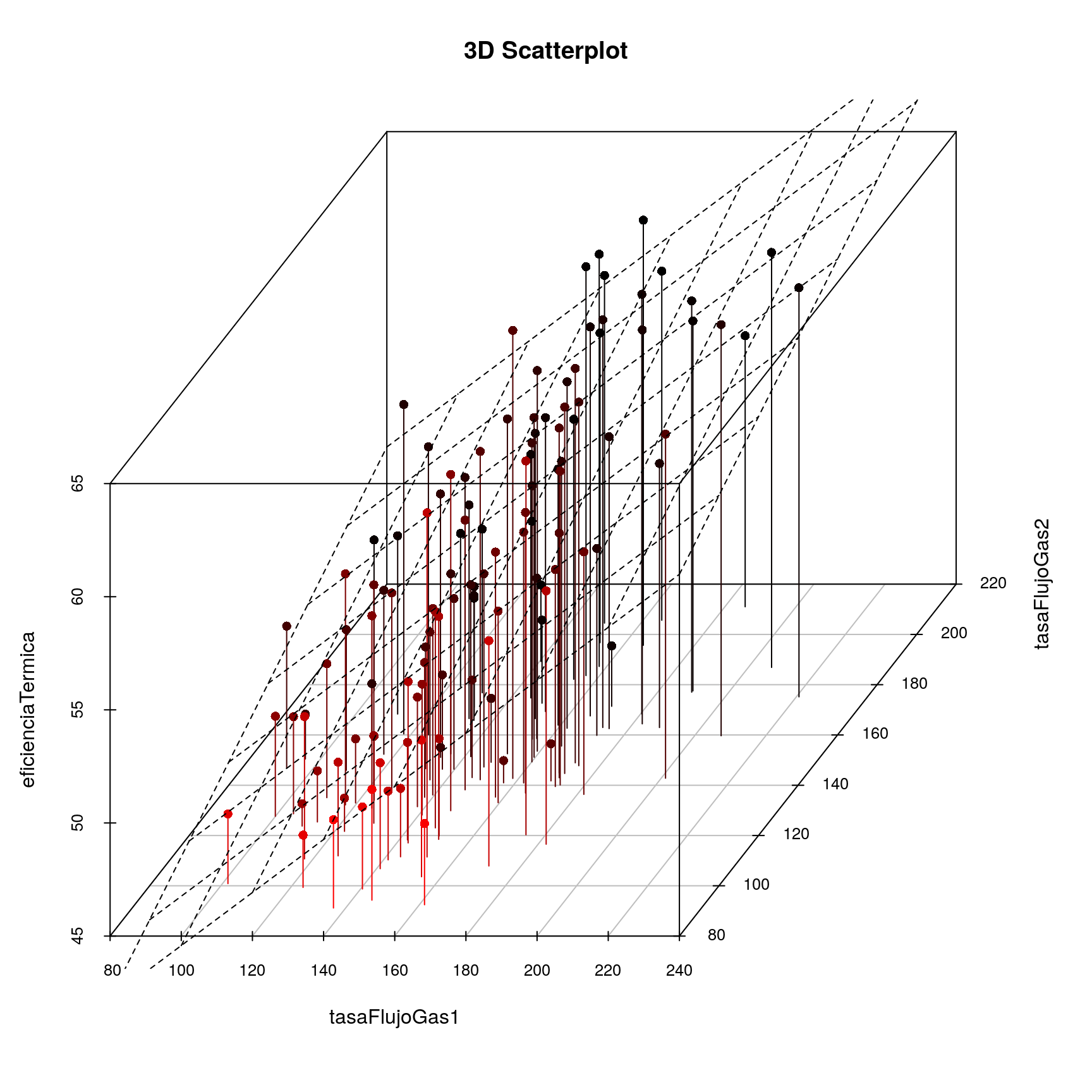
detach(ejemplo7)Utilizando el paquete rgl es posible mover una imagen 3d en el espacio mediante la sintaxis:
attach(ejemplo7)
library(rgl)
plot3d(tasaFlujoGas1,tasaFlujoGas2,eficienciaTermica, col="red",size=3)
detach(ejemplo7)Resumen de la estimación
varianza residual, errores estándar de los estimadores, contrastes, … Utilizamos directamente la función summary() de R:
regmult=lm(eficienciaTermica~tasaFlujoGas1+tasaFlujoGas2+aperturaBoq+tempGas,data=ejemplo7)
summary(regmult)##
## Call:
## lm(formula = eficienciaTermica ~ tasaFlujoGas1 + tasaFlujoGas2 +
## aperturaBoq + tempGas, data = ejemplo7)
##
## Residuals:
## Min 1Q Median 3Q Max
## -7.919 -1.459 0.126 1.223 7.772
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 7.5229 3.0454 2.47 0.0150 *
## tasaFlujoGas1 0.0529 0.0127 4.17 5.9e-05 ***
## tasaFlujoGas2 0.0345 0.0109 3.18 0.0019 **
## aperturaBoq 0.1535 0.0282 5.44 3.0e-07 ***
## tempGas 0.1249 0.0176 7.10 1.1e-10 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.77 on 115 degrees of freedom
## Multiple R-squared: 0.729, Adjusted R-squared: 0.719
## F-statistic: 77.3 on 4 and 115 DF, p-value: <2e-16Podemos además calcular intervalos de confianza para los parámetros:
confint(regmult)## 2.5 % 97.5 %
## (Intercept) 1.490609 13.555129
## tasaFlujoGas1 0.027774 0.078023
## tasaFlujoGas2 0.012985 0.056039
## aperturaBoq 0.097622 0.209292
## tempGas 0.090058 0.159753
© 2016 Angelo Santana, Carmen N. Hernández, Departamento de Matemáticas ULPGC