Inferencia estadística con R

Inferencias sobre la media en distribuciones normales: t.test

La función t.test() es la encargada de los procedimientos de inferencia sobre la media en poblaciones normales. Mediante esta función:

Podemos construir intervalos de confianza para una media y para la diferencia de medias entre dos poblaciones.
Podemos llevar a cabo contrastes de hipótesis, tanto unilaterales como bilaterales, sobre una media o sobre la diferencia de medias entre dos poblaciones.
En el caso particular de la comparación de dos poblaciones, permite elegir entre considerar las varianzas poblacionales iguales o distintas.

Veamos algunos ejemplos. Utilizaremos para ello algunas bases de datos incluídas en el paquete Lock5Data, que deberemos instalar previamente.

Inferencia sobre la media de una población normal

El conjunto de datos SleepStudy contiene 253 observaciones sobre patrones de sueño en estudiantes universitarios. Para ello se realizó un seguimiento de estos alumnos durante dos semanas. La variable AverageSleep contiene el número medio de horas de sueño de cada estudiante durante este periodo. En primer lugar leemos los datos y presentamos un histograma de esta variable:

library(Lock5Data)  # Cargamos el paquete que contiene los datos
data(SleepStudy)    # Cargamos los datos del estudio de sueño
hist(SleepStudy$AverageSleep, col="lightSalmon", xlab="Promedio de horas de sueño diarias", main="Estudio del sueño en \n estudiantes universitarios")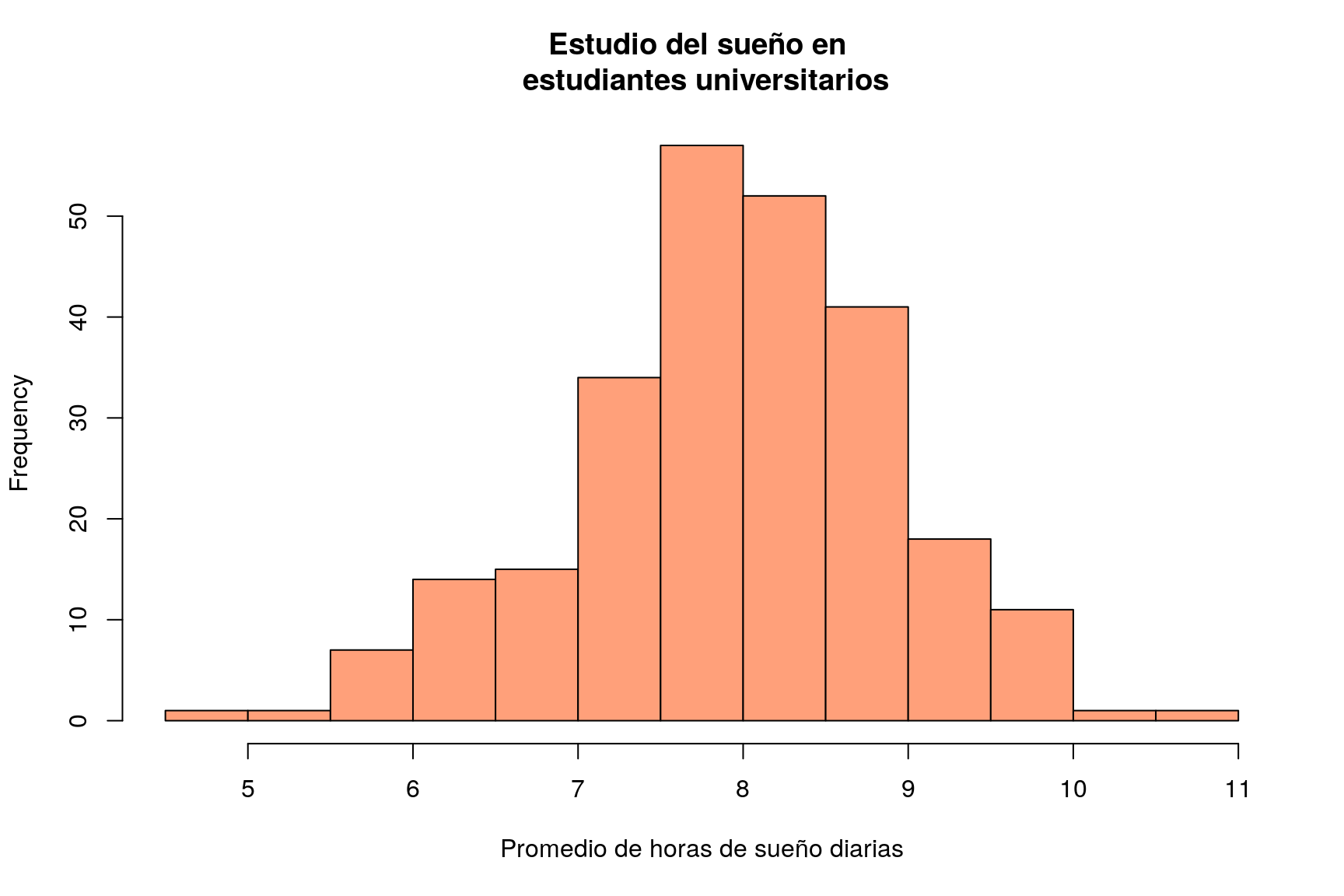

Contraste bilateral

Supongamos que queremos determinar si es admisible la hipótesis de que estos alumnos duermen por término medio 8 horas diarias. Utilizaríamos entonces la sintaxis:

t.test(SleepStudy$AverageSleep,  mu=8)

## 
##  One Sample t-test
## 
## data:  SleepStudy$AverageSleep
## t = -0.562, df = 252, p-value = 0.57
## alternative hypothesis: true mean is not equal to 8
## 95 percent confidence interval:
##  7.8465 8.0854
## sample estimates:
## mean of x 
##    7.9659

Obsérvese que para llevar a cabo el contraste basta con especificar la media que se desea poner a prueba mediante mu=8. Como resultado del procedimiento se muestra el valor del estadístico t, sus grados de libertad (df) y el p-valor del contraste (0.57483), que indica que la hipótesis planteada es admisible. Además obtenemos también la estimación del número medio de horas de sueño en la muestra (7.96593) y un intervalo de confianza al 95%. Podemos solicitar un intervalo a otro nivel de confianza especificándolo en la llamada al t.test:

t.test(SleepStudy$AverageSleep,  mu=8, conf.level=0.9)

## 
##  One Sample t-test
## 
## data:  SleepStudy$AverageSleep
## t = -0.562, df = 252, p-value = 0.57
## alternative hypothesis: true mean is not equal to 8
## 90 percent confidence interval:
##  7.8658 8.0661
## sample estimates:
## mean of x 
##    7.9659

Estructura del objeto `t.test`

Si ejecutamos:

tt=t.test(SleepStudy$AverageSleep,  mu=8)
str(tt)

## List of 9
##  $ statistic  : Named num -0.562
##   ..- attr(*, "names")= chr "t"
##  $ parameter  : Named num 252
##   ..- attr(*, "names")= chr "df"
##  $ p.value    : num 0.575
##  $ conf.int   : num [1:2] 7.85 8.09
##   ..- attr(*, "conf.level")= num 0.95
##  $ estimate   : Named num 7.97
##   ..- attr(*, "names")= chr "mean of x"
##  $ null.value : Named num 8
##   ..- attr(*, "names")= chr "mean"
##  $ alternative: chr "two.sided"
##  $ method     : chr "One Sample t-test"
##  $ data.name  : chr "SleepStudy$AverageSleep"
##  - attr(*, "class")= chr "htest"

podemos comprobar que el resultado de realizar un t-test es un objeto de clase htest compuesto por una lista de elementos (statistic, parameter, etc). Ello facilita la extracción de elementos particulares del test; por ejemplo, si sólo estuviésemos interesados en el intervalo de confianza o el p-valor bastaría ejecutar:

tt$conf.int

## [1] 7.8465 8.0854
## attr(,"conf.level")
## [1] 0.95

tt$p.value

## [1] 0.57483

o de manera equivalente:

tt["conf.int"]

## $conf.int
## [1] 7.8465 8.0854
## attr(,"conf.level")
## [1] 0.95

tt["p.value"]

## $p.value
## [1] 0.57483

Contraste unilateral

Si nuestro planteamiento original hubiese sido determinar si existe evidencia suficiente de que estos estudiantes duermen en promedio más de 7 horas diarias, plantearíamos un test unilateral, especificando el sentido de la hipótesis alternativa a contrastar (en este caso \(\mu>7\)):

t.test(SleepStudy$AverageSleep,  mu=7, alternative="greater")

## 
##  One Sample t-test
## 
## data:  SleepStudy$AverageSleep
## t = 15.9, df = 252, p-value <2e-16
## alternative hypothesis: true mean is greater than 7
## 95 percent confidence interval:
##  7.8658    Inf
## sample estimates:
## mean of x 
##    7.9659

Validación de la hipótesis de normalidad

El paquete car proporciona la función qqPlot() que nos permite evaluar gráficamente si puede aceptarse la hipótesis de normalidad de una variable:

library(car)

## Loading required package: carData

qqPlot(SleepStudy$AverageSleep)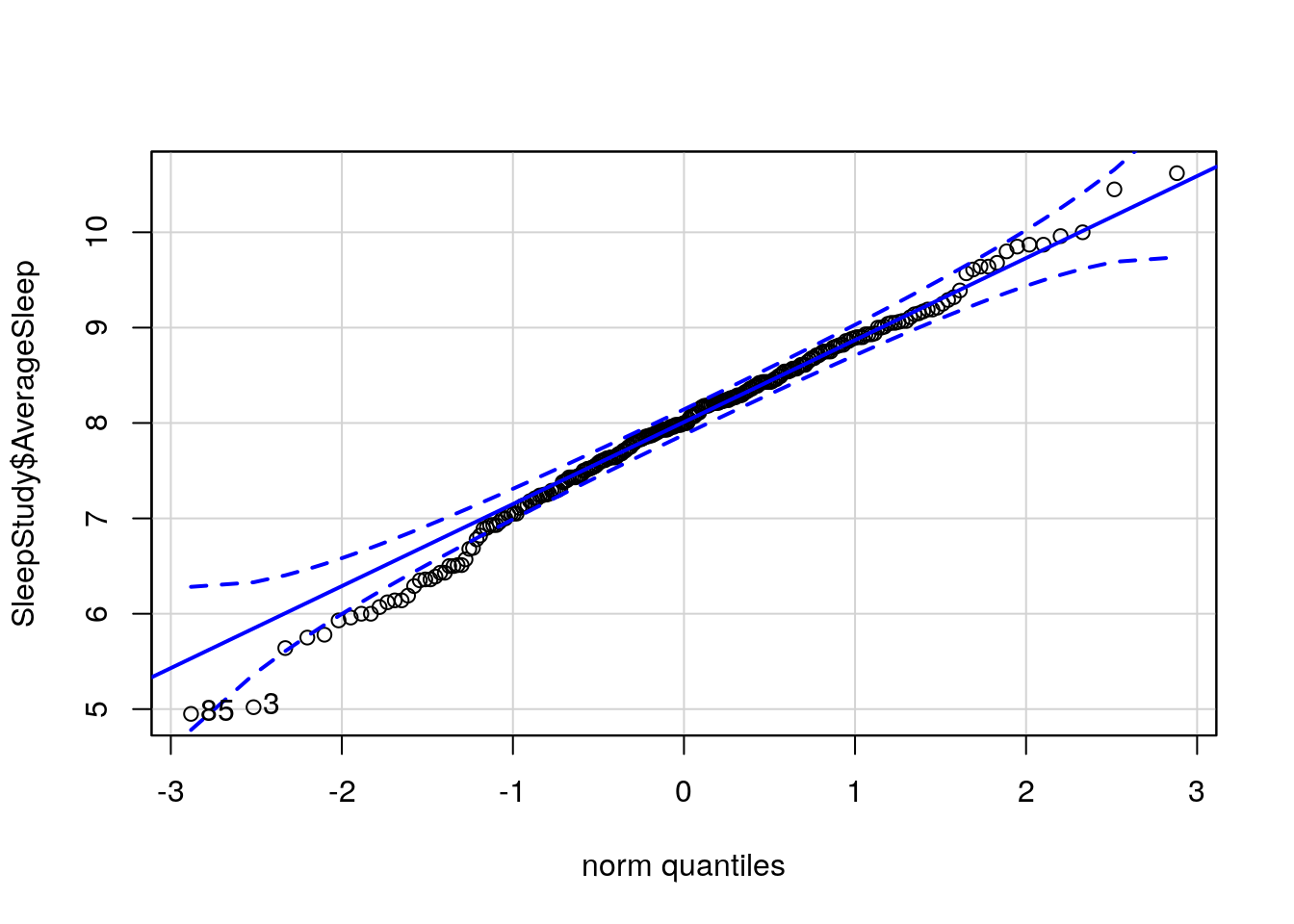

## [1] 85  3

En este caso se aprecia una ligera asimetría en la cola inferior de la distribución. No obstante, el test de Shapiro-Wilk permite aceptar la normalidad de esta variable:

shapiro.test(SleepStudy$AverageSleep)

## 
##  Shapiro-Wilk normality test
## 
## data:  SleepStudy$AverageSleep
## W = 0.99, p-value = 0.096

Diferencia de medias en dos poblaciones normales independientes

Podemos utilizar t.test() para contrastar la igualdad de medias en poblaciones normales. Por defecto, la función t.test() asume que la variable sobre la que se realiza el contraste tiene distinta varianza en los grupos que se comparan.

Comparación de grupos con varianzas distintas

Para contrastar con los datos del estudio anterior si existen diferencias en el promedio de horas de sueño diarias entre hombres y mujeres, asumiendo varianzas distintas, empleamos la siguiente sintaxis:

t.test(AverageSleep~Gender,data=SleepStudy)

## 
##  Welch Two Sample t-test
## 
## data:  AverageSleep by Gender
## t = 0.586, df = 227, p-value = 0.56
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -0.16905  0.31212
## sample estimates:
## mean in group 0 mean in group 1 
##          7.9948          7.9232

Como vemos, no existen diferencias significativas entre sexos (p-valor 0.55854). El boxplot que mostramos a continuación muestra que efectivamente ambos grupos son muy similares:

SleepStudy$Gender=factor(SleepStudy$Gender,levels=0:1,labels=c("Mujer","Hombre"))
boxplot(AverageSleep~Gender,data=SleepStudy,
        main="Promedio de horas de sueño diarias",col=c("lightpink","cyan"))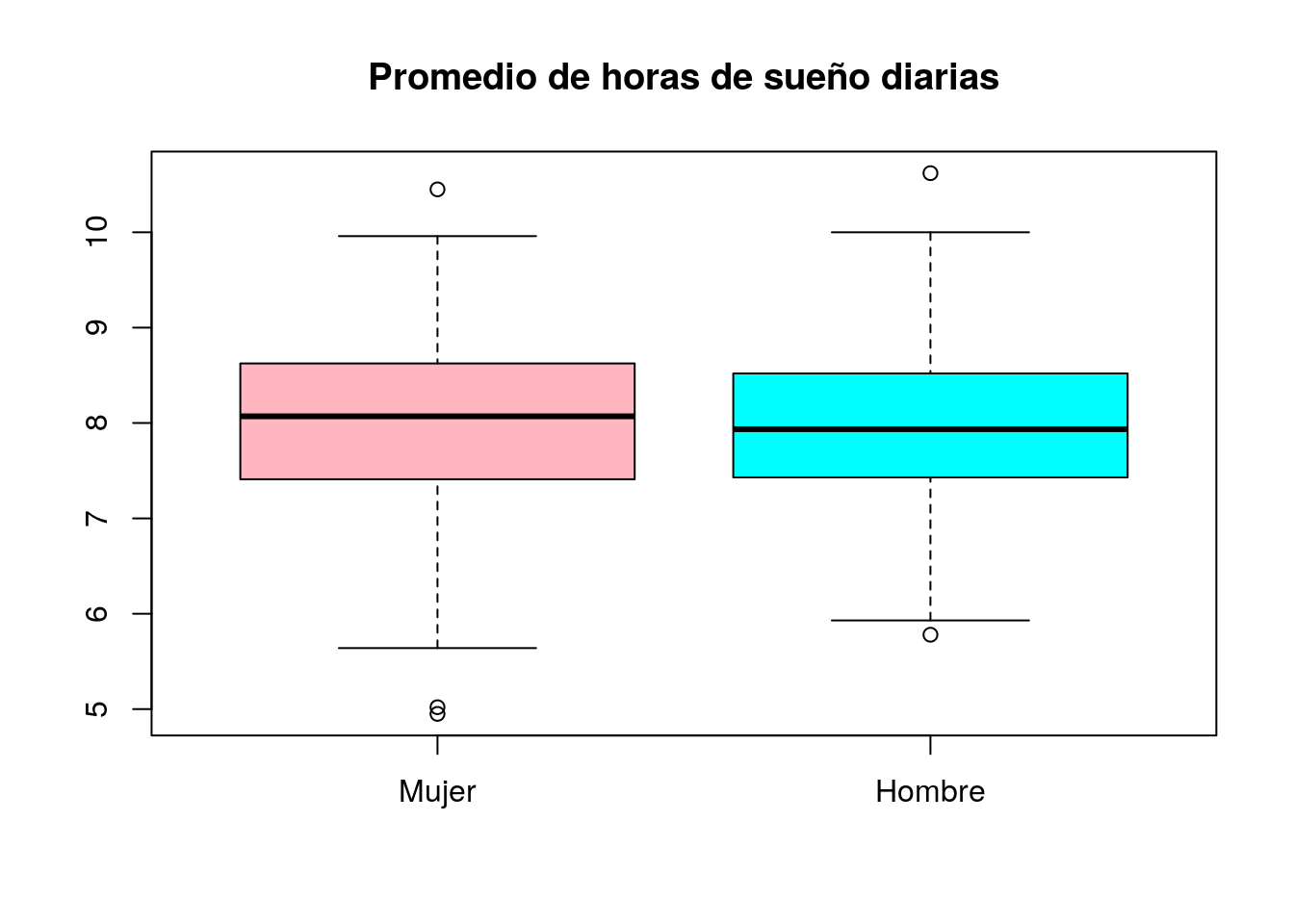

Para validar la aplicación del test, comprobamos la normalidad en cada grupo:

shapiro.test(SleepStudy$AverageSleep[SleepStudy$Gender=="Hombre"])

## 
##  Shapiro-Wilk normality test
## 
## data:  SleepStudy$AverageSleep[SleepStudy$Gender == "Hombre"]
## W = 0.986, p-value = 0.34

shapiro.test(SleepStudy$AverageSleep[SleepStudy$Gender=="Mujer"])

## 
##  Shapiro-Wilk normality test
## 
## data:  SleepStudy$AverageSleep[SleepStudy$Gender == "Mujer"]
## W = 0.986, p-value = 0.13

o, de una manera más sintética:

aggregate(AverageSleep~Gender,data=SleepStudy, function(x) shapiro.test(x)$p.value)

##   Gender AverageSleep
## 1  Mujer      0.13385
## 2 Hombre      0.34019

Sintaxis alternativa para el t-test

En el ejemplo anterior hemos realizado el t-test, describiendo la asignación de grupos mediante un objeto de clase formula. En general, una fórmula es un objeto descrito de la forma y~x. Cuando se emplea esta descripción es obligatorio además declarar el nombre del dataframe en que se encuentran los datos, tal como hemos hecho en nuestro ejemplo.

En ocasiones no tenemos los datos estructurados en un dataframe que incluya una variable que define el grupo de pertenencia, sino que simplemente tenemos los datos en dos vectores distintos; en tal caso, para realizar el t-test bastará con indicar los nombres de los vectores cuyas medias se pretende comparar:

chicos=c(7.55,8.57,8.49,7.56,7.38,8.85,7.82,8.13,6.77,7.88)
chicas=c(8.34,7.26,6.95,7.92,7.51,7.58,7.24,7.62,7.37,8.34)
t.test(chicos,chicas)

## 
##  Welch Two Sample t-test
## 
## data:  chicos and chicas
## t = 1.16, df = 16.5, p-value = 0.26
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -0.23422  0.80822
## sample estimates:
## mean of x mean of y 
##     7.900     7.613

Comparación de grupos con varianzas iguales

En caso de que queramos especificar que las varianzas son iguales, utilizaríamos la opción var.equal=TRUE:

t.test(AverageSleep~Gender,data=SleepStudy, var.equal=TRUE)

## 
##  Two Sample t-test
## 
## data:  AverageSleep by Gender
## t = 0.578, df = 251, p-value = 0.56
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -0.17233  0.31540
## sample estimates:
##  mean in group Mujer mean in group Hombre 
##               7.9948               7.9232

Especificación de una hipótesis alternativa unilateral.

En los ejemplos anteriores se contrasta si dos poblaciones difieren o no en media. Mediante t.test es posible especificar una alternativa unilateral.

Como ejemplo, analicemos los datos del conjunto FatMice18. Este dataframe corresponde a un experimento realizado para evaluar si la exposición de ratones a un número elevado de horas de luz influye en su ganancia de peso. El dataframe contieneddos variables medidas en 18 ratones:

Light: es un factor con dos niveles: LD (condiciones normales de luz) y LL (Luz de día y de noche)
WgtGain4: Ganancia de peso en gramos tras cuatro semanas sometidos a las condiciones experimentales.

Podemos ver los datos:

data(FatMice18)
FatMice18

##    Light WgtGain4
## 1     LL       10
## 2     LL       10
## 3     LL       11
## 4     LL        9
## 5     LL       12
## 6     LL        9
## 7     LL       11
## 8     LL        9
## 9     LL       17
## 10    LD        5
## 11    LD        6
## 12    LD        7
## 13    LD        8
## 14    LD        3
## 15    LD        8
## 16    LD        6
## 17    LD        6
## 18    LD        4

Si observamos la estructura del factor Light:

str(FatMice18$Light)

##  Factor w/ 2 levels "LD","LL": 2 2 2 2 2 2 2 2 2 1 ...

observamos que es un factor, con “LD” como primer nivel y “LL” como segundo. Es importante determinar el orden en que están codificados los niveles, ya que al aplicar el t-test, el primer grupo será el que corresponda al primer nivel del factor y el segundo grupo al otro. Para contrastar si los datos encierran evidencia suficiente de que la exposición a más horas de luz se asocia con un mayor incremento de peso planteamos el t-test de la forma:

t.test(WgtGain4~Light,data=FatMice18,alternative="less")

## 
##  Welch Two Sample t-test
## 
## data:  WgtGain4 by Light
## t = -4.94, df = 14, p-value = 0.00011
## alternative hypothesis: true difference in means is less than 0
## 95 percent confidence interval:
##     -Inf -3.2169
## sample estimates:
## mean in group LD mean in group LL 
##           5.8889          10.8889

(la hipótesis alternativa especificada es que los ratones en condiciones de luz normales ganan menos peso que en condiciones de luminosidad extendida). Como el p-valor es 1.091810^{-4} podemos asegurar que efectivamente a más luz mayor incremento de peso. Gráficamente:

boxplot(WgtGain4~Light,data=FatMice18,col=c("yellow3","yellow"))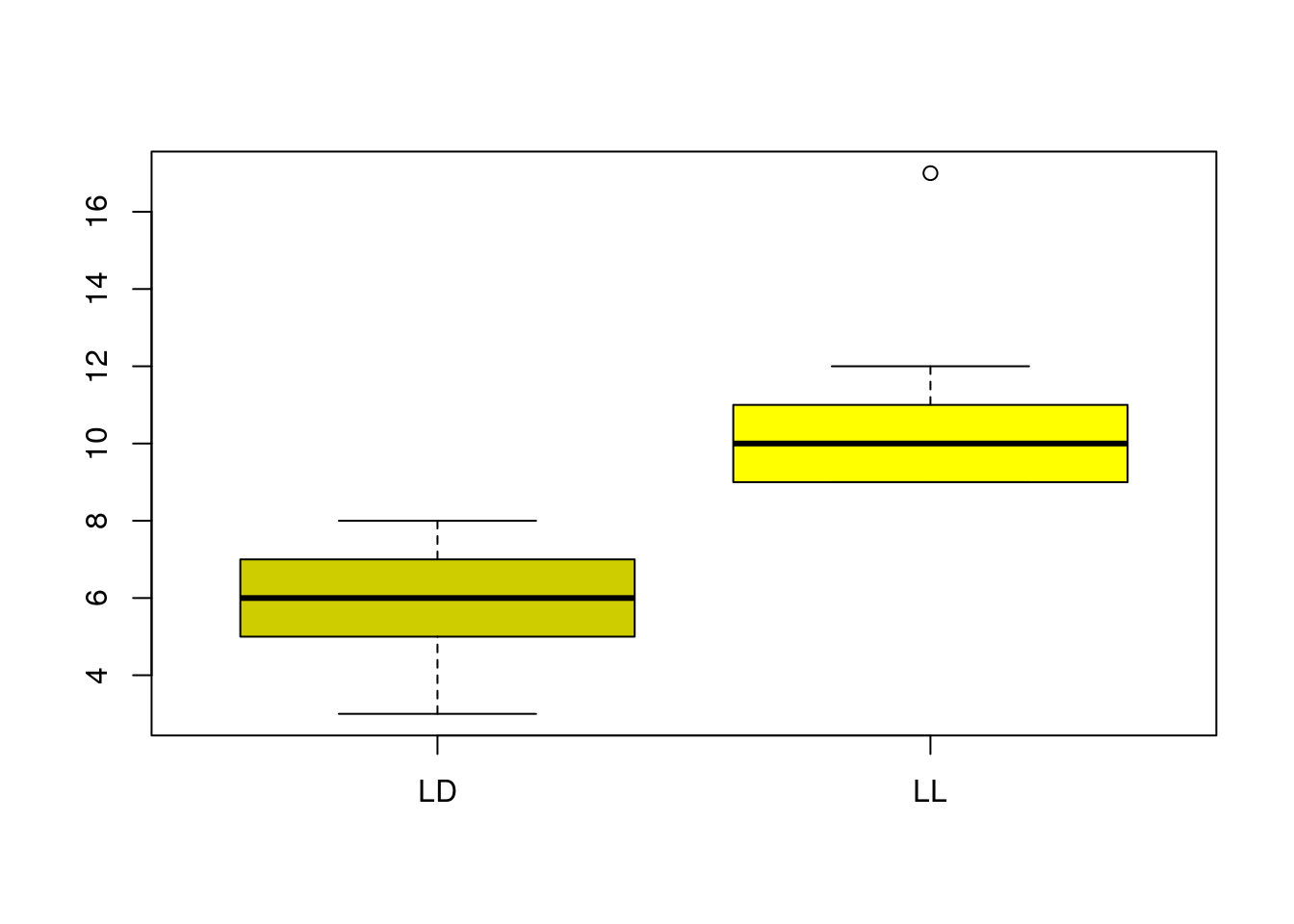

Dentro del paquete Lock5Data se encuentra también el dataframe NutritionStudy que contiene datos de un estudio de nutrición realizado en 315 individuos. Se desea determinar si existen diferencias significativas en el nivel medio de colesterol entre fumadores y no fumadores.

Comprueba que la variable Cholesterol no es normal en ninguno de los dos grupos.
Construye la variable lChol=log(Cholesterol) y comprueba que ahora sí que se cumple la hipótesis de normalidad.
Realiza el test de comparación de medias con la variable lChol.

Diferencia de medias en poblaciones normales emparejadas

Para comparar las medias de dos poblaciones en un diseño emparejado podemos utilizar t.test() con la opción paired=TRUE.

A modo de ejemplo, cargamos los datos QuizPulse10 también del paquete Lock5Data. Este archivo contiene los datos de pulsaciones por minuto de un grupo de 10 estudiantes en dos situaciones: durante la asistencia a una clase y durante la realización de un examen:

data(QuizPulse10)
QuizPulse10

##    Student Quiz Lecture
## 1        1   75      73
## 2        2   52      53
## 3        3   52      47
## 4        4   80      88
## 5        5   56      55
## 6        6   90      70
## 7        7   76      61
## 8        8   71      75
## 9        9   70      61
## 10      10   66      78

Para determinar si existen diferencias significativas en el número de pulsaciones por minuto en ambas situaciones utilizamos el t-test para muestras emparejadas:

with(QuizPulse10,t.test(Quiz,Lecture,paired=TRUE))

## 
##  Paired t-test
## 
## data:  Quiz and Lecture
## t = 0.86, df = 9, p-value = 0.41
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -4.4061  9.8061
## sample estimates:
## mean of the differences 
##                     2.7

NOTA: Obsérvese que en ese caso no podemos utilizar un objeto de clase formula para realizar la comparación, ya que no hay una variable factor que defina grupos a comparar sino que, de hecho, queremos comparar dos variables distintas. Como las variables se encuentran dentro del dataframe QuizPulse10, encapsulamos el comando t.test dentro de la función with para que R pueda acceder a los datos.

Potencia del t.test

Dados el nivel de significación \(\alpha\) de un test, la desviación típica de la variable cuya media se contrasta, el tipo de test (una muestra, dos muestras independientes o dos muestras emparejadas) y la hipótesis alternativa (unilateral o bilateral), la función power.t.test() permite:

Calcular la potencia del t-test para detectar una diferencia delta con un tamaño de muestra n prefijados.
Calcular el tamaño de la muestra necesario para detectar una diferencia delta con una potencia prefijada.
Calcular la diferencia máxima delta que es posible detectar con un tamaño de muestra n para una potencia específica.

La función power.t.test recibe como argumentos los valores de delta, n y power, y devuelve como resultado aquél que se declare como NULL (o se deje de declarar en la llamada a la función). Los siguientes ejemplos aclaran el funcionamiento de esta función

Ejemplos

¿Cuál es la potencia alcanzada en el test de la sección anterior en que aceptamos que la diferencia observada de 2.7 pulsaciones por minuto no era significativa?

sdif=with(QuizPulse10, sd(Quiz-Lecture))
power.t.test(n=10, delta=2.7, sd=sdif, sig.level=0.05, alternative="two.sided")

## 
##      Two-sample t test power calculation 
## 
##               n = 10
##           delta = 2.7
##              sd = 9.9337
##       sig.level = 0.05
##           power = 0.08319
##     alternative = two.sided
## 
## NOTE: n is number in *each* group

¿De qué tamaño debería ser la muestra si queremos alcanzar una potencia del 85% para detectar una diferencia de 8 pulsaciones por minuto a favor de una de las dos condiciones experimentales?

power.t.test(delta=8, power=0.85, sd=sdif, sig.level=0.05, alternative="one.sided")

## 
##      Two-sample t test power calculation 
## 
##               n = 22.878
##           delta = 8
##              sd = 9.9337
##       sig.level = 0.05
##           power = 0.85
##     alternative = one.sided
## 
## NOTE: n is number in *each* group

Necesitamos, por tanto, una muestra de tamaño 15

Cuál es la diferencia máxima en pulsaciones por minuto que es posible detectar con una muestra de tamaño 20 y una potencia del 90%?

power.t.test(n=20, power=0.9, sd=sdif, sig.level=0.05, alternative="two.sided")

## 
##      Two-sample t test power calculation 
## 
##               n = 20
##           delta = 10.45
##              sd = 9.9337
##       sig.level = 0.05
##           power = 0.9
##     alternative = two.sided
## 
## NOTE: n is number in *each* group

Más información y ejemplos en quick-R Power Analysis y en IDRE-UCLA

El test de Wilcoxon-Mann-Whitney

El test de Wilcoxon-Mann-Whitney contrasta si dos muestras proceden de la misma distribución o si, por el contrario, una de ellas tiende a producir valores más altos que la otra. Suele utilizarse como alternativa no paramétrica al t-test, cuando no se dan las condiciones de normalidad en las variables. Para realizar este test en R se utiliza la función wilcox.test de sintaxis muy parecida al t.test. Podemos repetir los contrastes de la sección anterior, utilizando ahora el test de Wilcoxon-Mann-Whitney:

wilcox.test(AverageSleep~Gender,data=SleepStudy)          # Muestras independientes

## 
##  Wilcoxon rank sum test with continuity correction
## 
## data:  AverageSleep by Gender
## W = 8170, p-value = 0.41
## alternative hypothesis: true location shift is not equal to 0

with(QuizPulse10,wilcox.test(Quiz,Lecture,paired=TRUE))   # Muestras emparejadas

## 
##  Wilcoxon signed rank test with continuity correction
## 
## data:  Quiz and Lecture
## V = 35.5, p-value = 0.44
## alternative hypothesis: true location shift is not equal to 0

Al igual que con el t-test podemos también especificar el sentido de la comparación. Por ejemplo, el dataframe HollywoodMovies2011 (también en el paquete Lock5Data) contiene datos relativos a la productura, ingresos, audiencias, etc, de 136 películas estrenadas en 2011. Queremos saber si estos datos muestran evidencia de que las grandes productoras generan más ingresos que las productoras independientes. La variable que codifica la productora es LeadStudio, y WorldGross es la variable que contiene los ingresos brutos obtenidos por la película. Una simple inspección de la variable LeadStudio nos muestra sus categorías:

data(HollywoodMovies2011)
table(HollywoodMovies2011$LeadStudio)

## 
##          20th Century Fox        Aardman Animations 
##                         9                         1 
##                 CBS Films                  Columbia 
##                         1                         3 
##                    Disney                DreamWorks 
##                         8                         2 
##      DreamWorks Animation       DreamWorks Pictures 
##                         1                         3 
##             Happy Madison Happy Madison Productions 
##                         2                         1 
##               Independent        Legendary Pictures 
##                        32                         2 
##                 Lionsgate             Miramax Films 
##                         5                         1 
##  Morgan Creek Productions           New Line Cinema 
##                         1                         1 
##                 Paramount                     Pixar 
##                         5                         1 
##       Regency Enterprises                Relativity 
##                         1                         4 
##               Relativity           Relativity Media 
##                         1                         8 
##    Reliance Entertainment                      Sony 
##                         1                         6 
##   Sony Pictures Animation    Spyglass Entertainment 
##                         1                         3 
##      Summit Entertainment     The Weinstein Company 
##                         2                         2 
##                 Universal     Vertigo Entertainment 
##                         9                         1 
## Village Roadshow Pictures                    Virgin 
##                         1                         1 
##               Warner Bros         Weinstein Company 
##                        12                         4

Definimos una nueva variable Studio con los valores “independent” o “major” para indicar si la película ha sido producida por los grandes estudios o no:

HollywoodMovies2011$Studio=ifelse(HollywoodMovies2011$LeadStudio=="Independent", "Independent", "Major")
HollywoodMovies2011$Studio=factor(HollywoodMovies2011$Studio,levels=c("Major","Independent"))
table(HollywoodMovies2011$Studio)

## 
##       Major Independent 
##         104          32

La introducción del comando factor tiene como objeto garantizar que R considera “Major” como primer nivel de la variable, e “Independent” como segundo.

Ahora contrastamos si las “majors” han generado más ingresos que las independientes:

wilcox.test(WorldGross~Studio,alternative="greater",data=HollywoodMovies2011)

## 
##  Wilcoxon rank sum test with continuity correction
## 
## data:  WorldGross by Studio
## W = 2440, p-value = 1.3e-05
## alternative hypothesis: true location shift is greater than 0

El p-valor (1.2546210^{-5}) indica que efectivamente hay evidencia suficiente para asegurar que las “major” generan más dinero.

Gráficamente:

boxplot(WorldGross~Studio, data=HollywoodMovies2011)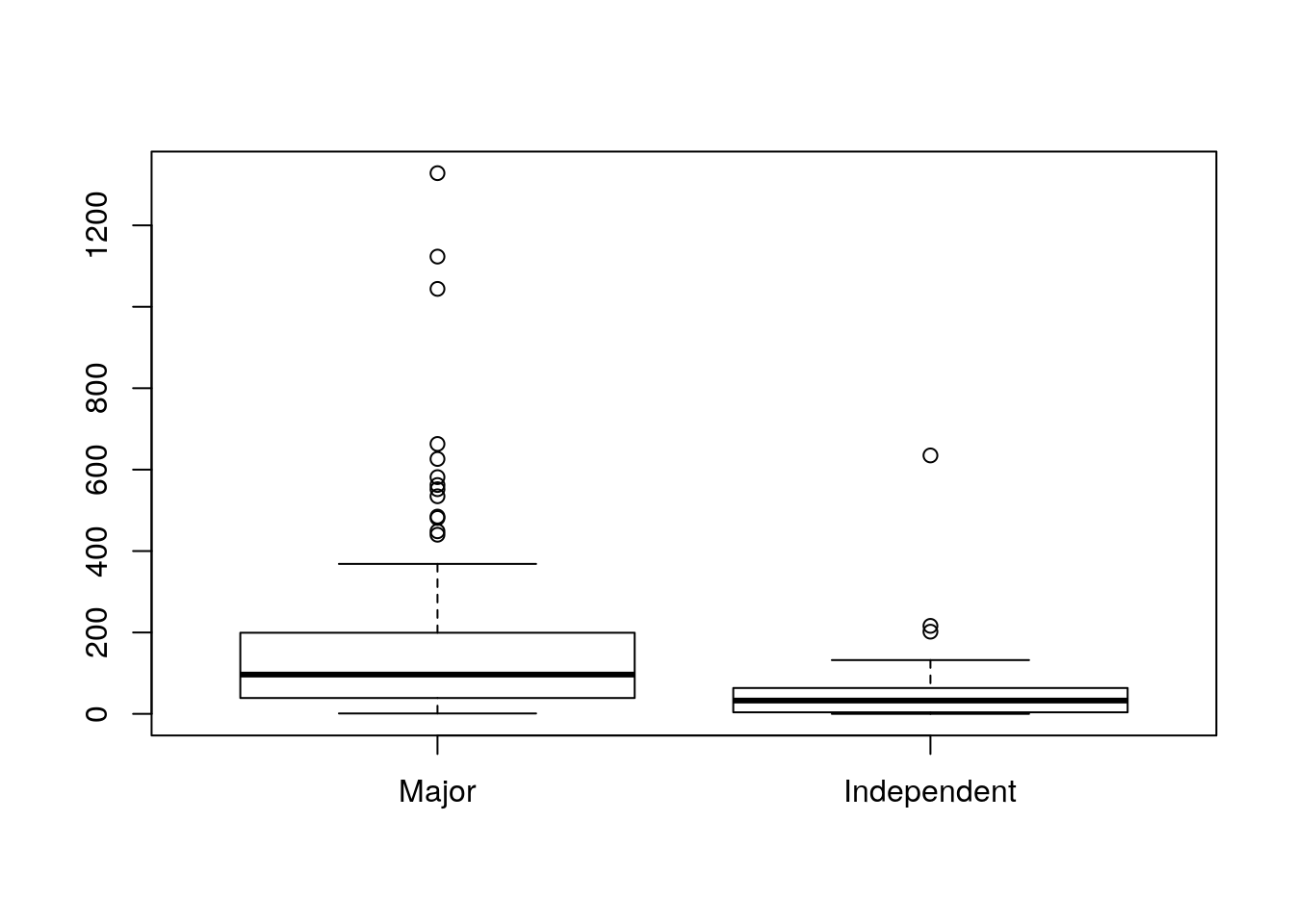

Inferencia sobre la varianza en poblaciones normales.

Contraste sobre la varianza de una variable con distribución normal

En la instalación básica de R no hay ninguna función para contrastar el valor de la varianza de una variable con distribución normal, o para construir un intervalo de confianza. Es preciso cargar el paquete TeachingDemos, que sí incluye la función sigma.test()

Ejemplo

Estamos interesados en determinar si en el estudio del sueño citado más arriba puede admitirse que la varianza del número de horas de sueño diario de los estudiantes es igual a 1:

library(TeachingDemos)
sigma.test(SleepStudy$AverageSleep, sigma=1)

## 
##  One sample Chi-squared test for variance
## 
## data:  SleepStudy$AverageSleep
## X-squared = 235, df = 252, p-value = 0.44
## alternative hypothesis: true variance is not equal to 1
## 95 percent confidence interval:
##  0.78758 1.11751
## sample estimates:
## var of SleepStudy$AverageSleep 
##                        0.93092

Por tanto puede admitirse dicha hipótesis (p-valor=0.44474). La función anterior nos proporciona además un intervalo de confianza al 95% para la varianza poblacional. Puede utilizarse la opción conf.level para especificar un nivel de confianza distinto.

Cociente de varianzas de poblaciones normales independientes.

La función var.test(), del paquete stats (no es necesario cargarlo, se carga por defecto al arrancar R) lleva a cabo un F test para comparar las varianzas de dos poblaciones normales independientes. Al igual que el t.test en la llamada a esta función se pueden incluir las dos variables a comparar o una fórmula en la que se especifica la variable factor que define los grupos que se comparan.

Ejemplo

Queremos decidira partir de los datos del estudio del sueño anterior si existe evidencia, al 5% de significación, de que la varianza del número de horas de sueño es menor entre los estudiantes varones que entre las mujeres. Las varianzas muestrales son las siguientes:

aggregate(AverageSleep~Gender,SleepStudy,var)

##   Gender AverageSleep
## 1  Mujer      0.98692
## 2 Hombre      0.85387

Con la codificación de la variable Gender el primer nivel de esta variable es Mujer. Por tanto el contraste deseado se lleva a cabo mediante:

var.test(AverageSleep~Gender,SleepStudy,alternative="greater")

## 
##  F test to compare two variances
## 
## data:  AverageSleep by Gender
## F = 1.16, num df = 150, denom df = 101, p-value = 0.22
## alternative hypothesis: true ratio of variances is greater than 1
## 95 percent confidence interval:
##  0.85136     Inf
## sample estimates:
## ratio of variances 
##             1.1558

El p-valor (0.21827) indica que aunque las mujeres presentan en la muestra más varianza que los hombres, la diferencia no es significativa.

Cociente de varianzas de poblaciones normales en muestras emparejadas.

Cuando se quiere comparar la varianza de muestras emparejadas puede utilizarse el test de Pitman-Morgan. En R este test se encuentra implementado en el paquete PairedData, en la función var.test().

Ejemplo:

Queremos contrastar si existen diferencias significativas entre las varianzas del número de pulsaciones por minuto de estudiantes según que estén haciendo un examen o atendiendo a una clase.

data(QuizPulse10)
library(PairedData)
with(QuizPulse10, var.test(Lecture,Quiz,paired=TRUE))

## 
##  F test to compare two variances
## 
## data:  Lecture and Quiz
## F = 1.05, num df = 9, denom df = 9, p-value = 0.95
## alternative hypothesis: true ratio of variances is not equal to 1
## 95 percent confidence interval:
##  0.26026 4.21848
## sample estimates:
## ratio of variances 
##             1.0478

Inferencia estadística con R

Angelo Santana & Carmen Nieves Hernández, Departamento de Matemáticas, ULPGC

Inferencias sobre la media en distribuciones normales: t.test

Inferencia sobre la media de una población normal

Contraste bilateral

Estructura del objeto t.test

Contraste unilateral

Validación de la hipótesis de normalidad

Diferencia de medias en dos poblaciones normales independientes

Comparación de grupos con varianzas distintas

Sintaxis alternativa para el t-test

Comparación de grupos con varianzas iguales

Especificación de una hipótesis alternativa unilateral.

Diferencia de medias en poblaciones normales emparejadas

Potencia del t.test

Ejemplos

El test de Wilcoxon-Mann-Whitney

Inferencia sobre la varianza en poblaciones normales.

Contraste sobre la varianza de una variable con distribución normal

Ejemplo

Cociente de varianzas de poblaciones normales independientes.

Ejemplo

Cociente de varianzas de poblaciones normales en muestras emparejadas.

Ejemplo:

Angelo Santana & Carmen Nieves Hernández,
Departamento de Matemáticas, ULPGC

Estructura del objeto `t.test`