En la página 35 de la guía didáctica de la asignatura aparece la siguiente tabla:

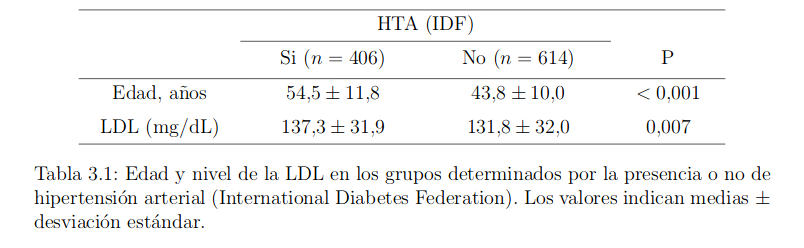
En esta tabla se puede apreciar que los sujetos con hipertensión tienen un mayor nivel de LDL en sangre que los normotensos (una media de LDL de 137.3 en los hipertensos frente a 131.8 en los normotensos, siendo esta diferencia significativa, p<0.05). Ello nos podría llevar a pensar que ambas variables están asociadas: la hipertensión puede intervenir de alguna manera en la elevación de los niveles de LDL, o a la inversa.

Ahora bien, la tabla nos muestra también que los hipertensos son, en media, de mayor edad que los normotensos (54.4 años, frente a 43.8 años, siendo esta diferencia significativa, p<0.05). Es sabido que la tensión arterial tiende a incrementarse con la edad; por ello cabe preguntarse aquí si la asociación entre LDL y HTA aparece simplemente porque la edad hace de factor de confusión (las personas mayores tienen más LDL y más HTA sin que exista relación causal entre ellas), o no. En caso de que la edad no bastase para explicar esta asociación se haría preciso indagar en la verdadera causa de la misma.

Vamos a utilizar nuevamente Jamovi y los datos del estudio de Telde para ver como el valor de la LDL depende de la edad del sujeto.

Una vez descargado el conjunto de datos endocrino.csv (se puede descargar de la web del curso, o directamente de aquí) podemos reproducir la tabla anterior pinchando en Exploration -> Descriptives, seleccionando EDAD y LDL como variables, indicando que se quiere separar ( Split by ) HTA_IDF, y marcando como estadísticos la media (Mean) y la desviación típica (Std. deviation):

 

 

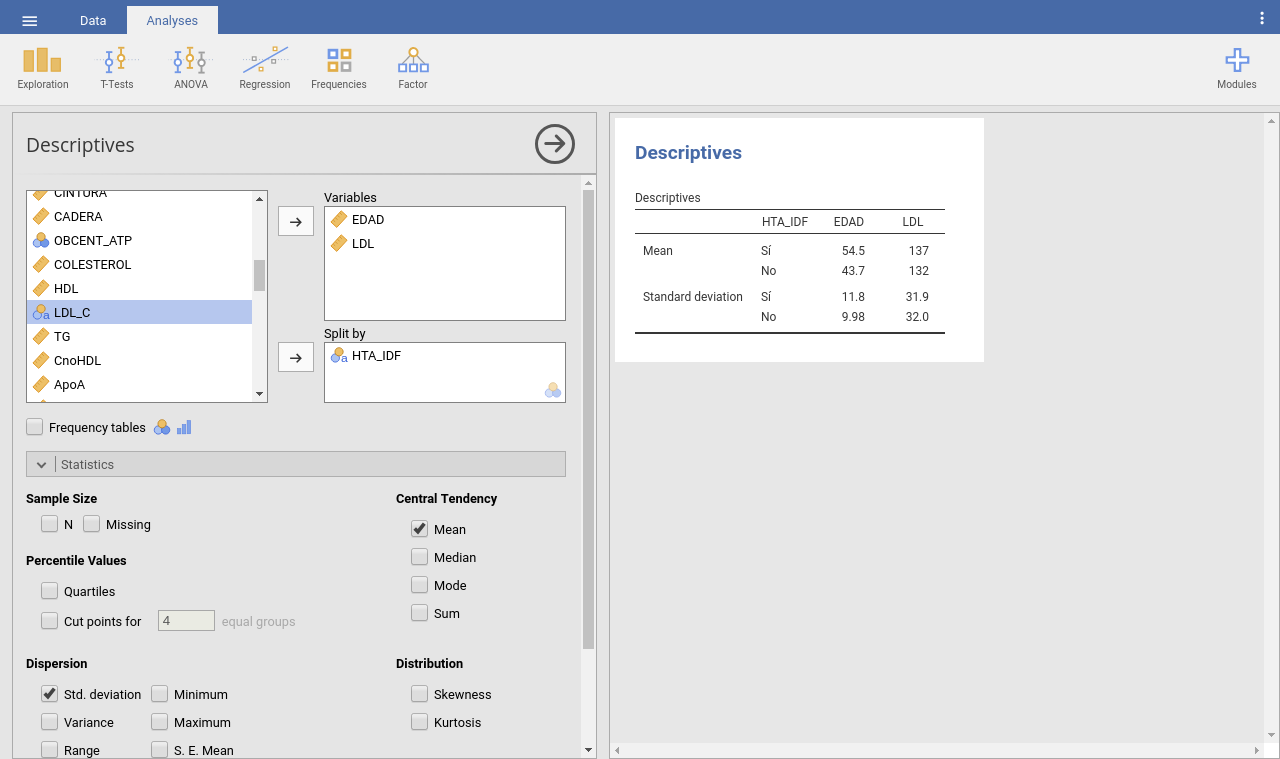
Ahora, para ver de manera más precisa como se relacionan LDL y Edad, vamos a hacer un gráfico de la LDL frente a la edad. Para ello hay que pinchar en el icono Exploration y a continuación Scatterplot (en caso de que la opción scatterplot no esté disponible hay que instalar el módulo scatr, pinchando en el icono “+” Modules, en la parte superior derrecha de la aplicación). Además marcamos la opción Linear en el submenú Regression Line a la izquierda. El resultado obtenido es el siguiente:

 

 

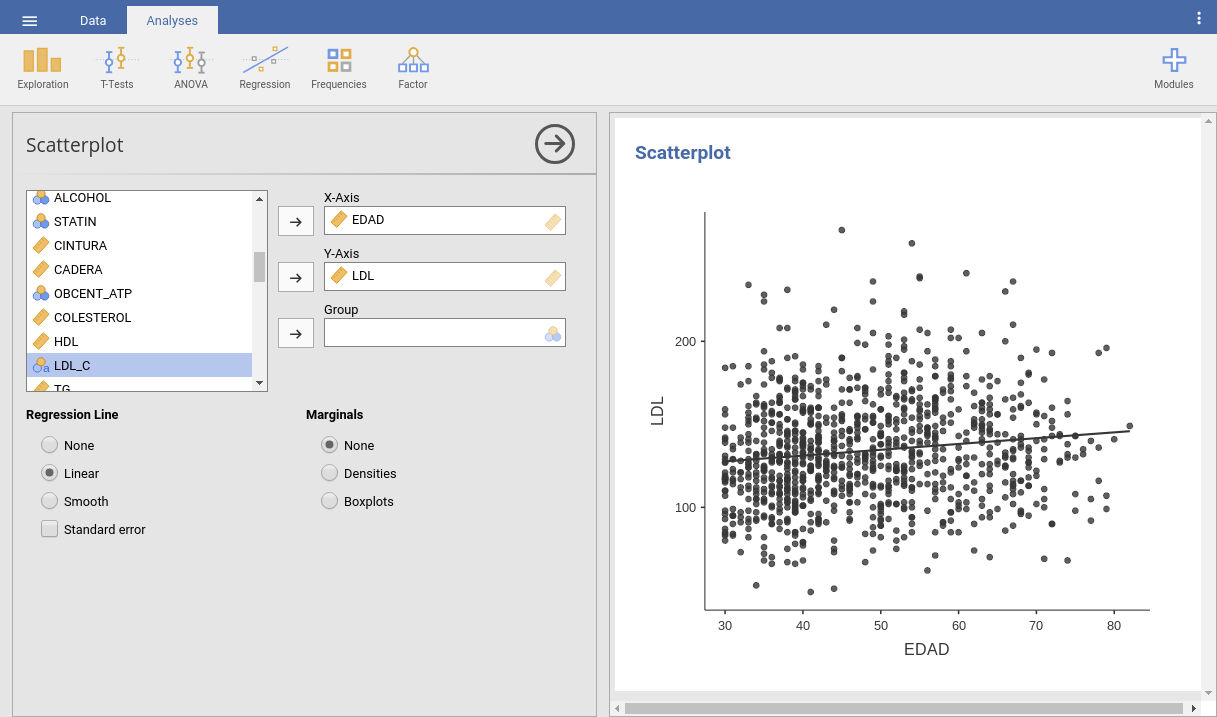
La imagen muestra que a medida que avanza la edad se incrementa la concentración de LDL en la sangre de los sujetos. También podemos usar Jamovi para calcular la recta de regresión que permita predecir el valor esperado de LDL en función de la edad:

\[LDL = b_0 + b_1\cdot Edad\] El valor de \(b_1\) se denomina pendiente y \(b_0\) ordenada (intercept) en inglés.

Para estimar estos coeficientes pinchamos en Regression -> Linear Regression, designamos LDL como variable dependiente y la Edad como covariable; además en Model Coefficients seleccionamos Confidence interval para que el programa nos muestre la precisión de las estimaciones. El resultado obtenido es:

 

 

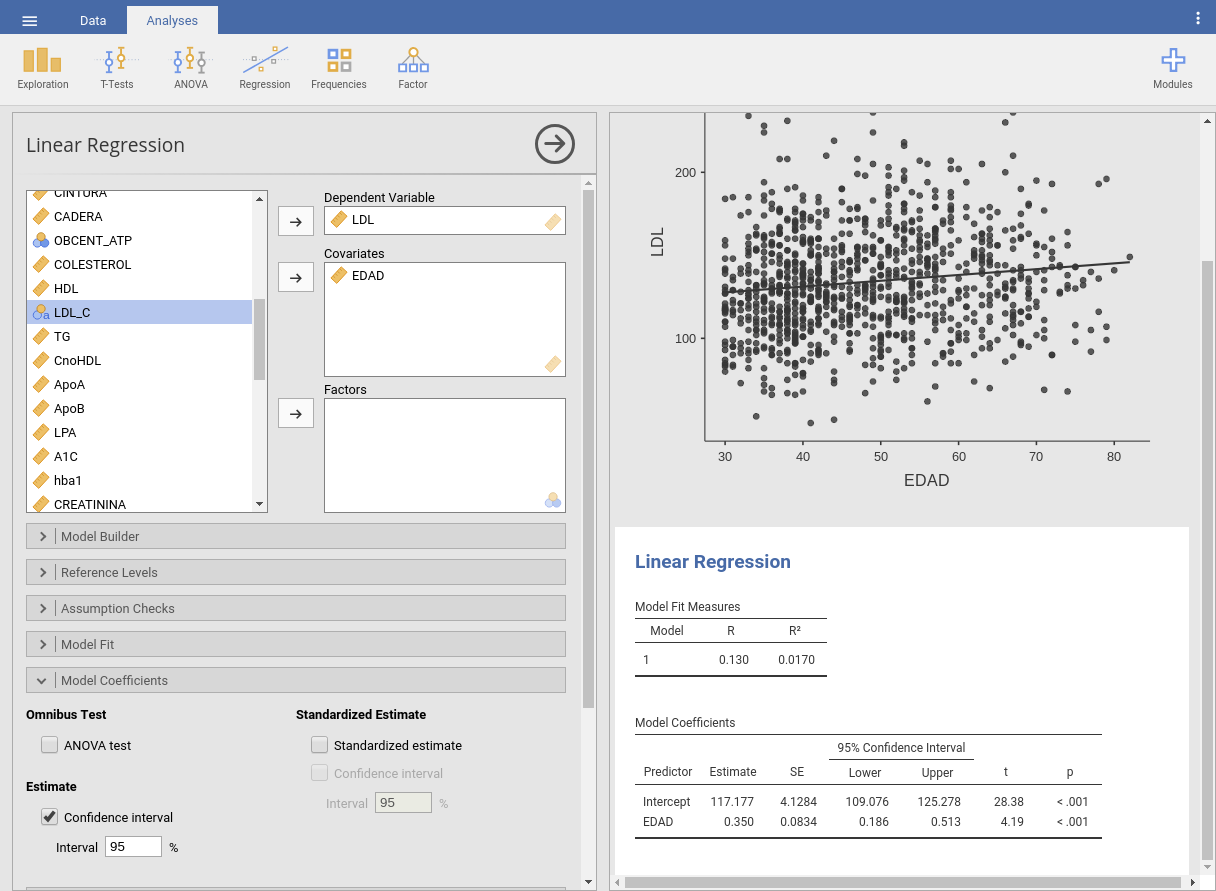
La estimación del modelo de regresión es, como vemos en la imagen:

\[LDL = 117.177 + 0.35\cdot Edad\]

lo que significa que por cada año transcurrido, el valor esperado de LDL en sangre se incrementa en 0.35 unidades. El p-valor asociado a este coeficiente es \(p<0.001\), lo que indica que este efecto de la edad sobre el nivel de LDL es significativo (no atribuíble al azar). El intervalo de confianza nos indica que el incremento estimado de 0.35 unidades de LDL por año tiene un margen de error (al 95% de confianza) tal que su valor real oscila probablemente entre 0.186 y 0.513 unidades de LDL por año.

Por cierto, el valor de \(R^2=0.017\) que muestra Jamovi puede interpretarse como la proporción de variabilidad en la LDL que se explica por la variación en la edad. En este caso, sólo un 1.7% de la variación en el LDL está explicado por la edad. Es un porcentaje realmente bajo si bien, como hemos visto, el efecto de la edad sobre el LDL es significativo. En realidad la lectura que extraemos de esta información es que, efectivamente, la edad puede tener influencia sobre el valor de LDL, pero dicha influencia no es mucha; probablemente hay otros factores que invluyan más.

 

En cualquier caso, la cuestión es ¿cómo interviene la HTA en la relación entre la edad y el nivel de LDL?. Podemos ver gráficamente la relación entre estas tres variables si volvemos al menú Exploration -> Scatterplot y añadimos HTA_IDF como variable de grupo:

 

 

Como vemos, la imagen sugiere una relación diferente entre el nivel de LDL y la edad según que los sujetos tengan o no HTA (según la IDF): en los sujetos sin HTA, el nivel medio de LDL aumenta con la edad, mientras que en los sujetos sin HTA, el nivel medio de LDL se mantiene casi constante (incluso disminuye un poco) a medida que aumenta la edad. En cualquier caso, para un mismo valor de edad, el promedio de LDL en hipertensos está muy próximo al promedio de LDL en normotensos. ¿Están tan próximos que la diferencia no es significativa, o la distancia es lo suficientemente grande como decidir dicha diferencia sí que es significativa?

Para responder a esta cuestión utilizaremos el modelo de análisis de la covarianza, que tiene por finalidad precisamente medir la asociación entre los niveles de LDL e hipertensión para sujetos de la misma edad, esto es, medir la asociación ajustada por la edad. Técnicamente este modelo es de la forma:

\[E[LDL | HTA, EDAD] = \theta + \alpha \cdot HTA + \beta \cdot EDAD\]

donde \(E[LDL | HTA, EDAD]\) es el valor esperado de LDL en un sujeto para unos valores fijos de HTA y EDAD; concretamente si:

\[HTA=\begin{cases} 0 & \textrm{Si el sujeto es normotenso}\\ 1 & \textrm{Si el sujeto es hipertenso} \end{cases}\]

En los individuos normotensos, como HTA=0, el modelo anterior se reduce a:

\[E[LDL | HTA=0, EDAD] = \theta + \beta \cdot EDAD\]

mientras que en los individuos hitertensos (HTA=1) nos queda:

\[E[LDL | HTA=1, EDAD] = \theta + \alpha + \beta \cdot EDAD\]

En otras palabras, el valor de \(\alpha\) mide la diferencia en LDL entre dos individuos de la misma edad, uno hipertenso y el otro normotenso. Si ocurriese que \(\alpha=0\), ello significaría que, a una misma edad, no hay diferencia en LDL entre normotensos e hipertensos. En la práctica, utilizaremos un software estadístico (en nuestro caso Jamovi) para que estime el valor de \(\alpha\) y contraste si puede aceptarse la hipótesis de que dicho valor es igual a cero:

Para llevar a cabo esta tarea en Jasmovi accedemos a Regression -> Linear Regression y especificamos el nivel de LDL como variable dependiente, la edad como covariable y la presencia o no de HTA como Factor:

 

 

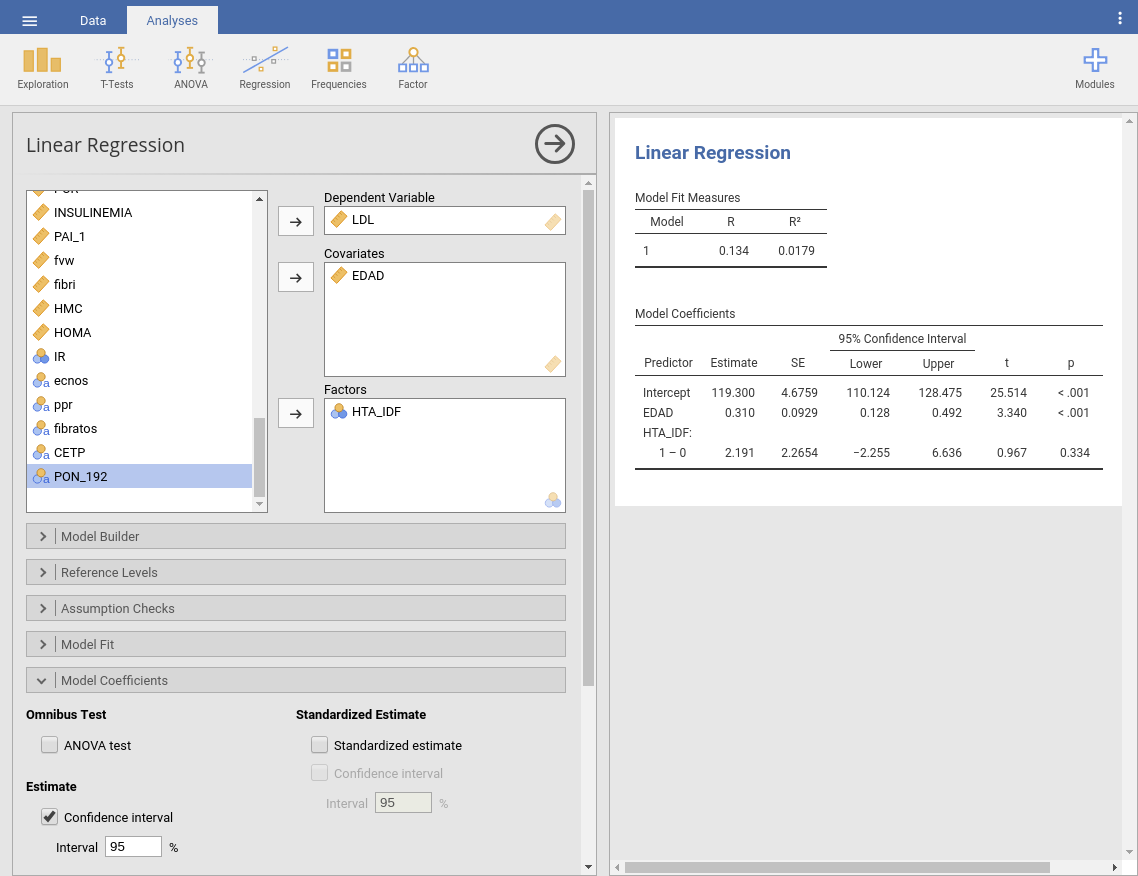
La correspondencia entre la tabla calculada por Jamovi y los elementos del modelo anterior es la siguiente:

\[\hat\theta=119.3\] \[\hat\beta=0.310\] \[\hat\alpha=2.191\]

Si atendemos al p-valor podemos concluir que aunque el valor estimado de \(\alpha\) sea 2.191, dicho valor no resulta significativo (p=0.334), lo que significa que no podemos asegurar que el valor de \(\alpha\) en la población sea distinto de cero. Si atendemos al intervalo de confianza observamos que éste va de -2.255 a 6.636; el intervalo indica lo mismo que el contraste: con el margen de error que se maneja en la muestra, no se puede asegurar que \(\alpha\) sea distinto de cero; por tanto podemos aceptar que \(\alpha=0\), es decir, los datos no muestran evidencia suficiente de que, a la misma edad, un hipertenso tenga un valor de LDL diferente de un normotenso. En otras palabras, una vez que se tiene en cuenta la edad, no hay relación entre hipertensión y LDL.