Odds-Ratio

En la tarea anterior vimos como utilizar Jamovi para calcular la odds-ratio entre dos variables en una tabla de doble entrada. A continuación, utilizaremos los datos del fichero endocrino.csv para calcular la odds-ratio entre las variables HTA_OMS y DM. Previamente, construimos la tabla de contingencia (utilizando en Jamovi el menú Frequencies/Contingency tables/Independent Samples) de ambas variables:

 

 

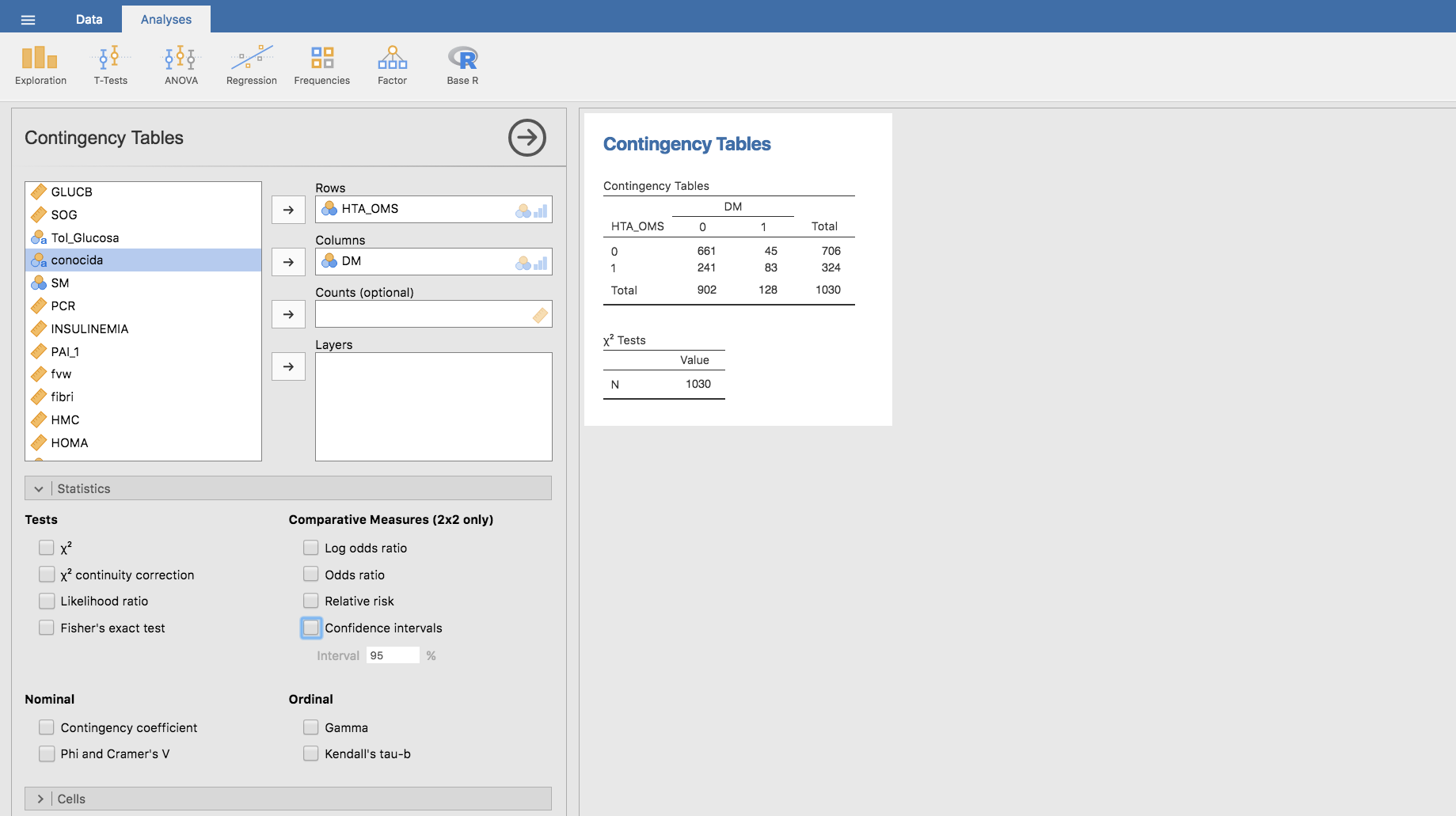
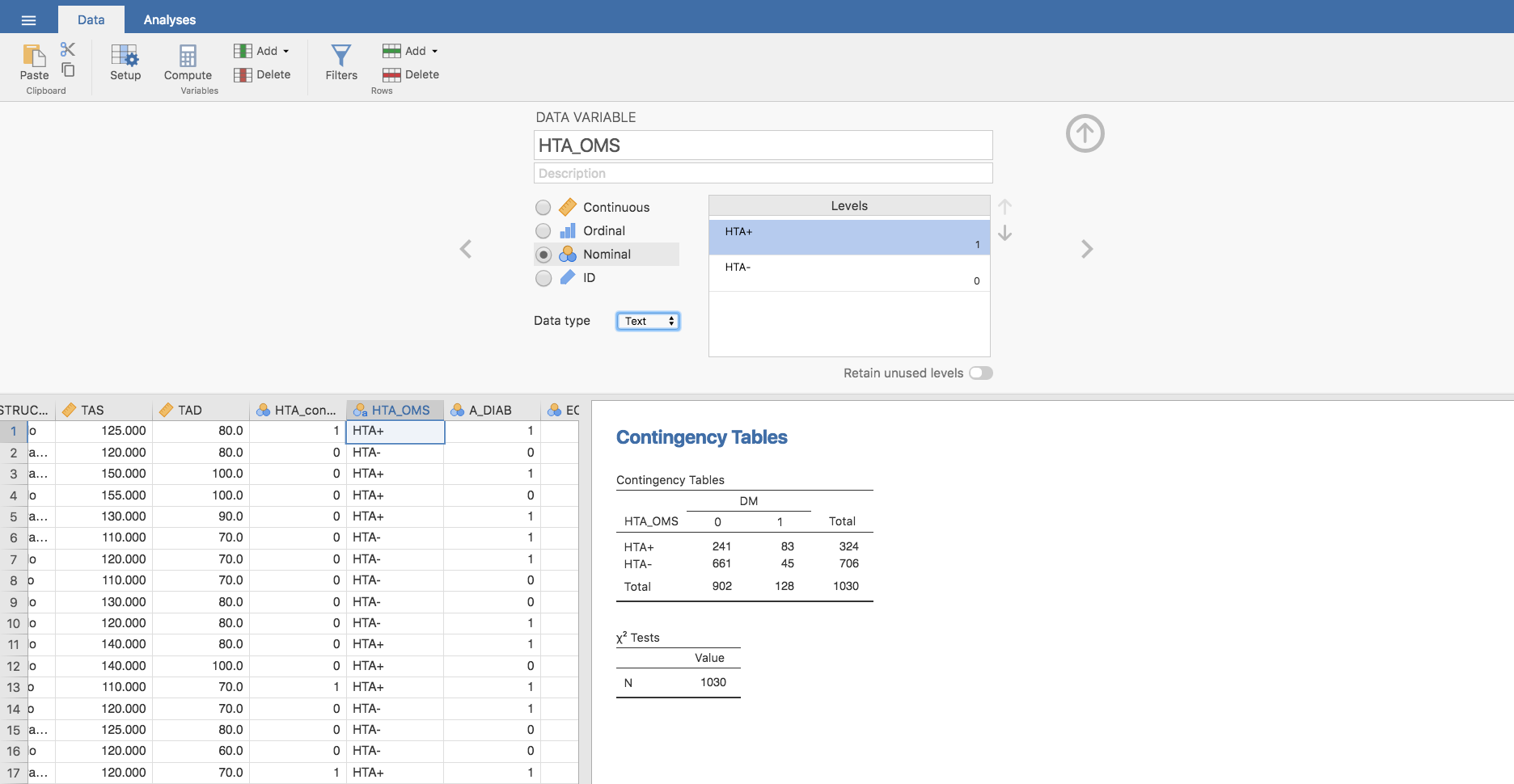
Recodificamos los niveles de HTA_OMS, sustituyendo el \(0\) por HTA- y el \(1\) por HTA+, y reordenamos esos niveles situando en primer lugar HTA+:

 

 

De forma análoga, procedemos con la variable DM para obtener la tabla que aparece a continuación:

 

 

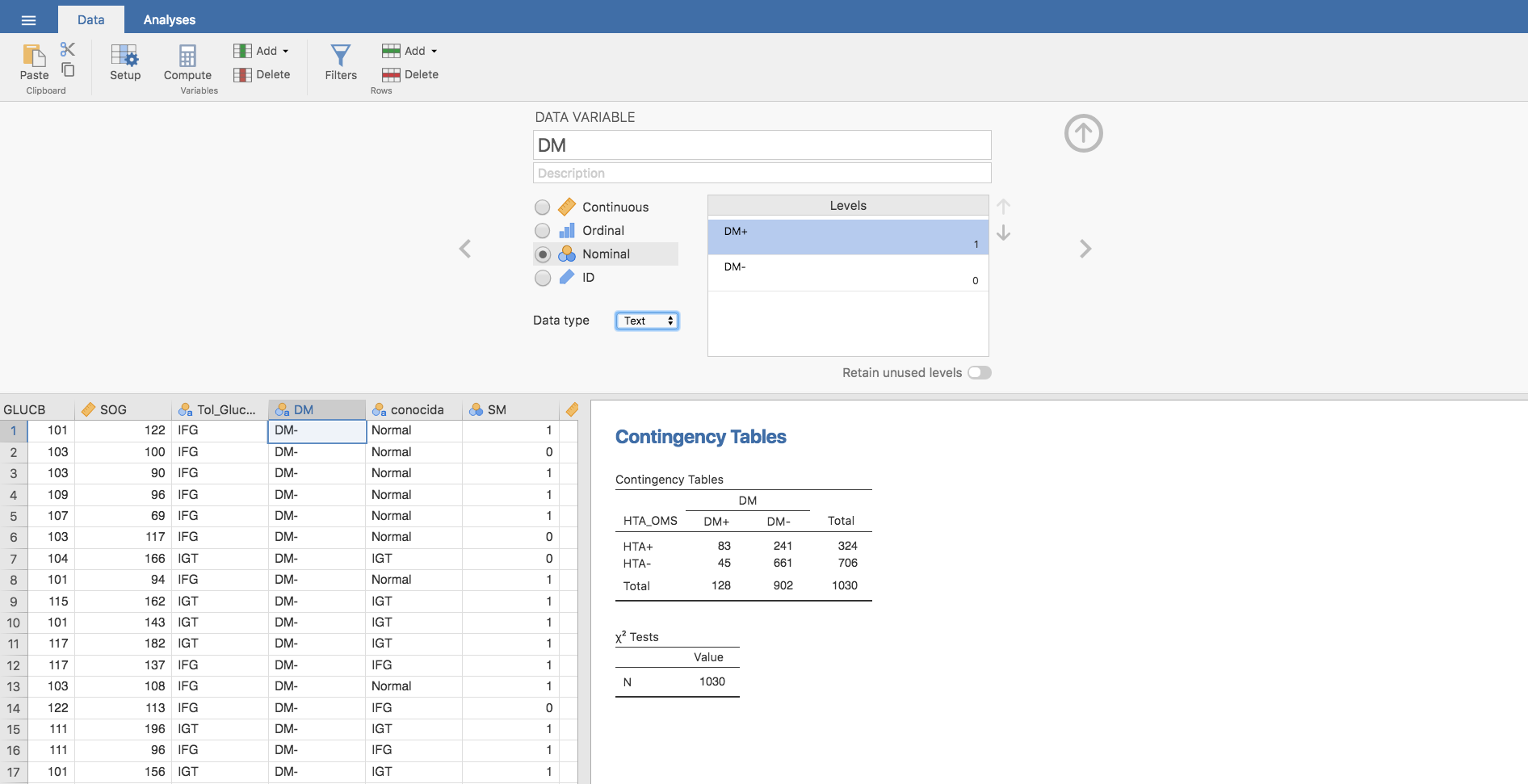
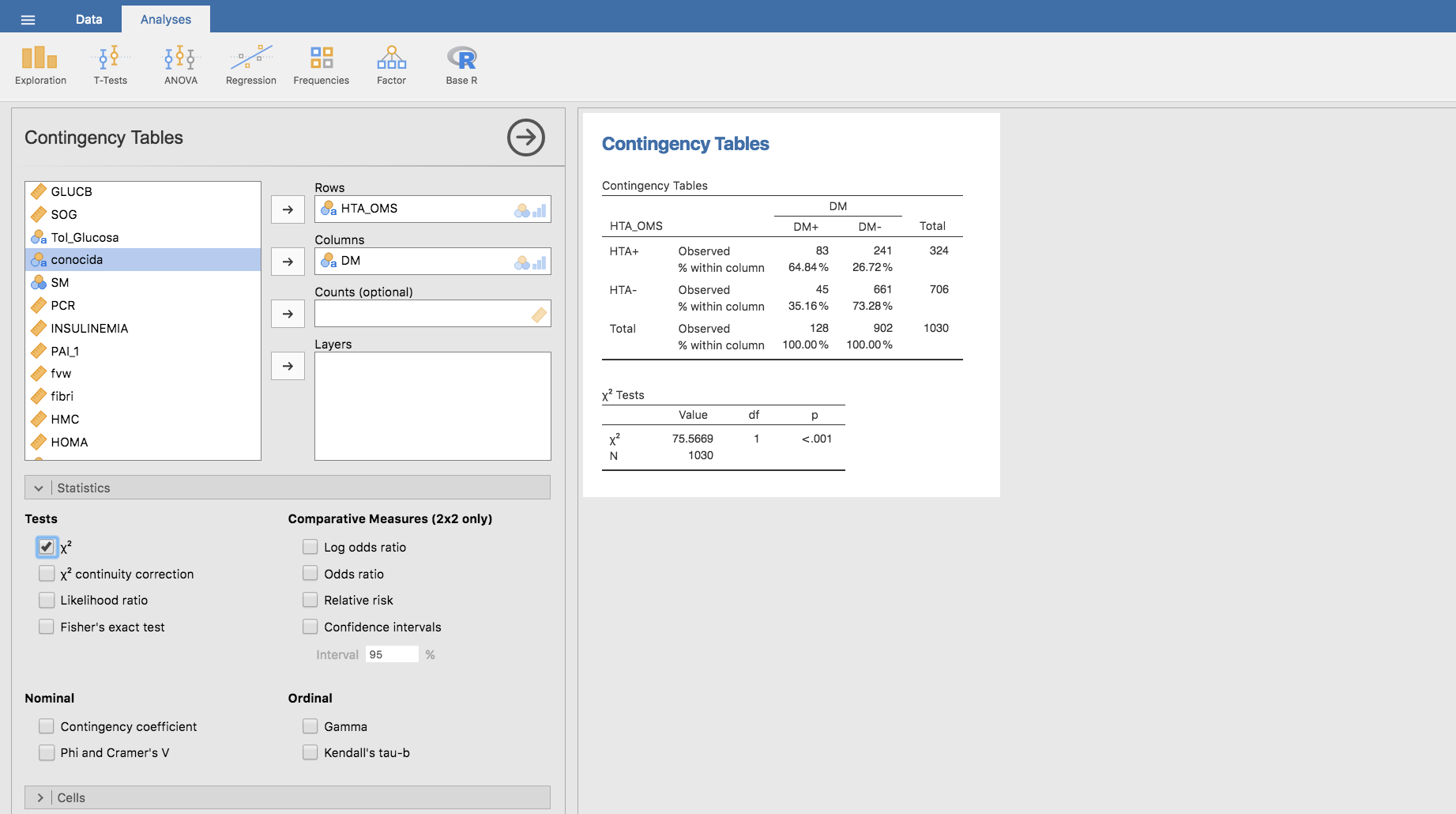
Seguidamente, calculamos las proporciones por columnas en nuestra tabla, que serán las respectivas proporciones de hipertensos entre los DM+ y los DM-:

 

 

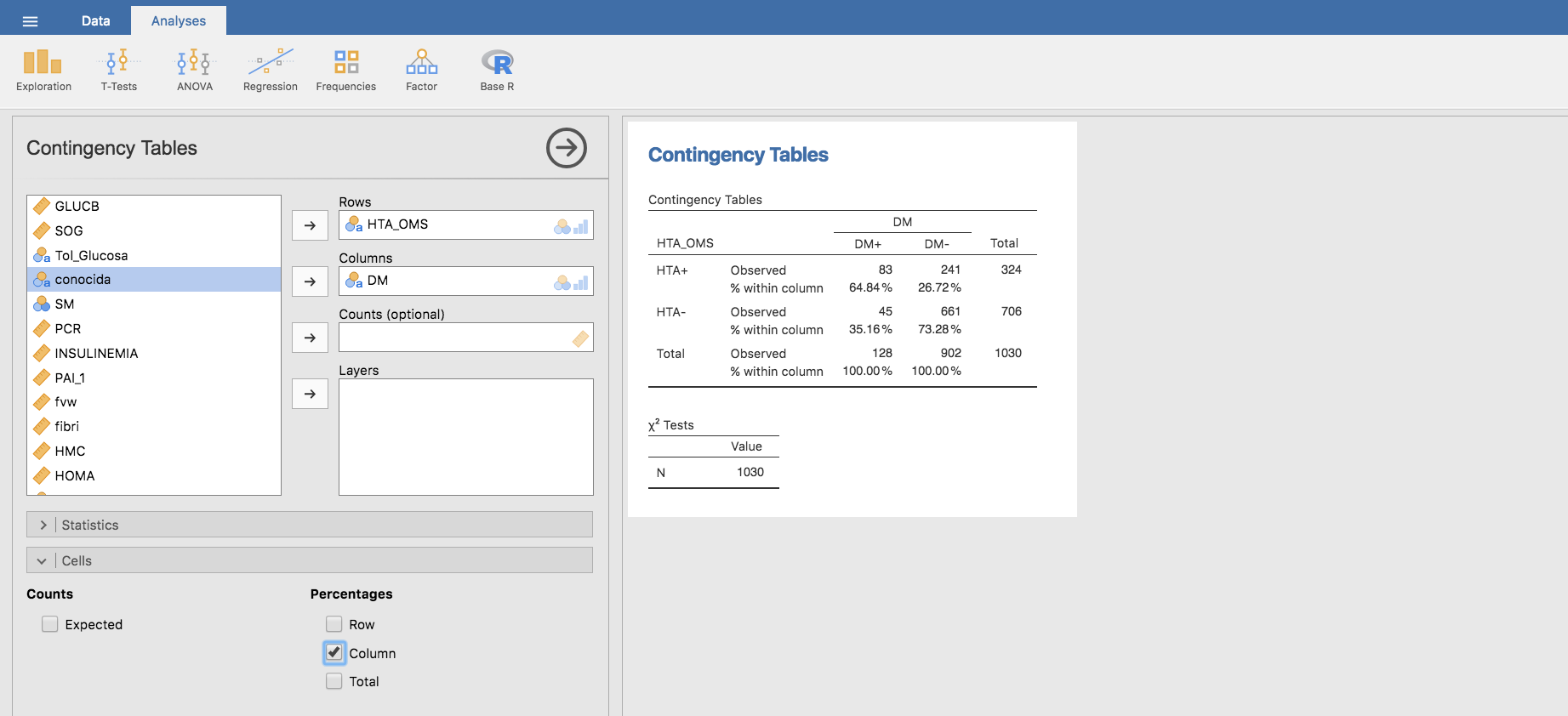
Observamos que la proporción de hipertensos es mucho mayor entre los diabéticos (64.84%) que entre los no diabéticos (26.72%). El siguiente test de la chi-cuadrado revela que esta asociación es significativa (no atribuíble al azar). Para realizar este test con Jamovi, expandimos la barra Statistics y hacemos clic en \(\chi^2\) en el apartado Tests:

 

 

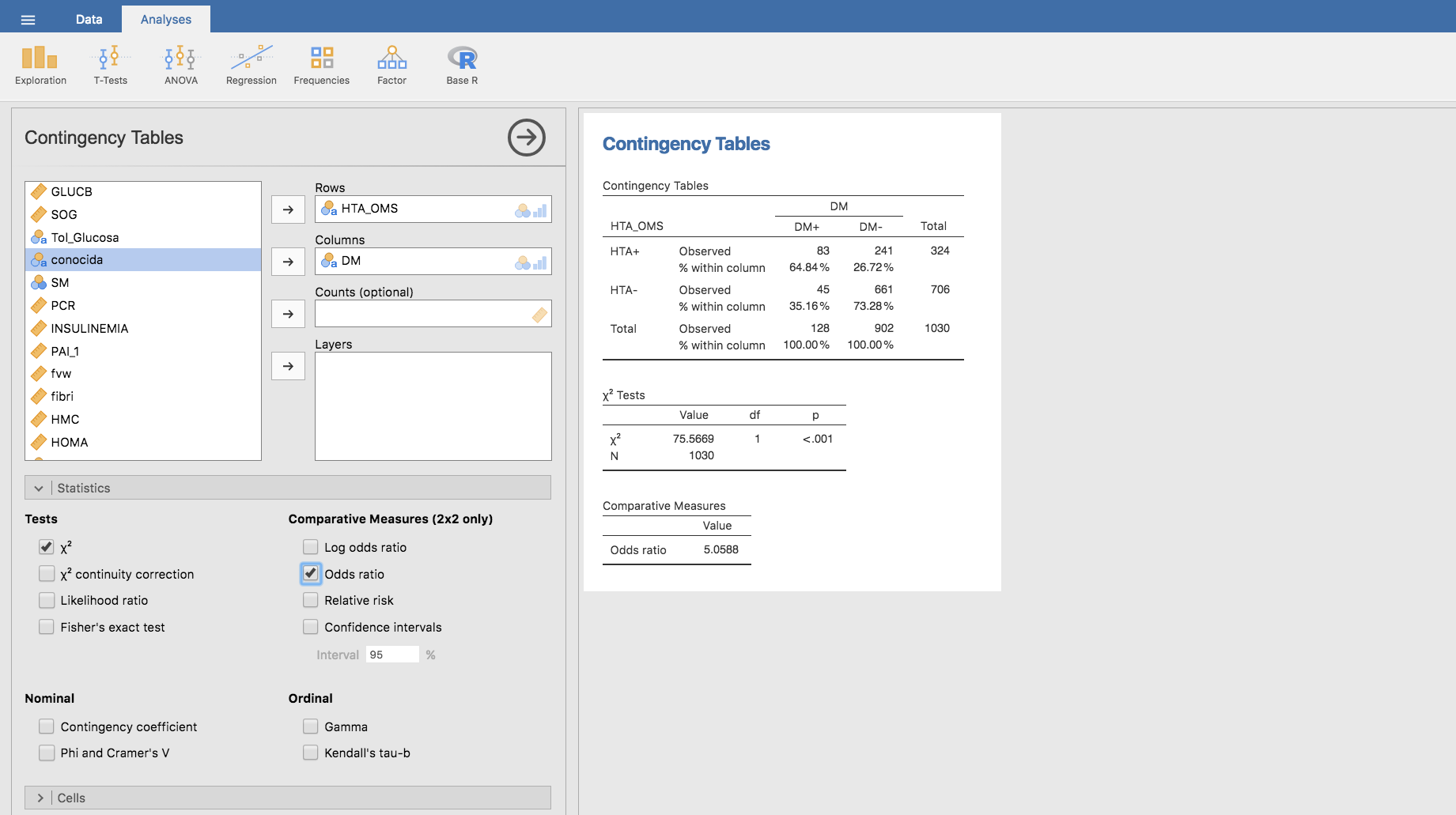
Finalmente, la odds-ratio la calculamos directamente sin más que seleccionar Odds ratio en el apartado Comparative measures:

 

 

 

 

Diagnóstico de la DM por A1C

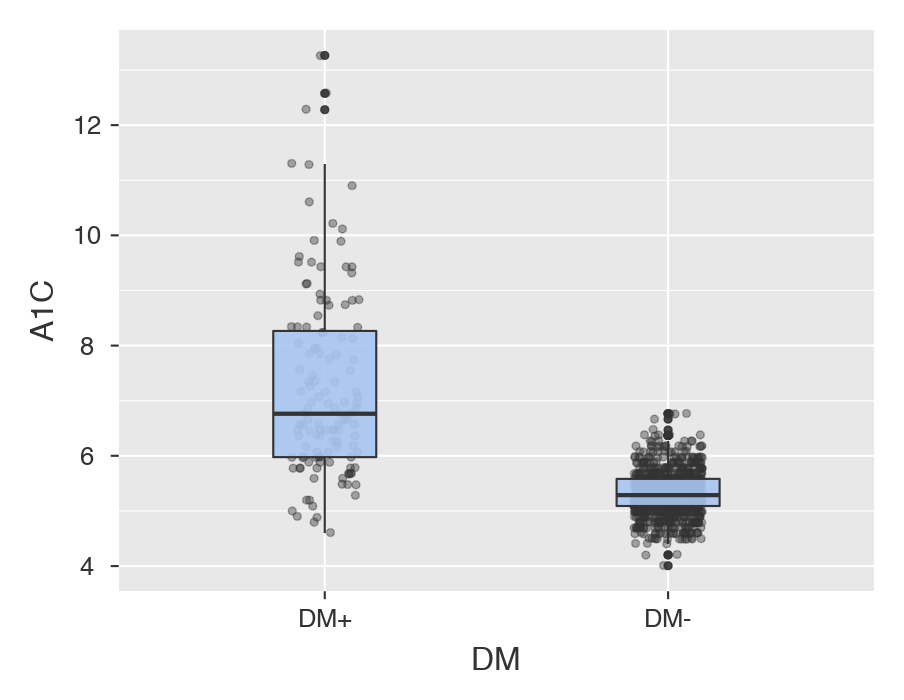
Supondremos en esta sección que disponemos de un marcador, que es una variable continua, cuyos valores difieren significativamente entre el grupo de las personas enfermas y el grupo de las sanas. Por ejemplo la hemoglobina glicosilada A1C difiere entre diabéticos y no diabéticos. Si representamos en un diagrama de cajas y bigotes los valores de esta variable en la muestra de Telde, según que los sujetos tengan o no DM, obtenemos la figura siguiente:

 

 

Para obtener este diagrama en Jamovi, en la pestaña Analyses utilizamos el menú Exploration/ Descriptives donde seleccionamos la variable A1C, clasificada en función de la variable DM. En la barra Statistics desmarcamos todas las opciones salvo el número de datos N, y en la barra Plots seleccionamos Box plot. Además, si seleccionamos la opción Data el diagrama se completa representando la distribución de los datos:

 

 

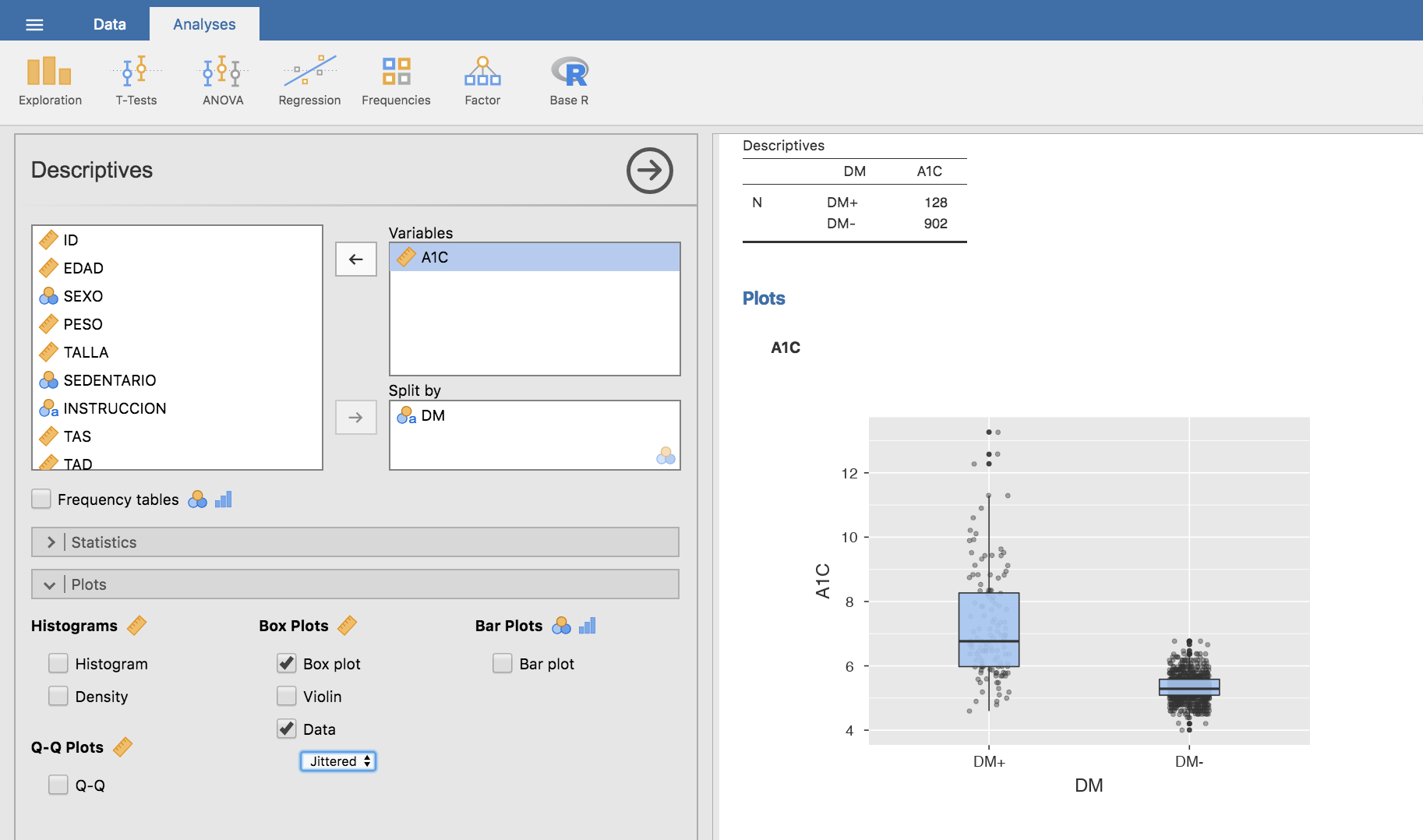
Si observamos la línea horizontal que representa un valor del \(6.5\)% de A1C, vemos que casi todos los sujetos con AIC menor que este valor están libres de DM, mientras que algo más de la mitad de los que tienen DM están por encima del mismo.

 

 

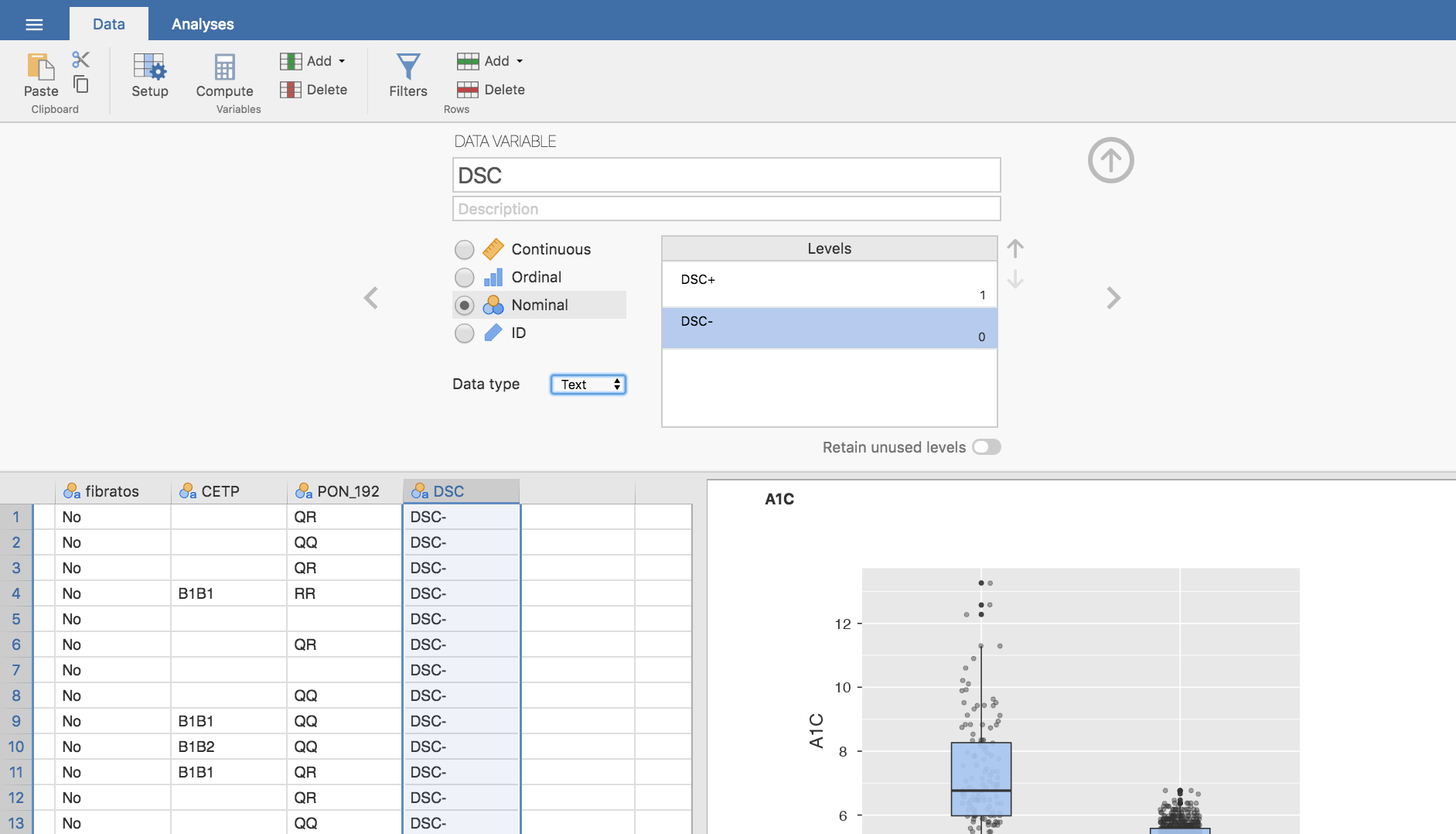
Podemos definir una nueva variable que llamaremos DSC (discriminante) que distinga si el sujeto tiene el valor de A1C por encima de \(6.5\)% o no; si está por debajo de \(6.5\)% entenderemos que el marcador es negativo (el gráfico indica que valores bajos se asocian con ausencia de DM), y por encima de \(6.5\)% es positivo. Al valor \(6.5\)% se le denomina valor cut-off del discriminante. En Jamovi ya sabemos cómo definir y codificar una variable, que para DSC es como sigue:

1. En la pestaña Data nos situamos en la primera columna libre después de los datos que tenemos, hacemos doble clic en esa columna, damos nombre a la variable y la definimos como un condicional. En principio, con valores \(1\) si A1C es mayor que \(6.5\)% y \(0\) si es menor.

 

 

2. Copiamos los datos que están en la columna que acabamos de añadir:

 

 

y los pegamos en la columna contigua:

 

 

3. Eliminamos la variable que habíamos llamado DSC.

 

4. En la última columna (llamada AZ en nuestro caso), hacemos doble clic en su nombre para recodificarla, llamando DSC- al nivel \(0\) y DSC+ al nivel \(1\), modificar su nombre y reordenar los niveles, situando DSC+ en primer lugar:

 

 

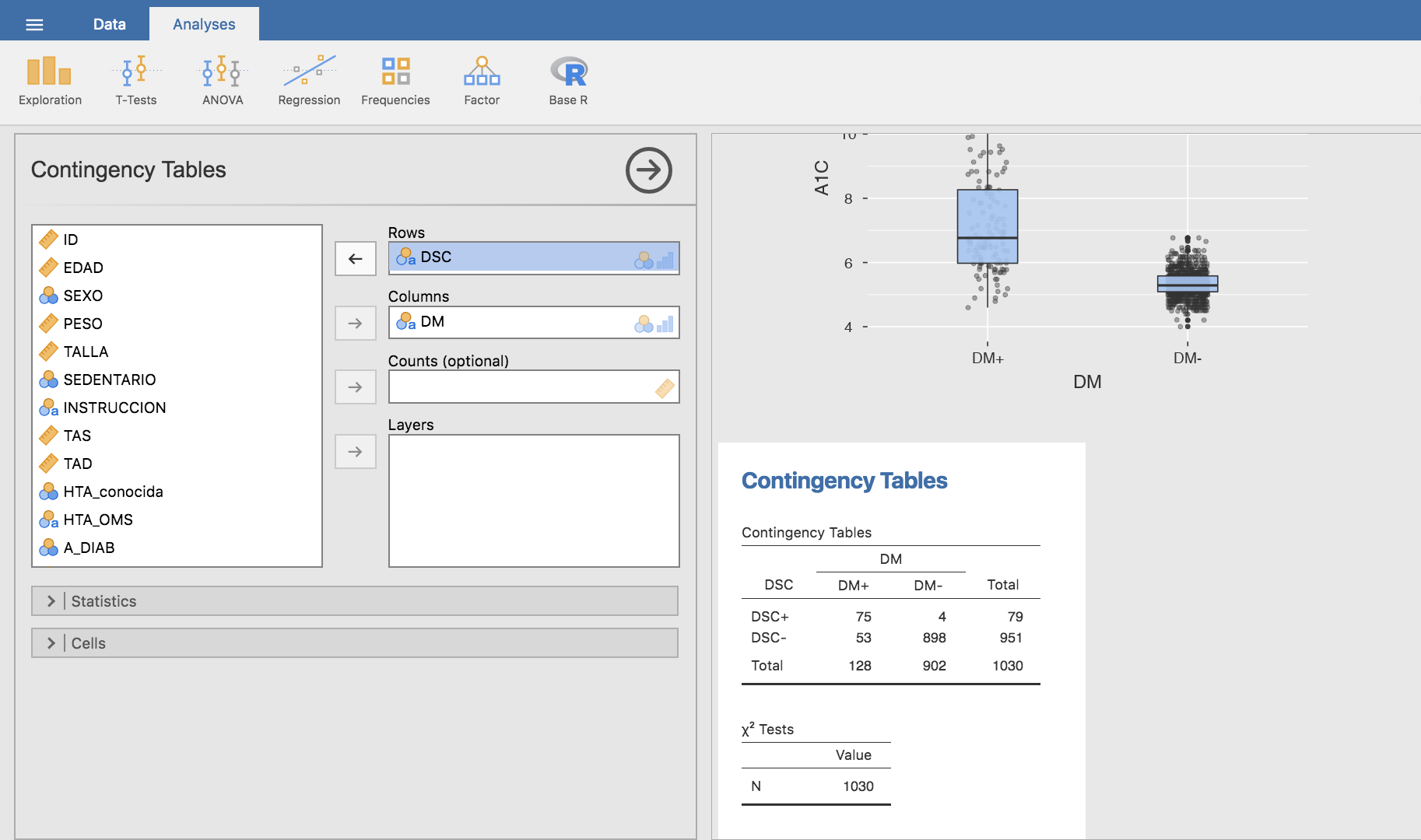
Si cruzamos esta variable con la DM obtenemos:

 

 

y en proporciones:

 

 

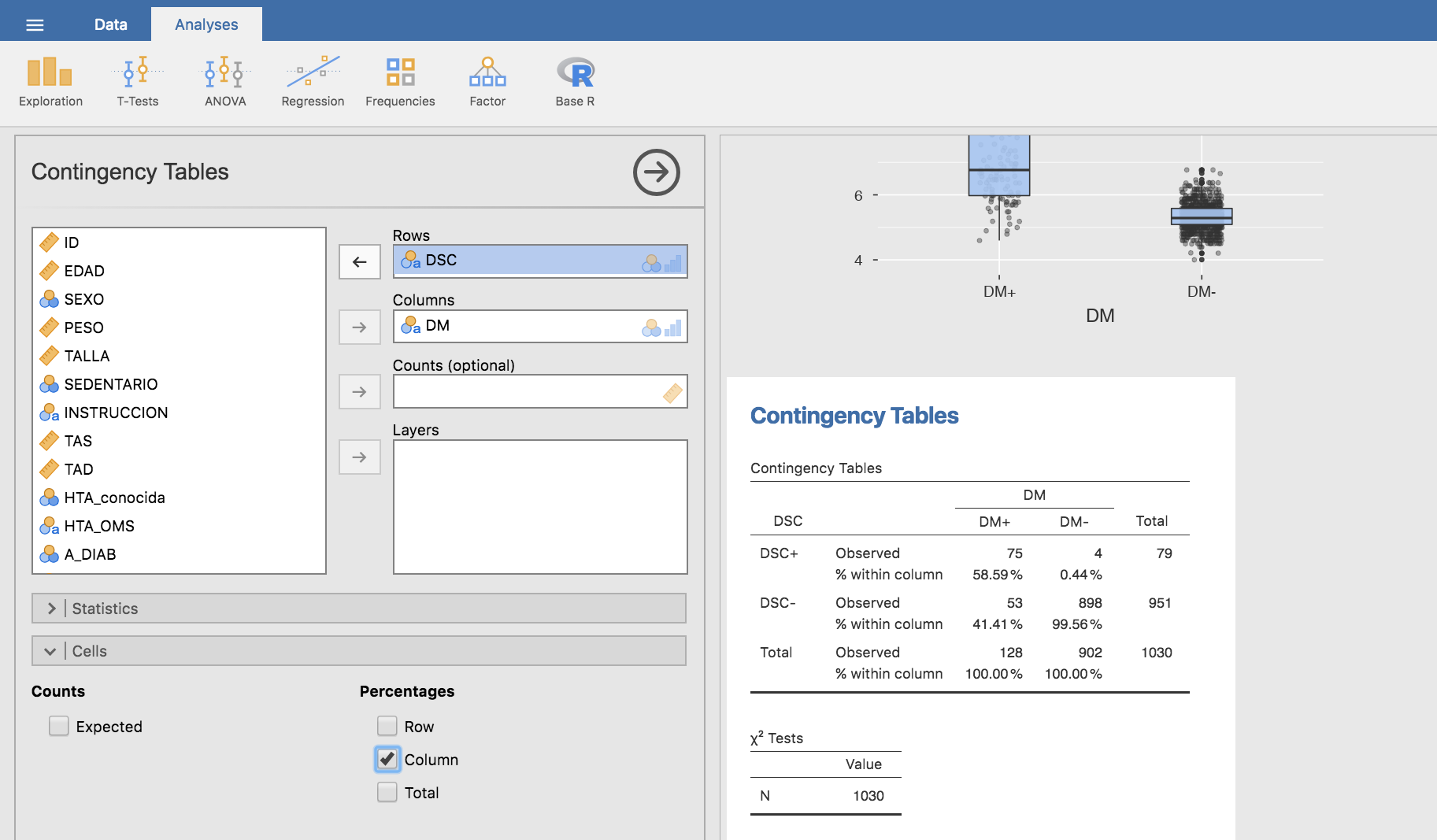
Por tanto, medir el valor de A1C y comprobar si está por encima o por debajo de \(6.5\)% constituye una prueba muy específica para la diabetes (la probabilidad estimada de que este marcador sea negativo si el sujeto es no diabético es del 99.56%), aunque poco sensible (la probabilidad estimada de que este marcador sea positivo si el sujeto es diabético es del 58.59%).

 

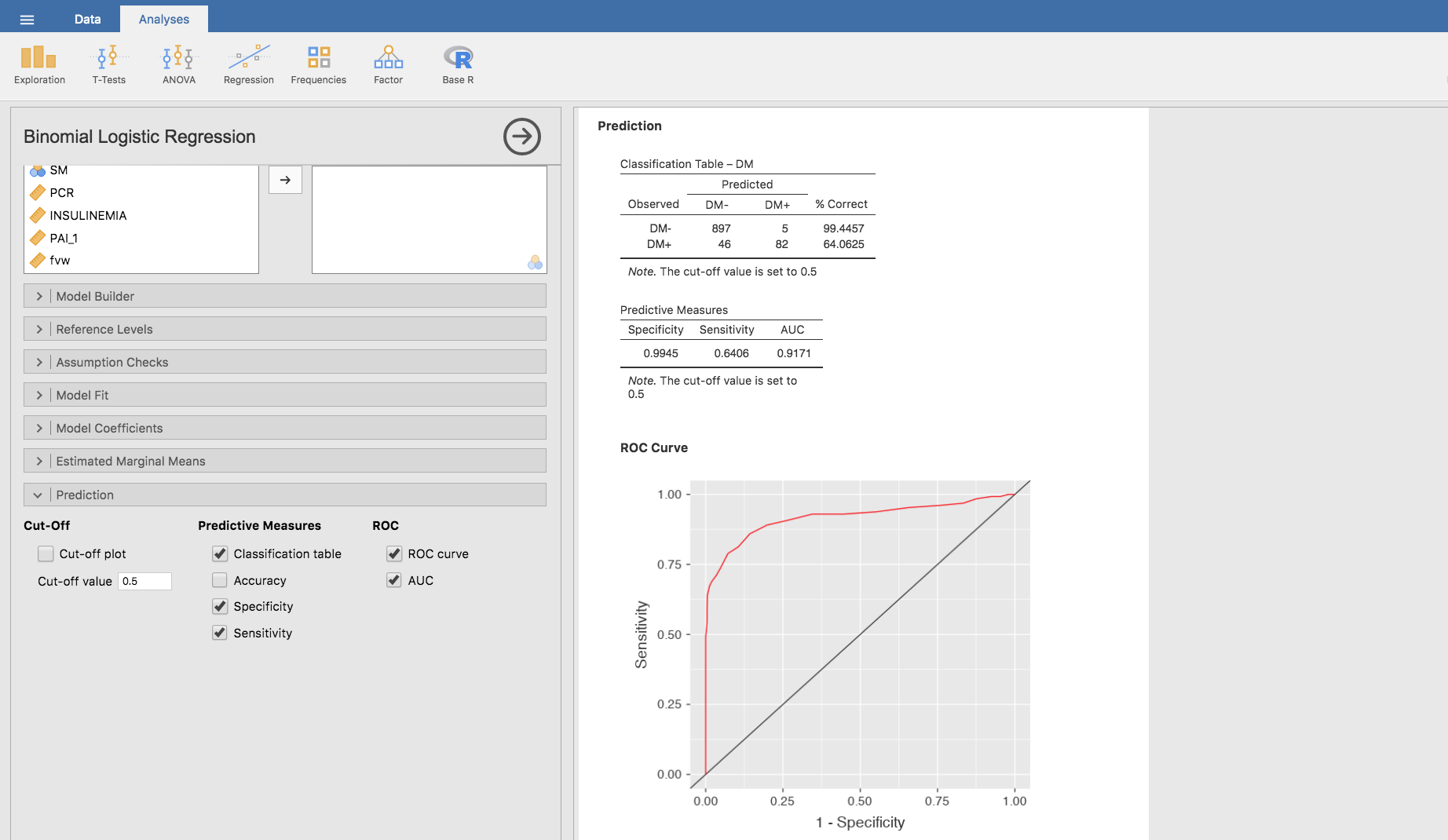
En el menú Regression/Logistic Regression/2 Outcomes tenemos la opción de calcular de manera directa la especificidad y sensibilidad, así como otras características, de una prueba diagnóstica. En nuestro caso, seleccionando DM como variable dependiente y DSC como Factors obtenemos una predicción de los coeficientes del modelo, y expandiendo la barra Prediction y haciendo clic en Specifity y Sensitivity obtenemos los valores buscados:

 

 

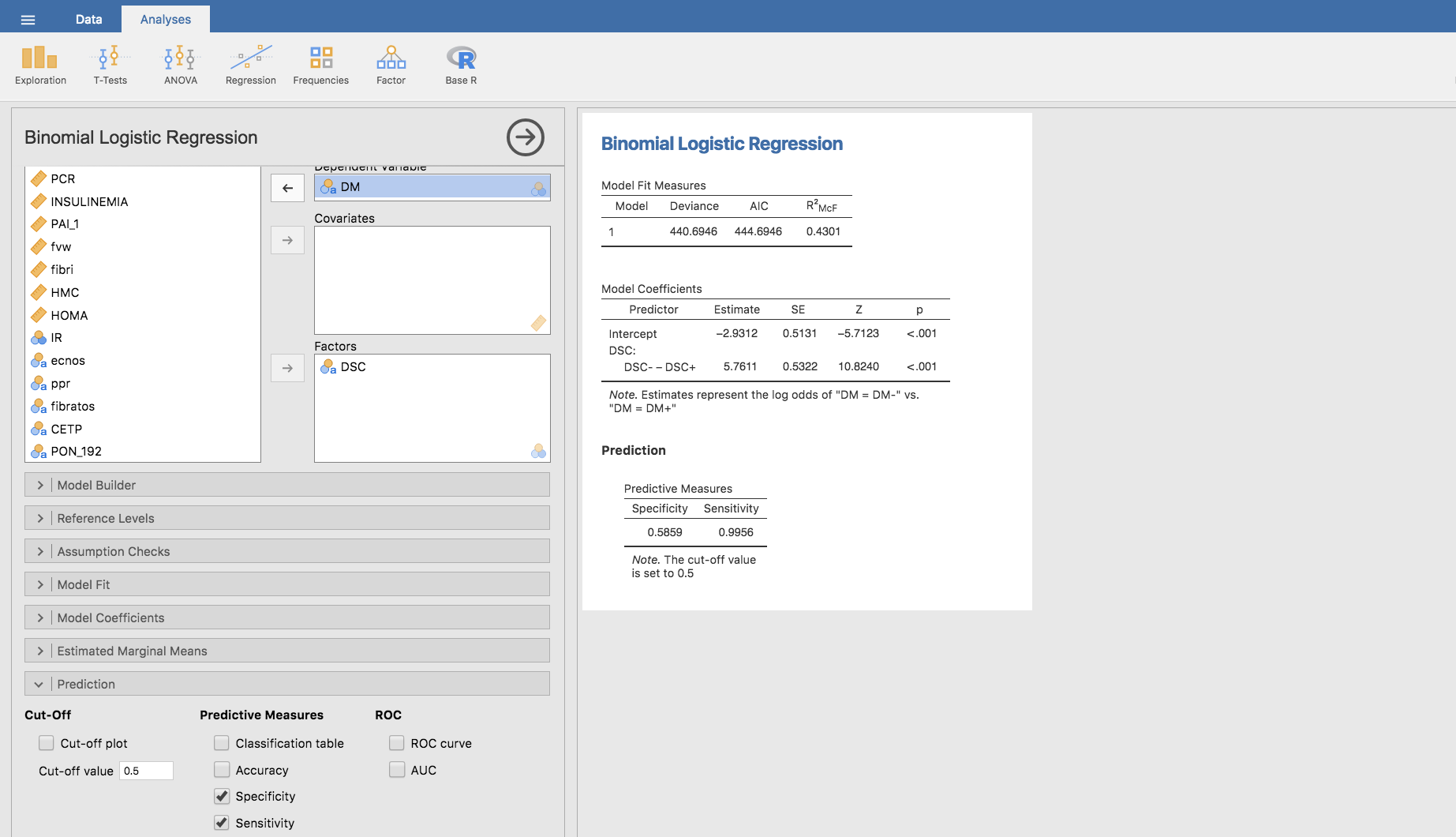
los cuales, efectivamente, coinciden con los calculados como proporciones por columnas en la tabla cruzada de DM y DSC.

 

Curva ROC

Para construir con Jamovi la curva ROC para la variable DM según se varía el umbral de la variable A1C, utilizamos el menú Regression / Logistic Regression / 2 Outcomes considerando DM como variable dependiente y A1C como Covariates. Además, en Reference Levels seleccionamos DM- como nivel de referencia:

 

 

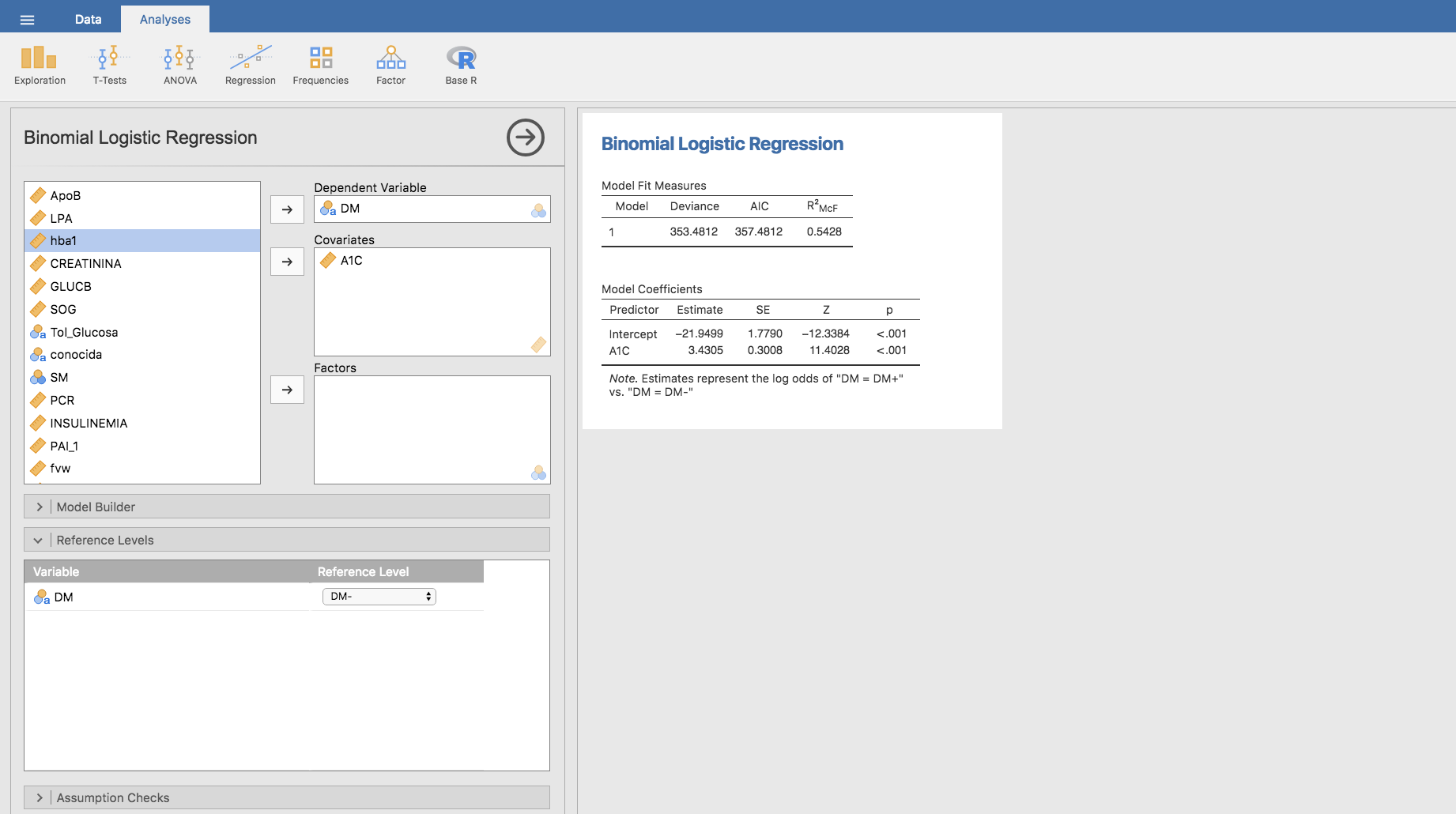
y en la barra Predictions seleccionamos ROC curve:

 

 

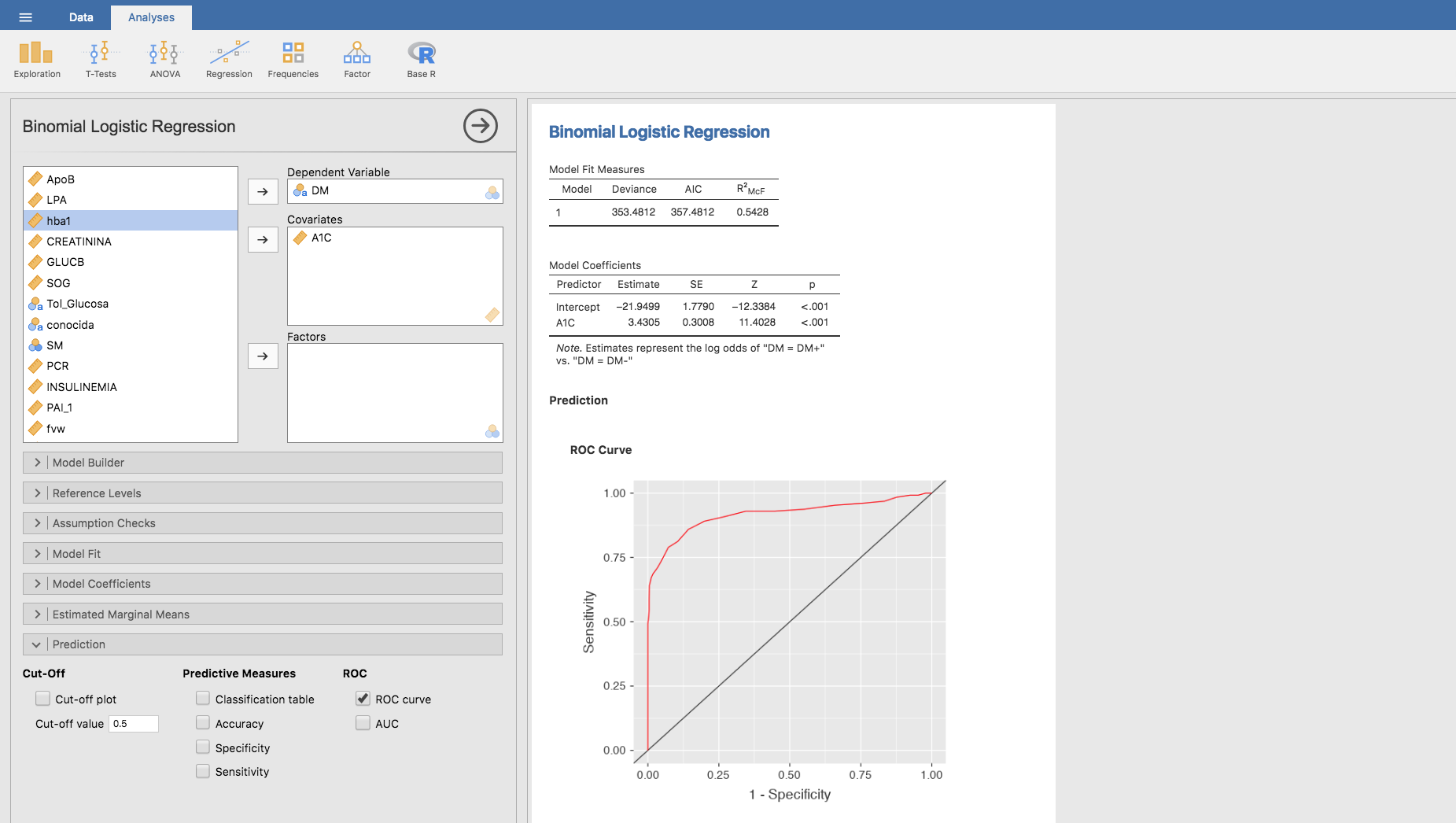
cuyo resultado gráfico es el siguiente:

 

 

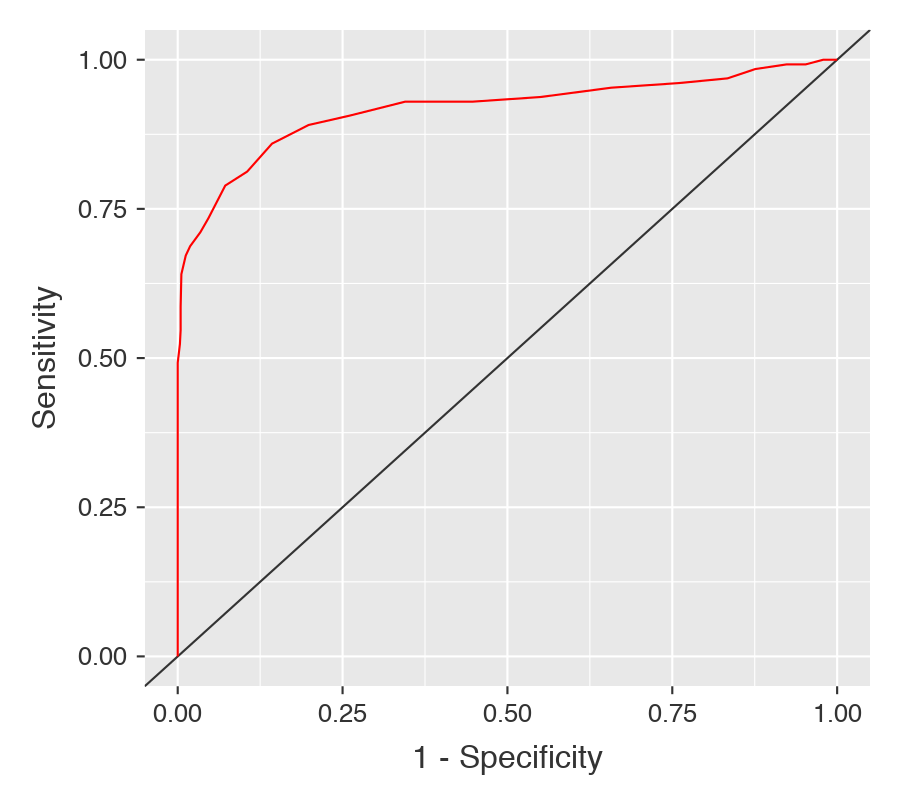
Si además, queremos cacular el área bajo la curva hacemos clic en AUC, justo debajo de ROC curve:

 

 

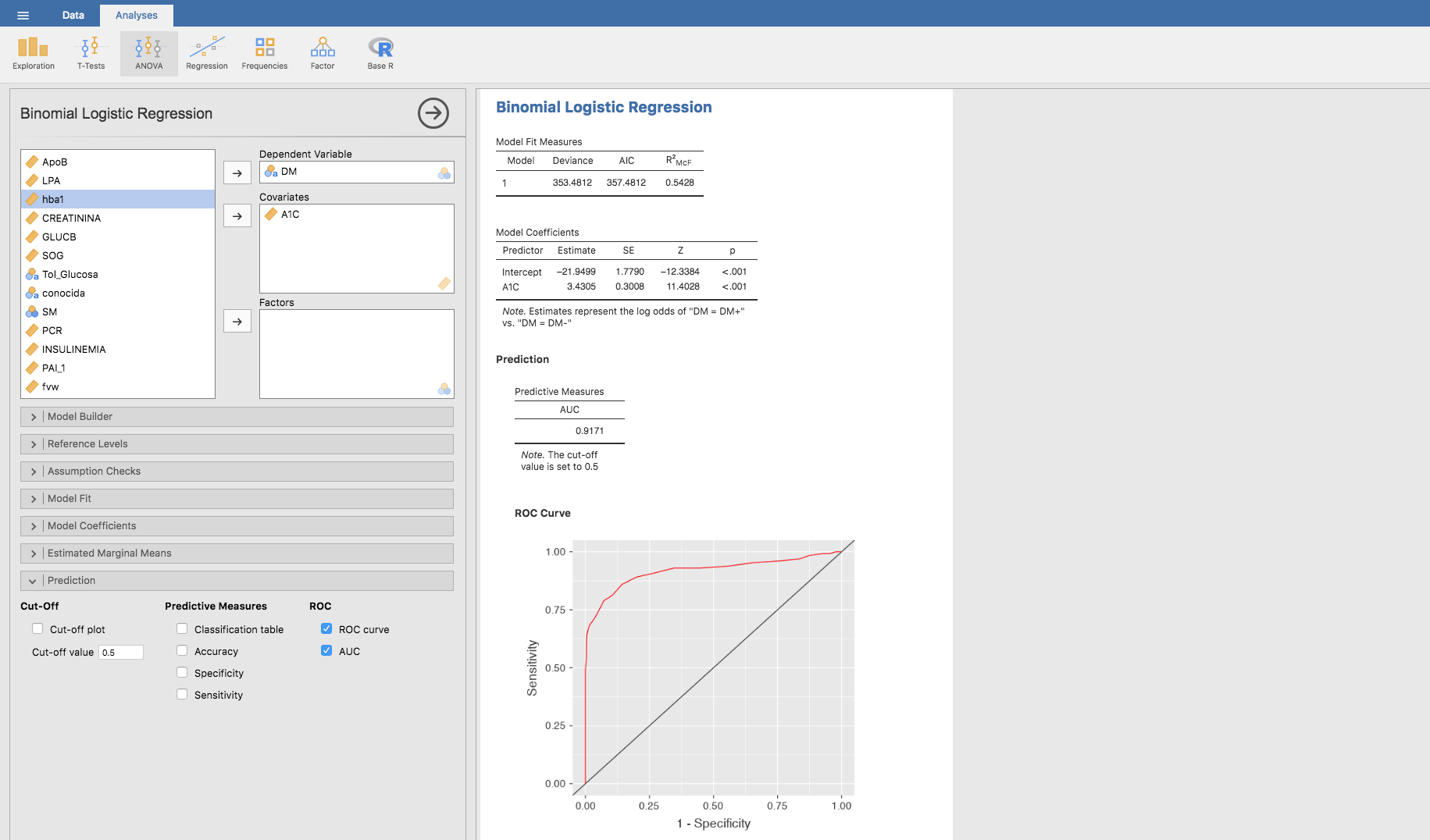
También podemos obtener una representación gráfica de las medias marginales, utilizando la barra Estimated Marginal Means como se indica a continuación:

 

 

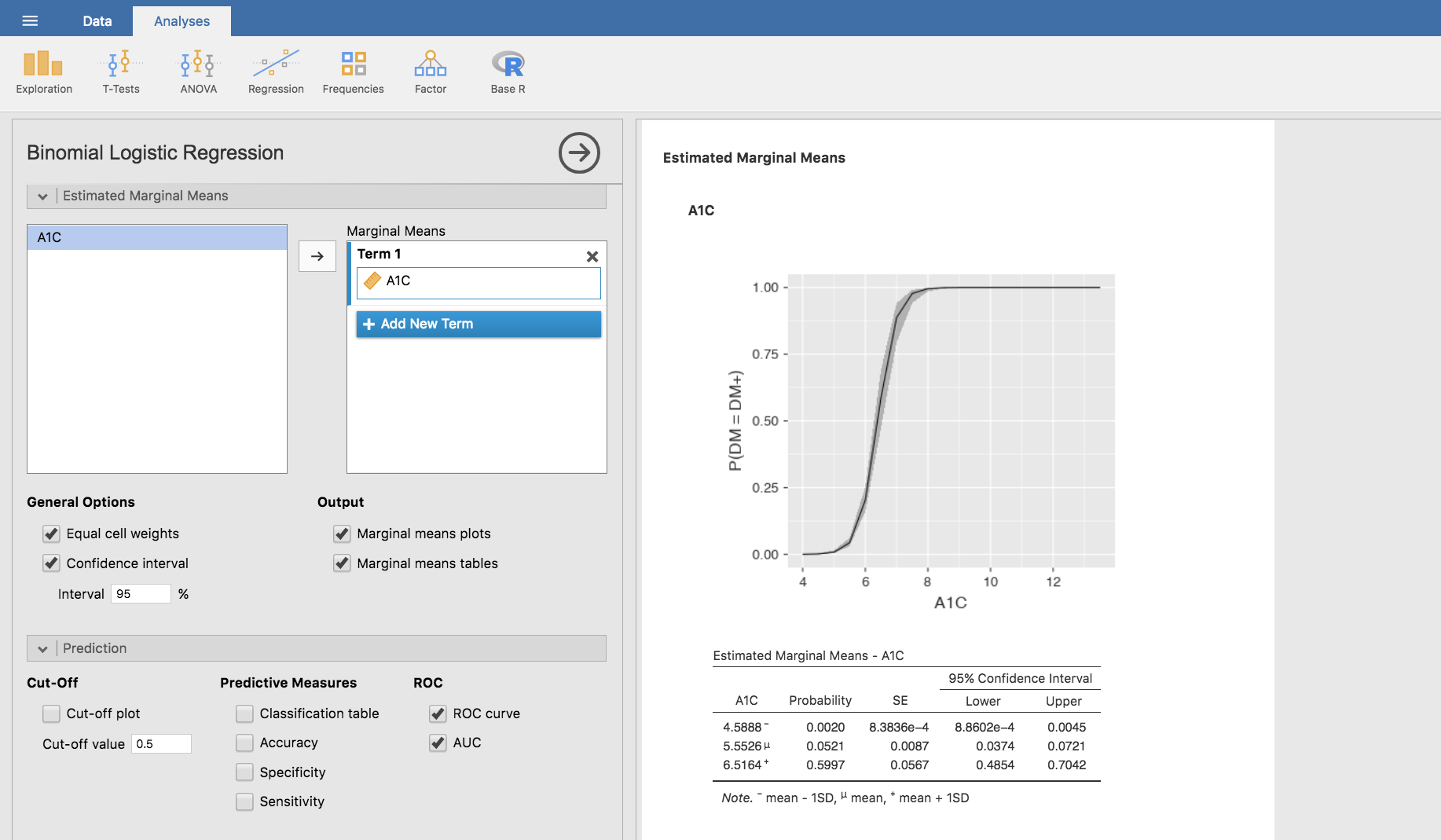
En lo que a medidas predictivas se refiere, volviendo a la barra Predictive Measures, calculamos la sensibilidad y especificidad de A1C como prueba diagnóstica para predecir la DM:

 

 

También puede interesarnos determinar el valor del cut-off en el que se “igualan/maximizan” sensibilidad y especificidad. La idea es encontrar aquel valor de la variable que al ser usado como punto de corte (cutoff) para discriminar entre sanos y enfermos, maximiza cierta función de la sensibilidad y la especificidad. Por defecto la función a maximizar es:

\[ {\left(1-sensitivity\right)}^2 + {\left(1-specificity\right)}^2\]

cuyo objetivo es conseguir que la sensibilidad y la especificidad se aproximen (simultáneamente) todo lo posible a \(1\).

Este valor óptimo es posible aproximarlo representando gráficamente las curvas de sensibilidad y especificidad, haciendo clic en Cut-off plot:

 

 

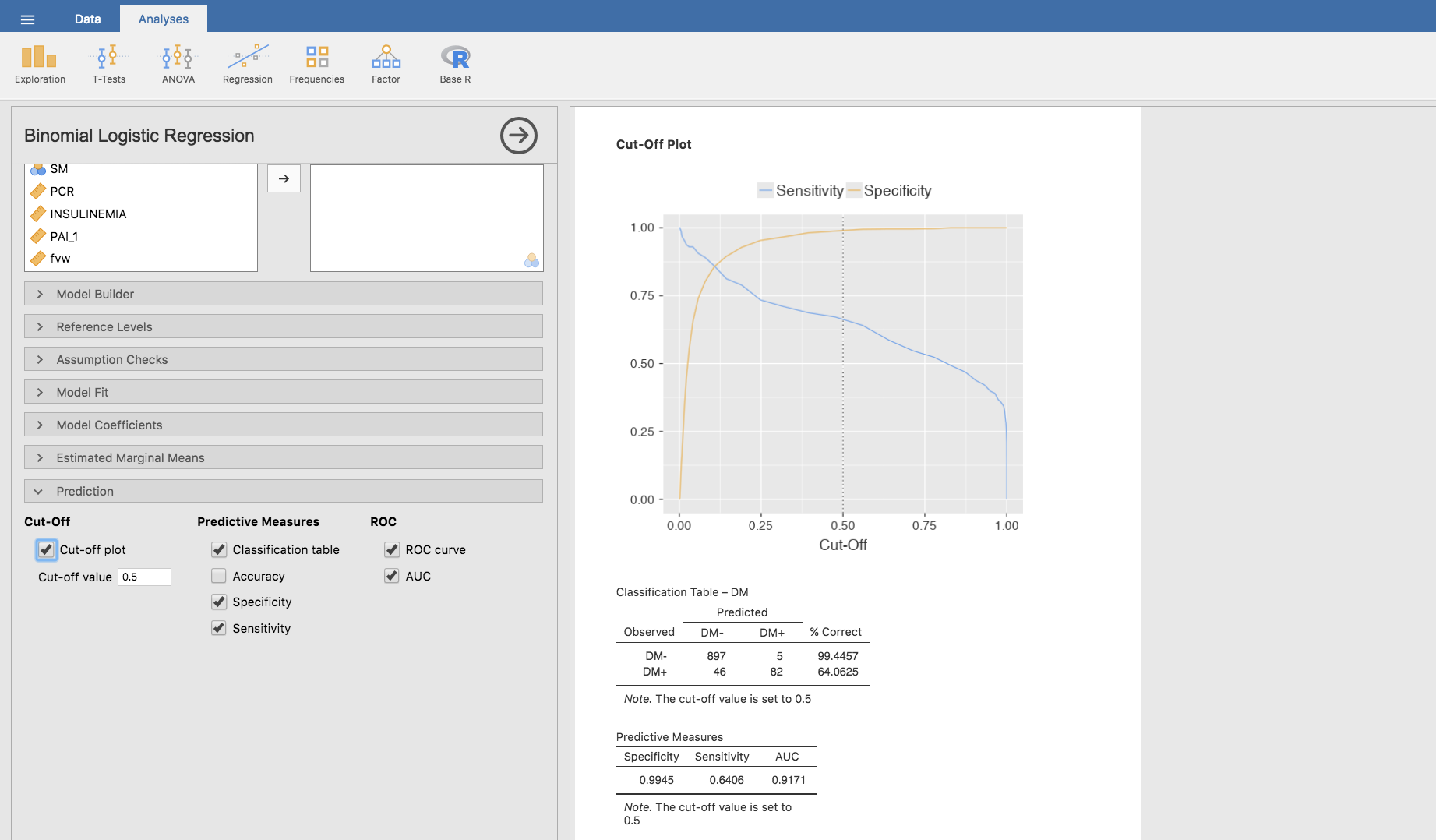
Tras tantear algunos valores, observamos que eligiendo \(0.1\) como cut-off value en Jamovi la línea vertical de trazo discontinuo que aparece en la gráfica se aproxima al punto de corte de ambas curvas. En realidad, el valor \(0.1\) representa la probabilidad \(P(DM+ / A1C)\), y no el valor del cut-off estrictamente hablando:

 

 

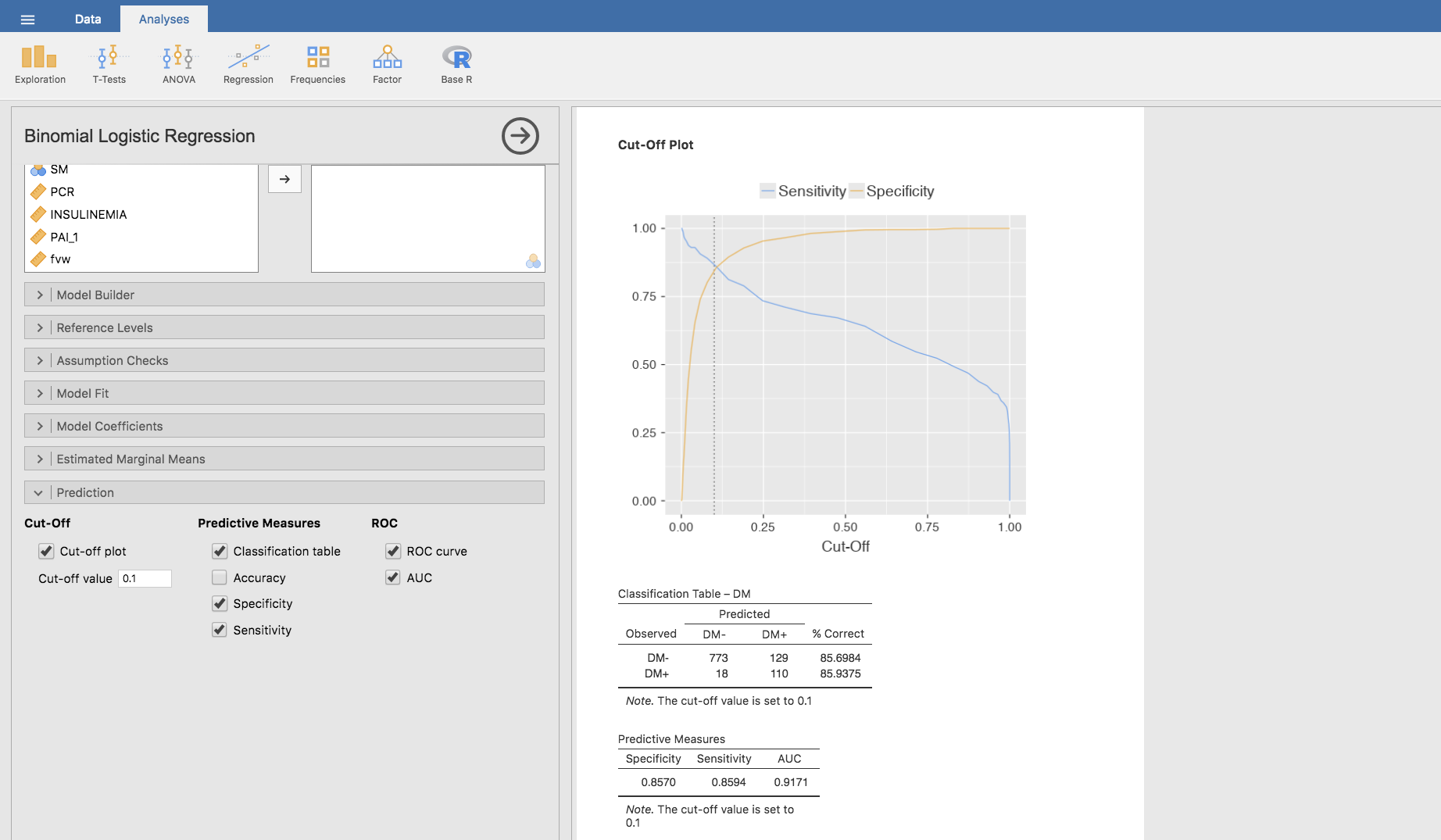
Ampliamos la representación gráfica:

 

 

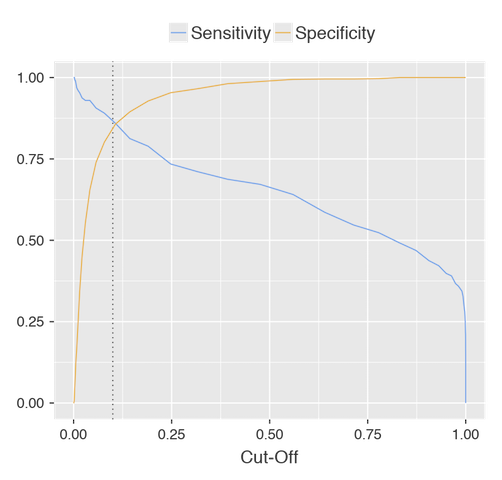
Además, al fijar el valor de esa probabilidad en \(0.1\), observamos como cambian y casi se igualan acercándose lo máximo posible a \(1\) la sensibilidad y la especificidad.

Ahora, para obtener el valor del cut-off óptimo de la variable A1C consideramos nuestro modelo de regresión logística:

\[ P(DM+/A1C)=\frac{e^{\beta_0 +\beta_1\cdot A1C}}{1+e^{\beta_0 +\beta_1\cdot A1C}}\]

donde conocemos \(\beta_0 = -21,9499\), \(\beta_1 = 3.4305\) (valores proporcionados por Jamovi en la tabla denominada Model Coefficients) y la probabilidad \(P(DM+/A1C)=0.1\). Por tanto:

\[ 0.1=\frac{e^{-21.9499 +3.4305\cdot A1C}}{1+e^{-21.9499 +3.4305\cdot A1C}}\Rightarrow \frac{0.1}{0.9}= e^{-21.9499 +3.4305\cdot A1C}\Rightarrow\]

 

\[ 0.11=e^{-21.9499 +3.4305\cdot A1C}\Rightarrow A1C=\frac{ln(0.11)+21.9499}{3.4305}=5.755\]

Llegados a este punto, podemos redefinir la regla discriminante (prueba diagnóstica) en función de este cutoff óptimo para A1C (5.75%), igual que hicimos más arriba con el 6.5%, considerando que la prueba es positiva si \(A1C>5.75\) y negativa en caso contrario.

 

 

 

Ejercicio.

1. HDL como predictor de la presencia del genotipo homocigoto B1/B1 en el polimorfismo Taq 1B. En el estudio de Telde se midió el polimorfismo Taq1B en el gen de la Cholesteryl ester transfer protein (CETP). Este polimorfismo tiene dos alelos, B1 y B2, por lo cual los posibles genotipos son B1/B1, B1/B2 y B2/B2. Estudios previos indican que los individuos homocigotos B1/B1 tienden a presentar valores más bajos de HDL.

1. Comprobar que en la base de datos de Telde, la variable CETP registra el genotipo de este polimorfismo en aquellas personas en que se pudo medir, mediante el cálculo de una tabla de frecuencias.

2. Construir una nueva variable Taq_1B que nos indique si el individuo es portador o no del genotipo B1/B1.

3. Representar un boxplot que muestre la posible asociación entre este genotipo y el valor del HDL, y confirme la presencia de valores ligeramente más bajos de HDL en los sujetos B1/B1.

4. Construir la curva ROC para evaluar la capacidad discriminante del valor de HDL como predictor de la presencia del genotipo homocigoto B1/B1 en el polimorfismo Taq1B del gen CETP. Determinar el cutoff óptimo así como los valores de sensibilidad y especificidad alcanzados para dicho cutoff.