Definición: Modelo Lineal
Un vector de variables aleatorias \(\mathbf{Y}= \left(y_1,y_2,\dots, y_n\right)'\) sigue un modelo lineal con variables independientes o explicativas \(X_1, X_2, \dots, X_p\) si:
\[\mathbf{Y} = \beta_{0}+\beta_{1}X_{1}+\beta_{2}X_{2}+\dots+\beta_{p}X_{p}+\varepsilon,\,\,\,\,\,\,\varepsilon\approx N
\left(0,\sigma_\varepsilon\right)\]
Definición: Modelo Lineal
Esto significa que si sobre los \(n\) objetos (o sujetos) de una muestra se han observado las variables \(X_1, X_2, \dots, X_p\) e \(Y\), entonces para el \(i\)-ésimo elemento de la muestra se tiene que:
\[y_{i}=\beta_{0}+\beta_{1}x_{1i}+\beta_{2}x_{2i}+\dots+\beta_{p}x_{pi}+e_{i}\] siendo \(y_i\) el valor de \(\mathbf{Y}\), y \(x_{ji}\) el valor de la variable \(X_j\) medidos en dicho objeto.
El valor de \(e_i\) es la diferencia entre \(y_i\) y el valor que se puede predecir a partir de las \(X_j\), esto es, \(\hat{y_i}=\beta_{0}+\beta_{1}x_{1i}+\beta_{2}x_{2i}+\dots+\beta_{p}x_{pi}\).
Asumiremos que los valores de \(e_i\) siguen una distribución \(N\left(0,\sigma_\varepsilon\right)\)
Ejemplo:
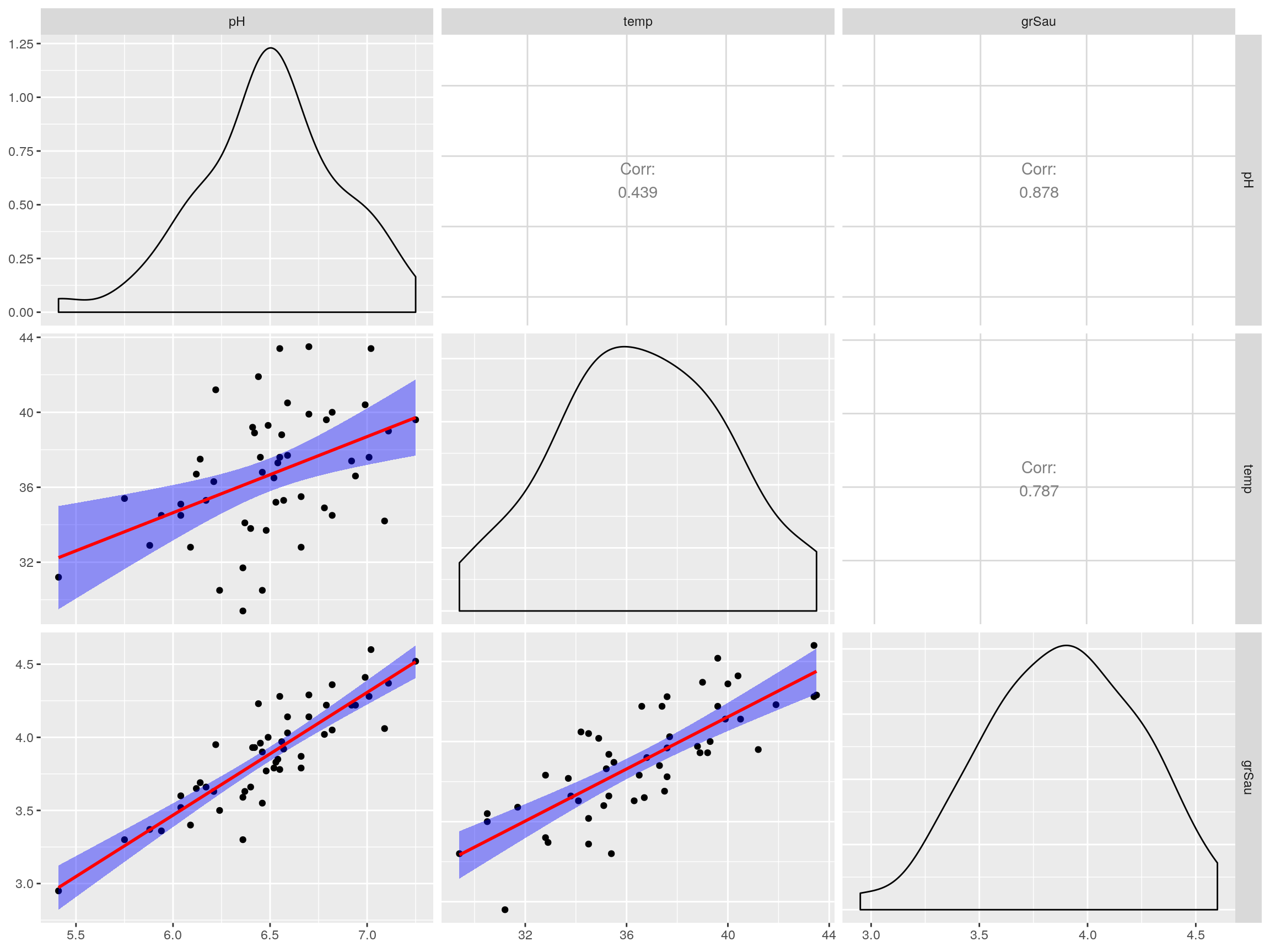
A continuación se muestran algunos de los datos obtenidos en un experimento para medir la velocidad de crecimiento de la bacteria S. aurea sobre un sustrato vegetal (verduras de ensalada) bajo diversas condiciones de pH y temperatura:
##
## ---------------------
## pH temp grSau
## ------ ------ -------
## 6.37 34.1 3.63
##
## 6.66 35.5 3.87
##
## 6.46 36.8 3.9
##
## 6.94 36.6 4.22
##
## 6.17 35.3 3.66
##
## 6.55 37.6 3.78
##
## 5.94 34.5 3.36
##
## 6.54 37.3 3.85
##
## 6.14 37.5 3.69
##
## 6.7 39.9 4.14
## ---------------------
La variable grSau es la velocidad de crecimiento de la bacteria (en cels/ml/min)
Gráficamente:
Estimación del modelo lineal.
El modelo lineal puede estimarse por Mínimos cuadrados: Este método consiste en encontrar los valores de los parámetros \(\beta_i\) que minimizan la distancia entre los valores observados y los predichos:
\[\underset{\beta_{0},\beta_{1},\dots,\beta_{p}}{min}\sum_{i=1}^{n}\left(y_{i}-\hat{y}_{i}\right)^{2}=\underset{\beta_{0},\beta_{1},\dots,\beta_{p}}{min}\sum_{i=1}^{n}\left(y_{i}-\beta_{0}-\beta_{1}x_{1i}+\beta_{2}x_{2i}+\dots+\beta_{p}x_{pi}\right)^{2}\]
Sólo en el caso de que los residuos del modelo sean normales e independientes puede llevarse a cabo adecuadamente la inferencia clásica sobre los parámetros del modelo.
Estimación del modelo lineal.
En R la estimación del modelo se realiza mediante:
##
## Call:
## lm(formula = grSau ~ pH, data = growth)
##
## Coefficients:
## (Intercept) pH
## -1.5682 0.8393
lm(grSau~temp,data=growth)
##
## Call:
## lm(formula = grSau ~ temp, data = growth)
##
## Coefficients:
## (Intercept) temp
## 0.90165 0.08131
lm(grSau~pH+temp,data=growth)
##
## Call:
## lm(formula = grSau ~ pH + temp, data = growth)
##
## Coefficients:
## (Intercept) pH temp
## -2.09547 0.63082 0.05133
Estimación del modelo lineal.
y de manera más completa:
modelo=lm(grSau~pH+temp,data=growth)
summary(modelo)
##
## Call:
## lm(formula = grSau ~ pH + temp, data = growth)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.186542 -0.037014 0.002805 0.044446 0.112115
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -2.095468 0.158264 -13.24 <2e-16 ***
## pH 0.630820 0.026616 23.70 <2e-16 ***
## temp 0.051333 0.002879 17.83 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.06187 on 47 degrees of freedom
## Multiple R-squared: 0.9706, Adjusted R-squared: 0.9693
## F-statistic: 775.1 on 2 and 47 DF, p-value: < 2.2e-16
En esta salida de R podemos apreciar varios elementos importantes del ajuste de un modelo de regresión:
- F-statistic y su p-valor: corresponden al contraste de hipótesis:
\[H_0:\beta_{1}=\beta_{2}=\dots=\beta_{p}=0\] Si p-valor<0.05 se acepta esta hipótesis, en caso contrario se rechaza. La aceptación de esta hipótesis implica que el modelo ajustado no tiene valor predictivo ni explicativo.
- \(R^2\) (múltiple R-squared) y \(R^2\) ajustado (adjusted R squared) miden la calidad del ajuste al modelo lineal; cuánto más se aproxime su valor a 1 mejor es el ajuste.
- Pr(>|t|): Contrastes individuales sobre los coeficientes del modelo. Valores menores que 0.05 indican que el efecto de la variable correspondiente es significativo; valores mayores o iguales que 0.05 indican que puede aceptarse que el coeficiente es nulo.
Intervalos de confianza para los coeficientes:
## 2.5 % 97.5 %
## (Intercept) -2.41385336 -1.77708196
## pH 0.57727519 0.68436502
## temp 0.04554181 0.05712507
Predicción
x0=data.frame(pH=6.75,temp=40)
- Predicción con intervalo de confianza para la media
predict(modelo,newdata=x0,interval="confidence")
## fit lwr upr
## 1 4.215906 4.190548 4.241263
- Predicción con intervalo de confianza para el valor predicho:
predict(modelo,newdata=x0,interval="prediction")
## fit lwr upr
## 1 4.215906 4.088891 4.34292
Visualización del grado de ajuste
Se puede “visualizar” el grado de ajuste alcanzado presentando gráficamente los valores predichos frente a los observados. Si el modelo es adecuado, los puntos así obtenidos deben disponerse en torno a la diagonal del primer cuadrante.
Ejemplo
ggplot(data.frame(obs=growth$grSau,pred=fitted(modelo)), aes(x=obs,y=pred)) + geom_point() +
geom_abline(intercept = 0,slope=1,color="red3")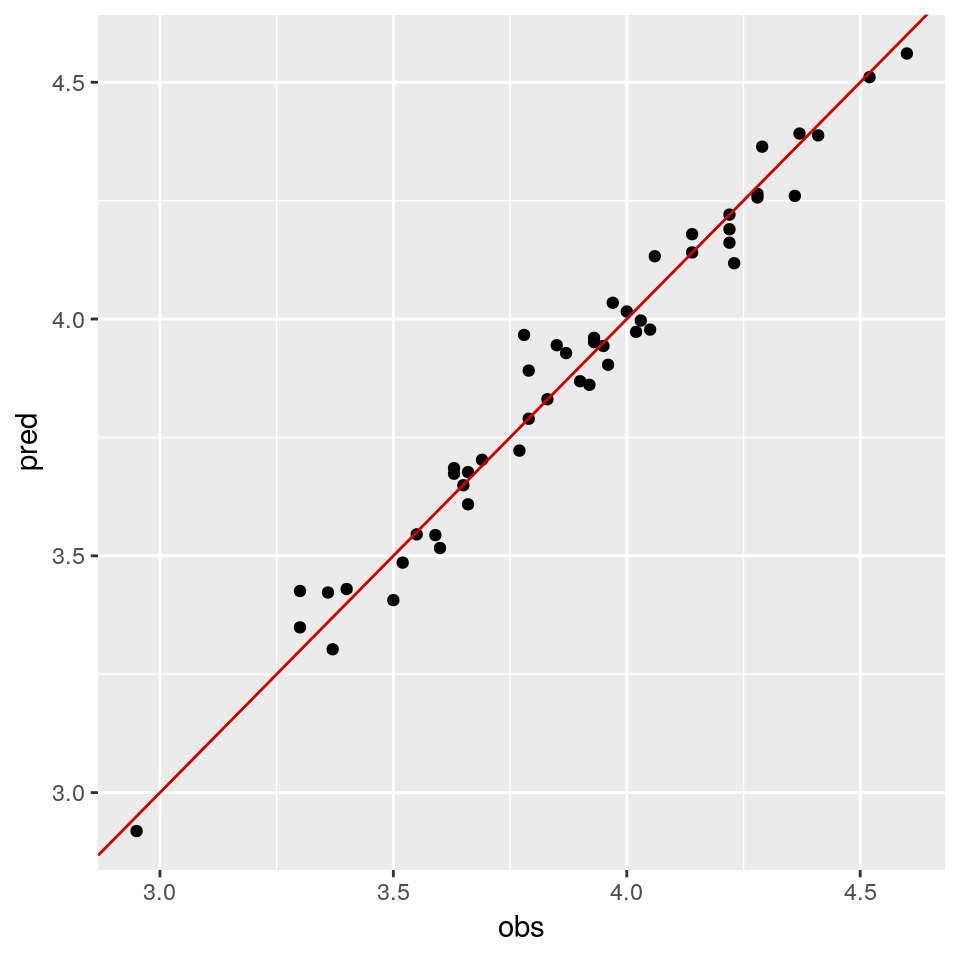
Validación del modelo.
Normalidad de los residuos
Podemos visualizar la normalidad mediante un histograma de los residuos:
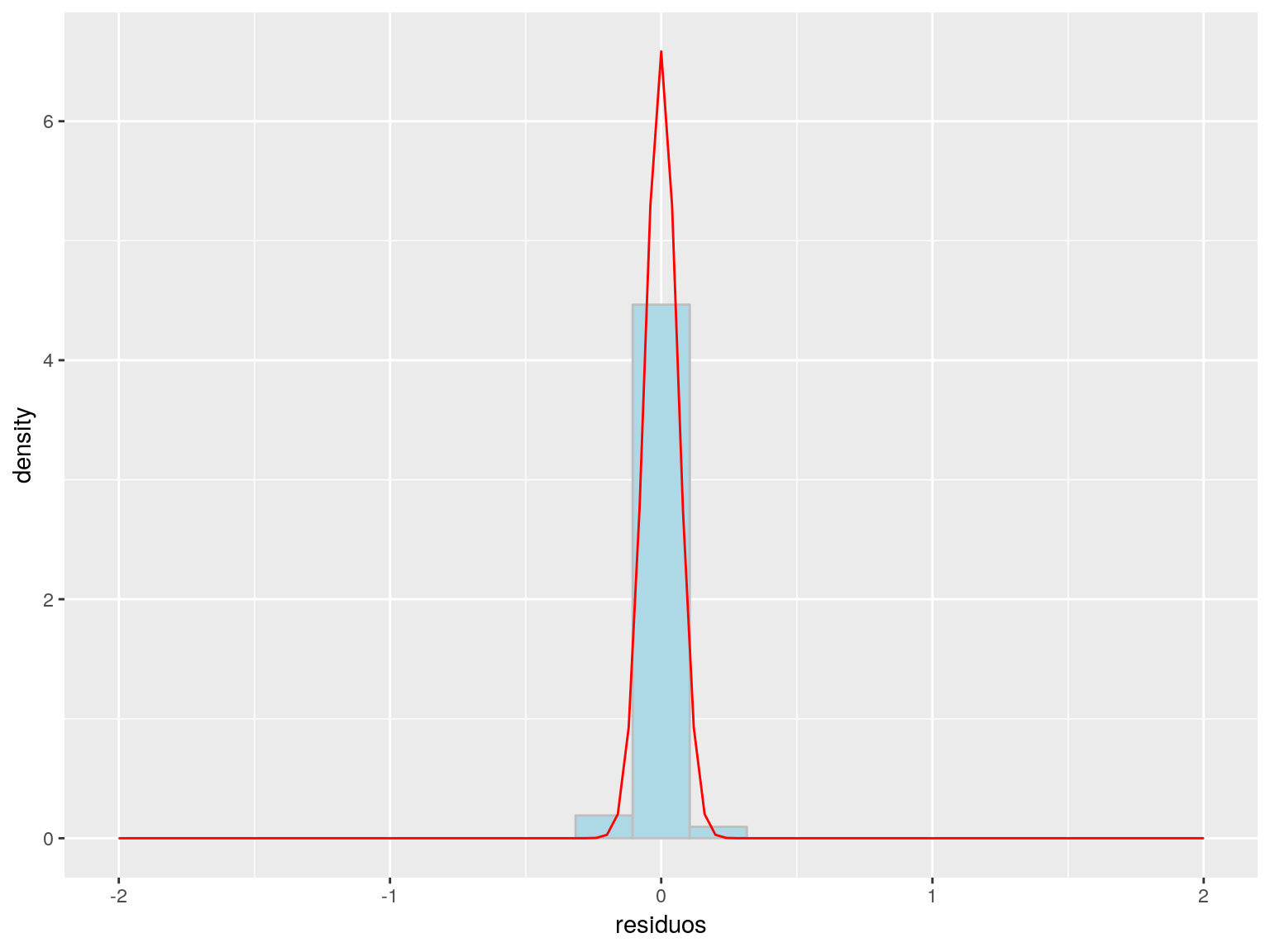
O mejor con un qqplot:
## Loading required package: carData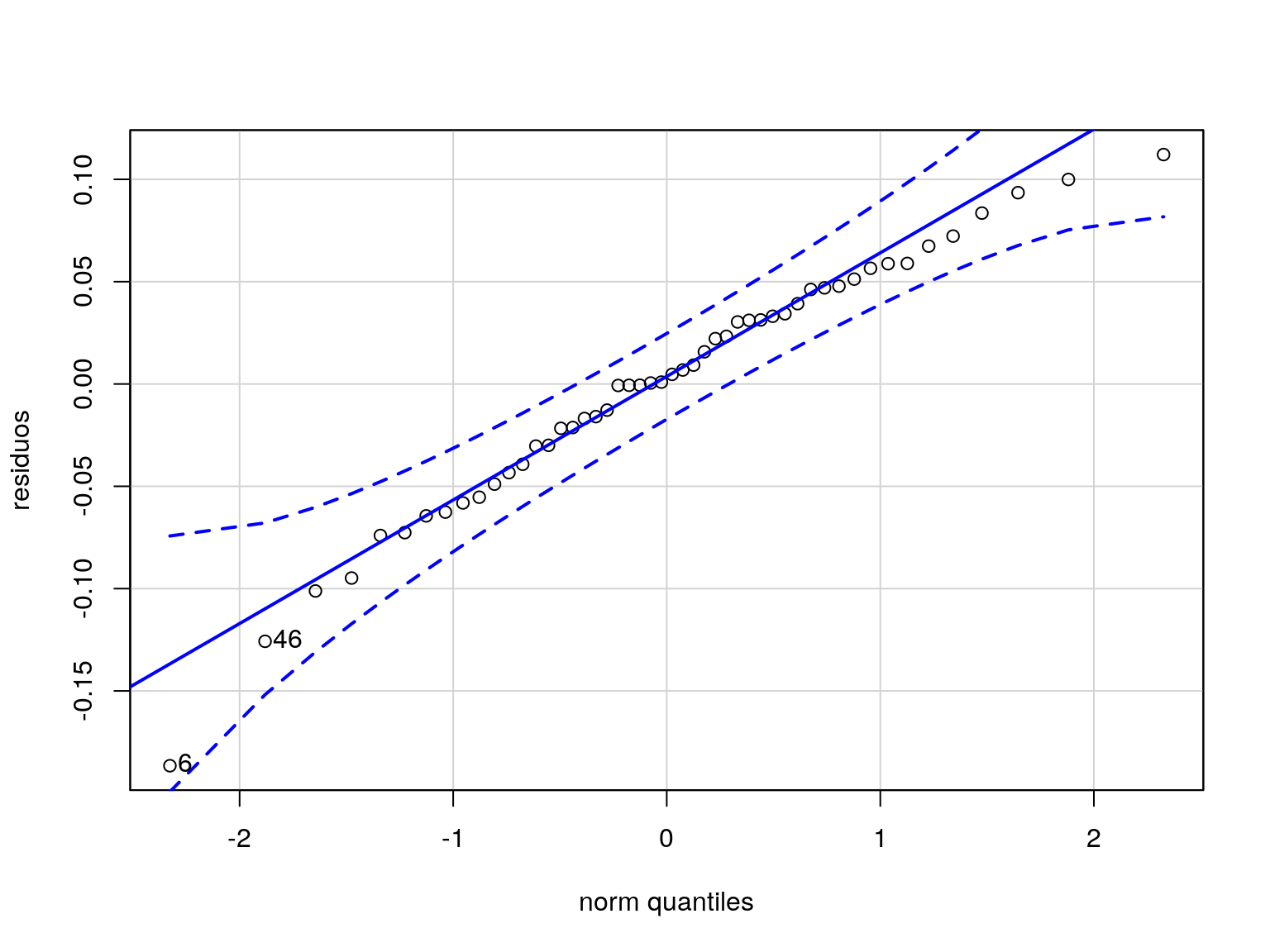
## [1] 6 46
El test de Shapiro-Wilk contrasta la normalidad de los residuos:
##
## --------------------------
## Test statistic P value
## ---------------- ---------
## 0.9756 0.3853
## --------------------------
##
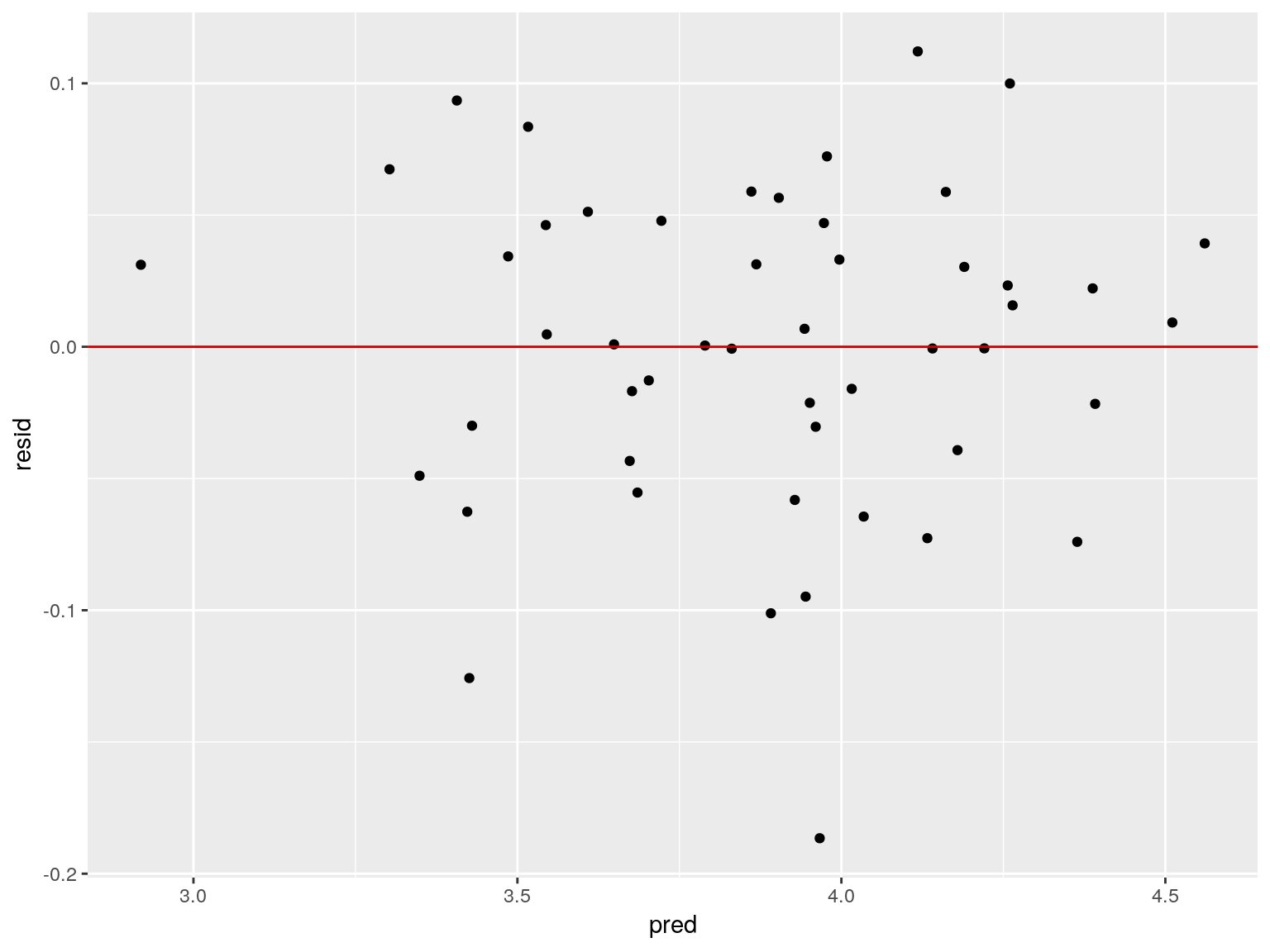
## Table: Shapiro-Wilk normality test: `residuos`
Podemos valorar la homoscedasticidad de los residuos graficando los residuos frente a los valores ajustados:
ggplot(data.frame(resid=residuos,pred=fitted(modelo)), aes(x=pred,y=resid)) + geom_point() +
geom_abline(intercept = 0,slope=0,color="red3")
