Tarea 2: Inferencia Estadística
Inferencia estadística. Intervalos de confianza y contraste de hipótesis
Las técnicas de estadística descriptiva, junto a la teoría de la Probabilidad y en particular los modelos de distribución de probabilidad, permiten abordar el estudio de la inferencia estadística. Los métodos básicos de la inferencia estadística son la estimación y el contraste de hipótesis. De forma esquemática, podría representarse como sigue:
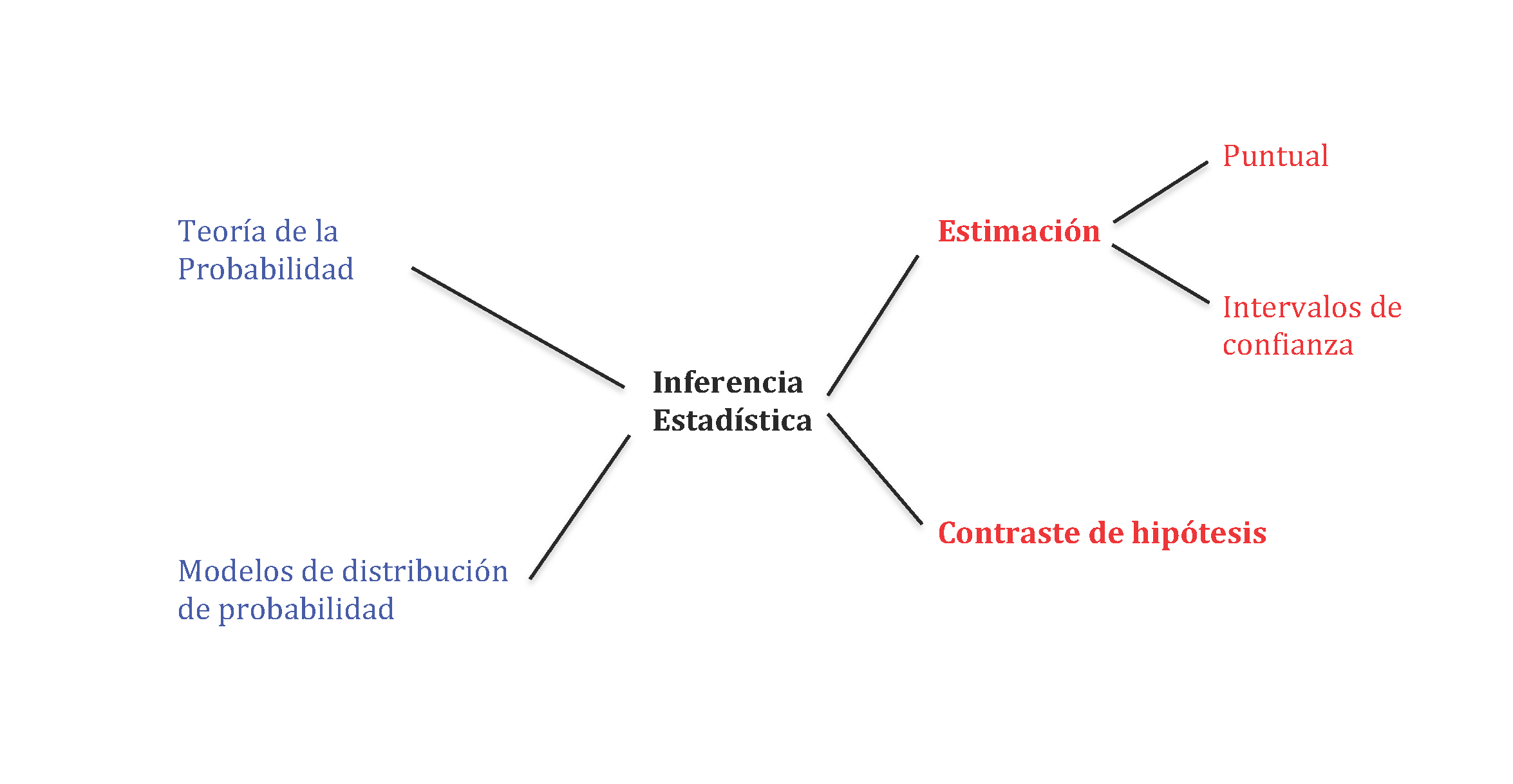
En lo que a estimación se refiere, existen dos formas de estimar parámetros: la estimación puntual y la estimación por intervalos de confianza. La primera trata de estimar un valor único para el parámetro que se está analizando, mientras que la segunda trata de estimar un intervalo que contenga al parámetro analizado con una probabilidad determinada, todo ello partiendo de la información que proporciona al investigador una muestra representativa de la población objeto de estudio.
Por otra parte, con respeto a contraste de hipótesis, éste trata de determinar si una hipótesis establecida por el investigador puede ser aceptada o no, teniendo en cuenta la información de la que dispone el investigador a partir de sus datos muestrales.
La siguiente tabla resume algunas de las técnicas más usuales para comparar y analizar la asociación de variables (la mayoría de estos procedimientos se plantean como un contraste de hipótesis):
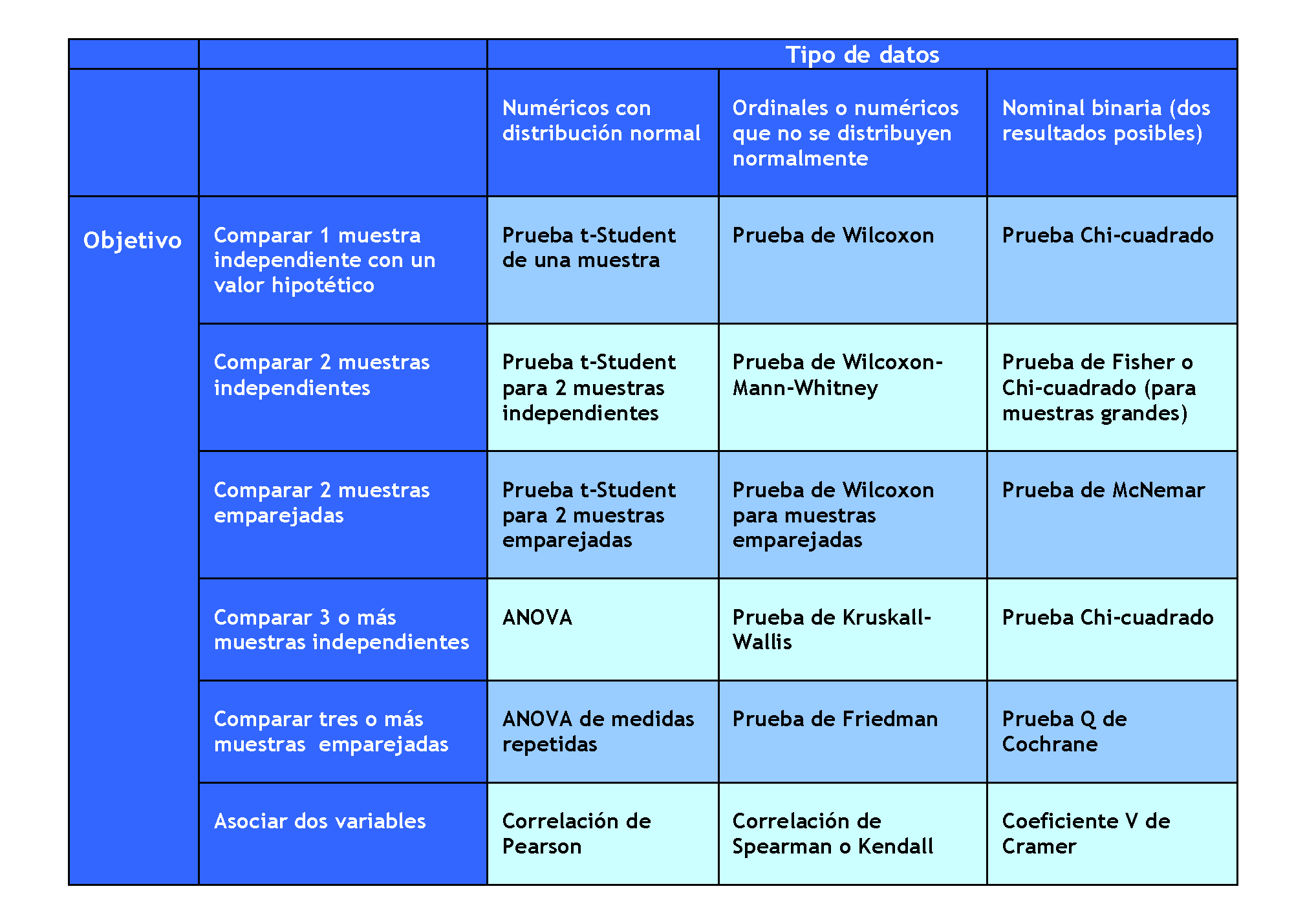
A continuación utilizaremos los recursos disponibles en Jamovi para la realización de contraste de hipótesis y el cálculo de intervalos de confianza. Para ello, haremos uso de los datos de los ficheros sargos.csv, endocrino.csv y MILLAC.sav.
Test de la t de Student: ¿Existe asociación entre el sexo de un pez y su longitud?
Para encontrar respuesta a esta pregunta, comenzamos por calcular el peso medio según el sexo de los peces, que nos proporciona la siguiente tabla:
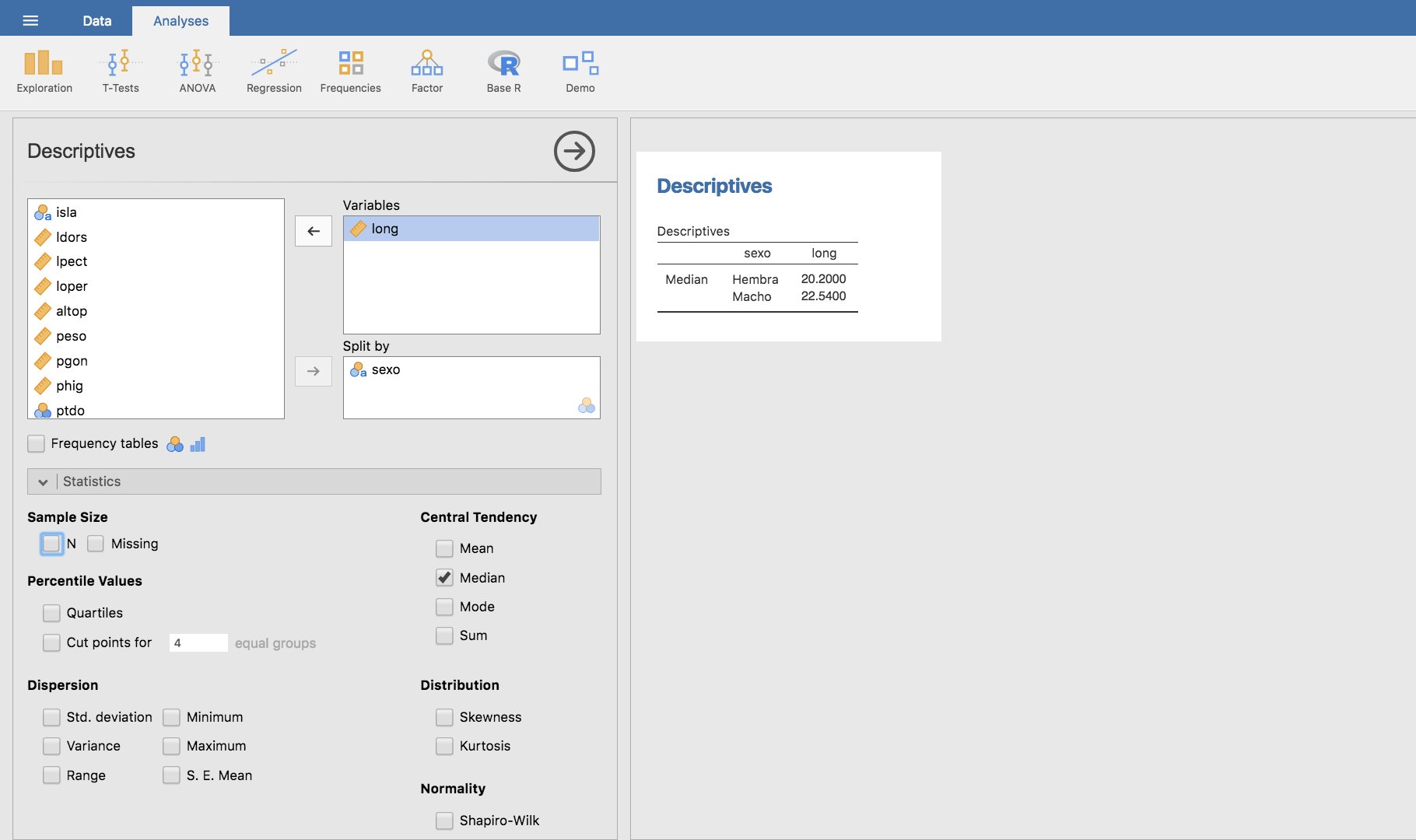
Gráficamente:
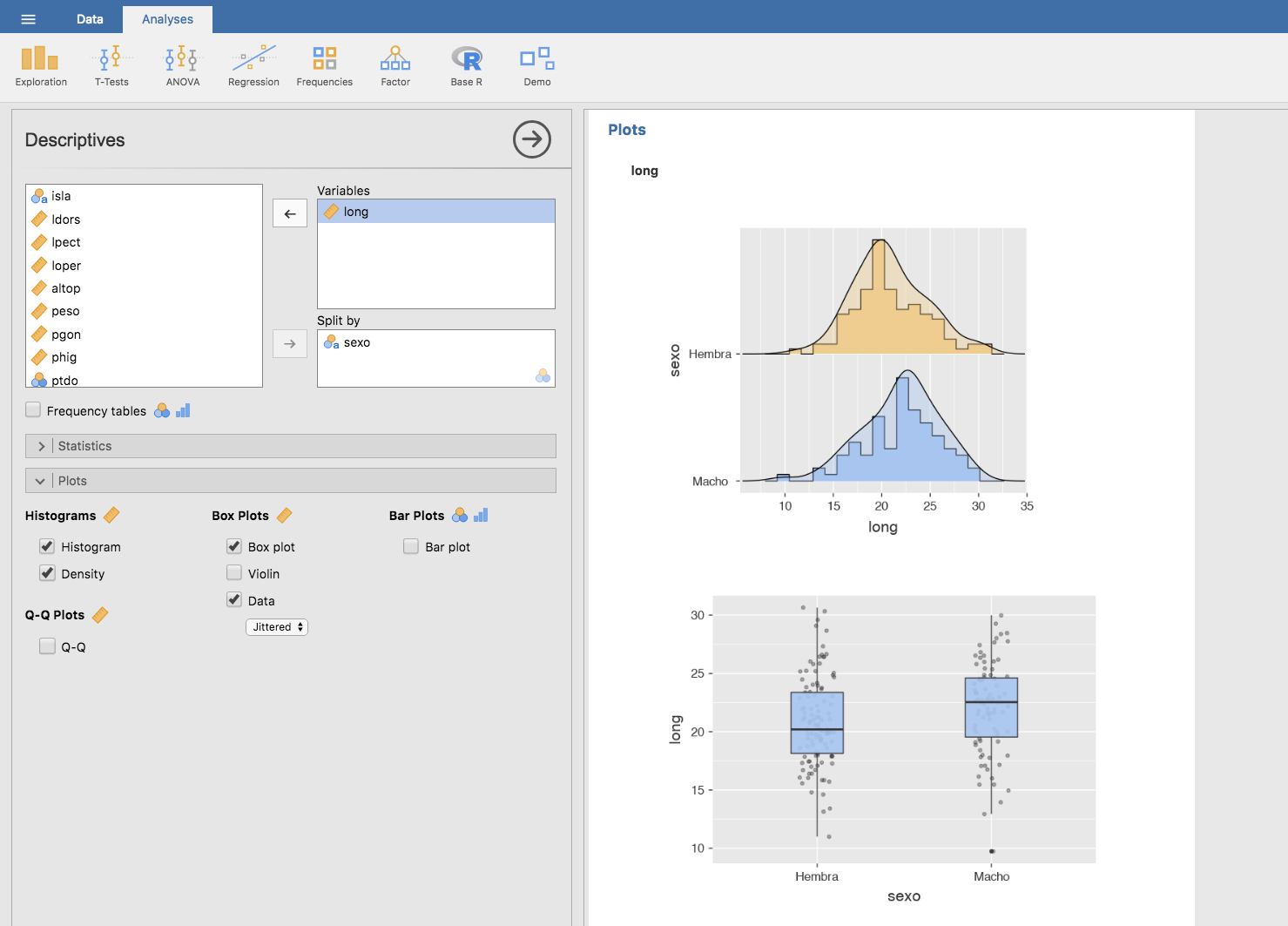
Se observa que la longitud media es mayor en los machos que en las hembras: ¿podría deberse esta diferencia a la variabilidad aleatoria del muestreo, o la diferencia es tan grande que solo puede explicarse porque en realidad una longitud mayor se asocia con ser macho?
Abordamos esta pregunta planteando el test de la t de Student:
La hipótesis nula es que la longitud no se asocia con el sexo de los peces; ello significaría que la longitud media sería la misma para hembras y machos. Si llamamos \(\mu_H\) a la longitud media en el primer grupo y \(\mu_M\) en el segundo, la hipótesis nula especifica que: \[\mu_H=\mu_M\]
La hipótesis alternativa es que la longitud media difiere entre hembras y machos. Consideramos, por ejemplo, que la hipótesis alternativa es:
\[\mu_M>\mu_H\] esto es que la longitud media es estrictamente mayor en machos que en hembras.
Para resolver este contraste de hipótesis podemos utilizar el test de la t de Student, siempre que las muestras a comparar se distribuyan normalmente y tengan varianzas iguales (en caso de que las varianzas difieran entre sí, se aplicaría el test de Welch).
Comprobamos si las distribuciones de la longitud en machos y hembras siguen una distribución normal utilizando el test de Shapiro-Wilk:
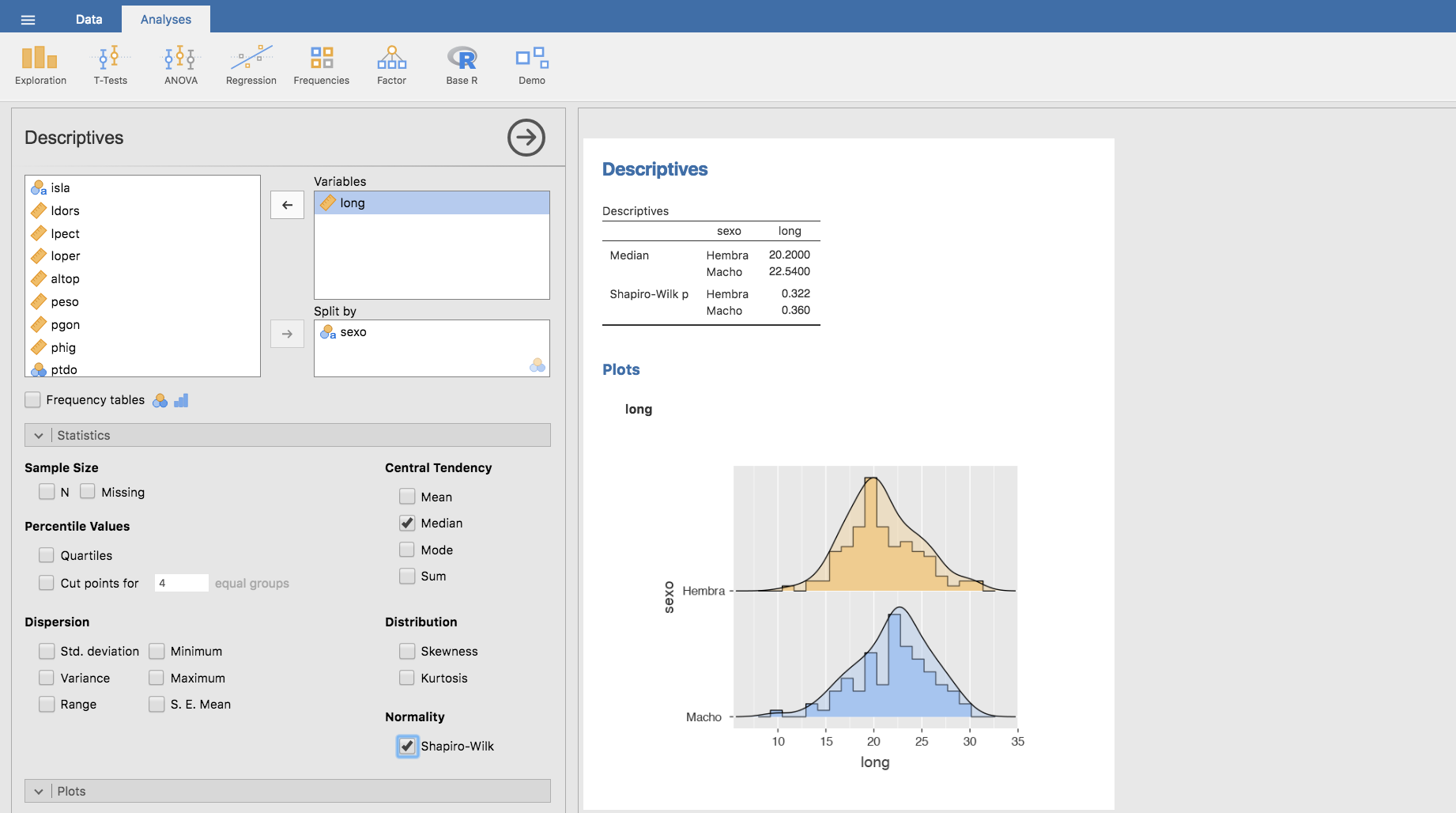
Y, efectivamente, los p-valores que proporciona Jamovi son mayores que 0.05 para machos y hembras. Esto significa que no podemos rechazar la hipótesis nula (la variable longitud sigue una distribución normal) en los tests de Shapiro-Wilk realizados en ambos grupos. Por tanto, concluimos que la longitud se distribuye normalmente tanto para hembras como para machos.
A continuación procedemos a realizar el test de la t de Student. Para ello, en la pestaña Analyses utilizamos el menú T-Tests y elegimos Independent Samples T-Test. Situamos la variable long como Dependent Variable y sexo como Grouping variable. Seguidamente, en el apartado Tests elegimos la opción Student’s, y en el apartado Hypothesis seleccionamos como hipótesis altenativa que la longitud de los machos es mayor que la de las hembras. En este punto, aún no hemos comprobado si se verifica la igualdad de varianzas entre ambos grupos. Por ello, en el apartado Assumption Checks seleccionamos Equality of variances para que Jamovi añada un test de Levene en nuestro análisis:
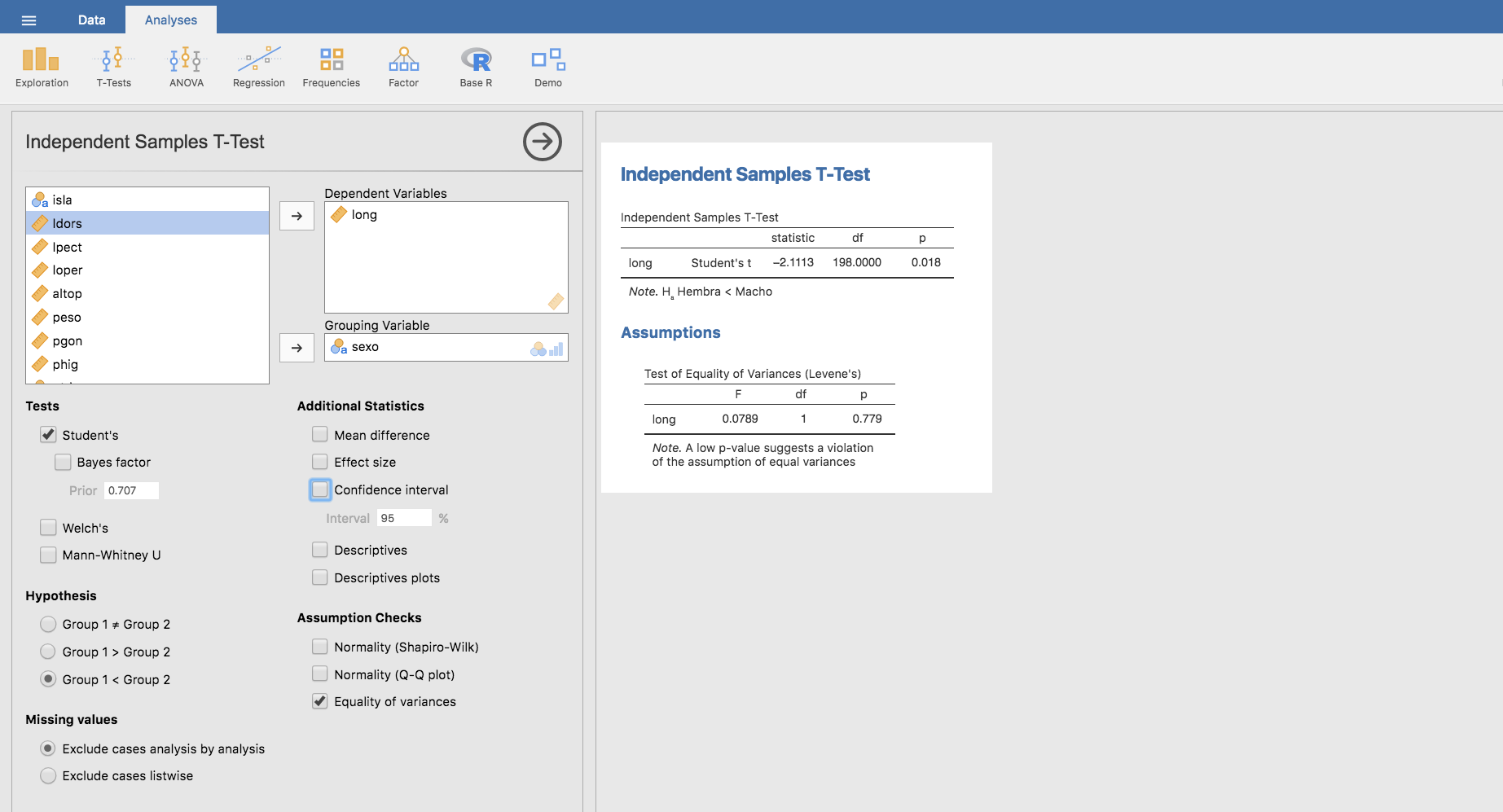
Los datos obtenidos permiten, en primer lugar, observar que podemos asumir que las varianzas en ambos grupos son iguales (el p-valor del test de Levene es p=0.779 > 0.05, por lo que no podemos rechazar la hipótesis nula de dicho test (\(H_0\) : las varianzas son iguales en ambos grupos)). Por tanto, se cumplen todos los requisitos para que se pueda aplicar el test de la t de Student tal y como hemos hecho. Finalmente, analizando el p-valor del test de la t de Student que hemos planteado, se concluye que dicho test es significativo (p-valor = 0.018 < 0.05). Por tanto, rechazamos la hipótesis nula y aceptamos la hipótesis alternativa: la longitud media en los machos es mayor que la longitud media en las hembras.
Nota: Como se mencionó anteriormente, en caso de que no se de la igualdad de varianzas entre los grupos, la alternativa es optar por plantear un test de Welch para comparar las longitudes medias entre machos y hembras.
Finalmente, el análisis anterior lo podemos completar solicitando a Jamovi que nos proporcione un intervalo de confianza para la diferencia de medias, una tabla descriptiva de cada grupo y una representación gráfica de los intervalos de confianza y las medianas para cada grupo:
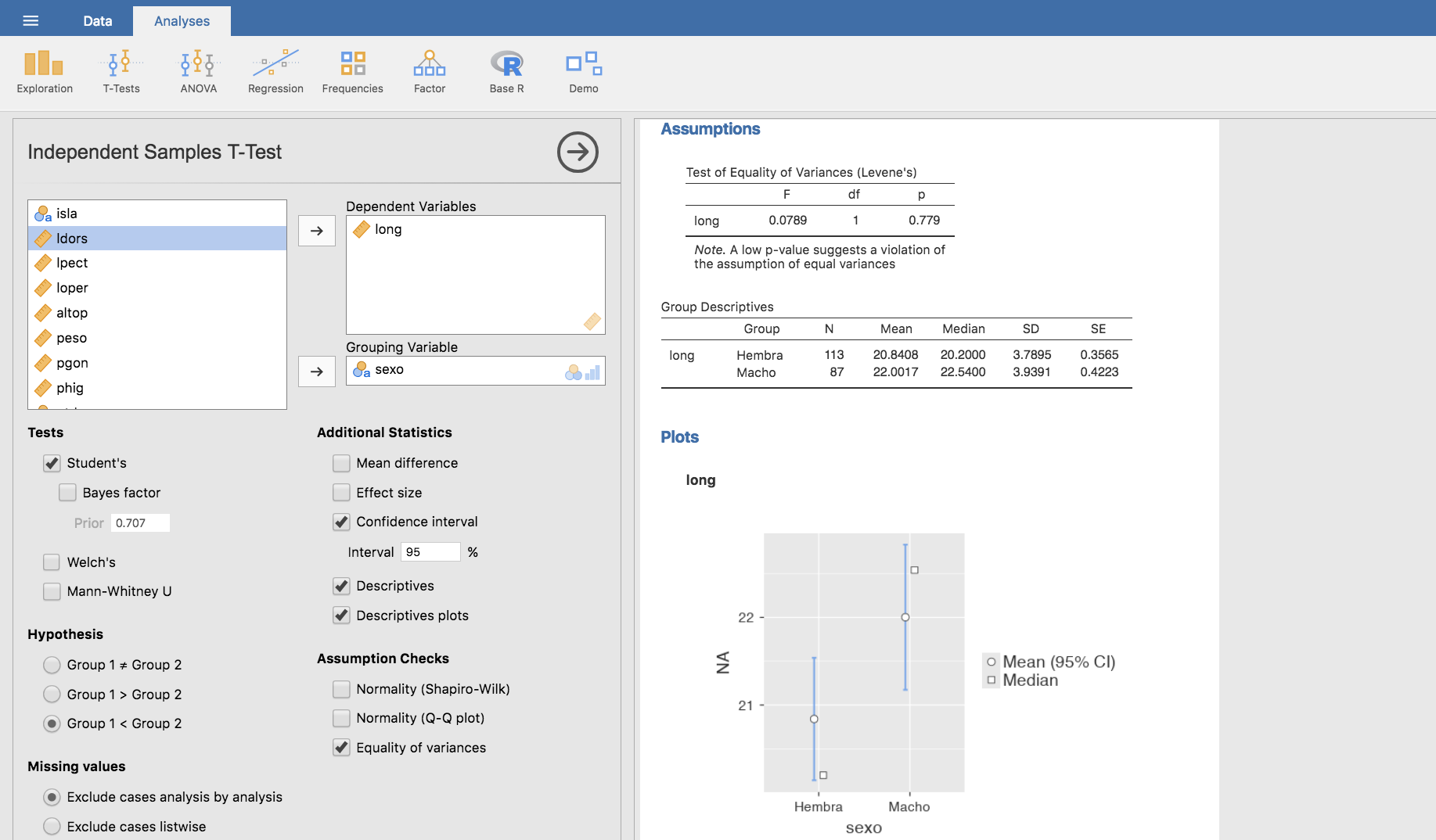
Test de la chi-cuadrado: ¿Existe asociación entre el sexo de un individuo y el padecer HTA?
Seguidamente, pasamos a utilizar los datos del fichero endocrino.csv, que recoge información de un estudio realizado con pacientes de Telde. El primer paso que damos con este fichero es el de recodificar la variable Sexo, denominando Mujer al nivel 0 y Hombre al nivel 1, situando a Hombre como primer nivel de la variable:
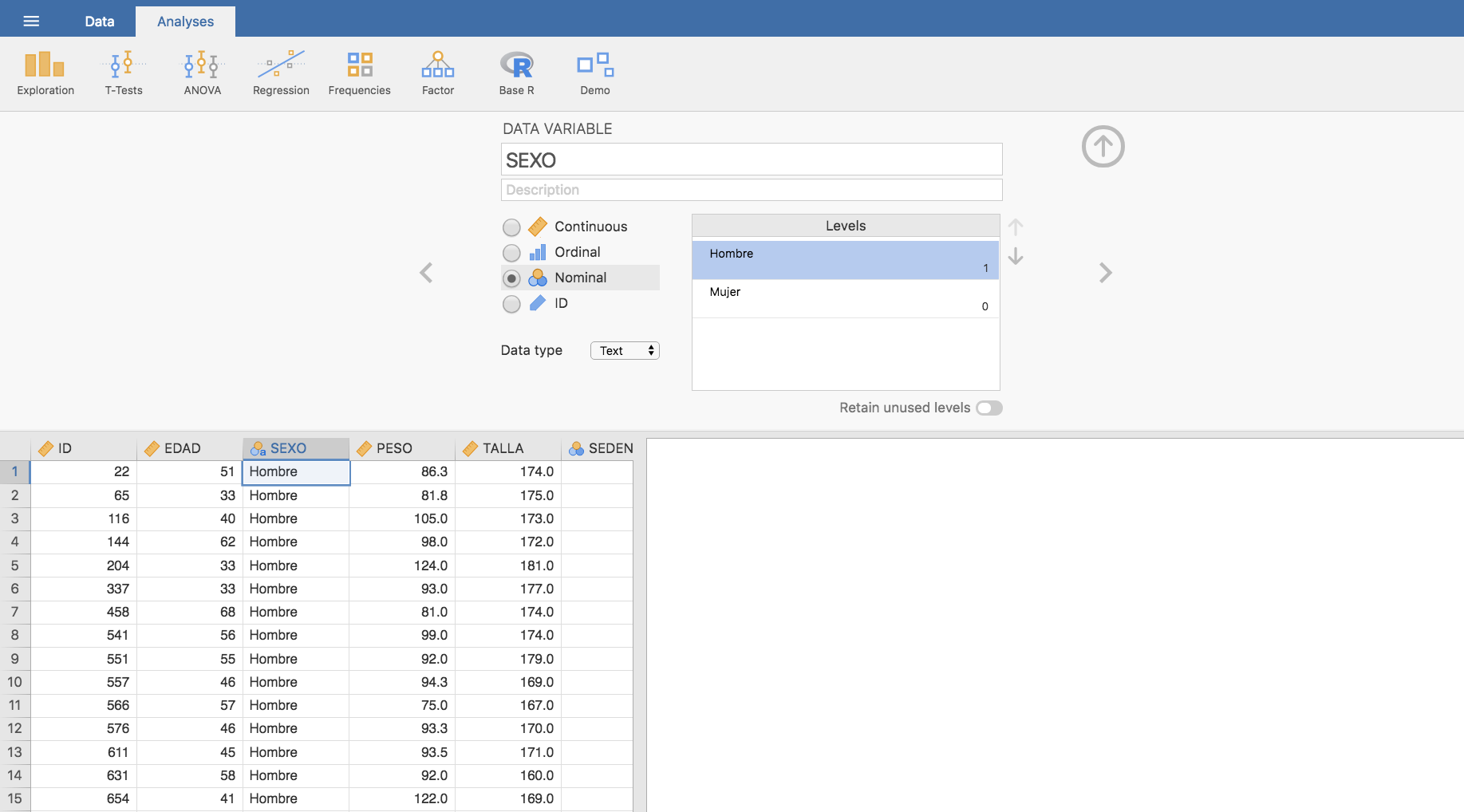
Para determinar si el sexo de una persona se asocia con el hecho de que esa persona padezca o no HTA comenzamos por copiar la columna de la variable HTA_OMS, pegar los datos en una columna vacía y llamar a la nueva variable HTA. Además, renombramos el nivel 0 como HTA- y el 1 como HTA+, y los reordenamos poniendo en primer lugar HTA+.
A continuación, construimos una tabla cruzada entre las variables HTA y SEXO:
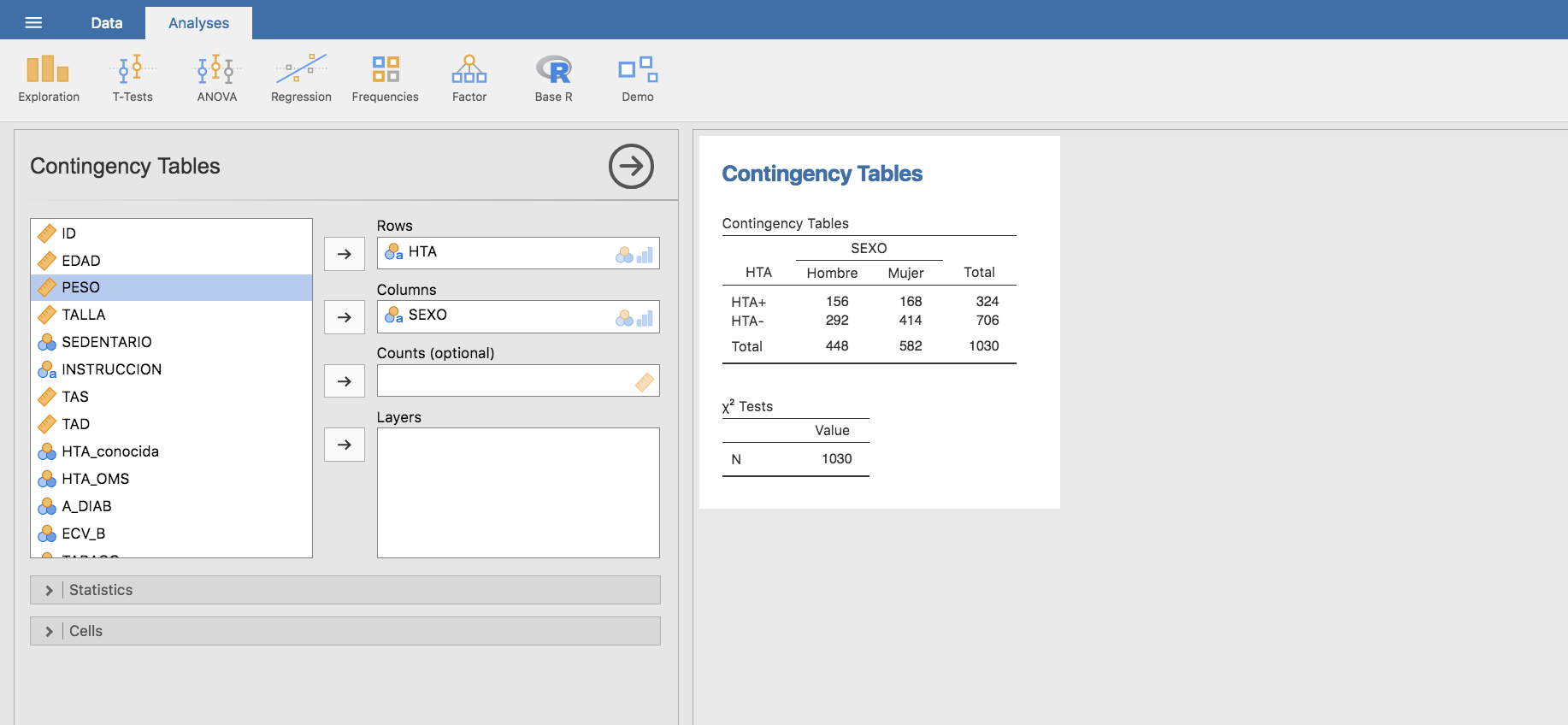
Y evaluamos las frecuencias relativas por columnas:
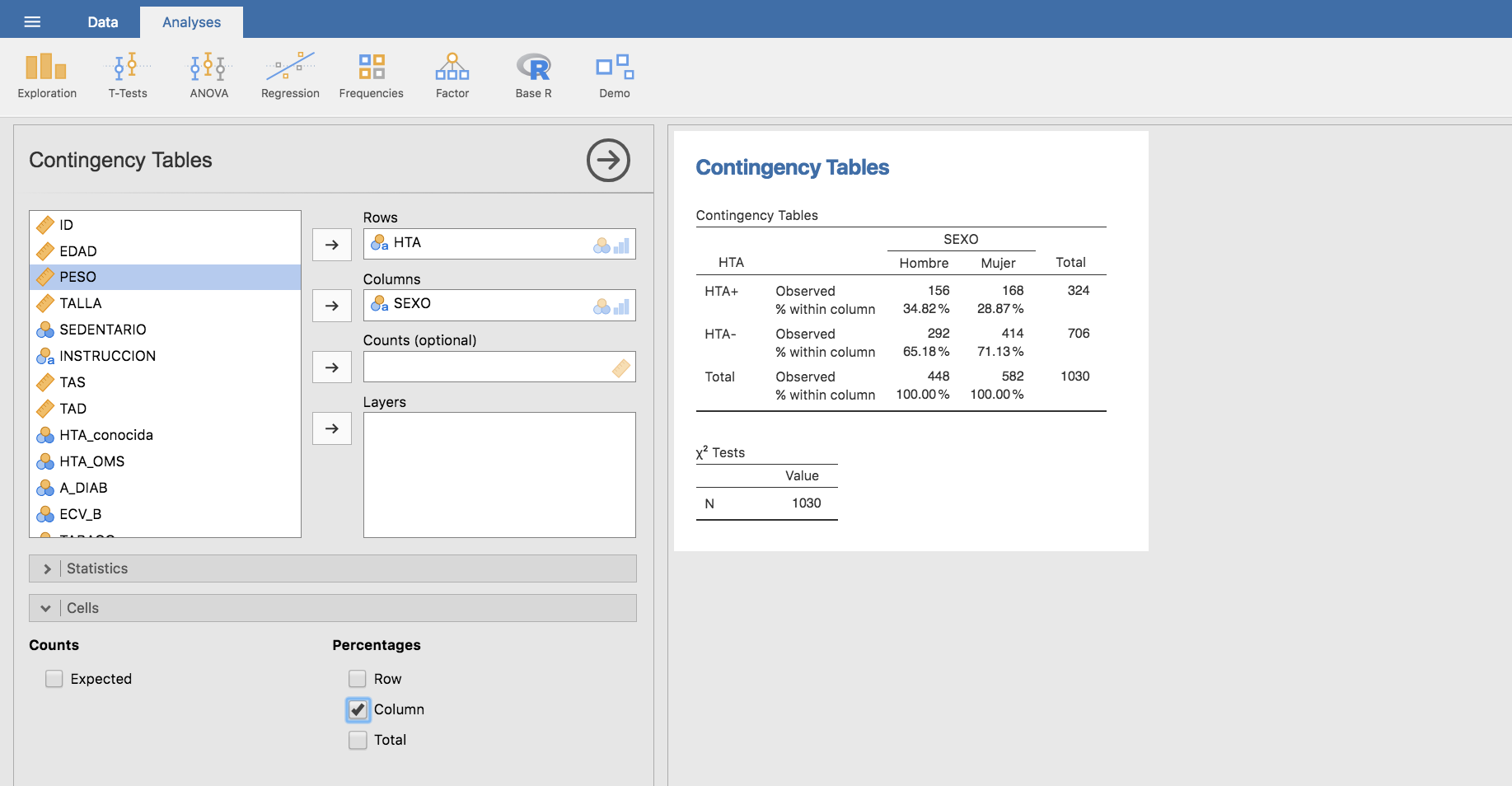
Esta tabla indica que un 34.82% de los hombres son hipertensos, frente a un 28.87% de las mujeres, lo que podría interpretarse como que el ser hombre es de algún modo un factor de riesgo de hipertensión. Podemos evaluar la asociación entre SEXO y HTA mediante la odds-ratio:
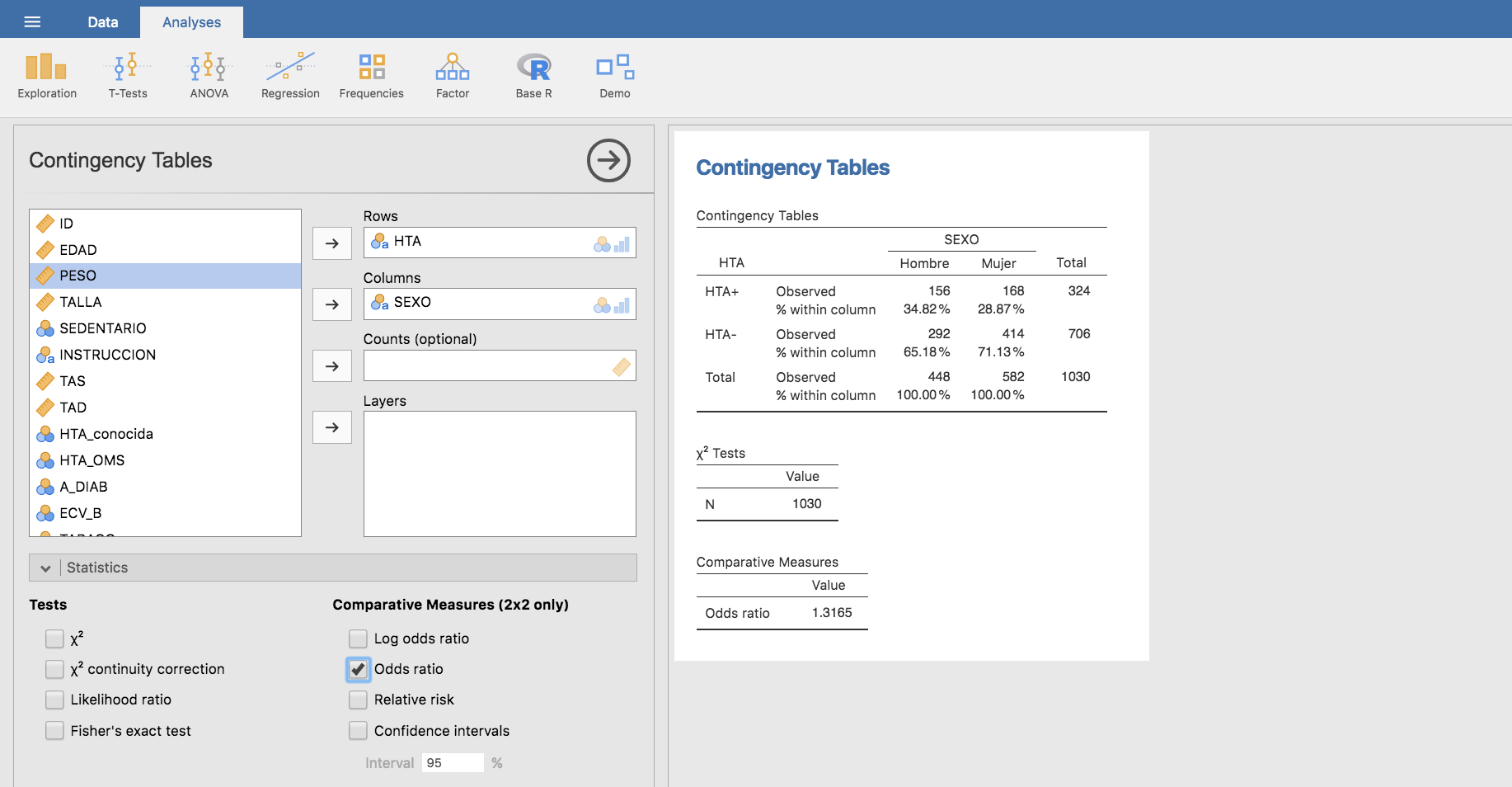
cuyo valor (mayor que la unidad) está efectivamente acorde con la presunción de que ser hombre incrementa el riesgo de HTA.
En cualquier caso la diferencia entre un 34.82% y un 28.87% no parece excesivamente elevada. Dado que los datos con los que estamos trabajando constituyen una muestra elegida al azar entre la población adulta de Telde cabe hacerse la siguiente pregunta: si la muestra hubiese sido otra ¿se habría observado la misma relación entre estos porcentajes (esto es mayor porcentaje de hipertensos entre los hombres que entre las mujeres), o quizás estos porcentajes podrían llegar incluso a invertirse? En otras palabras, la pregunta que nos hacemos es: ¿la diferencia observada puede explicarse simplemente por la variabilidad aleatoria presente en el muestreo, o necesariamente se debe a que en realidad la hipertensión es más común entre los hombres que entre las mujeres de Telde?
Para responder a esta pregunta debe utilizarse el test de la chi-cuadrado:
- La hipótesis nula es que la hipertensión afecta por igual a hombres y mujeres y por tanto que la diferencia observada entre los porcentajes se debe simplemente al azar; si \(\pi_M\) es la probabilidad de que una mujer sea hipertensa y \(\pi_H\) es la probabilidad de que un hombre sea hipertenso, la hipótesis nula establece que:
\[\frac{\pi_M}{\pi_H}=1\]
- La hipótesis alternativa es que la hipertensión afecta de manera diferente a hombres y mujeres, y por tanto que:
\[\frac{\pi_M}{\pi_H}\neq 1\]
La realización del test de la chi-cuadrado en Jamovi es muy simple, basta con seleccionar \(\chi^2\) continuity correction en el apartado Tests de la barra Statistics:
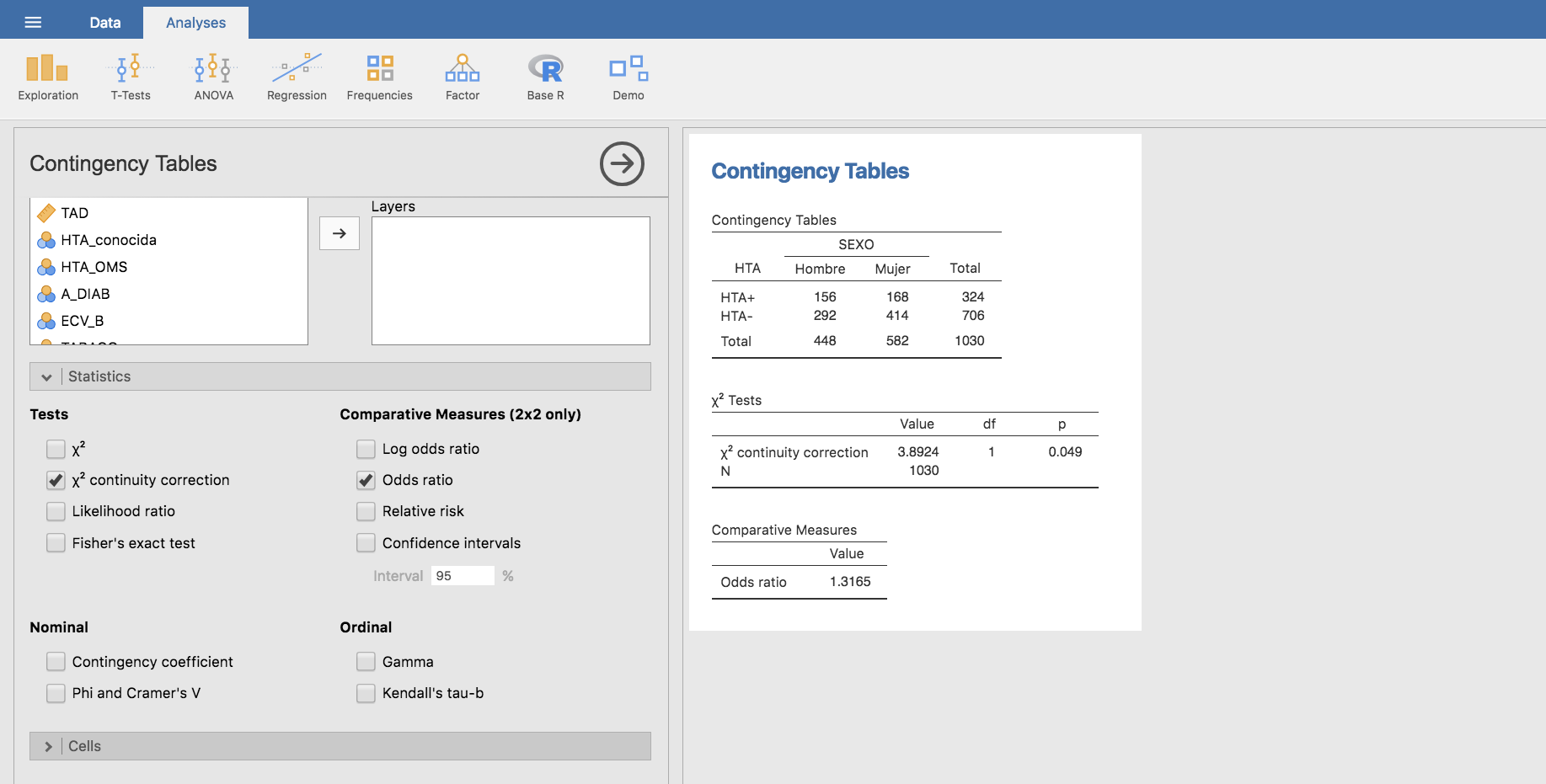
Y si deseamos calcular las frecuencias esperadas bajo la hipótesis nula (igual prevalencia de HTA en hombres y mujeres) podemos utilizar la opción Expected en el apartado Counts de la barra Cells:
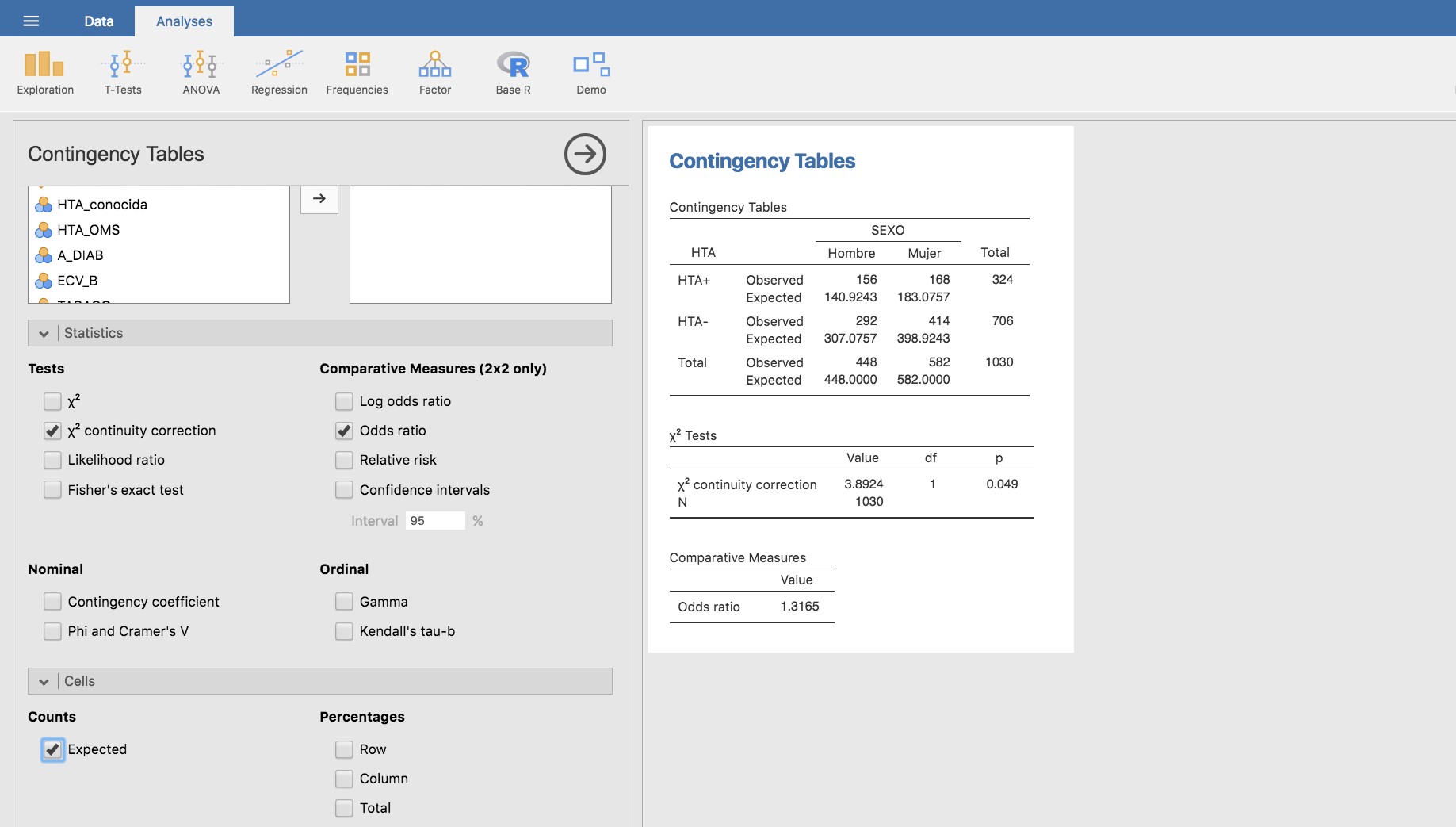
Test de la chi-cuadrado: ¿Existe asociación entre el nivel de instrucción de un individuo y el padecer HTA?
Para responder a esta pregunta podemos proceder del mismo modo que con la variable SEXO. Comenzamos por reordenar la variable INSTRUCCION de modo que el primer nivel sea Sin estudios, tal y como se indica a continuación:
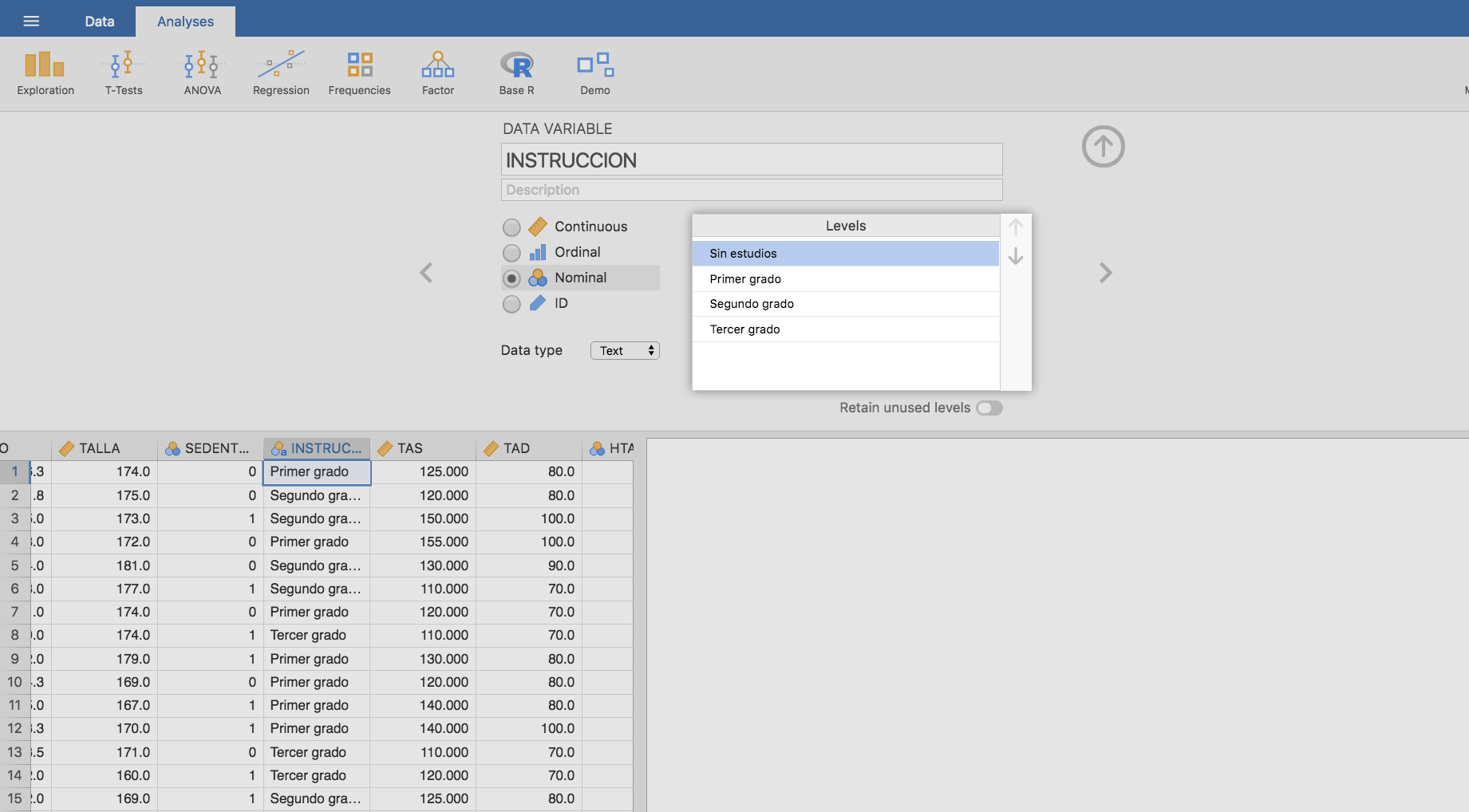
Como segundo paso, planteamos la tabla cruzada entre las variables HTA e INSTRUCCION, añadiendo el cálculo de frecuencias relativas por columnas:
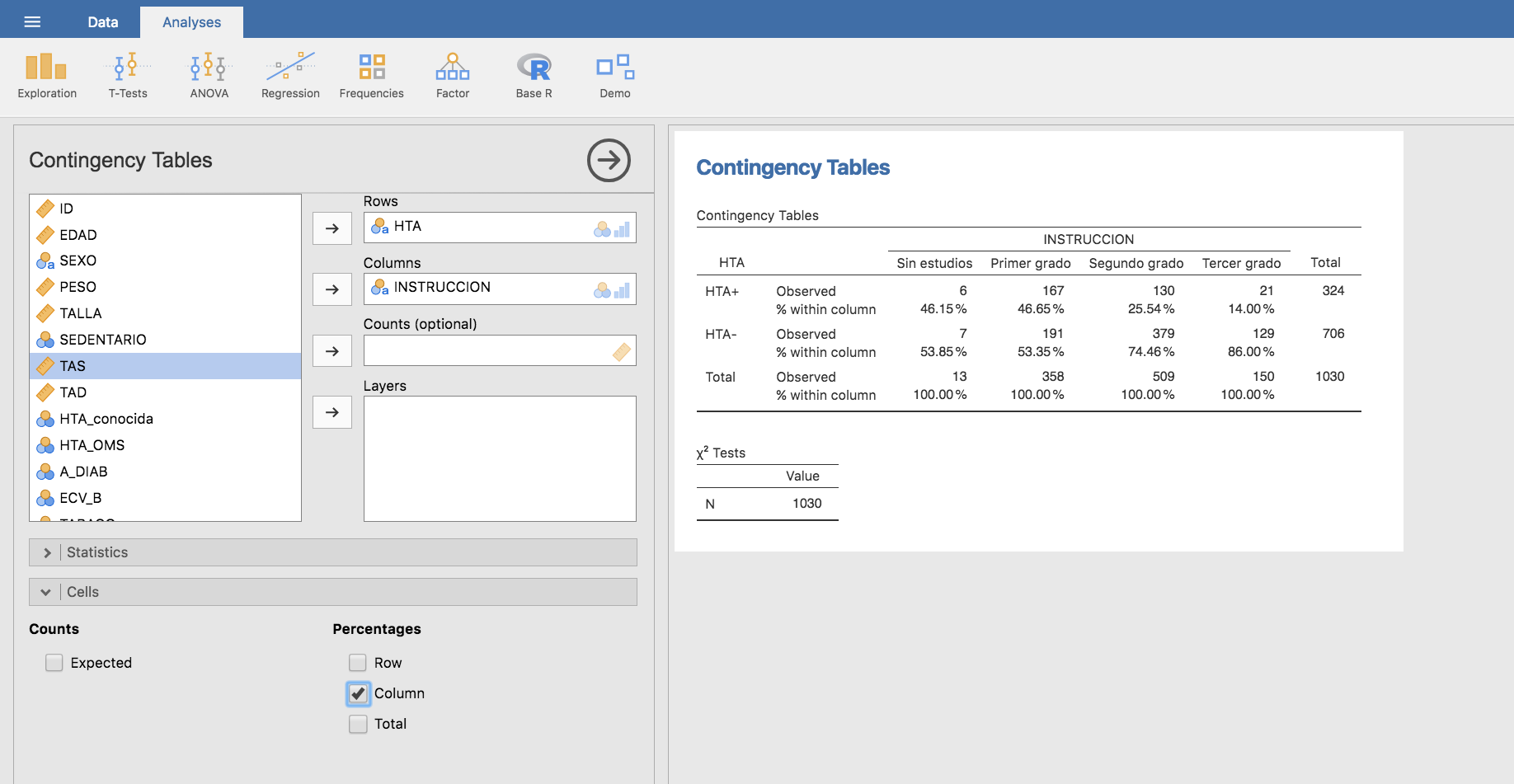
Esta última tabla muestra que, a medida que aumenta el nivel de instrucción aparentemente disminuye la probabilidad de padecer hipertensión.
Aplicamos el test de la chi-cuadrado:
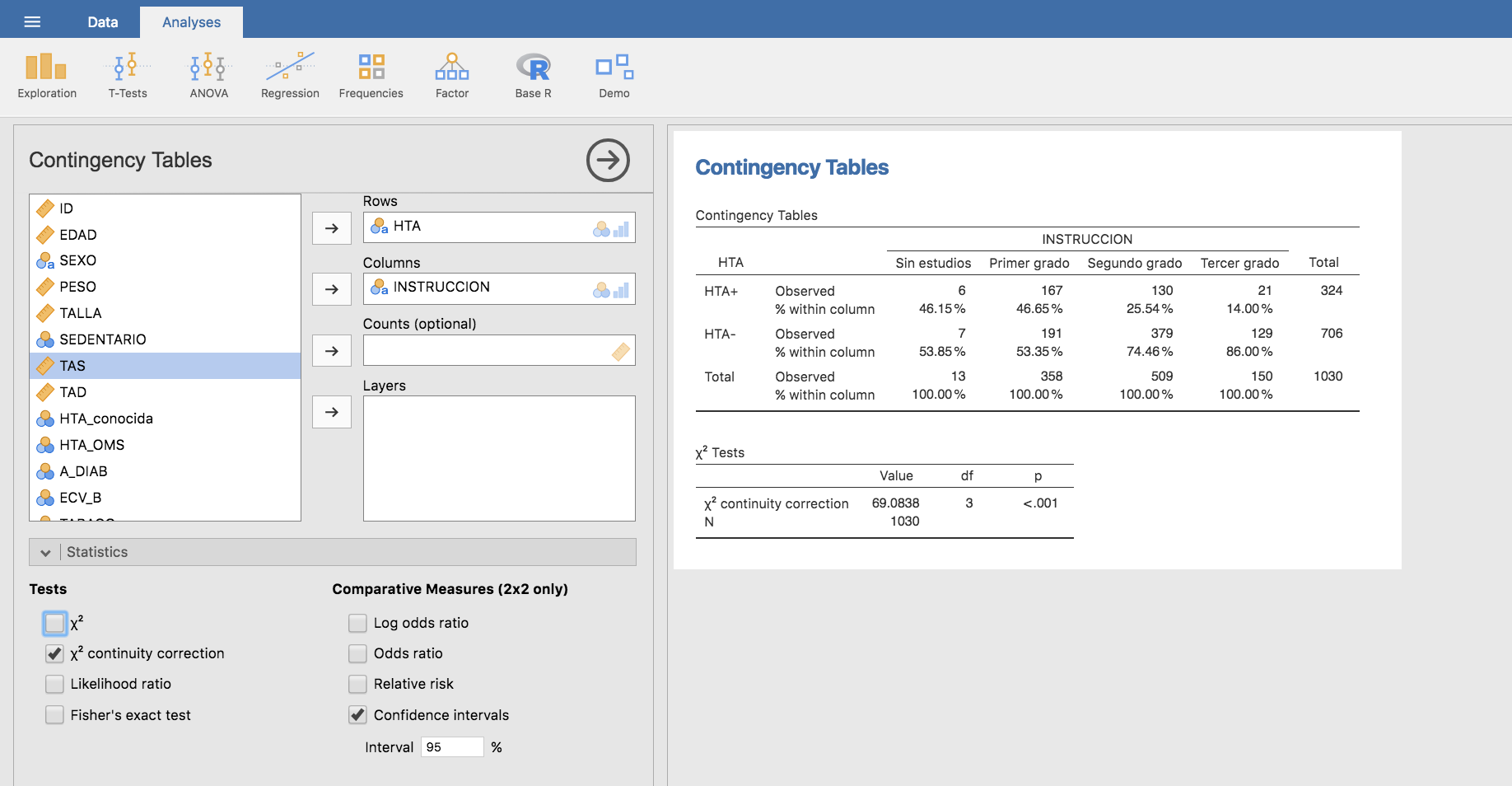
Y calculamos las frecuencias esperadas:
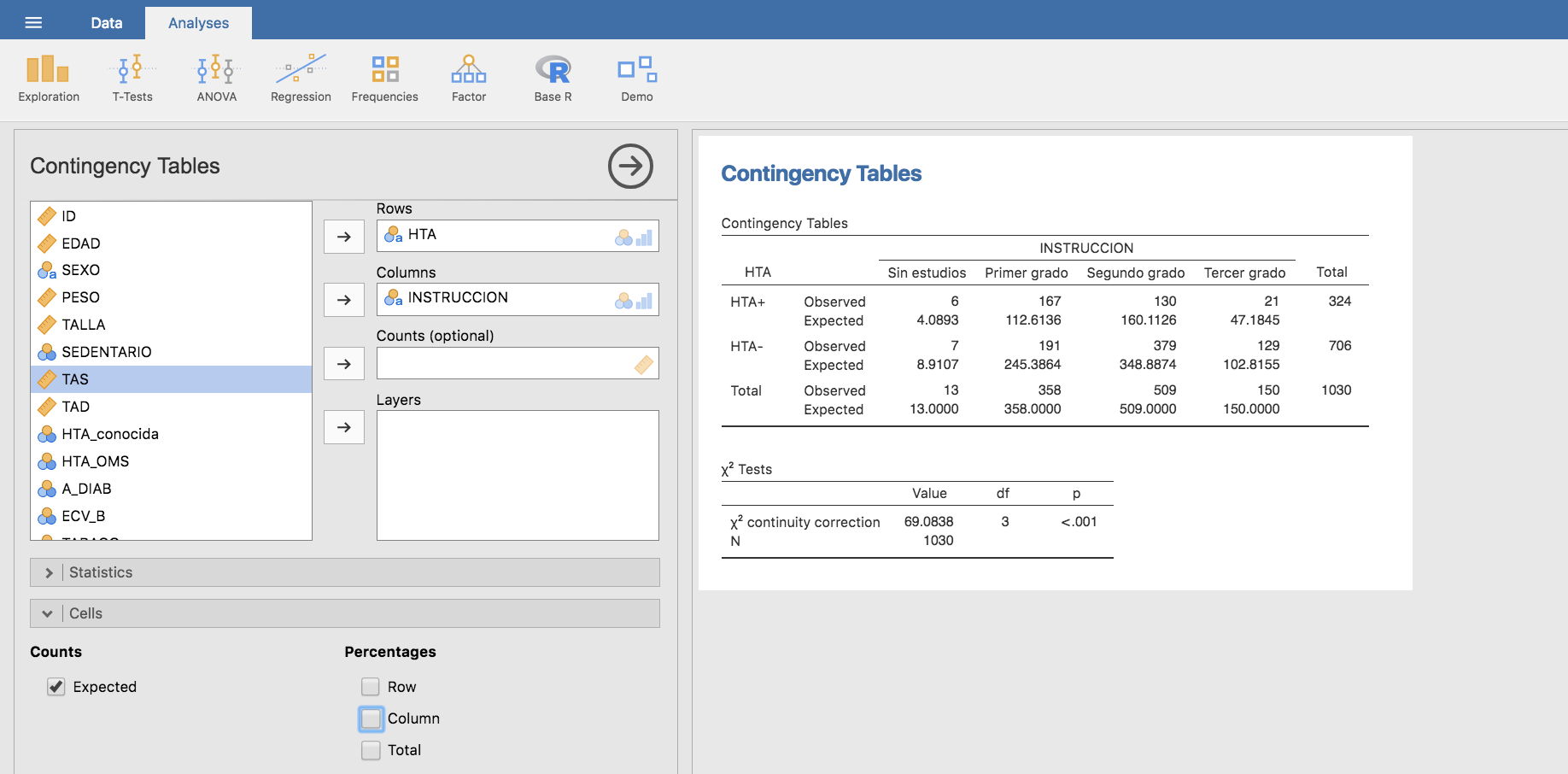
Nota: Las condiciones “técnicas” para la realización del test de la Chi-cuadrado requieren que ninguna frecuencia esperada sea menor que 1, y que al menos el 80 % de las frecuencias esperadas sean mayores que 5. En nuestro análisis hay una única frecuencia esperada menor que 5. En total hay 8 valores esperados, de los que 7 (esto es el 87.5%) son mayores que 5. Por tanto podemos confiar en el resultado del test y concluir que la asociación entre el nivel de instrucción y la HTA es significativa, esto es, no puede explicarse simplemente por efecto del azar.
Si no se cumpliesen las condiciones para la realización del test de la Chi-cuadrado, se debería proceder a agrupar categorías. Si hubiese ocurrido eso en nuestro, procederíamos como sigue: observamos que la categoría que puede causar problemas es “Sin estudios”, por lo que ésta podría fusionarse con la categoría “Primer grado” y crearíamos una nueva variable que llamamos INSTRUCCION2:
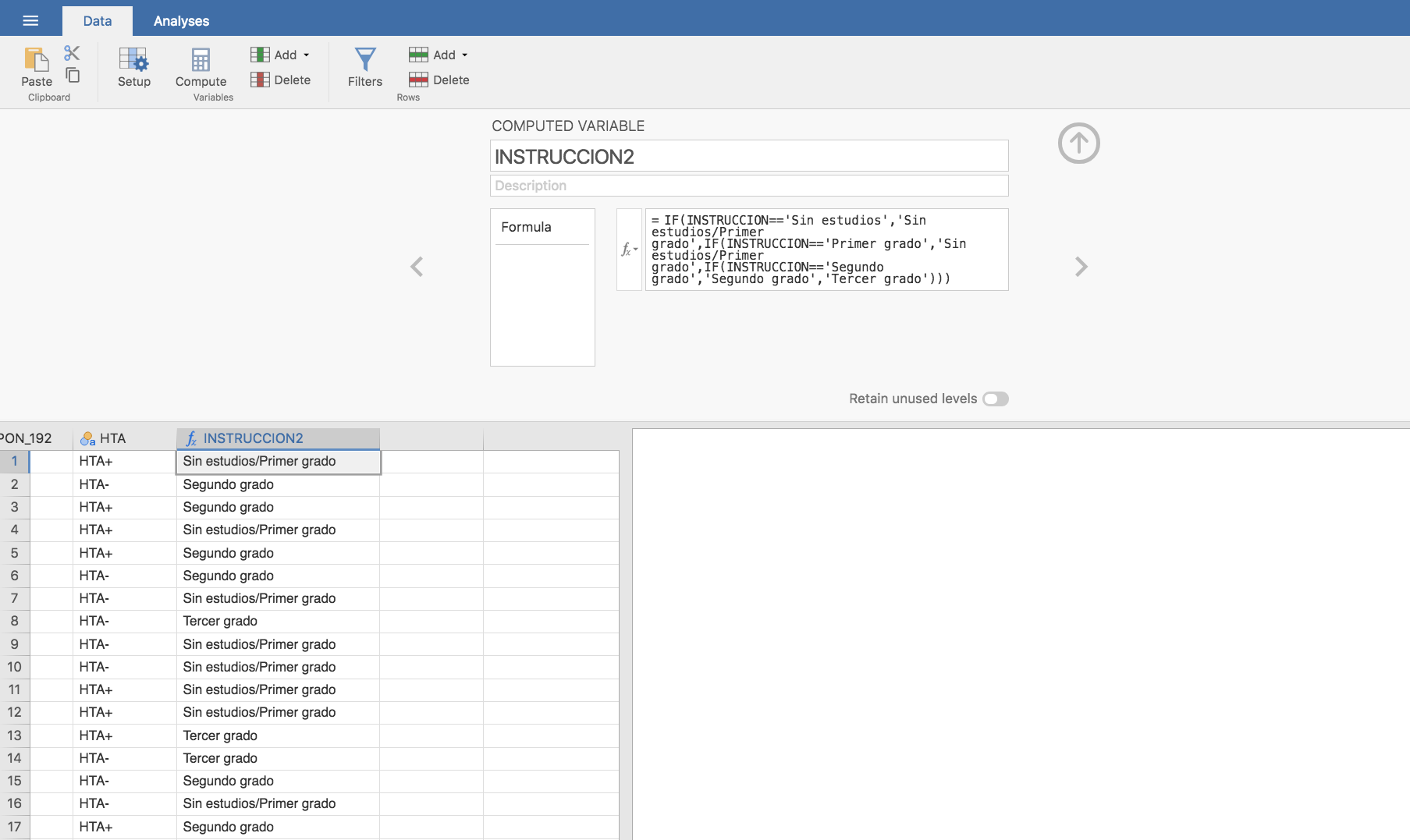
Una vez generada esta nueva variable, procederíamos siguiendo los mismos pasos dados para las variables HTA e INSTRUCCION, calculando la tabla de contingencia, frecuencias relativas por columnas y test de la Chi-cuadrado:
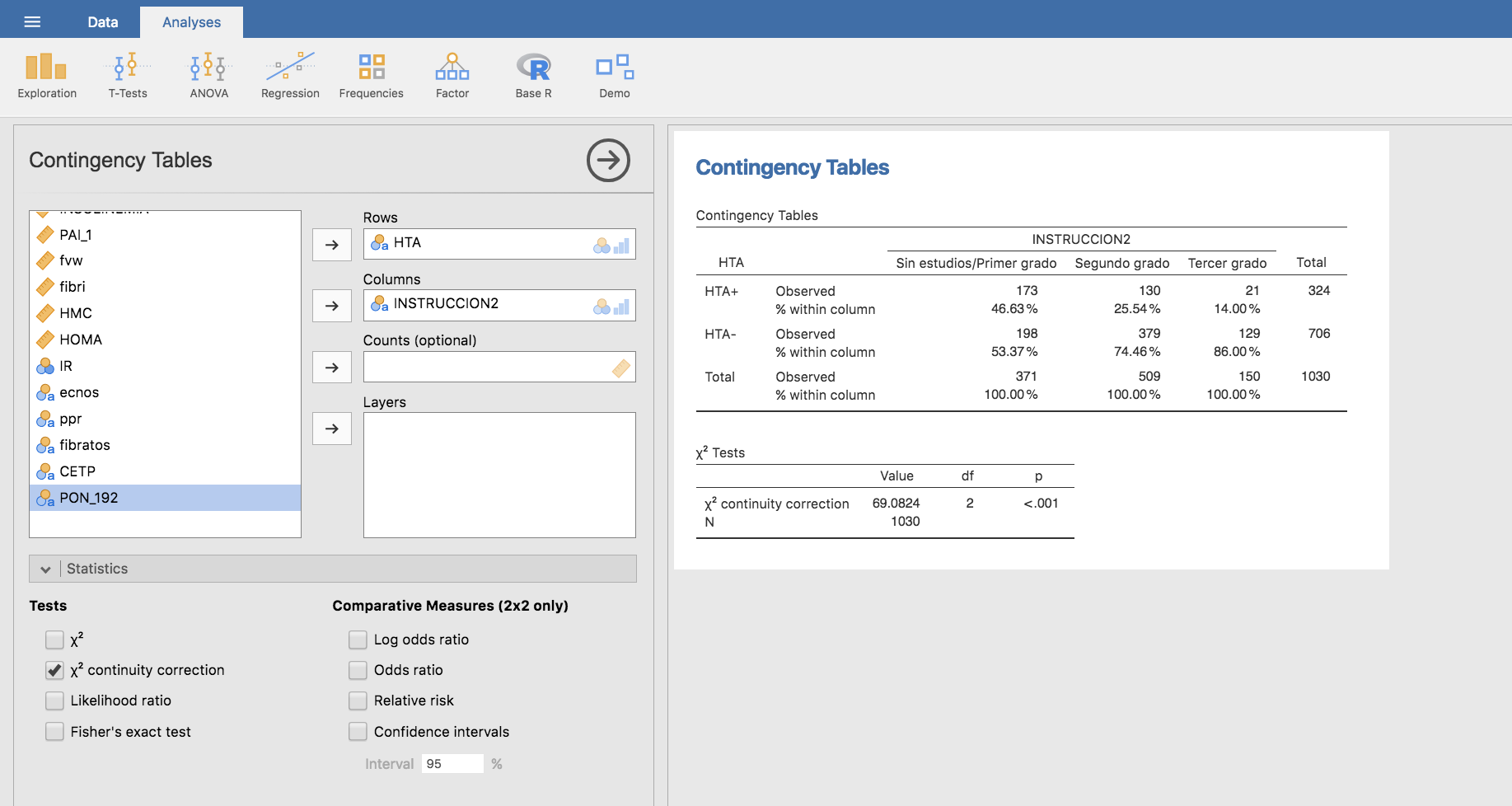
Test de Wilcoxon-Mann-Whitney: ¿Existe asociación entre el índice de masa corporal y la hipertensión arterial?
El índice de masa corporal se calcula como el peso (en kg) partido por la talla (en m) elevada al cuadrado. Podemos calcular el IMC de las personas de la muestra de Telde mediante:
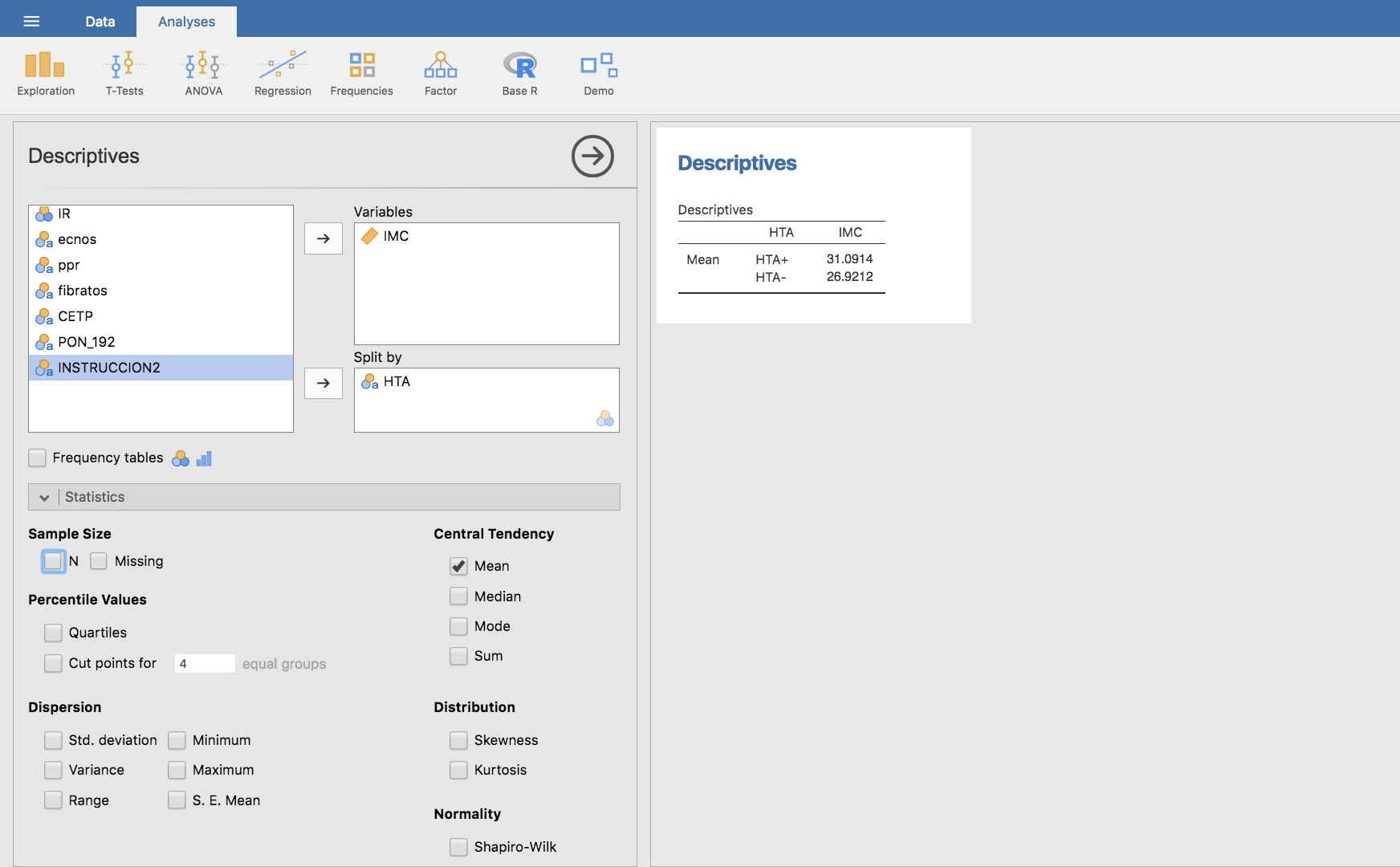
La siguiente tabla nos da el valor medio de IMC según las personas sean o no hipertensas:
Gráficamente:
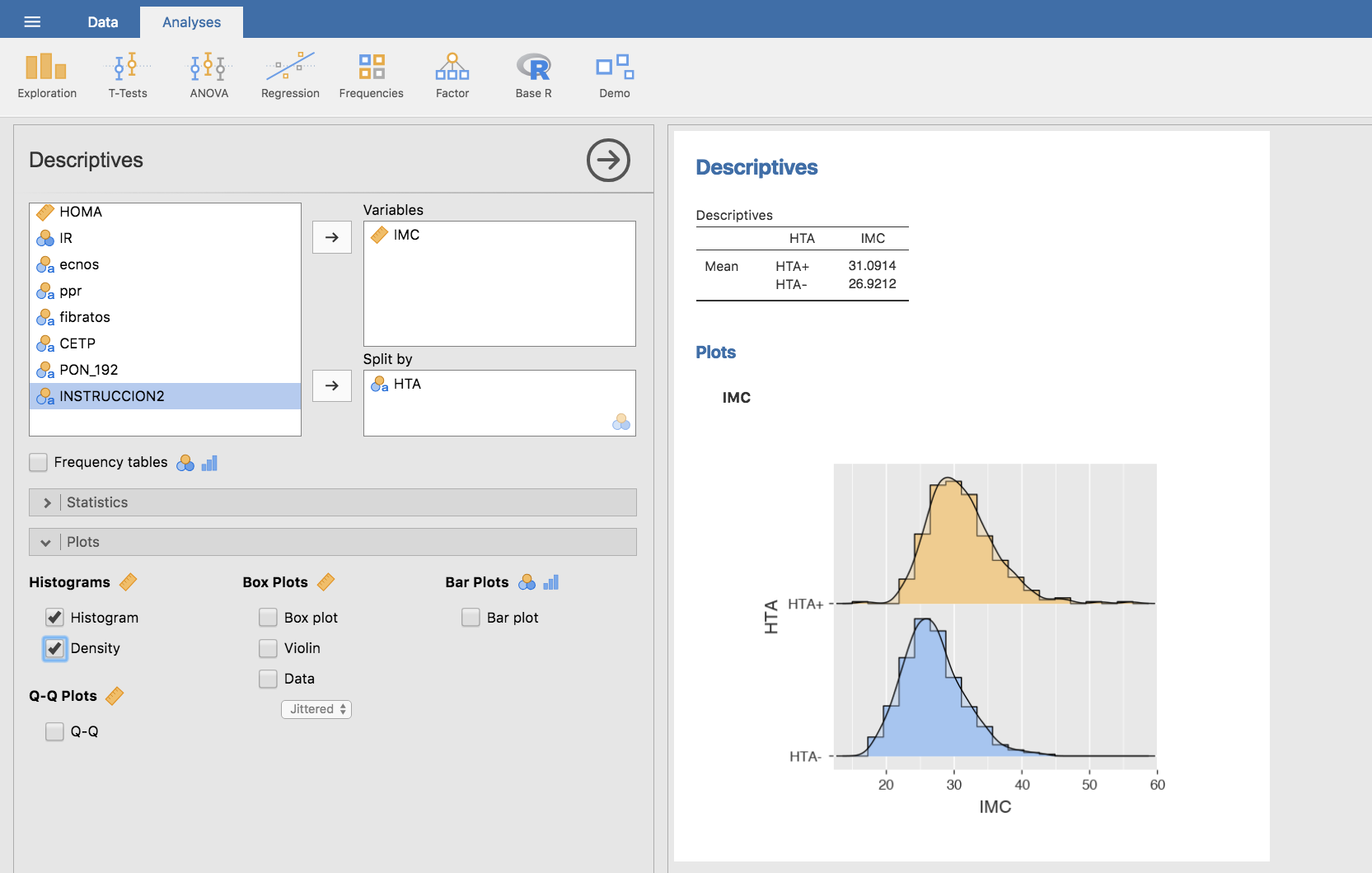
Vemos, pues, que el IMC medio es mayor en los hipertensos (31.10) que en los normotensos (26.92). Igual que en el caso anterior: ¿podría esta diferencia ser efecto de la variabilidad aleatoria del muestreo o la diferencia es tan grande que solo puede explicarse porque en realidad un mayor IMC se asocia con riesgo de HTA?
Para responder a esta pregunta planteamos el siguiente contraste de hipótesis:
La hipótesis nula es que la hipertensión no se asocia con el IMC; ello significaría que el valor medio de IMC sería el mismo para el grupo de hipertensos y para el grupo de normotensos. Si llamamos \(\mu_H\) al valor medio de IMC en el primer grupo y \(\mu_N\) en el segundo, la hipótesis nula especifica que: \[\mu_H=\mu_N\]
La hipótesis alternativa es que el valor medio de IMC difiere entre hipertensos y normotensos; podemos ser más específicos y considerar que la hipótesis alternativa es: \[\mu_H>\mu_N\]
esto es que el valor medio de IMC es estrictamente mayor en hipertensos que en normotensos.
Para resolver este contraste de hipótesis podemos utilizar el test de la t de Student, siempre que las muestras a comparar se distribuyan normalmente y tengan varianzas iguales; o bien, el test de Welch si las varianzas fuesen distintas. Comprobamos si ambas muestras siguen una distribución normal utilizando el test de Shapiro-Wilk:
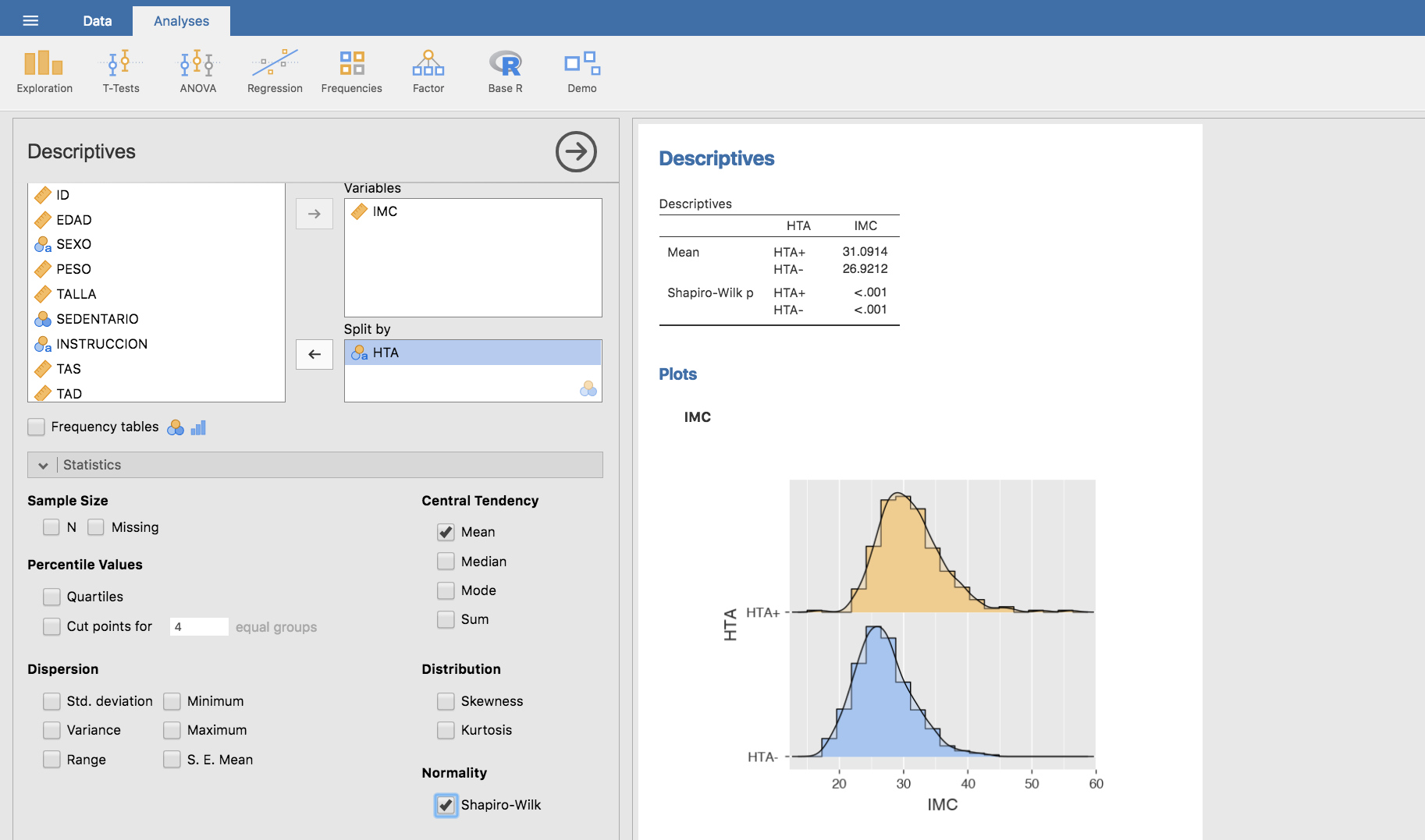
El resultado obtenido pone de manifiesto que los datos no se distribuyen normalmente ni para hipertensos ni para normotensos, ya que en ambos grupos el p-valor es menor que 0.05. Por tanto, no podremos utilizar los contrastes de hipótesis mencionados. En casos como este, utilizamos el test de Wilcoxon-Mann-Whitney (también denominado test de Mann-Whitney U) para comparar los valores de IMC entre normotensos e hipertensos, tomando como hipótesis alternativa que los valores en hipertensos son mayores que en normotensos:
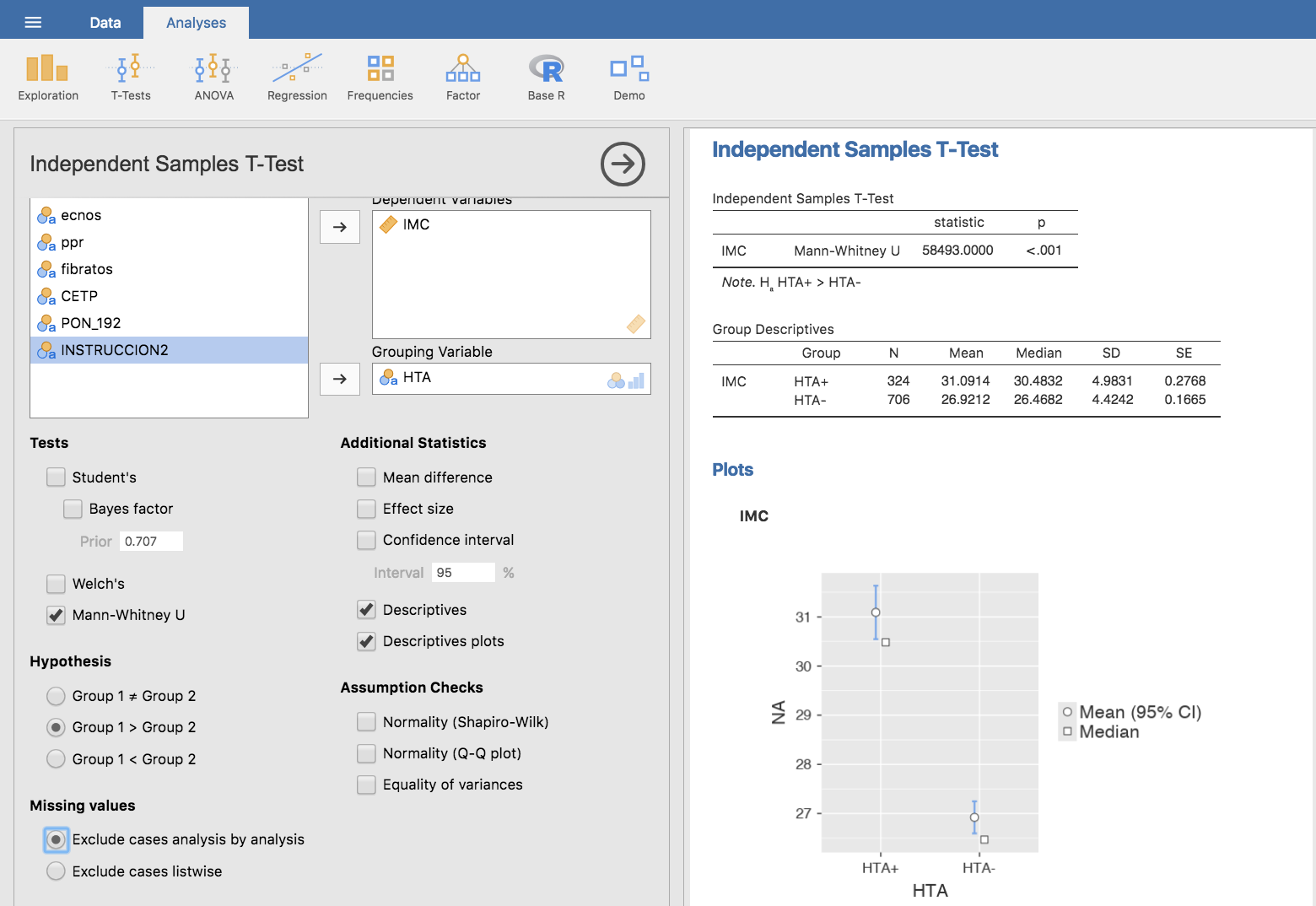
El p-valor que se obtiene aplicando el test de Wilcoxon-Mann-Whitney en las condiciones descritas es muy pequeño (p < 0.001), lo que indica que hay evidencia suficiente para asegurar que el valor de IMC en el grupo de hipertensos es mayor que en el grupo de normotensos; la diferencia observada no puede explicarse por el mero efecto del azar.
Jamovi también nos permite obtener un análisis descriptivo del IMC para hipertensos y normotensos, así como una gráfica con los intervalos de confianza para ambos grupos, los cuales podemos ver en la imagen anterior.
Test de Wilcoxon-Mann-Whitney: ¿Existe asociación entre el nivel de glucosa en sangre y la hipertensión arterial?
De igual modo que para el caso anterior podemos tratar de determinar la posible asociación entre el nivel de glucosa en sangre y la HTA. Los valores medios de glucosa en sangre en hipertensos y normotensos pueden obtenerse como:
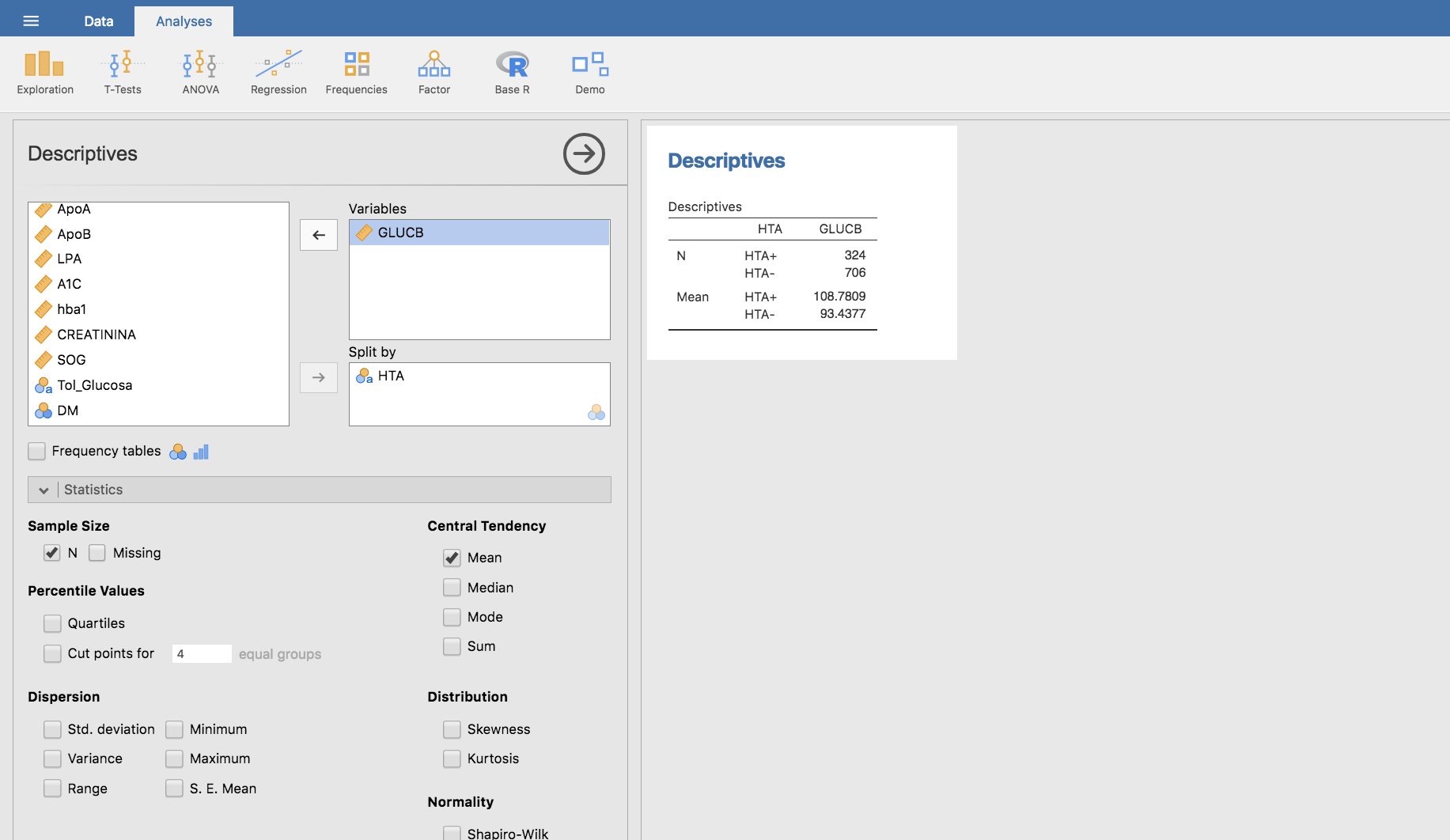
Gráficamente:
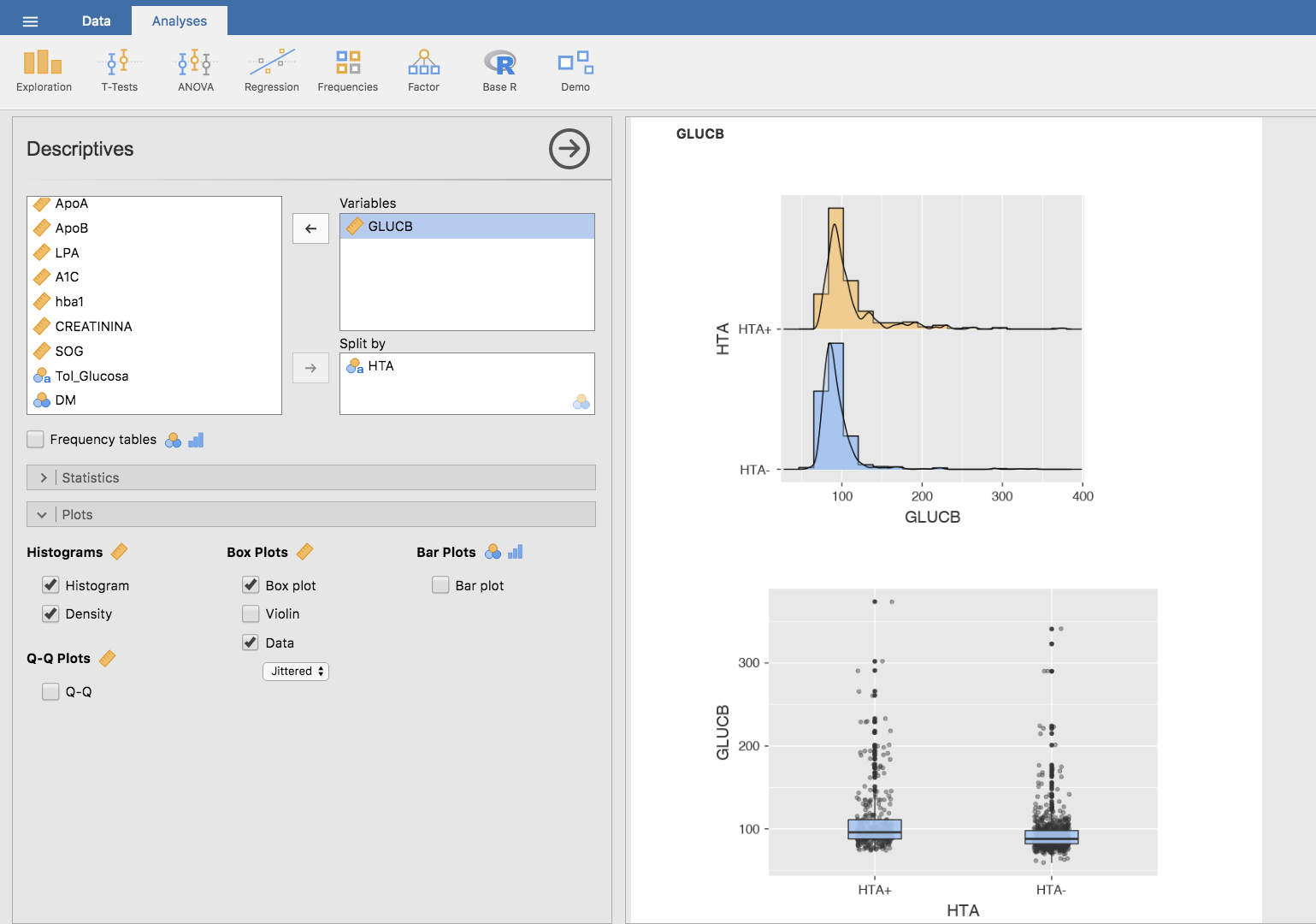
Estos gráficos indican que el nivel de glucosa en sangre tiene una distribución muy asimétrica en ambos grupos, lo que nos hace pensar que la variable bajo estudio (GLUCB) no sigue una distribución normal. De hecho, si planteamos el test de Shapiro-Wilk comprobamos que efectivamente así es:
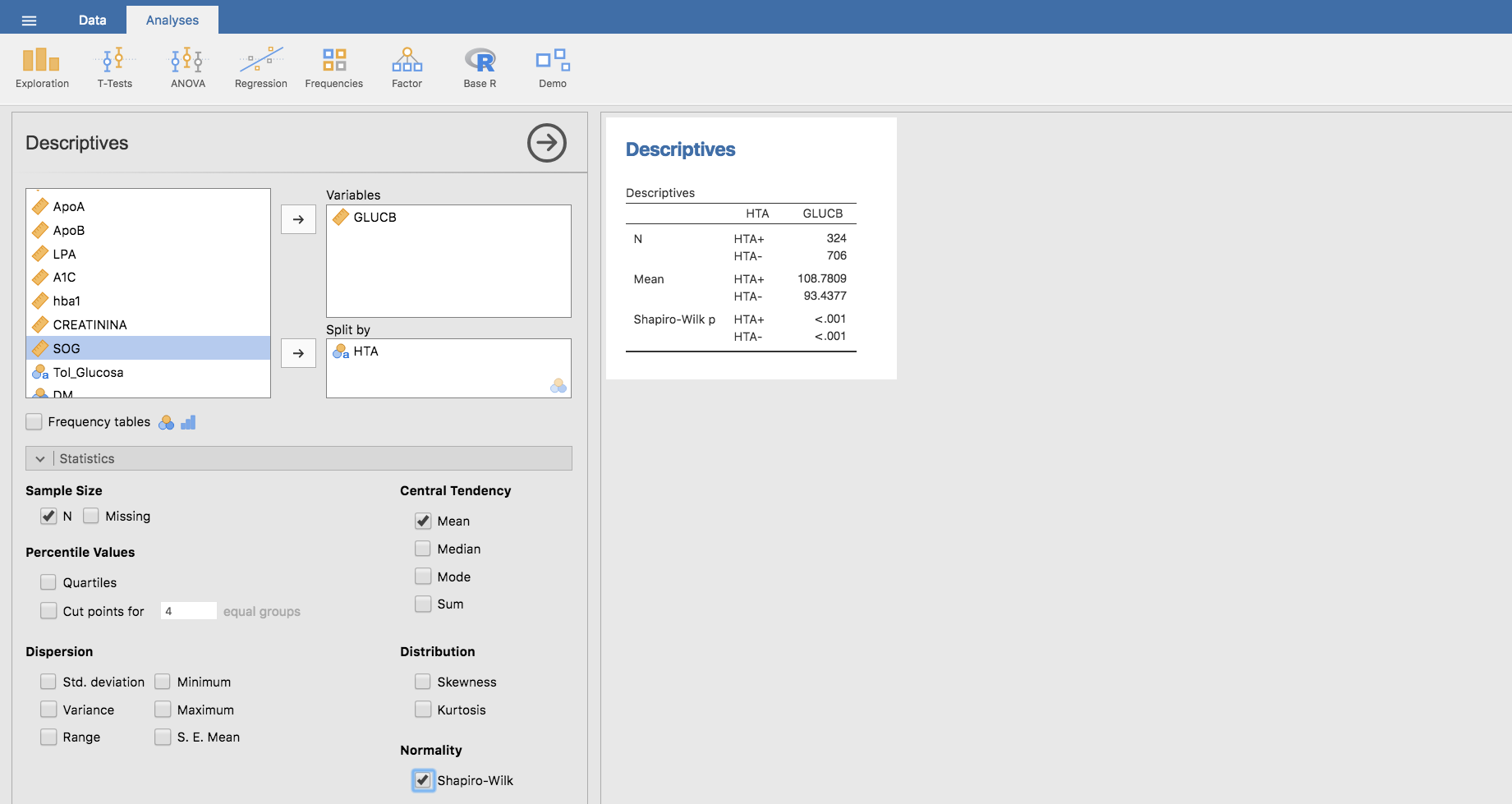
los p-valores que obtenemos indican que el nivel de glucosa en sangre no se distribuye según una normal ni para hipertensos ni para normotensos, por lo que no estamos en condiciones de aplicar el test de la t de Student.
Igual que en el caso anterior, optamos por realizar la comparación mediante el test de Wilcoxon-Mann-Whitney. La hipótesis nula en este test es que los valores de la variable tienden a ser similares en ambos grupos; la hipótesis alternativa es que los valores en uno de los grupos tienden a ser mayores que en el otro. Concretamente, si sospechamos que el nivel de glucosa es mayor en hipertensos, el contraste a realizar es:
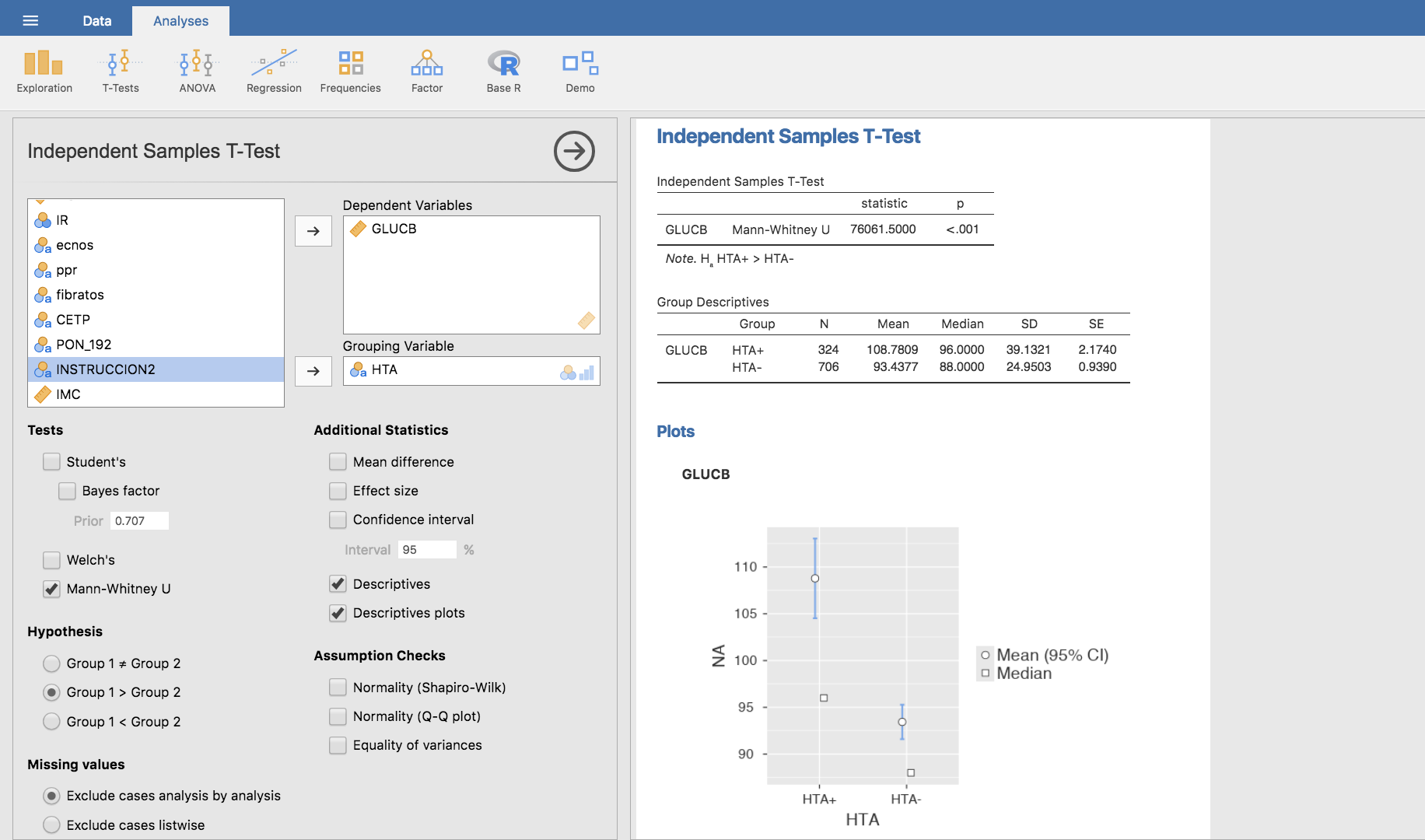
El p-valor indica que hay evidencia suficiente para asegurar que efectivamente en el grupo HTA+ el nivel de glucosa en sangre es mayor que en el grupo HTA-.
Datos emparejados
La siguiente base de datos que utilizaremos está en el fichero llamado MILLAC.sav:
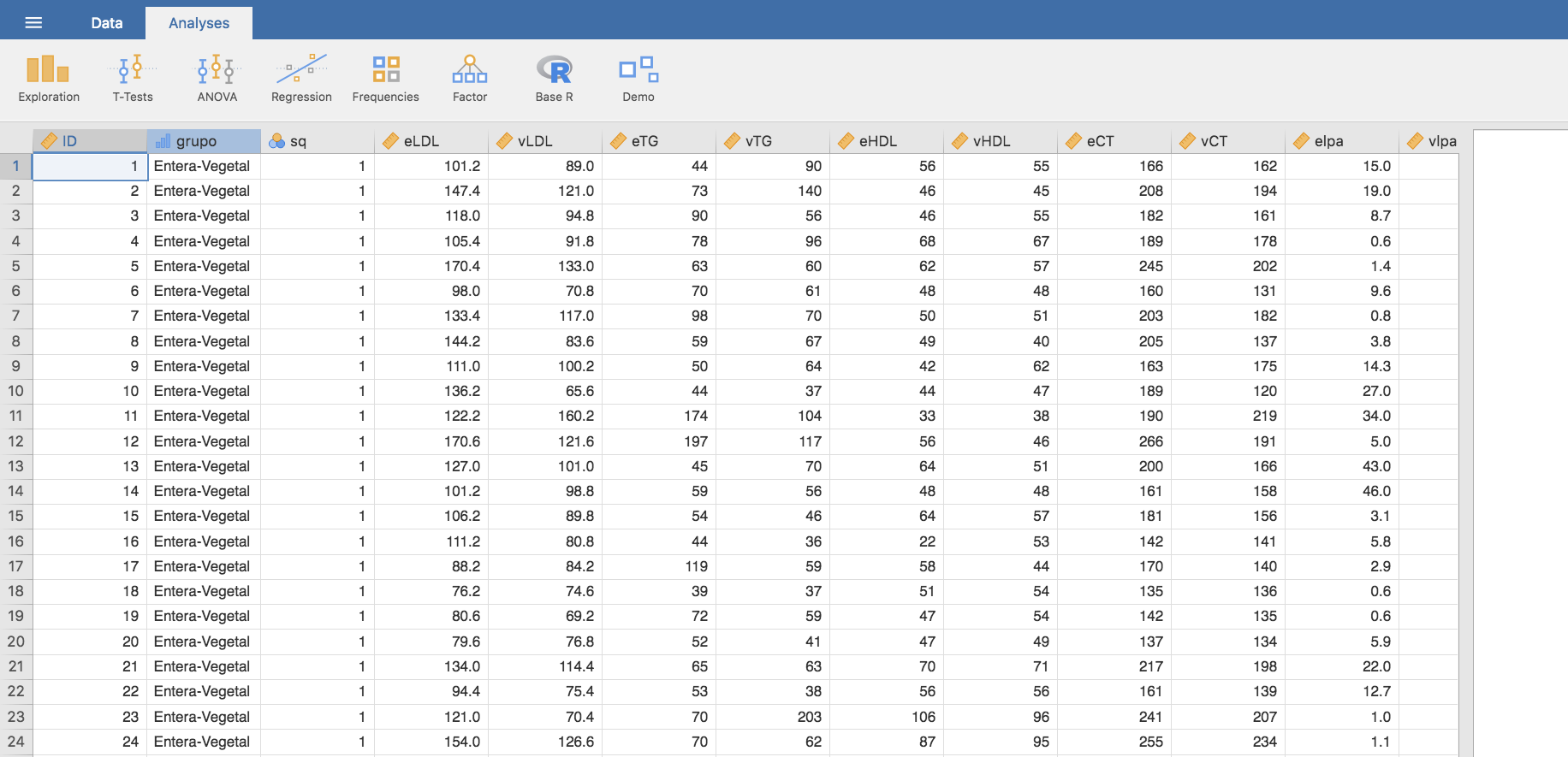
corresponde a un estudio sobre los niveles de HDL y LDL observados en niños dependiendo del tipo de leche que consumían. En concreto, el estudio se llevó a cabo mediante un diseño cruzado: los niños se dividieron aleatoriamente en dos grupos; en el primero (sq = 1) los niños consumieron leche entera durante 6 meses y leche desnatada (con grasa vegetal) durante los 6 meses siguientes; en el segundo grupo (sq = 2), durante los primeros 6 meses se consumió leche desnatada, y los siguientes 6 meses leche entera. Para cada niño se evaluaron los niveles de HDL y LDL al final de cada periodo de 6 meses. En lo que sigue denotamos por eLDL el valor de LDL tras el periodo de consumo de leche entera, y por vLDL el valor de LDL tras el consumo de leche desnatada enriquecida con grasa vegetal.
Los valores medios y desviaciones típicas de eLDL y vLDL, clasificados según la variable grupo, son:
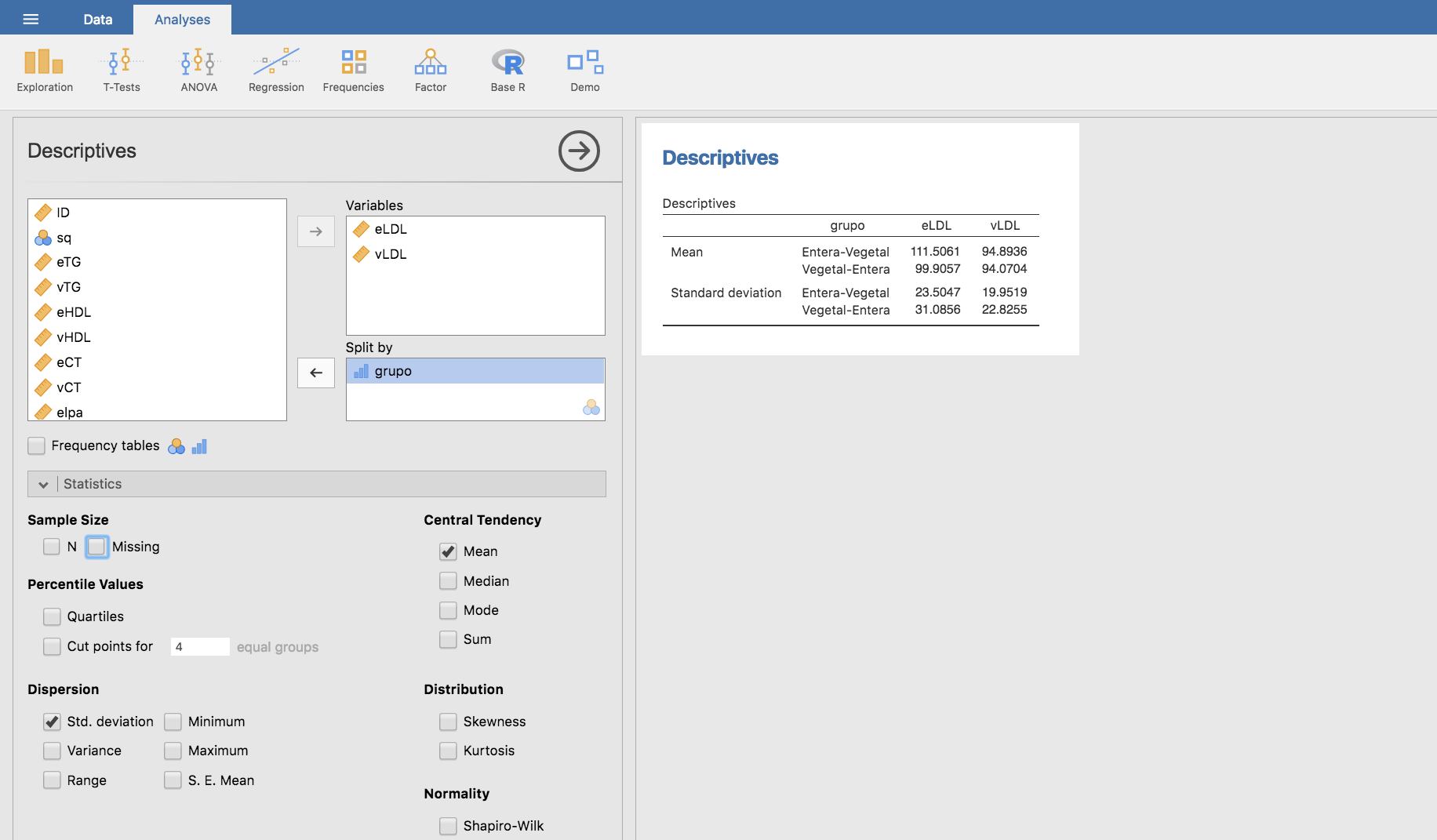
Así, los niveles de LDL tras la fase de consumo de leche entera (eLDL) fueron mayores en los niños que comenzaron con leche entera (LDL medio de 111.51) que en los que comenzaron con leche desnatada (LDL medio 99.91). Asimismo, los niveles de LDL tras la fase de consumo de leche desnatada (vLDL) fueron similares en los dos grupos (LDL medio de 94.89 entre los que hicieron la secuencia entera-vegetal, y 94.07 entre los que hicieron la secuencia vegetal-entera).
Gráficamente:
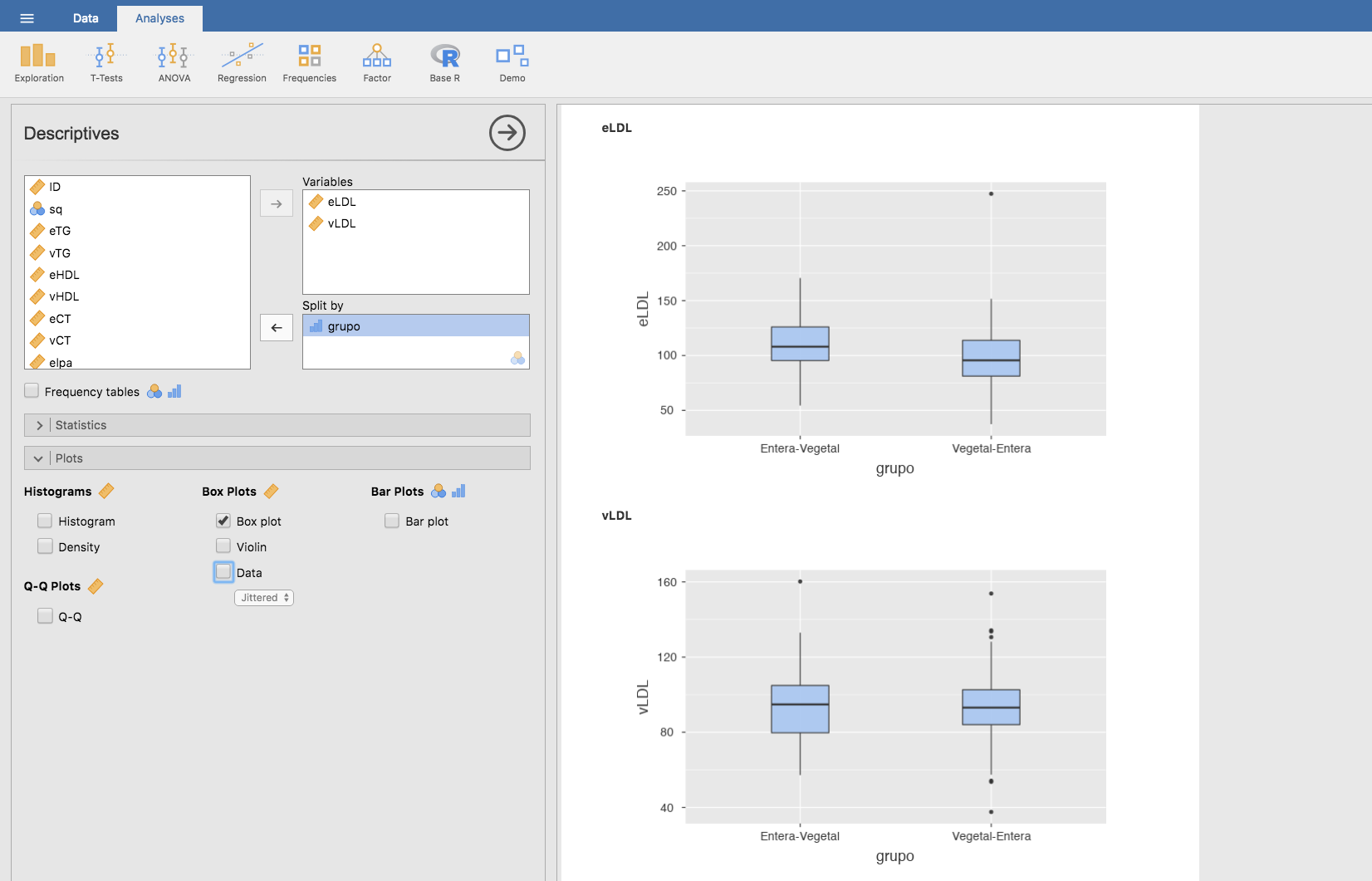
Los niños que han tomado leche en la secuencia Entera-Vegetal tuvieron un valor medio de LDL al terminar la fase entera de 111.51 unidades; esos mismos niños, al terminar la fase vegetal mostraron un valor medio de LDL de 94.89 unidades. ¿Es significativa esta diferencia? Es decir ¿puede explicarse por el mero efecto del azar o necesariamente debe atribuirse al efecto de haber cambiado el tipo de leche?
A diferencia de los casos anteriores para hacer esta comparación debe tenerse en cuenta que los datos están emparejados (cada niño se compara consigo mismo). Si suponemos que la variable LDL es aproximadamente normal, filtramos los datos de modo que nos quedemos solo con los niños del grupo sq = 1:
y aplicamos un test de la t de Student (para muestras emparejadas) para comparar la LDL en los niños del grupo seleccionado, en el que consideramos como hipótesis alternativa que la LDL es mayor en la primera fase que en la segunda:
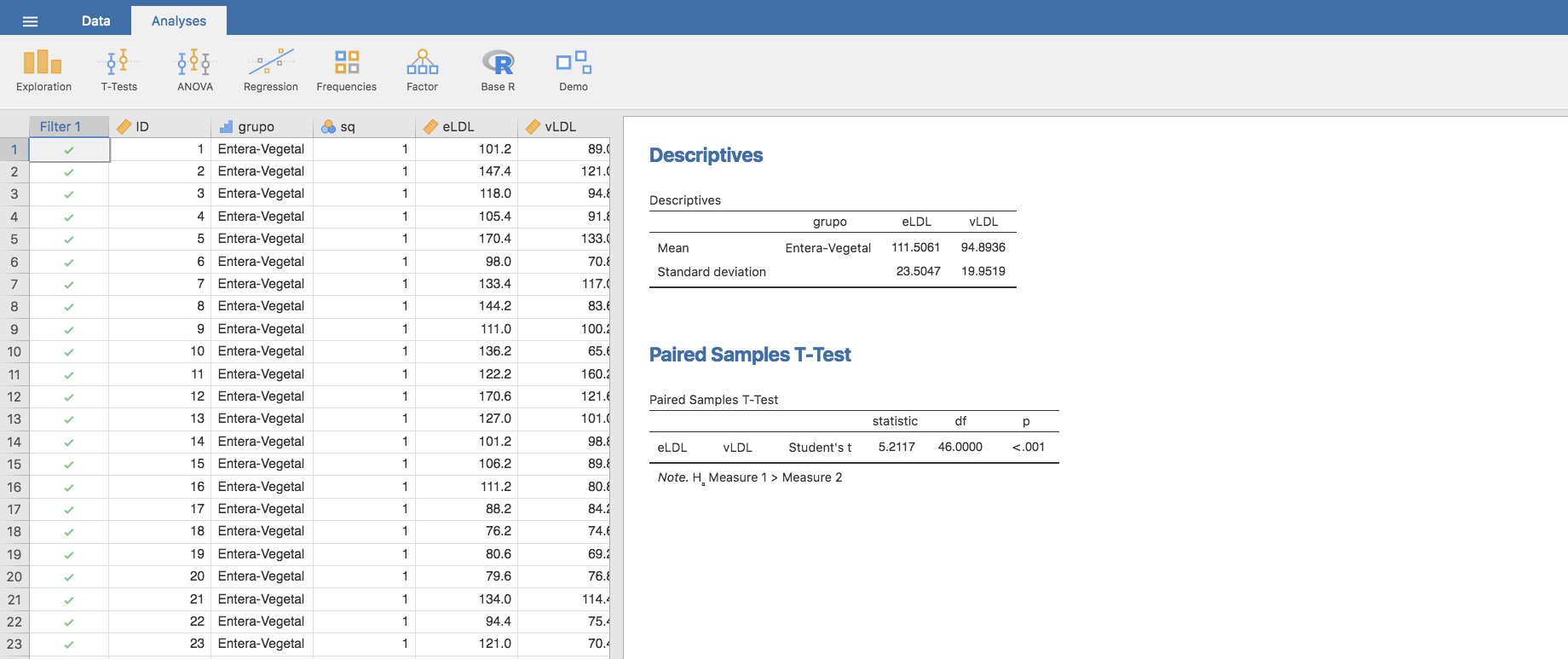
Los resultados indican que existe evidencia suficiente (p-valor < 0.01) para asegurar que se ha producido una disminución del LDL en el grupo analizado. La magnitud de dicha dismimución puede estimarse calculando la diferencia de medias y mediante un intervalo de confianza:
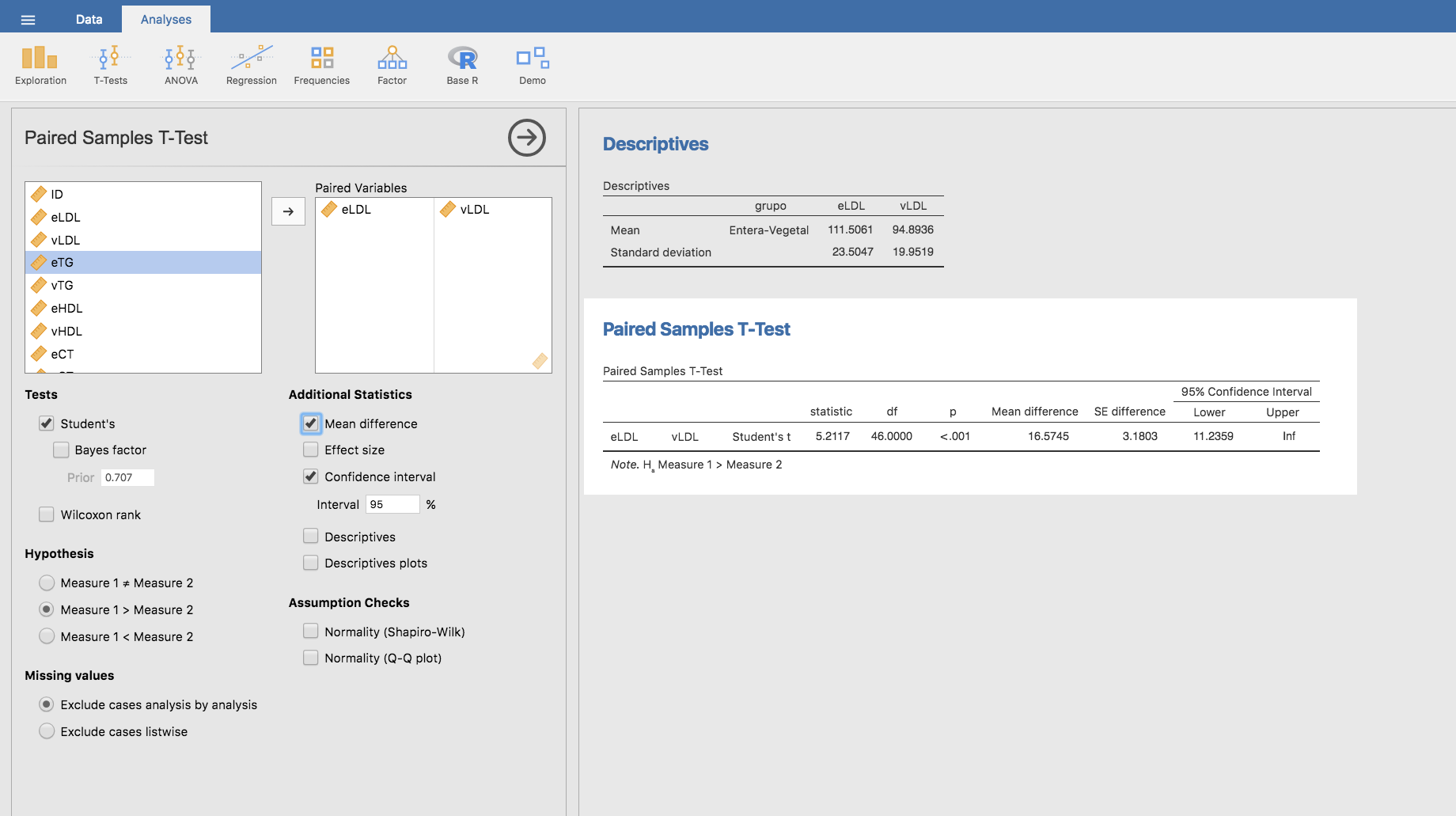
que pone de manifiesto que, con un 95% de confianza, se ha producido un incremento del LDL de al menos 11.236 unidades durante los meses en que los niños tomaban leche entera.
Por su parte, los niños que hicieron la secuencia inversa (primero leche desnadata-vegetal y luego leche entera), tenían un nivel medio de LDL al terminar la fase vegetal de 94.07, mientras que al terminar la fase entera el LDL había subido a 99.91. Nuevamente nos hacemos la pregunta: ¿es significativa esta diferencia?
Para responderla, al igual que antes, comparamos cada niño consigo mismo a través de un t-test para muestras emparejadas, suponiendo que los datos se distribuyen de forma aproximadamente normal. Previamente, filtramos los datos de modo que habilitamos solo los que corresponden al grupo que vamos a analizar (sq = 2):
Aplicando el test de la t de Student para muestras emparejadas a este grupo, tomando como hipótesis alternativa que la HDL es menor durante los seis primeros meses:
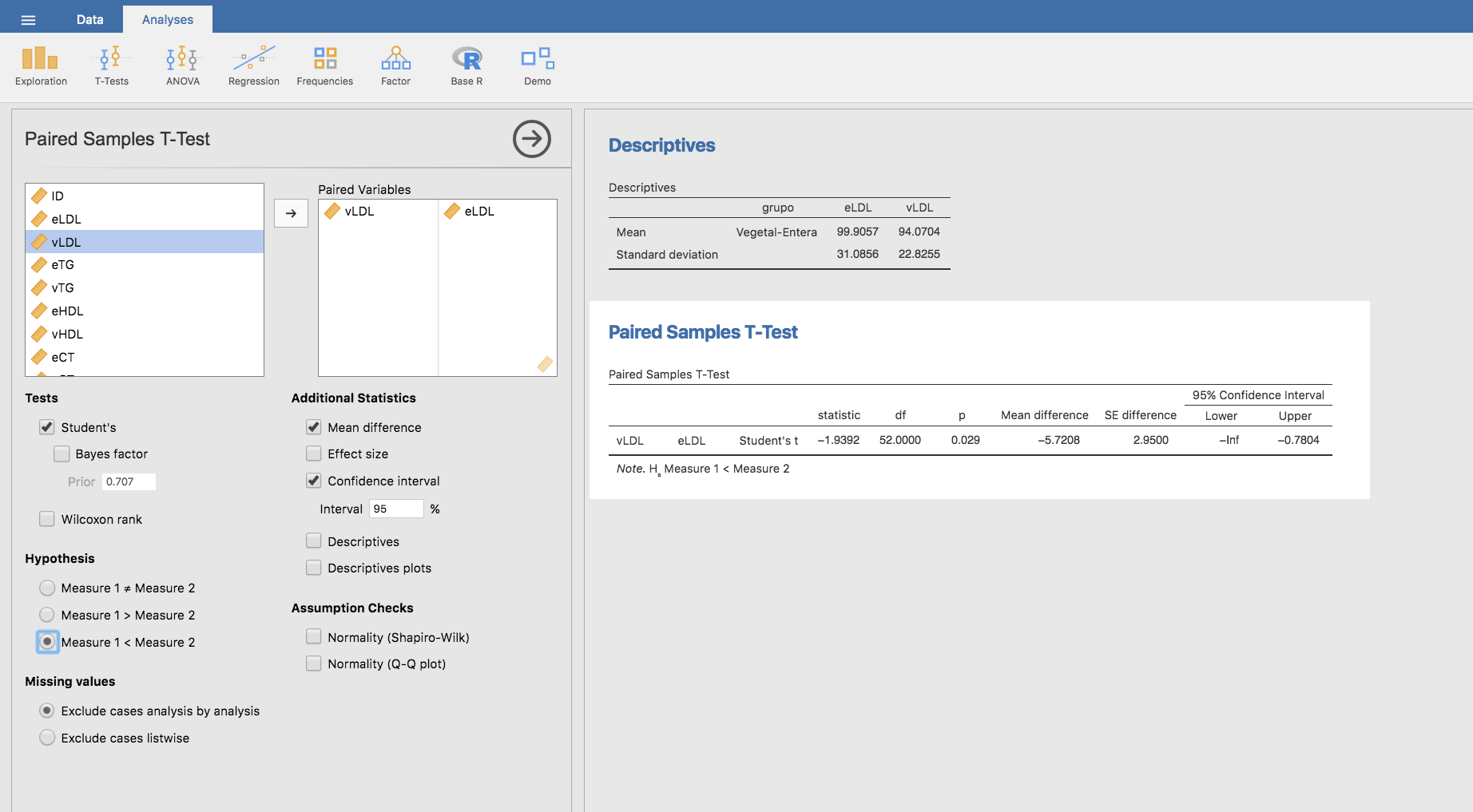
se obtiene que, efectivamente, se ha producido un incremento significativo del LDL durante los últimos seis meses de toma. Con un 95% de confianza, puede decirse que el incremento en LDL ha sido inferior a 0.78 unidades.
Ejercicios
Comprobar que la asociación entre las variables OBESIDAD (que se definió en uno de los ejercicios planteados en la tarea titulada Riesgo Relativo y Odds Ratio) y SEDENTARIO es significativa.
Comprobar que la asociación entre las variables OBESIDAD y DM es significativa.
¿Están asociadas las variables PESO y SEDENTARIO? En otras palabras, ¿el sedentarismo está asociado al aumento de peso?
¿Están asociadas las variables PESO y TABACO? En particular, ¿el hecho de ser fumador está asociado a una disminución de peso?