Tarea 1: Estadística descriptiva con Jamovi
Angelo Santana, Carmen Nieves Hernández, Juan Rocha
Introducción
La estadística descriptiva es el conjunto de métodos diseñados para organizar, resumir y representar los datos recogidos en el curso de algún estudio. Su finalidad es convertir los datos brutos en información que pueda ser fácilmente entendida y asimilada. En este sentido, la estadística descriptiva es una herramienta indispensable para la exploración de los datos: descubrir tendencias, asociaciones, características relevantes, …
Para poder aplicar los métodos de la estadística descriptiva de manera eficiente se hace necesario disponer de programas informáticos adecuados para ello, con capacidad para capturar datos desde distintas fuentes, procesarlos, transformarlos si es necesario, y generar tablas, gráficos y medidas de síntesis.
 \(\;\;\;\) R: http://www.r-project.org
\(\;\;\;\) R: http://www.r-project.org
\(\;\)  \(\;\;\;\) Jamovi: https://www.jamovi.org
\(\;\;\;\) Jamovi: https://www.jamovi.org
En este curso proponemos la utilización del software Jamovi, que cuenta con numerosas ventajas: es gratuito, se actualiza constantemente, interfaz amigable con la potencia de R, permite la realización de gráficos, permite al usuario desarrollar funciones a medida y funciona en todas las plataformas (Windows, Linux y Mac), la transferencia de ficheros es muy versatil permitiendo importar ficheros de SPSS, exportar código a Rstudio,…
Pretendemos además que este capítulo sea interactivo y que el alumno vaya aplicando las técnicas y métodos que en él se explican a medida que avanza en su lectura. Con este fin se han dispuesto en la web de la asignatura diversas bases de datos que pueden ser utilizadas libremente para el aprendizaje.
Objetivos
Al finalizar el estudio de este tema, se espera que el alumno sea capaz de:
Comprender la importancia de la exploración de los datos mediante tablas y gráficos.
Distinguir los distintos tipos de variables y sus características.
Calcular e interpretar correctamente la información aportada por las diferentes medidas de síntesis.
Conocer los métodos de estadística descriptiva para el estudio conjunto de dos variables.
Utilizar el programa Jamovi para la exploración y descripción de datos.
Población y Muestra
Cuando se realiza un estudio de cualquier tipo (de investigación, de mercado, de evaluación de calidad, etc.), generalmente se observan características o magnitudes correspondientes a los elementos de una población de interés. Normalmente dicha población no suele ser accesible en su totalidad, y el estudio ha de reducirse a unos cuantos elementos escogidos de la misma. El subconjunto de objetos (o sujetos) de la población que son incluidos en el estudio, recibe el nombre de muestra. Así, por ejemplo, en el ámbito de las Ciencias Marinas y Veterinaria:
El estudio de las poblaciones biológicas –cefalópodos, crustáceos, peces, mamíferos marinos, …– se realiza a partir de los datos aportados por los ejemplares que se capturan o se observan durante una campaña de muestreo.
El estudio de parámetros físicos o químicos –temperatura, salinidad, velocidad de corriente, concentración de \(CO_{2}\) disuelto, …– se realiza a partir de los datos obtenidos por sensores que se colocan en los lugares de interés durante periodos concretos.
El proceso mediante el cual los resultados particulares obtenidos en un muestreo se emplean para responder cuestiones generales sobre la población recibe el nombre de inferencia. Cuando el muestreo es aleatorio (todos los elementos de la población tienen, a priori, la misma probabilidad de formar parte de la muestra) el proceso de inferencia se lleva a cabo mediante métodos estadísticos basados en la probabilidad, y recibe el nombre de Inferencia Estadística. Ello garantiza al mismo tiempo que la muestra es representativa de la población, es decir, tiene sus mismas características generales. Un muestreo no aleatorio, en el que se seleccionan los objetos con unas características determinadas, puede resultar tendencioso y no representar para nada a la población de interés.
Tipos de datos
Las magnitudes o atributos medidos sobre cada objeto de la muestra reciben el nombre de variables estadísticas (longitud, peso, duración, temperatura, …). Los datos son los valores que toma la variable en cada objeto. Formalmente, una variable estadística \(X\) definida sobre una población \(\Omega\) y con valores en un conjunto \(V\) es una función \(X:\Omega\longrightarrow V\), que a cada objeto \(\omega\) de \(\Omega\), le asigna un único valor en \(V\). Cuando este conjunto es numérico (\(V\subseteq\mathbb{R}\)), la variable se dice cuantitativa o numérica, y en caso contrario cualitativa o categórica.
Las variables cuantitativas son continuas si pueden tomar cualquier valor dentro de un rango numérico (temperatura, peso, longitud, etc.); son discretas si no admiten todos los valores intermedios de un rango. Las variables discretas suelen tomar sólo valores enteros (número de hijos de una familia, número de fallos en un equipo técnico durante un año, etc.).
Las variables categóricas son binarias si solo toman dos valores (sano/enfermo, observado/no observado, sí/no, etc.). Pueden ser además nominales, si los datos corresponden a categorías sin relación de orden entre sí (color, sexo, profesión,…), u ordinales cuando sí que hay relación de orden (curso escolar, posición en una cola, nivel de dificultad,…).
Una vez que se han observado los valores que toman las variables de nuestro estudio es preciso guardar los datos en un archivo que pueda ser leido fácilmente por un programa estadístico, en nuestro caso Jamovi. Si la muestra está formada por \(n\) objetos \(\omega_{1},\omega_{2},\dots,\omega_{n}\), sobre los que se han medido \(p\) variables \(X_{1},X_{2},\dots,X_{p}\), los datos resultantes deberán organizarse, en general, en forma de una matriz con \(n\) filas (cada fila corresponde a un objeto) y \(p\) columnas (cada columna corresponde a una variable), tal como se muestra en la siguiente tabla. Denotamos por \(x_{ij}\) al valor observado de la variable \(X_{j}\) sobre el objeto \(\omega_{i}\).
| Objetos | Variables | |||||
|---|---|---|---|---|---|---|
| \(\;\) | \(X_{1}\) | \(X_{2}\) | \(\dots\) | \(X_{j}\) | \(\dots\) | \(X_{p}\) |
| \(\omega_{1}\) | \(x_{11}\) | \(x_{12}\) | \(\dots\) | \(x_{1j}\) | \(\dots\) | \(x_{ip}\) |
| \(\omega_{2}\) | \(x_{21}\) | \(x_{22}\) | \(\dots\) | \(x_{2j}\) | \(\dots\) | \(x_{2p}\) |
| \(\vdots\) | \(\vdots\) | \(\vdots\) | \(\ddots\) | \(\vdots\) | \(\vdots\) | \(\vdots\) |
| \(\omega_{i}\) | \(x_{i1}\) | \(x_{i2}\) | \(\dots\) | \(x_{ij}\) | \(\dots\) | \(x_{ip}\) |
| \(\vdots\) | \(\vdots\) | \(\vdots\) | \(\dots\) | \(\vdots\) | \(\ddots\) | \(\vdots\) |
| \(\omega_{n}\) | \(x_{n1}\) | \(x_{n2}\) | \(\dots\) | \(x_{nj}\) | \(\dots\) | \(x_{np}\) |
En la mayor parte de los casos la matriz de datos en bruto, aunque contiene toda la información recogida en el muestreo, no permite interpretar la información de forma clara. La percepción y resumen de las características de los datos se consigue fundamentalmente a través de:
- Tablas de Frecuencias.
- Representaciones Gráficas.
- Medidas de Síntesis de datos numéricos.
Datos de ejemplo: acceso y lectura
Para ilustrar los distintos métodos de la Estadística Descriptiva utilizaremos los datos que se encuentran en el archivo sargos.csv, que puede descargarse de la web de la asignatura. Este archivo corresponde a un muestreo de sargos realizado sobre capturas de esta especie en las Islas Canarias durante el año 2005. La tabla 2 muestra datos relativos a 10 ejemplares, si bien la base de datos completa contiene 200. Sobre cada ejemplar se han medido las variables: isla (donde fue capturado), sexo, long (longitud total), ldors (longitud medida desde el morro hasta la aleta dorsal), lpec (longitud hasta la aleta pectoral), loper (longitud hasta el opérculo), altop (altura del pez en la región del opérculo), peso (peso total), pgon (peso de las gónadas), phig (peso del hígado), ptdo (variable que vale 1 si el pez está parasitado por larvas de anisákidos y 0 si no lo está) y larvas (número de larvas de anisákidos encontradas en la cavidad abdominal del pez). Como puede apreciarse, el peso de las gónadas no está disponible para todos los peces. A estos valores no disponibles nos referiremos como valores perdidos.
| isla | sexo | long | ldors | lpect | loper | altop | peso | pgon | phig | ptdo | larvas |
|---|---|---|---|---|---|---|---|---|---|---|---|
| GC | Macho | 22,59 | 5,14 | 5,32 | 4,08 | 8 | 163,81 | 17,3 | 0 | 0 | |
| HI | Macho | 26,35 | 6,44 | 6,02 | 5,36 | 8,89 | 277,04 | 6,86 | 22,3 | 0 | 0 |
| FV | Macho | 21,23 | 5,11 | 4,63 | 4,39 | 6,39 | 135,69 | 1,98 | 5,4 | 0 | 0 |
| TF | Macho | 22,7 | 5,35 | 4,61 | 4,95 | 7,33 | 167,54 | 1,65 | 27 | 1 | 5 |
| LZ | Hembra | 20,2 | 4,84 | 4,58 | 4,38 | 6,63 | 131,68 | 7,1 | 0 | 0 | |
| TF | Macho | 21,6 | 5,5 | 5,56 | 3,83 | 6,08 | 176,21 | 4,54 | 22,9 | 0 | 0 |
| GC | Hembra | 25,18 | 5,73 | 5,52 | 5,72 | 8,14 | 257,38 | 37,01 | 12,4 | 0 | 0 |
| GC | Macho | 21,68 | 5,02 | 5,19 | 4,74 | 6,62 | 145,14 | 18,2 | 0 | 0 | |
| LP | Macho | 23,29 | 6,03 | 5,4 | 5,34 | 6,95 | 201,82 | 3,55 | 12,7 | 0 | 0 |
| TF | Hembra | 16,39 | 4,31 | 3,54 | 3,57 | 5,21 | 78,54 | 6,4 | 0 | 0 |
El archivo está en formato csv (Comma Separated Values), que es un archivo ASCII plano (es decir, sin información de formato de ningún tipo), en el que los distintos valores están separados por el símbolo punto y coma (;). Puede abrirse con cualquier editor de texto, si bien las hojas de cálculo estándar (OpenOffice o Microsoft Excel) nos lo muestran en forma de tabla visualmente más atractiva. En la primera fila del archivo se encuentran los nombres de las variables.
Supondremos que una vez descargado el archivo lo hemos guardado, por ejemplo, en el directorio:
C:/documents and settings/veterinaria/Est_Desc/
Suponemos que se utiliza un ordenador con sistema operativo Windows, que suele ser lo más habitual. En caso de utilizar Linux o Mac las rutas de directorio pueden ser ligeramente distintas. En lo que se refiere al funcionamiento de Jamovi, es idéntico en todos los sistemas operativos.
Para leer el archivo sargos.csv con Jamovi abrimos el programa, vamos al extremo superior izquierdo (pulsamos menú):
seguidamente Open:
luego This PC y Browse para llegar hasta el directorio en el que tenemos el fichero:
una vez estamos en nuestro directorio, elegimos el fichero sargos.csv y pulsamos “Open”:
a partir de ese momento, los datos estarían ya cargados en Jamovi:
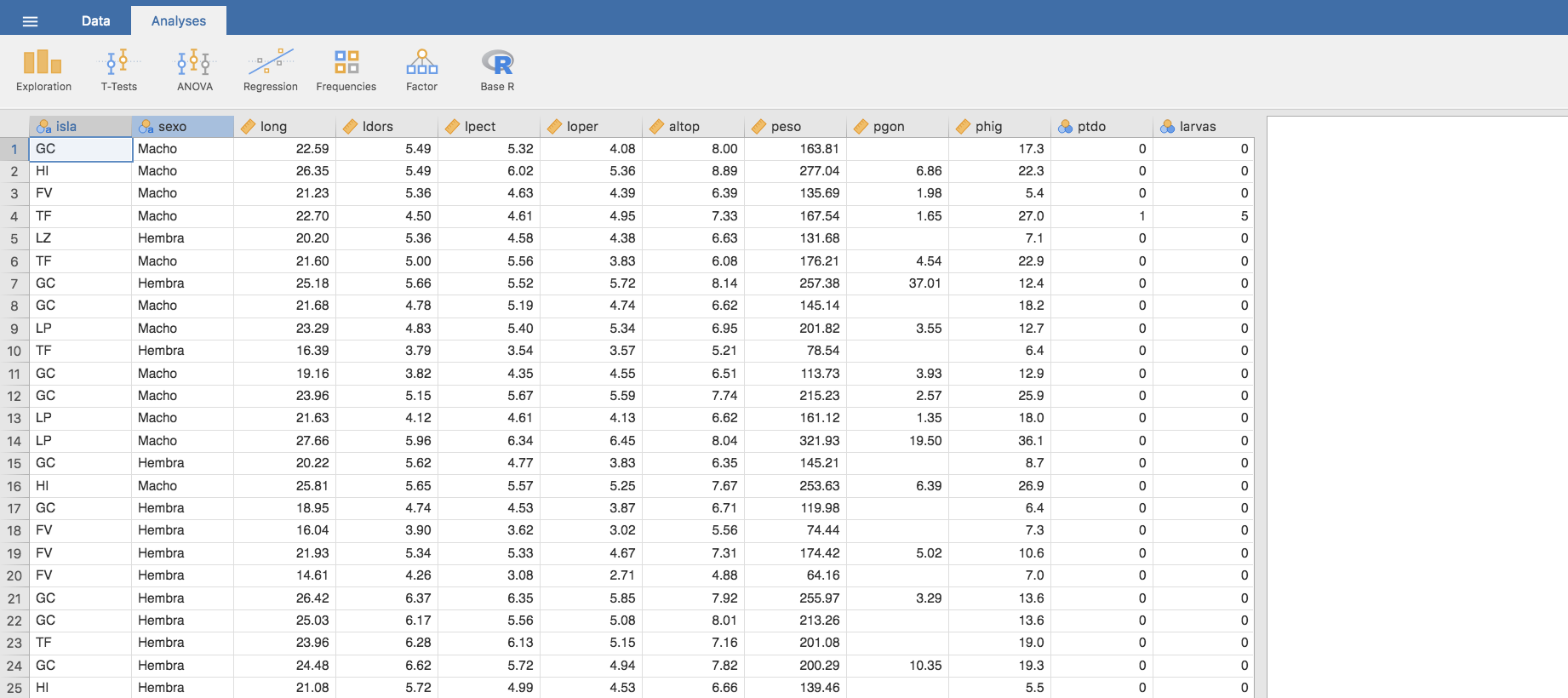
Acceso directo a las variables dentro de una matriz de datos
En general, para acceder a una variable en Jamovi es suficiente con hacer doble clic en el nombre de esa variable, o bien hacer clic en la columna que contiene los datos de esa variable y pulsar Data y luego Setup.
Por ejemplo, si queremos acceder a la variable isla optamos por hacer doble clic sobre su nombre, y aparece una ventana emergente con información sobre la misma.
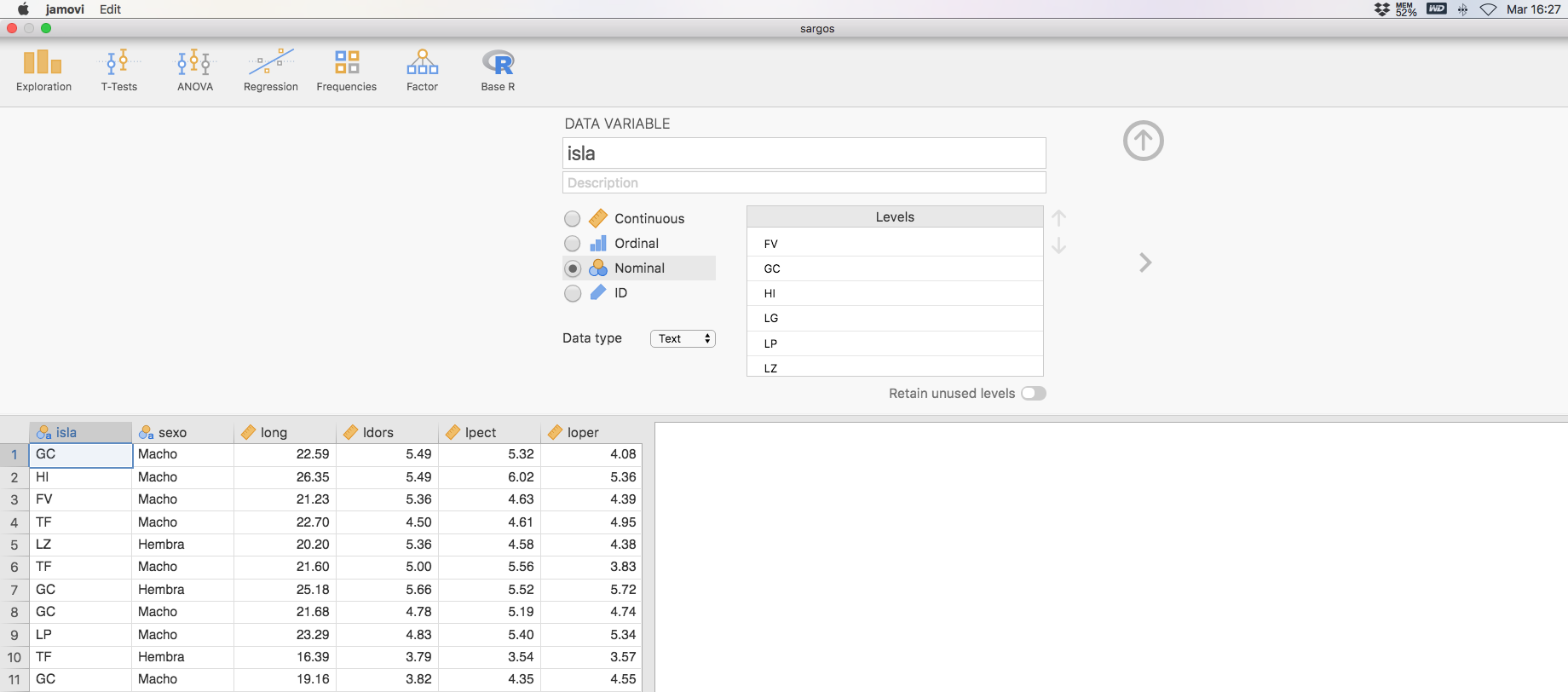
Tipos de datos en Jamovi
Hemos visto al comienzo de esta sección que las variables estadísticas pueden clasificarse en categóricas y numéricas, y estas últimas en discretas o continuas. Jamovi distingue las variables según su clase:
Continuous: variables numéricas continuas. Observa el icono que se asigna a las variables continuas:

Ordinal: variables ordinales, bien sean categóricas o numéricas discretas.

Nominal : variables categóricas nominales, aunque también puede asignarse a variables ordinales.
ID: variables que solo se utilizan para identificar cada registro, y que casi con total seguridad nunca se van a utilizar en ningún análisis estadístico (nombre o número de DNI de una persona, por ejemplo).

Podemos ver que las variables isla y sexo han sido identificadas como Nominal (en ambos casos, en Data type es Text); las variables long, ldors, lpect, loper, altop, peso, pgon y phig han sido identificadas como Continuous (valores reales, variables numéricas continuas, el “Data type” es Decimal); y las variables ptdo y larvas han sido identificadas como Nominal (valores enteros, variables numéricas discretas, Data type es Integer).
Observación: La variable ptdo ha sido considerada como Nominal por Jamovi, asignándole el tipo Integer. Sin embargo, no es una variable nominal en términos estrictos.
Recodificación y etiquetado de niveles
En muchas ocasiones, los niveles de una variable son poco ilustrativos de su significado. En los datos de nuestro ejemplo, la variable que indica si un pez está parasitado o no, ptdo, es dicotómica y toma los valores \(0\) y \(1\), y éstos son los valores que aparecerán en las tablas y gráficos que podamos hacer con ella. Sería deseable que en su lugar apareciesen los términos “No Parasitado” y “Parasitado”, ya que de esta forma la salida de resultados sería más clara e interpretable. Podemos conseguir este efecto creando una nueva variable a partir de ptdo, y asignando etiquetas a sus valores tal y como explicamos a continuación:
- Hacemos clic en la columna de la variable ptdo, pulsamos botón derecho del ratón (si estás con Windows) o Ctrl+clic al ratón (si estás con Mac) y la ventana emergente da la opción de copiar esa columna con los datos de la variable. Hacemos clic en Copy:
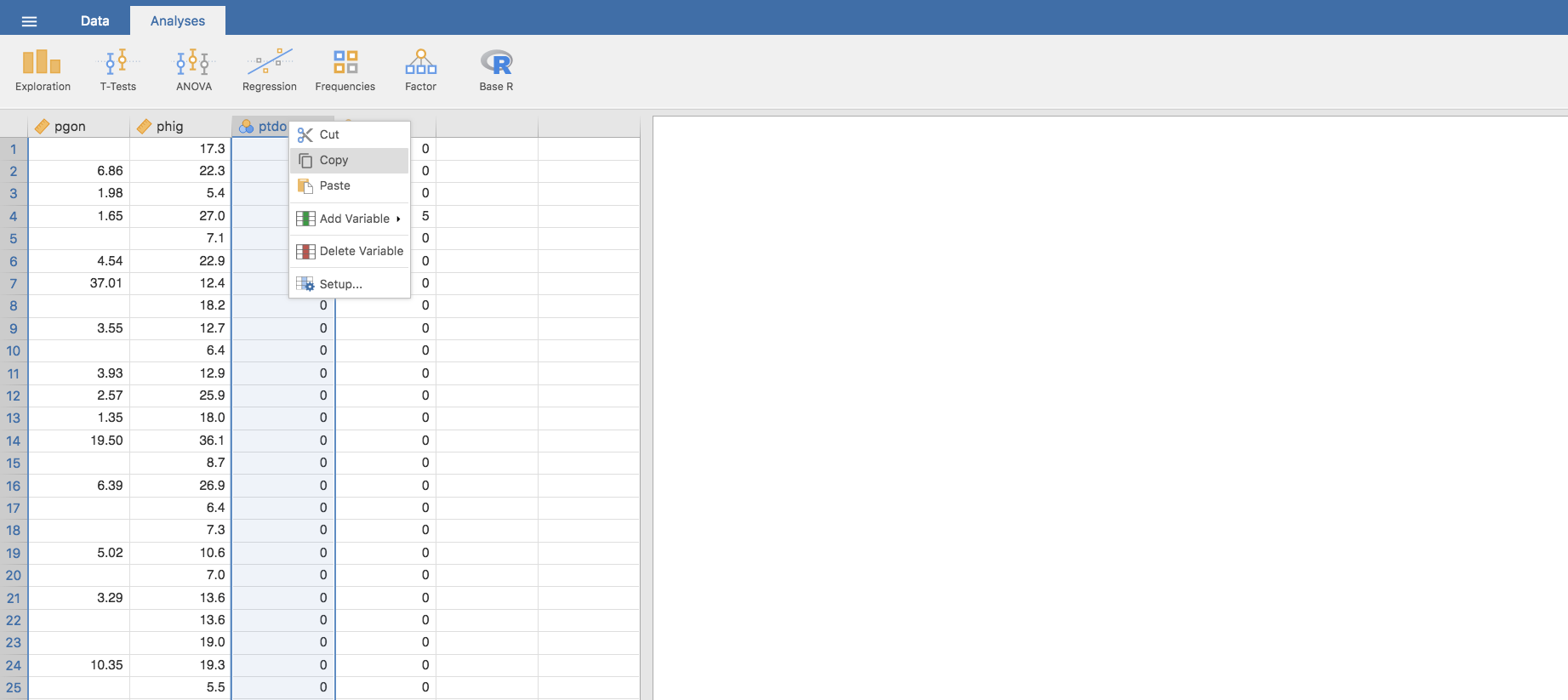
- Seleccionamos la columna en la que queremos copiar los datos y nuevamente: botón derecho del ratón o Ctrl+clic (en Mac) y luego pulsamos Paste
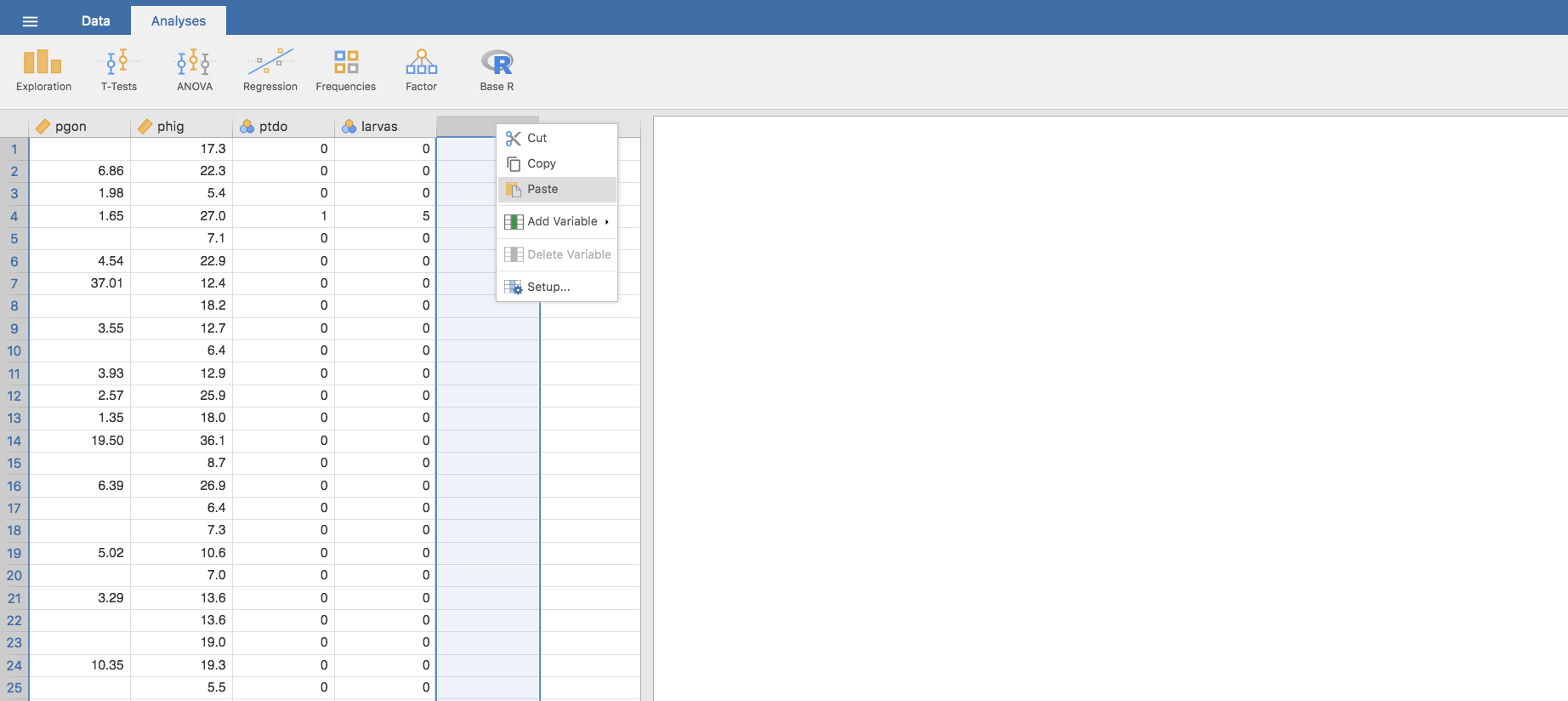
- La nueva variable se ubica en la columna elegida, y contiene los datos de la variable ptdo. El sistema le asigna como nombre la letra del alfabeto que corresponda a esa columna, en nuestro caso la M. Para recodificar los niveles hacemos doble clic en el nombre, aparece la ventana con los datos de la variable, y podemos darle un nombre y una descripción. La llamamos fptdo:
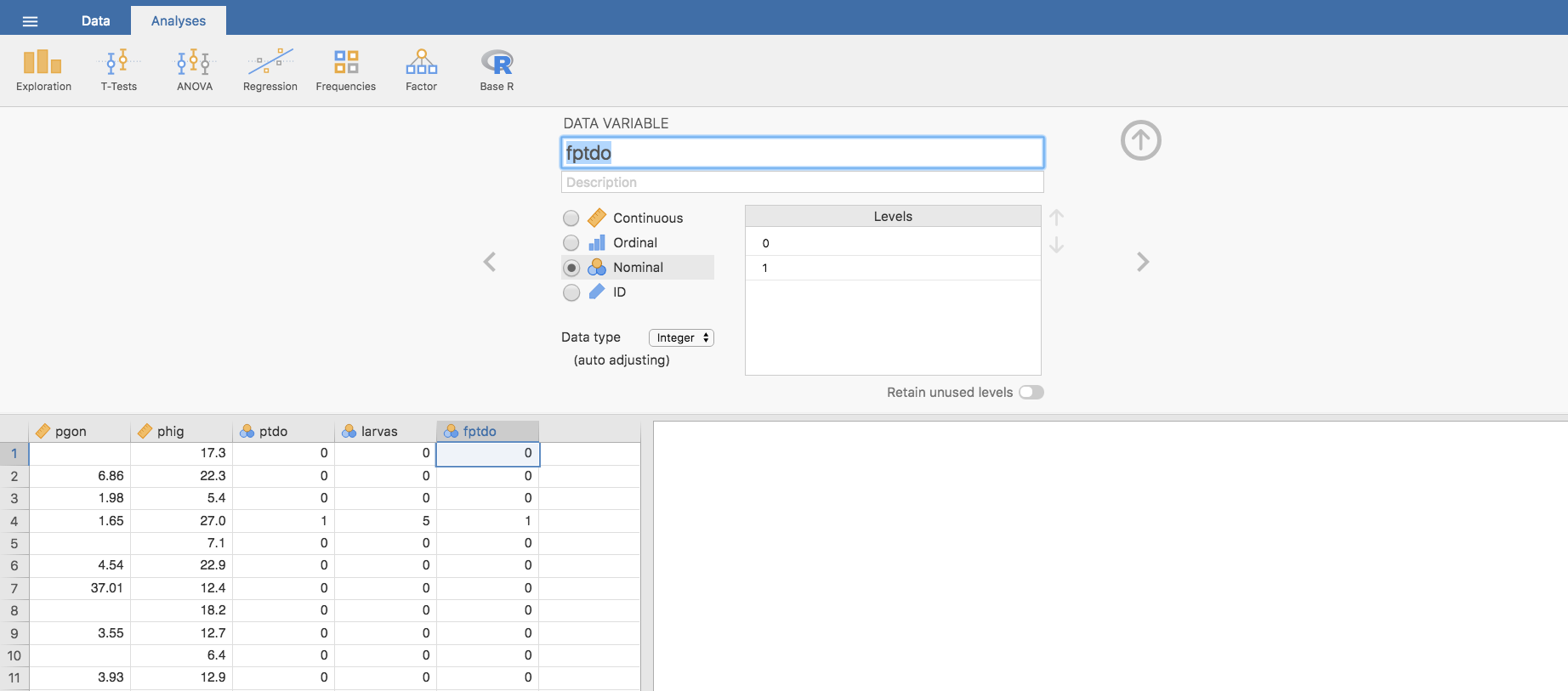
Además, podemos redefinir el tipo de variable: la consideraremos como una variable Ordinal con Data type como Text. Pulsamos en el nivel 0 y lo renombramos como No Parasitado y el 1 como Parasitado. Y ya hemos recodificado los niveles: observa como automáticamente aparecen los nuevos niveles en la columna que contiene los datos de la nueva variable.
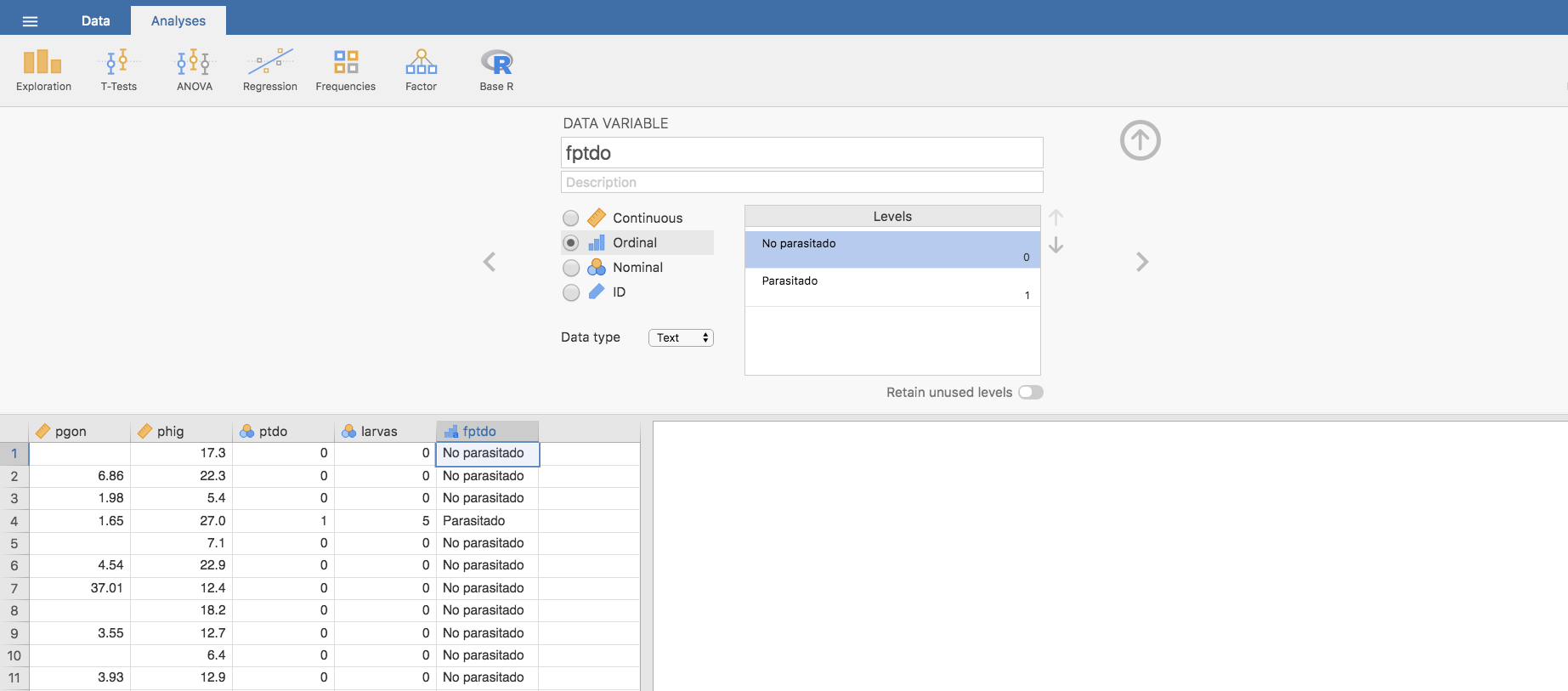
Como resultado final tenemos una nueva variable ordinal fptdo, construida a partir de ptdo, asignando a sus niveles originales, 0 y 1, unas nuevas etiquetas, No Parasitado y Parasitado. De esta manera, a partir de ahora, en todos los resultados que involucren a la variable fptdo (gráficos, tablas, etc.) sus valores aparecerán identificados como No Parasitado y Parasitado.
Crear variables o recodificar variables existentes
Acabamos de ver como se crea una variable (fptdo) a partir de una existente (ptdo). Si en lugar de crear la nueva variable, optamos por recodificar directamente sobre la variable ya existente (ptdo), en nuestro caso, ésta quedaría convertida en una variable Ordinal en la que sus niveles 0 y 1 son sustituidos por No parasitado y parasitado, respectivamente.
¿Es mejor crear nuevas variables o recodificar las que ya existen? Si somos principiantes en Jamovi lo mejor es crear nuevas variables; de esta forma las variables originales estarán siempre disponibles y en caso de error podemos volver a utilizarlas. Si las recodificamos y nos hemos equivocado en la recodificación, tendríamos que recuperar la variable original, lo que a veces puede resultar complicado.
Tablas de frecuencias y representaciones gráficas
Variables categóricas o numéricas discretas
Cuando se observan variables categóricas tales como la isla en que fue capturado un pez, su sexo, y si está o no parasitado, muchos de sus valores aparecen repetidos. La frecuencia absoluta de la \(i\)-ésima categoría es el número de veces \(n_{i}\) que se repite dicha categoría en el total de observaciones. La frecuencia relativa es la proporción: \[ f_{i}=\frac{n_{i}}{n} \]
siendo \(n=\sum_{i=1}^{k}n_{i}\) el número total de observaciones (\(k\) es el número de categorías). La frecuencia relativa suele también expresarse en porcentaje: \[ f_{i}=100\cdot\frac{n_{i}}{n}\% \]
Estas definiciones se extienden también a la construcción de tablas de frecuencias para variables numéricas discretas. En este último caso se suele considerar también la frecuencia acumulada hasta el valor \(x_{i}\) como el número \(N_{i}=\sum_{j=1}^{i}n_{j}\) de observaciones menores o iguales que \(x_{i}\). La frecuencia acumulada relativa es la proporción: \[ F_{i}=\frac{N_{i}}{n} \]
Estas frecuencias suelen presentarse en tablas similares a la siguiente. En la columna de la variable \(X\) se anotan sólo las \(k\) categorías o valores distintos que toma la variable, en orden creciente si \(X\) es numérica. Asimismo las frecuencias acumuladas sólo se incluyen cuando \(X\) es numérica.
| \(X\) | F. Absoluta | F. Relativa | F. Ac. Absol. | F. Ac. Rel. |
|---|---|---|---|---|
| \(x_{1}\) | \(n_{1}\) | \(f_{1}\) | \(N_{1}\) | \(F_{1}\) |
| \(x_{2}\) | \(n_{2}\) | \(f_{2}\) | \(N_{2}\) | \(F_{2}\) |
| \(\vdots\) | \(\vdots\) | \(\vdots\) | \(\vdots\) | \(\vdots\) |
| \(x_{k}\) | \(n_{k}\) | \(f_{k}\) | \(N_{k}\) | \(F_{k}\) |
Tablas de frecuencias para variables categóricas o discretas en Jamovi
A continuación mostramos como obtener tablas de frecuencias absolutas y relativas para la variable isla en la que se han capturado los peces de nuestro ejemplo:
- Una vez se ha cargado el fichero sargos.csv en Jamovi, en la pestaña Analyses hacer clic en Exploration y luego en Descriptives. Observa como a la derecha aparece una tabla vacía titulada Descriptives:
- En la ventana emergente elegimos isla y haciendo clic en la flecha superior, a la derecha de la ventana que contiene a las variables, la pasamos al cuadro denominado Variables.
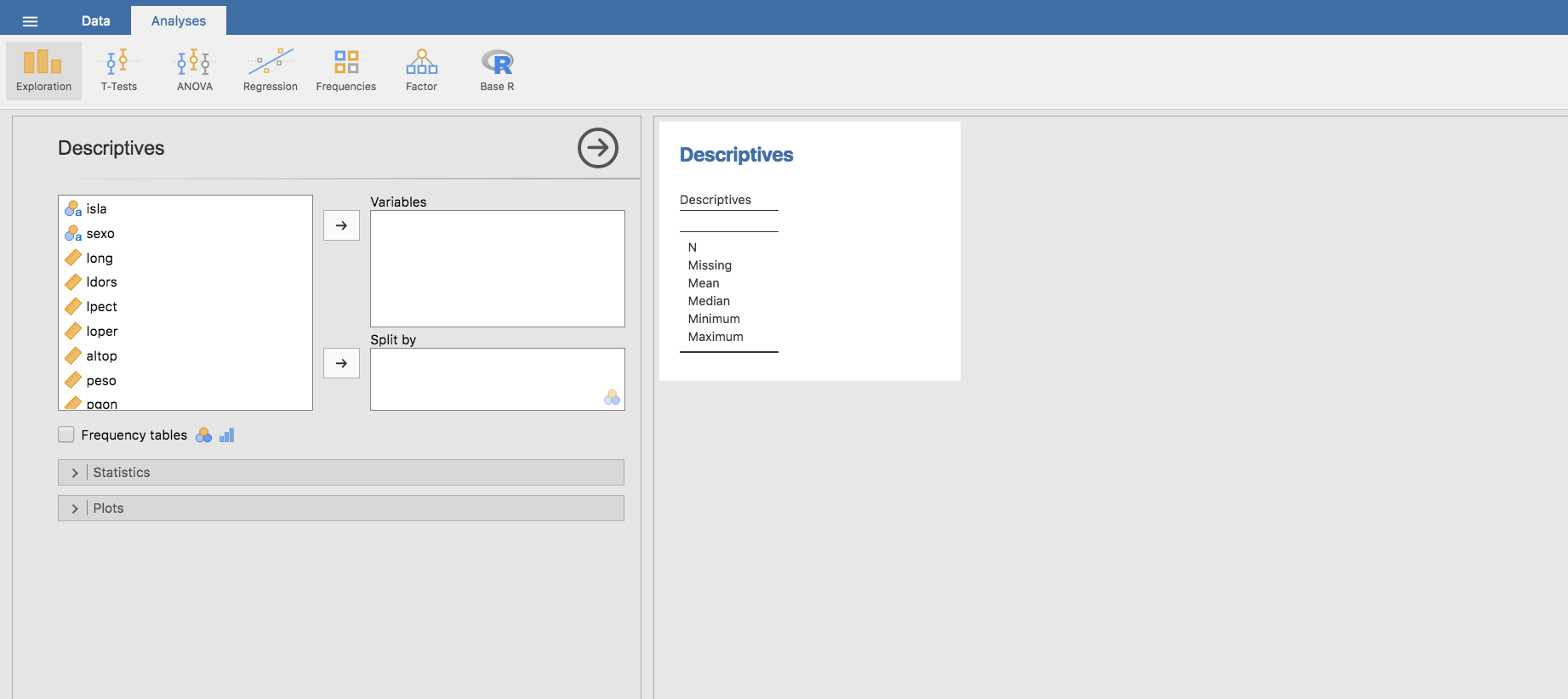
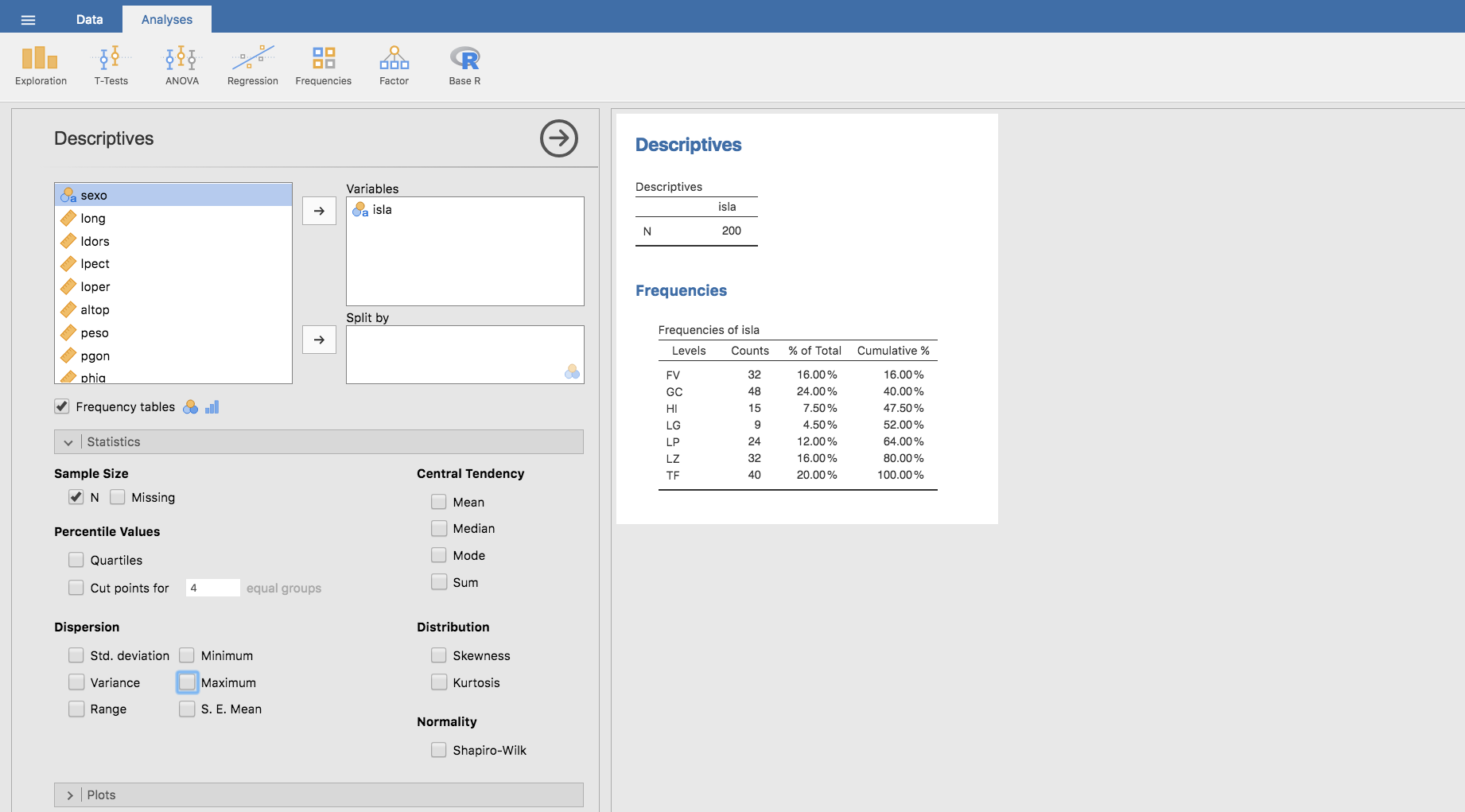
- Una vez seleccionada isla hacemos clic en Frequency tables y se muestra una tabla con las categorías (Levels), las frecuencias absolutas (Counts), porcentajes de cada categoría (% of Total) y porcentajes acumulados (Cumulative %):
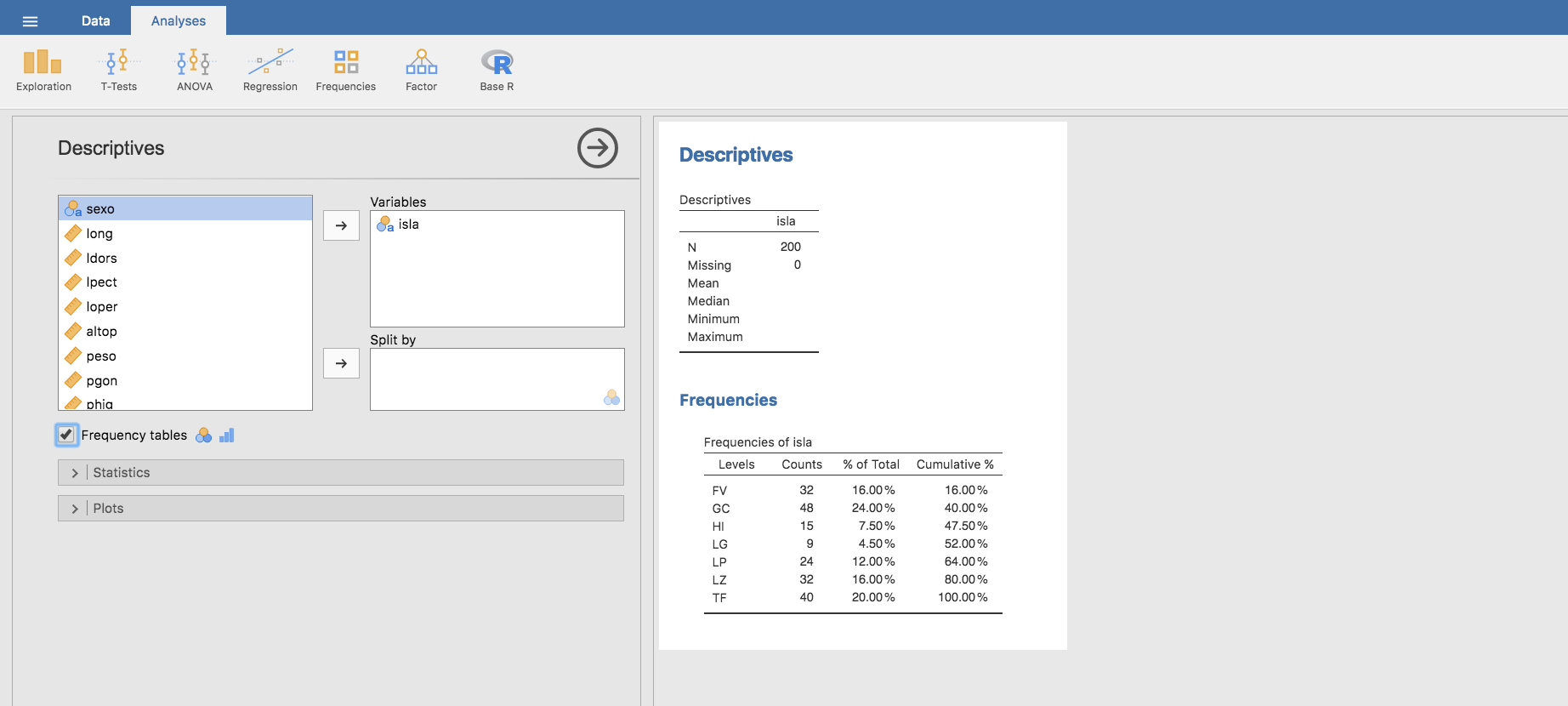
- Observamos que en la parte superior de la tabla de frecuencias obtenida, también hay una tabla titulada Descriptives. En ella se especifica N (número total de datos), Missing (número de datos perdidos) y varias medidas que corresponden a variables cuantitativas. Para evitar información superflua, vamos a eliminar lo que no nos interesa de esa tabla. Para ello, abajo a la izquierda pulsamos en la barra titulada Statistics:
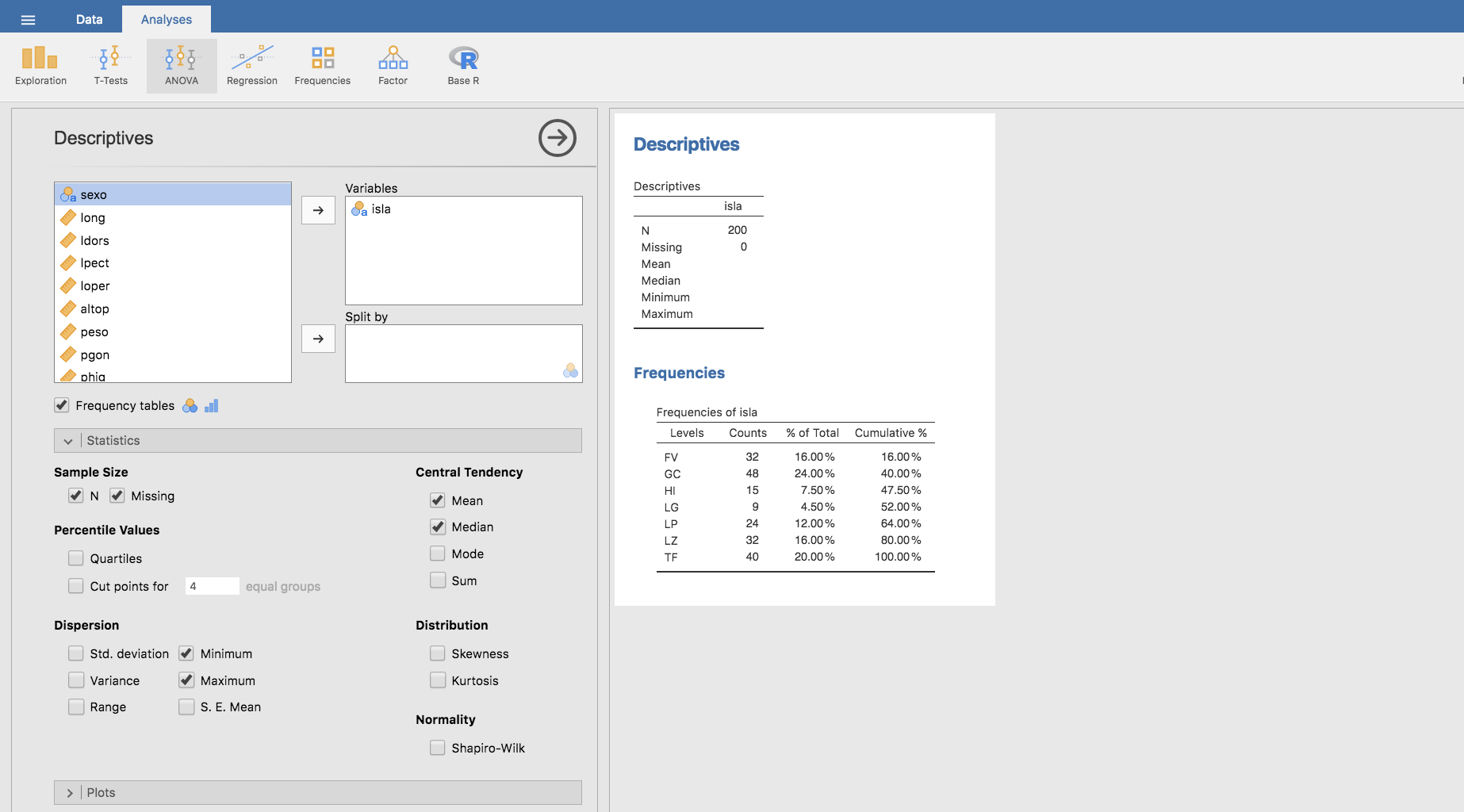
que muestra todas las medidas que podemos incluir en la tabla Descriptives. Ahora, podemos marcar o desmarcar opciones hasta quedarnos con la información que nos interesa. En nuestro caso, podemos elegir, por ejemplo, dejar solo el número total de datos incluidos en la variable isla (N). En caso de desmarcar todas las opciones de Statistics, desaparecería la tabla de la parte superior y solo quedaría la tabla de frecuencias. Pulsando sobre la barra Statistics se muestran u ocultan todas estas opciones.
Diagramas de barra para variables categóricas o discretas en Jamovi
En esta sección damos continuidad al análisis realizado hasta ahora con la variable isla, centrándonos ahora en la obtención de un diagrama de barras de isla.
- Para ello, basta con desplegar la barra Plots, que se ubica debajo de la barra Statistics:
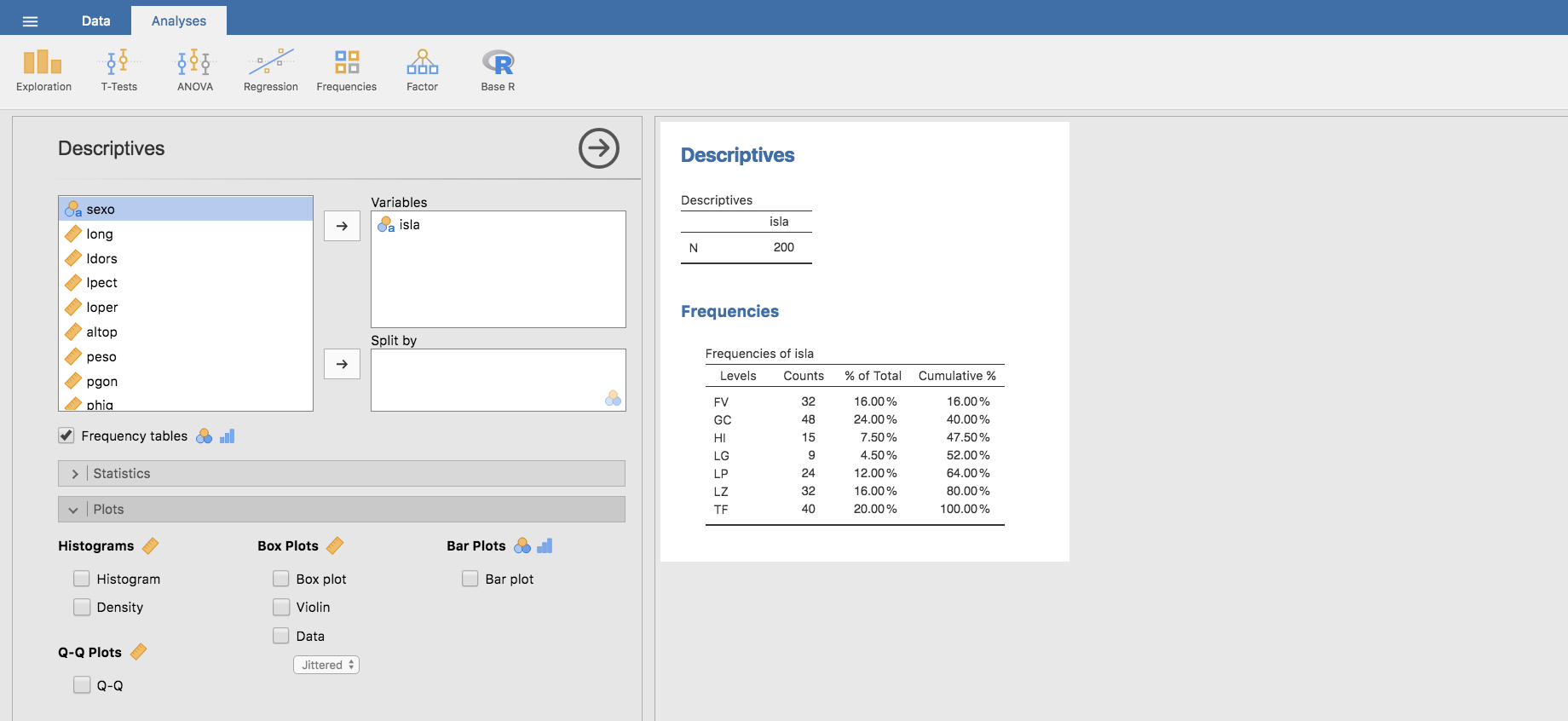
y hacer clic en la opción Bar plot y Jamovi muestra el diagrama de barras de la variable elegida. Observa como junto a la opción Bar plot aparecen los iconos correspondientes a variables de tipo Nominal y Ordinal, lo cual indica que este tipo de gráficos solo se aplican a ese tipo de variables. Igual con el resto de opciones gráficas, que solo serían adecuadas para variables de tipo Continuous.
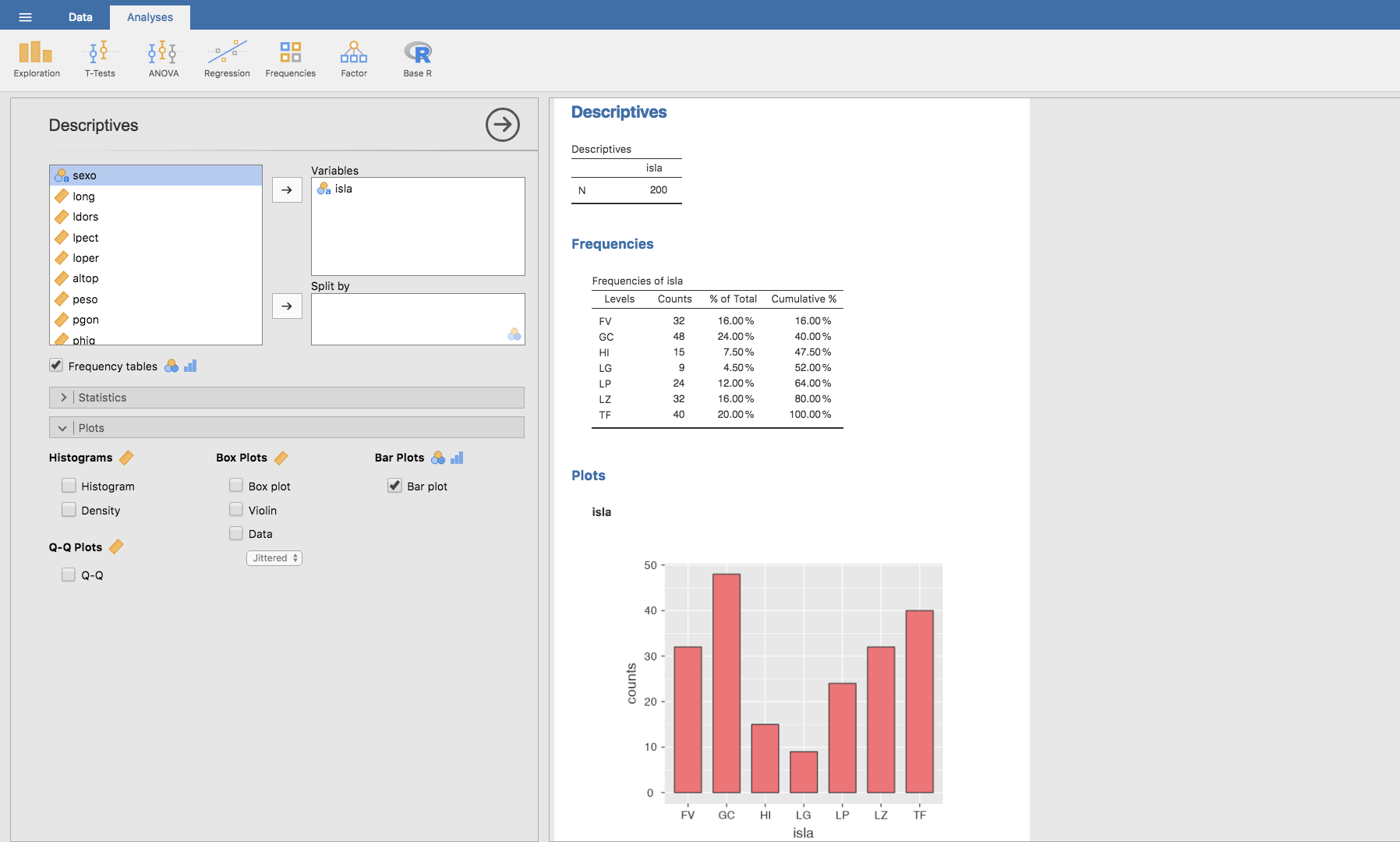
- Si queremos realizar algún cambio estético a la gráfica obtenida, existen algunas opciones que Jamovi ofrece. Haciendo clic en la esquina superior derecha
 se despliega el siguiente menú:
se despliega el siguiente menú:
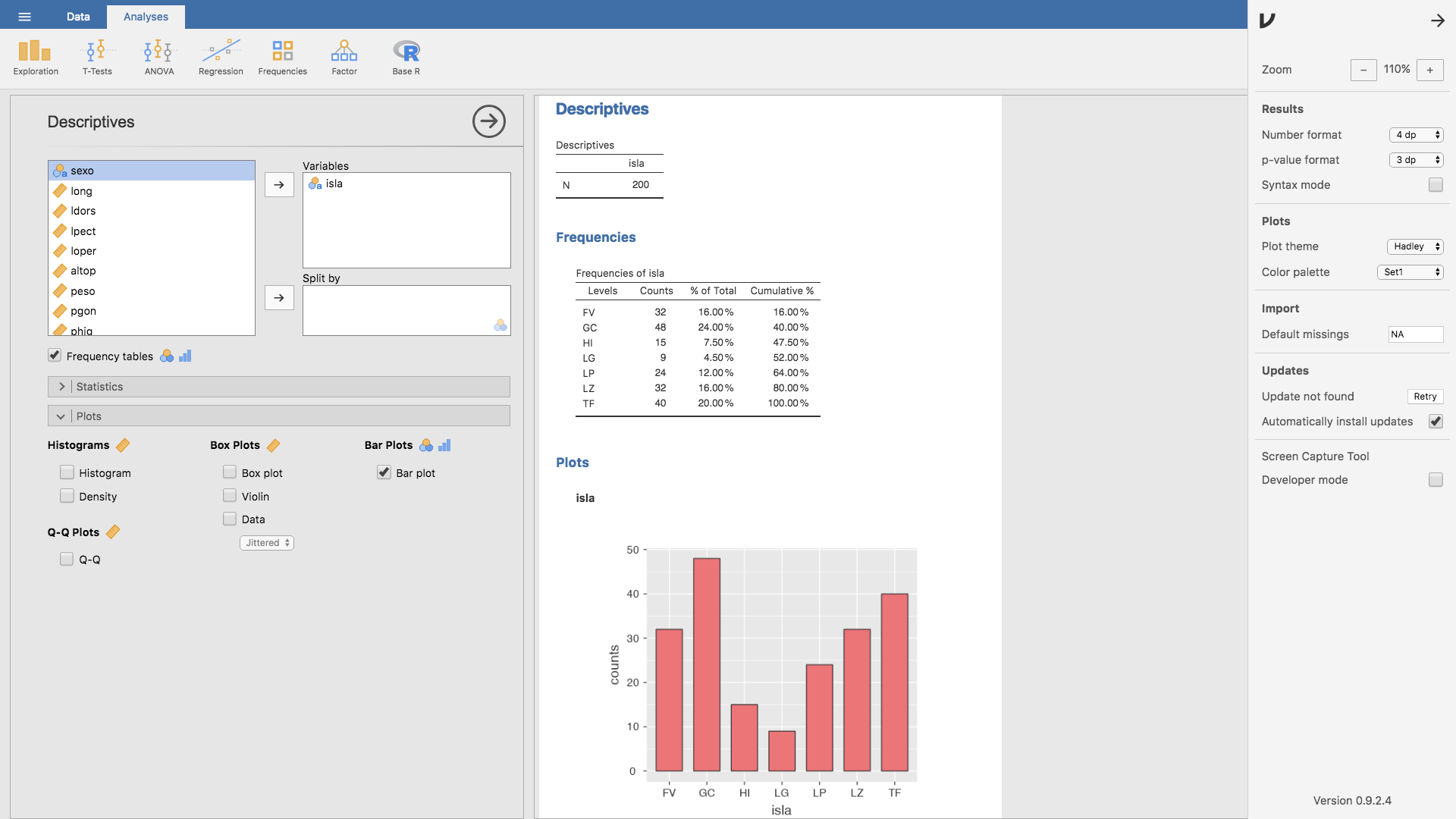
y el apartado Plots ofrece distintas opciones. Por ejemplo, si elegimos en Plot theme la opción Default y en Color palette elegimos jmv, la gráfica cambia de aspecto:
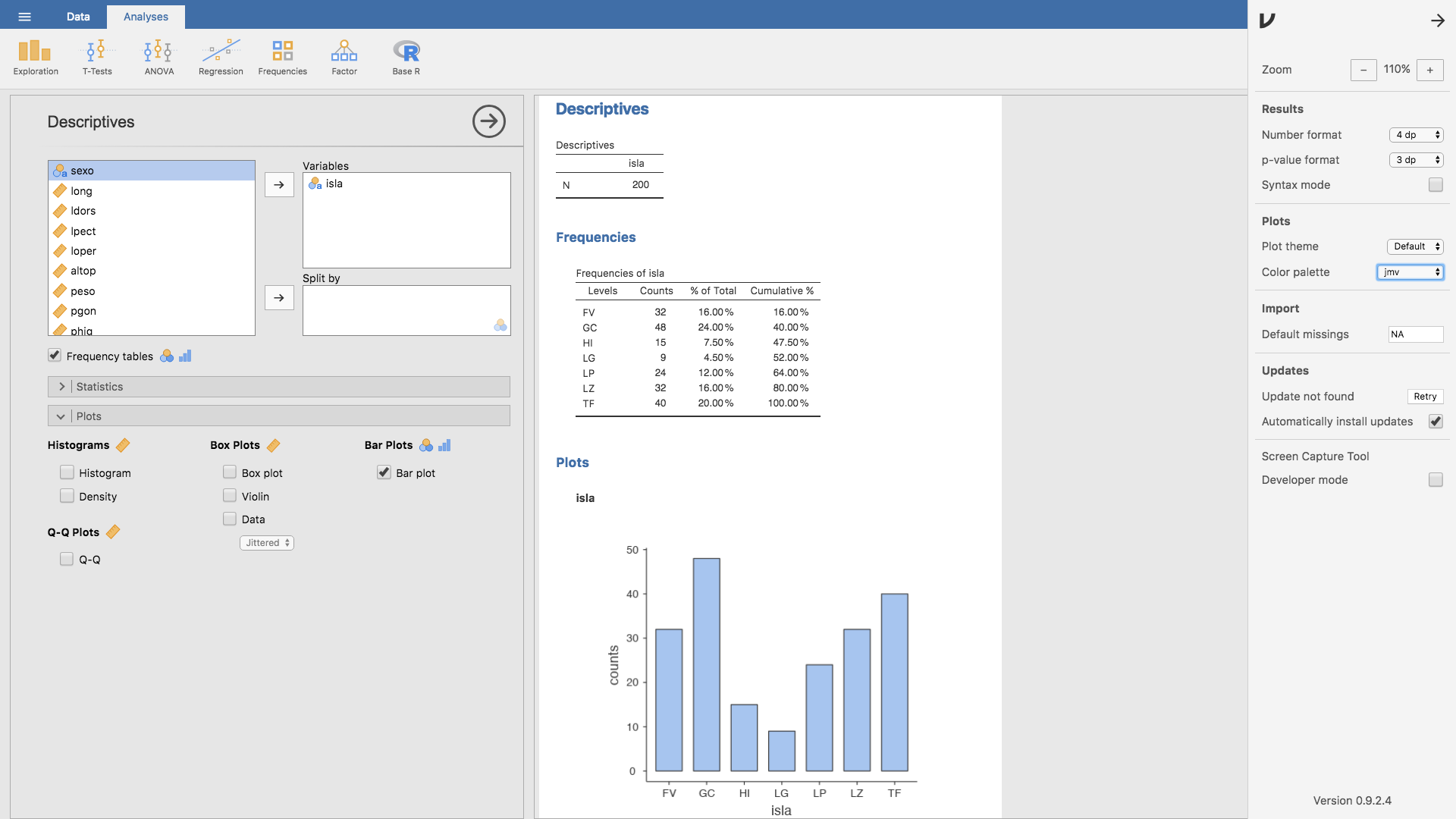
y así podemos seguir probando alternativas hasta encontrar la que se ajuste mejor a nuestras preferencias.
Procediendo de igual modo que se ha hecho con isla, se pueden obtener tablas de frecuencias y diagramas de barras para cualquier otra variable categórica o discreta de nuestro conjunto de datos.
Ejercicio: Utilizar Jamovi para obtener tabla de frecuencias y diagrama de barras de la variable larvas.
Mejorando la presentación de tablas y gráficos
Los gráficos anteriores, si bien representan correctamente las frecuencias observadas, podrían mejorar en algunas de sus características: las etiquetas de las barras o sectores (FV, GC, HI, etc) resultan poco claras (el lector del informe estadístico puede no saber qué significan estas siglas); estas etiquetas figuran en orden alfabético y quizás tuviese más sentido colocarlas en orden geográfico, con las islas de oeste a este.
Con Jamovi es sencillo mejorar aspectos de tablas y gráficos como los mencionados.
- Para reordenar las etiquetas de oeste a este en la variable isla, basta con hacer doble clic en la variable:
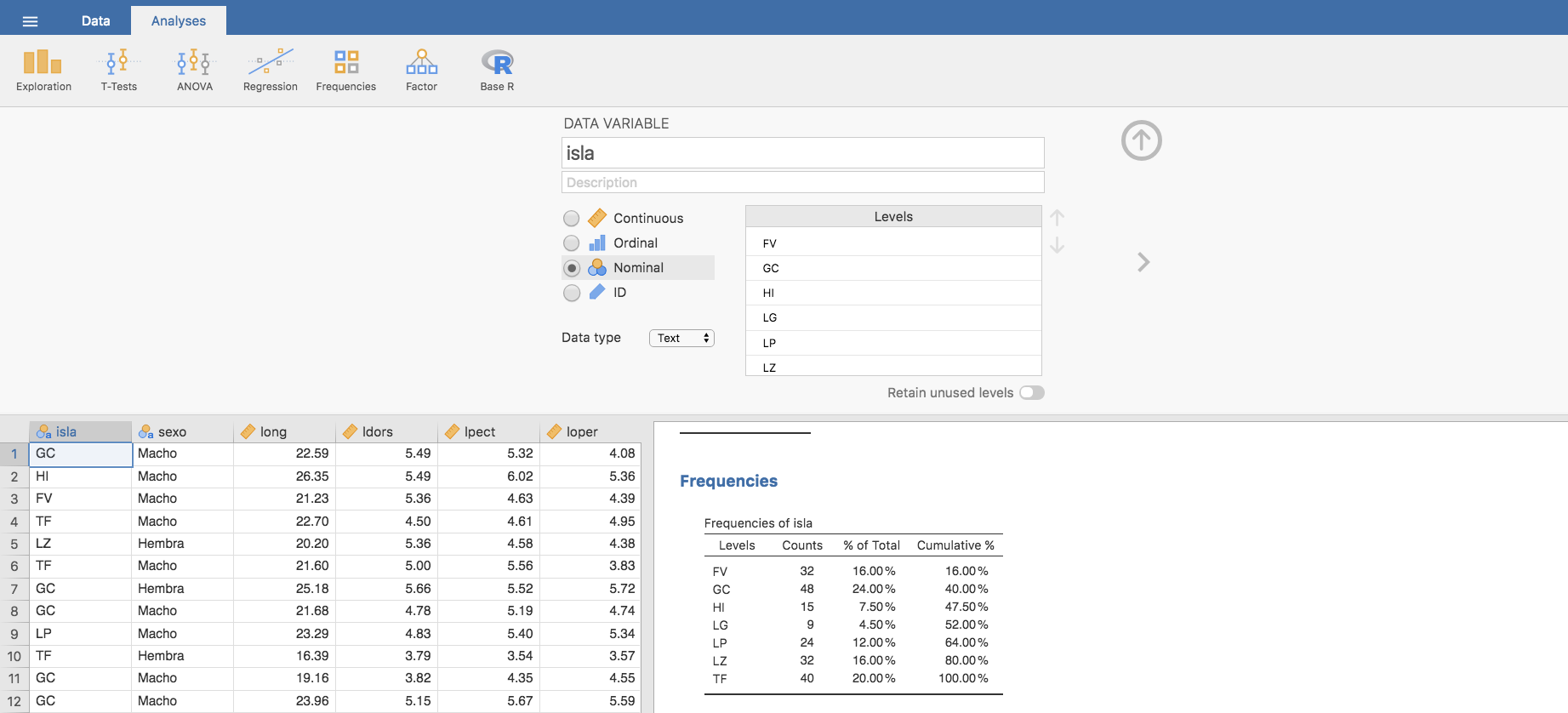
se despliega una ventana con las características de isla, y nos centramos en el cuadro titulado Levels. Hacemos clic en el primer nivel FV y lo situamos donde corresponda (sería la sexta isla si contamos de oeste a este) utilizando las flechas que aparecen a la derecha de la ventana Levels.
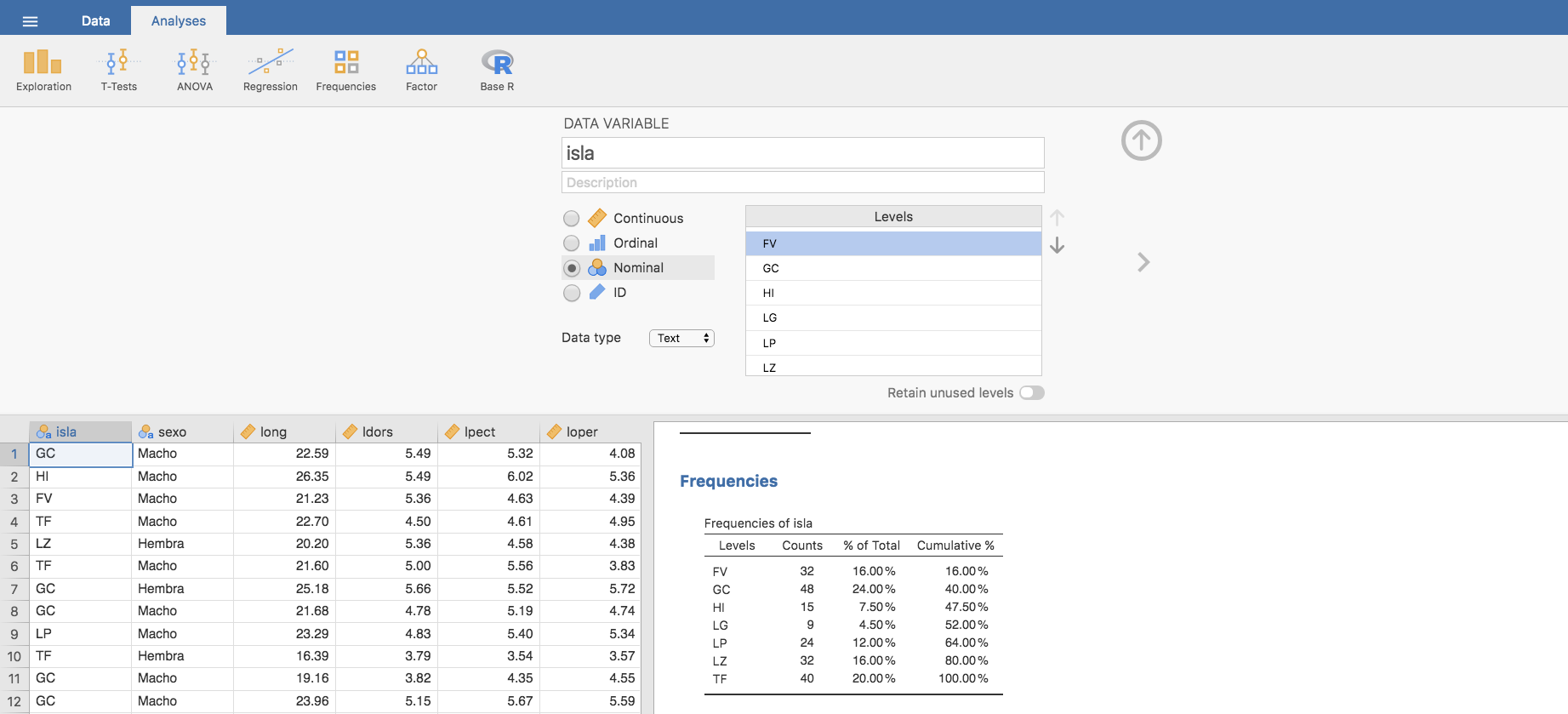
Igual con todos los demás niveles, hasta tener completada la reordenación:
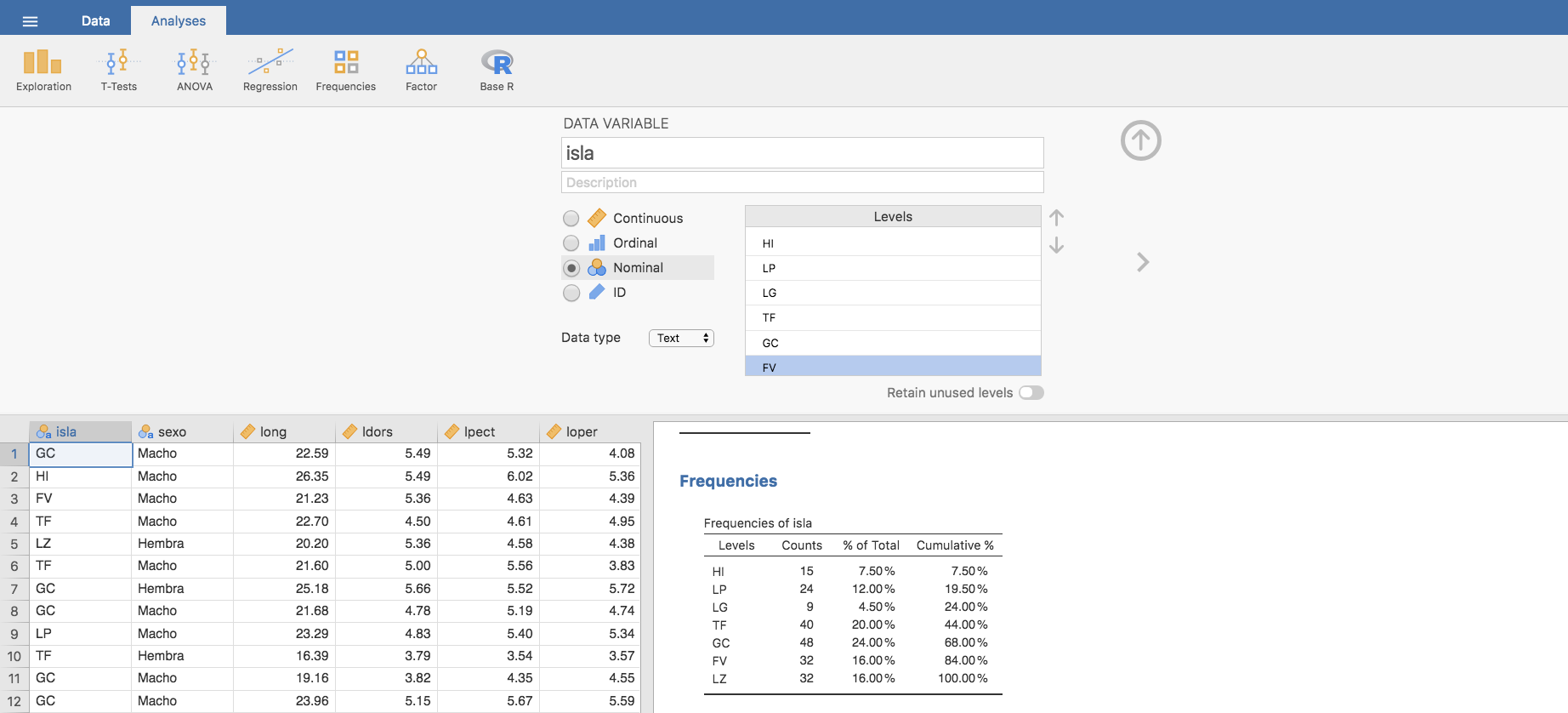
Automáticamente, observamos como la tabla de frecuencias se ha actualizado apareciendo en ella las islas ordenadas de oeste a este. Pero no solo la tabla de frecuencias, la reordenación también se ha realizado en el gráfico como muestra la siguiente imagen:
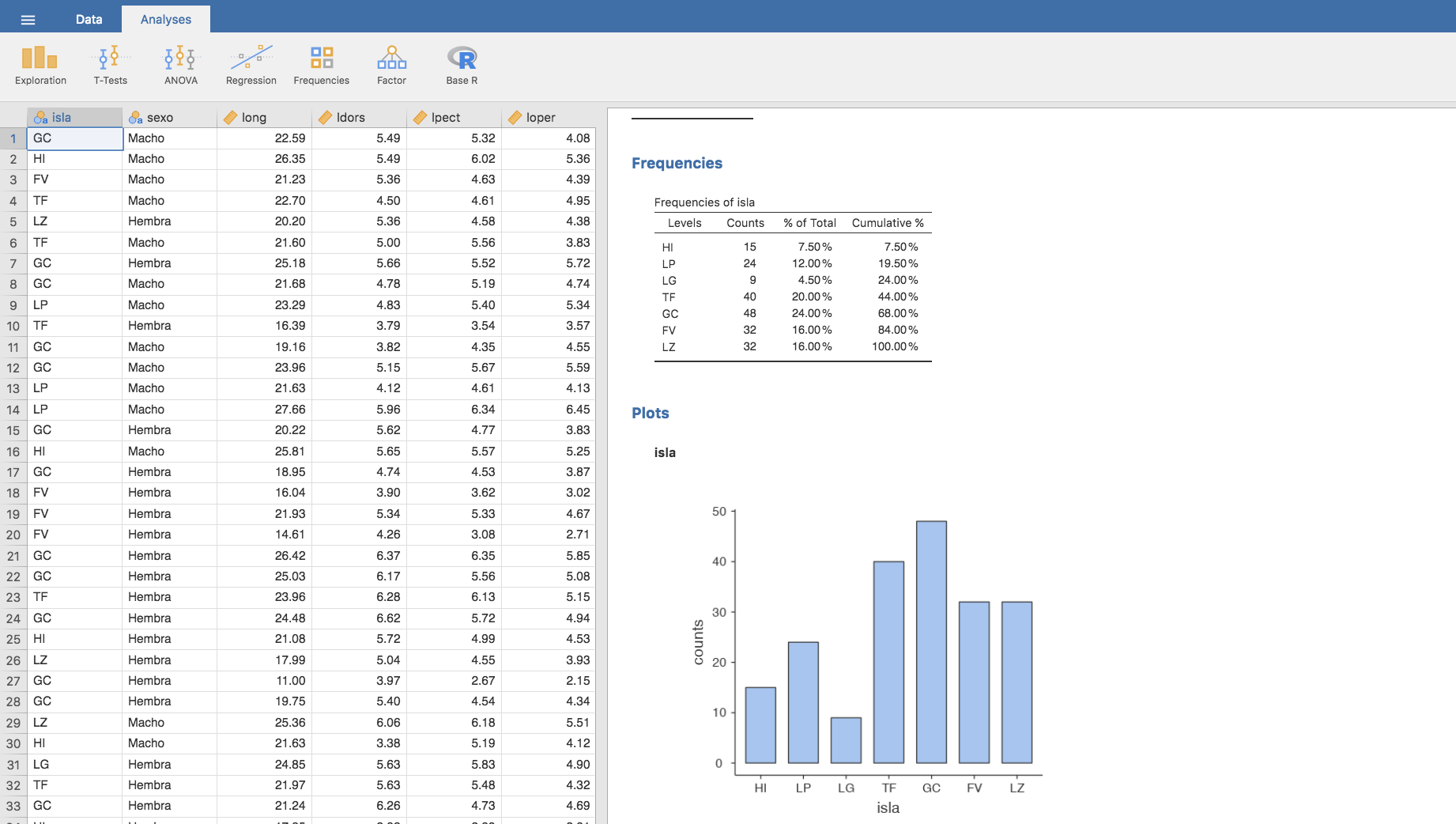
También podríamos haber optado por cambiar el tipo de variable a isla. Parece natural plantearse que al tratarse de una ordenación geográfica, isla pase de ser de tipo Nominal a tipo Ordinal. Independientemente del tipo que elijamos, los análisis que hagamos con esta variable reordenada funcionan correctamente.
- Si lo que queremos es especificar de forma más clara el nombre de cada isla, sería suficiente con sustituir las etiquetas que aparecen en la ventana Levels por el nombre completo que corresponda a cada isla, o bien por etiquetas que permitan identificarlas mejor. Optaremos por utilizar las que se indican en la siguiente imagen:
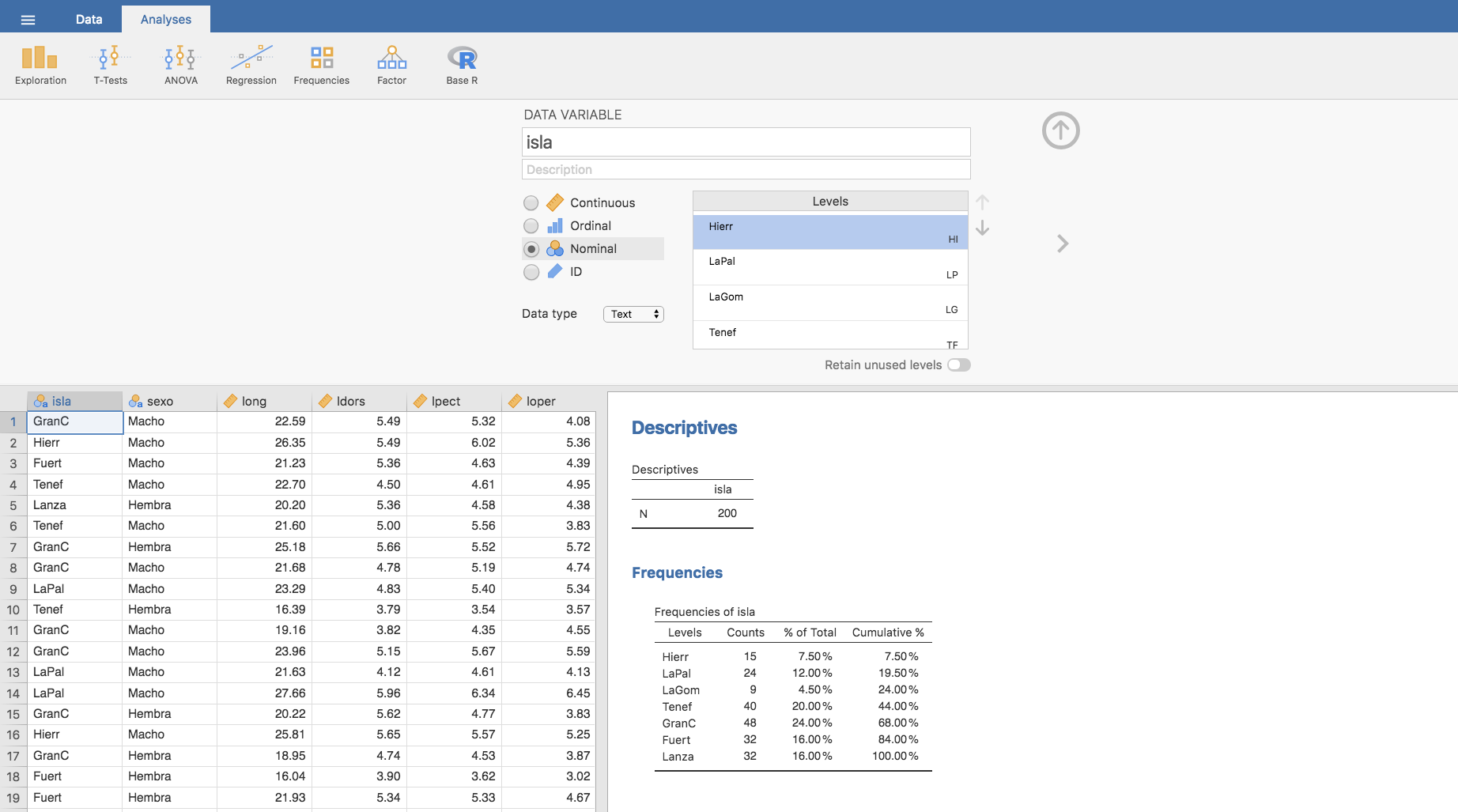
Nuevamente, de forma automática se actualizan esas etiquetas en tabla de frecuencias y diagrama de barras:
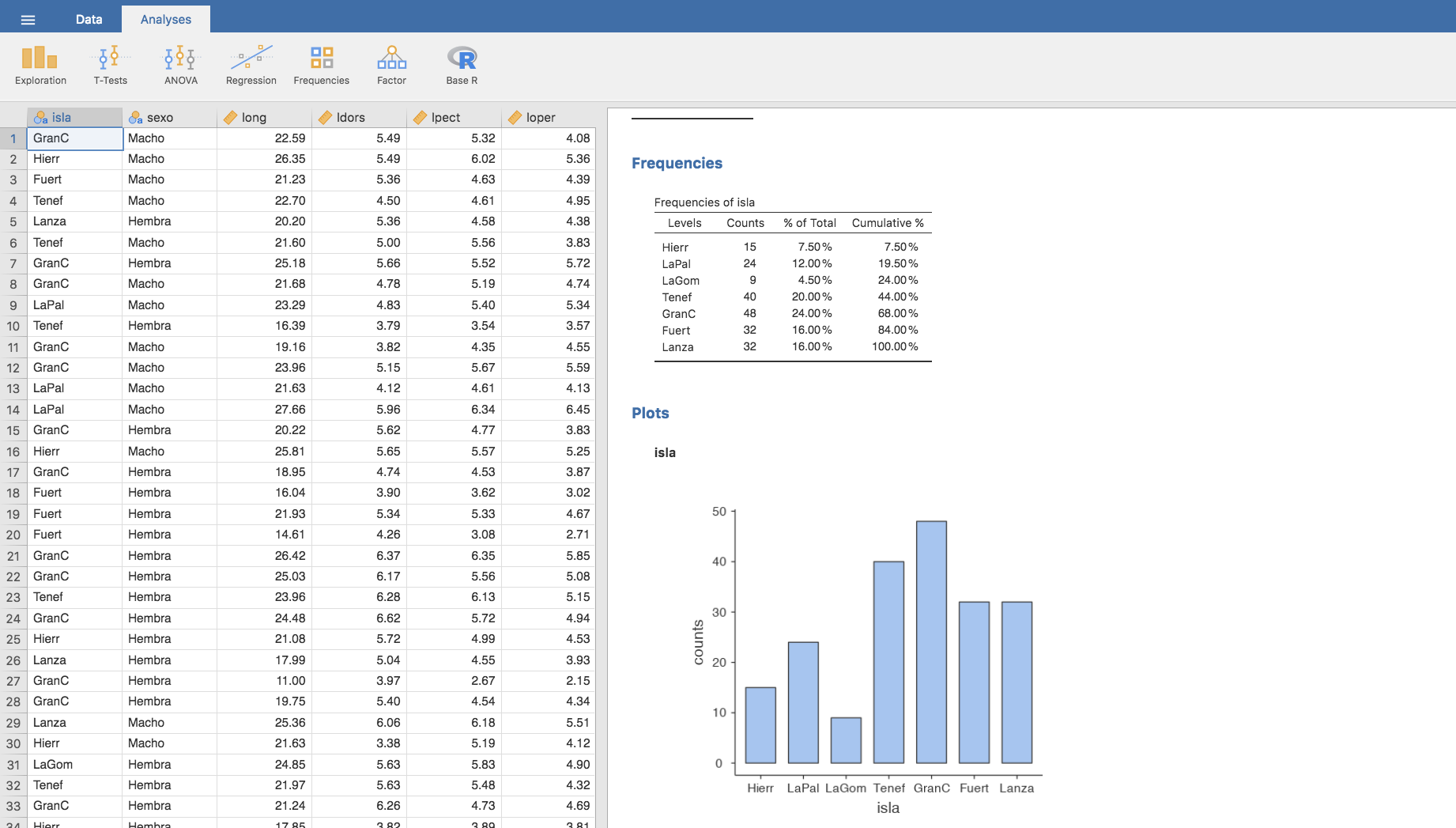
Tablas cruzadas para variables categóricas o numéricas discretas
Cuando se estudian conjuntamente dos variables categóricas o numéricas discretas, resulta de interés determinar qué valores aparecen juntos con más o menos frecuencia. Con este fin se construyen las tablas de frecuencias cruzadas, también denominadas tablas de contingencia. Si la variable \(X\) toma los valores \(x_{1},x_{2},\dots,x_{k}\) y la variable \(Y\) toma los valores \(y_{1},y_{2},\dots,y_{m}\), se denomina frecuencia absoluta del par \(\left(x_{i},y_{j}\right)\) al número de veces \(n_{ij}\) que dicha pareja de valores aparecen juntos en la muestra. Las frecuencias absolutas se suelen presentar en una tabla cruzada como se muestra a continuación:
| \(\;\) | \(y_{1}\) | \(y_{2}\) | \(\dots\) | \(y_{m}\) | Totales |
|---|---|---|---|---|---|
| \(x_{1}\) | \(n_{11}\) | \(n_{12}\) | \(\dots\) | \(n_{1m}\) | \(n_{1\bullet}\) |
| \(x_{2}\) | \(n_{21}\) | \(n_{22}\) | \(\dots\) | \(n_{2m}\) | \(n_{2\bullet}\) |
| \(\vdots\) | |||||
| \(x_{k}\) | \(n_{k1}\) | \(n_{k2}\) | \(\dots\) | \(n_{km}\) | \(n_{k\bullet}\) |
| Totales | \(n_{\bullet1}\) | \(n_{\bullet2}\) | \(n_{\bullet m}\) | \(n_{\bullet\bullet}\) |
El valor \(n_{i\bullet}\) representa el total de la fila \(i\), \(\left(n_{i\bullet}=\sum_{j=1}^{m}n_{ij}\right)\), y por tanto es la frecuencia absoluta con que se observa el valor \(x_{i}\). Asimismo, el valor \(n_{\bullet j}\) representa el total de la fila \(j\), \(\left(n_{\bullet j}=\sum_{i=1}^{k}n_{ij}\right)\), y por tanto es la frecuencia absoluta con que se observa el valor \(y_{j}\). Por último: \[n_{\bullet\bullet}=\sum_{i=1}^{k}\sum_{j=1}^{m}n_{ij}\] representa el total de valores observados y coincide con el tamaño de la muestra. Las frecuencias \(n_{i\bullet}\) y \(n_{\bullet j}\) reciben el nombre de frecuencias marginales de \(X\) e \(Y\), respectivamente.
A partir de una tabla de frecuencias cruzadas absolutas es posible construir tres clases de tablas de frecuencias relativas:
Frecuencias relativas globales: se calculan dividiendo cada frecuencia cruzada por el total de la tabla: \[f_{ij}=\frac{n_{ij}}{n_{\bullet\bullet}}\]
Frecuencias relativas por filas: se calculan dividiendo cada frecuencia cruzada por el total de su fila: \[ ff_{ij}=\frac{n_{ij}}{n_{i\bullet}} \] Representan la frecuencia relativa con que se produce cada valor de \(Y\) cuando se fija el valor \(X=x_{i}\). Por esta razón, suelen denominarse frecuencias relativas de \(Y\) condicionadas por \(X=x_{i}\).}
Frecuencias relativas por columnas: se calculan dividiendo cada frecuencia cruzada por el total de su columna: \[ fc_{ij}=\frac{n_{ij}}{n_{\bullet j}} \] Representan la frecuencia relativa con que se produce cada valor de \(X\) cuando se fija el valor \(Y=y_{j}\). Por esta razón, suelen denominarse frecuencias relativas de \(X\) condicionadas por \(Y=y_{j}\).
Tablas cruzadas en Jamovi
Las tablas cruzadas en Jamovi se generan en la pestaña Analyses, en el menú Frequencies/Contingency Tables/Independent Samples:
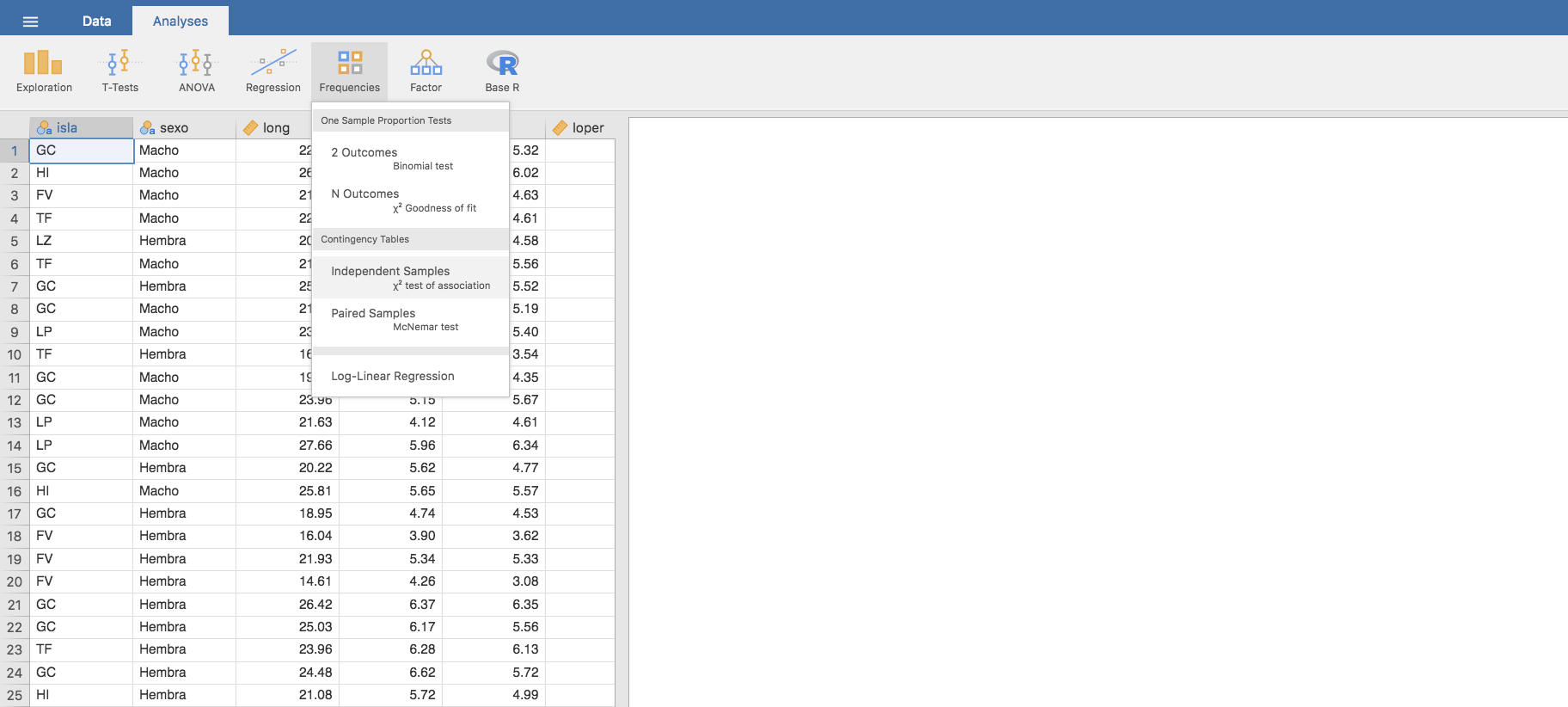
Al pulsar en Independent Samples la ventana emergente nos pide incluir las variables categóricas o numéricas discretas que vamos a estudiar conjuntamente:
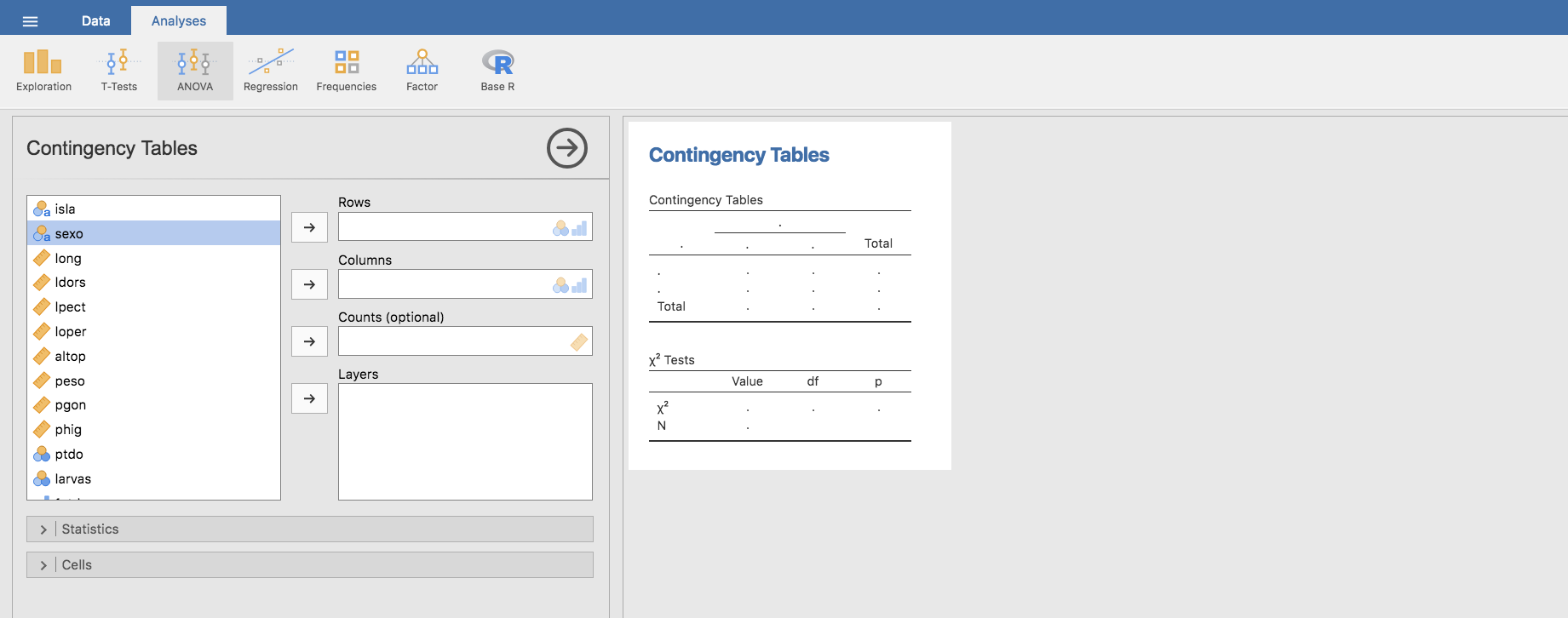
Por ejemplo, con nuestros datos, si queremos evaluar frecuencias absolutas de peces parasitados por anisakis capturados en cada una de las islas durante nuestra campaña de muestreo, ubicamos las categorías de la variable fptdo por filas (Rows) y las de isla por columnas (Columns):
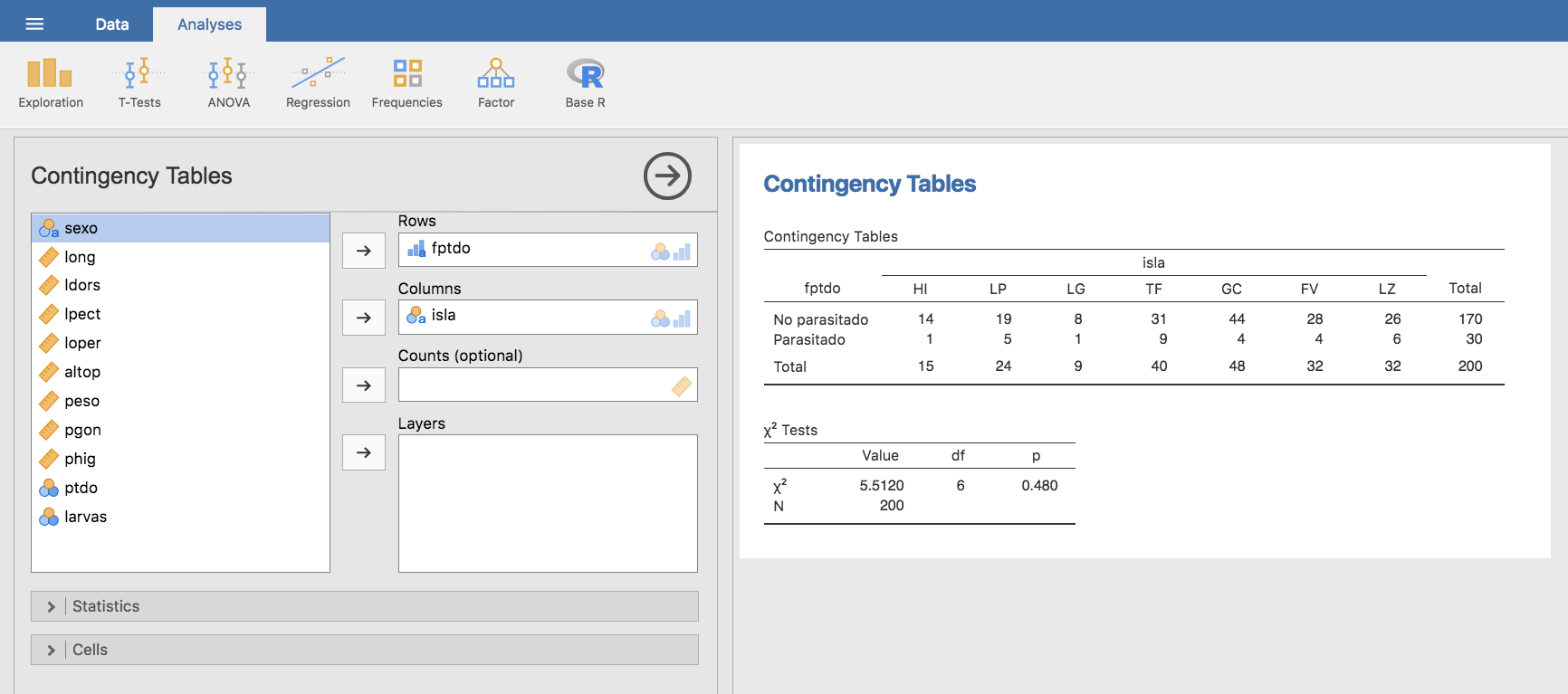
y Jamovi genera la tabla de contingencia para las variables elegidas. Observamos que Jamovi también muestra un test en la parte inferior de la tabla de contingencia. En esta parte del curso obviaremos este test, y lo simplificamos yendo a la barra Statistics y desmarcando la opción \(\chi^2\), de manera que ese test solo muestre el número total de datos de la tabla de contingencia:
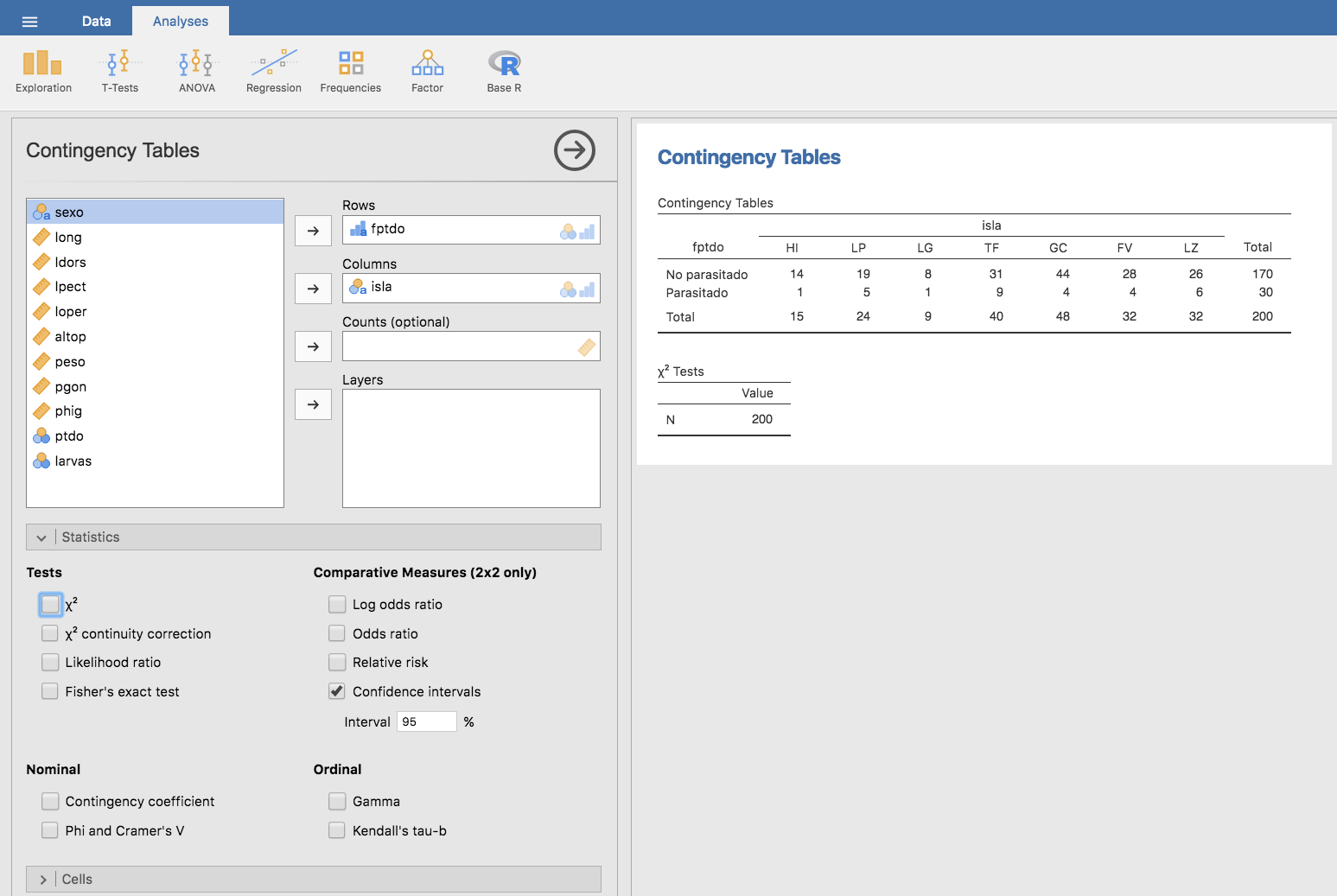
Podemos añadir las frecuencias relativas expandiendo la barra Cells, ubicada debajo de las variables, y en Percentages hacemos clic en Row, Column o Total para calcular las frecuencias relativas por filas, columnas o totales, respectivamente.
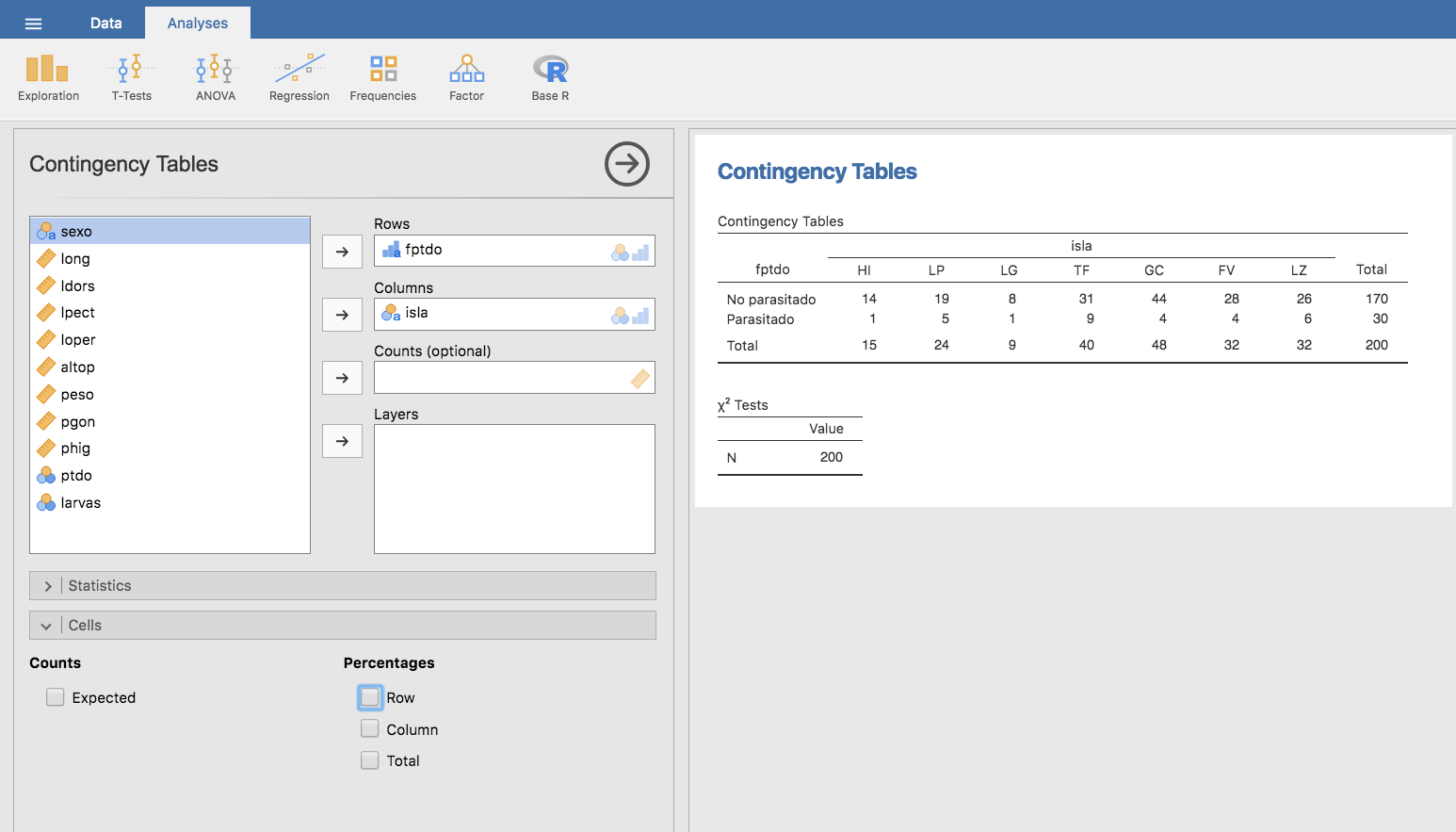
Por ejemplo, para calcular las frecuencias relativas por filas:
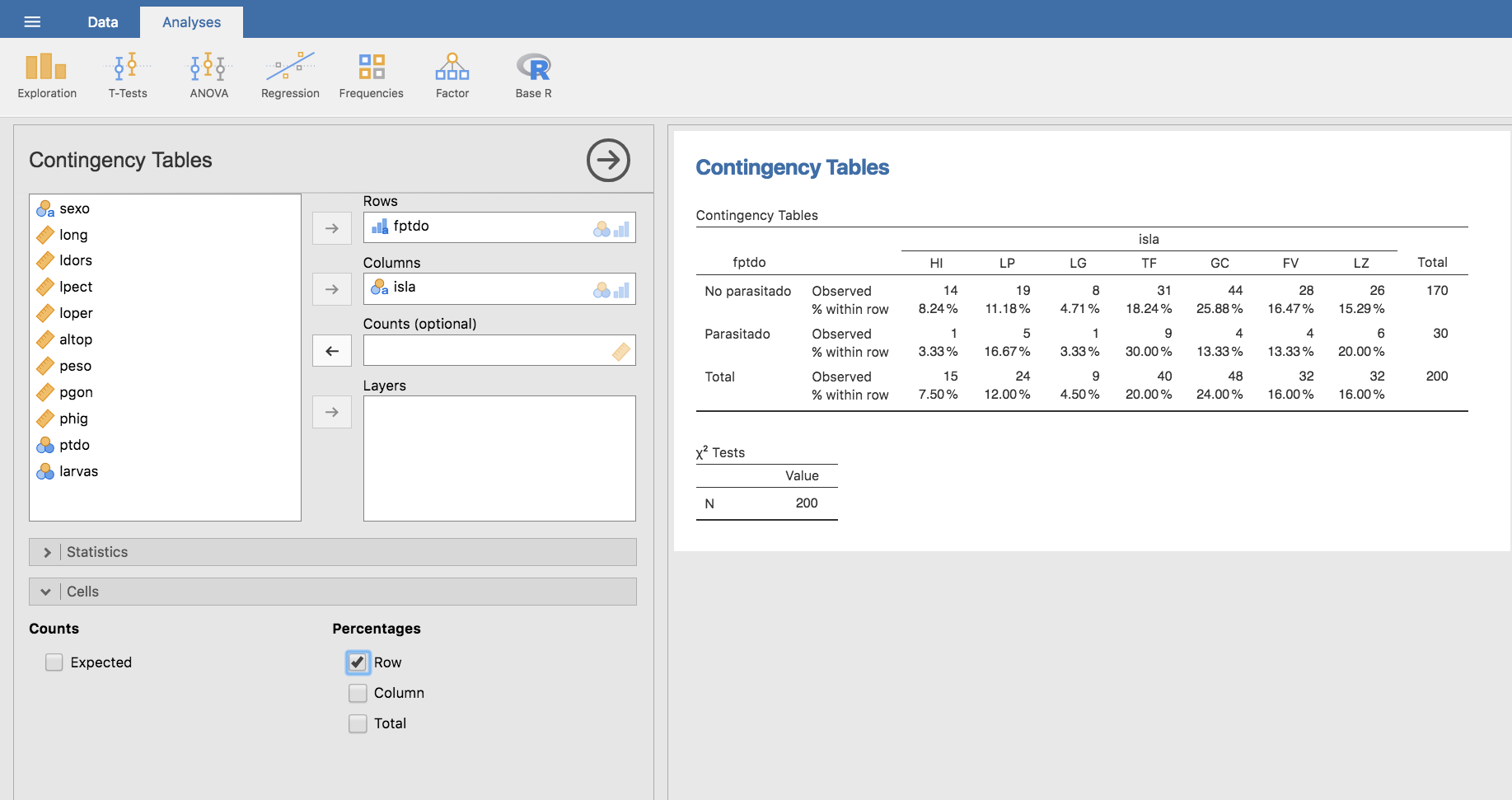
En el caso de frecuencias relativas por columnas:
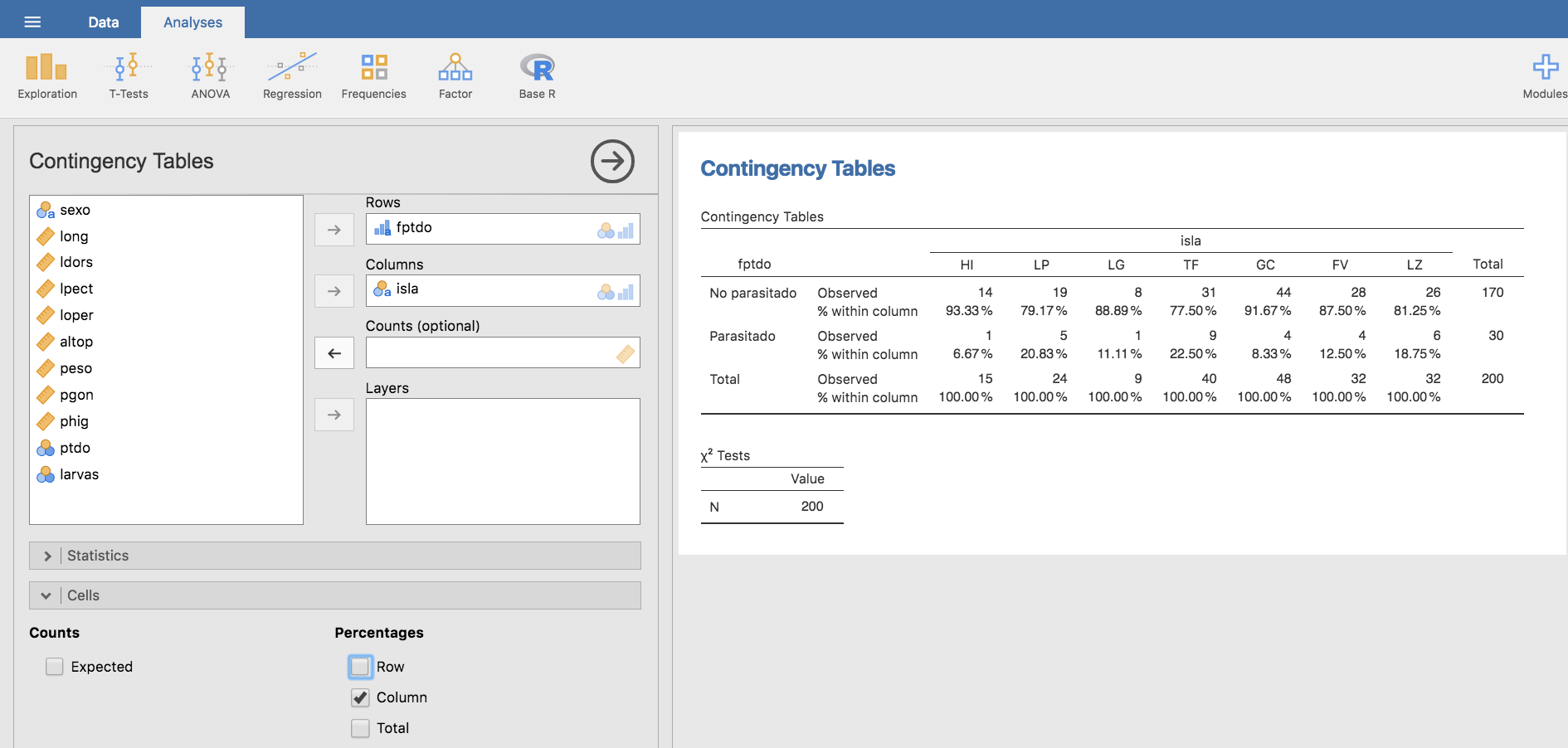
Jamovi evalúa todas las frecuencias relativas que se seleccionen, pudiéndose calcular todas en la misma tabla:
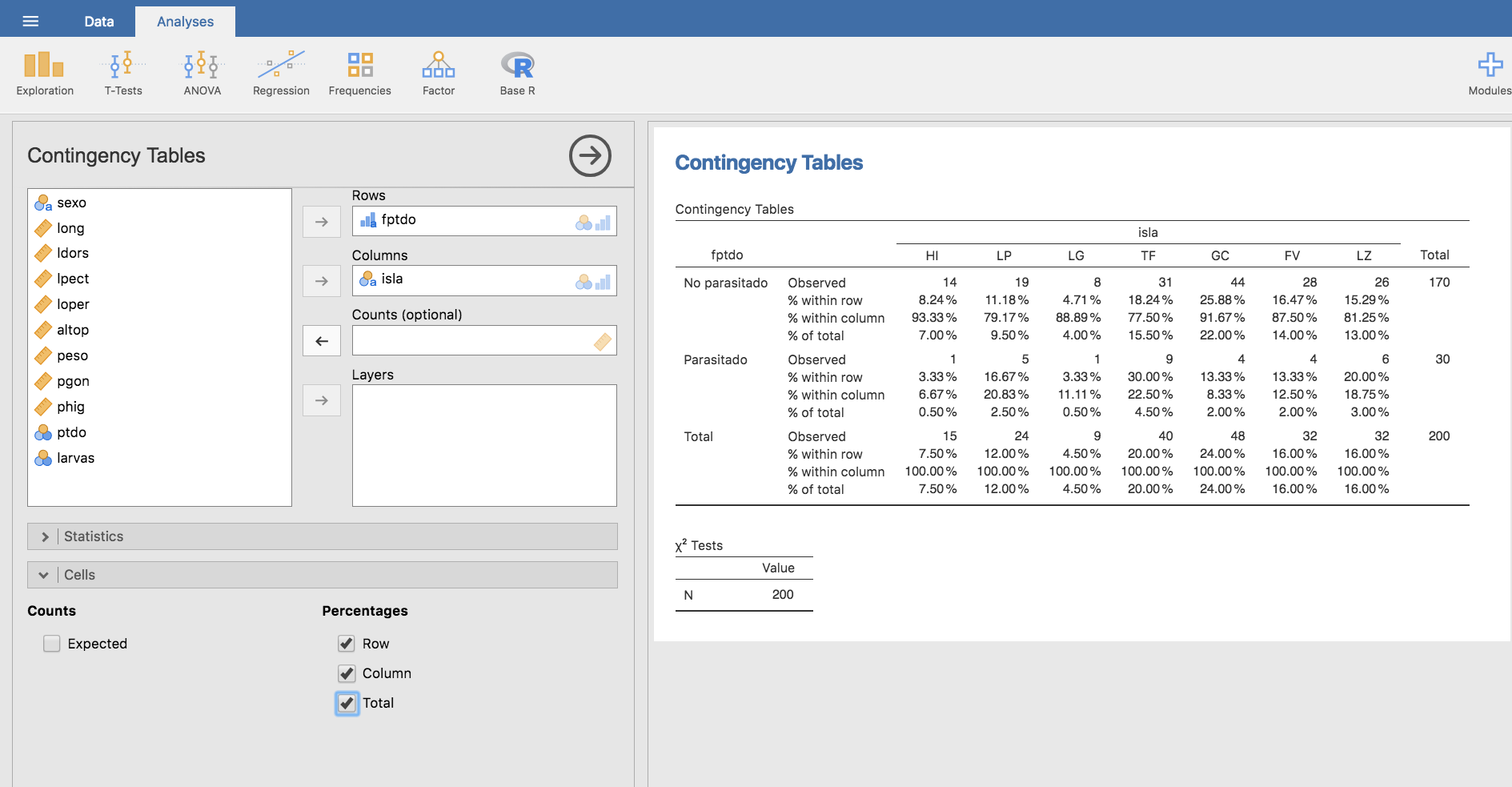
Presentación gráfica de tablas cruzadas
Las tablas de frecuencias cruzadas también pueden representarse gráficamente mediante diagramas de barras. Por ejemplo, si planteamos la tabla cruzada entre las variables isla y sexo, estaríamos interesados en obtener una representación gráfica que muestre la distribución de sexos por isla, en este caso un diagrama de barras, que puede obtenerse con Jamovi como se indica a continuación:
Seguimos los pasos realizados para obtener una tabla de frecuencias y diagrama de barras para el caso de una sola variable. Es decir, clicamos en el menú Exploration y luego en Descriptives.
Seleccionamos la variable isla y, además, indicamos a Jamovi que distribuya la variable seleccionada por sexo: para eso añadimos la variable sexo en la ventana Split by.
Finalmente, clicamos en Frequency tables, en la barra Statistics desmarcamos todas las opciones y en la barra Plots seleccionamos Bar plot, obteniéndose:
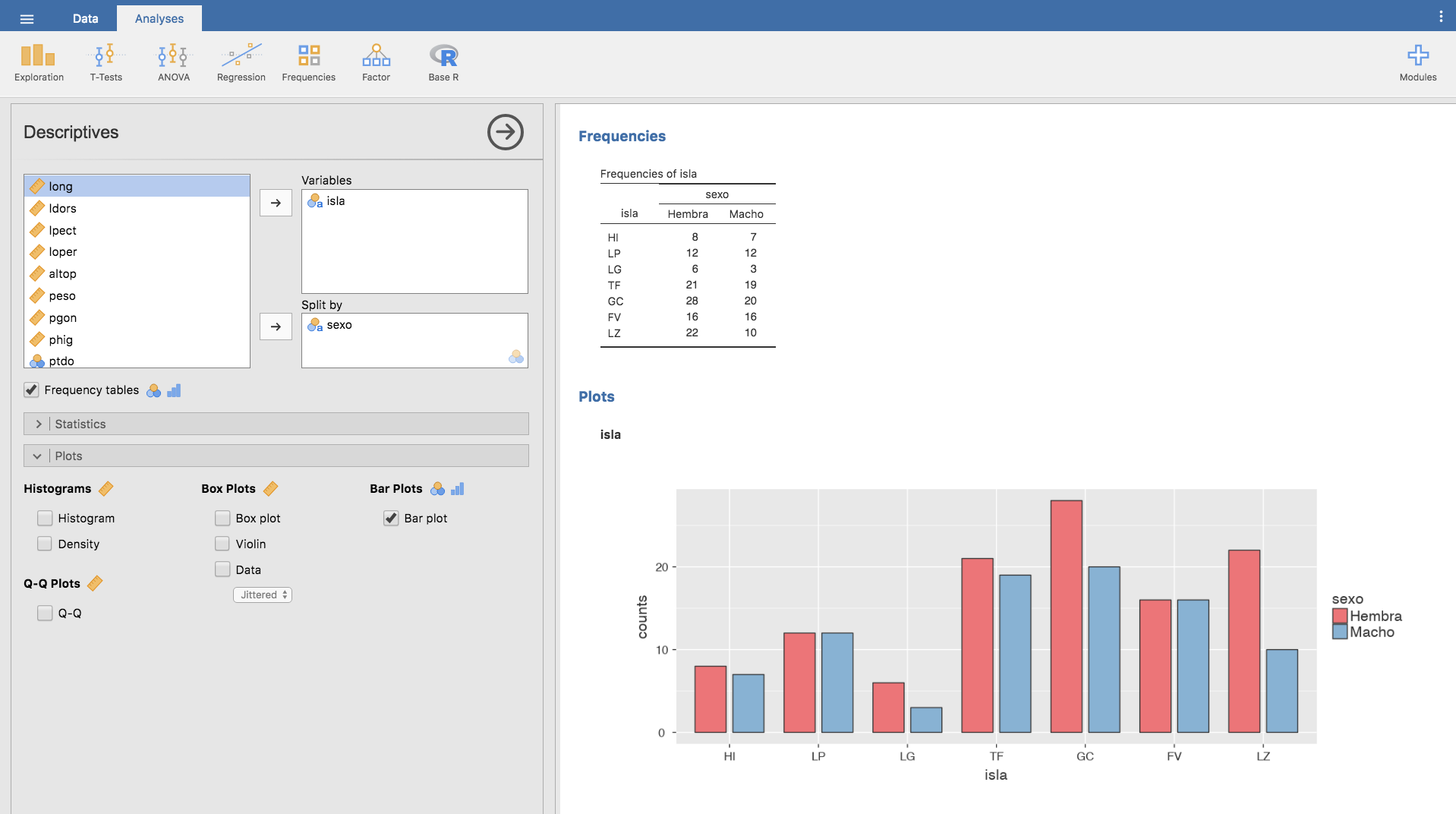
Variables numéricas continuas
Si la variable numérica es continua, no cabe esperar repeticiones de un mismo valor de la variable. En este caso, conviene sintetizar el conjunto de valores mediante agrupaciones de la variable en intervalos de clase \(\left(x_{i-1},x_{i}\right]\). En general, los intervalos deben ser de la misma longitud. Denominaremos marca de clase al punto medio del intervalo de clase, \(m_{i}=\frac{x_{i-1}+x_{i}}{2}\). Para determinar el número de intervalos a construir suele emplearse la regla empírica de Sturges que consiste en tomar como número de intervalos un valor próximo a \(k\approx1+3.22\log(n)\), siendo \(n\) el número total de valores observados. Esta regla es la que emplea Jamovi por defecto en la construcción de gráficos para variables continuas.
Tablas de Frecuencias para variables continuas
Una vez agrupados los datos en intervalos de clase, el cálculo de las frecuencias es análogo al caso anterior, con la única diferencia de que ahora \(n_{i}\) es el número de observaciones dentro del intervalo \(\left(x_{i-1},x_{i}\right]\), tal como se muestra en la siguiente tabla:
| \(X\) (Intervalo) | Marca de clase | F. Absoluta | F. Relativa | F. Abs. Acum. | F. Rel. Acum. |
|---|---|---|---|---|---|
| \(\left[x_{0},x_{1}\right]\) | \(m_{1}\) | \(n_{1}\) | \(f_{1}\) | \(N_{1}\) | \(F_{1}\) |
| \(\left(x_{1},x_{2}\right]\) | \(m_{2}\) | \(n_{2}\) | \(f_{2}\) | \(N_{2}\) | \(F_{2}\) |
| \(\vdots\) | \(\vdots\) | \(\vdots\) | \(\vdots\) | \(\vdots\) | \(\vdots\) |
| \(\left(x_{k-1},x_{k}\right]\) | \(m_{k}\) | \(n_{k}\) | \(f_{k}\) | \(N_{k}\) | \(F_{k}\) |
La configuración básica de Jamovi no dispone de ninguna función específica para la construcción de tablas de frecuencias para variables continuas.
Representación gráfica de variables continuas
Histogramas
La distribución de frecuencias de variables continuas se representa habitualmente en un histograma. Este gráfico se construye levantando sobre cada intervalo un rectángulo de área proporcional a la frecuencia que se pretende representar. En Jamovi podemos obtener el histograma de las longitudes de los sargos de nuestra muestra por medio del menú Descriptives, donde elegimos la variable long y en la barra Plots seleccionamos Histogram, obteniendo:
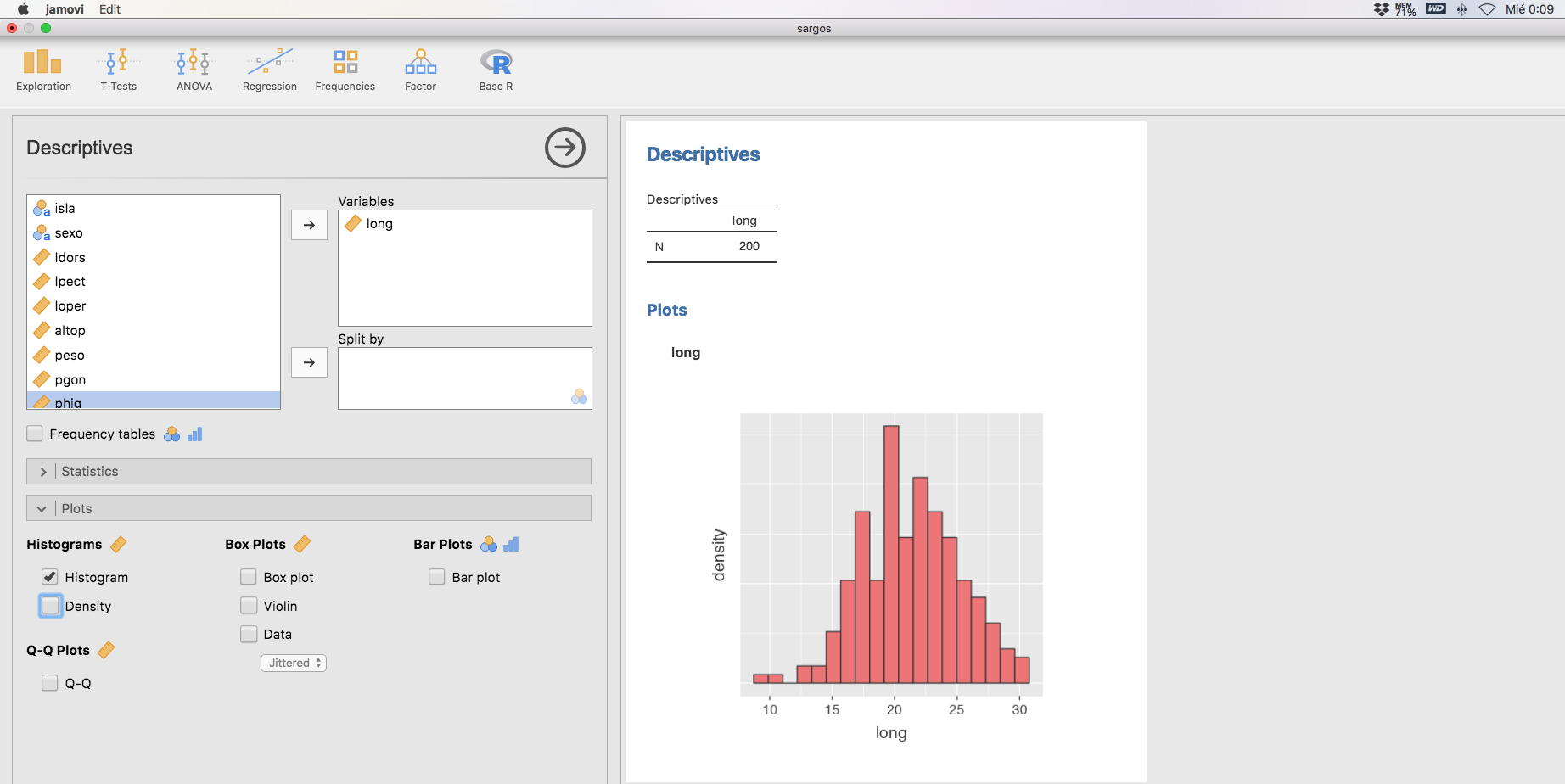
Gráficos de densidad
Los gráficos de densidad permiten visualizar cómo se distribuyen los datos en un intervalo continuo. Puede decirse que es un histograma suavizado. En un gráfico de densidad, los picos ayudan a localizar los valores más frecuentes del intervalo.
En Jamovi los gráficos de densidad se construyen fácilmente, de igual forma que los histogramas. Basta con seleccionar la opción Density ubicada debajo de Histogram:
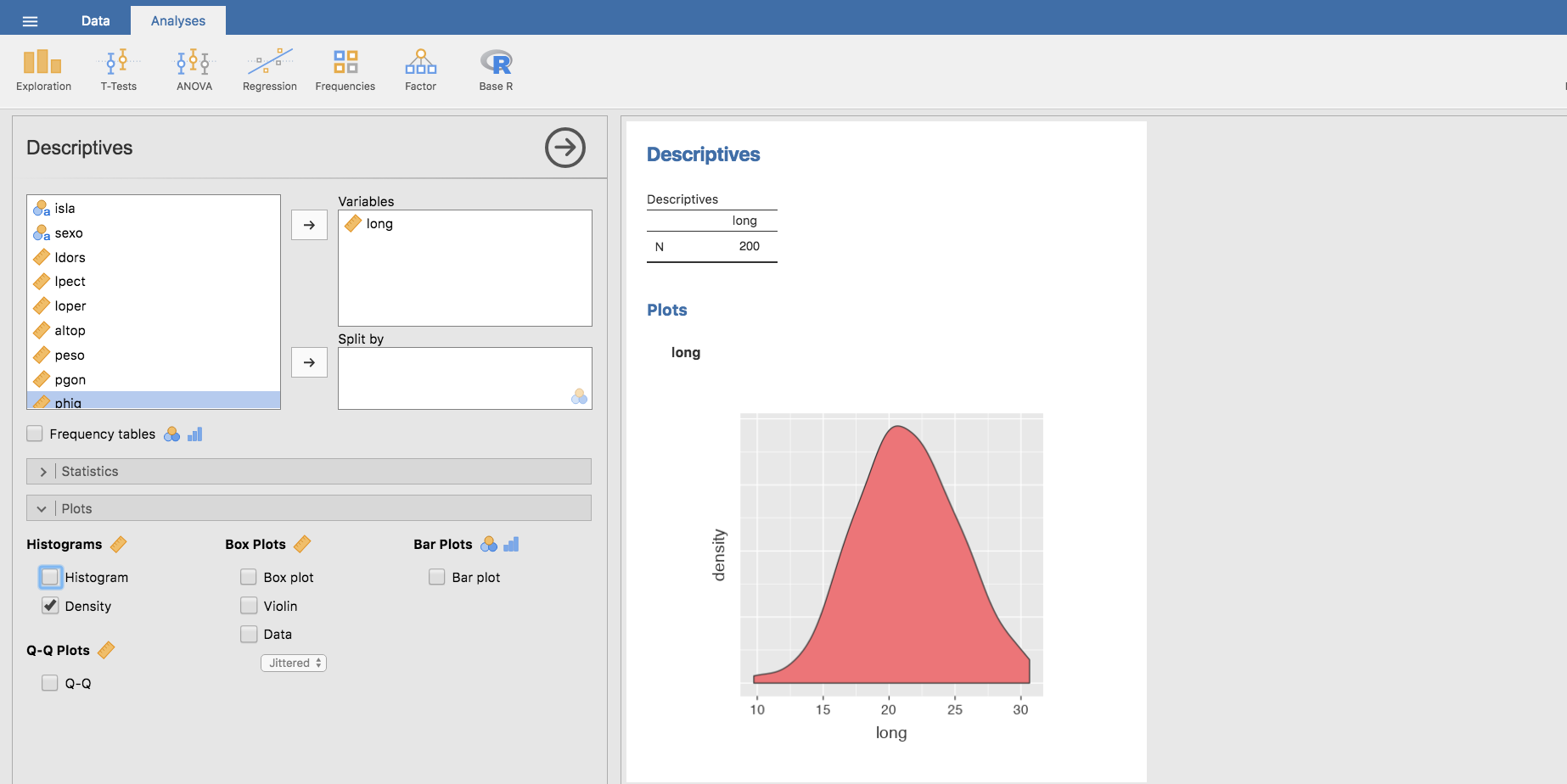
Pueden superponerse histograma y gráfico de densidad sin más que elegir ambas opciones:
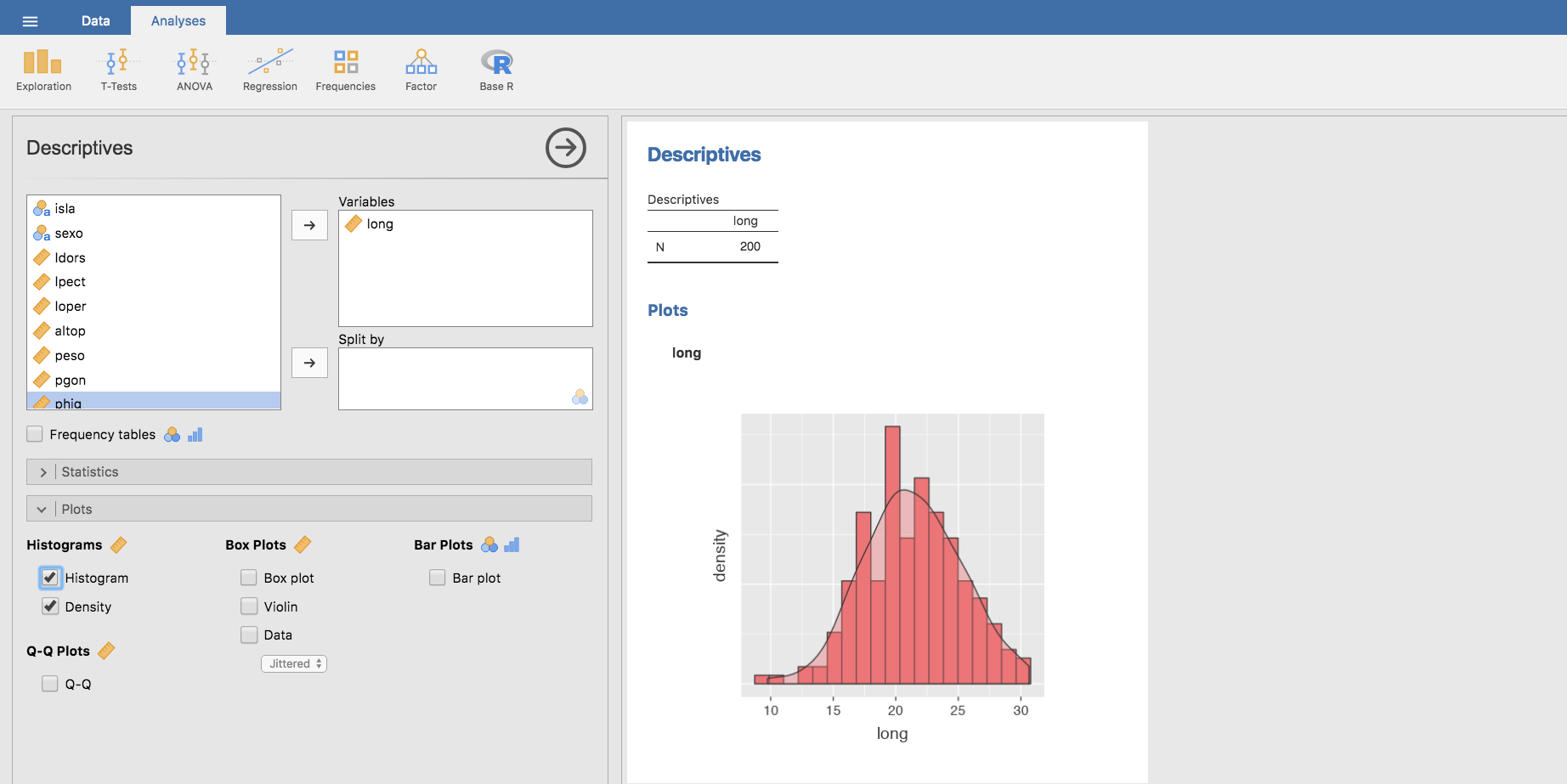
Medidas de síntesis o resumen de variables numéricas
Las variables numéricas pueden resumirse a través de diversas medidas que describen sus características de:
Posición: Percentiles y cuartiles.
Tendencia~central: Media, mediana y moda.
Dispersión: Varianza, desviación típica (o estándar), coeficiente de variación y rango.
Forma: Asimetría, Apuntamiento (curtosis).
Pasamos a describir cada una de estas medidas.
Medidas de posición
El \(k\)-ésimo percentil es un valor \(P_{k}\) tal que el \(k\)% de las observaciones de la variable tienen un valor menor o igual que \(P_{k}\). Los percentiles 25, 50 y 75 reciben el nombre de primer, segundo y tercer cuartiles, respectivamente.
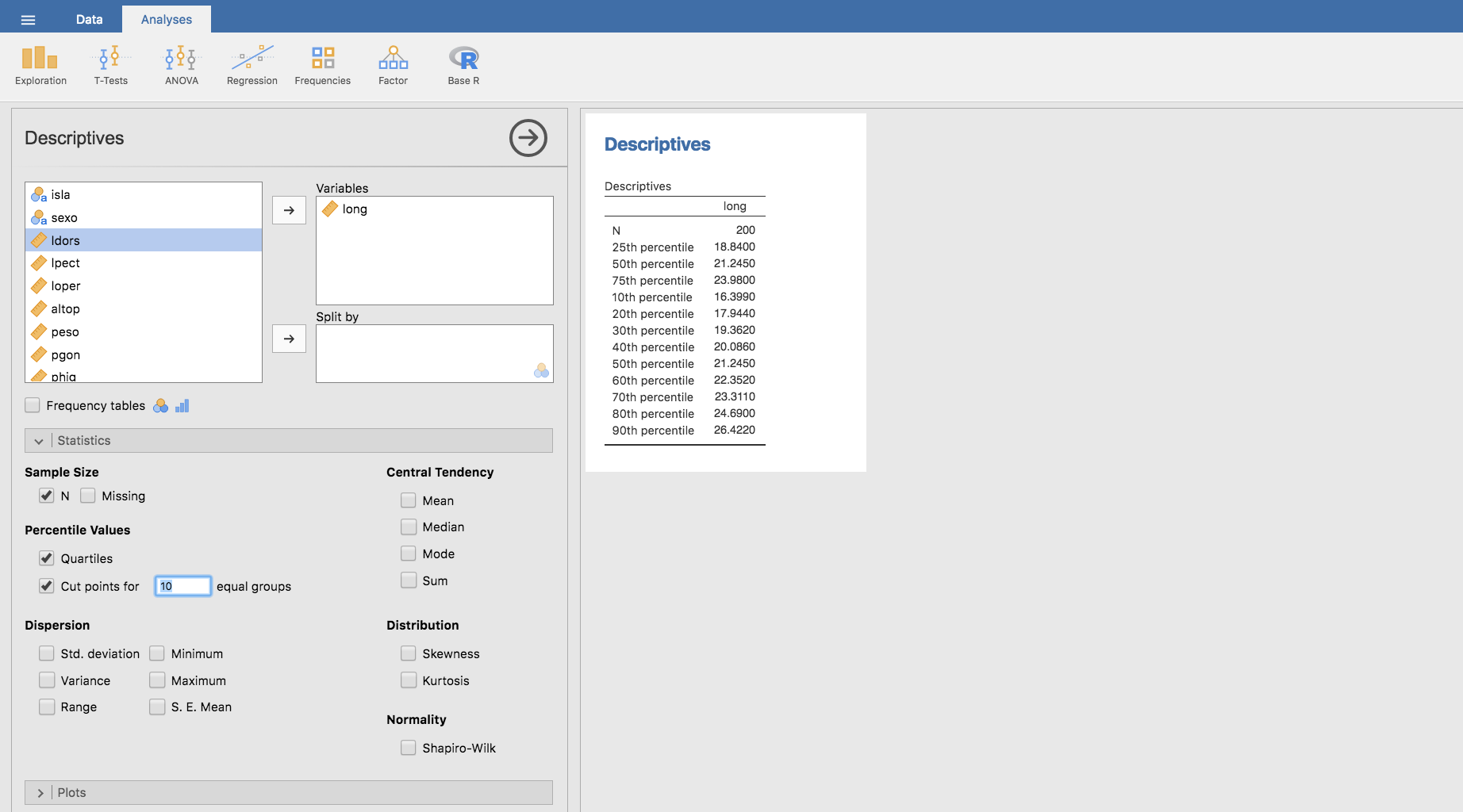
Los percentiles en Jamovi se calculan a través del menú Exploration/Descriptives. Así, para calcular los percentiles \(0.1\), \(0.25\), \(0.50\), \(0.75\), \(0.8\) y \(0.9\) de la longitud de los peces obtenidos durante la campaña de muestreo:
- Elegimos la variable long.
- En la barra Statistics, en el apartado Percentile values elegimos Quartiles y obtenemos tres cuartiles, y eligiendo \(10\) como el número de puntos de corte (Cut points…), completamos la lista de los percentiles buscados.
Medidas de tendencia central
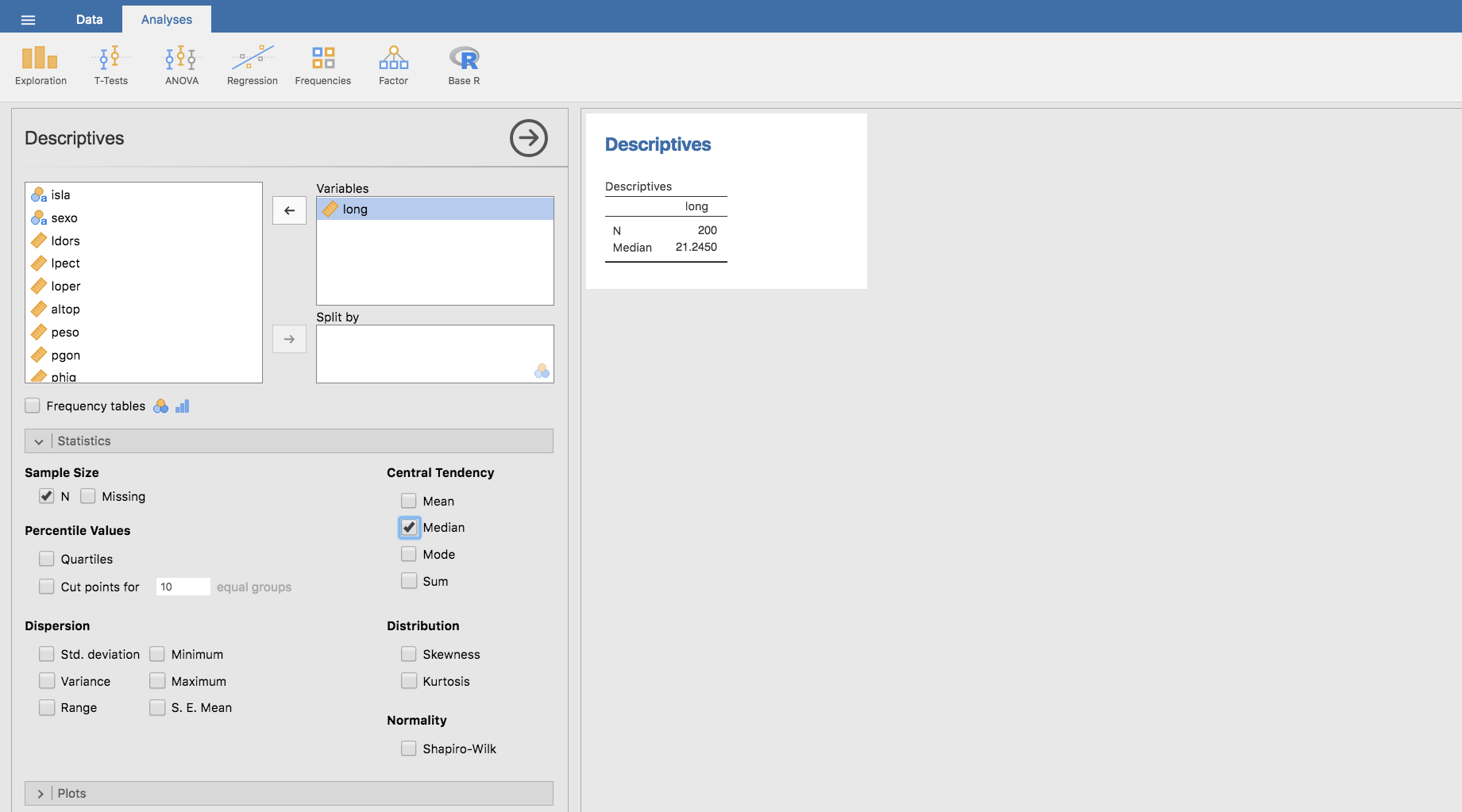
- Mediana: Es el valor que ocupa la posición intermedia del conjunto de datos una vez que éstos se han ordenado de menor a mayor. La mediana es, por tanto, aquel valor que es mayor que la primera mitad de los datos, y menor que la segunda mitad. Obviamente, por su definición, coincide con el percentil 50, \(P_{50}\) y con el segundo cuartil.
Si el número de datos es impar, se toma como mediana el valor que deja a derecha e izquierda el mismo número de datos. Si el número de datos es par, entonces la mediana es igual al promedio de los dos valores centrales.
En Jamovi la mediana se calcula en la barra Statistics, igual que los percentiles, clicando Median en el apartado Central Tendency. Así, la longitud mediana de los sargos de la muestra es \(21,245\):
- Media aritmética: Si en una muestra de una variable \(X\) se han observado los valores \(x_{1},x_{2},\)\(\dots,\)\(x_{k}\), siendo \(n_{1},n_{2},\dots,n_{k}\) sus frecuencias absolutas (número de veces que se ha observado cada valor), se define la media aritmética como: \[ \overline{x}=\frac{x_{1}n_{1}+x_{2}n_{2}+\dots,+x_{k}n_{k}}{n}=\sum_{i=1}^{k}x_{i}\frac{n_{i}}{n}=\sum_{i=1}^{k}x_{i}f_{i} \] siendo \(n=\sum_{i=i}^{k}n_{i}\) el número total de observaciones y \(f_{i}\) la frecuencia relativa del valor \(x_{i}\).
La media aritmética representa el centro de gravedad de los datos, por lo que efectivamente puede entenderse como medida de tendencia central.
En Jamovi la media aritmética se calcula igual que la mediana, pero clicando en Mean, y ambos valores se pueden obtener simultaneamente:
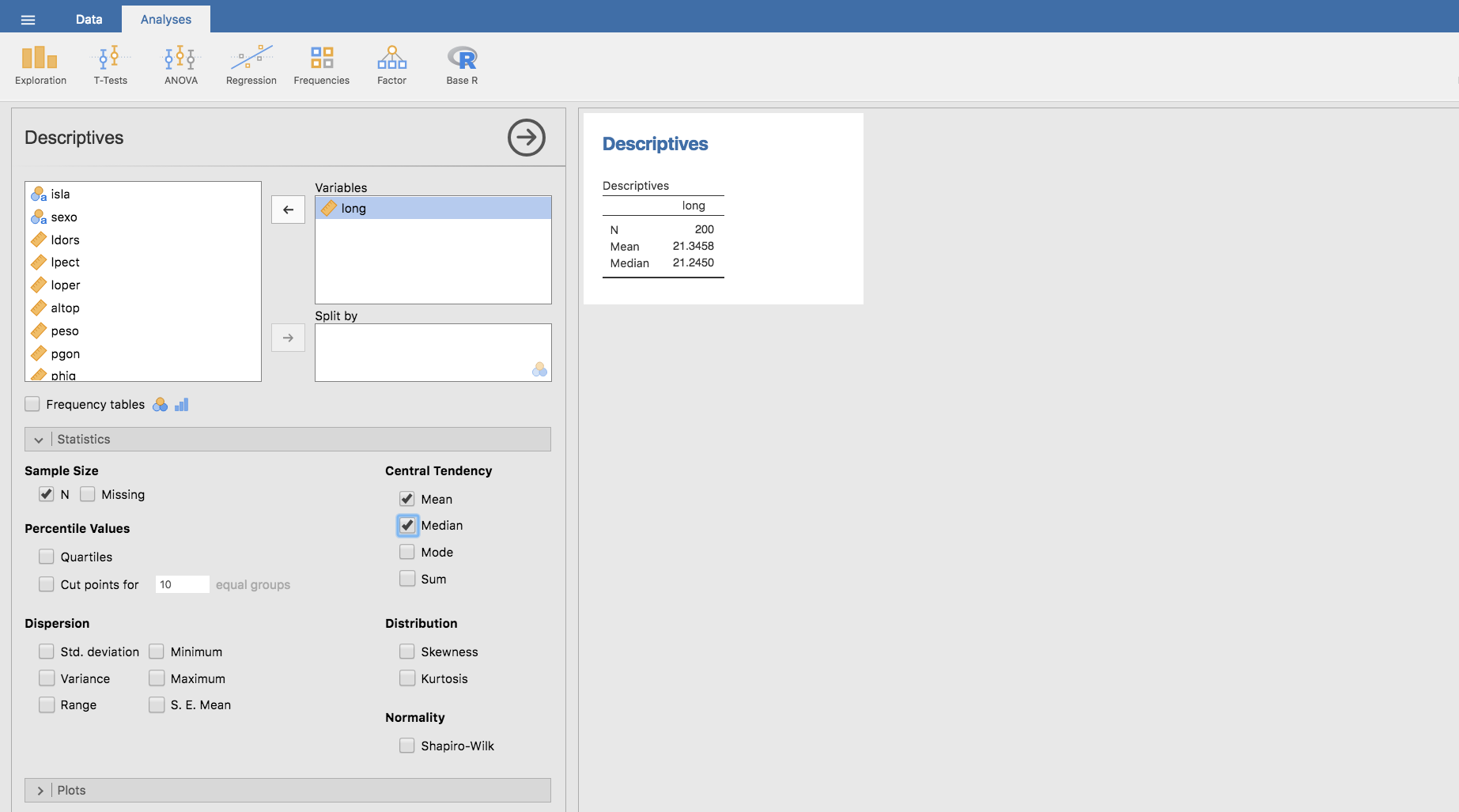
- Moda: Es el valor que más veces se repite (esto es, el valor con mayor frecuencia absoluta). En el caso de datos agrupados suele sustituirse la moda por el intervalo modal, que se corresponde con el intervalo de mayor frecuencia absoluta observada. Tanto la moda como el intervalo modal pueden no ser únicos.
Jamovi permite calcular la moda de igual modo que la mediana y la media aritmética. En este caso, para obtener la moda basta con hacer clic en Mode:
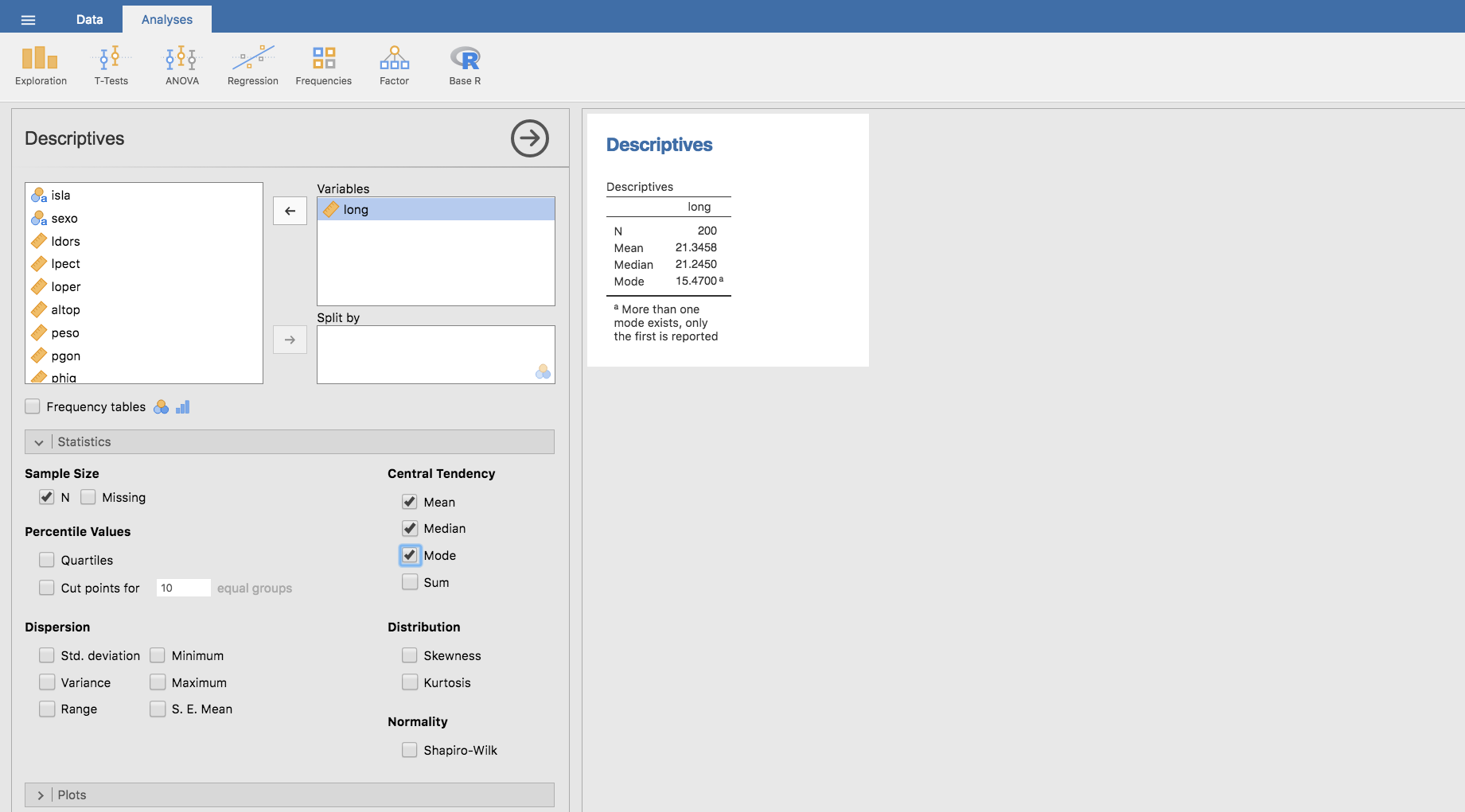
Observamos que Jamovi nos indica que existe más de una moda en nuestros datos.
- Media geométrica: Se define como: \[ \gamma=\left\{ x_{1}\cdot x_{2}\cdot\cdots\cdot x_{n}\right\} ^{1/n} \] Suele utilizarse para promediar incrementos relativos, tales como los que se observan frecuentemente en Economía o Demografía. Por ejemplo, si el tamaño de una población se ha incrementado en un 50% en un primer año, y ha disminuido un 50% al año siguiente, la aplicación ingenua de la media aritmética nos llevaría a concluir que, por término medio, el tamaño de la población no cambia. Sin embargo un análisis más atento nos revela que si la población parte inicialmente de, digamos, 1000 individuos, el incremento inicial del 50% significa una cifra de 1500 individuos al acabar el primer año, y la disminución posterior del 50% deja la población en 750 individuos; por tanto, en los dos años ha habido un decremento global del 25%. En realidad, la tasa media de variación interanual en este caso debe calcularse mediante la media geométrica: \[\gamma=\left(1.50\cdot0.50\right)^{1/2}=0.866.\]
Su interpretación es que, por término medio, cada año el tamaño de la población es un 86.6% del tamaño del año anterior; dos años sucesivos con esta tasa media producen una tasa acumulada de \(0.866\cdot0.866=0.75\), o lo que es lo mismo, un 75% del tamaño inicial, lo que sí coincide con la cifra observada.
Si en la definición de media geométrica tomamos logaritmos resulta: \[ \log\gamma=\frac{1}{n}\sum_{i=i}^{n}\log\left(x_{i}\right) \]
Por tanto el logaritmo de la media geométrica coincide con la media aritmética de los logaritmos de los datos originales.
Jamovi no dispone de ninguna función para el cálculo de la media geométrica. No obstante, es muy fácil de calcular utilizando la propiedad anterior. Por ejemplo, si el objetivo fuese calcular la media geométrica de la variable long, podemos calcular una nueva variable que contenga los logaritmos de la longitud:
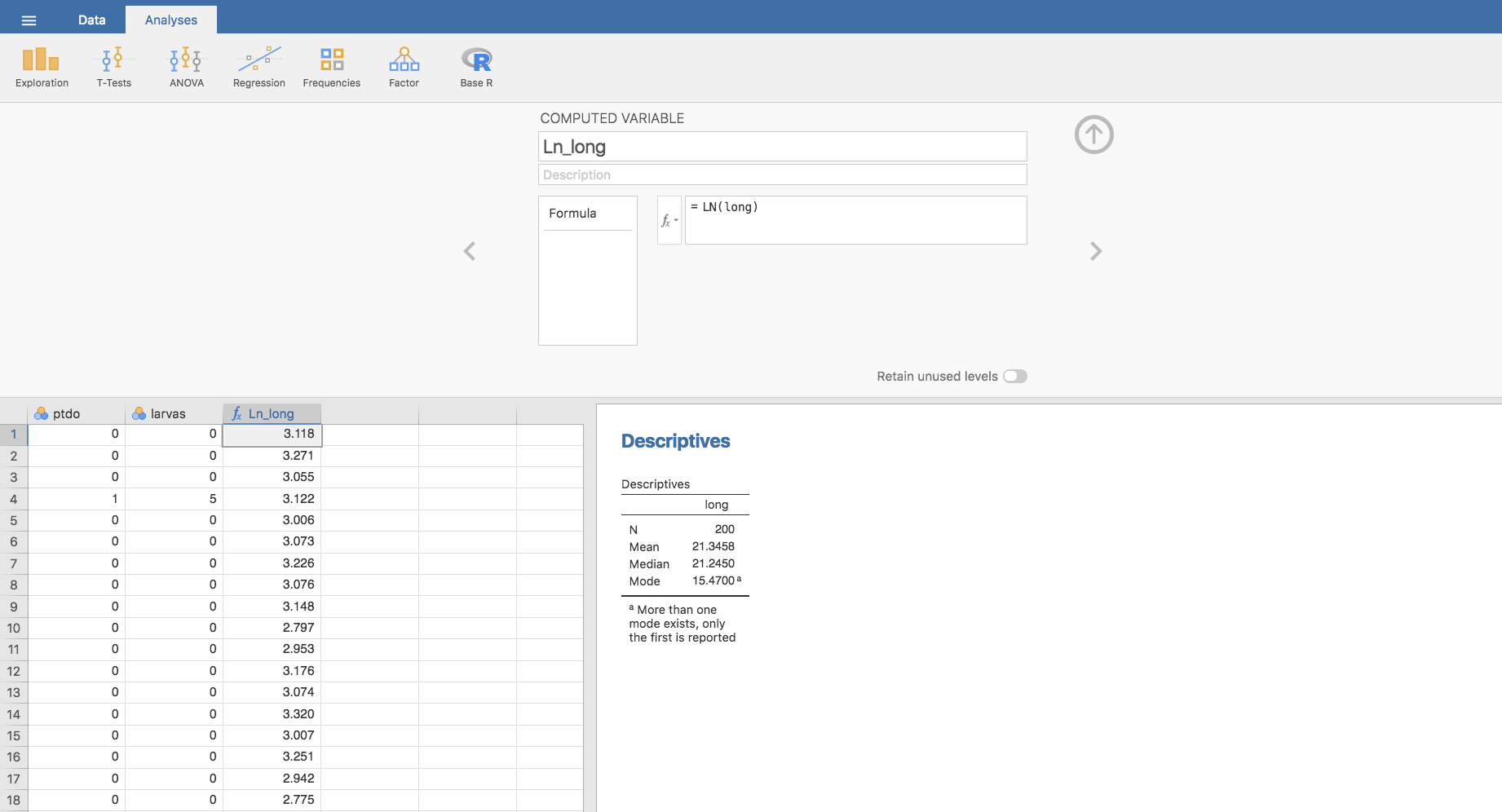
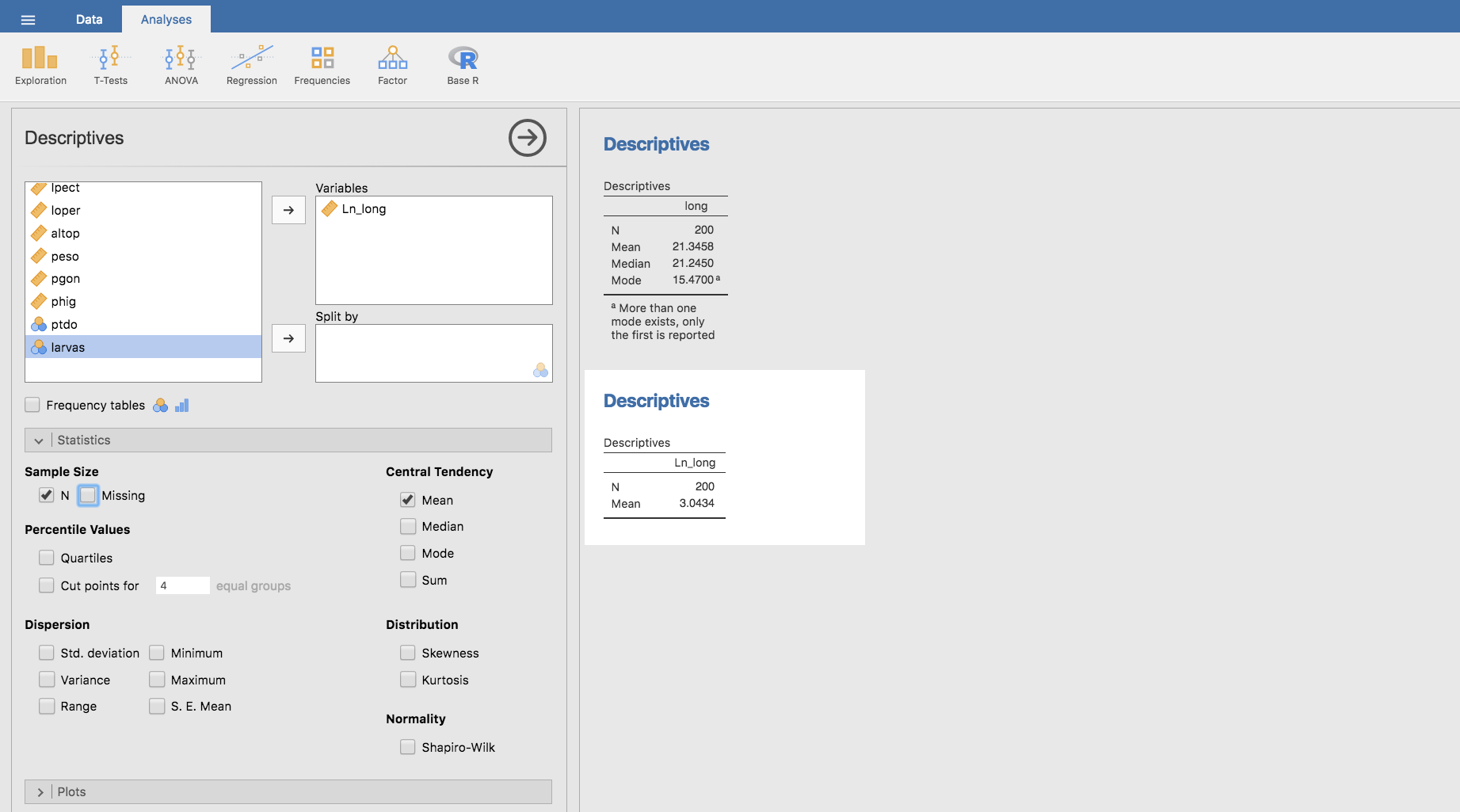
y calculando la media aritmética a Ln_long obtenemos el logaritmo neperiano de la media geométrica: \(3.0434\). En este punto, con un simple cálculo podríamos obtener la media geométrica.
Medidas de Dispersión
- Varianza: Si en una muestra de una variable \(X\) se han observado los valores \(x_{1},x_{2},\)\(\dots,\)\(x_{k}\), siendo \(n_{1},n_{2},\dots,n_{k}\) sus frecuencias absolutas (número de veces que se ha observado cada valor), se define la varianza muestral (o cuasi-varianza) como: \[ s^{2}= var\left(X\right)=\frac{1}{n-1}\sum\limits _{i=1}^{k}(x_{i}-\overline{x})^{2}n_{i}=\frac{n}{n-1}\sum\limits _{i=1}^{k}(x_{i}-\overline{x})^{2}\frac{n_{i}}{n}=\frac{n}{n-1}\sum\limits _{i=1}^{k}(x_{i}-\overline{x})^{2}f_{i} \]
siendo \(n=\sum_{i=i}^{k}n_{i}\) el número total de observaciones y \(f_{i}\) la frecuencia relativa del valor \(x_{i}\). Obviamente la varianza es una medida de dispersión ya que cuanto más alejados entre sí se encuentren los valores \(x_{i}\) más lejos estarán de su media aritmética y mayor será el valor de la varianza; y a la inversa, cuánto más próximos entre sí, más cerca estarán de la media y menor será la varianza.
En Jamovi la varianza se calcula igual que la media y mediana en el apartado anterior, seleccionando Variance en el apartado Dispersion de la barra Statistics:
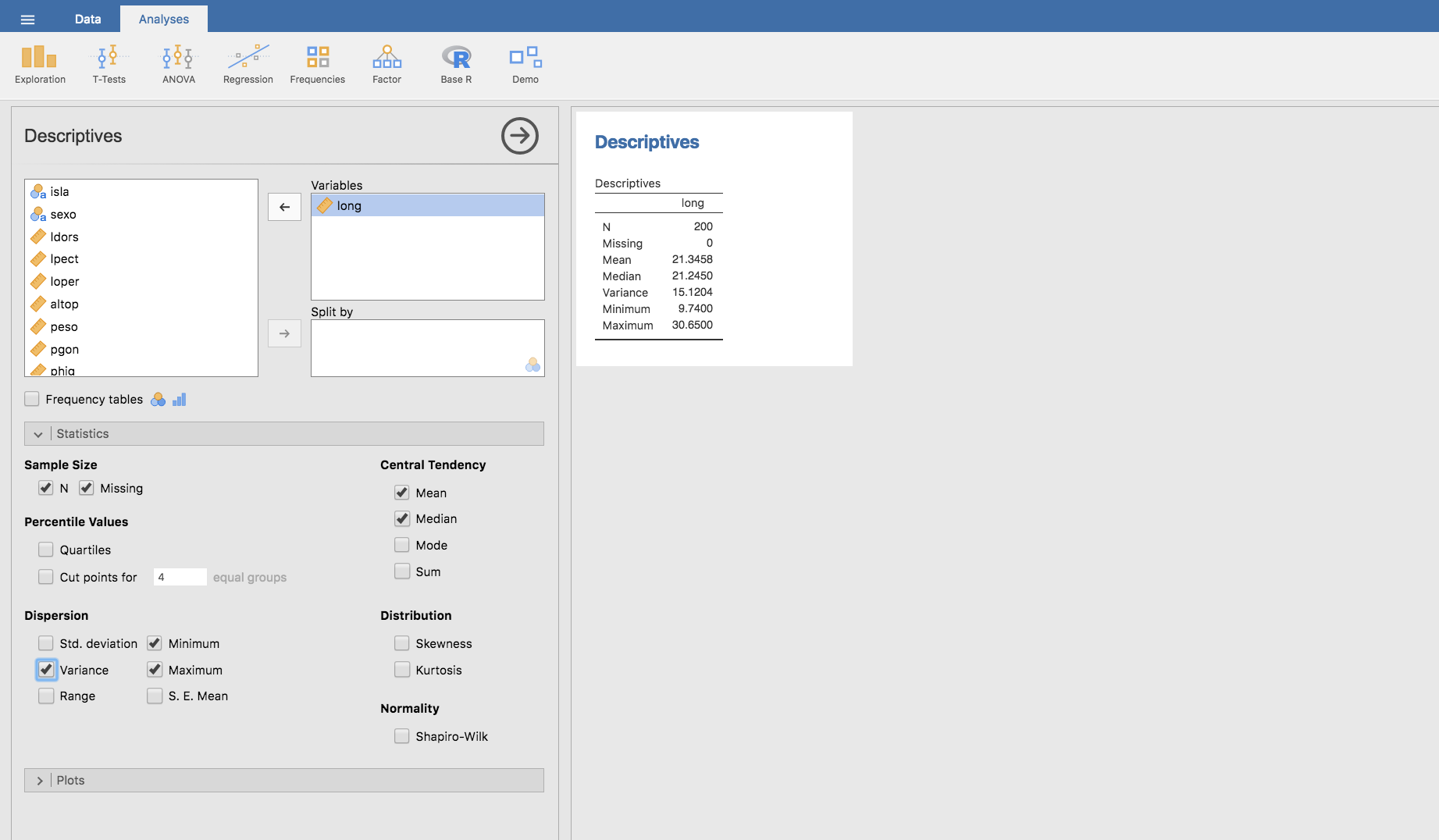
- Desviación típica (o Desviación estándar): Es la raiz cuadrada de la varianza. Se obtiene así una medida de dispersión en las mismas unidades que la variable original: \[ s=\sqrt{s^{2}} \]
En Jamovi se obtiene seleccionando Std. deviation en el mismo apartado anteriore, en el que calculamos la varianza:
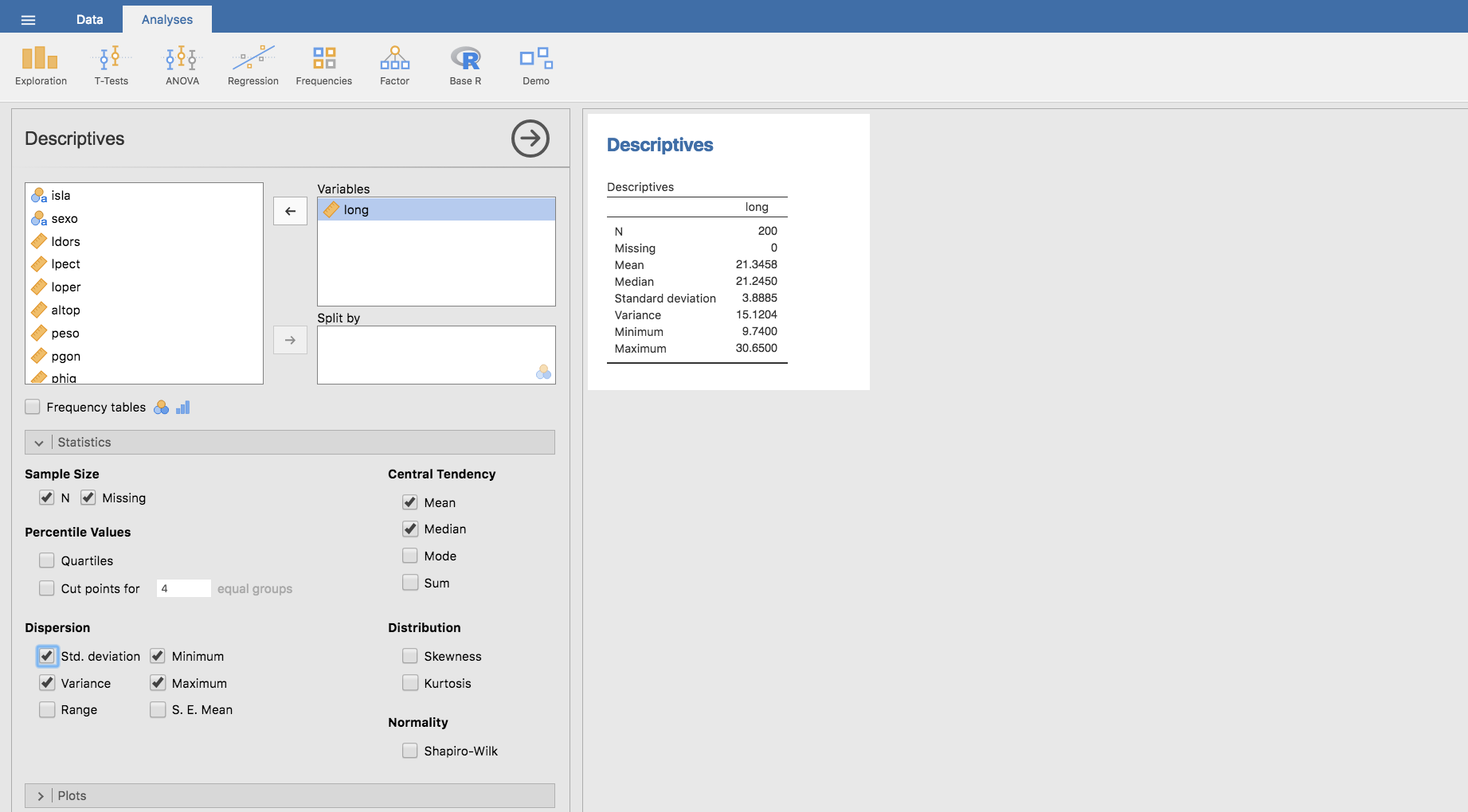
- Coeficiente de variación: La varianza y la desviación estándar son medidas de dispersión dependientes de las unidades en las que se mida la variable. El coeficiente de variación es una medida de dispersión adimensional que se define como: \[ cv(X)=\frac{s}{\overline{x}} \] (siempre que \(\overline{x}\ne0\)).
El coeficiente de variación resulta especialmente útil para comparar el grado de dispersión de variables que se miden en unidades diferentes. Por ejemplo si, en la muestra que estamos utilizando, queremos saber si los sargos presentan más dispersión en longitud o en peso, no tiene sentido comparar sus desviaciones típicas, medidas en centímetros y en gramos respectivamente. Sin embargo sus coeficientes de variación:
\[\frac{S_{long}}{\overline{long}}=0.1821669\]
\[\frac{S_{peso}}{\overline{peso}}=0.4552767\]
nos indican una mayor variabilidad en peso. Jamovi no ofrece ningún método específico para obtener el coeficiente de variación de una variable.
- Rango y rango intercuartílico: El rango de una variable se define como la distancia entre los valores mínimo y máximo: \[ \textrm{rango}\left(X\right)=\max\left(X\right)-\min\left(X\right) \] Asimismo, el rango intercuartílico es la distancia entre los cuartiles primero y tercero (\(P_{75}-P_{25}\) ).
Para obtener el rango de una variable, con Jamovi, basta con seleccionar Range en el mismo apartado que utilizamos para obtener la varianza y la desviación típica:
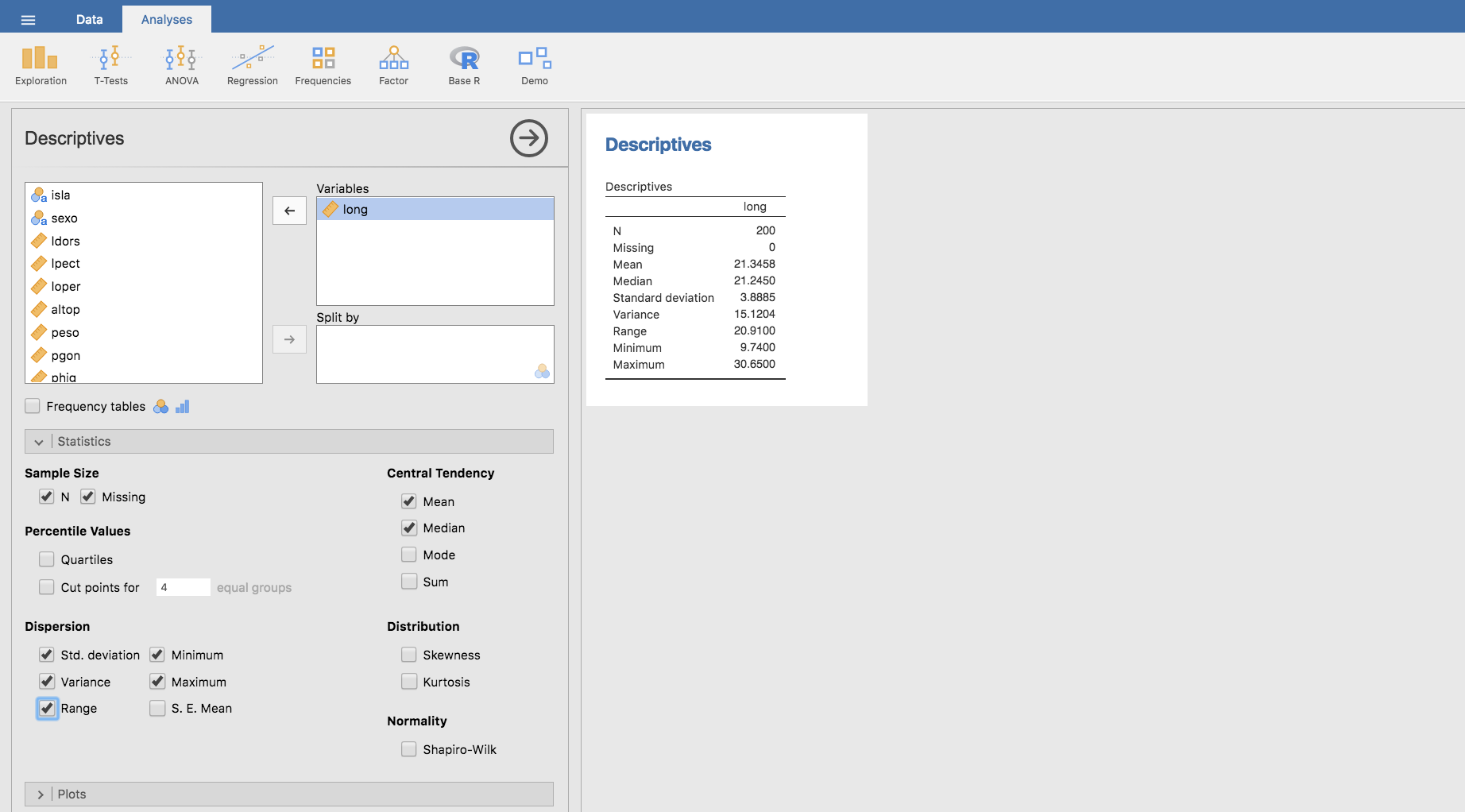
Para el rango intercuartílico, no hay comando específico, por lo que evaluaremos los cuartiles y a partir de ellos haremos la diferencia entre el primero y el tercer cuartil.
Medidas de forma
- Coeficiente de asimetría: En los casos en que los datos estén distribuidos de forma simétrica, la media y mediana son medidas aproximadamente similares. Sin embargo, cuando los datos muestran largas colas a la derecha (valores altos muy alejados del resto de los datos), el valor de la media tenderá a ser mayor que el de la mediana. Así por ejemplo, para el conjunto de datos ${ 1,2,2,3,3,3,4,4,5} $ media y mediana coinciden en el valor \(3\). Por el contrario, si el conjunto de datos es ${1,2,2,3,3,3,4,4,50} $, la mediana sigue siendo el valor \(3\), mientras que la media aritmética se desplaza al valor \(8\). En estos casos, la mediana representa (localiza) mejor el centro de la distribución que la media aritmética.
Dada una muestra de una variable \(X\) formada por \(n\) observaciones, siendo \(\overline{x}\) su media aritmética y \(s\) su desviación típica, la asimetría de la variable puede cuantificarse a través del coeficiente de asimetría de Fisher, definido como:
\[ a_{F}=\frac{\frac{1}{n}\sum\limits _{i=1}^{n}\left(x_{i}-\bar{x}\right)^{3}}{\left(\frac{1}{n}\sum\limits _{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}\right)^{3/2}} \]
si bien en la práctica es preferible utilizar la siguiente versión corregida: \[ a_{F}=\frac{n\sqrt{\left(n-1\right)}}{n-2}\frac{\sum\limits _{i=1}^{n}\left(x_{i}-\overline{x}\right)^{3}}{\left(\sum\limits _{i=1}^{n}\left(x_{i}-\overline{x}\right)^{2}\right)^{3/2}}=\frac{n}{\left(n-1\right)\left(n-2\right)}\frac{\sum\limits _{i=1}^{n}\left(x_{i}-\overline{x}\right)^{3}}{s^{3}} \]
ya que esta última expresión tiende a producir valores más próximos a la asimetría de la variable en la población de la que se ha extraído la muestra. Cuando los datos son perfectamente simétricos este coeficiente es nulo. Cuando los valores se concentran a la derecha, con largas colas a la izquierda este coeficiente es negativo (asimetría a la izquierda o negativa); y cuando los valores tienden a concentrarse a la izquierda, con largas colas a la derecha, el coeficiente es positivo (asimetría a la derecha o positiva).
Para el cálculo de la asimetría de las variables ldors y phig con Jamovi, seleccionamos ambas variables y en el apartado Distribution de la barra Statistics hacemos clic en Skewness:
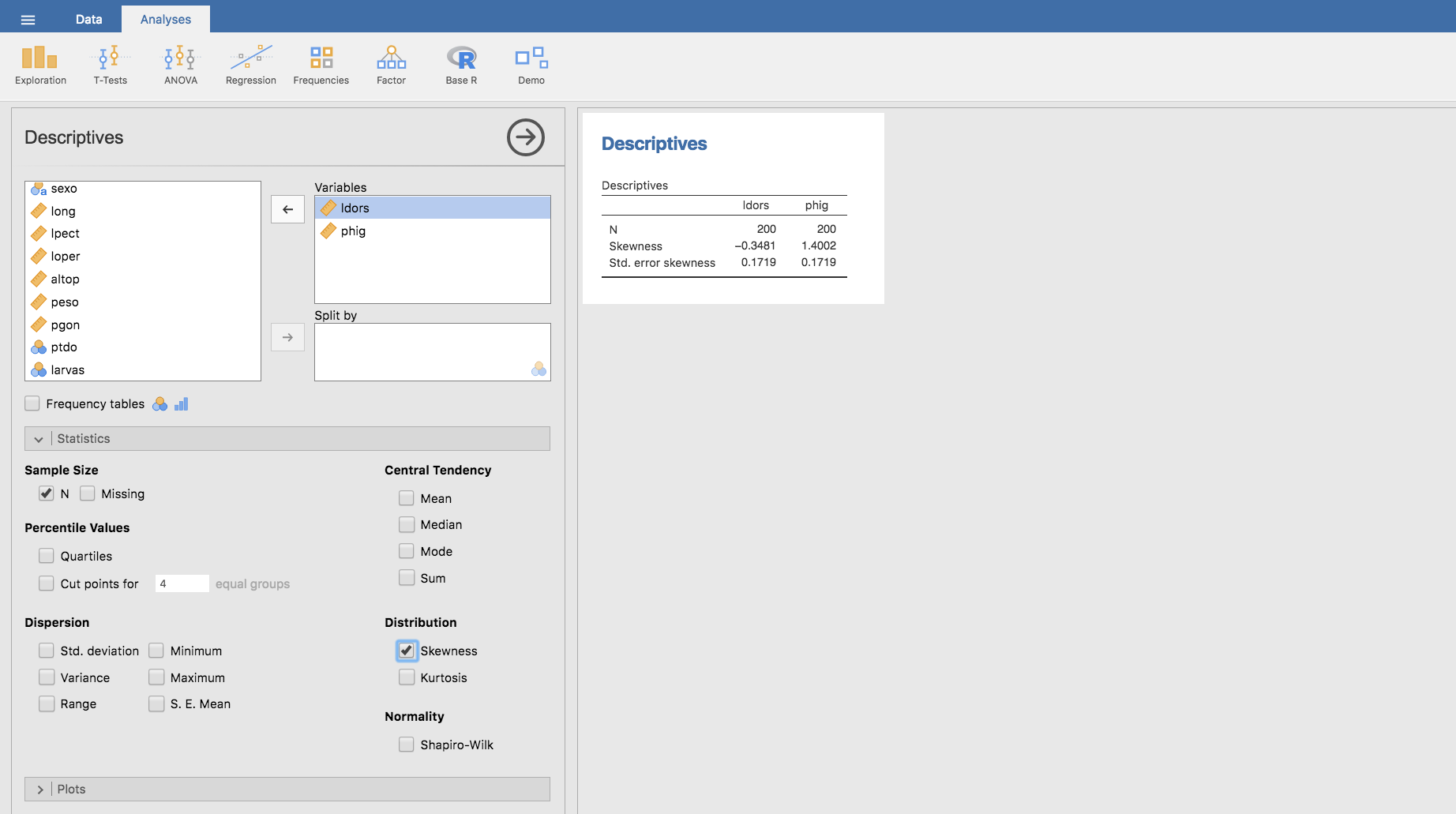
Como vemos, la distancia desde el morro del pez a la aleta dorsal (ldors) presenta asimetría negativa y el peso del hígado (phig) asimetría positiva.
En la siguiente representación gráfica podemos observar los histogramas de ambas variables, y comprobar que son efectivamente asimétricos:
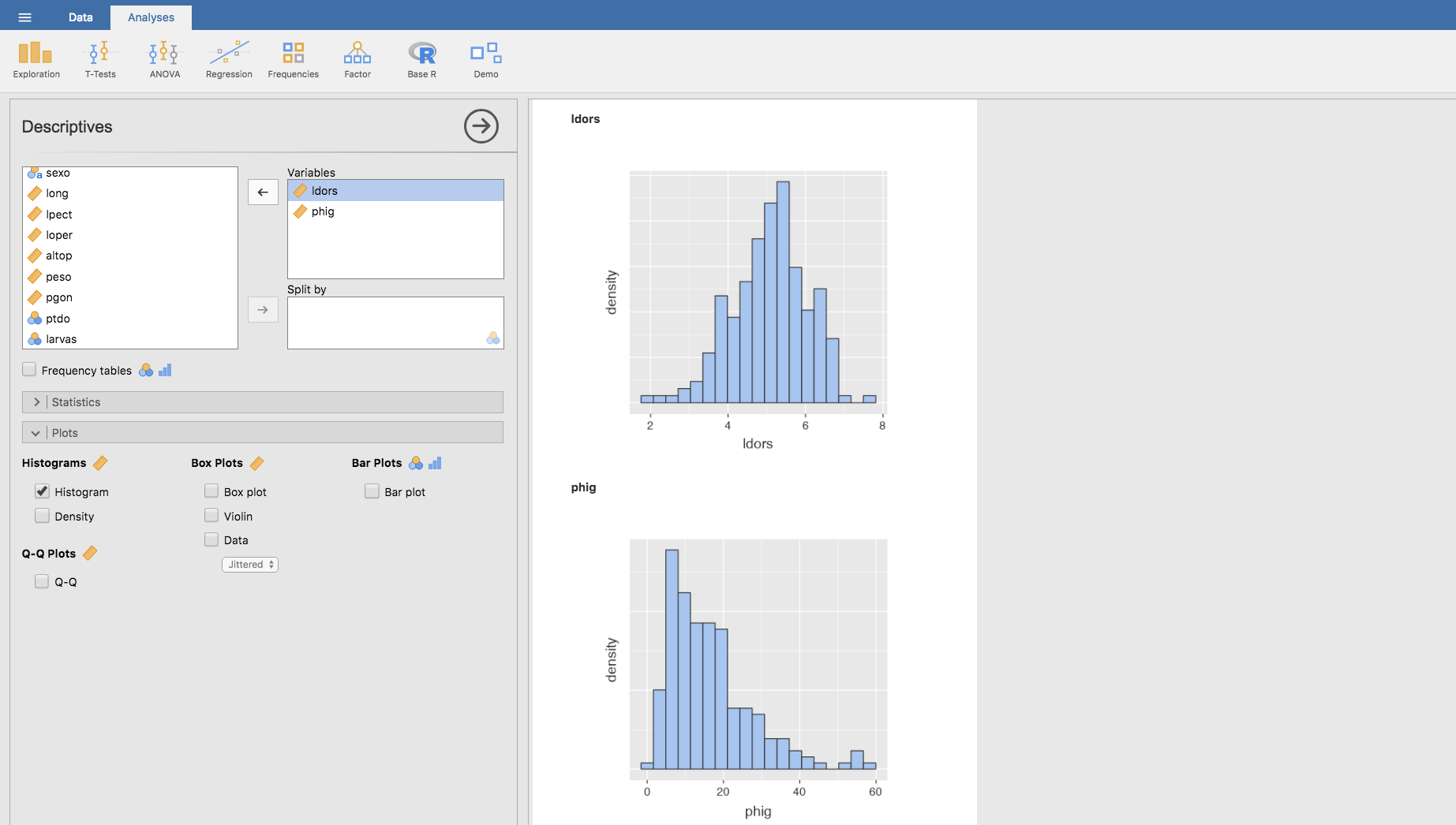
- Coeficiente de apuntamiento (curtosis): mide el grado de concentración que presentan los valores alrededor de la zona central del conjunto de datos. La definición habitual de curtosis es: \[ \kappa=\frac{\frac{1}{n}\sum\limits _{i=1}^{n}\left(x_{i}-\bar{x}\right)^{4}}{\left(\frac{1}{n}\sum\limits _{i=1}^{n}\left(x_{i}-\bar{x}\right)^{2}\right)^{2}}-3 \]
si bien, como ocurre con la asimetría, en la práctica se emplea una versión corregida (cuando \(n\) es grande produce prácticamente el mismo valor que la anterior, pero para valores de \(n\) pequeños tiende a producir valores de curtosis más próximos al verdadero valor en la población de la que se ha extraído la muestra): \[ \kappa=\frac{n\left(n+1\right)}{\left(n-1\right)\left(n-2\right)\left(n-3\right)}\frac{\sum\limits _{i=1}^{n}\left(x_{i}-\bar{x}\right)^{4}}{S^{4}}-3\frac{\left(n-1\right)^{2}}{\left(n-2\right)\left(n-3\right)} \]
Si \(\kappa>0\) la forma del conjunto de datos es “puntiaguda” (leptocúrtica); por el contrario, si \(\kappa<0\), la forma es “aplastada” (platicúrtica). El caso \(\kappa=0\) corresponde a una forma “normal” (mesocúrtica), ni muy apuntada ni muy aplastada.
Al igual que ocurría con la asimetría, Jamovi calcula de un modo muy simple la curtosis, por ejemplo, para las variables ldors y phig:
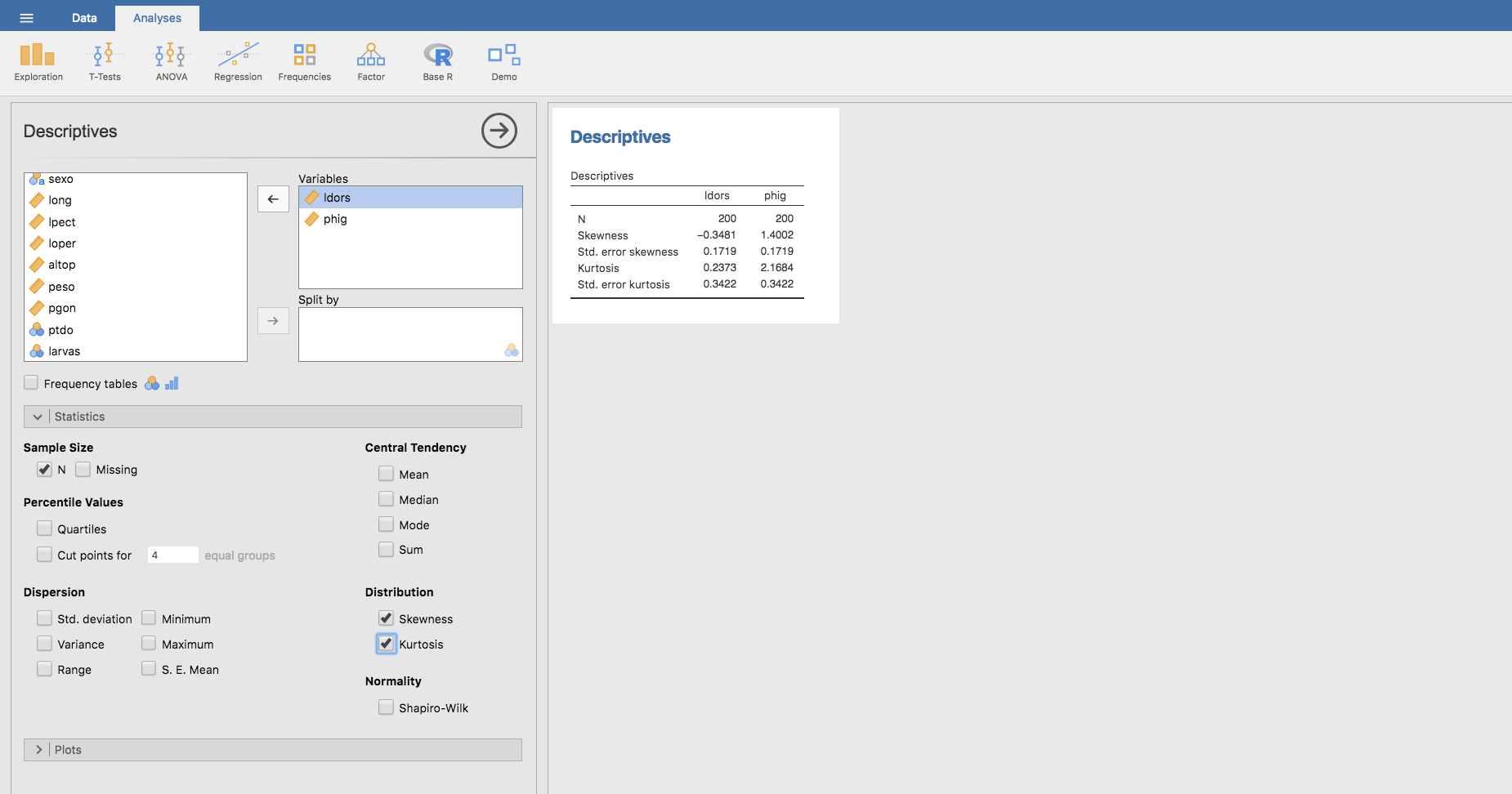
Como vemos, ambas variables presentan apuntamiento positivo (corresponden a distribuciones leptocúrticas), tal como podemos apreciar visualmente en los histogramas mostrados anteriormente.
Diagrama de cajas y barras (boxplot)
Estos diagramas representan los percentiles de una variable y son especialmente útiles para una comparación gráfica de varias poblaciones, así como para la detección de posibles valores anómalos (). Su construcción se realiza de la siguiente forma: sea ${ x_{1},,x_{n}} $ el conjunto de datos correspondientes a una variable numérica \(X\), y representemos por \(P_{25}\), \(P_{50}\) y \(P_{75}\) los percentiles \(25\), \(50\) y \(75\) respectivamente; se dibuja un rectángulo vertical cuyos lados inferior y superior corresponden a \(P_{25}\) (primer cuartil) y \(P_{75}\) (tercer cuartil) respectivamente; a la altura \(P_{50}\) (mediana) se traza un segmento horizontal. Por último el rectángulo se une mediante lineas a dos barras correspondientes los extremos de la distribución, trazadas a alturas respectivas \(b\) y \(B\):
Los valores de los datos que quedan fuera de las barras superior e inferior se marcan con puntos y se entenderá que pueden ser anómalos, y deben ser revisados por si constituyeran errores de medida, datos correspondientes a otra población, etc.
Para obtener en Jamovi el boxplot de la variable longitud, por ejemplo, haríamos exactamente lo mismo que para obtener su histograma, solo que en este caso seleccionamos la opción Box plot en la barra Plots:
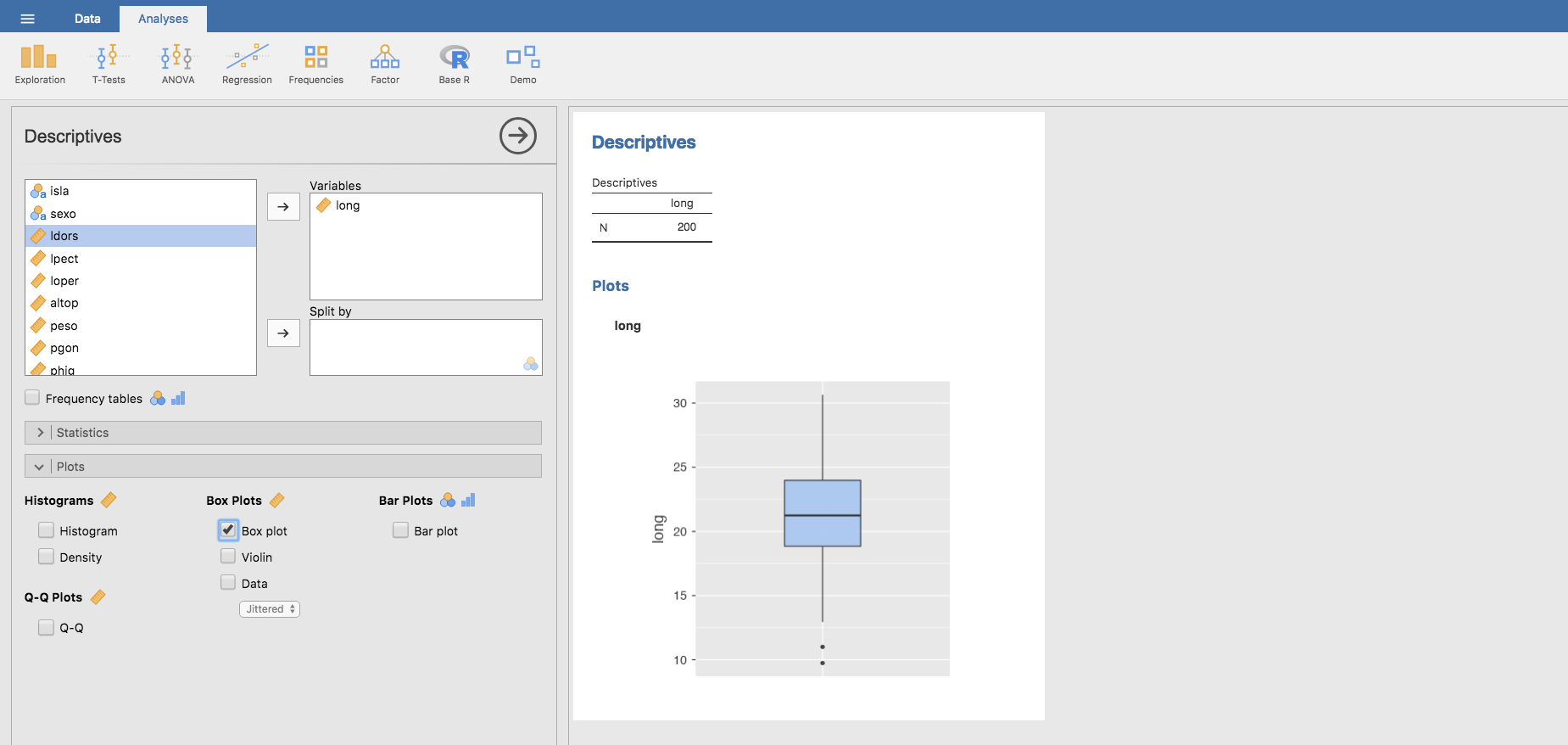
Medidas de síntesis en subgrupos de la muestra
En muchas ocasiones los objetos de la muestra pueden clasificarse según los valores de alguna variable categórica. Así, en los datos de nuestro ejemplo, podríamos clasificar los sargos en función de la isla de procedencia, o en función de su sexo. En la sección Variables categóricas ya hemos visto como construir tablas cruzadas para esta clase de variables. Cuando lo que nos interesa es calcular las distintas medidas de síntesis sobre cada uno de los grupos que forman la muestra, podemos hacerlo de un modo sencillo con Jamovi.
Así, por ejemplo, para calcular la longitud media de los sargos según sexo seleccionaríamos la variable long, la cual distribuimos por sexo situando la variable sexo en la ventana titulada Split by, y finalmente en la barra Statistics indicamos a Jamovi que calcule la media (Mean):
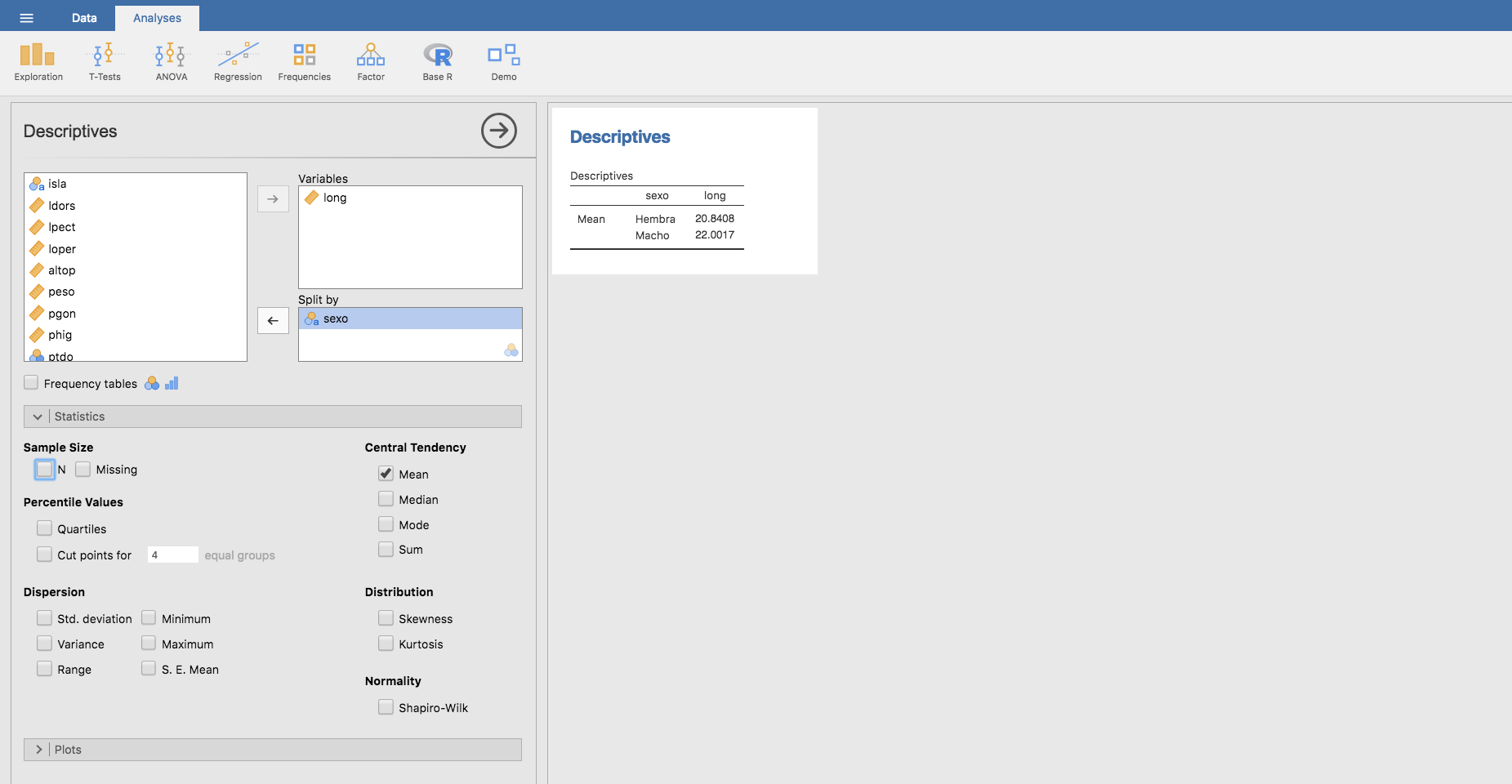
Si quisiéramos calcular varias medidas de síntesis sobre los subgrupos de la muestra sería suficiente con elegir las medidas a calcular; así, por ejemplo, si quisiéramos obtener la media, desviación típica, mínimo y máximo de la variable long clasificadas por la variable sexo:
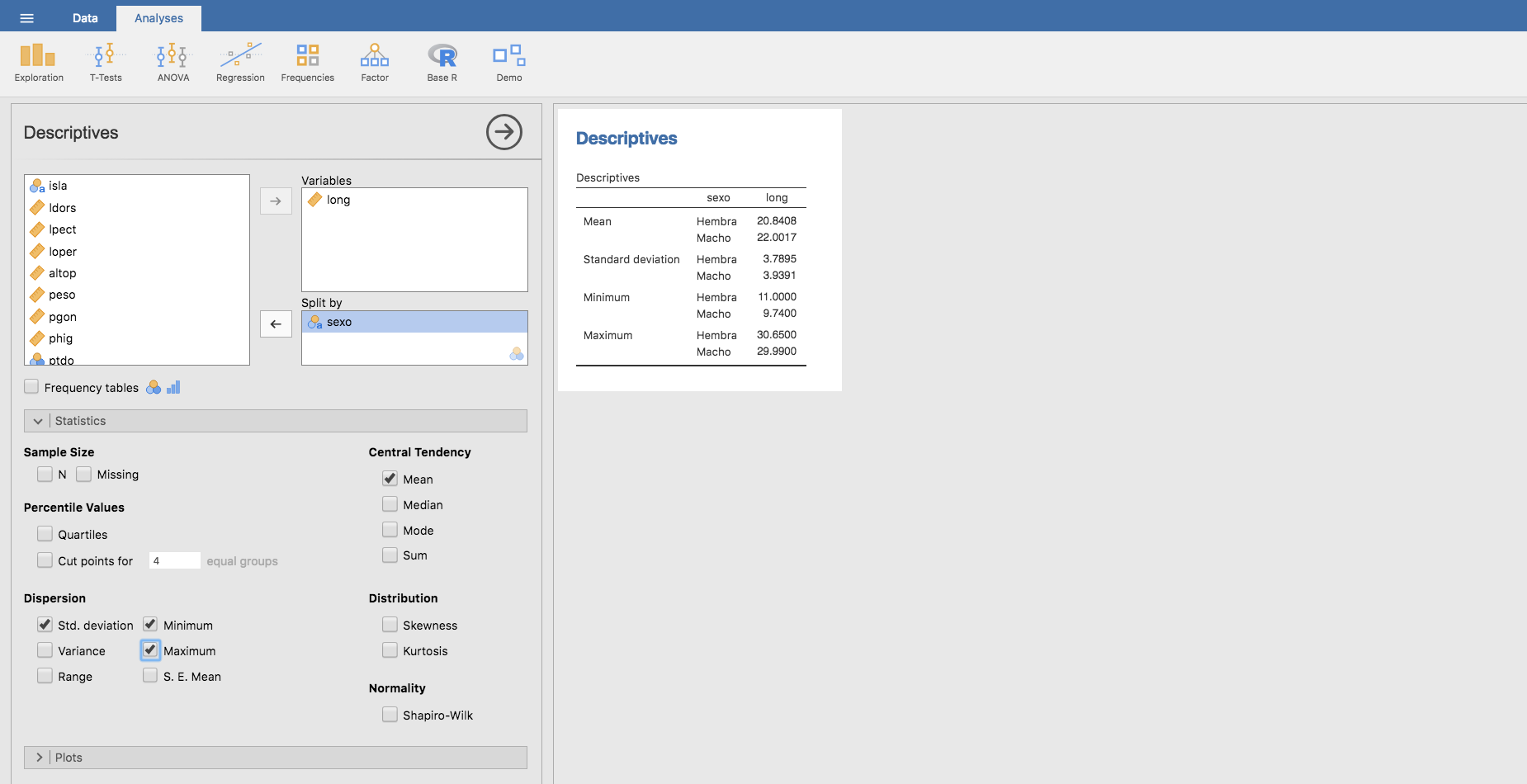
También podemos obtener medidas por subgrupos clasificadas por varias variables. Por ejemplo, si quisiéramos calcular las medidas elegidas anteriormente pero clasificándolas por sexo y por isla:
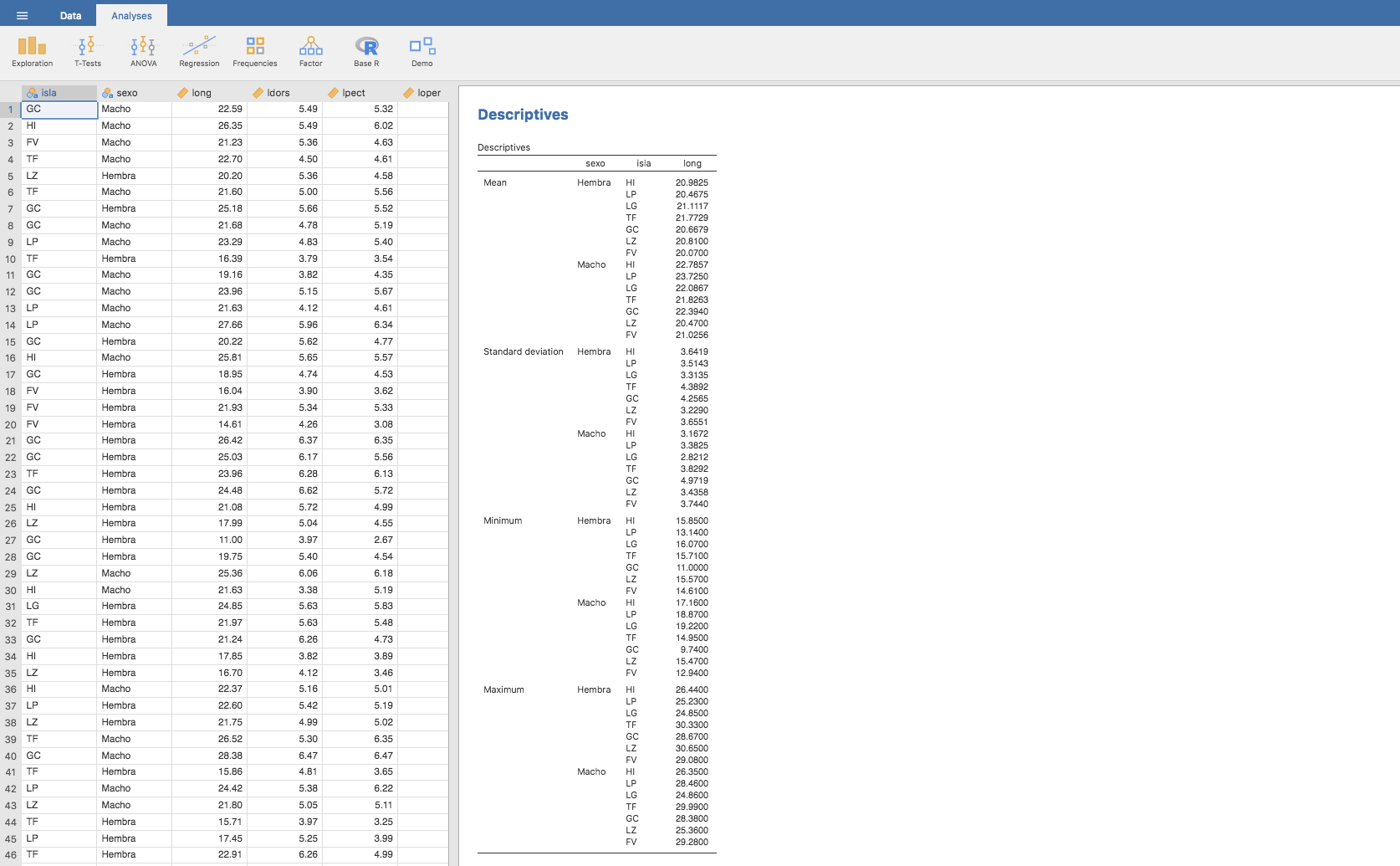
Para concluir esta sección citemos que es posible hacer diagramas de cajas y barras según subgrupos de la muestra. Por ejemplo, para representar el peso según el sexo:
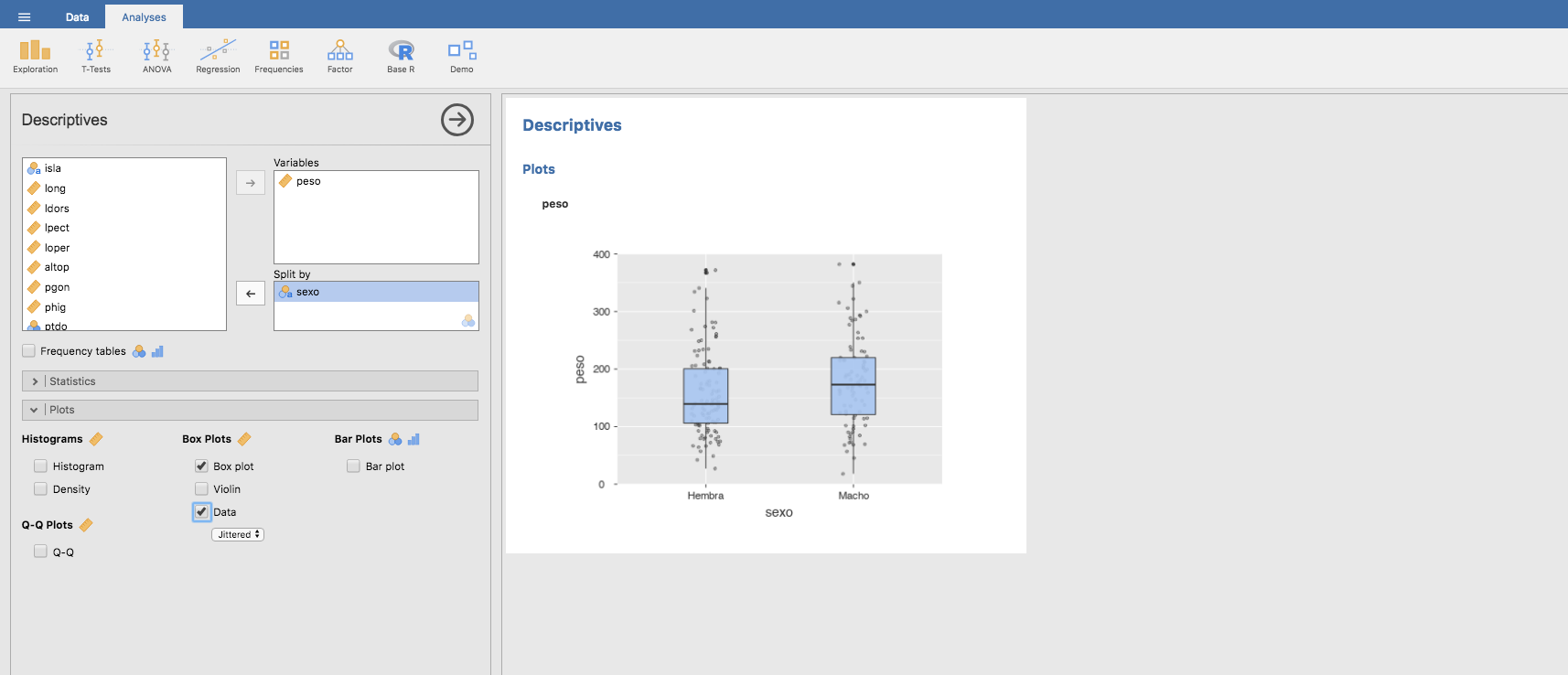
O para el sexo según la isla:
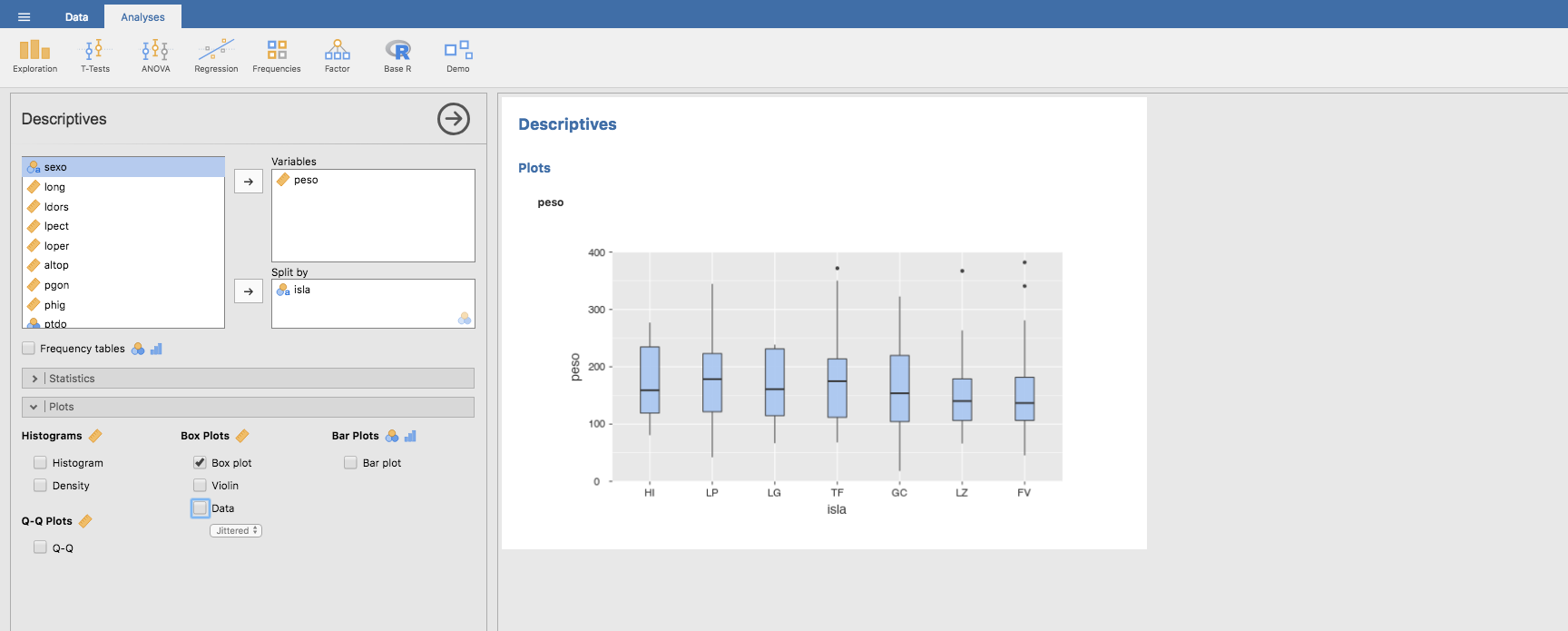
También, para el peso según el sexo y la isla:
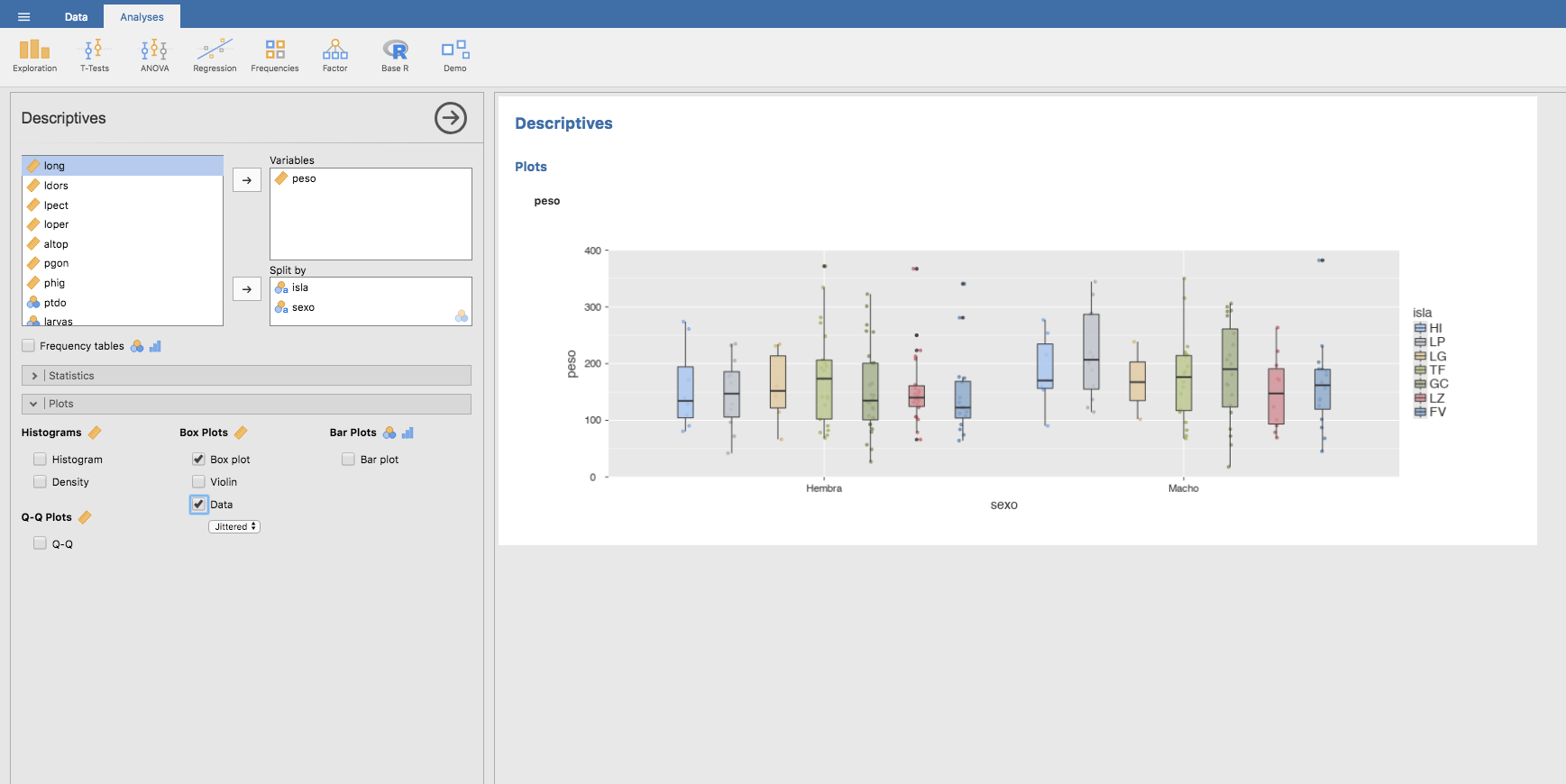
Asociación entre variables continuas
En la sección Variables numéricas continuas hemos llevado a cabo la descripción de datos correspondientes a variables continuas: tablas de frecuencias, histogramas, boxplots,…
Asimismo, en la sección Medidas de síntesis hemos presentado las medidas de síntesis que nos permiten resumir las características de estas variables en unos pocos valores. En ambos casos, el análisis de los datos ha sido univariante: cada variable se estudia aisladamente, sin conexión con las restantes variables continuas medidas en la muestra. Todo lo más, en síntesis-grupos hemos visto como varía una variable continua en varios grupos definidos por una variable categórica.
Ahora bien, cuando se realiza el estudio conjunto de dos variables, normalmente el objetivo es determinar si existe algún tipo de asociación entre ellas o si, por el contrario, son independientes. En términos prácticos, la asociación significa que el conocimiento de los valores de una de las variables proporciona alguna información sobre los valores de la otra. Por ejemplo, conocer la estatura de una persona nos informa sobre su peso, ya que las personas más altas tienen, en general, un peso mayor que las personas más bajas. Esta asociación estadística, obviamente no es exacta: dos personas de la misma altura no tienen que tener exactamente el mismo peso, y una persona más alta puede pesar menos que una más baja. La gráfica siguiente (denominada nube de puntos) ilustra este tipo de asociación: valores altos de la variable \(loper\) tienden a ir acompañados de valores altos de la variable \(lpect\), a la vez que valores bajos de \(loper\) tienden a ir acompañados de valores bajos de \(lpect\), si bien no de manera exacta.
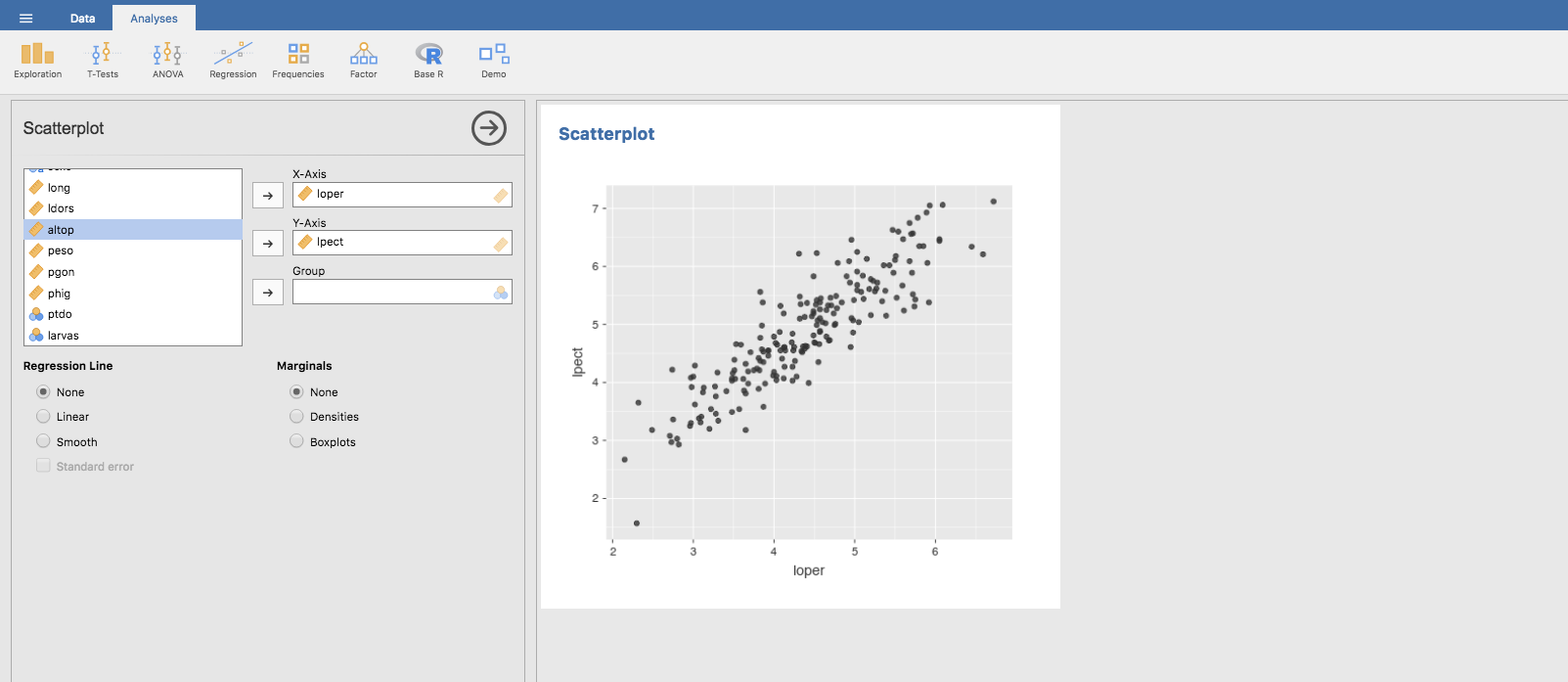
Al estudiar la asociación entre variables continuas podemos encontrarnos ante dos problemas distintos, según cuál sea el objetivo de nuestro estudio:
Análisis de regresión: nuestro objetivo es construir un modelo para predecir el valor de una variable \(Y\) cuando se conoce el valor de otra variable \(X\). Esto es, si para el sujeto \(i\)-ésimo de la muestra sabemos que \(X=x_{i}\), queremos hallar una función \(f\) tal que el valor de \(Y\) predicho para ese sujeto sea \(y_{i}=f\left(x_{i}\right)+\varepsilon_{i}\). Los términos \(\varepsilon_{i}\) representan los errores de predicción. Cuando la función \(f\left(X\right)\) es lineal nos hallamos ante un problema de regresión lineal. En caso contrario estaríamos ante un problema de regresión no lineal.
Análisis de correlación: nuestro objetivo es medir la intensidad de la asociación lineal entre dos variables \(X\) e \(Y\). Una correlación alta indicaría una fuerte asociación y una correlación baja, una asociación débil. Las variables son tratadas de forma simétrica, no hay una variable predictora y una variable a predecir.
En un análisis de correlación ambas variables \(X\) e \(Y\) son aleatorias, lo que significa que sus valores no se conocen hasta haberlas observado. El observador usa la correlación para medir la asociación entre estas variables tal como se produce en la naturaleza. En la muestra que venimos utilizando como ejemplo, para cada sargo se mide su longitud y su peso; antes de tomar la muestra estos valores son desconocidos, por lo que ambas variables son aleatorias. Sin embargo, en un análisis de regresión, si bien ambas variables pueder ser también aleatorias, es frecuente que el observador (o experimentador) fije de antemano los valores de la variable \(X\) y mida a continuación como responde la variable \(Y\), que sería en tal caso la única aleatoria. Es importante señalar que en estas condiciones la asociación que se produzca entre \(X\) e \(Y\) puede ser muy distinta de la que se observa en condiciones naturales.
Nota: tanto en el caso de la regresión como en el de la correlación no debe confundirse asociación con causalidad. Podemos usar una regresión para predecir la edad de un niño a partir de su estatura, ya que niños más altos probablemente tienen mayor edad; pero evidentemente, la altura no es la causa de la edad. Podemos detectar una correlación –asociación– fuerte entre altos niveles de glucosa en sangre e hipertensión; sin embargo ello no quiere decir que la diabetes cause la hipertensión o que la hipertensión cause la diabetes; no puede descartarse la posibilidad de que exista una causa común –en este caso, el síndrome metabólico– que sea en realidad la que da lugar a la asociación entre ambas enfermedades.
Sólo los estudios experimentales pueden probar de manera concluyente una posible relación causal entre dos variables: en estos estudios el experimentador controla todos los posibles factores de confusión (terceras variables que puedan influir en la asociación) y las posibles fuentes de ruido en los datos; si en tales condiciones la modificación de \(X\) produce un cambio en \(Y\), y se cuenta además con un mecanismo para explicar como se produce tal efecto, entonces y sólo entonces se puede hablar de causalidad, o al menos de influencia de \(X\) sobre \(Y\).
Regresión lineal
Una de las formas más comunes de asociación entre variables es la asociación lineal. Los valores representados en la última gráfica (nube de puntos) muestran precisamente este tipo de asociación. En la práctica resulta de interés determinar la ecuación de la recta que define esta relación y que permite aproximar el valor de \(Y\) cuando se conoce el valor de \(X\). Esta recta se denomina recta de regresión de \(Y\) sobre \(X\), y su ecuación es de la forma \(Y=b_{0}+b_{1}X\).
La variable \(X\) recibe el nombre de variable explicativa (o independiente) y la \(Y\) el de variable respuesta (o dependiente). El valor de \(b_{1}\) es la pendiente y \(b_{0}\) es la ordenada en el origen. La pendiente representa el incremento (si \(b_{1}\) es positivo) o decremento (si \(b_{1}\) es negativo) que experimenta el valor promedio de \(Y\) por cada unidad de incremento en el valor de \(X\). Asimismo, la ordenada en el origen \(b_{0}\) es el valor de \(Y\) cuando \(X=0\). Hay que señalar que, desde el punto de vista del análisis de los datos, esta interpretación solo debe realizarse cuando el valor \(X=0\) ha sido efectivamente observado. Si, por ejemplo, \(Y\) fuese el peso de una persona de altura \(X\) y se dispusiera de una recta de regresión \(Y=b_{0}+b_{1}X\) que relacionase ambas variables, dado que no existen personas de estatura \(X=0\) no tiene sentido decir que \(b_{0}\) es el peso aproximado de tales personas.
Para calcular la recta de regresión de \(Y\) sobre \(X\) se utiliza habitualmente el método de los mínimos cuadrados. Supongamos que sobre una muestra de \(n\) objetos hemos medido el par de variables \(\left(X,Y\right)\), y que los valores observados han sido ${(x_{1},y_{1}),(x_{2},y_{2}),,(x_{n},y_{n})} $. Supongamos además que estos puntos se encuentran alineados a lo largo de una recta de ecuación \(Y=b_{0}+b_{1}X\), y llamemos \(\hat{y}_{i}=b_{0}+b_{1}x_{i}\) al valor que corresponde sobre la recta al punto \(x_{i}\) (valor predicho por la recta). El error de predicción sería entonces \(e_{i}=y_{i}-\hat{y_{i}}\). El criterio de los mínimos cuadrados consiste en determinar los valores de \(b_{0}\) y \(b_{1}\) de forma que la suma de distancias al cuadrado entre observaciones y predicciones sea mínima, esto es:
\[ \min\sum\limits _{i=1}^{n}e_{i}^{2}=\min\sum\limits _{i=1}^{n}\left(y_{i}-\hat{y}_{i}\right)^{2}=\underset{b_{0},b_{1}}{\min}\sum\limits _{i=1}^{n}\left(y_{i}-\left(b_{0}+b_{1}x_{i}\right)\right)^{2} \]
De esta forma se consigue que la recta pase simultáneamente lo más cerca posible de todos los puntos observados. La figura siguiente ilustra gráficamente esta idea.
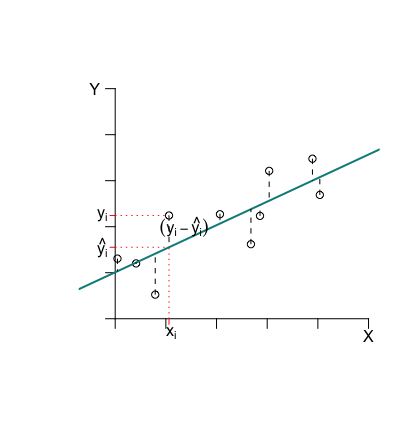
Llamemos: \[ L(b_{0},b_{1})=\sum\limits _{i=1}^{n}{(y_{i}-b_{0}-b_{1}x_{i})^{2}} \]
Para obtener los valores de \(b_{0}\) y \(b_{1}\) que minimizan esta expresión derivamos con respecto a \(b_{0}\) y a \(b_{1}\) e igualamos a 0, obteniendo las llamadas ecuaciones normales de mínimos cuadrados:
\[ \begin{array}{ccccc} {\frac{{\partial L(b_{0},b_{1})}}{{\partial b_{0}}}} & = & {-2\sum\limits _{i=1}^{n}{(y_{i}-b_{0}-b_{1}x_{i})}} & = & 0\\ {\frac{{\partial L(b_{0},b_{1})}}{{\partial b_{1}}}} & = & {-2\sum\limits _{i=1}^{n}{(y_{i}-b_{0}-b_{1}x_{i})x_{i}}} & = & 0 \end{array} \]
De la primera ecuación se tiene:
\[ \begin{array}{l} -2\sum\limits _{i=1}^{n}{(y_{i}-b_{0}-b_{1}x_{i})}=0\Rightarrow\sum\limits _{i=1}^{n}{(y_{i}-b_{0}-b_{1}x_{i})}=0\Rightarrow\sum\limits _{i=1}^{n}y_{i}-\sum\limits _{i=1}^{n}b_{0}-\sum\limits _{i=1}^{n}{b_{1}x_{i}}=0\\ \Rightarrow\sum\limits _{i=1}^{n}{y_{i}}-nb_{0}-b_{1}\sum\limits _{i=1}^{n}{x_{i}}=0\Rightarrow b_{0}=\frac{{\sum\limits _{i=1}^{n}{y_{i}}}}{n}-b_{1}\frac{{\sum\limits _{i=1}^{n}{x_{i}}}}{n}\Rightarrow b_{0}=\bar{y}-b_{1}\bar{x} \end{array} \]
Sustituyendo en la segunda ecuación: \[ \begin{eqnarray*} -2\sum\limits _{i=1}^{n}{(y_{i}-b_{0}-b_{1}x_{i})}x_{i} & = & 0\Rightarrow\sum\limits _{i=1}^{n}{(y_{i}-\left(\bar{y}-b_{1}\bar{x}\right)-b_{1}x_{i})}x_{i}=0\Rightarrow \end{eqnarray*} \]
\[ \sum\limits _{i=1}^{n}\left(y_{i}-\overline{y}\right)x_{i}-b_{1}\sum\limits _{i=1}^{n}\left(x_{i}-\overline{x}\right)x_{i}=0\Rightarrow b_{1}=\frac{\sum\limits _{i=1}^{n}\left(y_{i}-\overline{y}\right)x_{i}}{\sum\limits _{i=1}^{n}\left(x_{i}-\overline{x}\right)x_{i}}=\frac{\sum\limits _{i=1}^{n}y_{i}x_{i}-\overline{y}\sum\limits _{i=1}^{n}x_{i}}{\sum\limits _{i=1}^{n}x_{i}^{2}-\overline{x}\sum\limits _{i=1}^{n}x_{i}} \]
Si tenemos en cuenta que: \[ \bar{x}=\frac{{\sum\limits _{i=1}^{n}{x_{i}}}}{n}\Rightarrow\sum\limits _{i=1}^{n}{x_{i}}=n\bar{x} \]
podemos sustituir en la expresión anterior y nos queda:
\[ b_{1}=\frac{{\sum\limits _{i=1}^{n}{x_{i}y_{i}}-n\bar{x}\bar{y}}}{{\sum\limits _{i=1}^{n}{x_{i}^{2}}-n\bar{x}^{2}}} \]
Una vez obtenido el valor de \(b_{1}\), el valor de \(b_{0}\) se despeja de:
\[ b_{0}=\bar{y}-b_{1}\bar{x} \]
En Jamovi es muy sencillo obtener la recta de regresión para las variables peso y longitud. Para ello, en la pestaña Analyses seleccionamos el menú Regression, luego Linear Regression y seleccionamos el peso como variable dependiente, y long como variable independiente:
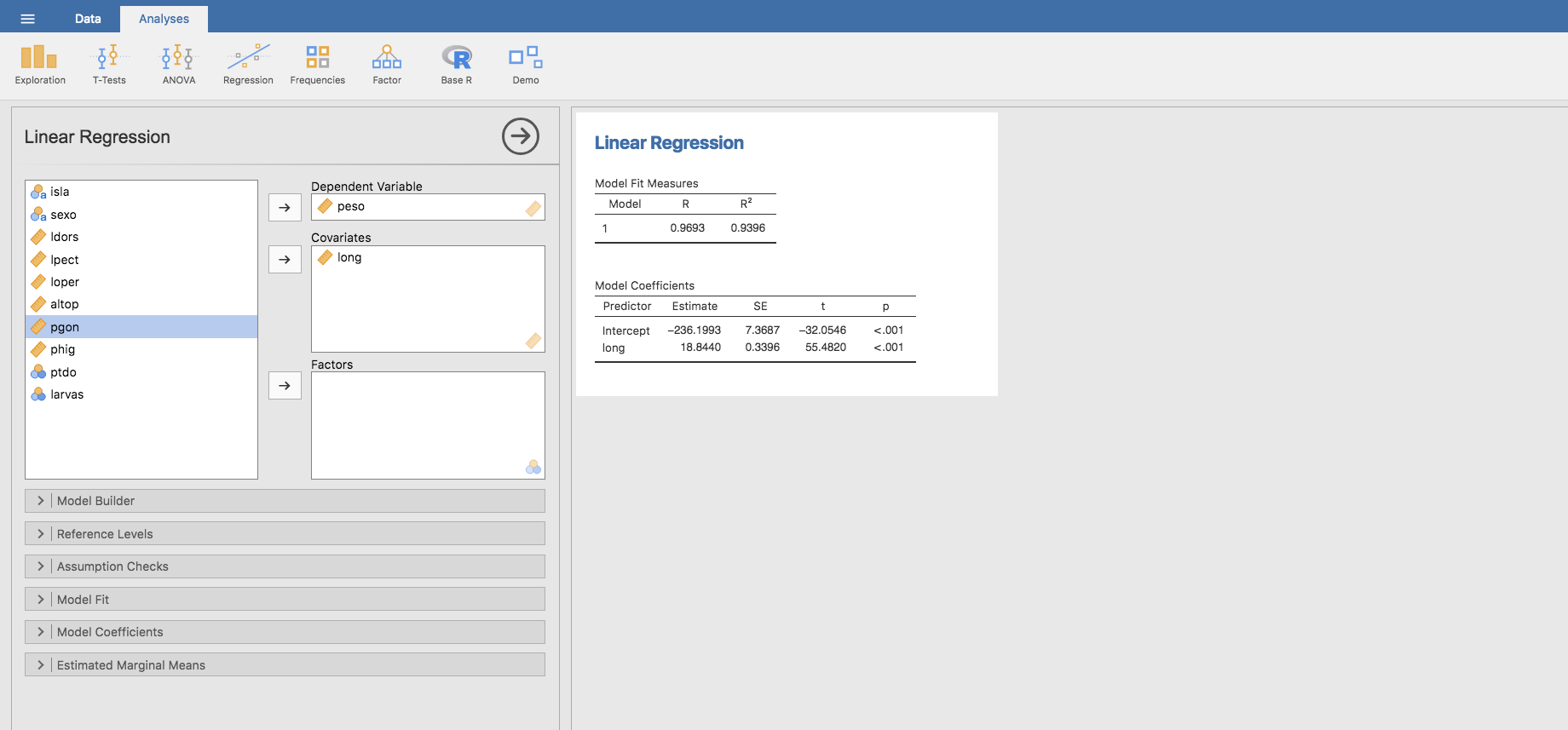
El valor indicado como intercept (-236.1993) es la ordenada en el origen \(b_{0}\), mientras que el valor bajo el nombre de la variable (18.8440) es la pendiente \(b_{1}\). Para representar esta recta gráficamente podemos utilizar la barra Estimated Marginal Means, seleccionamos la variable long y la ubicamos en la ventana titulada Marginal Means, para finalmente seleccionar Marginal means plots en el apartado Outputs.
Con Jamovi es posible dibujar en un mismo gráfico nubes de puntos correspondientes a distintos grupos de datos, mostrando el ajuste de regresión para cada uno. Por ejemplo, para el caso de las variables long y ldors, vamos a representar la nube de puntos y la recta de regresión pero dibujando de color distinto machos y hembras, y ajustando una recta de regresión a cada grupo. Para poder hacerlo necesitamos instalar en Jamovi el módulo denominado scatr (pulsar en la esquina superior derecha Modules, luego Jamovi library e instalar scatr si fuera necesario). Una vez lo tenemos instalado: en el menú Exploration seleccionamos Scatterplot y ubicamos long en el eje X, ldors en el eje Y y la variable sexo en Group, para obtener la siguiente gráfica:
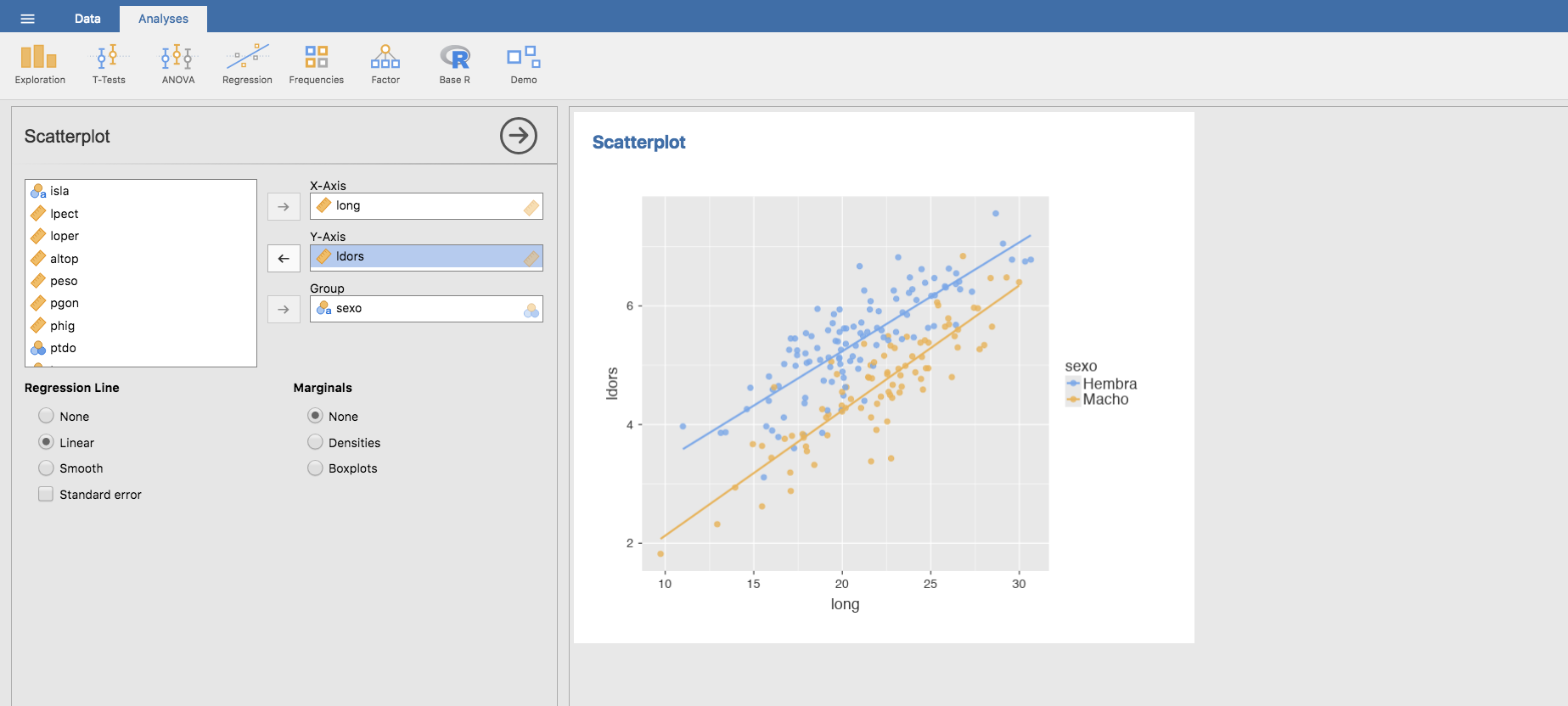
que nos proporciona las rectas de regresión para la distancia desde el morro a la aleta dorsal frente a la longitud total del pez, ajustadas para cada sexo.
Si queremos obtener los valores numéricos de las ecuaciones de ambas rectas (para hembras y machos) podemos proceder como sigue: En la pestaña Data seleccionamos el menú Filters, y filtramos los datos escribiendo en Filter 1 sexo==‘Hembra’. Así, lo que se consigue es que nuestra base de datos inicial quede activada solo para los datos en los que el sexo es Hembra, desactivándose todos los que son machos:
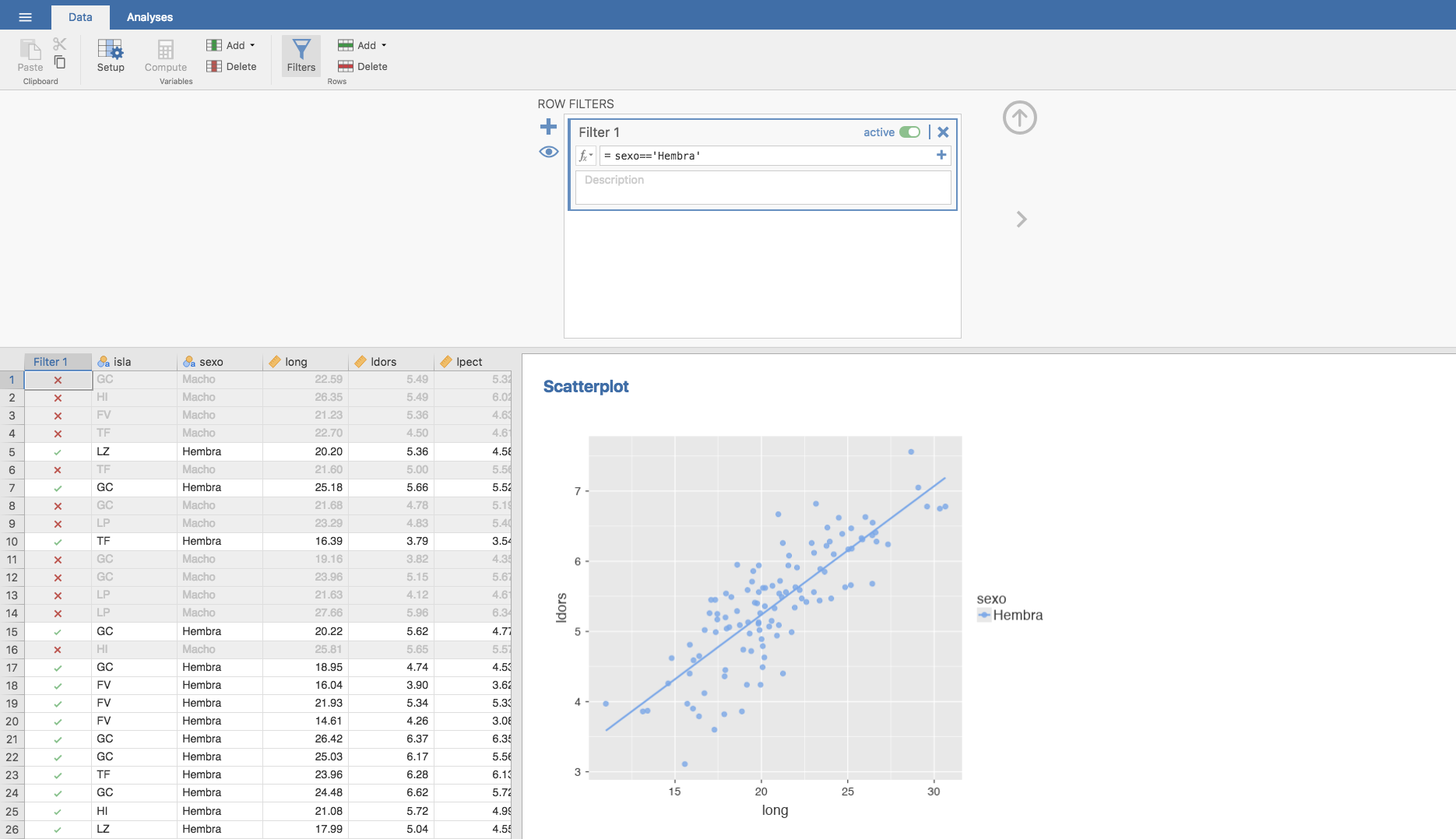
Una vez filtrados los datos regresamos a la pestaña Analyses, en el menú Regression seleccionamos Linear Regression, y volvemos a situar las variables según corresponda, obteniéndose:
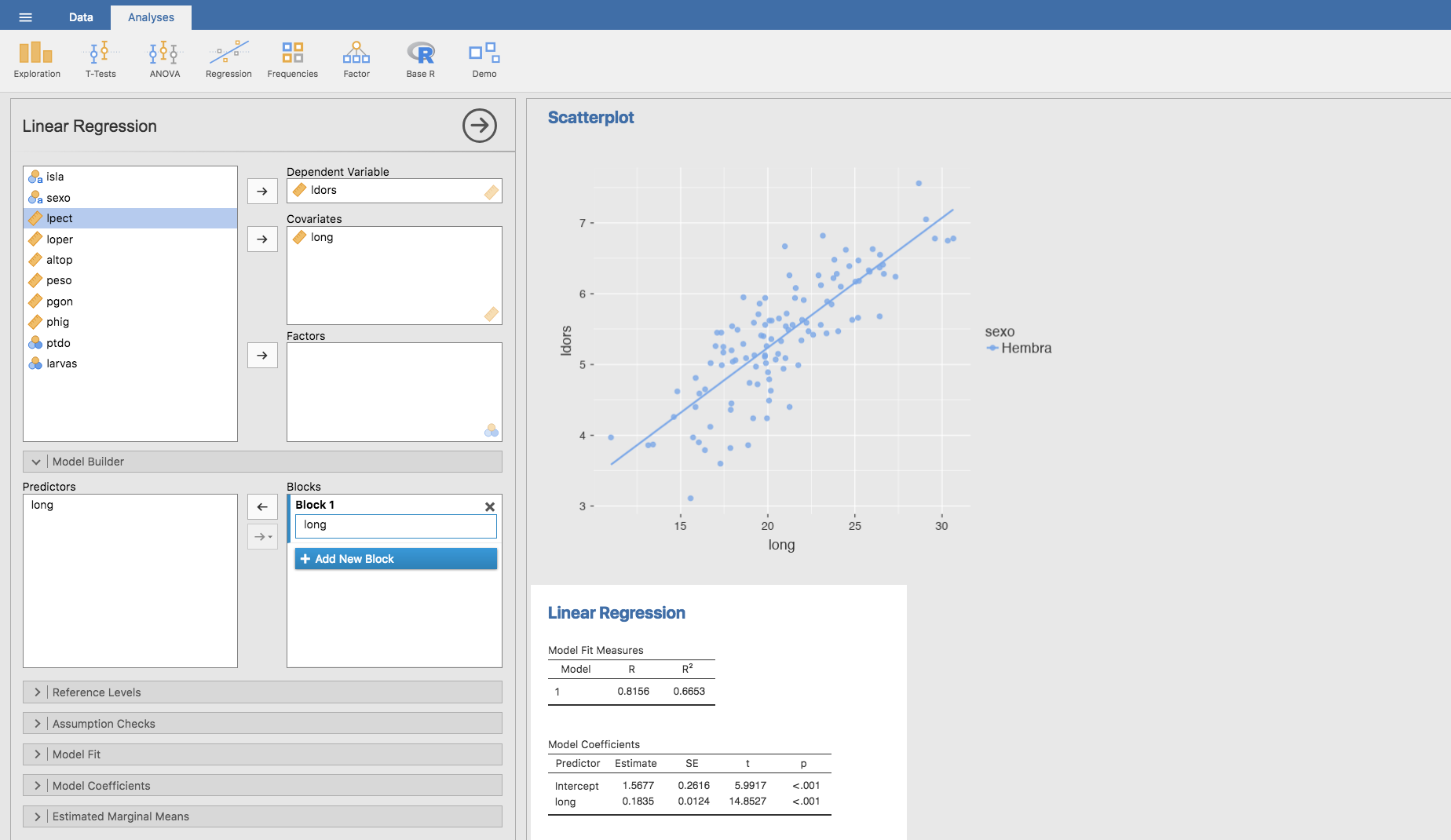
que nos proporciona los coeficientes de la recta de regresión para las hembras: \(b_0 = 1.5677\) y \(b_1 = 0.1835\). Análogamente se obtienen los coeficientes de la recta de regresión para los machos, filtrando los datos:
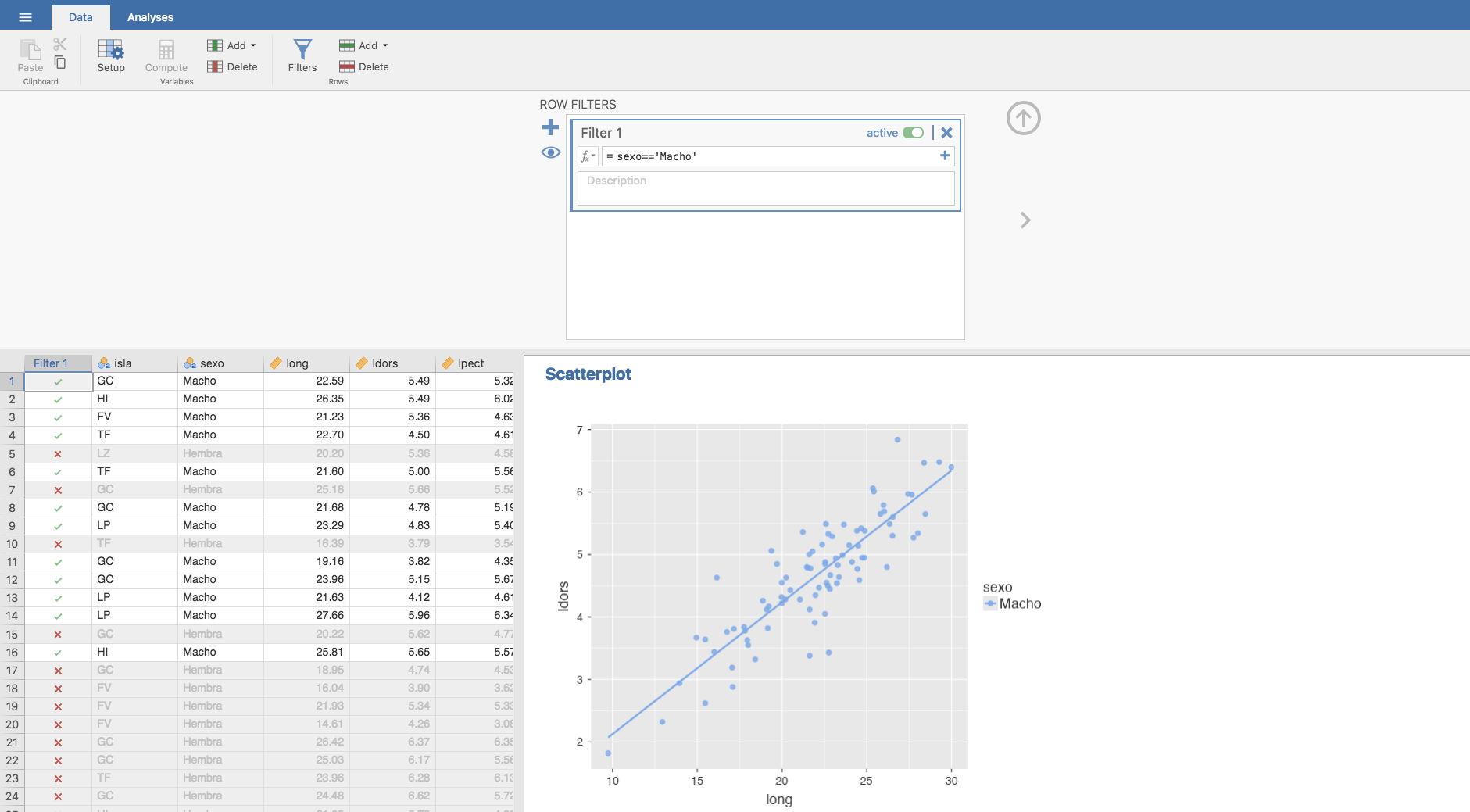
y procediendo igual que en el caso de las hembras:
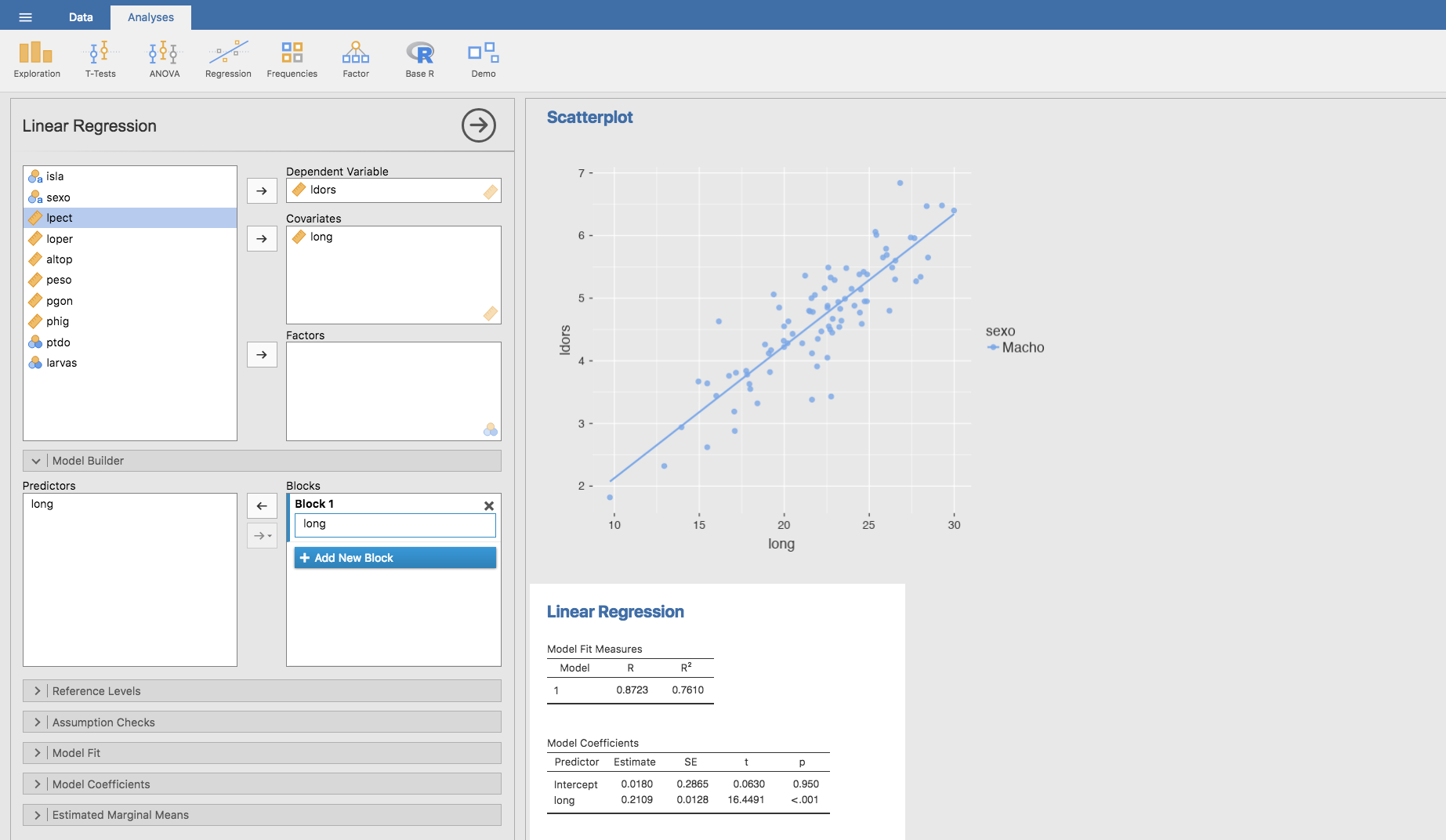
En este caso, los coeficientes de la recta de regresión para las machos es: \(b_0 = 0.0180\) y \(b_1 = 0.2109\).
Covarianza y correlación
La siguiente figura nos muestra dos nubes de puntos. Se aprecia claramente que los datos de la nube (a) muestran una asociación lineal muy fuerte, mientras que en la nube (b) esta asociación es más débil.
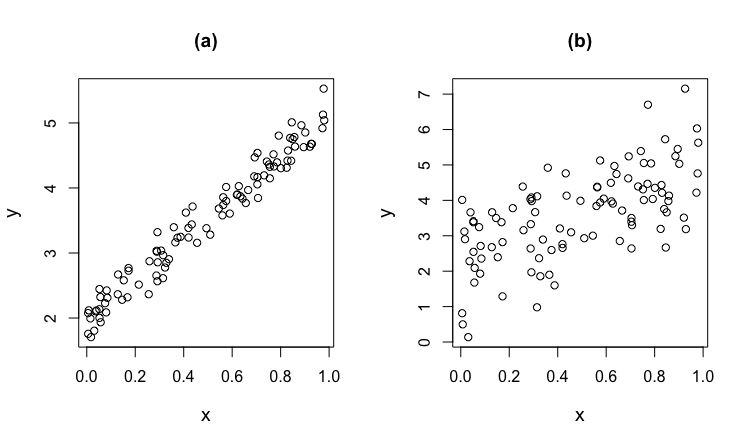
Para medir numéricamente la intensidad de la asociación lineal entre dos variables se utiliza la covarianza, definida como: \[ S_{XY}=\frac{1}{{n-1}}\sum\limits _{i=1}^{n}{(x_{i}-\bar{x})(y_{i}-\bar{y})}=\frac{1}{{n-1}}\left({\sum\limits _{i=1}^{n}{x_{i}y_{i}}-n\cdot\bar{x}\,\bar{y}}\right) \]
Esta medida es positiva si los datos presentan tendencia lineal creciente; es negativa si presentan tendencia lineal decreciente; y es nula si los datos no presentan tendencia lineal.
Nota: La ausencia de tendencia lineal no significa que no exista algún otro tipo de asociación (no lineal) entre \(X\) e \(Y.\)
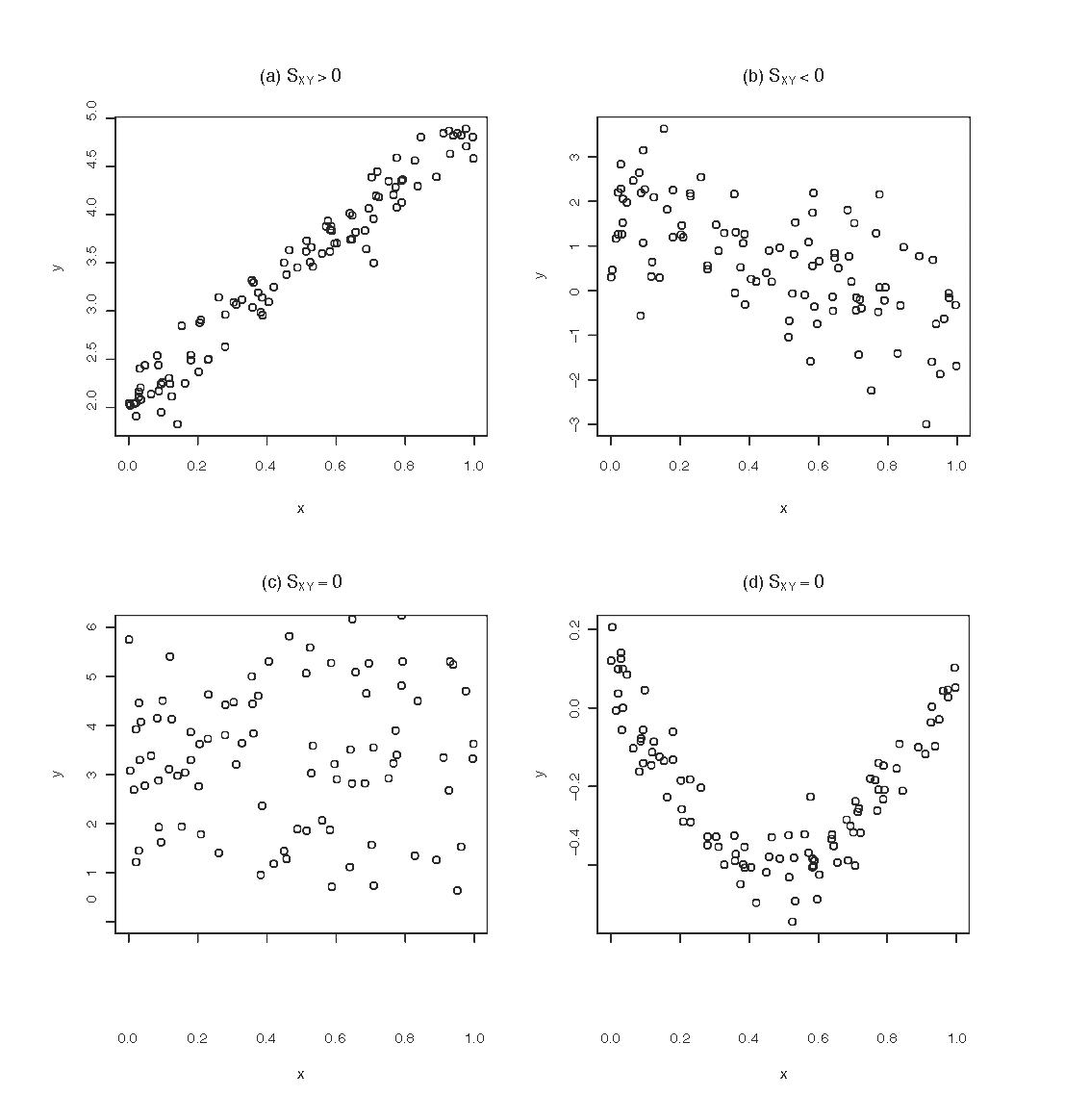
La figura siguiente muestra cuatro nubes de puntos con distinta covarianza. La figuras (a) y (b) presentan asociación lineal, el caso (a) con pendiente positiva, y por tanto con covarianza positiva, y el caso (b) con pendiente (y por tanto covarianza) negativa. A su vez las figuras (c) y (d) presentan covarianza nula; en el caso (c) porque no existe asociación entre \(X\) e \(Y\), y en el caso (d) porque, aún existiendo asociación, esta es claramente no lineal.
La covarianza, como medida de la asociación lineal entre variables presenta un problema práctico: depende de las unidades de \(X\) e \(Y\), y por tanto su magnitud, en términos absolutos, sea grande o pequeña puede depender más de las escalas de medida que de la fuerza de la asociación lineal entre ambas variables (por ejemplo, si \(X\) e \(Y\) son longitudes, el valor de la covarianza entre ambas será un número mucho mayor si \(X\) e \(Y\) se miden en centímetros que si se miden en metros). Por tanto es preciso introducir una nueva medida de asociación lineal que no dependa de las unidades de \(X\) e \(Y\). Esta medida es el coeficiente de correlación de Pearson, definido como:
\[ r=\frac{{S_{XY}}}{{S_{X}S_{Y}}} \]
siendo \(S_{X}\) y \(S_{Y}\) las desviaciones típicas respectivas de las variables \(X\) e \(Y\). Como éstas son siempre positivas, es obvio que el signo de \(r\) coincide con el signo de \(S_{XY}\). Además, se cumple que: \[ -1\le r\le1 \] siendo el valor absoluto de \(r\) igual a \(1\) cuando los puntos están exactamente sobre una recta. La siguiente figura muestra cuatro nubes de puntos con distintos valores de correlación lineal.
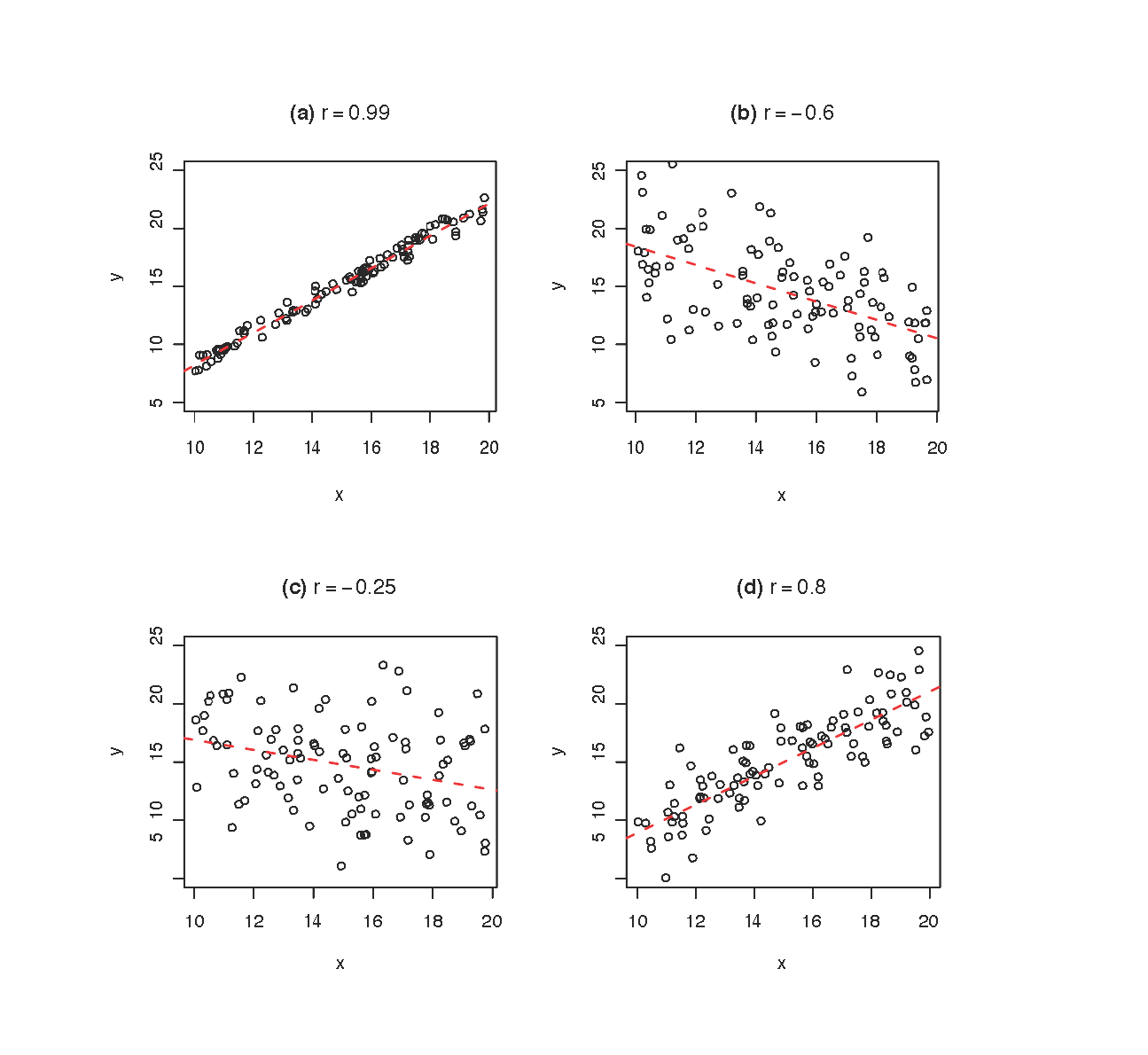
Así pues:
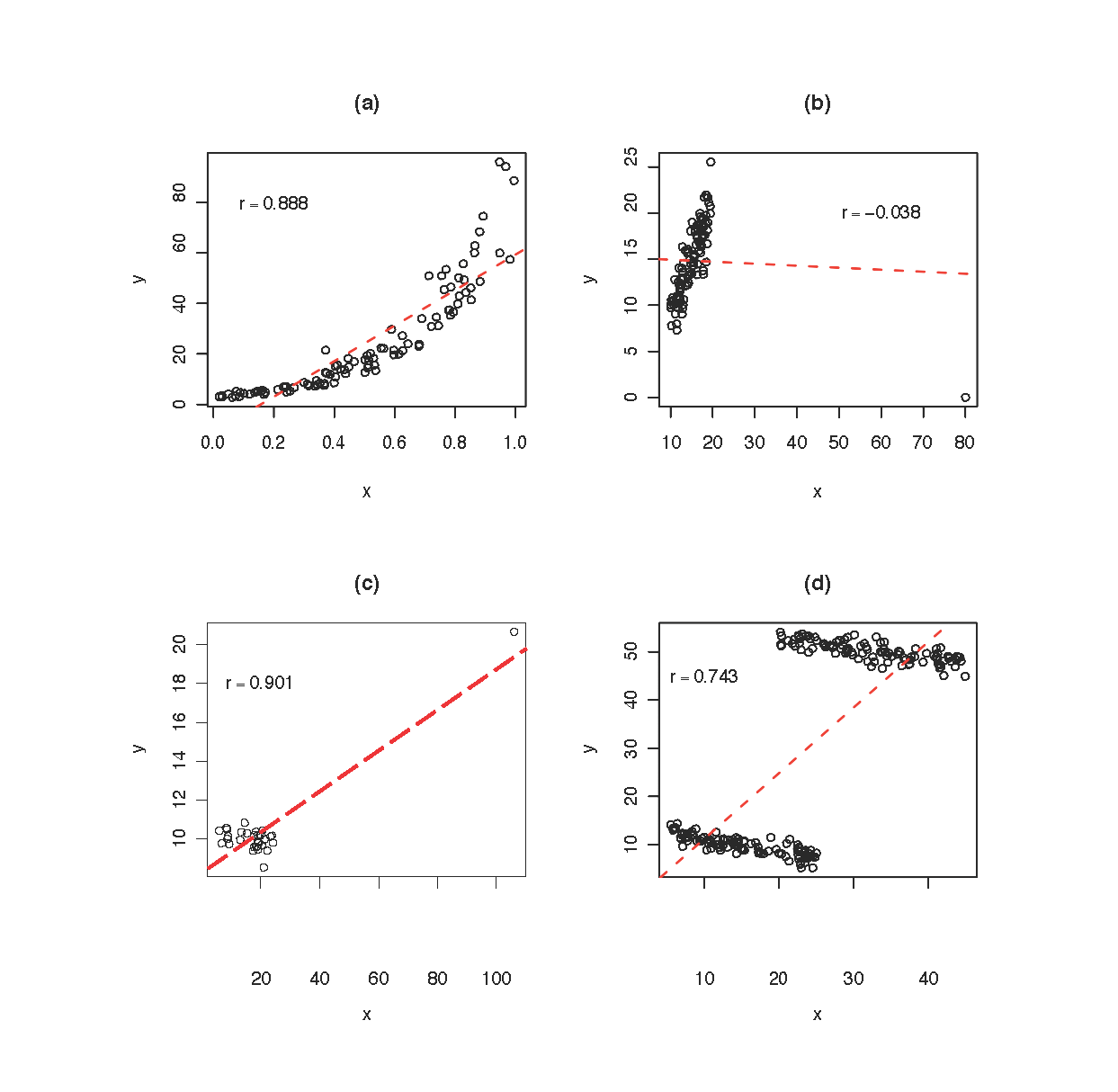
Para determinar si el coeficiente de correlación es una medida adecuada de la asociación entre variables, el primer paso debe ser siempre dibujar un gráfico de la nube de puntos correspondiente a las observaciones.En los siguientes casos no es apropiado utilizar el coeficiente de correlación:
En Jamovi la correlación se calcula en la pestaña Analyses, menú Regression/Linear Regression, eligiendo las variables (por ejemplo, long como variable explicativa y ldors como variable respuesta), y en la barra Model Fit marcamos R en el apartado Fit Measures:
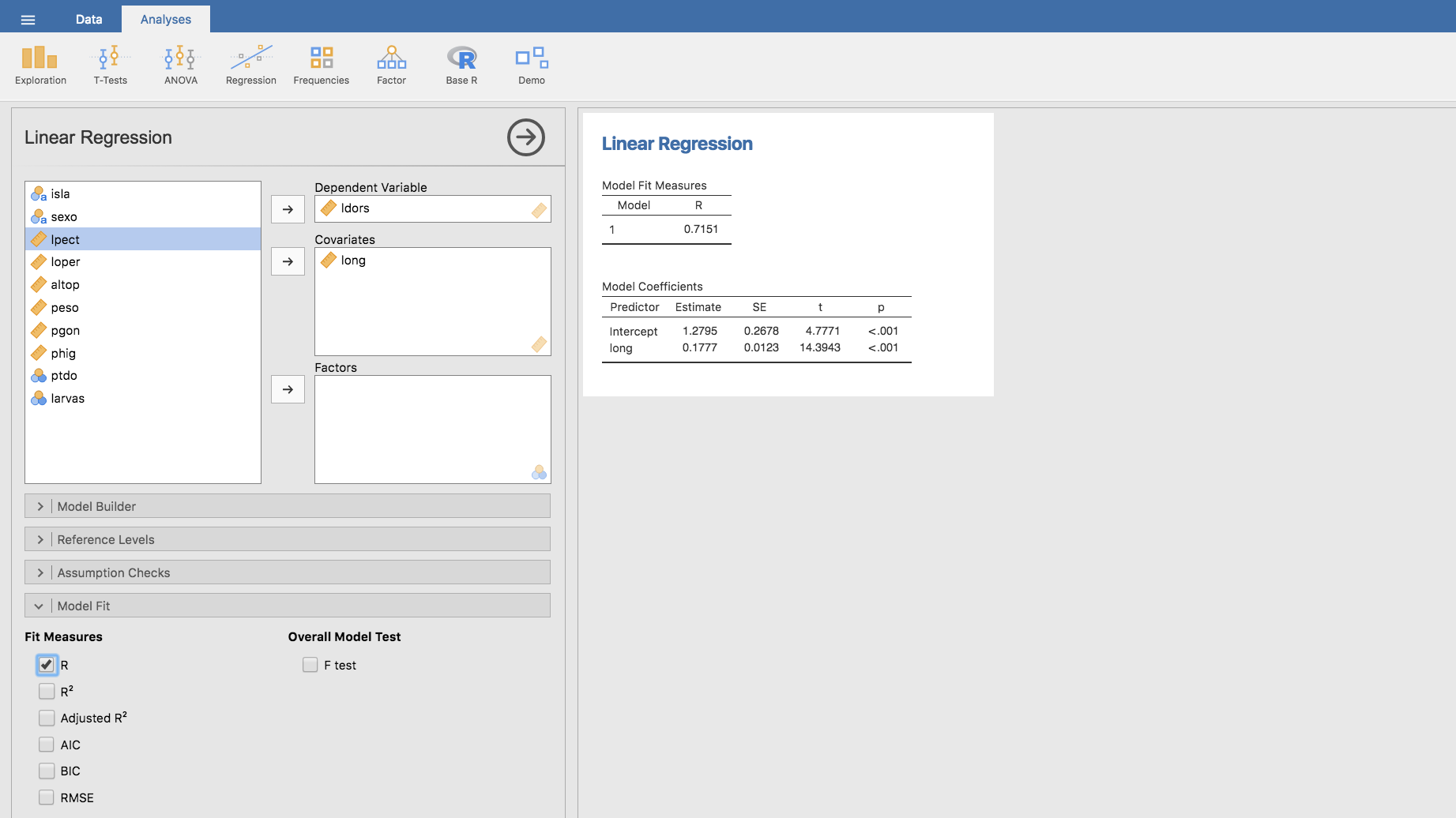
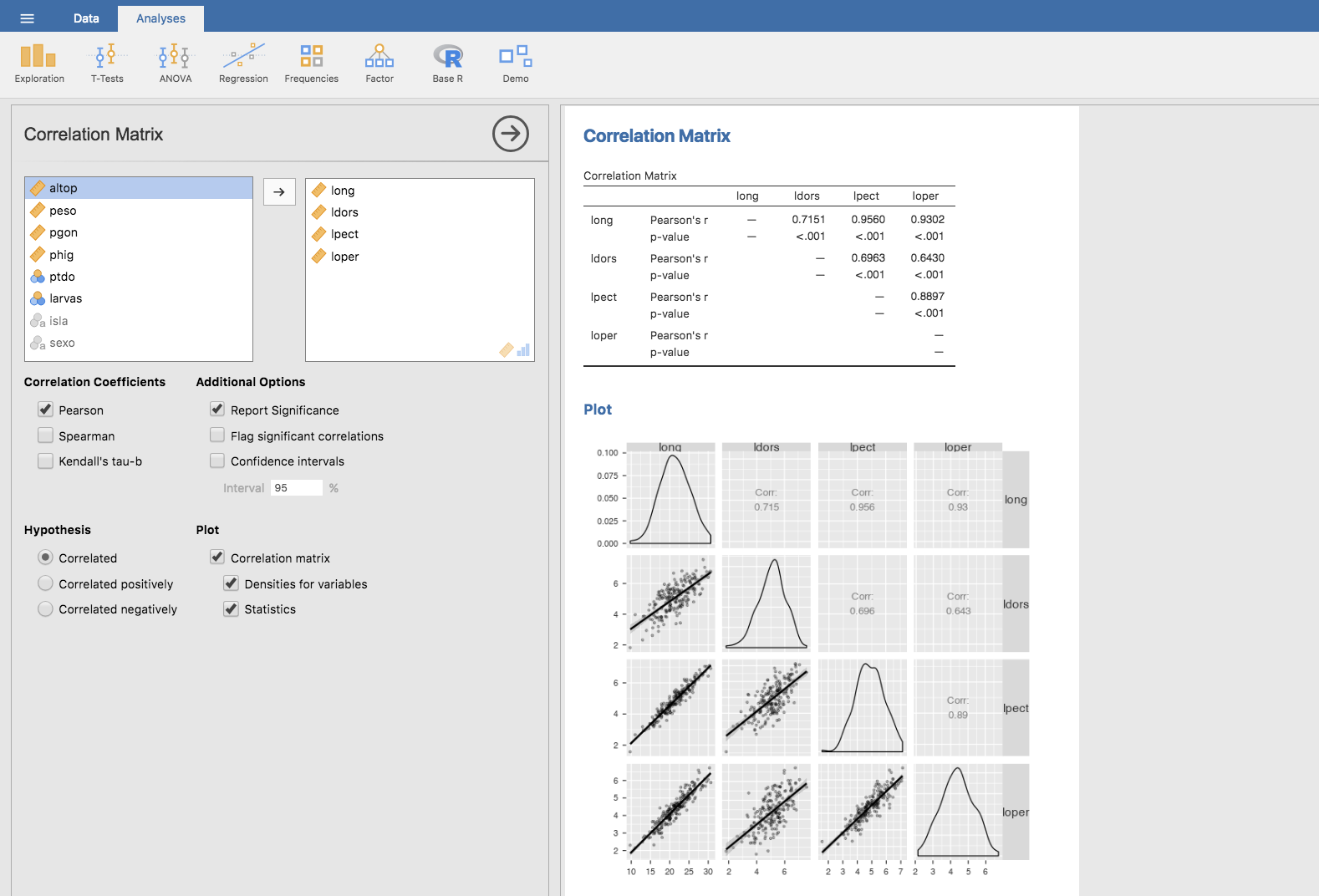
En este ejemplo obtenemos que el coeficiente de correlación de Pearson es 0.7151.
Finalmente, la correlación puede aplicarse a más de dos variables, en cuyo caso se obtienen las correspondientes matrices de correlaciones. Para ello, utilizamos Analyses/Regression/Correlation Matrix, elegimos las variables que queremos cruzar para analizar su correlación y, en el apartado Plot, marcamos Correlation matrix, Density for variables y Statistics. Así conseguimos que Jamovi genere una matriz con los valores de los coeficientes de Pearson para cada par de variables, y con las representación gráfica de sus correspondientes nubes de puntos y gráficos de densidad.