Metodología Estadística: Probabilidad y Medidas de Asociación y Riesgo
Angelo Santana
Bioestadística. Master SASA. Curso 2023-24
PROBABILIDAD
Probabilidad: Medida de la incertidumbre asociada a la ocurrencia de determinado suceso o evento.
En términos matemáticos una probabilidad es una función \(P\) que satisface:
- La probabilidad del suceso seguro es 1.
- Si dos sucesos A y B son incompatibles (no pueden ocurrir simultáneamente) entonces: \[P\left(A \cup B \right) =P\left(A\right)+P\left(B\right)\]
PROBABILIDAD CONDICIONADA E INDEPENDENCIA DE SUCESOS
Para un suceso \(A\) tal que \(Pr\left( A \right) > 0\), la probabilidad de otro suceso \(B\) condicionada por \(A\) se define por:
\[Pr\left(\textrm{B}\left|\textrm{A}\right.\right)=\frac{Pr\left(\textrm{A}\cap\textrm{B}\right)}{Pr\left(\textrm{A}\right)}\]
Dos sucesos \(A\) y \(B\) se dicen independientes si:
\[Pr\left(\textrm{B}\left|A\right.\right)=Pr\left(B\right)\] En caso contrario, ambos sucesos están asociados.
PROBABILIDAD: Ejemplo
| HTA_OMS |
|
|
|
| Sí |
324 (31.46) |
83 (64.84) |
241 (26.72) |
| No |
706 (68.54) |
45 (35.16) |
661 (73.28) |
De esta tabla deducimos:
\[ Pr\left(DM\right)=\frac{128}{1030}=0.124 \;\;\;\;\;\;\; Pr\left(HTA\right)=\frac{324}{1030}=0.314 \]
\[Pr\left(\textrm{DM}\left|\textrm{HTA}\right.\right)=\frac{N\left(\mathrm{DM}\cap\mathrm{HTA}\right)}{N\left(\mathrm{HTA}\right)}=\frac{83}{83+241}=\frac{83}{324}=0.256\]
\[Pr\left(\textrm{HTA}\left|\textrm{DM}\right.\right)=\frac{N\left(\mathrm{DM}\cap\mathrm{HTA}\right)}{N\left(\mathrm{DM}\right)}=\frac{83}{83+45}=\frac{83}{128}=0.648\]
Teorema de la probabilidad total
Sea \(A_{1},A_{2},\ldots,A_{n}\) un sistema completo de sucesos y sea B un suceso arbitrario. Entonces:
\[P(B)=\sum\limits _{i=1}^{n}{P\left(B\left|A_{i}\right.\right)P\left({A_{i}}\right)}\]
- Aplicación: A partir de un estudio sobre la epilepsia idiopática en diversas razas caninas, se estima que la prevalencia de esta enfermedad en Golden Retrievers es del 6%; en caniches es del 8%, en cockers es del 9% y en el resto de razas es del 2%. En una región en la que el censo canino comprende un 10% de caniches, un 5% de golden retrievers, un 12% de cockers y el resto corresponde a otras razas, ¿cuál es la prevalencia estimada de epilepsia idiopática?
En este caso la prevalencia de la enfermedad en cada raza es:
\[P\left(Epi\left|Golden\,R\right.\right)=0.06 \;\;\;\;\; P\left(Epi\left|Caniche\right.\right)=0.08\]
\[P\left(Epi\left|Cocker\right.\right)=0.09 \;\;\;\;\; P\left(Epi\left|Otro\right.\right)=0.02\]
La proporción que representa cada raza dentro del total de perros es:
\[P\left(Golder\,R\right)=0.05 \;\;\;\;\; P\left(Caniche\right)=0.10\]
\[P\left(Cocker\right)=0.12 \;\;\;\;\; P\left(Otra\,raza\right)=0.73\]
Para resolver el problema anterior aplicamos el teorema de la probabilidad total (siendo \(P\left(R_i\right)\) la proporción de cada raza):
\[Pr\left(Epi\right)=\sum\limits _{i=1}^{n}{P\left(Epi\left|R_{i}\right.\right)P\left({R_{i}}\right)}=\]
\[ = 0.06\cdot 0.05 +0.08 \cdot 0.10 + 0.09 \cdot 0.12 + 0.02\cdot 0.73= 0.0364\]
Por tanto la prevalencia de esta enfermedad en la región es del 3.64%
Teorema de Bayes
En las condiciones del Teorema de la Probabilidad Total, el Teorema de Bayes permite calcular la probabilidad de un suceso \(A_j\) una vez que se ha observado que ha ocurrido un suceso \(B\) (lo que se conoce como probabilidad a posteriori de \(A_j\)):
\[P\left(A_{j}\left|B\right.\right)=\frac{P\left(B\left|A_{j}\right.\right)P\left(A_j\right)}{\sum\limits _{i=1}^{n}{P\left(B\left|A_{i}\right.\right)P\left({A_{i}}\right)}}\]
En el ejemplo anterior, de entre todos los perros con epilepsia idiopática, ¿Cuál es la proporción de Cockers?
\[P\left(Cocker\left|Epi\right.\right)=\frac{P\left(Epi\left|Cocker\right.\right)P\left(Cocker\right)}{\sum\limits _{i=1}^{n}{P\left(Epi\left|R_{i}\right.\right)P\left({R_{i}}\right)}}=\frac{0.09\cdot0.12}{0.0364}=0.2967\]
Por tanto, aunque los Cockers suponen un 12% de la población de perros de la región, son casi un 30% de los perros epilépticos.
Asociación entre eventos: Riesgo Relativo (RR)
La asociación entre dos sucesos puede medirse mediante el riesgo relativo, definido como:
\[RR=\frac{P\left(B\left|A\right.\right)}{P\left(B\left|A^{c}\right.\right)}\]
(\(A^c\) es el suceso contrario de \(A\))
Nótese que:
RR = 1 : No hay asociación
RR > 1 : La ocurrencia de A incrementa la probabilidad de B. (riesgo)
RR < 1 : La ocurrencia de A disminuye la probabilidad de B. (protección)
Asociación entre eventos: Riesgo Relativo (RR)
Ejemplo
¿Cuál es el riesgo relativo de Epilepsia en los Cocker frente a los que no son Cocker?
\[RR=\frac{P\left(Epi\left|Cocker\right.\right)}{P\left(Epi\left|Cocker^{C}\right.\right)}=\frac{0.09}{0.0291}=3.09\]
donde:
- \(P\left(Epi\left|Cocker\right.\right)=0.09\)
- \(P\left(Epi\left|Cocker^{C}\right.\right)=\frac{P\left(Cocker^{C}\left|Epi\right.\right)P\left(Epi\right)}{P\left(Cocker^{C}\right)}=\frac{\left(1-P\left(Cocker\left|Epi\right.\right)\right)P\left(Epi\right)}{1-P\left(Cocker\right)}=\) \[=\frac{\left(1-0.2967\right)\cdot0.0364}{1-0.12}=0.0291\]
Asociación entre eventos: Riesgo Relativo (RR)
El RR como medida de asociación no es una medida simétrica: no es lo mismo el riesgo relativo de B según la presencia/ausencia de A que el riesgo relativo de A según la presencia/ausencia de B.
Veamos un ejemplo:
Asociación entre eventos: Riesgo Relativo (RR)
| DM |
|
|
|
| Sí |
128 (12.43) |
83 (25.62) |
45 (6.37) |
| No |
902 (87.57) |
241 (74.38) |
661 (93.63) |
A partir de estos datos queremos calcular:
El riesgo relativo de padecer DM según se tenga o no HTA.
El riesgo relativo de padecer HTA según se tenga o no DM.
Asociación entre eventos: Riesgo Relativo (RR)
| DM |
|
|
|
| Sí |
128 (12.43) |
83 (25.62) |
45 (6.37) |
| No |
902 (87.57) |
241 (74.38) |
661 (93.63) |
\[P\left(DM\left|HTA\right.\right)=0.2562 \;\;\;\;\;\;\;\;\;\;\; P\left(DM\left|{HTA}^c\right.\right)=0.0637\]
El riesgo relativo de padecer DM cuando hay HTA es entonces: \[ RR=\frac{P\left(DM\left|HTA\right.\right)}{P\left(DM\left|{HTA}^{c}\right.\right)}=\frac{0.2562}{0.0637}=4.02\]
El riesgo de DM es 4 veces más alto entre los hipertensos.
Asociación entre eventos: Riesgo Relativo (RR)
| HTA_OMS |
|
|
|
| Sí |
324 (31.46) |
83 (64.84) |
241 (26.72) |
| No |
706 (68.54) |
45 (35.16) |
661 (73.28) |
\[P\left(HTA\left|DM\right.\right)=0.6484 \;\;\;\;\;\;\;\;\;\;\; P\left(HTA\left|{DM}^c\right.\right)=0.2672\]
El riesgo relativo de padecer HTA cuando hay DM es entonces: \[ RR=\frac{P\left(HTA\left|DM\right.\right)}{P\left(HTA\left|{DM}^{c}\right.\right)}=\frac{0.6484}{0.2672}=2.43\]
El riesgo de HTA es 2.43 veces más alto entre los diabéticos.
Asociación entre eventos: Riesgo Relativo (RR)
El riesgo relativo no debe utilizarse como medida de asociación en estudios de Caso-Control.
Para entender por qué, volvamos a nuestro ejemplo del estudio de Telde.
Supongamos que en el estudio de Telde se hubiese realizado como un estudio de casos y controles, siendo los casos los sujetos con DM y los controles los sujetos sin DM. Tanto el número de casos (128) como el número de controles (902) son elegidos arbitrariamente por el investigador.
¿Qué ocurriría si el investigador hubiese decidido elegir 4000 casos en lugar de los 128 actuales?
Si la proporción de sujetos con HTA entre los DM hubiese sido la misma que la ya observada (64.84%) ello significaría que entre los 4000 diabéticos habría 2594 sujetos con HTA y 1406 sin HTA. La tabla resultante en este caso sería de la forma:
Asociación entre eventos: Riesgo Relativo (RR)
| HTA_OMS |
|
|
|
| Sí |
2835 |
2594 |
241 |
| No |
2067 |
1406 |
661 |
Entonces: \[P\left(DM\left|HTA\right.\right)=\frac{2594}{2835}=0.9150 \;\;\;\;\;\;\; P\left(DM\left|{HTA}^c\right.\right)=\frac{1406}{2067}=0.6802\]
El riesgo relativo de DM cuando hay HTA es entonces: \[ RR=\frac{P\left(DM\left|HTA\right.\right)}{P\left(DM\left|{HTA}^{c}\right.\right)}=\frac{0.9150}{0.6802}=1.34\]
Así pues, el riesgo se ha reducido casi a la mitad, ¡solo por haber aumentado el tamaño de la muestra de casos!
Asociación entre eventos: Odds-Ratio (OR)
Definición de odd (ventaja): mide cuanto más probable es la ocurrencia de un suceso B frente a la no ocurrencia del mismo suceso: \[odd(B)=\frac{P\left(B\right)}{P\left(B^C\right)}\]
Definición de odds-ratio: evalúa el cociente de las odds (ventajas) de \(B\) según que ocurra o no un segundo suceso \(A\): \[OR=\frac{odd(B\left|A\right.)}{odd(B\left|A^C\right.)}=\frac{P\left(B\left|A\right.\right)\left/P\left(B^{C}\left|A\right.\right)\right.}{P\left(B\left|A^{C}\right.\right)\left/P\left(B^{C}\left|A^{C}\right.\right)\right.}=\frac{P\left(B\left|A\right.\right)\cdot P\left(B^{C}\left|A^{C}\right.\right)}{P\left(B^{C}\left|A\right.\right)\cdot P\left(B\left|A^{C}\right.\right)}\]
Una OR>1 significa que \(A\) favorece la ocurrencia de \(B\) (\(A\) es factor de riesgo para \(B\))
Una OR<1 significa que \(A\) dificulta la ocurrencia de \(B\) (\(A\) es factor de protección frente a \(B\))
Una OR=1 significa que \(A\) no favorece ni dificulta la ocurrencia de \(B\) (No hay asociación entre ambos sucesos)
Asociación entre eventos: Odds-Ratio (OR)
Los datos para el cálculo de la OR se suelen presentar en una tabla como la siguiente:
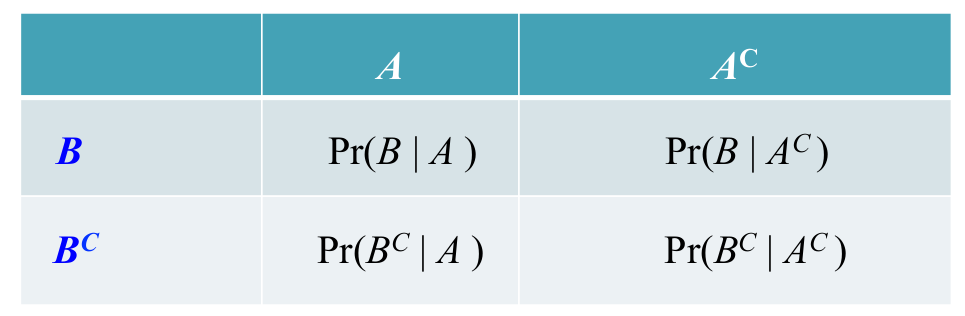
Nótese que los sucesos \(B\) y \(A\) ocupan, respectivamente, la primera fila y la primera columna de esta tabla
La odds-ratio se calcula entonces como el producto de la diagonal principal dividido entre el producto de la diagonal inversa:
\[OR=\frac{P\left(B\left|A\right.\right)\cdot P\left(B^{C}\left|A^{C}\right.\right)}{P\left(B^{C}\left|A\right.\right)\cdot P\left(B\left|A^{C}\right.\right)}\]
Asociación entre eventos: Odds-Ratio (OR)
Se puede probar que la OR es una medida de asociación simétrica: \[OR=\frac{odd(B\left|A\right.)}{odd(B\left|A^{C}\right.)}=\frac{P\left(B\left|A\right.\right)\cdot P\left(B^{C}\left|A^{C}\right.\right)}{P\left(B^{C}\left|A\right.\right)\cdot P\left(B\left|A^{C}\right.\right)}=\] \[=\frac{P\left(A\left|B\right.\right)\cdot P\left(A^{C}\left|B^{C}\right.\right)}{P\left(A^{C}\left|B\right.\right)\cdot P\left(A\left|B^{C}\right.\right)}=\frac{odd(A\left|B\right.)}{odd(A\left|B^{C}\right.)}\]
La validez de este resultado se deduce del Teorema de Bayes.
Asociación entre eventos: Odds-Ratio (OR)
| HTA_OMS |
|
|
|
| Sí |
324 (31.46) |
83 (64.84) |
241 (26.72) |
| No |
706 (68.54) |
45 (35.16) |
661 (73.28) |
\[OR=\frac{P\left(HTA\left|DM\right.\right)/P\left(HTA^{c}\left|DM\right.\right)}{P\left(HTA\left|DM^{c}\right.\right)/P\left(HTA^{c}\left|DM^{c}\right.\right)}\] \[ = \frac{0.6484/0.3516}{0.2672/0.7328}=\frac{1.844}{0.3646}=5.06\]
Asociación entre eventos: Odds-Ratio (OR)
| DM |
|
|
|
| Sí |
128 (12.43) |
83 (25.62) |
45 (6.37) |
| No |
902 (87.57) |
241 (74.38) |
661 (93.63) |
\[OR=\frac{P\left(DM\left|HTA\right.\right)/P\left(DM^{c}\left|HTA\right.\right)}{P\left(DM\left|HTA^{c}\right.\right)/P\left(DM^{c}\left|HTA^{c}\right.\right)}\] \[ = \frac{0.2562/0.7438}{0.0637/0.9363}=\frac{0.3444}{0.068}=5.06\]
Asociación entre eventos: Odds-Ratio (OR)
Cálculo de la OR a partir de una tabla de frecuencias:

Odds-Ratio (OR): Ejemplo de aplicación a la diagnosis clínica
La existencia de asociación entre el resultado de una prueba y la presencia de una enfermedad es un requisito previo para que dicha prueba pueda servir como herramienta de diagnosis. La siguiente gráfica muestra la asociación entre la prueba PSA y el cáncer de próstata:
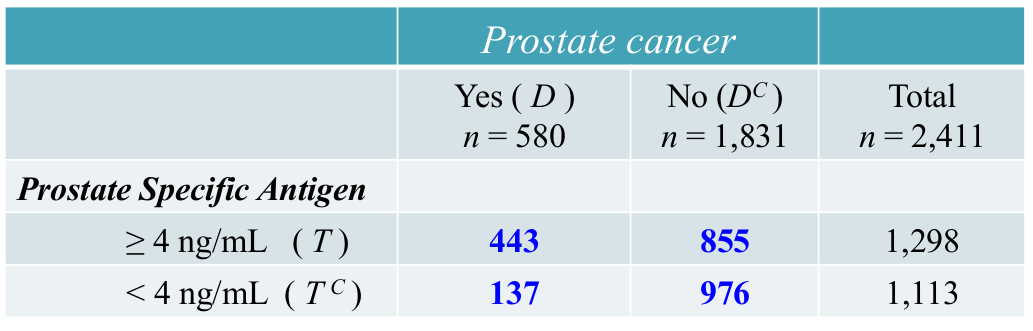
Es fácil comprobar en este caso que :
OR=3.69
Otras medidas de calidad de una prueba diagnóstica:
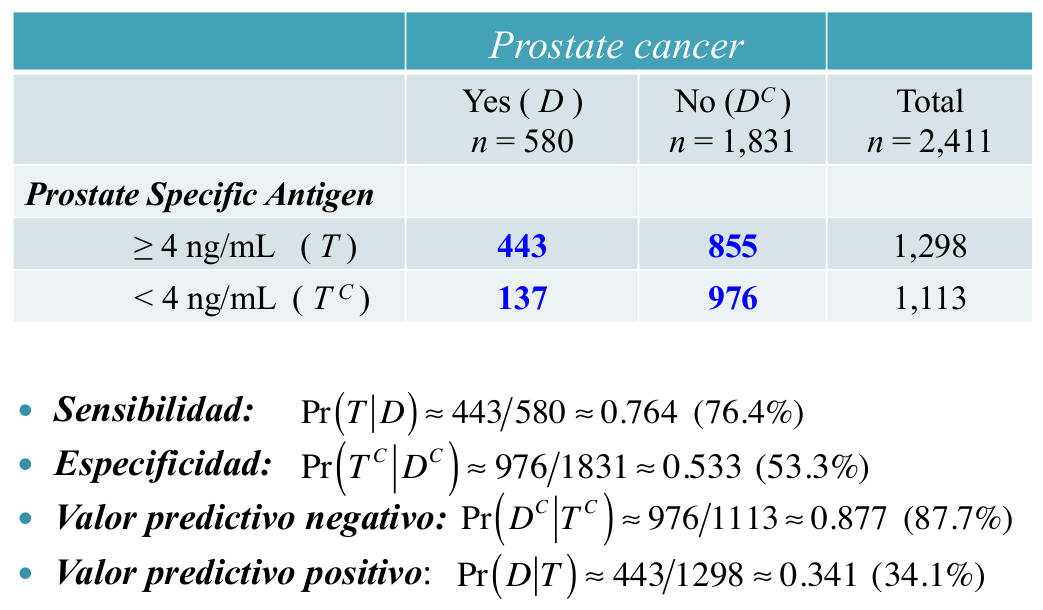
Valores Predictivos de una prueba
OJO: VPP y VPN calculados de esta manera solo son válidos si la proporción de enfermos en el estudio es igual a la prevalencia de la enfermedad en la población. Si la prevalencia en la población es \(P(D)\) y se conocen la sensibilidad \(P(T|D)\) y especificidad \(P(T^C|D^C)\), el VPN y el VPP se calculan mediante el teorema de Bayes:
\[VPP=P\left(D\left|T\right.\right)=\frac{P\left(T\left|D\right.\right)P\left(D\right)}{P\left(T\left|D\right.\right)P\left(D\right)+P\left(T\left|D^{C}\right.\right)P\left(D^{C}\right)}\]
\[VPN=P\left(D^{c}\left|T^{c}\right.\right)=\frac{P\left(T^{c}\left|D^{c}\right.\right)P\left(D^{c}\right)}{P\left(T^{c}\left|D^{c}\right.\right)P\left(D^{c}\right)+P\left(T^{c}\left|D\right.\right)P\left(D\right)}\]
Valores Predictivos de una prueba
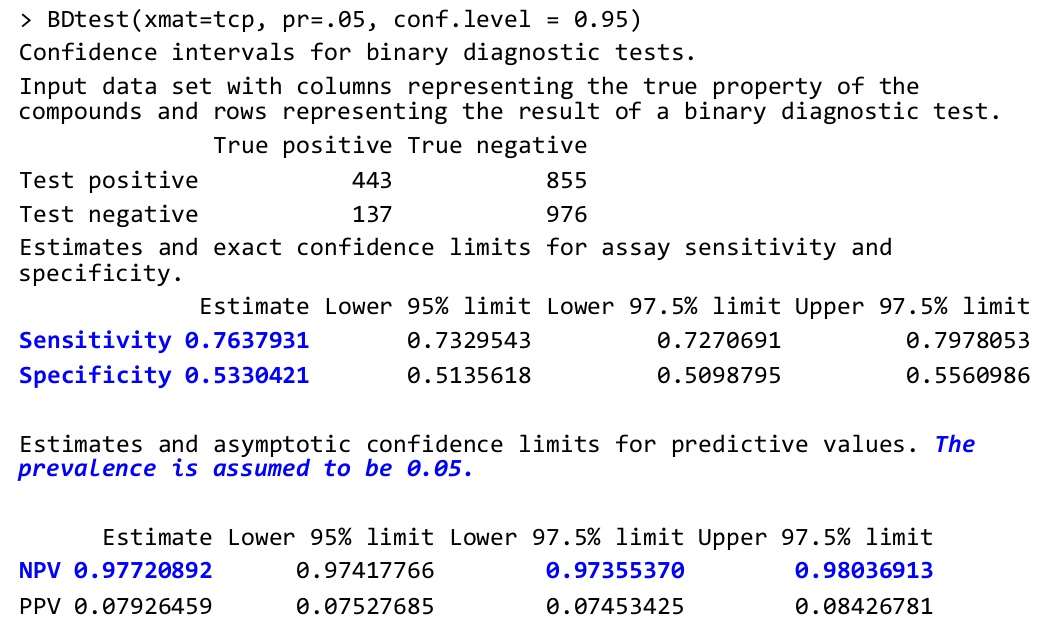
Diagnosis clínica: A1C% como predictor de DM:
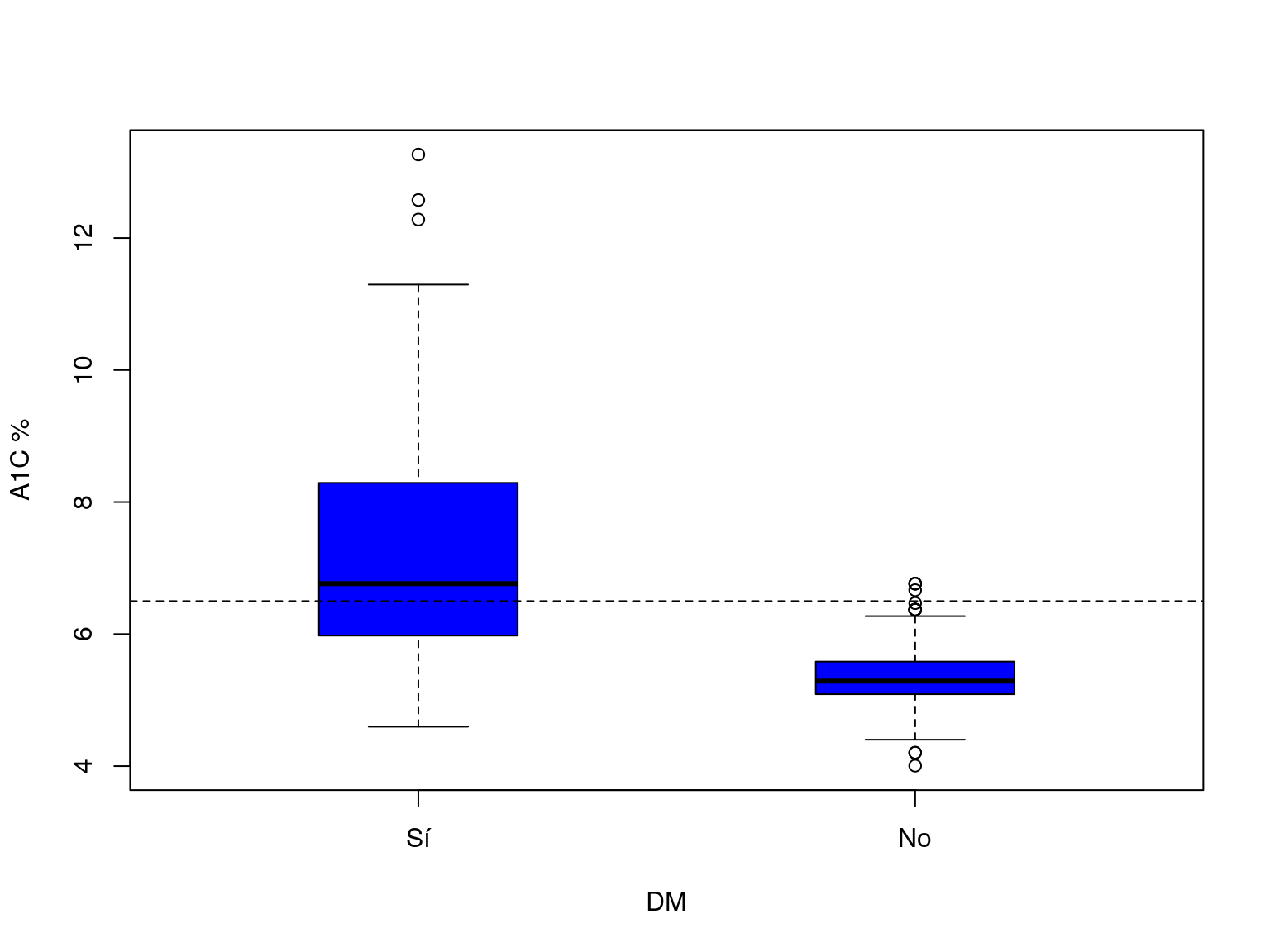
El valor de hemoglobina glicosilada A1C% se mide en escala continua. Debemos definir un valor límite o umbral de tal forma que aquellos pacientes que lo superan se diagnostican como DM, y los que no lo alcanzan como No DM. En la figura se ha elegido como umbral el valor 6.5%.
Diagnosis clínica: A1C% como predictor de DM:
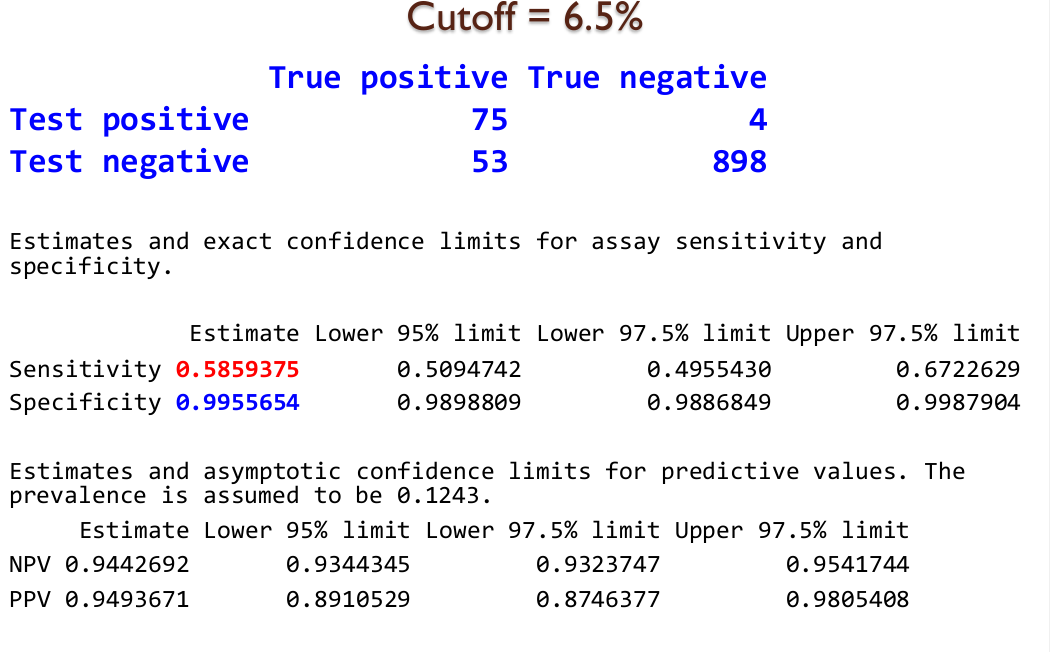
Diagnosis clínica: curvas ROC (Receiver Operating Characteristic)
Sea \(X\) un marcador para una enfermedad.
Supongamos que la enfermedad se asocia con un incremento en el valor del marcador \(X\)
En este contexto, un individuo será considerado positivo si y sólo sí \(X>C\) donde \(C\) recibe el nombre de cutoff (punto de corte)
Cada posible cutoff determina una sensibilidad (\(P\left(T\left|D\right.\right)\)) y especificidad (\(P\left(T^C\left|D^C\right.\right)\))
La curva ROC es la representación gráfica de la sensibilidad frente a la especificidad de la prueba para un conjunto continuo de posibles valores del cutoff.
Cuanto más se aproxime a 1 el área bajo la curva más fácil será encontrar un cutoff para el que se consigan simultáneamente alta sensibilidad y alta especificidad.
Diagnosis clínica: curvas ROC (Receiver Operating Characteristic)
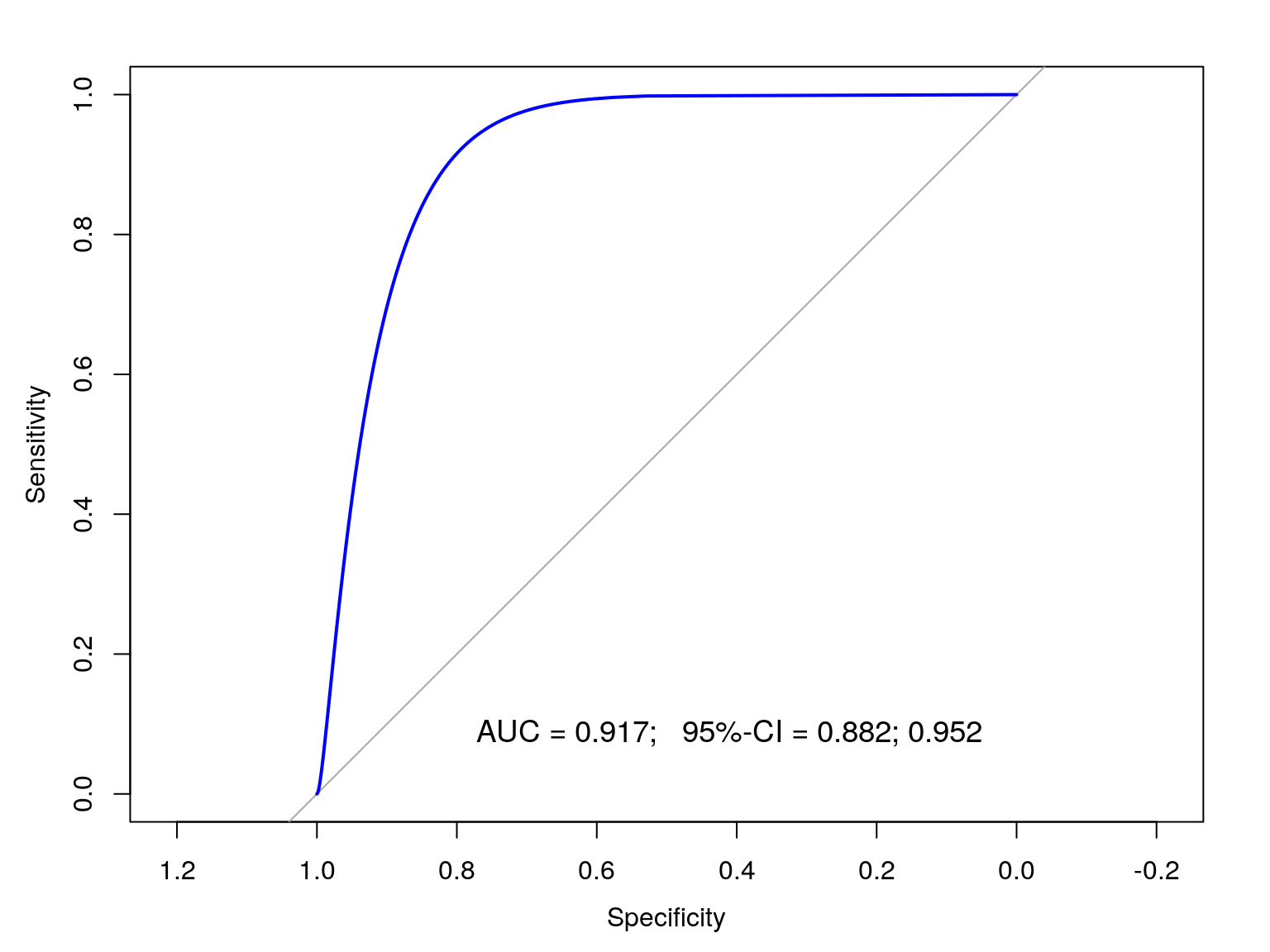
Nótese en la figura como el eje de la especificidad va en sentido decreciente, desde 1 a 0.
Asociación entre variables continuas: correlación
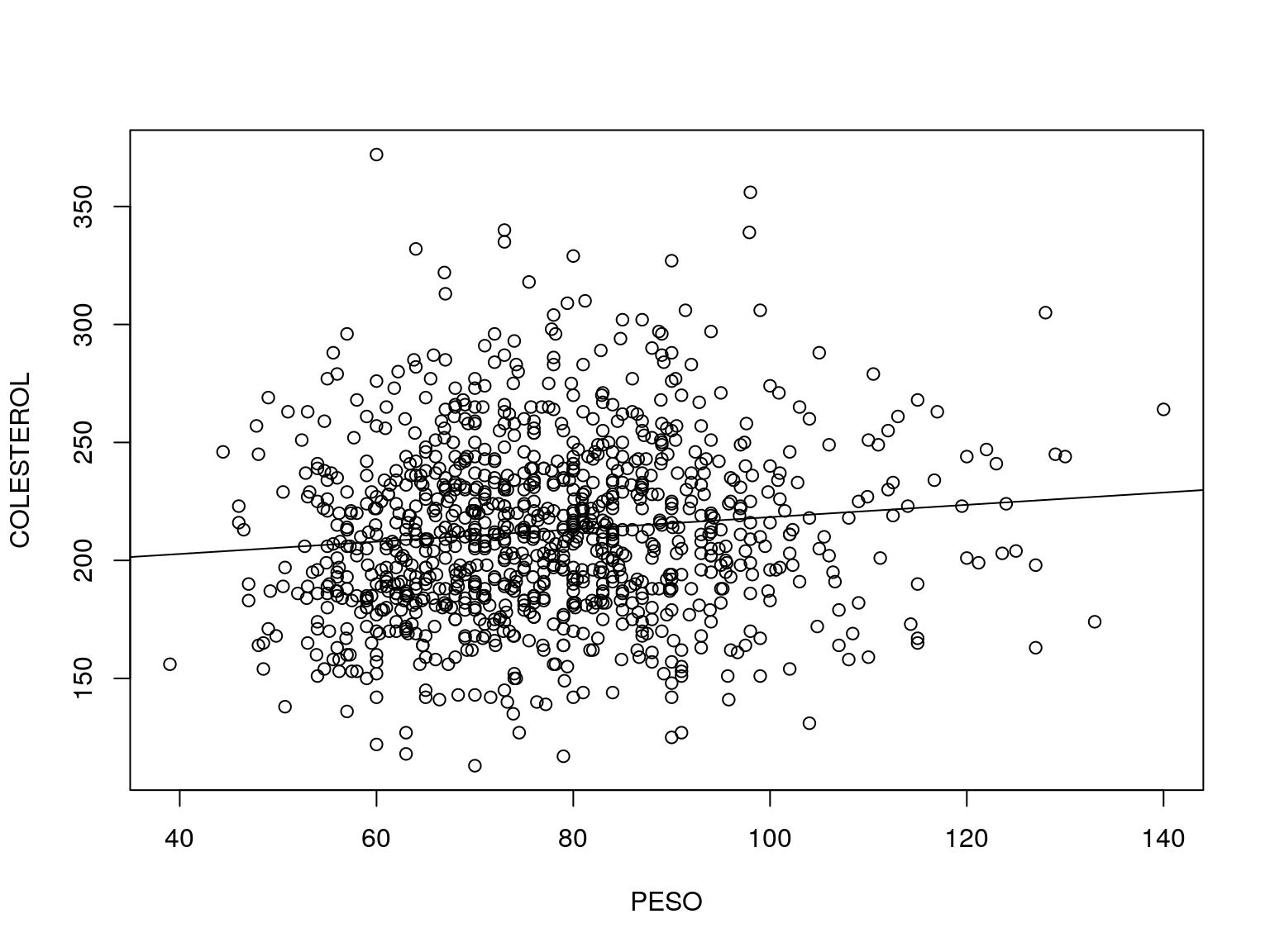
## correlación
## 0.1062269
Asociación entre variables continuas: correlación
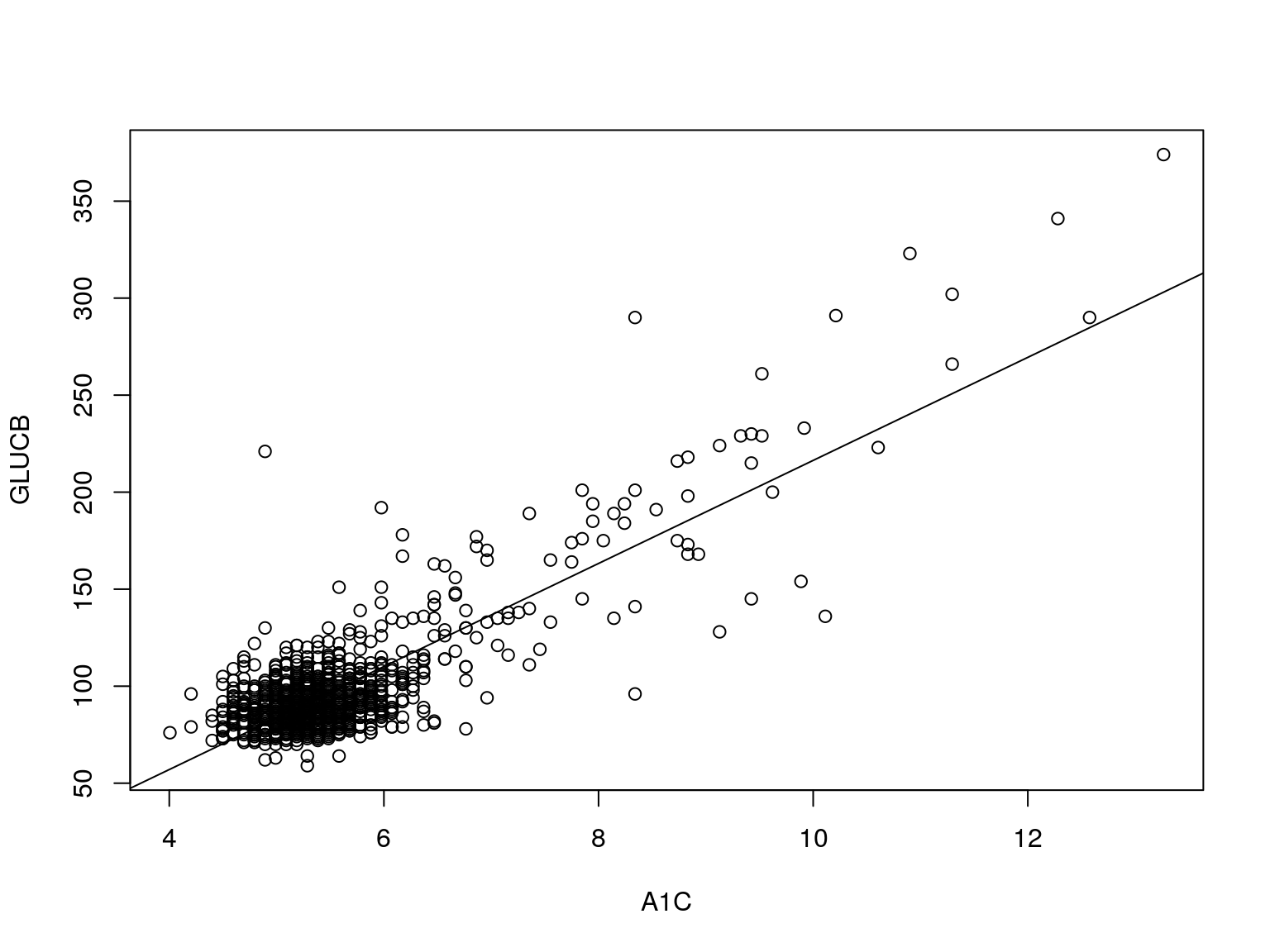
## correlación
## 0.8269498









