Concepto de variable aleatoria. Distribución binomial.

Una variable aleatoria es una cantidad cuyo valor depende del azar. A modo de ejemplo, si la prevalencia de cierta enfermedad en una población es \(\pi=\) 0.30, esto significa que la probabilidad de que una persona elegida al azar padezca esa enfermedad es 0.3. Si elegimos al azar 3 personas de esa población, podrá ocurrir:

• Que ninguna esté enferma. Este suceso tiene probabilidad \(p_0=(1-\pi)^3\)
• Que solo haya una enferma: \(p_1=3\pi\left(1-\pi\right)^2\).
• Que haya dos enfermas: \(p_2=3\pi^2\left(1-\pi\right)\).
• Que las tres estén enfermas: \(p_3=\pi^3\)

En este contexto, \(X=\) “número de enfermos entre las tres personas elegidas al azar”" es una variable aleatoria en el sentido que se acaba de definir. Concretamente, si el hecho de que un sujeto esté enfermo es independiente de que el resto de sujetos esté enfermo o no, el reparto (o distribución) de probabilidades entre los distintos valores de la variable \(X\) recibe el nombre de distribución binomial, en este caso particular, de parámetros \(n=3\) y \(\pi=0.3\), y se suele denotar de la forma \(X\approx b\left(n,\pi\right)\)

Podemos calcular las probabilidades anteriores como sigue:

\(p_0=(1-0.3)^3=0.343\), \(p_1=3\cdot 0.3\cdot (1-0.3)^2=0.441\), \(p_2=3\cdot (0.3^2)\cdot (1-0.3)=0.189\) y \(p_3=0.3^3=0.027\)

Estas cuatro probabilidades suman 1: \[ p_0+p_1+p_2+p_3=1 \]

Estudio de Telde: prevalencia de HTA

En el estudio de Telde tenemos una muestra de \(n=\) 1030 personas. El número de personas con HTA entre estas 1030 es una variable aleatoria con distribución binomial \(b\left(1030, \pi\right)\), donde \(\pi\) es la probabilidad de que una persona elegida al azar de esta población padezca HTA. El valor de \(\pi\) en la población adulta de Telde es desconocido, pero podemos estimarlo (obtener un valor aproximado) a partir de los datos de nuestra muestra, usando como estimador la prevalencia observada de HTA. Dicha prevalencia puede calcularse a partir de la tabla de frecuencias de la variable HTA_OMS:

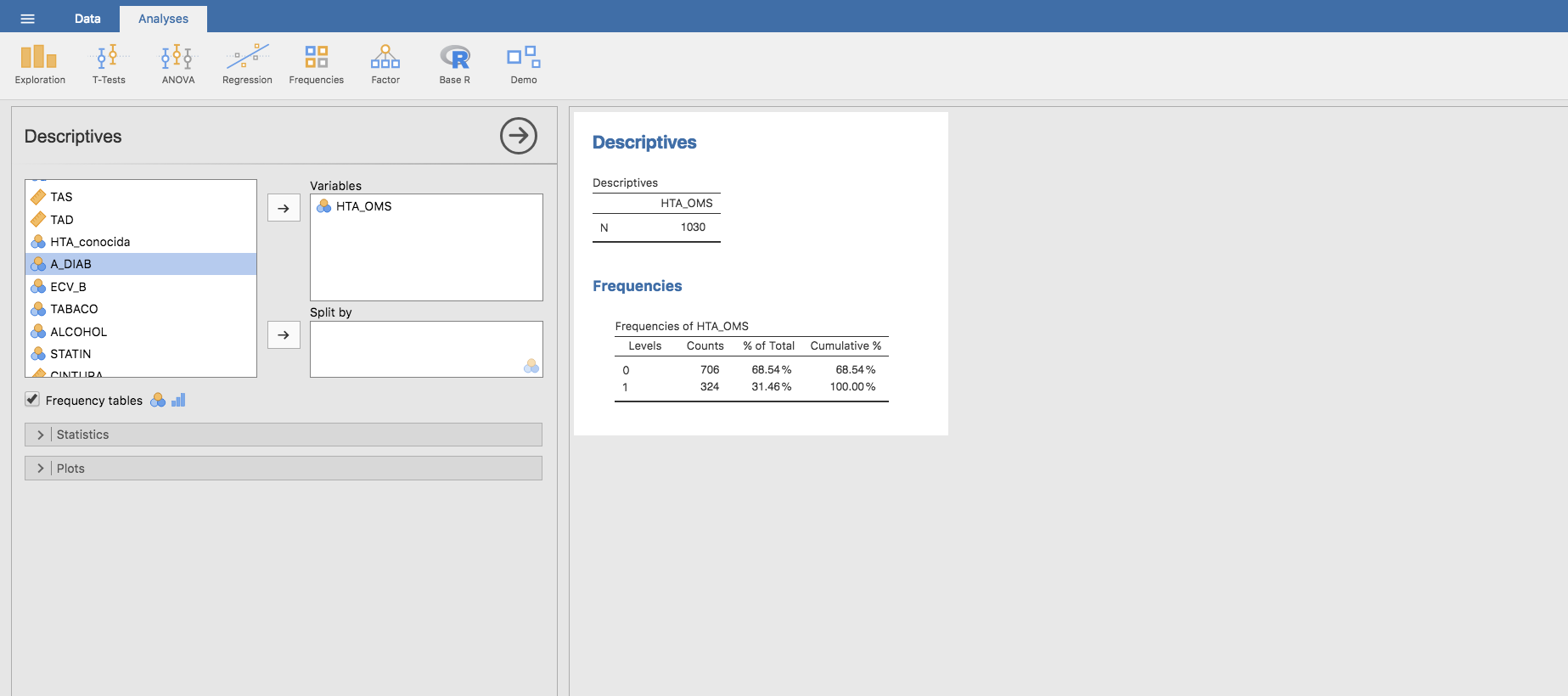
Por tanto de acuerdo con nuestros datos, la prevalencia de HTA en Telde ronda un 31.46% (esto es, la probabilidad de que una persona elegida al azar en la población adulta de Telde tenga HTA es aproximadamente 0.3146).

Asimismo podemos estimar la prevalencia de HTA de acuerdo a la presencia/ausencia de T2DM, a partir de la tabla cruzada entre las variable DM y HTA_OMS, en la que añadimos las frecuencias relativas por filas:

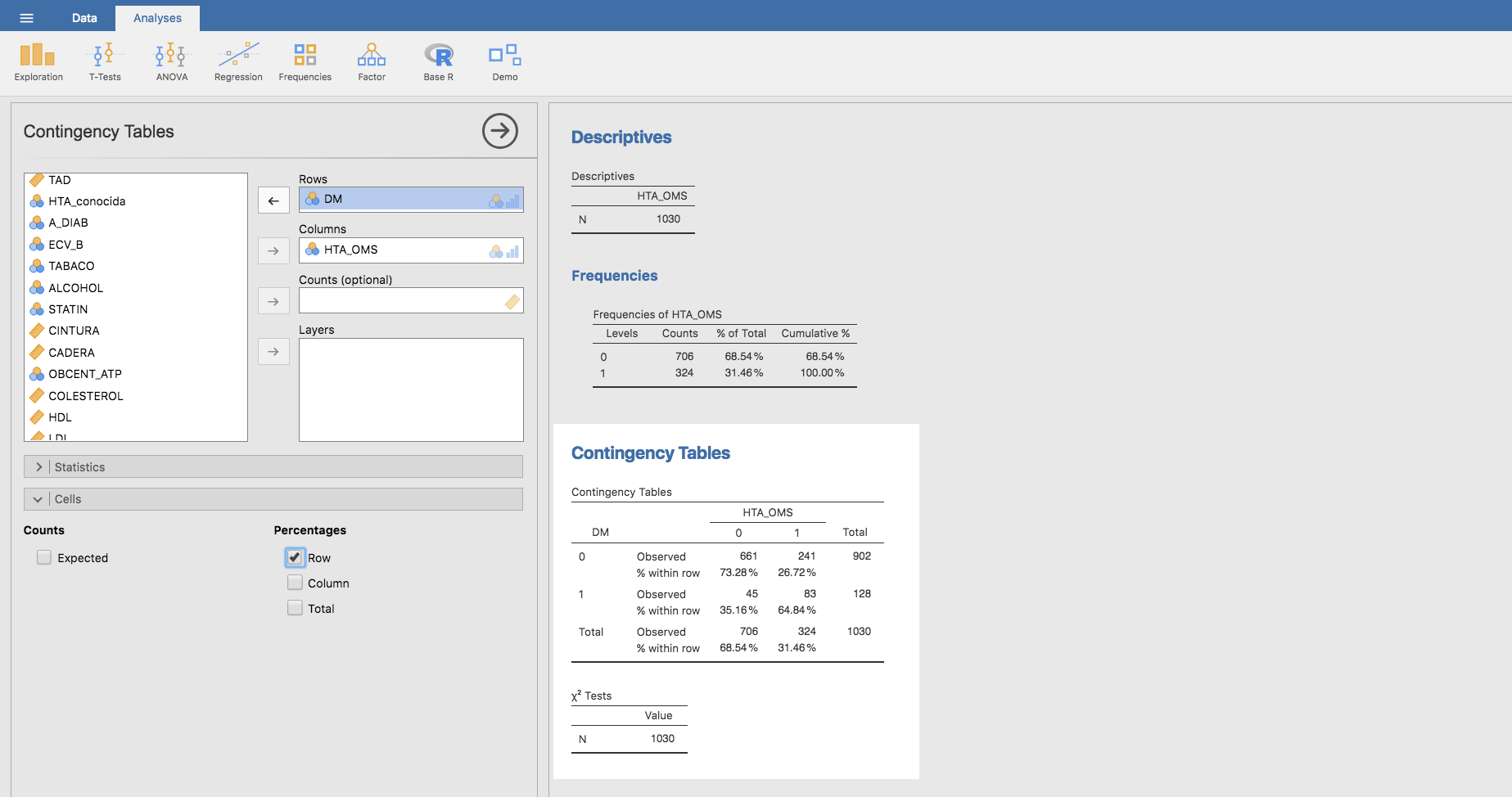
Esta tabla nos indica que entre los diabéticos hay un 64.84% de hipertensos (83 hipertensos de un total de 83+45=128 sujetos); asimismo entre los no diabéticos (241+661=902) hay 241 hipertensos, lo que da lugar a una prevalencia de HTA de un 26.72% entre los no diabéticos. Este resultado muestra bien a las claras que la probabilidad de que una persona tenga HTA depende de si dicha persona tiene o no DM: es más probable ser hipertenso cuando se es diabético que cuando no se es diabético.

Modelo de regresión logística con una única variable explicativa: HTA según DM

En primer lugar, cambiamos los niveles de la variable DM: el 0 por DM- y el 1 por DM+. Seguidamente, construimos el modelo de regresión logística para predecir la prevalencia de HTA según la presencia/ausencia de diabetes con Jamovi. Para ello utilizamos Analyses/Regression/Logistic Regression/2 Outcomes (Binomial), que nos proporciona la siguiente estimación:

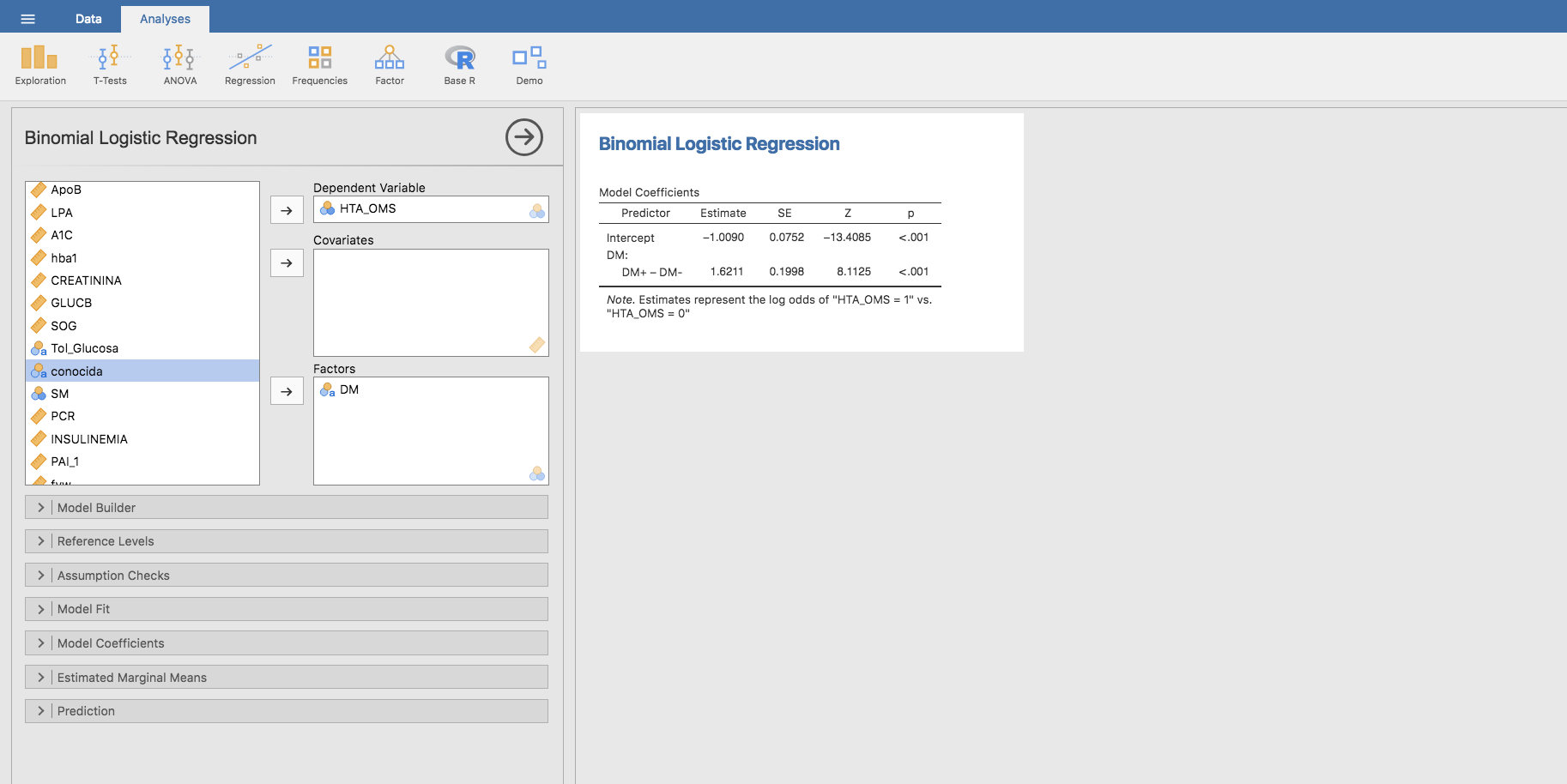
Las predicciones de este modelo se obtienen mediante la barra Estimated Marginal Means, seleccionando la variable DM y marcando todas las opciones del apartado Output:

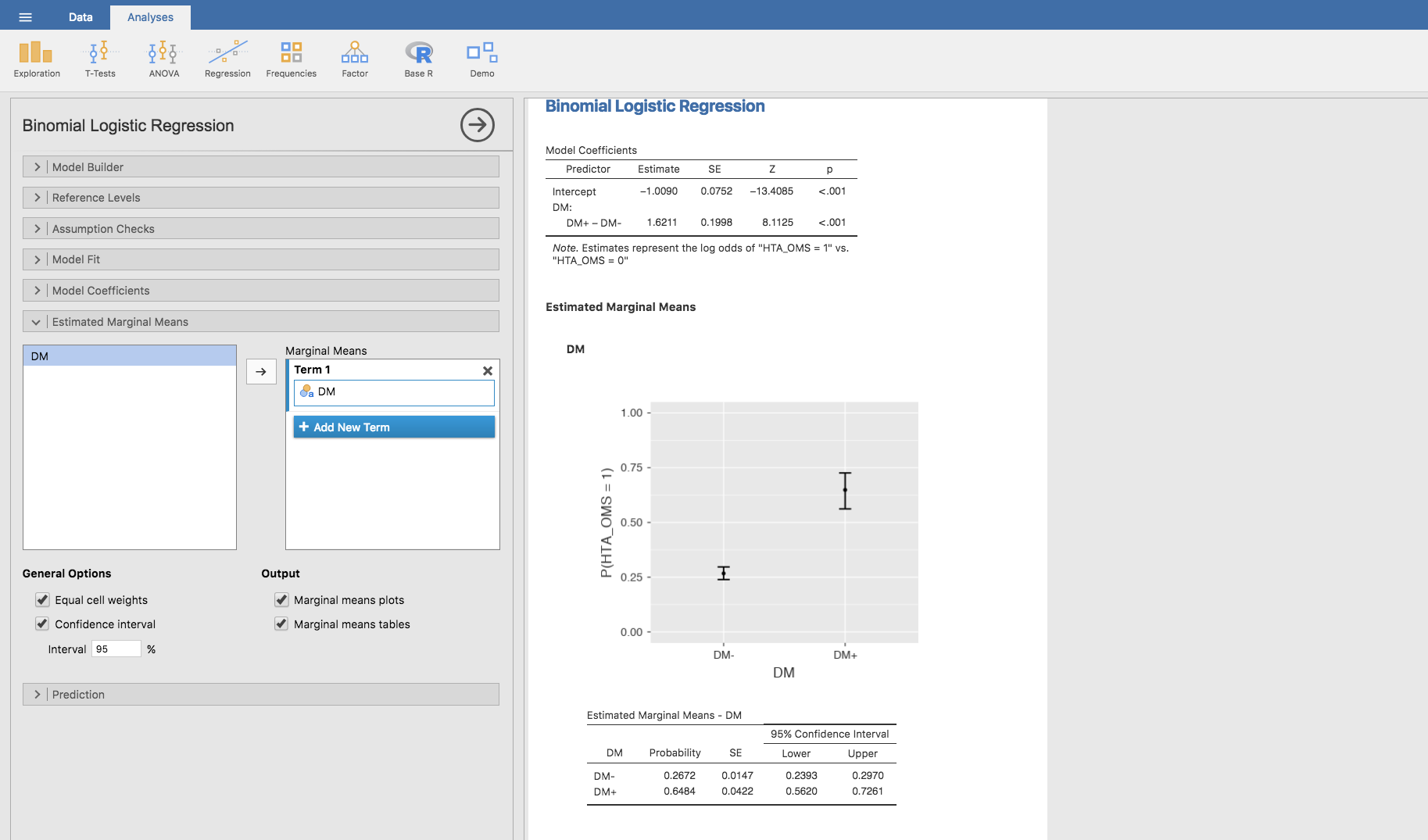
Podemos observar que la predicción es exacta, esto es, se predicen exactamente los valores de las prevalencias observadas y obtener la representación gráfica de los intervalos de confianza para cada categoría.

Modelo de regresión logística multivariante: HTA según IR y DM

Introduzcamos a continuación en el modelo anterior, además del efecto de la T2DM, el efecto de la resistencia a la insulina. Así, siguiendo los mismos pasos dados anteriormente construimos el modelo de regresión logística para nuestro caso con Jamovi, que nos proporciona la siguiente estimación:

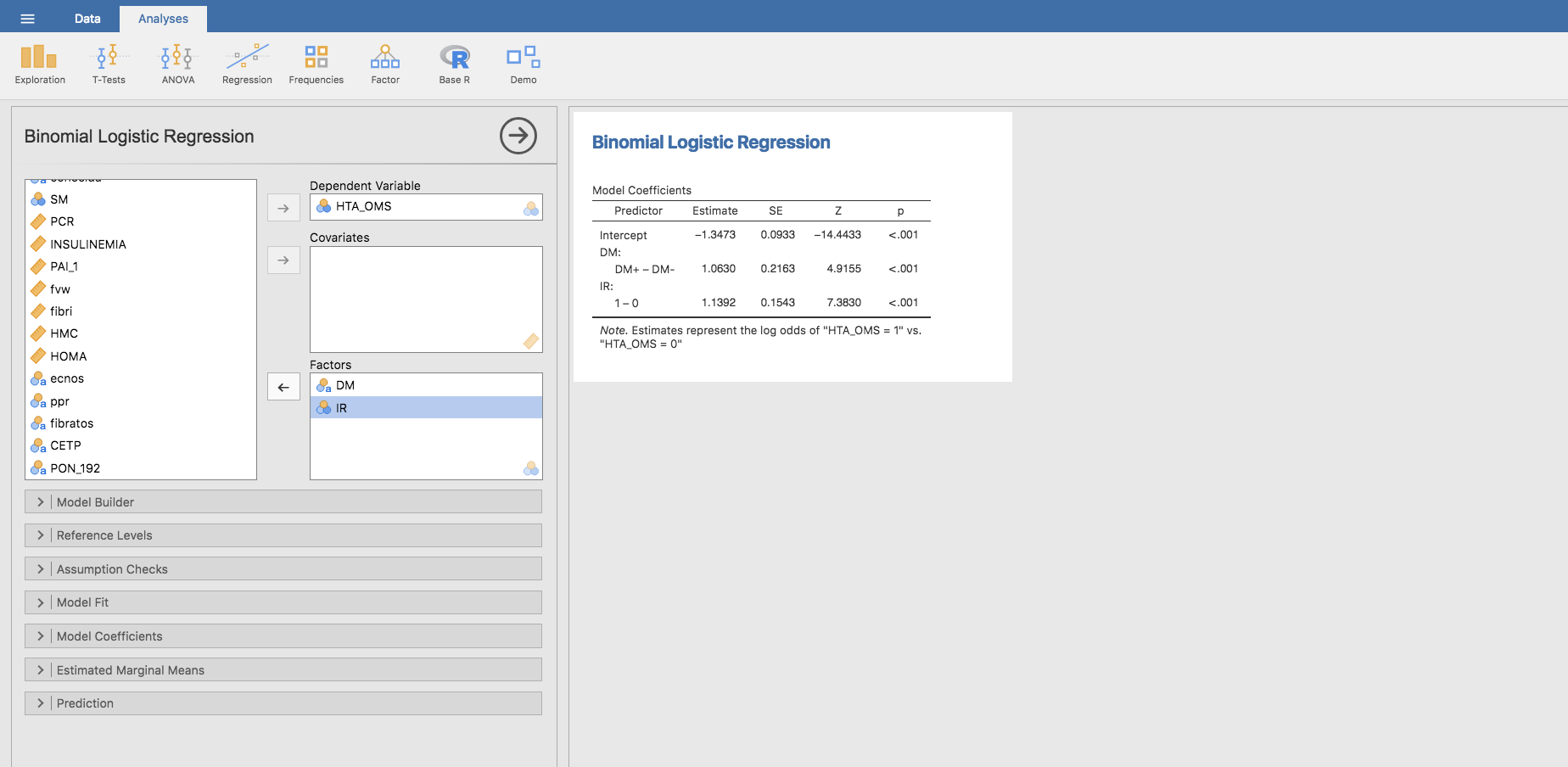
cuyas predicciones se obtienen igual que en el caso anterior, y son las siguientes (obsérvese que ahora ya no coinciden con las proporciones observadas):

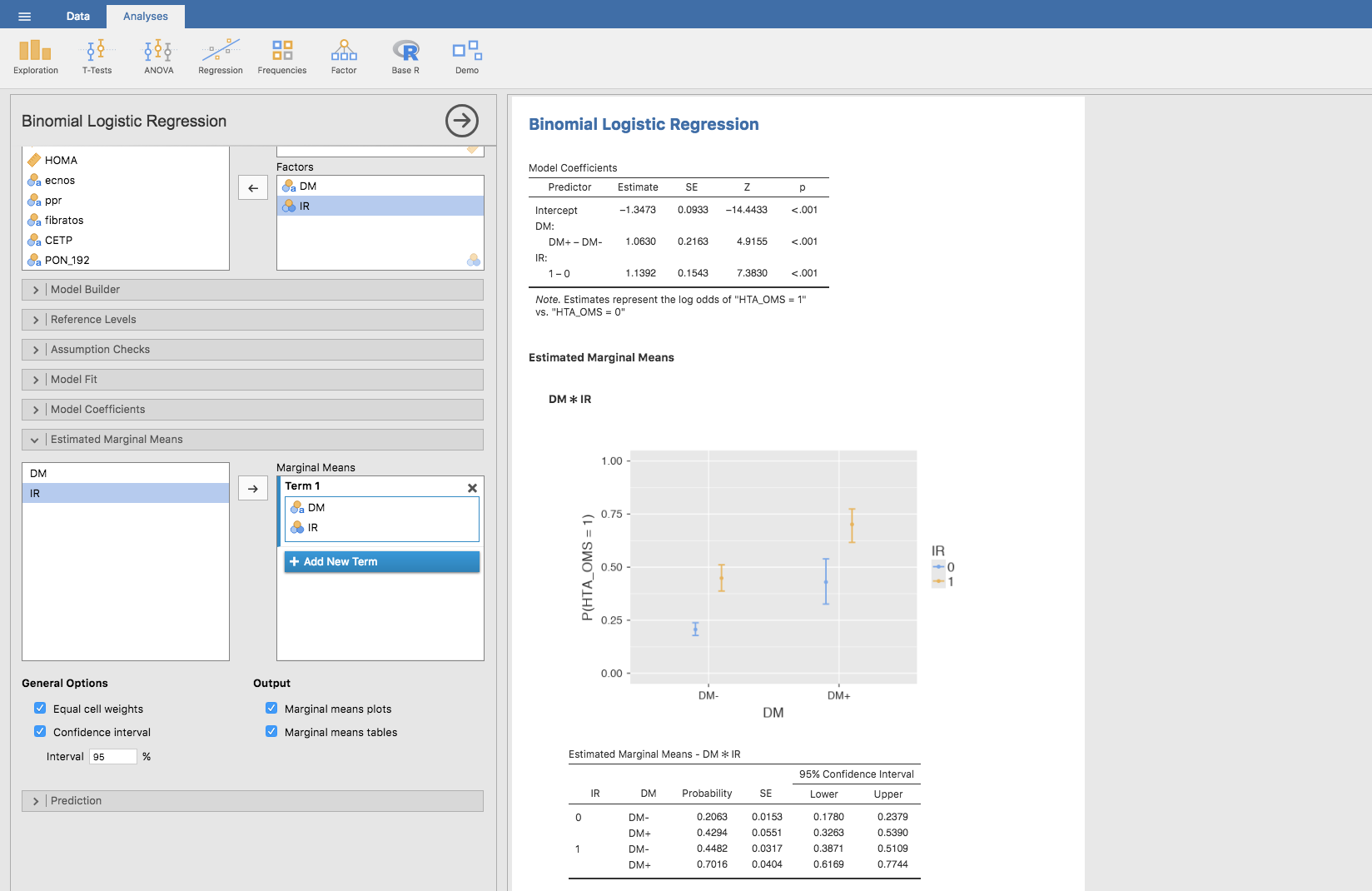
Regresión logística multivariante: Prevalencia de HTA según incluyendo DM y edad:

De forma análoga a los casos anteriores, planteamos el modelo de regresión logística binaria utilizando como variable dependiente la HTA y como variables explicativas la DM y la EDAD. Jamovi proporciona la siguiente estimación:

 

 

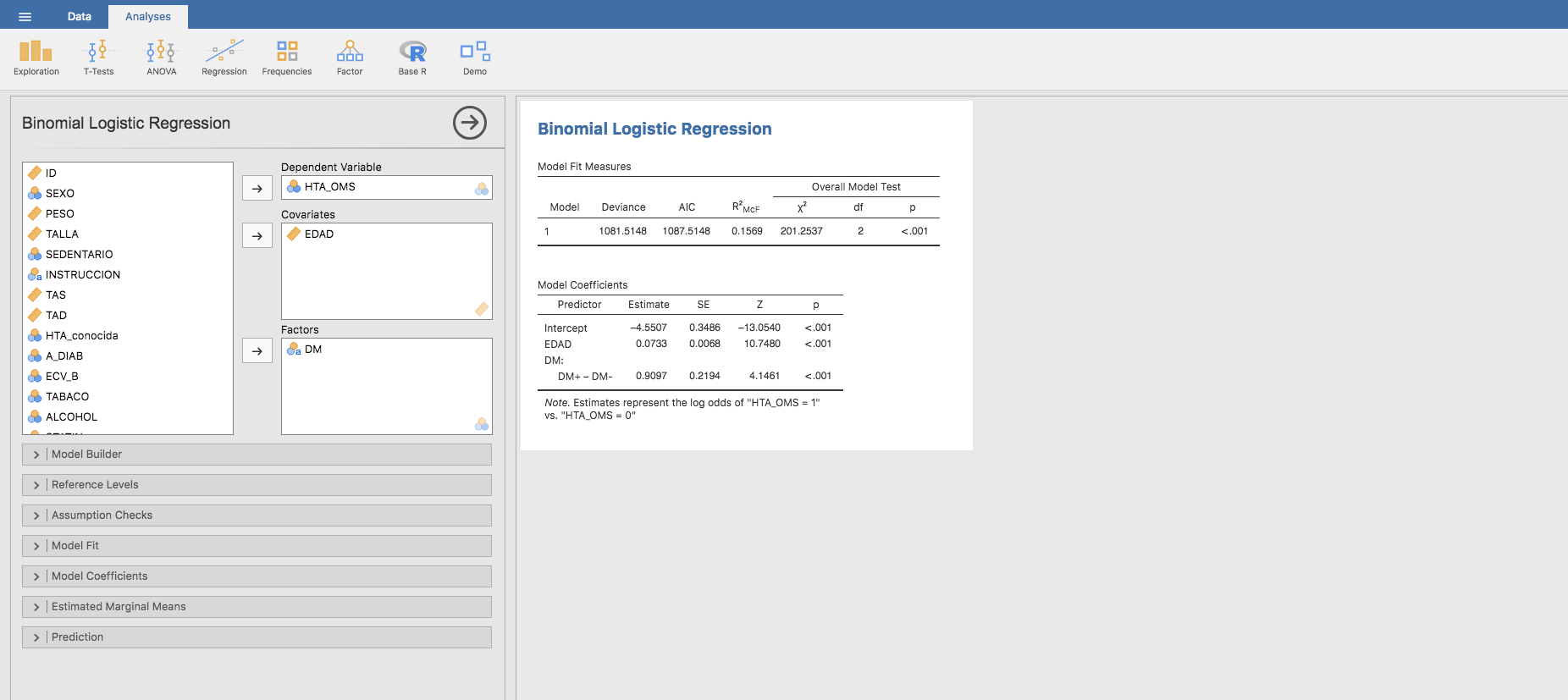
Podemos representar gráficamente el efecto de la edad en cada grupo (DM+ y DM-) del siguiente modo:

 

 

 

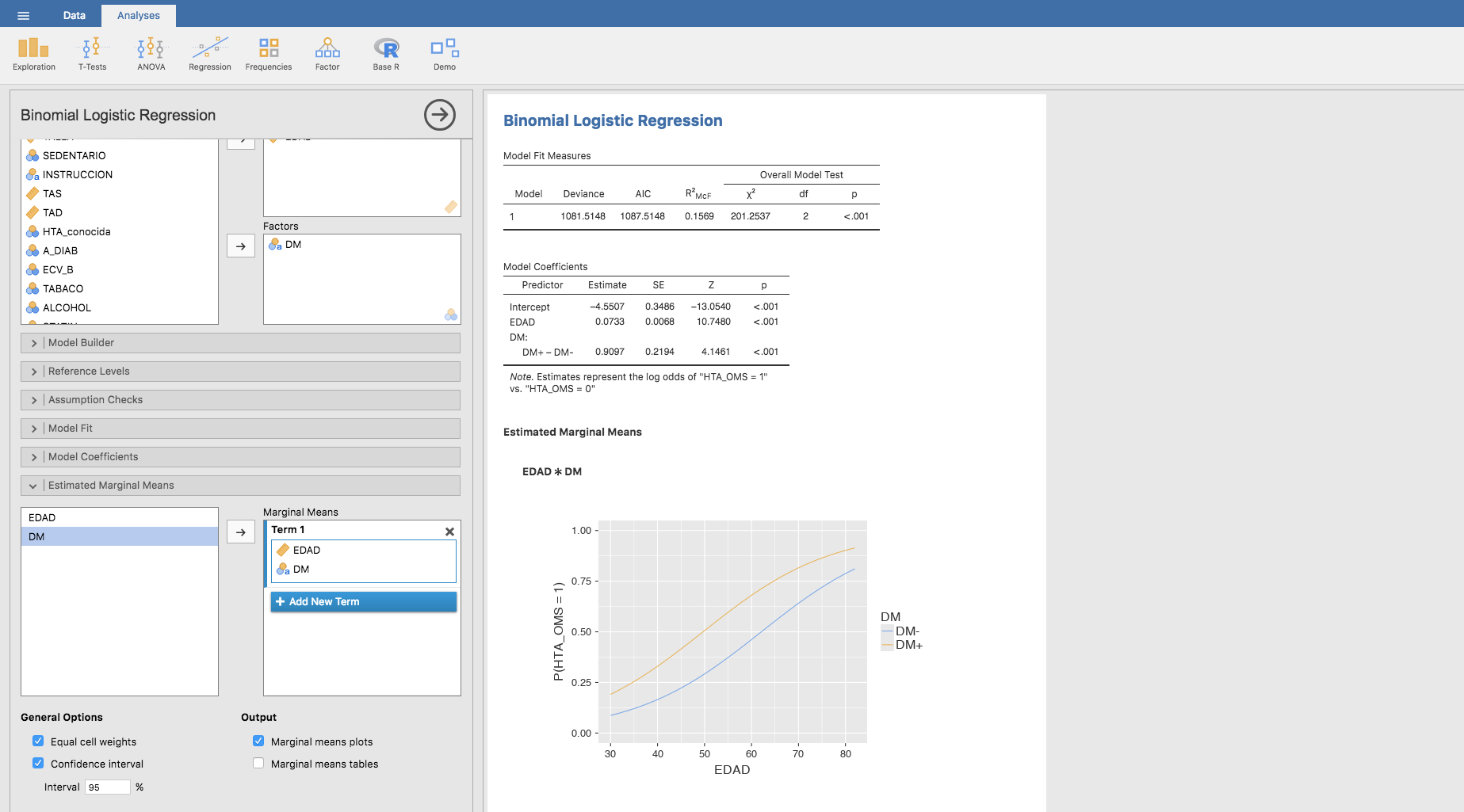
Regresión logística multivariante: Prevalencia de HTA según incluyendo DM, IR y edad:

En este caso, añadimos la variable IR para estimar el modelo de regresión logística:

 

 

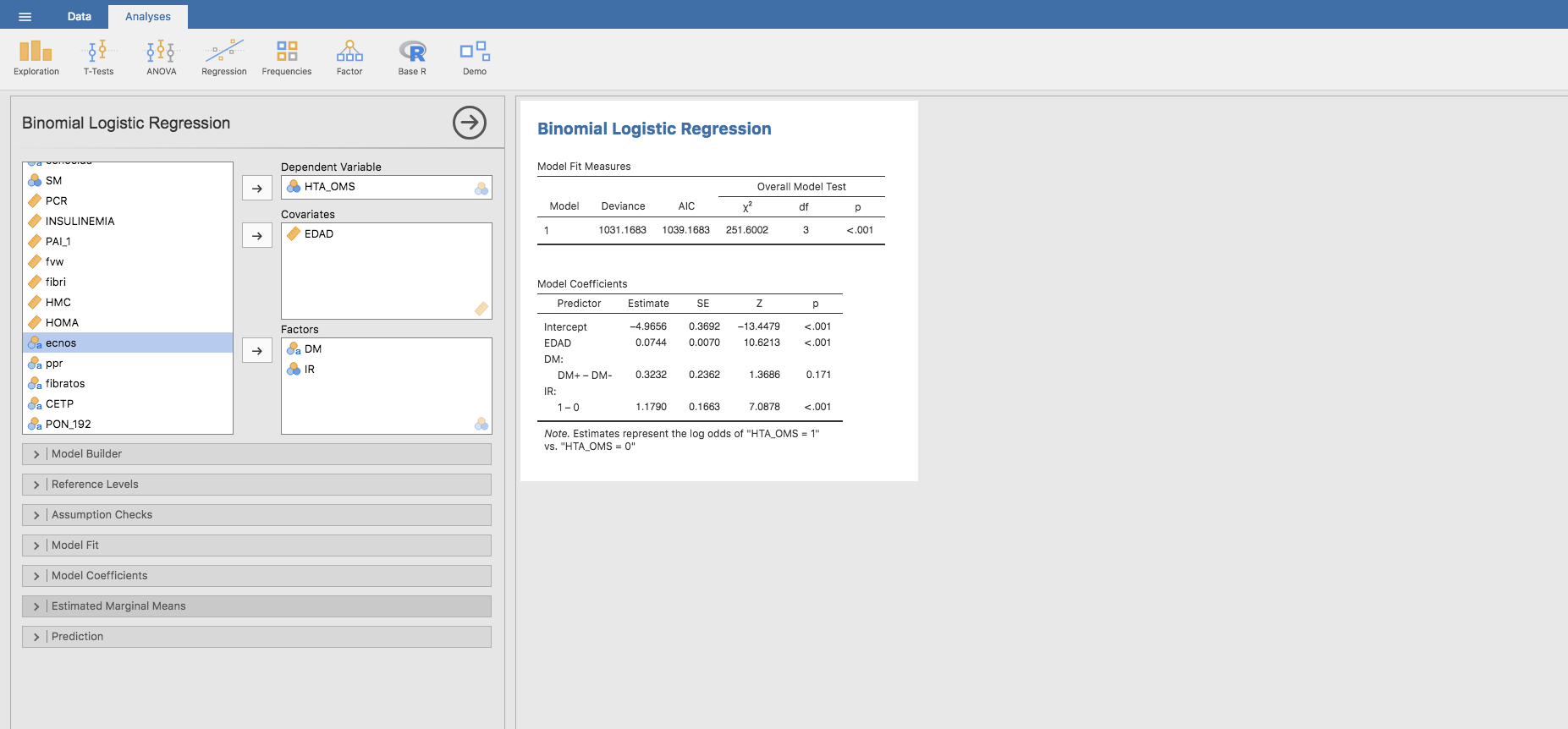
Gráficamente:

• Representamos primero los sujetos Insulino-Resistentes. Para ello, filtramos los datos considerando solo los pacientes cuya IR = 1:

 

 

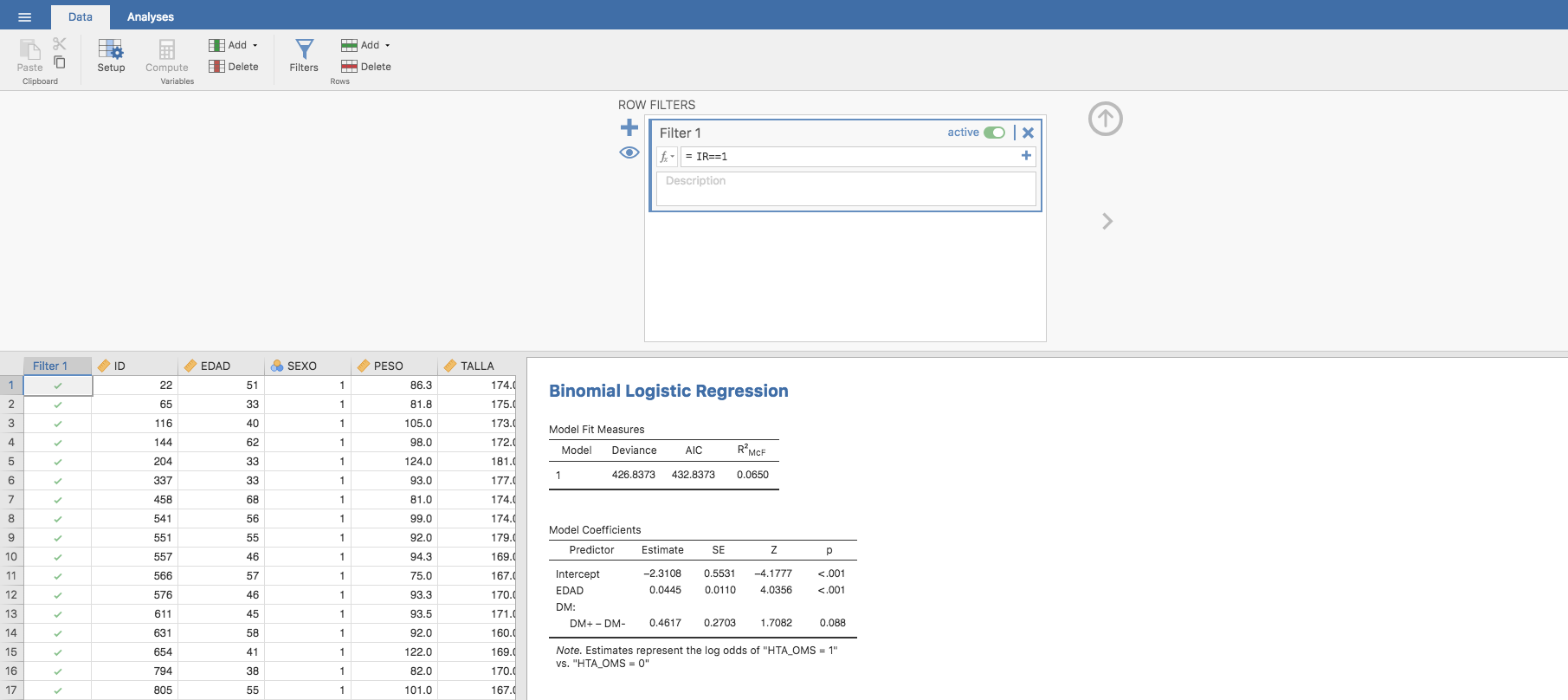
Para estos pacientes, obtenemos la siguiente gráfica:

 

 

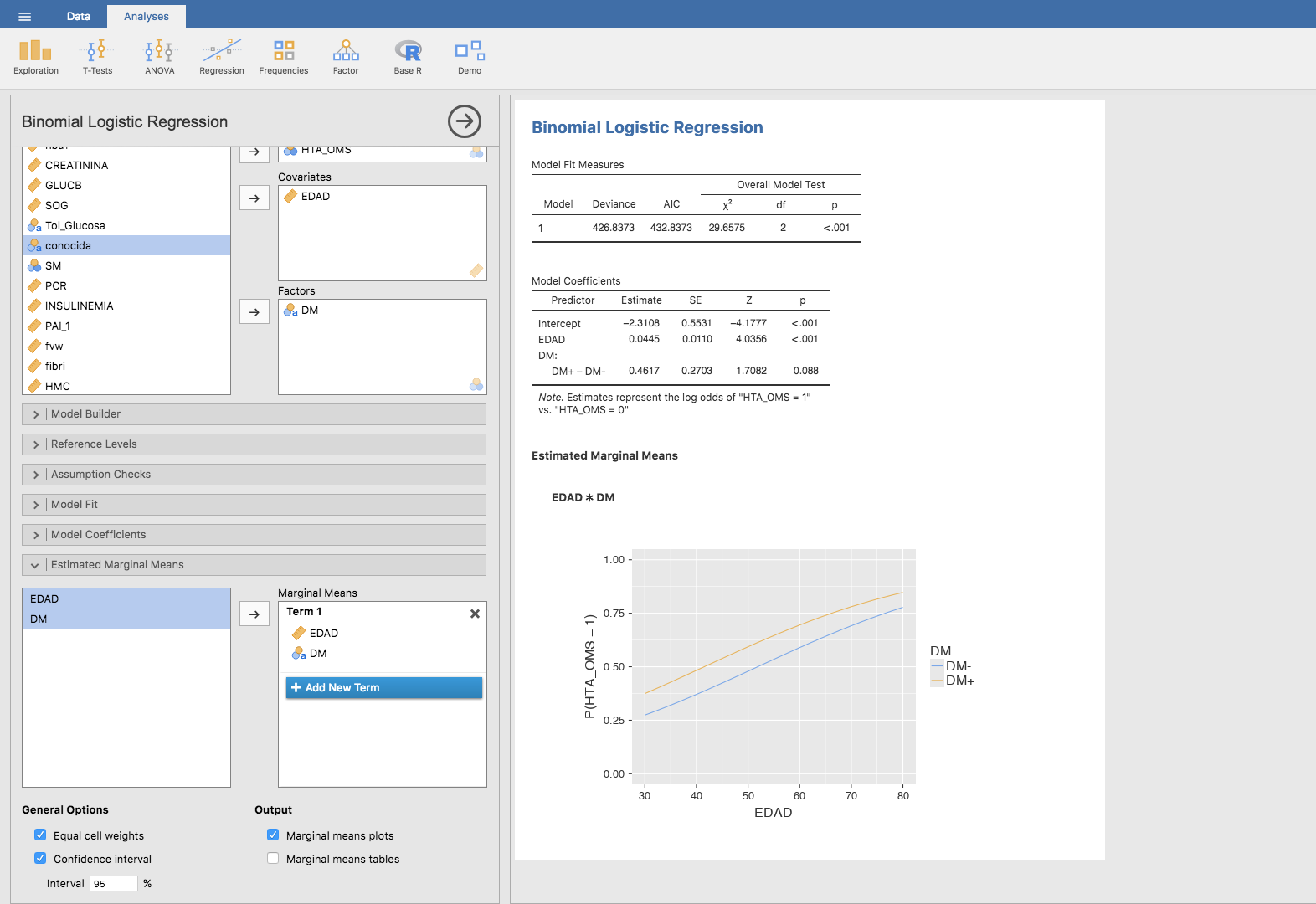
• Y ahora los no Insulino-Resistentes: repetimos el procedimiento anterior, filtrando los datos para los pacientes con IR = 0:

 

 

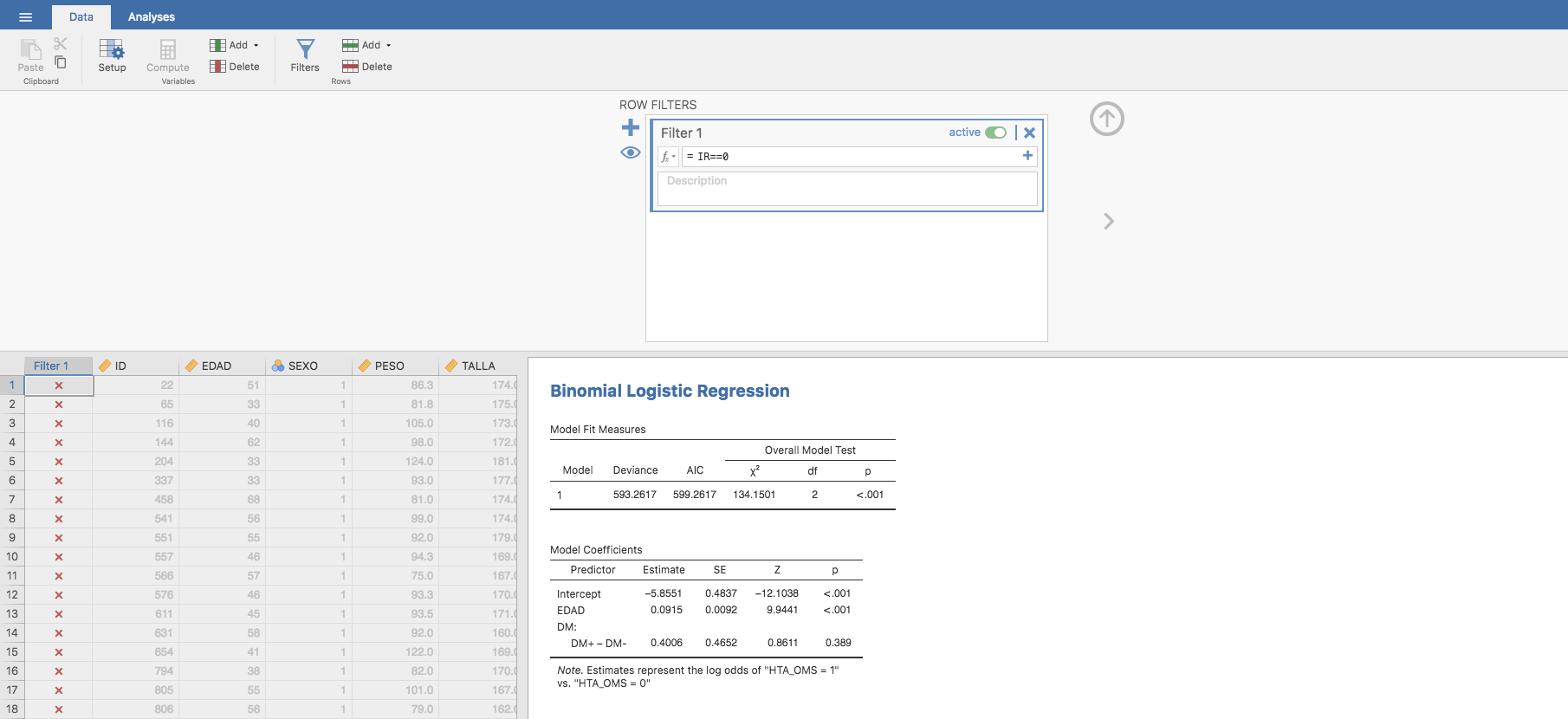
para los que se tiene el siguiente resultado gráfico: