Introducción.

Consideremos la siguiente situación: queremos determinar la tasa de remisión que se consigue con cierto tratamiento para una enfermedad. No es factible aplicar dicho tratamiento a todos los posibles pacientes afectados, por lo que solo se aplica en una muestra de \(n\) pacientes elegidos al azar. Transcurrido el tiempo de aplicación del tratamiento, evaluamos a los pacientes tratados y determinamos para cada uno de ellos si la enfermedad ha remitido o no. Si la enfermedad ha remitido en \(n_R\) de los \(n\) pacientes iniciales, nuestra estimación (valor aproximado) de la tasa de remisión conseguida con el tratamiento será:

\[p = \frac{n_R}{n}\]

Surgen de inmediato varias preguntas: ¿este procedimiento proporciona realmente un valor aproximado de la tasa de remisión que se consiguiría con el tratamiento si se aplicara a todos los pacientes y no solo a una muestra? ¿Qué margen de error tiene esta aproximación? ¿Cuál es el tamaño adecuado de la muestra?

En este documento utilizaremos las herramientas de simulación que ofrece R para ayudarnos a entender las ideas subyacentes al problema de estimación de parámetros. A partir de estas ideas trataremos de dar respuesta a las preguntas que nos hemos hemos planteado.

 

 

Simulación de variables aleatorias.

R permite simular de manera muy sencilla el comportamiento de una variable aleatoria en el muestreo. Si la distribución de probabilidad de dicha variable aleatoria depende de un parámetro (desconocido) \(\theta\), esta simulación nos ayuda a entender qué información podemos obtener de dicho parámetro a partir de los datos muestrales.

En primer lugar aclaremos qué significa la frase “simular el comportamiento de una variable aleatoria en el muestreo”:

• Una variable aleatoria es una cantidad cuyo valor observado depende del azar. En el ejemplo anterior, la variable aleatoria es la tasa de remisión que se observa en la muestra de pacientes; a priori no podemos predecir en qué pacientes se producirá la remisión y en qué pacientes no, y por tanto no podemos conocer el valor exacto de dicha tasa hasta que termine el estudio.

• El muestreo es el proceso mediante el cual se observan valores de la variable aleatoria. En el ejemplo, es el procedimiento por el cual se seleccionan los pacientes que participan en el estudio, se les aplica el tratamiento y se determina en cuántos se ha conseguido la remisión.

• El comportamiento de la variable aleatoria en el muestreo se refiere a la caracterización de los valores que puede presentar dicha variable en el muestreo: cuales son los valores posibles, con qué frecuencia puede aparecer cada uno, si son valores muy parecidos entre sí, si son valores muy distintos, si tienden a estar agrupados alrededor de algún valor concreto … Debe quedar claro que aquí no nos referimos a un valor particular observado en una muestra concreta, sino a la colección de posibles valores susceptibles de ser observados en las distintas muestras que podrían obtenerse al llevar a cabo el muestreo. Volviendo a nuestro ejemplo, si decidimos tomar una muestra de 30 pacientes, hay muchísimas formas de elegir 30 pacientes de entre todos los afectados por la enfermedad, y por tanto hay muchas muestras posibles de 30 pacientes; en una de esas muestras la tasa de remision podria ser el 68%, en otra el 76%, en otra el 54%, …

• Simular la variable aleatoria significa utilizar R para generar valores de dicha variable con un comportamiento lo más parecido posible a lo que ocurriría en observaciones reales de la misma. Si, en nuestro ejemplo, suponemos que la tasa de remisión con el tratamiento empleado es del 70%, ello significa que para cada paciente individual, la probabilidad de que la enfermedad le remita es 0.7 y la probabilidad de que no le remita es 0.3. Lo que le ocurre a un individuo es muy fácil de simular en R. Una posible forma de hacerlo es la siguiente:

  sample(c("remite","no remite"), size=1,prob=c(0.7,0.3))

  ## [1] "no remite"

  Si queremos simular lo que le ocurre a 10 pacientes especificamos size=10 e indicamos replace=TRUE lo que significa que cada valor (“remite” o “no remite”) puede ocurrir varias veces en la muestra:

  sample(c("remite","no remite"), size=10, prob=c(0.7,0.3), replace=TRUE)

  ##  [1] "remite"    "no remite" "remite"    "no remite" "no remite"
  ##  [6] "remite"    "remite"    "remite"    "remite"    "remite"

  Si repetimos la simulación no obtendremos el mismo resultado, ya que representaría otra muestra de 10 pacientes distintos (que obviamente no producen los mismos valores que los 10 primeros):

  sample(c("remite","no remite"), size=10, prob=c(0.7,0.3), replace=TRUE)

  ##  [1] "remite"    "no remite" "no remite" "remite"    "remite"   
  ##  [6] "remite"    "remite"    "remite"    "no remite" "no remite"

  Podemos simplificar el código anterior, codificando como “1” la remisión y como “0” la no remisión:

  muestra=sample(c(1,0), size=10, prob=c(0.7,0.3), replace=TRUE)
  muestra

  ##  [1] 1 0 0 0 0 1 0 1 1 1

  De esta forma, la suma de los valores de la muestra nos proporcionaría justamente el número de personas de esta muestra en las que se ha producido la remisión:

  sum(muestra)

  ## [1] 5

  y si dividimos por el tamaño muestral obtendríamos la tasa de remisión observada en esta muestra particular:

  sum(muestra)/10

  ## [1] 0.5

 

 

Simulación de la tasa de remisión

El procedimiento de simulación anterior, aunque es simple, se puede simplificar aún más si tenemos en cuenta que la variable en la que estamos interesados:

\(n_R\) = “Número de pacientes de una muestra de tamaño \(n\) en los que se produce la remisión.”

es una variable aleatoria con distribución binomial de parámetros \(n\) y \(\pi\), siendo \(\pi\) la tasa de remisión (en la práctica, desconocida) del tratamiento.

R dispone de una función específica para simular variables con distribución de probabilidad binomial; si la tasa de remisión real fuese del 70%, podemos simular una observación de \(n_R\) en una muestra de tamaño \(n=10\) como:

nR=rbinom(1,10,0.7)
nR

## [1] 9

y la tasa de remisión en esta muestra sería:

tasaMuestral=nR/10
tasaMuestral

## [1] 0.9

Si queremos que R simule el resultado de observar la tasa de remisión en 100 muestras, cada una de tamaño \(n=10\), con \(\pi=0.7\), bastará con ejecutar:

n=10
pi=0.7
tasaMuestral=rbinom(100,n,pi)/n
tasaMuestral

##   [1] 0.6 0.7 0.9 0.7 0.8 0.6 0.5 0.7 0.7 0.7 0.7 0.6 0.6 1.0 0.9 0.8 0.6
##  [18] 0.8 0.6 0.6 0.4 0.4 0.8 0.7 0.5 0.8 0.7 0.7 0.4 0.5 0.6 0.7 0.5 0.9
##  [35] 0.9 0.8 0.7 0.7 0.8 0.9 1.0 0.7 0.7 0.6 0.7 0.7 0.6 0.6 0.8 0.7 0.5
##  [52] 0.5 0.7 0.5 0.8 0.7 0.8 0.7 0.8 0.8 0.6 0.6 0.6 0.6 0.7 0.7 1.0 0.4
##  [69] 0.9 0.7 0.9 0.4 0.6 0.7 0.7 0.7 0.9 0.7 0.9 0.9 0.7 0.6 0.7 0.8 0.3
##  [86] 0.8 0.7 0.6 0.7 0.6 0.6 0.7 0.8 0.7 0.7 0.6 0.9 0.5 0.7 0.6

Podemos presentar estos resultados en una tabla:

ttm=table(tasaMuestral)
library(pander)
pander(ttm)

0.3	0.4	0.5	0.6	0.7	0.8	0.9	1
1	5	8	22	35	15	11	3

Es decir, de las 100 muestras, se ha observado una tasa de remisión de 0.3 en 1 de ellas, una tasa 0.4 en 5, 0.5 en 8, etc. En particular, la tasa 0.7 se ha observado en 35 muestras. Gráficamente:

barplot(prop.table(ttm),col="skyblue")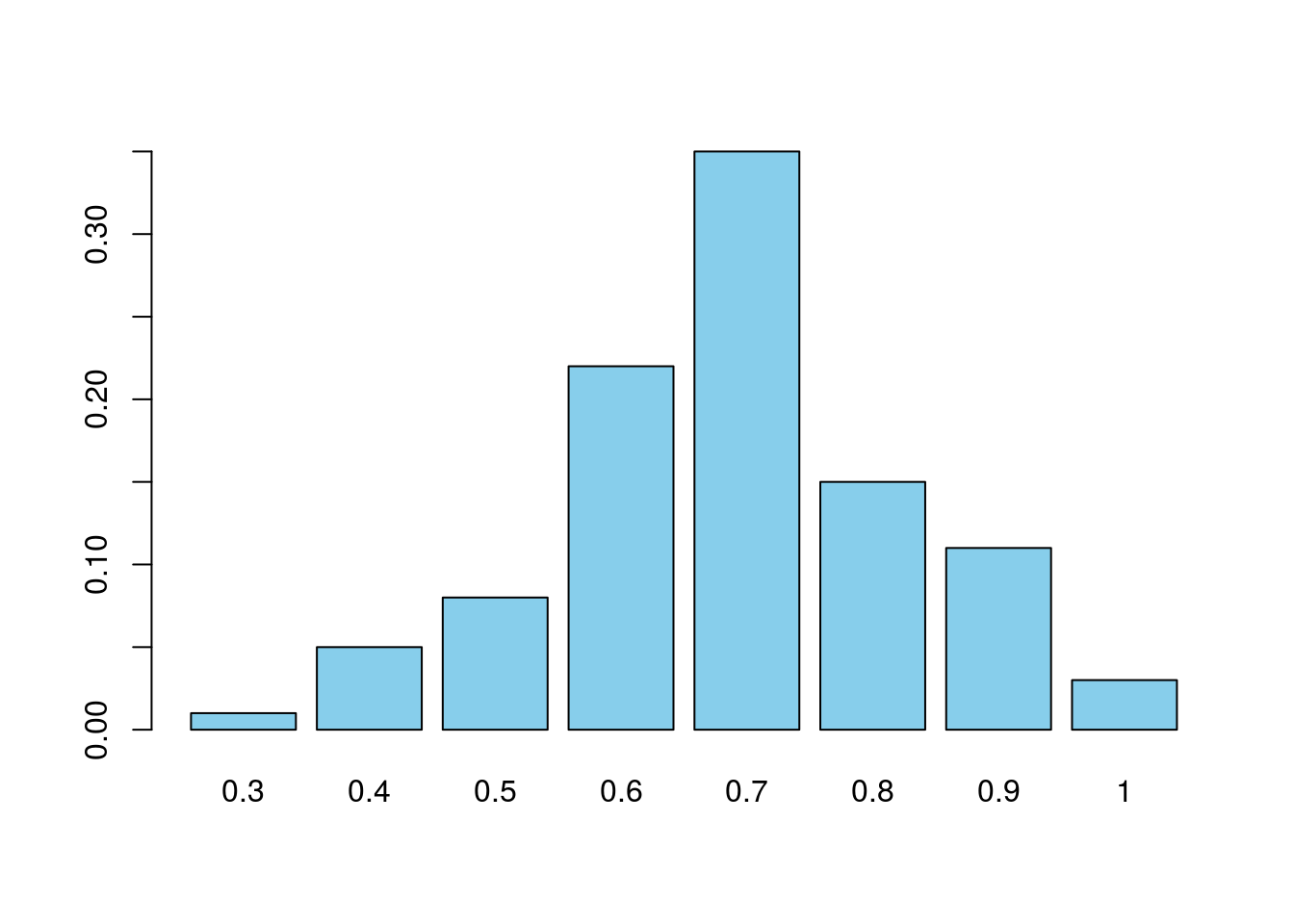

Podemos conseguir más información si en lugar de 100 muestras de tamaño 10, simulamos 10000 muestras de tamaño 10:

n=10
pi=0.7
tasaMuestral=rbinom(10000,n,pi)/n
pander(table(tasaMuestral))

0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1
8	93	403	1025	2038	2666	2317	1189	261

barplot(prop.table(table(tasaMuestral)), col="skyblue")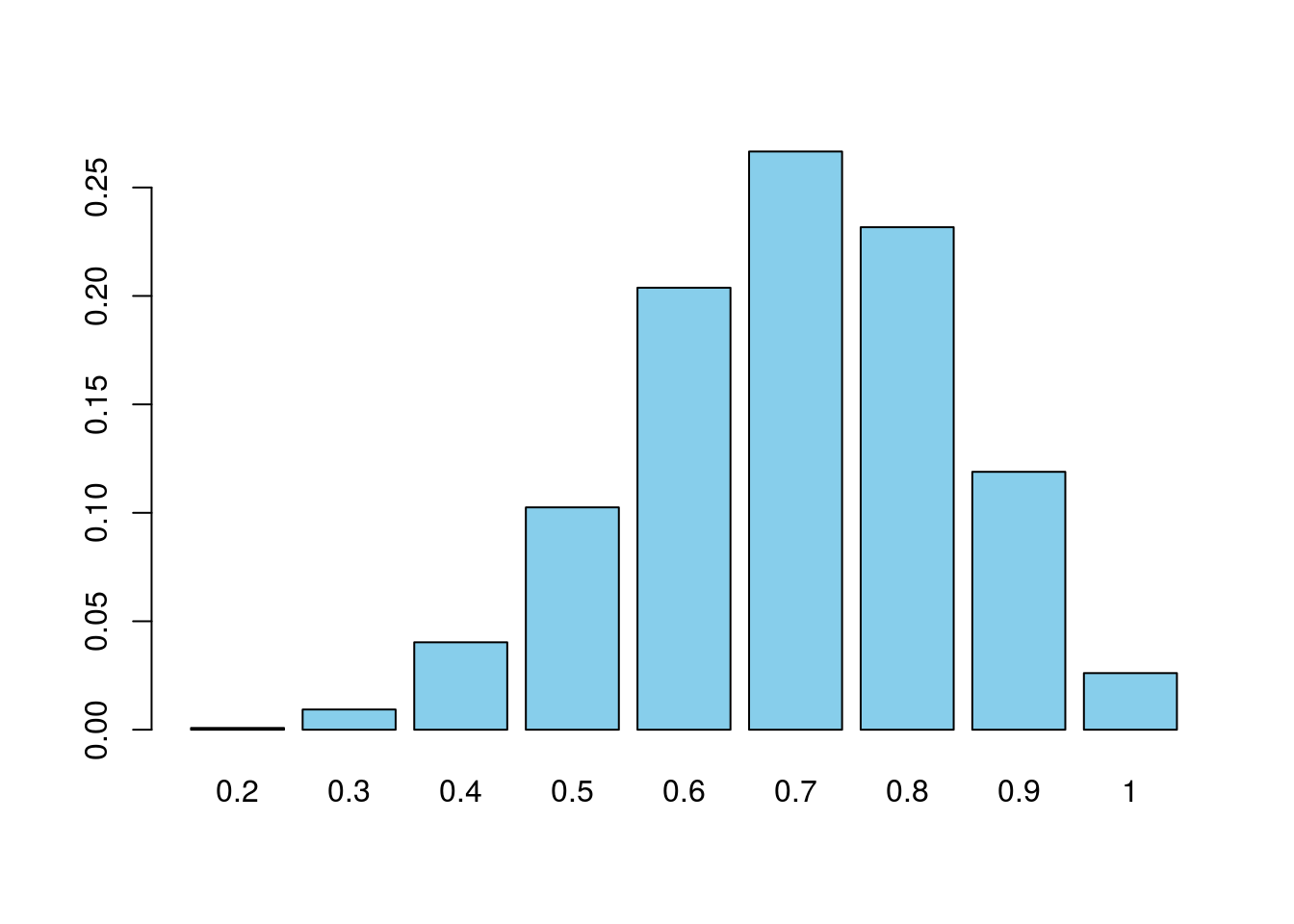

¿Qué nos indican esta tabla y este gráfico? Básicamente que si la muestra disponible para estimar la prevalencia es de tamaño 10, aunque la mayor parte de las veces el valor estimado es 0.6, 0.7 ó 0.8, no resulta demasiado extraño que aparezcan estimaciones como 0.4, 0.9 o incluso 1. Si calculamos los percentiles 2.5 y 97.5, nos dan un intervalo dentro del cuál aparece el 95% de los valores de prevalencia estimados en las distintas muestras:

quantile(tasaMuestral, probs=c(0.025,0.975))

##  2.5% 97.5% 
##   0.4   1.0

En otras palabras, esta simulación nos informa de que si la verdadera tasa de remisión fuese 0.7, una muestra de tamaño 10 el 95% de las veces produce valores estimados entre 0.4 y 1. Si pensamos que cuando tomamos una muestra no conocemos el verdadero valor de la tasa de remisión, estos resultados indican que si la tasa de remisión muestral que observamos fuese 0.4, sería perfectamente posible, incluso problable, que la tasa de remisión “real” fuese 0.7, lo que significa que nuestra estimación tendría un error de 0.3 unidades.

Veamos qué ocurre si tomamos muestras de tamaños 20, 50, 100, 200, 500, 1000, 2000 y 5000 (mostramos sólo los gráficos y una versión animada de éstos):

par(mfrow=c(2,2))
pi=0.7
for (n in c(20, 50, 100, 200, 500, 1000, 2000, 5000)){
  tasaMuestral=rbinom(10000,n,pi)/n
  hist(tasaMuestral, freq=FALSE, main=paste("Tamaño de muestra n =",n),
       xlim=c(0.2,1), ylim=c(0,40), col="yellow", xlab="Tasa de remisión")
  abline(v=0.7,col="red",lwd=2,lty=2)
}

 

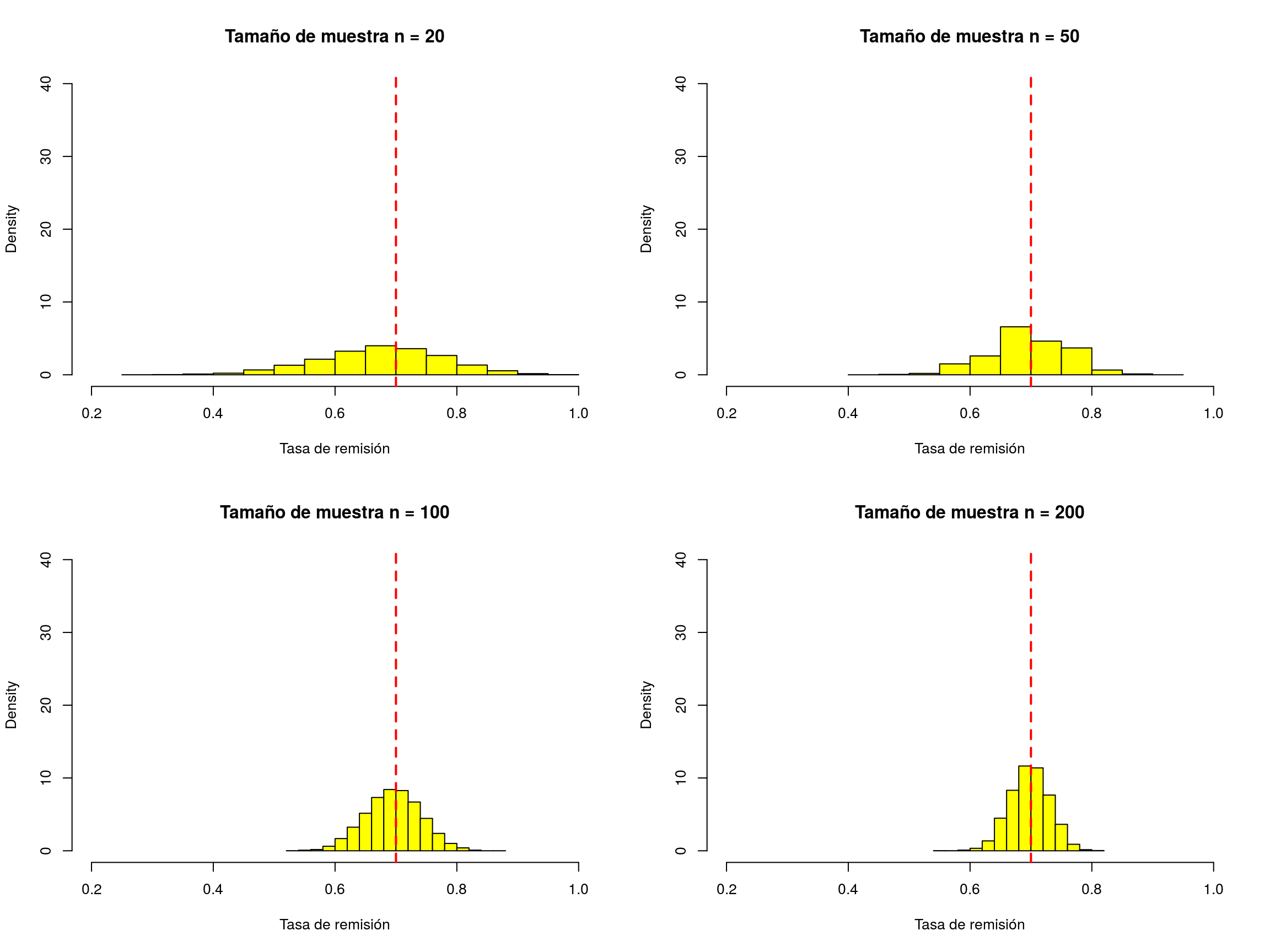
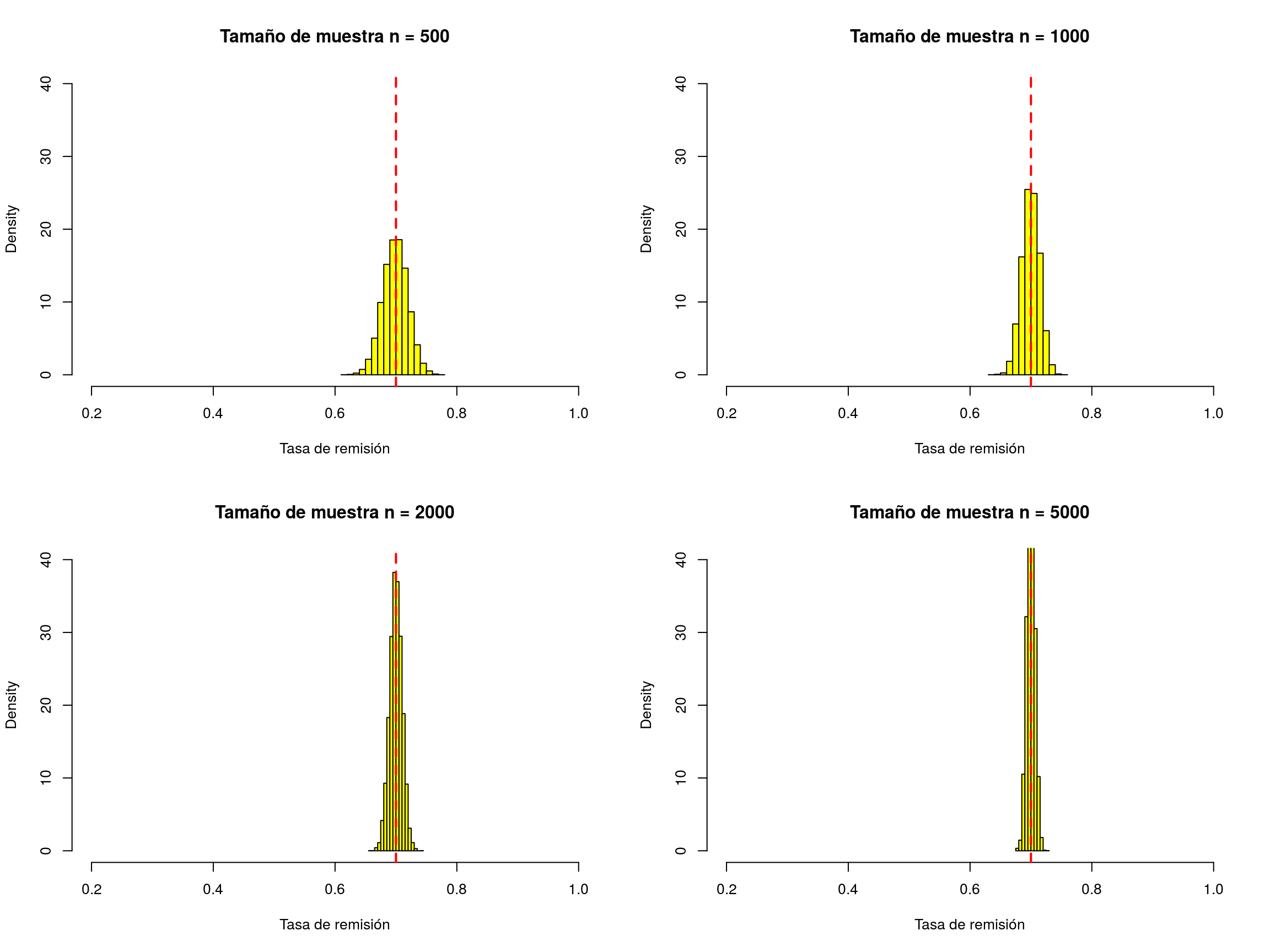
Estas figuras muestran que a medida que aumenta el tamaño de la muestra:

• Los valores muestrales de la tasa de remisión están siempre en torno al verdadero valor de la tasa de remisión (0.7).

• A medida que aumenta el tamaño de la muestra, la dispersión es menor, esto es, los valores de tasa de remisión muestrales aparecen cada vez más concentrados en torno al verdadero valor de la tasa de remisión. Ello nos indica que cuando por fin hagamos el muestreo real (no las simulaciones), cualquiera que sea la muestra particular que obtengamos finalmente, podemos estar bastante seguros de que, si la muestra es lo suficientemente grande, el valor estimado de la tasa de remisión será muy próximo al valor real de dicha tasa.

 

Para tener una idea de la proximidad entre las estimaciones y el verdadero valor de la tasa de remisión, podemos calcular los percentiles 2.5 y 97.5 para las estimaciones obtenidas con los distintos tamaños de muestra:

tab=NULL
for (n in c(20, 50, 100, 200, 500, 1000, 2000, 5000)){
  tasaMuestral=rbinom(10000,n,pi)/n
  tab=rbind(tab,c(n,quantile(tasaMuestral, probs=c(0.025,0.975))))
}
tab

##             2.5%  97.5%
## [1,]   20 0.5000 0.9000
## [2,]   50 0.5800 0.8200
## [3,]  100 0.6100 0.7900
## [4,]  200 0.6400 0.7600
## [5,]  500 0.6600 0.7400
## [6,] 1000 0.6710 0.7290
## [7,] 2000 0.6800 0.7195
## [8,] 5000 0.6872 0.7128

Así pues:

• Si la muestra es de tamaño 20, el 95% de las estimaciones muestrales están entre 0.5 y 0.9; dicho de otra forma, el 95% de las estimaciones realizadas con una muestra de tamaño 20 tendrán un error máximo de ±0.2.

• Si la muestra es de tamaño 50, el 95% de las estimaciones muestrales están entre 0.58 y 0.82; dicho de otra forma, el 95% de las estimaciones realizadas con una muestra de tamaño 20 tendrán un error máximo de ±0.12.

• Si la muestra es de tamaño 100, el 95% de las estimaciones muestrales están entre 0.61 y 0.79; dicho de otra forma, el 95% de las estimaciones realizadas con una muestra de tamaño 20 tendrán un error máximo de ±0.09.

• Si la muestra es de tamaño 500, el 95% de las estimaciones muestrales están entre 0.66 y 0.74; dicho de otra forma, el 95% de las estimaciones realizadas con una muestra de tamaño 20 tendrán un error máximo de ±0.04.

• Si la muestra es de tamaño 1000, el 95% de las estimaciones muestrales están entre 0.671 y 0.729; dicho de otra forma, el 95% de las estimaciones realizadas con una muestra de tamaño 20 tendrán un error máximo de ±0.029.

 

Por tanto:

• Si, siendo la verdadera tasa de remisión 0.7, un error de 0.2 (un 20%) es admisible, una muestra de tamaño 20 es suficiente.

• Si queremos que el error máximo de estimación sea de 0.04 (un 4%) la muestra debe ser de tamaño 500.

 

Pueden ejecutarse simulaciones como las anteriores variando los valores de \(\pi\) y \(n\) para determinar el valor de \(n\) adecuado que permitiría estimar \(\pi\) con el error que deseemos.