Tarea 6: Evaluación de pruebas diagnósticas y Curvas ROC
Evaluación de pruebas diagnósticas y Curvas ROC
Odds-Ratio
Ya hemos visto en una tarea anterior como calcular la odds-ratio entre dos variables en una tabla 2 por 2. Por ejemplo, si queremos calcular la odds-ratio entre HTA y DM en la base de datos de Telde, procedemos del modo siguiente:
library(openxlsx)
telde <- read.xlsx("endocrino.xlsx",sheet=1)
telde$DM <- ordered(telde$DM, levels=c(1,0), labels=c("DM+", "DM-"))
telde$HTA_OMS <- ordered(telde$HTA_OMS, levels=c(1,0), labels=c("HTA+", "HTA-"))
thd=with(telde, table(HTA_OMS,DM))
thd## DM
## HTA_OMS DM+ DM-
## HTA+ 83 241
## HTA- 45 661Si calculamos las proporciones por columnas obtendremos las proporciones respectivas de hipertensos entre los DM+ y los DM-:
round(prop.table(thd,2),3)## DM
## HTA_OMS DM+ DM-
## HTA+ 0.648 0.267
## HTA- 0.352 0.733Vemos que la proporción de hipertensos en mucho mayor entre los diabéticos (64.8%) que entre los no diabéticos (26.7%). El test de la chi-cuadrado revela que esta asociación es significativa (no atribuíble al azar):
chisq.test(thd, correct=FALSE)##
## Pearson's Chi-squared test
##
## data: thd
## X-squared = 75.567, df = 1, p-value < 2.2e-16Recordemos que en R la odds-ratio puede calcularse utilizando la función epi.2by2 de la librería epiR:
library(epiR)
epi.2by2(thd)## Outcome + Outcome - Total Inc risk *
## Exposed + 83 241 324 25.62
## Exposed - 45 661 706 6.37
## Total 128 902 1030 12.43
## Odds
## Exposed + 0.3444
## Exposed - 0.0681
## Total 0.1419
##
## Point estimates and 95 % CIs:
## -------------------------------------------------------------------
## Inc risk ratio 4.02 (2.87, 5.64)
## Odds ratio 5.06 (3.42, 7.48)
## Attrib risk * 19.24 (14.16, 24.33)
## Attrib risk in population * 6.05 (3.35, 8.76)
## Attrib fraction in exposed (%) 75.12 (65.11, 82.26)
## Attrib fraction in population (%) 48.71 (35.86, 58.99)
## -------------------------------------------------------------------
## X2 test statistic: 75.567 p-value: < 0.001
## Wald confidence limits
## * Outcomes per 100 population units
Diagnóstico de la DM por A1C
Supondremos en esta sección que disponemos de un marcador, que es una variable continua, cuyos valores difieren significativamente entre el grupo de las personas enfermas y el grupo de las sanas. Por ejemplo la hemoglobina glicosilada A1C difiere entre diabéticos y no diabéticos. Si representamos en un boxplot los valores de esta variable en la muestra de Telde, según que los sujetos tengan o no DM obtenemos la figura siguiente:
boxplot(A1C ~ DM, data=telde, xlab="T2DM",ylab="A1C %",boxwex=.5,col="skyblue")
abline(h=6.5,lty=2) # Traza una linea horizontal en el punto de abcisa 6.5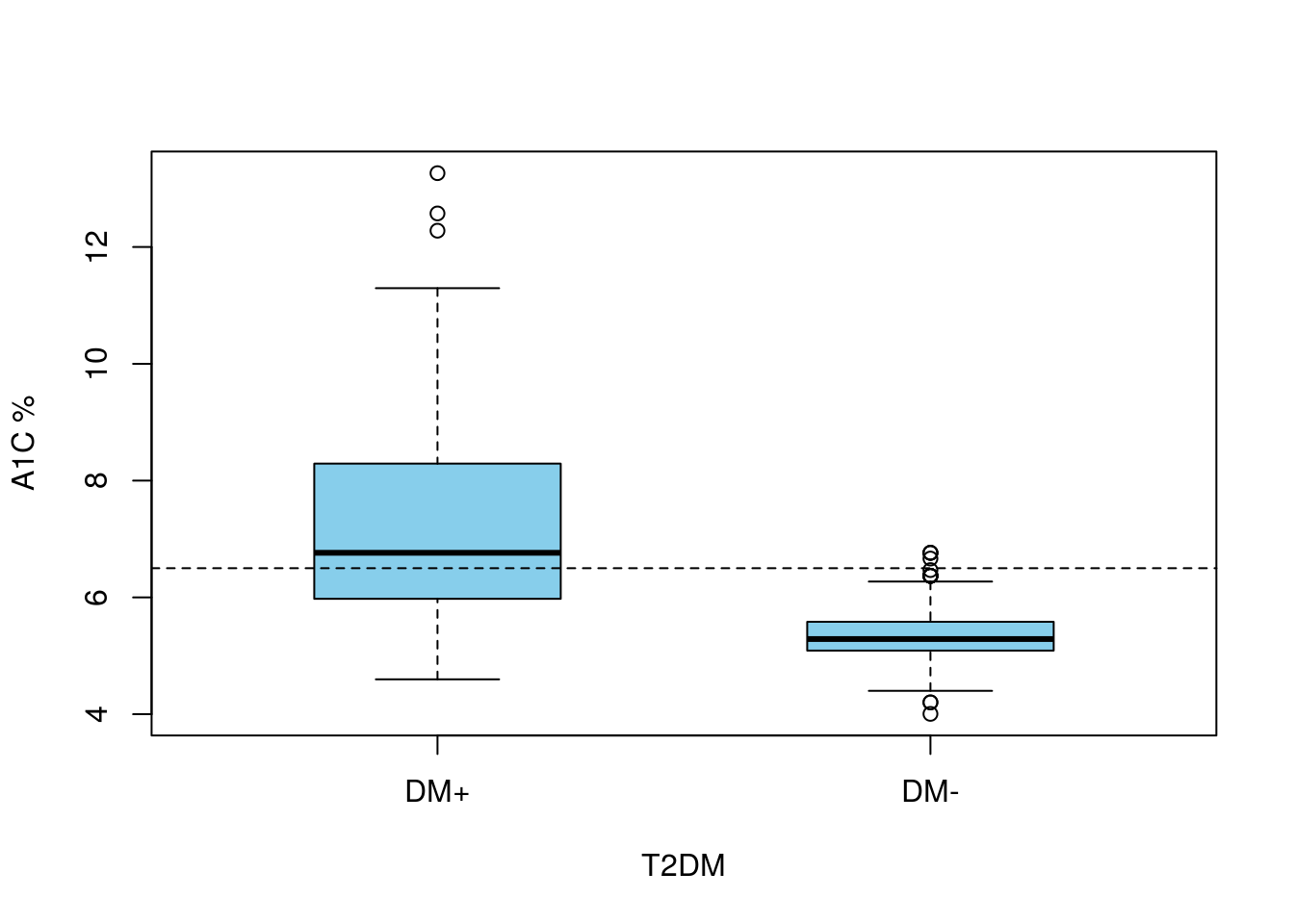
donde hemos representado una línea horizontal para un valor de A1C del 6.5%. Tal como vemos, casi todos los sujetos con AIC menor que este valor están libres de DM, mientras que algo más de la mitad de los que tienen DM están por encima del mismo.
Podemos definir una nueva variable que llamaremos DSC (discriminante) que distinga si el sujeto tiene el valor de A1C por encima de 6.5 o no; si está por debajo de 6.5 entenderemos que el marcador es negativo (el gráfico indica que valores bajos se asocian con ausencia de DM), y por encima de 6.5 es positivo. En R la codificación sería la siguiente:
telde$DSC <- ifelse(telde$A1C>6.5, 1, 0)
telde$DSC <- ordered(telde$DSC, levels=c(1,0), labels=c("DSC+","DSC-"))
table(telde$DSC)##
## DSC+ DSC-
## 79 951Si cruzamos esta variable con la DM obtenemos:
tdd <- with(telde,table(DSC,DM))
tdd## DM
## DSC DM+ DM-
## DSC+ 75 4
## DSC- 53 898y en proporciones:
round(prop.table(tdd,2),3)## DM
## DSC DM+ DM-
## DSC+ 0.586 0.004
## DSC- 0.414 0.996Por tanto medir el valor de A1c y comprobar si está por encima o por debajo de 6.5 constituye una prueba muy específica para la diabetes (la probabilidad estimada de que este marcador sea negativo si el sujeto es no diabético es del 99.6%), aunque poco sensible (la probabilidad estimada de que este marcador sea positivo si el sujeto es diabético es del 58.6%).
La función BDtest del paquete bdpv permite calcular de manera directa la especificidad y sensibilidad, así como otras características, de una prueba diagnóstica. Si no lo tenemos instalado, podemos instalarlo mediante:
install.packages("bdpv")
Un vez instalado, podemos calcular la sensibilidad y especificidad de la prueba mediante la sintaxis que se especifica a continuación. Nótese que hemos de convertir la tabla tdd en un objeto de clase matrix (ya que en caso contrario la función BDtest no procesa la tabla), y además debemos proporcionar una estimación de la prevalencia en la población. En este caso utilizamos como estimación de prevalencia la proporción de diabéticos observada en la muestra.
library(bdpv) # Cargamos la librería
preval.Diab <- prop.table(table(telde$DM))[1] # Estimador de la prevalencia de diabetes en Telde
class(tdd) <- "matrix" # se convierte la tabla tdd a la clase `matrix`
BDtest(tdd, pr=preval.Diab, conf.level = 0.95)## Confidence intervals for binary diagnostic tests.
## Input data set with columns representing the true property of the compounds and rows representing the result of a binary diagnostic test.
## True positive True negative
## Test positive 75 4
## Test negative 53 898
## Estimates and exact confidence limits for assay sensitivity and specificity.
## Estimate Lower 95% limit Lower 97.5% limit Upper 97.5% limit
## Sensitivity 0.5859375 0.5094742 0.4955430 0.6722629
## Specificity 0.9955654 0.9898809 0.9886849 0.9987904
## Estimates and asymptotic confidence limits for predictive values. The prevalence is assumed to be 0.1243.
## Estimate Lower 95% limit Lower 97.5% limit Upper 97.5% limit
## NPV 0.9442692 0.9344345 0.9323747 0.9541744
## PPV 0.9493671 0.8910529 0.8746377 0.9805408
Curva ROC
Para construir la curva ROC necesitamos instalar el paquete pROC en caso de que aún no lo tengamos:
install.packages("pROC")La curva ROC se obtiene mediante:
library(pROC)
rocA1C <- with(telde,roc(DM,A1C))
plot(rocA1C, col="red", print.auc=TRUE)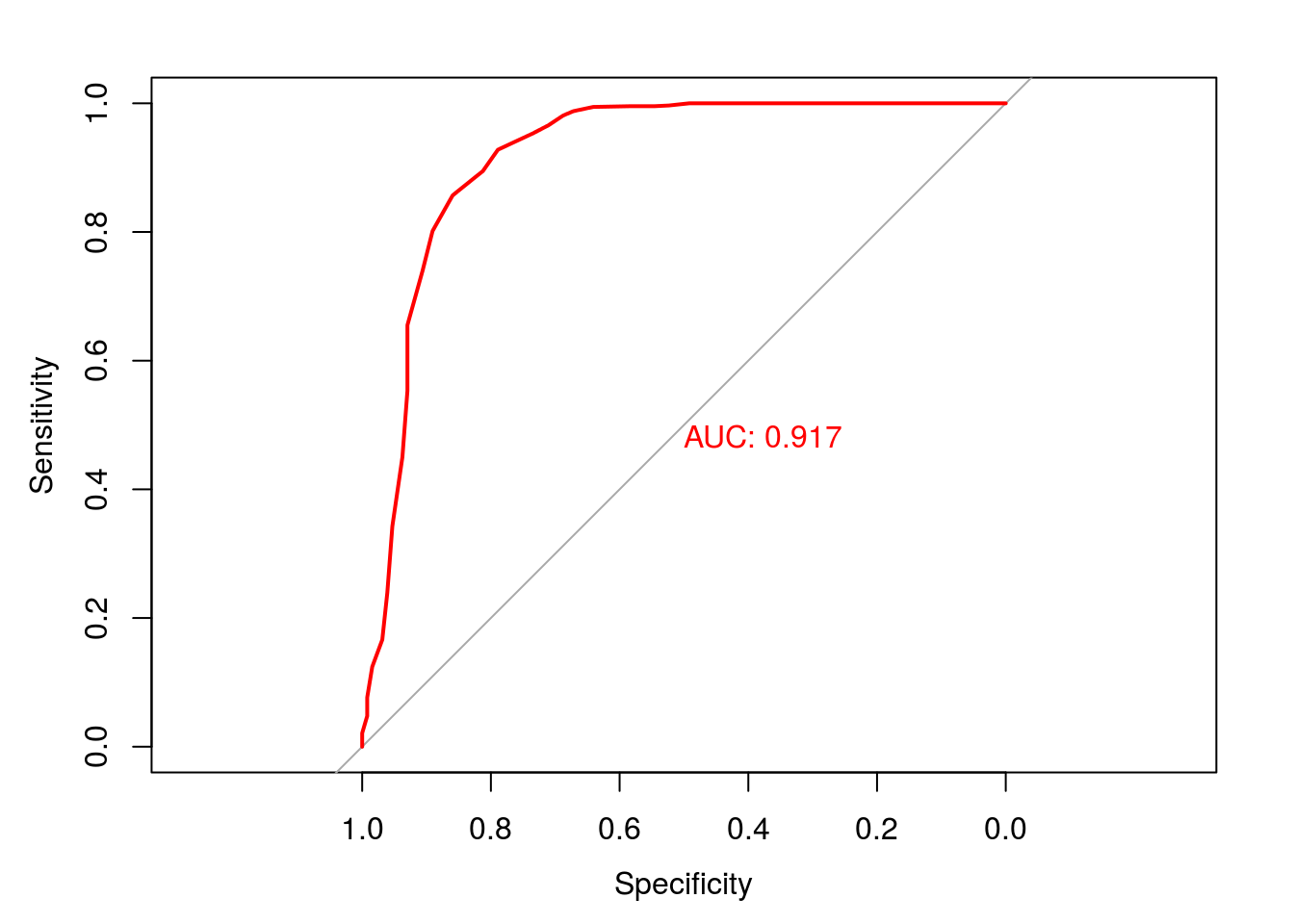
##
## Call:
## roc.default(response = DM, predictor = A1C)
##
## Data: A1C in 128 controls (DM DM+) > 902 cases (DM DM-).
## Area under the curve: 0.9171Un intervalo de confianza para el área bajo la curva se obtiene mediante:
ci.auc(rocA1C)## 95% CI: 0.8821-0.9521 (DeLong)y una gráfica “suavizada” de la curva ROC:
plot.roc(smooth(rocA1C),col="blue", print.auc=TRUE)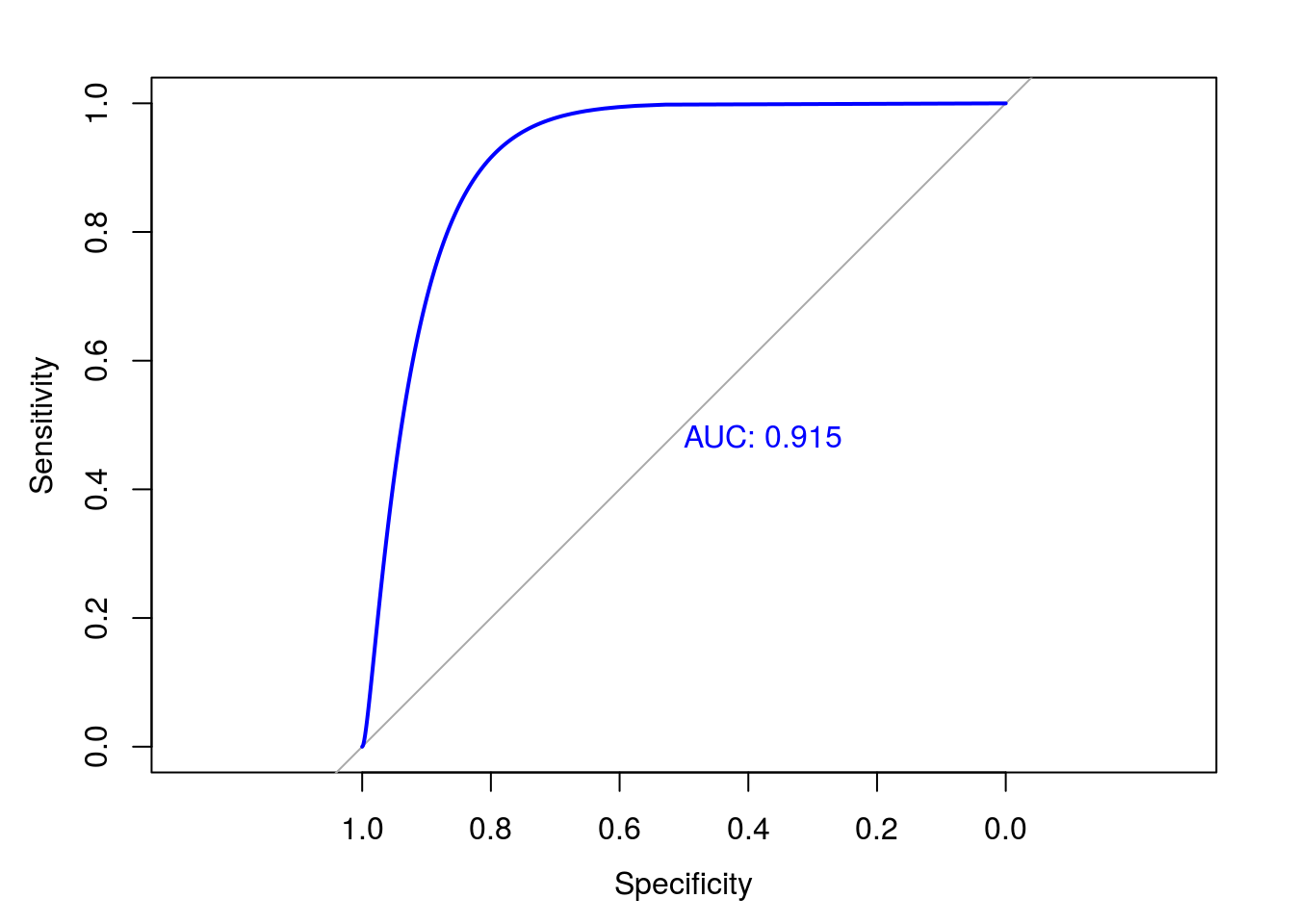
##
## Call:
## smooth.roc(roc = rocA1C)
##
## Data: A1C in 128 controls (DM DM+) > 902 cases (DM DM-).
## Smoothing: binormal
## Area under the curve: 0.9154Unas pocas líneas de código permiten añadir el área y el intervalo de confianza a la gráfica, dejándola lista para publicación:
ci <- as.numeric(ci.auc(rocA1C)) # Valores numéricos del área y el intervalo de confianza
a<-plot.roc(smooth(rocA1C),col="blue")
legend(0.85,.15, sprintf("AUC = %.3f; 95%%-CI = %.3f; %.3f",ci[2],ci[1],ci[3]),bty="n",cex=1.15)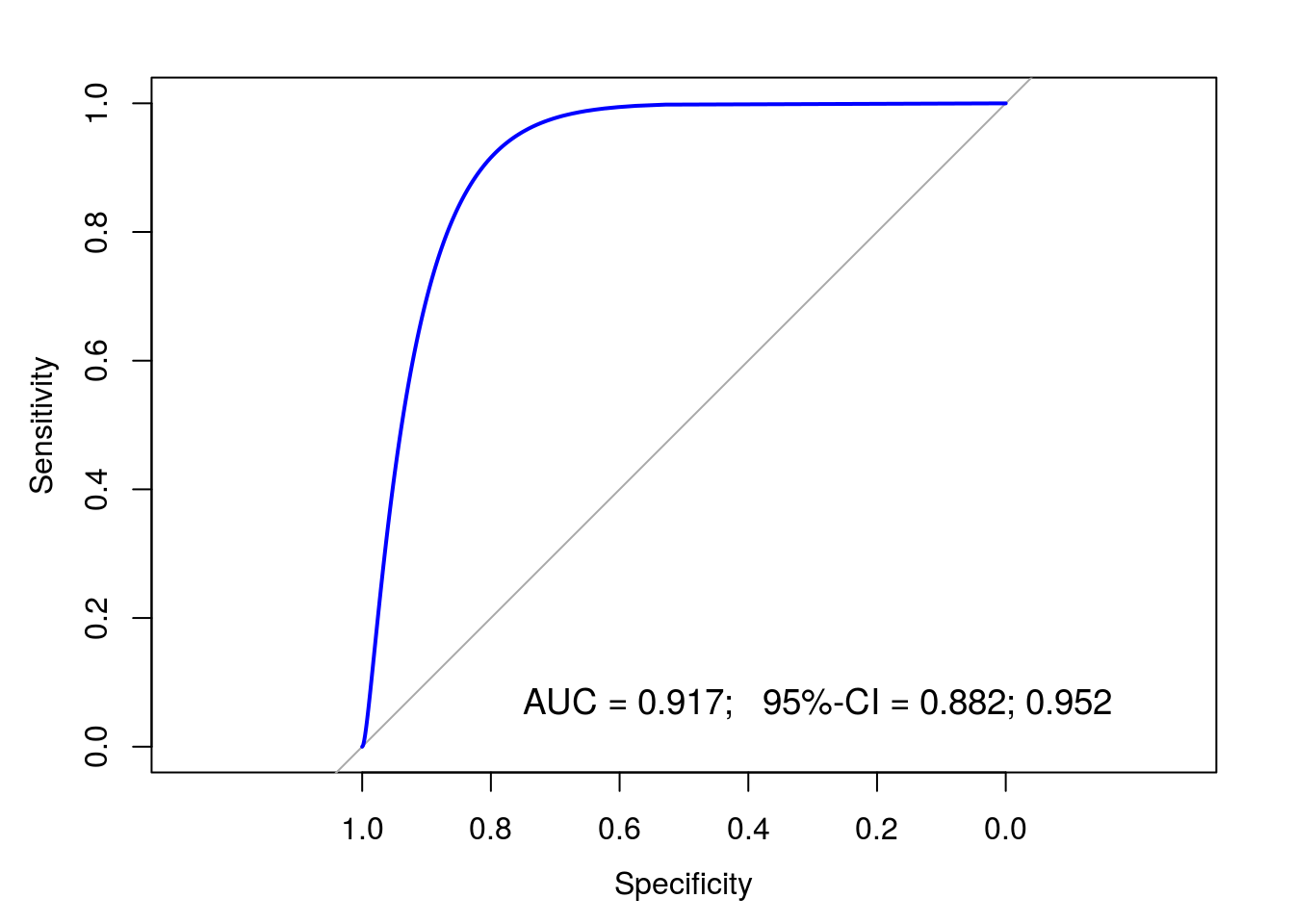
La función coords permite encontrar aquel valor de la variable que al ser usado como punto de corte (cutoff) para discriminar entre sanos y enfermos, maximiza cierta función de la sensibilidad y la especificidad. Por defecto la función a maximizar es:
\[ {\left(1-sensitivity\right)}^2 + {\left(1-specificity\right)}^2\]
cuyo objetivo es conseguir que la sensibilidad y la especificidad se aproximen (simultáneamente) todo lo posible a 1. Al aplicar esta función a nuestros datos resulta:
closest <- coords(rocA1C,"b",ret=c("threshold","specificity","sensitivity","npv","ppv"),
best.method="closest.topleft")
closest## threshold specificity sensitivity npv ppv
## 5.7297500 0.8593750 0.8569845 0.4602510 0.9772440
Podemos definir la regla discriminante (prueba diagnóstica) en función de este cutoff (5.73%), igual que hicimos más arriba con el 6.5%, considerando que la prueba es positiva si A1C>5.73 y negativa en caso contrario:
telde$DSC <- ifelse(telde$A1C>closest[1], 1, 0)
telde$DSC <- ordered(telde$DSC, levels=c(1,0), labels=c("DSC+","DSC-"))
table(telde$DSC)##
## DSC+ DSC-
## 239 791boxplot(A1C ~ DM, data=telde, xlab="T2DM",ylab="A1C %",boxwex=.5,col="skyblue")
abline(h=closest[1],lty=2)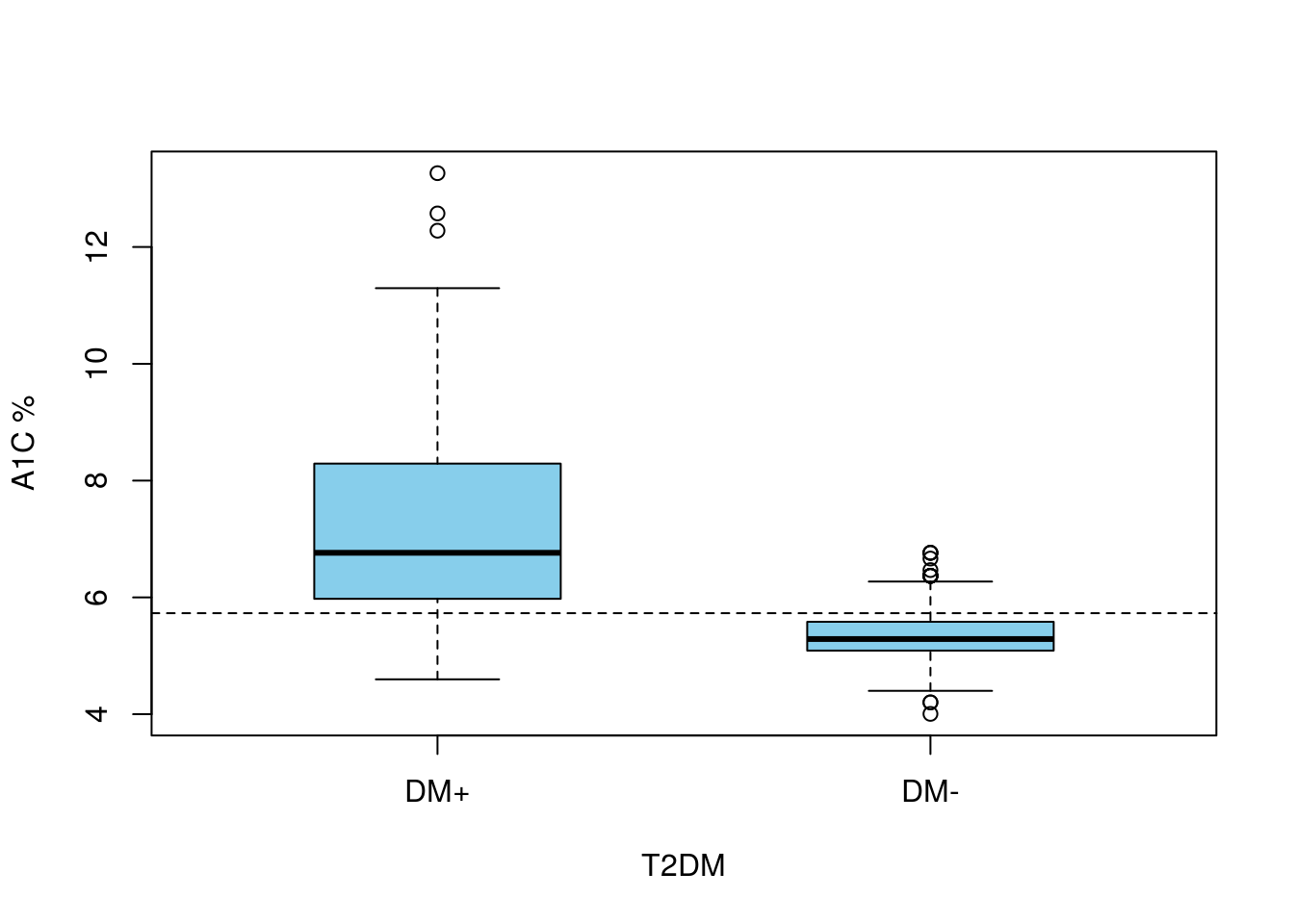
Por último, evaluamos la sensibilidad, especificidad, VPP, VPN de esta prueba diagnóstica mediante BDtest:
tdd <- with(telde,table(DSC,DM))
tdd## DM
## DSC DM+ DM-
## DSC+ 110 129
## DSC- 18 773class(tdd) <- "matrix"
BDtest(tdd, pr=preval.Diab, conf.level = 0.95)## Confidence intervals for binary diagnostic tests.
## Input data set with columns representing the true property of the compounds and rows representing the result of a binary diagnostic test.
## True positive True negative
## Test positive 110 129
## Test negative 18 773
## Estimates and exact confidence limits for assay sensitivity and specificity.
## Estimate Lower 95% limit Lower 97.5% limit Upper 97.5% limit
## Sensitivity 0.8593750 0.7986299 0.7868852 0.9144768
## Specificity 0.8569845 0.8363907 0.8324189 0.8791902
## Estimates and asymptotic confidence limits for predictive values. The prevalence is assumed to be 0.1243.
## Estimate Lower 95% limit Lower 97.5% limit Upper 97.5% limit
## NPV 0.977244 0.9676985 0.9654712 0.9850649
## PPV 0.460251 0.4241572 0.4173220 0.5037780
Ejercicios.
- La siguiente tabla muestra los datos de un estudio sobre la utilización de la PSA (Prostate Specific Antigen) como prueba diagnóstica de la presencia de cáncer de próstata:
| D+ | D- | |
|---|---|---|
| ≥ 4 ng/mL (T+) | 443 | 855 |
| < 4 ng/mL (T-) | 137 | 976 |
Utilizar R para calcular la sensibilidad, especificidad, valor predictivo negativo y valor predictivo positivo de esta prueba diagnóstica en los siguientes casos:
- Cuando la prevalencia del cáncer de próstata en la población es del 5%
- Cuando esta prevalencia es del 1%
- cuando esta prevalencia es del 10%
- HDL como predictor de la presencia del genotipo homocigoto B1/B1 en el polimorfismo Taq 1B. En el estudio de Telde se midió el polimorfismo Taq1B en el gen de la Cholesteryl ester transfer protein (CETP). Este polimorfismo tiene dos alelos, B1 y B2, por lo cual los posibles genotipos son B1/B1, B1/B2 y B2/B2. Estudios previos indican que los individuos homocigotos B1/B1 tienden a presentar valores más bajos de HDL.
Podemos comprobar que en la base de datos de Telde, la variable CETP registra el genotipo de este polimorfismo en aquellas personas en que se pudo medir:
table(telde$CETP)##
## B1B1 B1B2 B2B2
## 200 175 52sum(table(telde$CETP))## [1] 427Construiremos un nuevo factor Taq_1B que nos indique si el individuo es portador o no del genotipo B1/B1:
telde$Taq_1B=factor(ifelse(telde$CETP=="B1B1","B1/B1","No B1/B1"))
table(telde$Taq_1B)##
## B1/B1 No B1/B1
## 200 227Un sencillo boxplot nos muestra la posible asociación entre este genotipo y el valor del HDL, y confirma la presencia de valores ligeramente más bajos de HDL en los sujetos B1/B1:
boxplot(HDL ~ Taq_1B,data=telde, xlab="Taq 1B",ylab="HDL (mg/dL)",boxwex=.4,col="steelblue")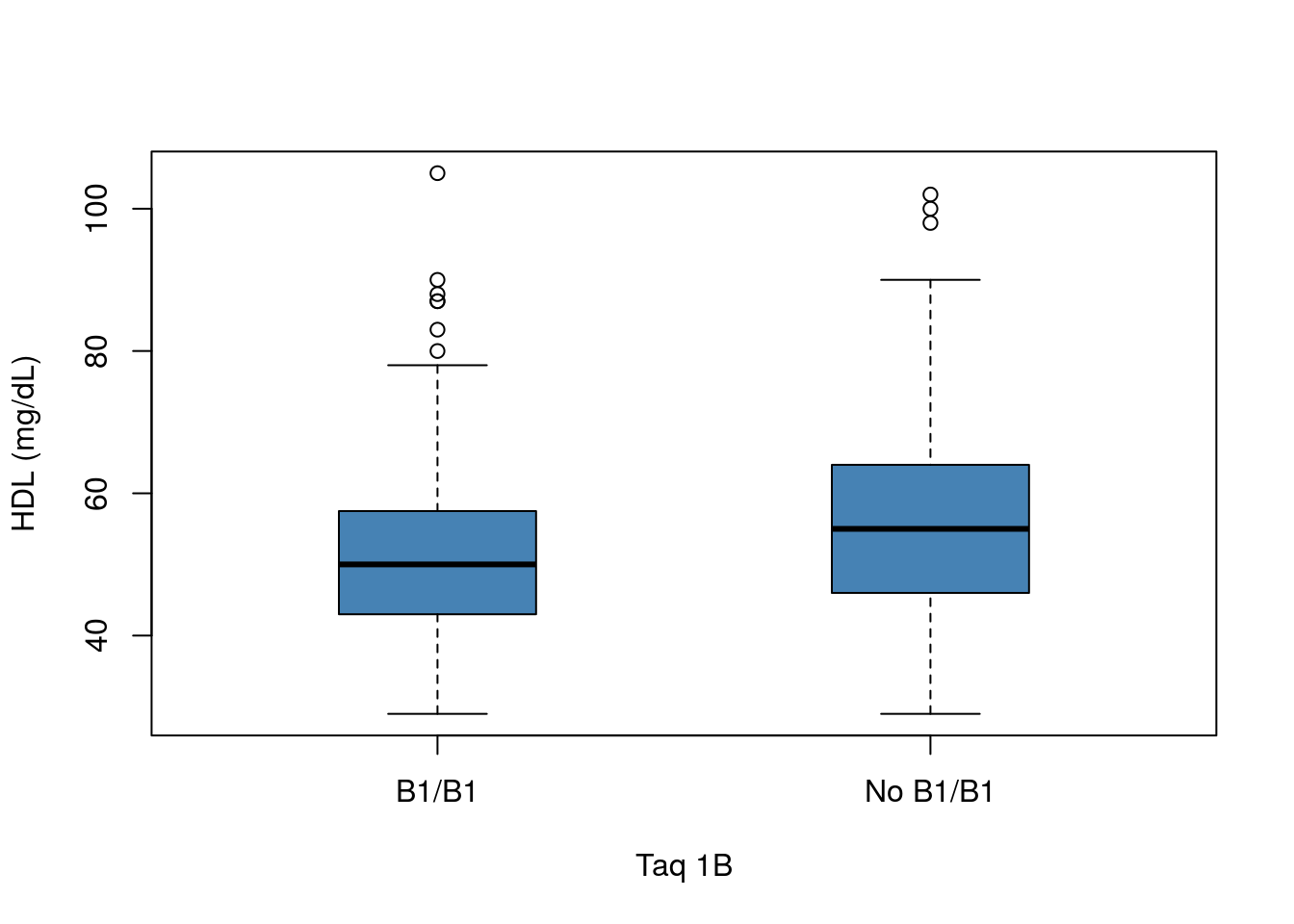
Construir la curva ROC para evaluar la capacidad discriminante del valor de HDL como predictor de la presencia del genotipo homocigoto B1/B1 en el polimorfismo Taq1B del gen CETP. Determinar el cutoff óptimo así como los valores de sensibilidad y especificidad alcanzados para dicho cutoff.