Tarea 5: Riesgo Relativo y Odd Ratio
Riesgo Relativo y Odds Ratio
A Case-Control Study of Factors Associated with HIV Infection among Black Women
Data collection. Trained interviewers used standardized questionnaires to collect epidemiologic, behavioral, socio-economic and demographic data for the 12-month period preceding either the date of diagnosis for the cases and for their male partners, or the date of interview for the controls.
Los datos disponibles se muestran en la siguiente tabla:
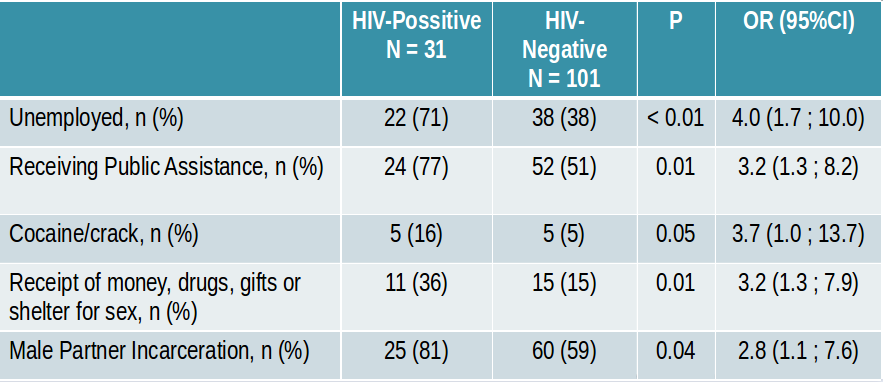
A partir de estos datos calcularemos el riesgo relativo (RR) de padecer HIV según estén presentes o no los distintos factores de riesgo considerados. Para ello tengamos en cuenta que el RR de HIV para el factor T se define como:
\[ RR=\frac{P\left(HIV+\left|T+\right.\right)}{P\left(HIV+\left|T-\right.\right)} \]
donde \(HIV+\) significa que el sujeto padece la enfermedad, \(T+\) significa que el posible factor de riesgo está presente y \(T-\) que está ausente.
Desempleo
- Cuando el factor de riesgo es el desempleo (Unemployed) la tabla nos indica que de las 31 mujeres con HIV, 22 estaban desempleadas, de donde se sigue que las otras 9 tenían empleo; asimismo de las 101 sin HIV, 38 estaban desempleadas, lo que significa que las restantes 101-38=63 tenían empleo. Podemos construir una tabla cruzada con estos datos del siguiente modo:
tabla1=array(c(22,9,38,63),dim=c(2,2))
colnames(tabla1)=c("HIV+","HIV-")
rownames(tabla1)=c("T+","T-")
tabla1## HIV+ HIV-
## T+ 22 38
## T- 9 63Puede mejorarse la presentación con pander:
library(pander)
pander(tabla1)| HIV+ | HIV- | |
|---|---|---|
| T+ | 22 | 38 |
| T- | 9 | 63 |
Si calculamos las proporciones por columnas:
pc <- prop.table(tabla1,2)
pander(round(pc,2)) # Redondeamos a dos dígitos decimales| HIV+ | HIV- | |
|---|---|---|
| T+ | 0.71 | 0.38 |
| T- | 0.29 | 0.62 |
confirmamos que, efectivamente el 71% de las mujeres HIV+ estaban desempleadas, y también lo estaban el 38% de las HIV-, tal como figura en la tabla original. Ahora bien, para calcular el riesgo relativo necesitamos la probabilidad \(P\left(HIV+\left|T+\right.\right)\), es decir, la probabilidad de padecer HIV cuando se está en desempleo, y \(P\left(HIV+\left|T-\right.\right)\), la probabilidad de padecer HIV cuando NO se está en desempleo. Por tanto necesitamos las probabilidades por filas de la tabla anterior:
pf <- prop.table(tabla1,1)
pander(round(pf,4))| HIV+ | HIV- | |
|---|---|---|
| T+ | 0.3667 | 0.6333 |
| T- | 0.125 | 0.875 |
El riesgo relativo es, por tanto:
\[ RR=\frac{P\left(HIV+\left|T+\right.\right)}{P\left(HIV+\left|T-\right.\right)} = \frac{0.3667}{0.125}\]
que puede calcularse directamente con R mediante:
RR <- pf[1,1]/pf[2,1]
RR## [1] 2.933333Por tanto, el riesgo de padecer HIV es casi el triple entre las mujeres negras desempleadas que entre las que tienen empleo.
¿Es correcto calcular el Riesgo Relativo en este contexto (estudio caso-control)?
Para responder a esta pregunta observemos lo siguiente: en un estudio de casos y controles es el investigador el que decide cuántos casos y cuántos controles se seleccionan. Supongamos que hubiésemos decidido (o hubiésemos podido) tomar 310 casos (mujeres con HIV) en lugar de los 31 que tenemos, y 303 controles (en lugar de los 101 que tenemos). En otras palabras, multiplicamos por 10 el tamaño de la muestra de casos y por 3 el tamaño de la muestra de controles. Supongamos además que las proporciones de mujeres empleadas y desempleadas siguen siendo las mismas en ambos grupos. En tal caso, los datos disponibles serían:
tabla2=array(c(220,90,114,189),dim=c(2,2))
colnames(tabla2)=c("HIV+","HIV-")
rownames(tabla2)=c("T+","T-")
pander(tabla2)| HIV+ | HIV- | |
|---|---|---|
| T+ | 220 | 114 |
| T- | 90 | 189 |
Podemos comprobar que las proporciones por columnas coinciden con las mostradas en la tabla anterior:
pc2 <- prop.table(tabla2,2)
pander(round(pc2,2))| HIV+ | HIV- | |
|---|---|---|
| T+ | 0.71 | 0.38 |
| T- | 0.29 | 0.62 |
Pero ahora las proporciones por filas son distintas:
pf2 <- prop.table(tabla2,1)
pander(round(pf2,4))| HIV+ | HIV- | |
|---|---|---|
| T+ | 0.6587 | 0.3413 |
| T- | 0.3226 | 0.6774 |
y también lo es el riesgo relativo:
RR <- pf2[1,1]/pf2[2,1]
RR## [1] 2.041916que ha disminuído a 2.04. Por tanto el riesgo relativo ha disminuido en una tercera parte (de casi 3 a 2 y poco) simplemente por haber cambiado el número de casos y controles elegidos, aún cuando las prevalencias del factor de riesgo no han cambiado en cada grupo. Así pues, en los estudios de casos y controles, el riesgo relativo depende de los tamaños de muestra elegidos arbitrariamente por el investigador, y no es por tanto una característica intrínseca de la asociación entre la enfermedad y el factor de riesgo. Por tanto no puede ser un indicador útil del valor de dicha asociación, y no puede usarse con el objetivo de medir dicho valor.
¿Es el riesgo relativo realmente una medida de asociación?
Señalemos además que el riesgo relativo no es propiamente una medida de asociación en sentido estricto. De una medida de asociación se espera que la asociación entre A y B sea la misma que entre B y A, lo que no ocurre con el riesgo relativo. Podemos comprobar esta afirmación de manera muy simple: hemos visto que en el estudio original, el riesgo relativo de padecer HIV (A) según que la mujer esté o no desempleada (B) es 2.9333; para calcular ahora el riesgo de que una mujer esté desempleada (B) según que tenga o no HIV (A), deberíamos partir de la tabla traspuesta de la original:
tabla3 <- t(tabla1)
tabla3## T+ T-
## HIV+ 22 9
## HIV- 38 63y procediendo igual que antes, calcular las proporciones por filas, y a partir de ellas el RR:
pf3 <- prop.table(tabla3,1)
pander(round(pf3,4))| T+ | T- | |
|---|---|---|
| HIV+ | 0.7097 | 0.2903 |
| HIV- | 0.3762 | 0.6238 |
RR <- pf3[1,1]/pf3[2,1]
RR[1] 1.886248
Como vemos este riesgo no coincide con el calculado inicialmente: el riesgo de HIV condicionado por el desempleo (asociación de A con B) no coindice con el riesgo de desempleo condicionado por el HIV (asociación de B con A), lo que confirma que el riesgo relativo no es simétrico
Odds ratio
La odds-ratio que mide la asociación entre dos eventos A y B se define como:
\[OR\left(A,B\right)=\frac{P({A}\;|\;{B})/P({{A}^{c}}\;|\;{B})}{P({A}\;|\;{{B}^{c}})/P({{A}^{c}}\;|\;{{B}^{c}})}\]
Puede comprobarse que la odds-ratio sí que es una medida simétrica y que:
\[OR\left(A,B\right)=OR\left(B,A\right)=\frac{P({B}\;|\;{A})/P({{B}^{c}}\;|\;{A})}{P({B}\;|\;{{A}^{c}})/P({{B}^{c}}\;|\;{{A}^{c}})}\]
A modo de ejemplo, si volvemos a la relación entre HIV y desempleo del ejemplo anterior, si consideramos que el suceso \(A\) es el HIV+, entonces el contrario \(A^c\) es el HIV-. Asimismo, si el suceso \(B\) es estar desempleada (\(T+\)), el \(B^c\) sería tener empleo (\(T-\)). Entonces, podríamos calcular la OR mediante:
\[OR\left(HIV,T\right)= \frac{P({HIV+}\;|\;{T+})/P({HIV-}\;|\;{T+})}{P({HIV+}\;|\;{T-})/P({HIV-}\;|\;{T-})}\]
Para obtener este valor de OR partimos nuevamente de la tabla:
pander(tabla1)| HIV+ | HIV- | |
|---|---|---|
| T+ | 22 | 38 |
| T- | 9 | 63 |
y de sus proporciones por fila:
pf=prop.table(tabla1,1)
pander(round(pf,4))| HIV+ | HIV- | |
|---|---|---|
| T+ | 0.3667 | 0.6333 |
| T- | 0.125 | 0.875 |
Tenemos entonces:
\[OR = \frac{0.3667 / 0.6333}{0.125 / 0.875}=\frac{0.5789474}{0.1428571}= 4.0526\]
que en R se obtiene como:
(pf[1,1]/pf[1,2]) / (pf[2,1]/pf[2,2])## [1] 4.052632
Si queremos calcular:
\[OR\left(T,HIV\right)= \frac{P({T+}\;|\;{HIV+})/P({T-}\;|\;{HIV+})}{P({T+}\;|\;{HIV-})/P({T-}\;|\;{HIV-})}\]
volvemos a partir de la tabla:
pander(tabla1)| HIV+ | HIV- | |
|---|---|---|
| T+ | 22 | 38 |
| T- | 9 | 63 |
pero ahora habremos de calcular las proporciones por columnas:
pc=prop.table(tabla1,2)
pander(round(pc,4))| HIV+ | HIV- | |
|---|---|---|
| T+ | 0.7097 | 0.3762 |
| T- | 0.2903 | 0.6238 |
Tenemos entonces:
\[OR = \frac{0.7097 / 0.0.2903}{0.3762 / 0.6238}=\frac{2.4444444}{0.6031746}= 4.0526\]
que en R se obtiene como:
(pc[1,1]/pc[1,2]) / (pc[2,1]/pc[2,2])## [1] 4.052632
Así pues, este ejemplo confirma la simetría de la odds-ratio: \[OR\left(HIV,T\right) = OR\left(T,HIV\right) = 4.0526316\]
Señalemos por último que la odds-ratio puede obtenerse también a partir de la tabla cruzada de frecuencias absolutas:
| B+ | B- | |
|---|---|---|
| A+ | n[1,1] | n[1,2] |
| A- | n[2,1] | n[2,2] |
sin necesidad de calcular proporciones por filas ni por columnas, mediante:
\[OR = \frac{n[1,1]\cdot n[2,2]}{n[1,2]\cdot n[2,1]}\]
NOTA: esto sólo es verdad si en la tabla la categoría positiva es la primera tanto en filas como en columnas.
Si calculamos la OR de esta manera en la tabla1 anterior:
tabla1## HIV+ HIV-
## T+ 22 38
## T- 9 63(tabla1[1,1]*tabla1[2,2])/(tabla1[1,2]*tabla1[2,1])## [1] 4.052632volvemos a obtener el mismo resultado.
Cálculo de la Odds-Ratio con el paquete epiR
El paquete epiR contiene algunas funciones que permiten obtener fácilmente la OR y el RR a partir de una tabla cruzada. En primer lugar cargamos la librería:
library(epiR)y podemos obtener inmediatamente la odds-ratio de HIV frente a desempleo mediante la función epi.2by2 aplicada a la tabla1:
pander(tabla1)| HIV+ | HIV- | |
|---|---|---|
| T+ | 22 | 38 |
| T- | 9 | 63 |
epi.2by2(tabla1)## Outcome + Outcome - Total Inc risk *
## Exposed + 22 38 60 36.7
## Exposed - 9 63 72 12.5
## Total 31 101 132 23.5
## Odds
## Exposed + 0.579
## Exposed - 0.143
## Total 0.307
##
## Point estimates and 95 % CIs:
## -------------------------------------------------------------------
## Inc risk ratio 2.93 (1.46, 5.88)
## Odds ratio 4.05 (1.69, 9.71)
## Attrib risk * 24.17 (9.78, 38.56)
## Attrib risk in population * 10.98 (0.47, 21.50)
## Attrib fraction in exposed (%) 65.91 (31.64, 83.00)
## Attrib fraction in population (%) 46.77 (12.12, 67.76)
## -------------------------------------------------------------------
## X2 test statistic: 10.637 p-value: 0.001
## Wald confidence limits
## * Outcomes per 100 population unitsNotas importantes:
Para que el cálculo sea correcto la tabla de partida (
tabla1en este ejemplo) debe estar ordenada de forma que las categorías “positivas” (tener la enfermedad, tener el factor de riesgo, …) sean las primeras en cada variable.La función
epi.2by2, por defecto devuelve también el riesgo relativo. Es responsabilidad del investigador tener en cuenta que el RR en este problema (diseño caso-control), carece de sentido.
Cálculo de la odds-ratio y riesgo relativo para variables incluídas en bases de datos (data.frames)
Cuando se desea calcular la odds-ratio entre dos variables que forman parte de un data.frame lo único que habremos de hacer es construir la tabla cruzada para dichas variables, con la precaución de que los valores positivos (presencia de la enfermedad, presencia del factor de riesgo, presencia de la exposición) deben situarse en primer lugar en las filas y columnas de la tabla, y los valores negativos (ausencia de enfermedad, factor de riesgo o exposición) en segundo lugar. Para ello utilizaremos la función ordered.
A modo de ejemplo, calculemos la odds-ratio entre diabetes e hipertensión para los datos de Telde. En primer lugar leemos la base de datos:
library(openxlsx)
telde=read.xlsx("endocrino.xlsx")Ordenamos los valores de DM y HTA:
telde$DM <- ordered(telde$DM, levels=c(1,0), labels=c("DM+","DM-"))
telde$HTA_OMS <- ordered(telde$HTA_OMS, levels=c(1,0), labels=c("HTA+","HTA-"))Construimos la tabla cruzada:
tadh <- with(telde, table(DM, HTA_OMS))
tadh## HTA_OMS
## DM HTA+ HTA-
## DM+ 83 45
## DM- 241 661Y por último aplicamos la función epi.2by2 a dicha tabla para calcular la odds-ratio:
epi.2by2(tadh)## Outcome + Outcome - Total Inc risk *
## Exposed + 83 45 128 64.8
## Exposed - 241 661 902 26.7
## Total 324 706 1030 31.5
## Odds
## Exposed + 1.844
## Exposed - 0.365
## Total 0.459
##
## Point estimates and 95 % CIs:
## -------------------------------------------------------------------
## Inc risk ratio 2.43 (2.05, 2.87)
## Odds ratio 5.06 (3.42, 7.48)
## Attrib risk * 38.13 (29.36, 46.89)
## Attrib risk in population * 4.74 (0.69, 8.79)
## Attrib fraction in exposed (%) 58.80 (51.30, 65.14)
## Attrib fraction in population (%) 15.06 (10.77, 19.15)
## -------------------------------------------------------------------
## X2 test statistic: 75.567 p-value: < 0.001
## Wald confidence limits
## * Outcomes per 100 population units
Ejercicios.
Calcular las odds-ratio para los restantes factores de riesgo considerados en el estudio original del HIV en mujeres negras (Recibir ayudas sociales, consumir cocaína/crack, prostitución o encarcelamiento de la pareja)
Utilizando la base de datos de Telde, calcular la odds-ratio entre las variables TABACO y ALCOHOL
Utilizando la base de datos de Telde, calcula el IMC del siguiente modo:
telde$IMC=telde$PESO/(telde$TALLA/100)^2y construye la variable OBESIDAD con los valores OB+ para los sujetos con IMC>30 y OB- cuando el IMC es menor o igual que 30:
telde$OBESIDAD=ifelse(telde$IMC>30,"OB+","OB-")
table(telde$OBESIDAD)##
## OB- OB+
## 698 332Calcula la OR entre obesidad y sedentarismo, y entre obesidad y DM.