Tablas univariantes

Para construir una tabla de frecuencias absolutas utilizamos la funcion table(). Por ejemplo, para contar el número de diabéticos y no diabéticos en la muestra:

table(telde$DM)

## 
##   0   1 
## 902 128

Obsérvese que el nombre de la variable (DM) va precedido por el nombre del data.frame telde y el símbolo $. Ello permite utilizar simultáneamente varios data.frames que contengan información de las mismas variables (por ejemplo, podríamos tener un estudio similar cargado en otro data.frame llamado arucas, y accederíamos a la variable como arucas$DM).

De la misma forma, podemos contar el número de hombres y de mujeres:

table(telde$SEXO)

## 
##   0   1 
## 582 448

Esta tabla resulta poco informativa ya que a priori no sabemos quienes son los hombres y quienes las mujeres, ya que la variable SEXO toma los valores 0 y 1. Sabiendo que el 0 corresponde a los hombres y el 1 a las mujeres, podemos hacer la recodificación mediante:

telde$SEXO=factor(telde$SEXO,levels=c(0,1),labels=c("Hombre","Mujer"))

De esta forma, si repetimos la tabla, resultará mucho más clara:

table(telde$SEXO)

## 
## Hombre  Mujer 
##    582    448

Si en lugar de las frecuencias absolutas (número de hombres y mujeres, o número de diabéticos) queremos las frecuencias relativas (proporciones), utilizamos la función prop.table():

prop.table(table(telde$DM))

## 
##         0         1 
## 0.8757282 0.1242718

prop.table(table(telde$SEXO))

## 
##    Hombre     Mujer 
## 0.5650485 0.4349515

Podemos representar las tablas mediante diagramas de barras, en las que se pueden especificar colores, etiquetas para los ejes, títulos, etc:

barplot(table(telde$SEXO), col=c("lightblue","pink"),
        xlab="Sexo", ylab="Frecuencia", 
        main="Estudio de Telde.\n Distribución por sexos.")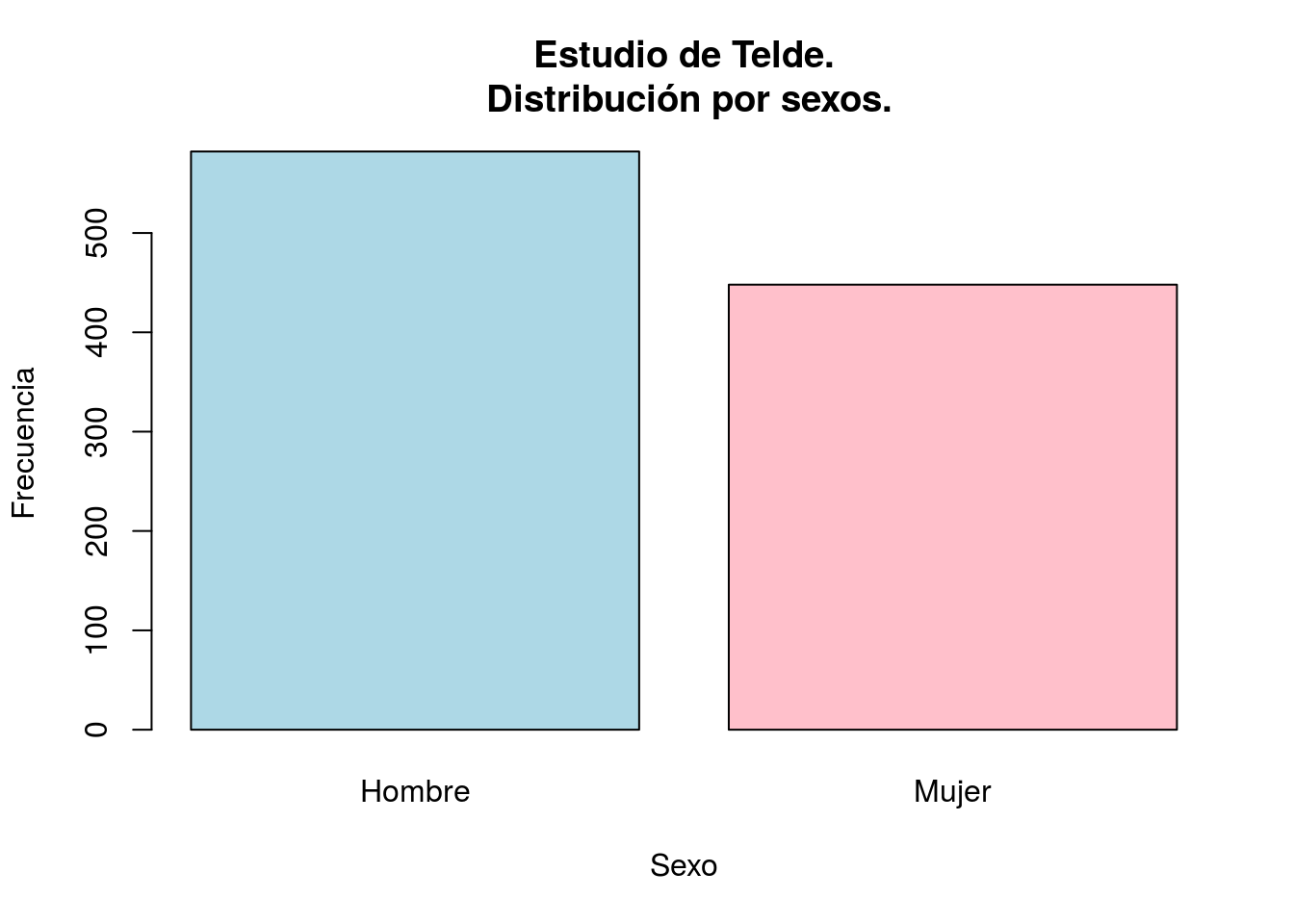

Otra representación habitual es mediante diagramas de sectores:

pie(table(telde$SEXO), col=c("lightblue","pink"),
        main="Estudio de Telde.\n Distribución por sexos.")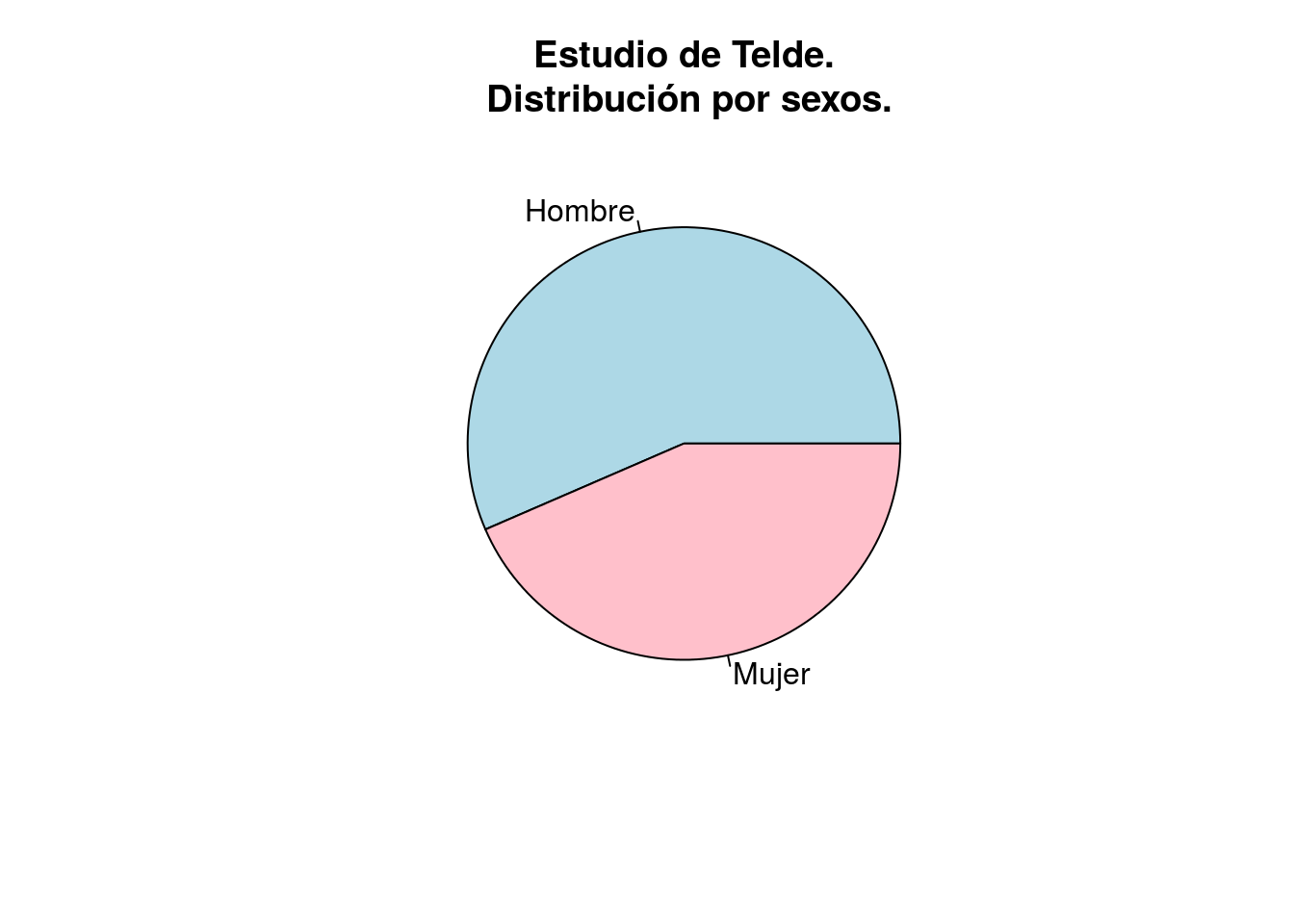

 

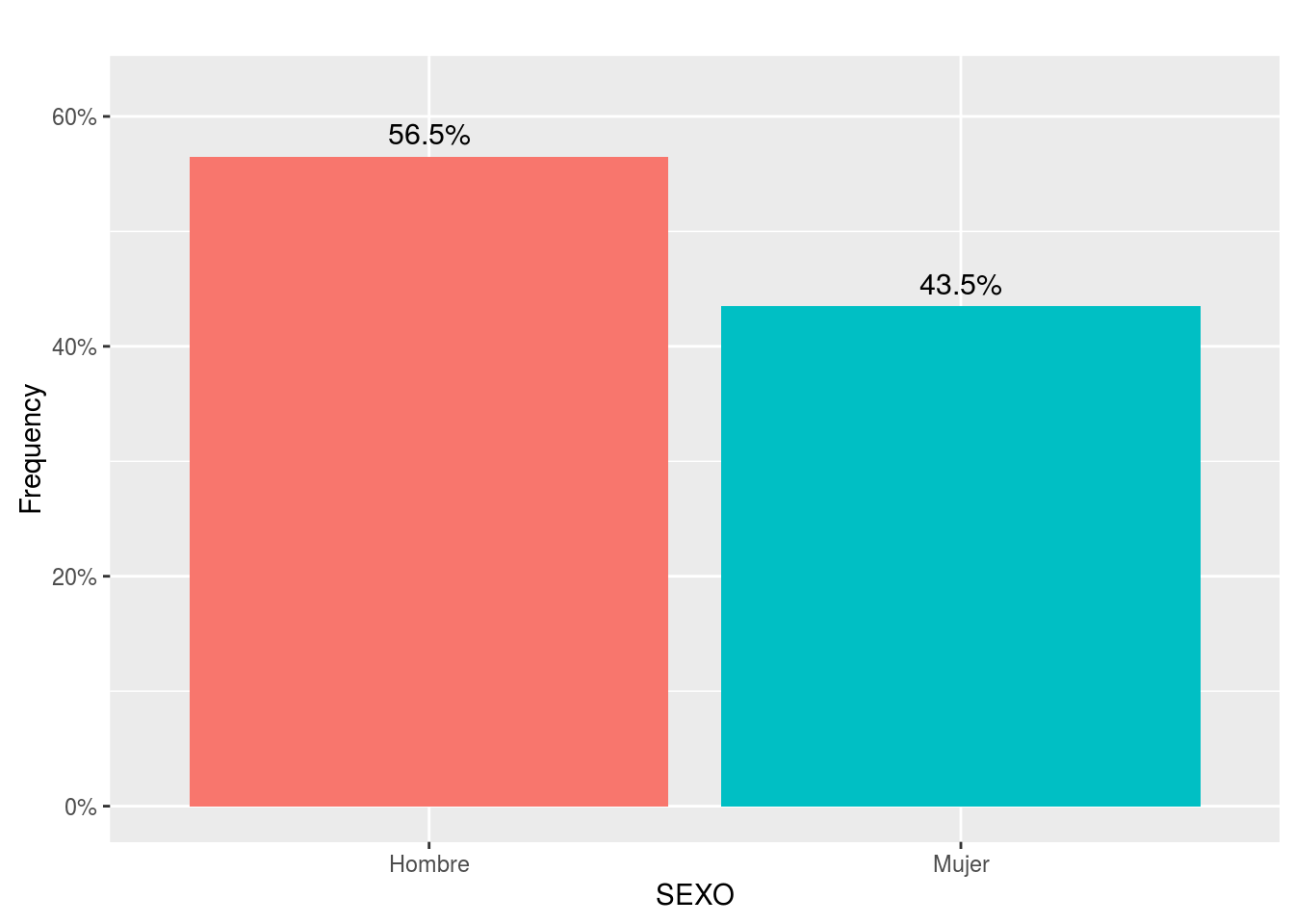
El paquete ULPGCmisc calcula tablas y gráficos conjuntamente con la función freqTable():

library(ULPGCmisc) # Cargamos la librería ULPGCmisc
freqTable(telde$SEXO)

Data are summarized in absolute frequencies and percentages, n(%)

Variable (levels)	All data (n=1030)
SEXO
Hombre	582 (56.50)
Mujer	448 (43.50)

 

 

Tablas cruzadas

La función table() también permite calcular las frecuencias cruzadas de dos variables. Basta simplemente con indicar los dos nombres. Así, por ejemplo, para calcular el número de diabéticos y no diabéticos según el sexo podemos utilizar:

table(telde$SEXO,telde$DM)

##         
##            0   1
##   Hombre 528  54
##   Mujer  374  74

o bien:

with(telde,table(SEXO,DM))

##         DM
## SEXO       0   1
##   Hombre 528  54
##   Mujer  374  74

 

Para calcular las frecuencias relativas puede resultar más cómodo asignar un nombre a la tabla cruzada:

tbSexDM <- with(telde,table(SEXO,DM))

Las frecuencias relativas pueden calcularse entonces:

• Para toda la tabla:

prop.table(tbSexDM)

##         DM
## SEXO              0          1
##   Hombre 0.51262136 0.05242718
##   Mujer  0.36310680 0.07184466

 

• Por filas: En la tabla cruzada, cada fila corresponde a uno de los dos sexos; si queremos calcular, para para cada sexo por separado, cuáles son las proporciones respectivas de diabéticos y no diabéticos ejecutamos la siguiente función:

prop.table(tbSexDM,1)

##         DM
## SEXO              0          1
##   Hombre 0.90721649 0.09278351
##   Mujer  0.83482143 0.16517857

que nos indica que entre los hombres hay un 9.27% de diabéticos y entre las mujeres un 16.52% de diabéticas:

 

• Por columnas: La siguiente tabla nos muestra cuáles son las proporciones relativas de hombres y mujeres entre las personas diabéticas, así como entre las no diabéticas:

prop.table(tbSexDM,2)

##         DM
## SEXO             0         1
##   Hombre 0.5853659 0.4218750
##   Mujer  0.4146341 0.5781250

Esta tabla nos indica que entre los diabéticos el 42.19% son hombres y el 57.81% mujeres; asimismo, entre los no diabéticos el 58.54% son hombres y el restante 41,46% mujeres.

 

 

Podemos representar gráficamente estas tablas mediante diagramas de barras:

• Frecuencias absolutas totales:

barplot(with(telde,table(SEXO,DM)),beside=TRUE,legend=TRUE,
        xlab="Presencia de DM2", ylab="Frecuencia",
        col=c("lightblue","pink"), main="Estudio de Tede \n DM2 según sexo")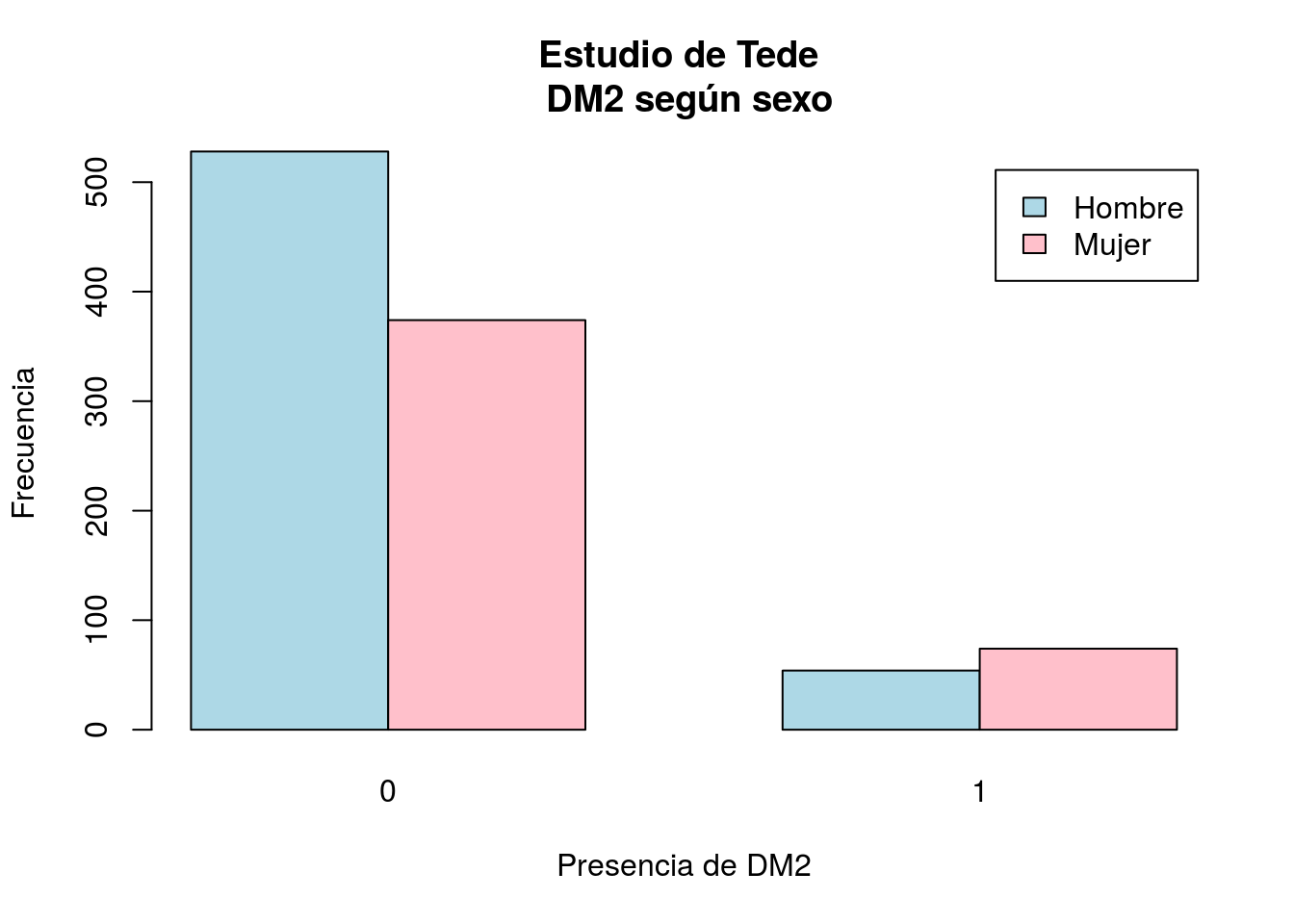

 

• Frecuencias relativas por columnas:

tb2=with(telde,prop.table(table(SEXO,DM),2))
barplot(tb2,beside=TRUE,legend=TRUE,ylim=c(0,1),
        xlab="Presencia de DM2", ylab="Proporción muestral",
        col=c("lightblue","pink"), 
        main="Estudio de Tede \nDistribución de sexos según presencia de DM2")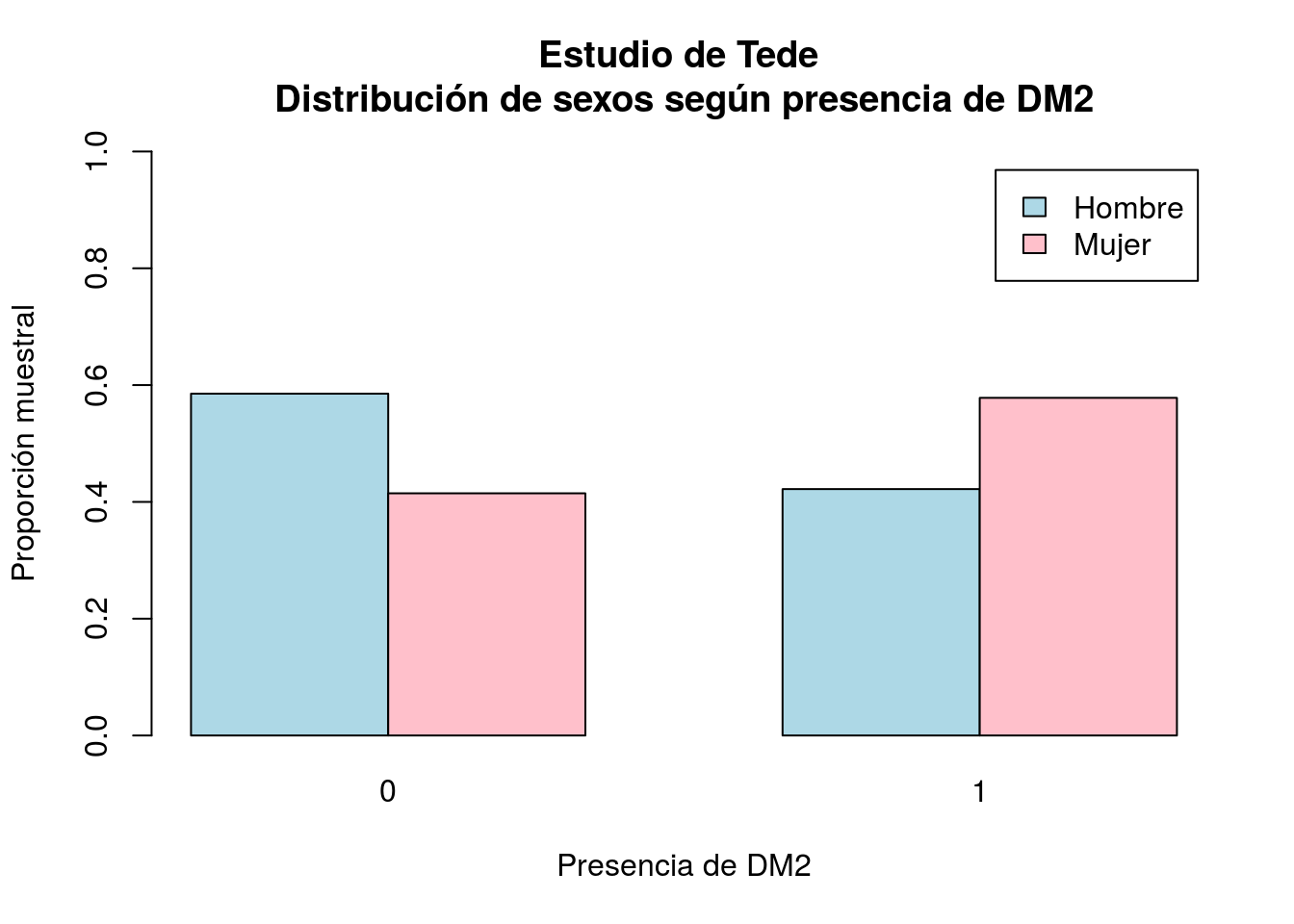

 

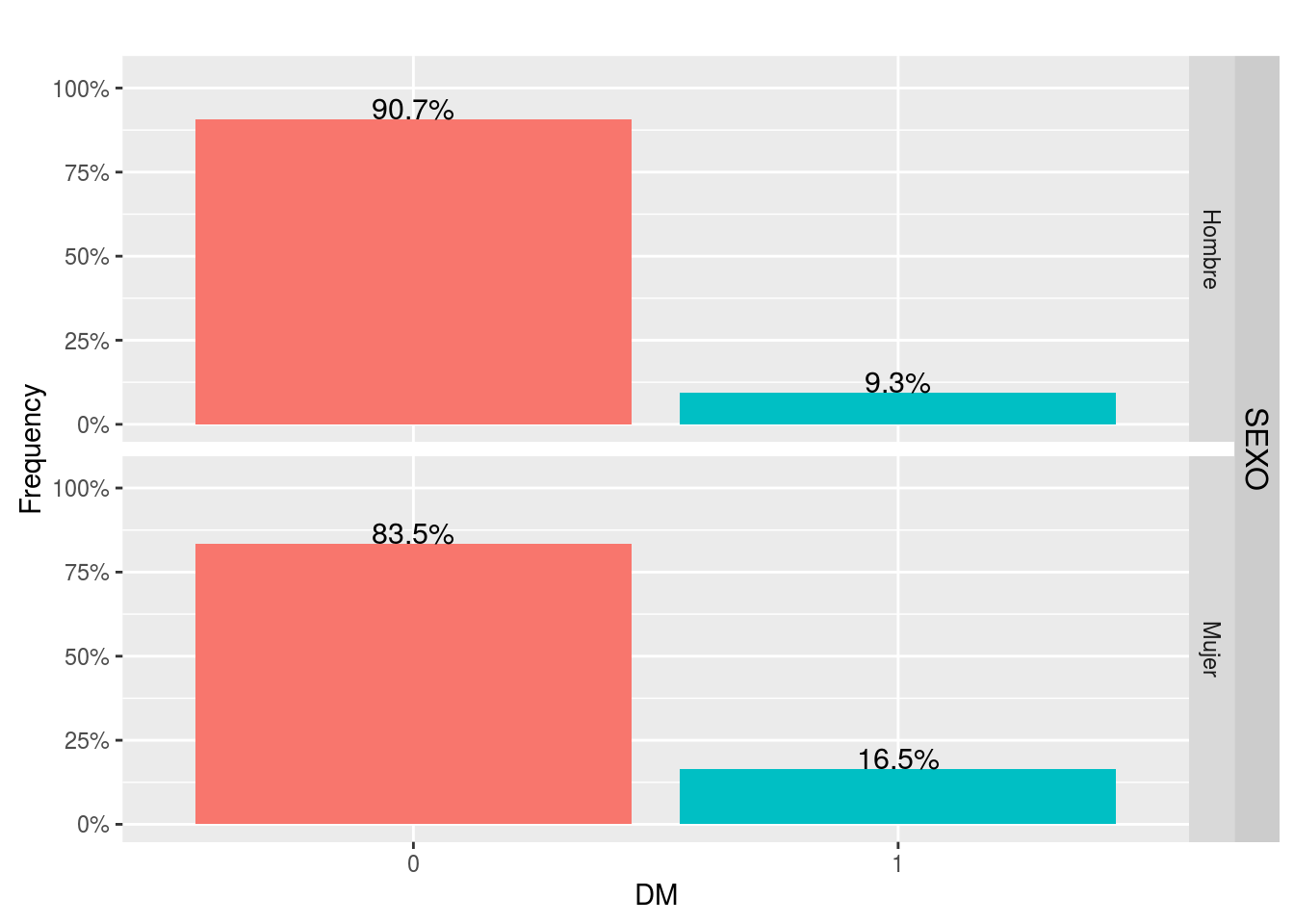
La función freqTable() del paquete ULPGCmisc construye tablas y gráficos conjuntamente:

with(telde, freqTable(DM, by=SEXO))

Data are summarized in absolute frequencies and percentages, n(%)

Variable (levels)	All data (n=1030)	SEXO = Hombre (n=582)	SEXO = Mujer (n=448)	Chi-Squared test P
DM				0.0007
‌ 0	902 (87.57)	528 (90.72)	374 (83.48)
‌ 1	128 (12.43)	54 (9.28)	74 (16.52)

 

 

telde$DM2=ordered(telde$DM,levels=c(1,0),c("Sí","No"))
with(telde,table(DM2))

## DM2
##  Sí  No 
## 128 902

with(telde,table(SEXO,DM2))

##         DM2
## SEXO      Sí  No
##   Hombre  54 528
##   Mujer   74 374

barplot(table(telde$DM2), col=c("red3","green3"),
        xlab="DM2", ylab="Frecuencia", 
        main="Estudio de Telde.\n Distribución de DM.")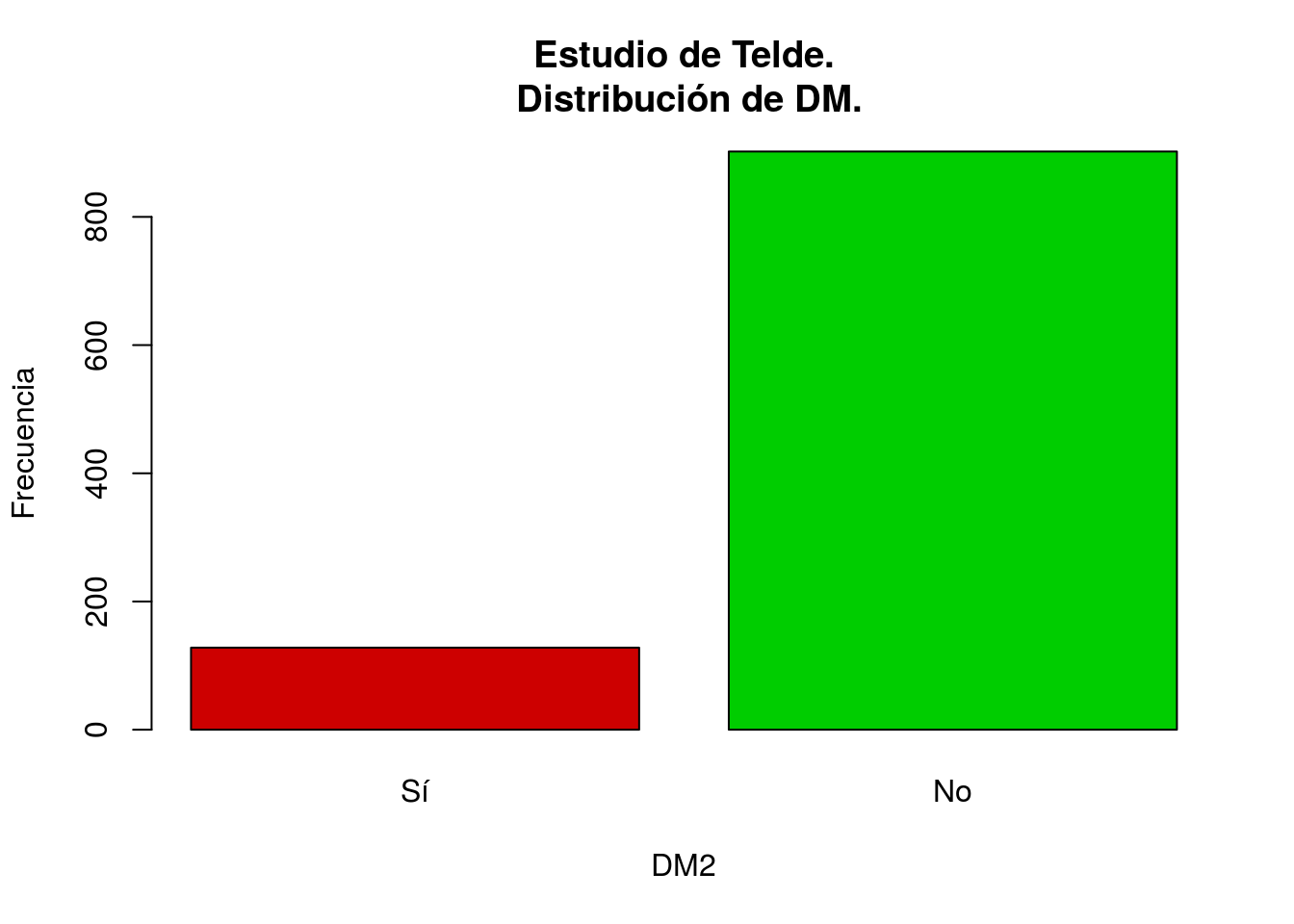

Ejercicios

1. Cuántas personas con HTA hay en el estudio de Telde. ¿Cuál es la frecuencia relativa de hipertensos y no hipertensos?

2. ¿Cuántas personas tienen HTA y DM? ¿Cuántas no son HTA ni DM? Construye la tabla cruzada de ambas variables.

3. ¿Cuál es la proporción de personas hipertensas entre las que tienen DM?

4. ¿Cuál es la proporción de personas diabéticas entre las que tienen HTA?