Tarea 7: Regresión logística binaria
Distribucion binomial y regresion logistica
Concepto de variable aleatoria. Distribución binomial.
Una variable aleatoria es una cantidad cuyo valor depende del azar. A modo de ejemplo, si la prevalencia de cierta enfermedad en una población es \(\pi=\) 0.30, ello significa que la probabilidad de que una persona elegida al azar padezca esa enfermedad es 0.3. Si elegimos al azar 3 personas de esa población, podrá ocurrir:
- Que ninguna esté enferma. Este suceso tiene probabilidad \(p_0=(1-\pi)^3\)
- Que solo haya una enferma: \(p_1=3\pi\left(1-\pi\right)^2\).
- Que haya dos enfermas: \(p_2=3\pi^2\left(1-\pi\right)\).
- Que las tres estén enfermas: \(p_3=\pi^3\)
En este contexto, \(X=\) “número de enfermos entre las tres personas elegidas al azar”" es una variable aleatoria en el sentido que se acaba de definir. Concretamente, si el hecho de que un sujeto esté enfermo es independiente de que el resto de sujetos esté enfermo o no, el reparto (o distribución) de probabilidades entre los distintos valores de la variable \(X\) recibe el nombre de distribución binomial, en este caso particular, de parámetros \(n=3\) y \(\pi=0.3\), y se suele denotar de la forma \(X\approx b\left(n,\pi\right)\)
Podemos calcular las probabilidades anteriores con R:
p0=(1-0.3)^3; p0## [1] 0.343p1=3*0.3*(1-0.3)^2; p1## [1] 0.441p2=3*(0.3^2)*(1-0.3); p2## [1] 0.189p3=0.3^3; p3## [1] 0.027Estas cuatro probabilidades suman 1:
p0+p1+p2+p3## [1] 1Esperanza de una variable aleatoria (discreta):
Se define como:
\[E\left[X\right]=\sum_{k=0}^{n} k\cdot p\left(X=k\right)\]
En el caso de la variable aleatoria de nuestro ejemplo:
0*p0+1*p1+2*p2+3*p3## [1] 0.9Se puede demostrar que para la distribución binomial \(b\left(n,\pi\right)\) la ecuación anterior puede simplificarse como:
\[E\left[X\right]=n\cdot\pi\]
En nuestro ejemplo \(n\cdot \pi=3\cdot0.3=0.9\) que coincide con el valor que se acaba de calcular.
Podemos interpretar intuitivamente el concepto de esperanza en este caso considerando que en lugar de una muetra de 3 personas tenemos una muestra de 300; si la probabilidad de que una persona elegida al azar esté enferma es del 30% (esto es, \(\pi=0.3\)), cabe esperar que un 30% de las 300 personas (esto es, 90 personas) estén enfermas. Este valor esperado coincide precisamente con \(E\left[X\right]=n\cdot\pi=300\cdot 0.3= 90\).
Otra manera de interpretar la esperanza es como el valor medio de la variable en muchas muestras. R permite simular con facilidad valores de variables aleatorias; en particular, si \(X\approx b\left(300,0.3\right)\) (esto es, \(X\) es el número de enfermos entre 300 personas elegidas al azar cuando la probabilidad de estar enfermo es 0.3), puede simularse un valor de \(X\) como:
rbinom(1,300,0.3)## [1] 100La siguiente sintaxis simula el número de enfermos en cada una de 10 muestras de 300 personas cada una:
rbinom(10,300,0.3)## [1] 86 96 85 84 84 88 95 91 111 91Y ahora generamos 1000 muestras de tamaño 300 y contamos el número de enfermos en cada una:
enfermos=rbinom(1000,300,0.3)Si calculamos el número medio de enfermos en estas muestras de tamaño 300:
mean(enfermos)## [1] 89.763obtenemos un valor muy próximo a la esperanza calculada más arriba (0.9)
Varianza de una variable aleatoria (discreta)
Se define como:
\[{Var}\left(X\right)=\sum_{k=0}^{n} \left(k-E[X]\right)^2\cdot p\left(X=k\right)\]
La varianza es una medida de la variabilidad presente en una variable aleatoria. En el caso particular de la distribución binomial \(b\left(n,\pi\right)\) la ecuación anterior puede simplificarse como:
\[{Var}\left(X\right)=n\cdot \pi\cdot \left(1-\pi \right)\]
La desviación típica es la raiz cuadrada de la varianza:
\[{sd}\left(X\right)=\sqrt{n\cdot\pi\cdot\left(1-\pi \right)}\]
Calculamos la varianza para una variable \(b\left(300,0.3\right)\):
300*0.3*(1-0.3)## [1] 63y la desviación típica:
sqrt(300*0.3*(1-0.3))## [1] 7.937254
Podemos calcular la varianza y desviación típica en las 1000 muestras anteriores y comprobar que son similares a estos valores teóricos:
var(enfermos)## [1] 57.99883sd(enfermos)## [1] 7.615696
Estudio de Telde: prevalencia de HTA
Cargamos los datos del estudio de Telde:
library(openxlsx)
setwd("c:/Users/aulas/Downloads/")
telde = read.xlsx("endocrino.xlsx") En el estudio de Telde tenemos una muestra de \(n=\) 1030 personas. El número de personas con HTA entre estas 1030 es una variable aleatoria con distribución binomial \(b\left(1030, \pi\right)\), donde \(\pi\) es la probabilidad de que una persona elegida al azar de esta población padezca HTA. El valor de \(\pi\) en la población adulta de Telde es desconocido, pero podemos estimarlo (obtener un valor aproximado) a partir de los datos de nuestra muestra, usnado como estimador la prevalencia observada de HTA. Dicha prevalencia puede calcularse mediante:
tb=table(telde$HTA_OMS)
tb##
## 0 1
## 706 324ptb=prop.table(tb)
ptb##
## 0 1
## 0.6854369 0.3145631Por tanto de acuerdo con nuestros datos, la prevalencia de HTA en Telde ronda un 31.46% (esto es, la probabilidad de que una persona elegida al azar en la población adulta de Telde tenga HTA es aproximadamente 0.3146).
Asimismo podemos estimar la prevalencia de HTA de acuerdo a la presencia/ausencia de T2DM:
tb2 <- with(telde,table(DM,HTA_OMS))
tb2## HTA_OMS
## DM 0 1
## 0 661 241
## 1 45 83prop.table(tb2,1)## HTA_OMS
## DM 0 1
## 0 0.7328160 0.2671840
## 1 0.3515625 0.6484375Esta tabla nos indica que entre los diabéticos hay un 64.8% de hipertensos (83 hipertensos de un total de 83+45=128 sujetos); asimismo entre los no diabéticos (241+661=902) hay 241 hipertensos, lo que da lugar a una prevalencia de HTA de un 26.7% entre los no diabéticos). Este resultado muestra bien a las claras que la probabilidad de que una persona tenga HTA depende de si dicha persona tiene o no DM: es más probable ser hipertenso cuando se es diabético que cuando no se es diabético.
Modelo de regresión logística con una única variable explicativa: HTA según DM
Preparamos un data.frame con los sujetos según tengan o no T2DM, indicando en cada grupo (con DM y sin DM), el número de sujetos con HTA, y el número total de sujetos (Nt).:
freqHTA=aggregate(HTA_OMS~DM, telde,
function(x){c(con.HTA=sum(x),Nt=length(x),pHTA=sum(x)/length(x))})
freqHTA=data.frame(DM=freqHTA[,1],freqHTA[,-1])
rownames(freqHTA)=c("DM-","DM+")
freqHTA## DM con.HTA Nt pHTA
## DM- 0 241 902 0.2671840
## DM+ 1 83 128 0.6484375La siguiente sintaxis permite construir el modelo de regresión logística para predecir la prevalencia de HTA según la presencia/ausencia de diabetes:
mlog <- glm(pHTA ~ DM, data=freqHTA ,weights=Nt, family=binomial)
summary(mlog)##
## Call:
## glm(formula = pHTA ~ DM, family = binomial, data = freqHTA, weights = Nt)
##
## Deviance Residuals:
## [1] 0 0
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -1.00896 0.07525 -13.408 < 2e-16 ***
## DM 1.62114 0.19983 8.113 4.96e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 6.9666e+01 on 1 degrees of freedom
## Residual deviance: 5.4179e-14 on 0 degrees of freedom
## AIC: 16.228
##
## Number of Fisher Scoring iterations: 2Las predicciones de este modelo se obtienen mediante:
PrHTA=mlog$fit
PrHTA## DM- DM+
## 0.2671840 0.6484375Podemos observar que la predicción es exacta, esto es, se predicen exactamente los valores de las prevalencias observadas.
Gráficamente:
boxplot(PrHTA~names(PrHTA), ylim=c(0,1),boxwex=0.4,medcol=c("darkgreen","red"), ylab="Pr(HTA)",
boxlty = 0, whisklty = 0, staplelty = 0)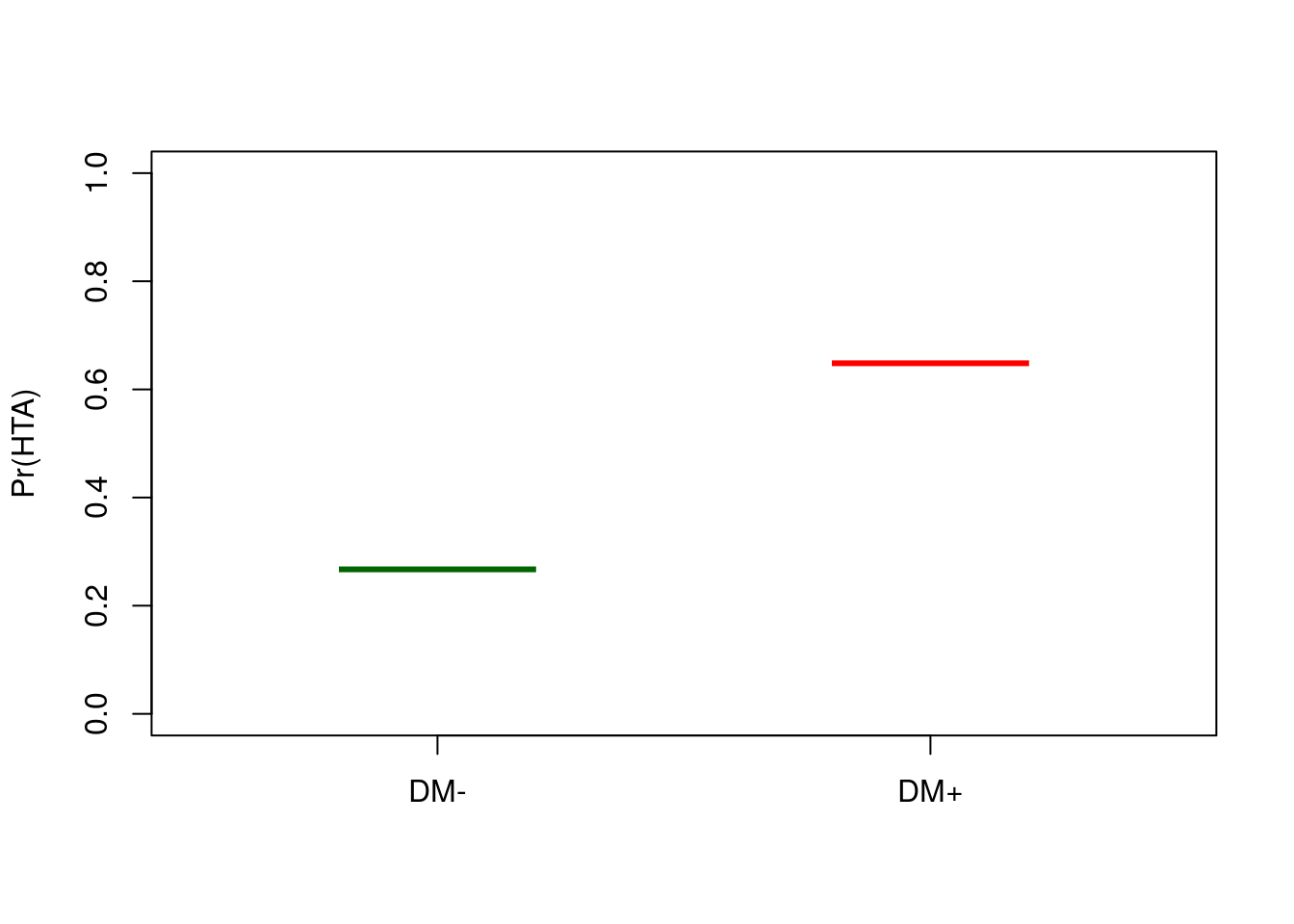
Para calcular la regresión logística anterior hemos construido una tabla resumen con las proporciones observadas de padecer HTA según se padezca o no DM. Podemos obtener el mismo resultado (ya que el modelo es el mismo) si se utiliza directamente la base de datos del estudio de Telde; en este caso la estimación del modelo se lleva a cabo de manera muy simple:
mlogB <- glm(HTA_OMS ~ DM, data=telde , family=binomial)
summary(mlogB)##
## Call:
## glm(formula = HTA_OMS ~ DM, family = binomial, data = telde)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.4459 -0.7885 -0.7885 0.9308 1.6247
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -1.00896 0.07525 -13.408 < 2e-16 ***
## DM 1.62114 0.19983 8.113 4.96e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 1282.8 on 1029 degrees of freedom
## Residual deviance: 1213.1 on 1028 degrees of freedom
## AIC: 1217.1
##
## Number of Fisher Scoring iterations: 4y ahora la predicción se realiza para cada sujeto por separado; para cada sujeto se predice la probabilidad de que padezca HTA en función de que tenga o no DM. Mostramos a continuación las predicciones para los sujetos 1, 2, 900, 901, 1001, 1002,1028,1029 (elegimos estos sujetos a modo de ejemplo, para no tener que mostrar las predicciones de los 1030 que componen la muestra completa):
mlogB$fit[c(1, 2, 900, 901, 1001, 1002,1028,1029)]## 1 2 900 901 1001 1002 1028
## 0.2671840 0.2671840 0.2671840 0.2671840 0.6484375 0.6484375 0.6484375
## 1029
## 0.6484375
Modelo de regresión logística multivariante: HTA según IR y DM
Introduzcamos a continuación en el modelo anterior, además del efecto de la T2DM, el efecto de la resistencia a la insulina. Para ello construimos en primer lugar una tabla que nos da el número de hipertensos para cada una de las cuatro posibles combinaciones de T2DM e IR:
freqHTA=aggregate(HTA_OMS~IR+DM, telde,
function(x){c(con.HTA=sum(x),Nt=length(x),pHTA=sum(x)/length(x))})
freqHTA=data.frame(freqHTA[,(1:2)],freqHTA[,-(1:2)])
rownames(freqHTA)=c("IR-/DM-","IR+,DM-","IR-/DM+","IR+/DM+")
freqHTA## IR DM con.HTA Nt pHTA
## IR-/DM- 0 0 136 675 0.2014815
## IR+,DM- 1 0 105 227 0.4625551
## IR-/DM+ 0 1 14 25 0.5600000
## IR+/DM+ 1 1 69 103 0.6699029El modelo de regresión logística para esta tabla se calcula mediante:
mlog2 <- glm(pHTA ~ DM + IR, data=freqHTA, weights=Nt, family=binomial)
summary(mlog2)##
## Call:
## glm(formula = pHTA ~ DM + IR, family = binomial, data = freqHTA,
## weights = Nt)
##
## Deviance Residuals:
## IR-/DM- IR+,DM- IR-/DM+ IR+/DM+
## -0.3115 0.4353 1.3104 -0.6964
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -1.34726 0.09328 -14.443 < 2e-16 ***
## DM 1.06299 0.21625 4.915 8.86e-07 ***
## IR 1.13921 0.15430 7.383 1.55e-13 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 126.0959 on 3 degrees of freedom
## Residual deviance: 2.4885 on 1 degrees of freedom
## AIC: 29.534
##
## Number of Fisher Scoring iterations: 3cuyas predicciones son las siguientes (obsérvese que ahora ya no coinciden con las proporciones observadas):
PrHTA2=mlog2$fit
PrHTA2## IR-/DM- IR+,DM- IR-/DM+ IR+/DM+
## 0.2063183 0.4481725 0.4294062 0.7016004Gráficamente:
boxplot(PrHTA2~names(PrHTA2), ylim=c(0,1),boxwex=0.4,medcol=c("darkgreen","red"), ylab="Pr(HTA)",
boxlty = 0, whisklty = 0, staplelty = 0)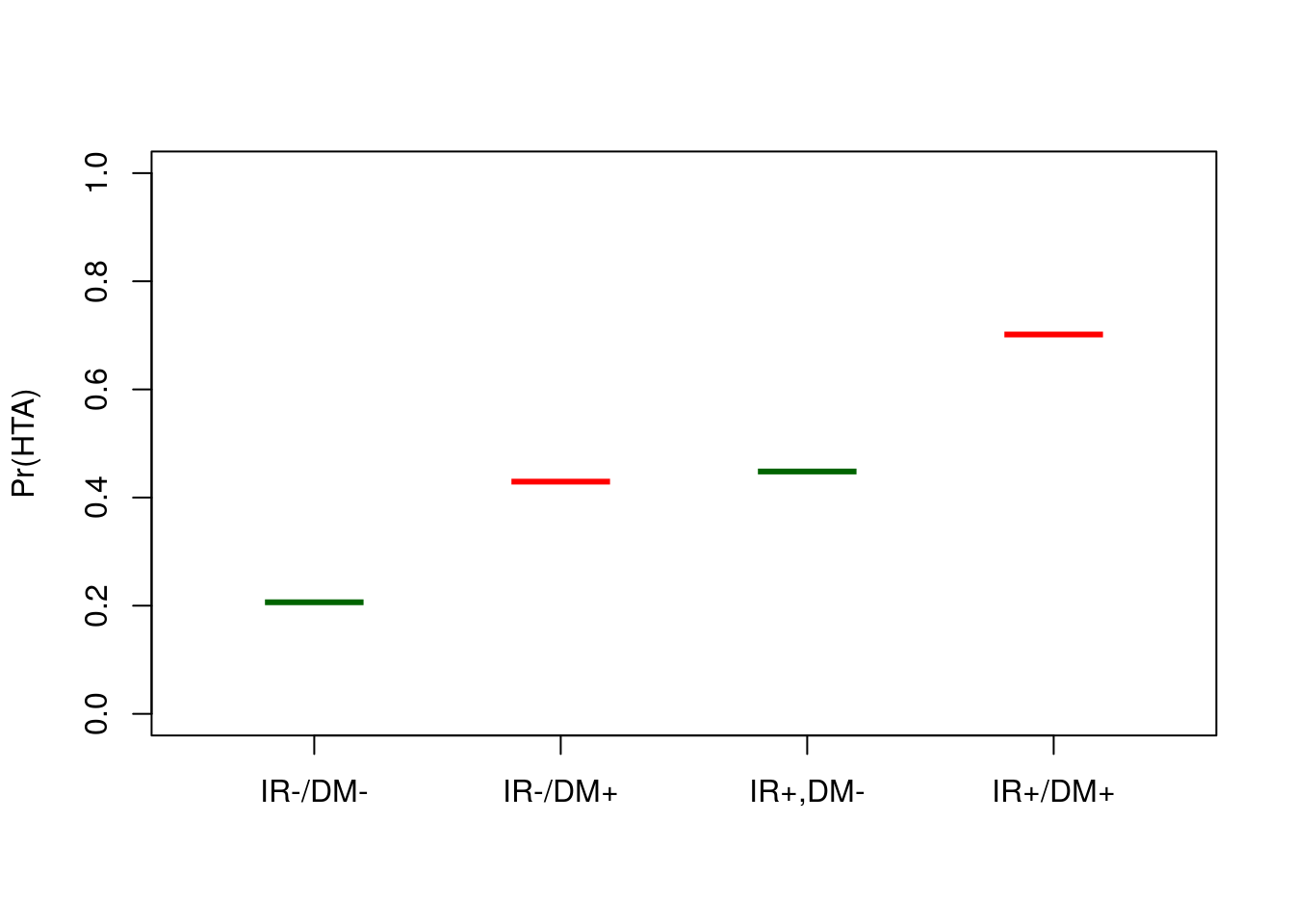
El modelo con interacciones sí que hace predicciones exactas:
mlog3 <- glm(pHTA ~ DM * IR, data=freqHTA, weights=Nt, family=binomial)
summary(mlog3)##
## Call:
## glm(formula = pHTA ~ DM * IR, family = binomial, data = freqHTA,
## weights = Nt)
##
## Deviance Residuals:
## [1] 0 0 0 0
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -1.37706 0.09596 -14.350 < 2e-16 ***
## DM 1.61822 0.41418 3.907 9.34e-05 ***
## IR 1.22700 0.16410 7.477 7.59e-14 ***
## DM:IR -0.76042 0.48288 -1.575 0.115
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 1.2610e+02 on 3 degrees of freedom
## Residual deviance: -5.3513e-14 on 0 degrees of freedom
## AIC: 29.046
##
## Number of Fisher Scoring iterations: 3mlog3$fit## IR-/DM- IR+,DM- IR-/DM+ IR+/DM+
## 0.2014815 0.4625551 0.5600000 0.6699029
Del mismo modo que antes, la regresión logística puede estimarse a partir de la base de datos original mediante:
mg <- glm(HTA_OMS ~ DM + IR , data =telde, family=binomial)
summary(mg)##
## Call:
## glm(formula = HTA_OMS ~ DM + IR, family = binomial, data = telde)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.5552 -0.6798 -0.6798 0.8419 1.7767
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -1.34726 0.09328 -14.443 < 2e-16 ***
## DM 1.06299 0.21625 4.915 8.86e-07 ***
## IR 1.13921 0.15430 7.383 1.55e-13 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 1282.8 on 1029 degrees of freedom
## Residual deviance: 1159.2 on 1027 degrees of freedom
## AIC: 1165.2
##
## Number of Fisher Scoring iterations: 4Ahora lo que se predice para cada sujeto es la probabilidad de que sea hipertenso según que tenga o no T2DM, y según que tenga o no IR; para los mismos sujetos de antes, las predicciones son:
mg$fit[c(1, 2, 900, 901, 1001, 1002,1028,1029)]## 1 2 900 901 1001 1002 1028
## 0.4481725 0.4481725 0.2063183 0.2063183 0.7016004 0.7016004 0.4294062
## 1029
## 0.4294062
Regresión logística multivariante: Prevalencia de HTA según incluyendo DM y edad:
mg <- glm(HTA_OMS ~ DM + EDAD, data=telde, family=binomial)
summary(mg)##
## Call:
## glm(formula = HTA_OMS ~ DM + EDAD, family = binomial, data = telde)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.1255 -0.7804 -0.5432 0.9044 2.2104
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -4.550680 0.348603 -13.054 < 2e-16 ***
## DM 0.909660 0.219401 4.146 3.38e-05 ***
## EDAD 0.073285 0.006818 10.748 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 1282.8 on 1029 degrees of freedom
## Residual deviance: 1081.5 on 1027 degrees of freedom
## AIC: 1087.5
##
## Number of Fisher Scoring iterations: 4Podemos representar gráficamente el efecto de la edad en cada grupo (DM+ y DM-) del siguiente modo:
telde$pHTA=mg$fitted # Añadimos las predicciones a la base de datos
telde=telde[order(telde$EDAD), ] # Ordenamos por edad
si.DM=subset(telde,DM==1) # Subconjunto de diabéticos
no.DM=subset(telde,DM==0) # Subconjunto de no diabéticos
plot(pHTA~EDAD,telde, type="n", xlab="EDAD", ylab="pr(HTA)") # Gráfico en blanco
lines(no.DM$EDAD,no.DM$pHTA,type="l",col="darkgreen",lwd=2,lty=2)
lines(si.DM$EDAD,si.DM$pHTA,type="l",col="red3",lwd=2,lty=1)
legend("bottomright", c("DM+","DM-"), lty=c(1,2), col=c("red3","darkgreen"), lwd=2, bty="n")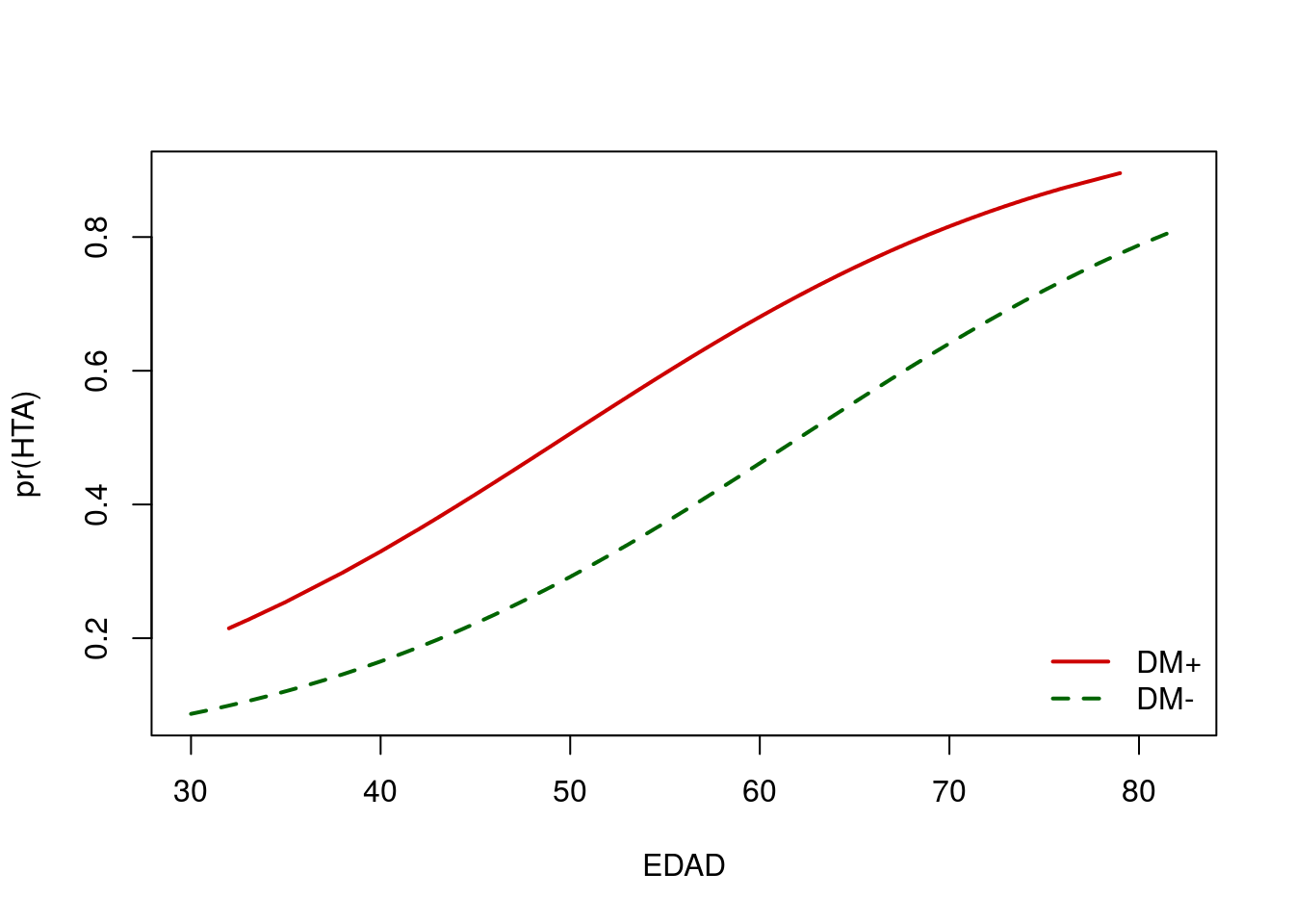
Regresión logística multivariante: Prevalencia de HTA según incluyendo DM, IR y edad:
mg2 <- glm(HTA_OMS ~ DM + IR + EDAD, data=telde, family=binomial)
summary(mg2)##
## Call:
## glm(formula = HTA_OMS ~ DM + IR + EDAD, family = binomial, data = telde)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.0154 -0.7342 -0.4717 0.8531 2.3655
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -4.965598 0.369248 -13.448 < 2e-16 ***
## DM 0.323218 0.236159 1.369 0.171
## IR 1.178958 0.166337 7.088 1.36e-12 ***
## EDAD 0.074358 0.007001 10.621 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 1282.8 on 1029 degrees of freedom
## Residual deviance: 1031.2 on 1026 degrees of freedom
## AIC: 1039.2
##
## Number of Fisher Scoring iterations: 4Gráficamente:
telde$pHTA=mg2$fitted # Añadimos las predicciones a la base de datos
telde=telde[order(telde$EDAD), ] # Ordenamos por edad- Representamos primero los sujetos insulino resistentes:
teldeIR=subset(telde,IR==1)
si.DM=subset(teldeIR,DM==1) # Subconjunto de diabéticos e IR
no.DM=subset(teldeIR,DM==0) # Subconjunto de no diabéticos e IR
plot(pHTA~EDAD,telde, type="n", xlab="EDAD", ylab="pr(HTA)",
main="Sujetos con Insulino-Resistencia")
lines(no.DM$EDAD,no.DM$pHTA,type="l",col="darkgreen",lwd=2,lty=2)
lines(si.DM$EDAD,si.DM$pHTA,type="l",col="red3",lwd=2,lty=1)
legend("bottomright", c("DM+","DM-"), lty=c(1,2), col=c("red3","darkgreen"), lwd=2, bty="n")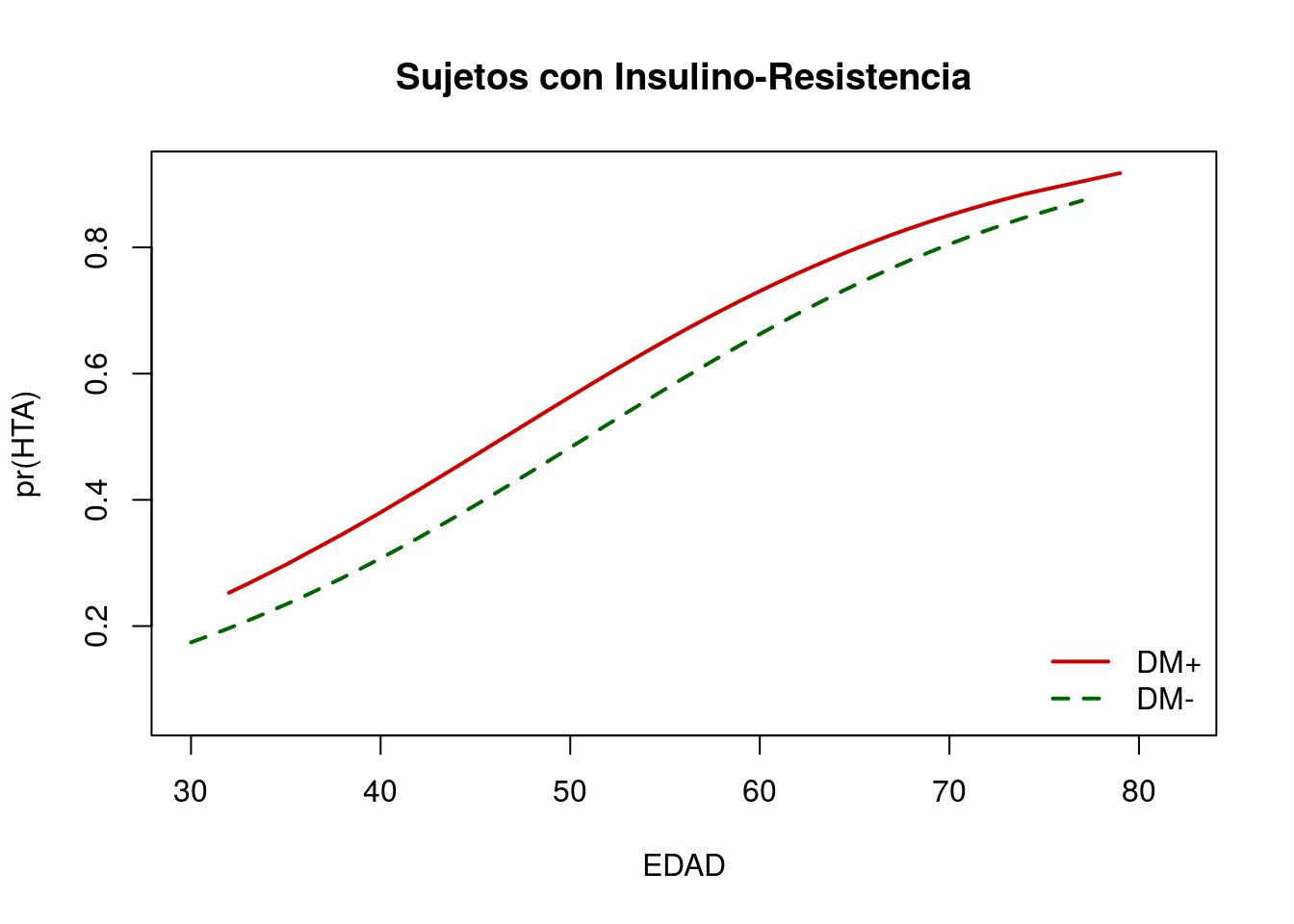
- Y ahora los no Insulino-Resistentes:
telde.noIR=subset(telde,IR==0)
si.DM=subset(telde.noIR,DM==1) # Subconjunto de diabéticos e IR
no.DM=subset(telde.noIR,DM==0) # Subconjunto de no diabéticos e IR
plot(pHTA~EDAD,telde, type="n", xlab="EDAD", ylab="pr(HTA)",
main="Sujetos SIN Insulino-Resistencia")
lines(no.DM$EDAD,no.DM$pHTA,type="l",col="darkgreen",lwd=2,lty=2)
lines(si.DM$EDAD,si.DM$pHTA,type="l",col="red3",lwd=2,lty=1)
legend("bottomright", c("DM+","DM-"), lty=c(1,2), col=c("red3","darkgreen"), lwd=2, bty="n")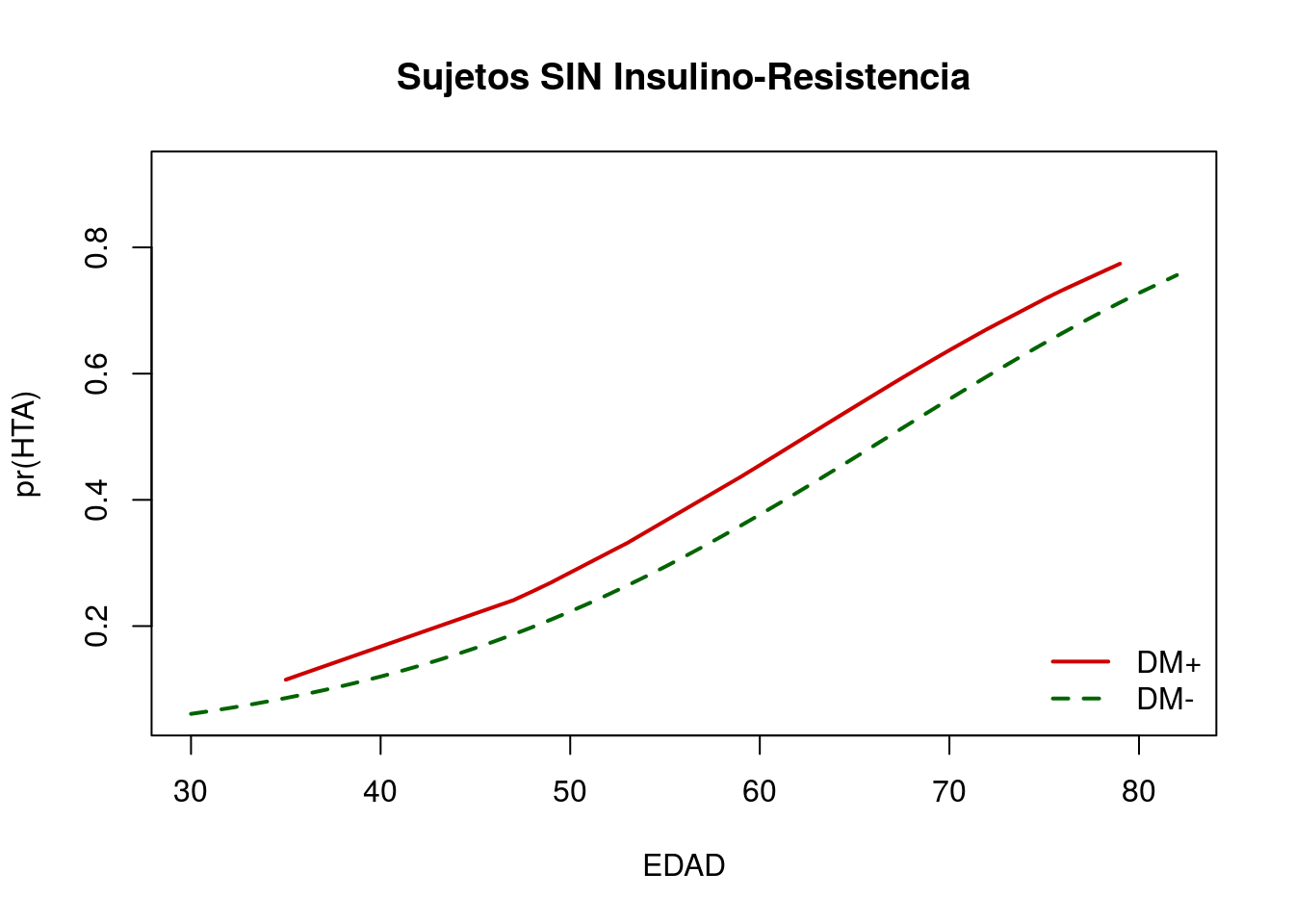
Cálculo de las odds-ratio a partir de la regresión logística.
Ya hemos visto como podemos usar epiR para calcular la odds-ratio entre HTA_OMS y DM:
library(epiR)
fDM=ordered(telde$DM,levels=c(1,0),labels=c("DM+","DM-"))
fHTA=ordered(telde$HTA_OMS,levels=c(1,0),labels=c("HTA+","HTA-"))
tb <- table(fDM,fHTA)
tb## fHTA
## fDM HTA+ HTA-
## DM+ 83 45
## DM- 241 661epi.2by2(tb)## Outcome + Outcome - Total Inc risk *
## Exposed + 83 45 128 64.8
## Exposed - 241 661 902 26.7
## Total 324 706 1030 31.5
## Odds
## Exposed + 1.844
## Exposed - 0.365
## Total 0.459
##
## Point estimates and 95 % CIs:
## -------------------------------------------------------------------
## Inc risk ratio 2.43 (2.05, 2.87)
## Odds ratio 5.06 (3.42, 7.48)
## Attrib risk * 38.13 (29.36, 46.89)
## Attrib risk in population * 4.74 (0.69, 8.79)
## Attrib fraction in exposed (%) 58.80 (51.30, 65.14)
## Attrib fraction in population (%) 15.06 (10.77, 19.15)
## -------------------------------------------------------------------
## X2 test statistic: 75.567 p-value: < 0.001
## Wald confidence limits
## * Outcomes per 100 population unitso directamente a partir de la tabla cruzada:
OR=tb[1,1]*tb[2,2]/(tb[1,2]*tb[2,1])
OR## [1] 5.058829La odds ratio es, como vemos, 5.058829. El modelo logístico para predecir la prevalencia de HTA_OMS a partir de DM es:
mg <- glm(HTA_OMS~DM, data=telde, family=binomial)
summary(mg)##
## Call:
## glm(formula = HTA_OMS ~ DM, family = binomial, data = telde)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.4459 -0.7885 -0.7885 0.9308 1.6247
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -1.00896 0.07525 -13.408 < 2e-16 ***
## DM 1.62114 0.19983 8.113 4.96e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 1282.8 on 1029 degrees of freedom
## Residual deviance: 1213.1 on 1028 degrees of freedom
## AIC: 1217.1
##
## Number of Fisher Scoring iterations: 4Los valores de las odds-ratio se obtienen como el resultado de calcular el valor del número e elevado a los coeficientes estimados del modelo:
exp(coef(mg))## (Intercept) DM
## 0.3645991 5.0588290y podemos ver que el valor así obtenido coincide con el ya calculado a partir de la tabla anterior.
El empleo de la regresión logística nos permite obtener las odds-ratio ajustadas por otras variables:
mg2 <- glm(HTA_OMS ~ DM + IR + EDAD, data=telde, family=binomial)
exp(coef(mg2))## (Intercept) DM IR EDAD
## 0.006973777 1.381565898 3.250984231 1.077192451Se pueden también obtener intervalos de confianza y contrastes de significación para las odds-ratio:
library(pander)
library(MASS) # Para el cálculo de intervalos de confianza
smg<-summary(mg2)
pv=smg$coef[,4] # p-valores de los coeficientes
pval=c(ifelse(pv<.001,"< .001",round(pv,3)))
b=smg$coef[,1]
sb=smg$coef[,2]
bs=array(sprintf("%.3f (%.3f)",b,sb),dim=c(length(b),1))
OR=exp(b)
OR.ci=exp(confint(mg))
IC95=array(sprintf("%.3f (%.3f,%.3f)",OR,OR.ci[,1],OR.ci[,2]),dim=c(length(OR),1))
ta5 <- data.frame(bs,pval,IC95)
names(ta5)=c("Coeficiente (SE)","P","OR (IC-95%)")
pander(ta5)| Coeficiente (SE) | P | OR (IC-95%) | |
|---|---|---|---|
| (Intercept) | -4.966 (0.369) | < .001 | 0.007 (0.314,0.422) |
| DM | 0.323 (0.236) | 0.171 | 1.382 (3.437,7.535) |
| IR | 1.179 (0.166) | < .001 | 3.251 (0.314,0.422) |
| EDAD | 0.074 (0.007) | < .001 | 1.077 (3.437,7.535) |