library(openxlsx) 
setwd("c:/Users/aulas/Downloads/") 
telde = read.xlsx("endocrino.xlsx") 

Test de la chi-cuadrado: ¿Existe asociación entre el sexo de un individuo y el padecer HTA?

Para determinar si el sexo de una persona se asocia con el hecho de que esa persona padezca o no HTA comenzamos por la construcción de una tabla cruzada de ambas variables:

telde$SEXO=ordered(telde$SEXO,levels=c(1,0),labels=c("Hombre","Mujer"))
telde$HTA=ordered(telde$HTA_OMS,levels=c(1,0),labels=c("HTA+","HTA-"))

tb=with(telde,table(HTA,SEXO))
tb

##       SEXO
## HTA    Hombre Mujer
##   HTA+    156   168
##   HTA-    292   414

prop.table(tb,2)

##       SEXO
## HTA       Hombre     Mujer
##   HTA+ 0.3482143 0.2886598
##   HTA- 0.6517857 0.7113402

Esta tabla indica que un 34.8% de los hombres son hipertensos, frente a un 28.9% de las mujeres, lo que podría interpretarse como que el ser hombre es de algún modo un factor de riesgo de hipertensión. Podemos evaluar la asociación entre sexo y HTA mediante la odds-ratio:

tb[1,1]*tb[2,2]/(tb[1,2]*tb[2,1])

## [1] 1.316536

cuyo valor (mayor que la unidad) está efectivamente acorde con la presunción de que ser hombre incrementa el riesgo de HTA.

En cualquier caso la diferencia entre un 34.8% y un 28.9% no parece excesivamente elevada. Dado que los datos con los que estamos trabajando constituyen una muestra elegida al azar entre la población adulta de Telde cabe hacerse la siguiente pregunta: si la muestra hubiese sido otra ¿se habría observado la misma relación entre estos porcentajes (esto es mayor porcentaje de hipertensos entre las mujeres que entre los hombres), o quizás estos porcentajes podrían llegar incluso a invertirse? En otras palabras, la pregunta que nos hacemos es: ¿la diferencia observada puede explicarse simplemente por la variabilidad aleatoria presente en el muestreo, o necesariamente se debe a que en realidad la hipertensión es más común entre los hombres que entre las mujeres de Telde?

Para responder a esta pregunta debe utilizarse el test de la chi-cuadrado:

• La hipótesis nula es que la hipertensión afecta por igual a hombres y mujeres y por tanto que la diferencia observada entre los porcentajes se debe simplemente al azar; si \(\pi_M\) es la probabilidad de que una mujer sea hipertensa y \(\pi_H\) es la probabilidad de que un hombre sea hipertenso, la hipótesis nula establece que:

\[\frac{\pi_M}{\pi_H}=1\]

• La hipótesis alternativa es que la hipertensión afecta de manera diferente a hombres y mujeres, y por tanto que:

\[\frac{\pi_M}{\pi_H}\neq 1\]

La realización del test de la chi-cuadrado en R es muy simple: se utiliza la función chisq.test a la que se le pasa como argumento la tabla con los datos disponibles:

chisq.test(tb)

## 
##  Pearson's Chi-squared test with Yates' continuity correction
## 
## data:  tb
## X-squared = 3.8924, df = 1, p-value = 0.0485

 

Si deseamos calcular las frecuencias esperadas bajo la hipótesis nula (igual prevalencia de HTA en hombres y mujeres) podemos utilizar:

chisq.test(tb)$expected

##       SEXO
## HTA      Hombre    Mujer
##   HTA+ 140.9243 183.0757
##   HTA- 307.0757 398.9243

 

 

Test de la chi-cuadrado: ¿Existe asociación entre el nivel de instrucción de un individuo y el padecer HTA?

Para responder a esta pregunta podemos proceder del mismo modo que con el sexo:

telde$INSTRUCCION=ordered(telde$INSTRUCCION,levels=c("Sin estudios","Primer grado",
                                                     "Segundo grado","Tercer grado"))
tb=with(telde,table(HTA,INSTRUCCION))
tb

##       INSTRUCCION
## HTA    Sin estudios Primer grado Segundo grado Tercer grado
##   HTA+            6          167           130           21
##   HTA-            7          191           379          129

prop.table(tb,2)

##       INSTRUCCION
## HTA    Sin estudios Primer grado Segundo grado Tercer grado
##   HTA+    0.4615385    0.4664804     0.2554028    0.1400000
##   HTA-    0.5384615    0.5335196     0.7445972    0.8600000

Esta última tabla muestra que a medida que aumenta el nivel de instrucción aparentemente disminuye la probabilidad de padecer hipertensión.

Aplicamos el test de la chi-cuadrado:

chisq.test(tb)

## Warning in chisq.test(tb): Chi-squared approximation may be incorrect

## 
##  Pearson's Chi-squared test
## 
## data:  tb
## X-squared = 69.084, df = 3, p-value = 6.705e-15

Observemos que R nos muestra una advertencia relativa a que la aproximación chi-cuadrado puede ser incorrecta. Ello es debido a que las condiciones “técnicas” de realización del test requieren que ninguna frecuencia esperada sea menor que 1 y que al menos el 80 % de las frecuencias esperadas son mayores que 5. Las frecuencias esperadas en este caso son:

chisq.test(tb)$expected

## Warning in chisq.test(tb): Chi-squared approximation may be incorrect

##       INSTRUCCION
## HTA    Sin estudios Primer grado Segundo grado Tercer grado
##   HTA+      4.08932     112.6136      160.1126     47.18447
##   HTA-      8.91068     245.3864      348.8874    102.81553

En este caso hay una única frecuencia esperada menor que 5; en total hay 8 valores esperados de los que 7, esto es el 87.5%, son mayores que 5. Por tanto podemos confiar en el resultado del test y concluir que la asociación entre el nivel de instrucción y la HTA es significativa, esto es, no puede explicarse simplemente por efecto del azar.

En caso de que no se hubiesen cumplido las condiciones para la realización del test, se debería proceder a agrupar categorías; en este caso, como la categoría que puede causar problemas es la categoría “Sin estudios”, ésta podría fusionarse con la categoría “Primer grado”:

telde$INSTRUCCION2=ifelse((telde$INSTRUCCION=="Sin estudios")|(telde$INSTRUCCION=="Primer grado"),"Sin Estudios/Primer grado",as.character(telde$INSTRUCCION))
tb=with(telde,table(HTA,INSTRUCCION2))
tb

##       INSTRUCCION2
## HTA    Segundo grado Sin Estudios/Primer grado Tercer grado
##   HTA+           130                       173           21
##   HTA-           379                       198          129

prop.table(tb,2)

##       INSTRUCCION2
## HTA    Segundo grado Sin Estudios/Primer grado Tercer grado
##   HTA+     0.2554028                 0.4663073    0.1400000
##   HTA-     0.7445972                 0.5336927    0.8600000

chisq.test(tb)

## 
##  Pearson's Chi-squared test
## 
## data:  tb
## X-squared = 69.082, df = 2, p-value = 9.976e-16

 

 

Test de la t de Student (t.test): ¿Existe asociación entre el índice de masa corporal y la hipertensión arterial?

El índice de masa corporal se calcula como el peso (en kg) partido por la talla (en m) elevada al cuadrado. Podemos calcular el IMC de las personas de la muestra de Telde mediante:

telde$IMC=telde$PESO/(telde$TALLA/100)^2

La siguiente tabla nos da el valor medio de IMC según las personas sean o no hipertensas:

aggregate (IMC~HTA, telde, mean)

##    HTA      IMC
## 1 HTA+ 31.09140
## 2 HTA- 26.92119

Gráficamente:

library(ULPGCmisc)
summarize(telde$IMC,by=telde$HTA, showSummary = FALSE)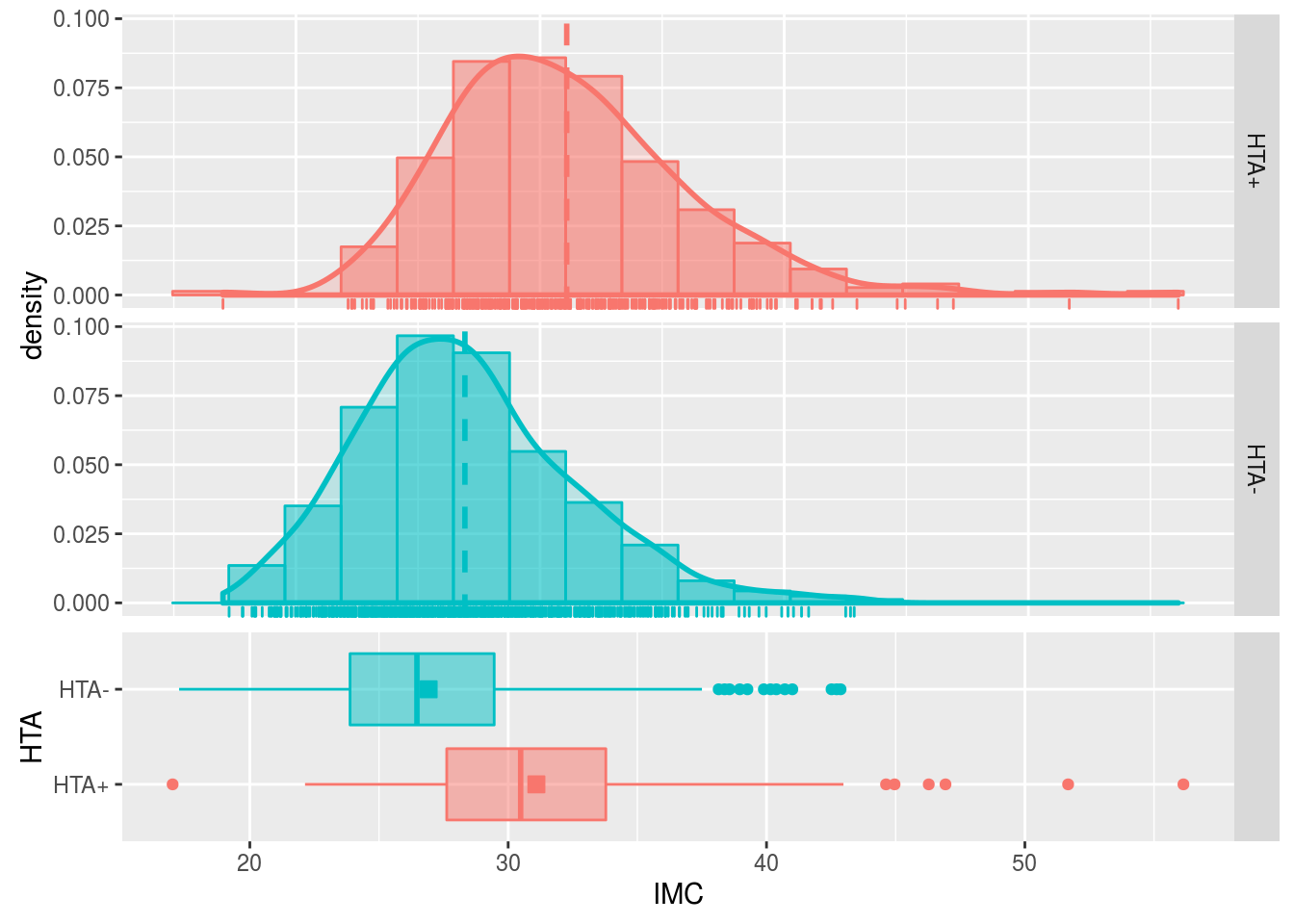

Vemos, pues, que el IMC medio es mayor en los hipertensos (31.10) que en los normotensos (26.92). Igual que en el caso anterior: ¿podría esta diferencia ser efecto de la variabilidad aleatoria del muestreo o la diferencia es tan grande que solo puede explicarse porque en realidad un mayor IMC se asocia con riesgo de HTA?

Para responder a esta pregunta podemos utilizar el test de la de Student:

• La hipótesis nula es que la hipertensión no se asocia con el IMC; ello significaría que el valor medio de IMC sería el mismo en el grupo de hipertensos y en el grupo de normotensos. Si llamamos \(\mu_H\) al valor medio de IMC en el primer grupo y \(\mu_N\) en el segundo, la hipótesis nula especifica que: \[\mu_H=\mu_N\]

• La hipótesis alternativa es que el valor medio de IMC difiere entre hipertensos y normotensos; podemos ser más específicos y considerar que la hipótesis alternativa es: \[\mu_H>\mu_N\]

esto es que el valor medio de IMC es estrictamente mayor en hipertensos que en normotensos. Para resolver este contraste ejecutamos la siguiente función en R:

t.test(IMC~HTA,data=telde,alternative="greater")

## 
##  Welch Two Sample t-test
## 
## data:  IMC by HTA
## t = 12.909, df = 565.08, p-value < 2.2e-16
## alternative hypothesis: true difference in means is greater than 0
## 95 percent confidence interval:
##  3.637958      Inf
## sample estimates:
## mean in group HTA+ mean in group HTA- 
##           31.09140           26.92119

El p-valor es muy pequeño (<0.0001) lo que indica que hay evidencia suficiente para asegurar que el valor de IMC en el grupo de hipertensos es mayor que en el grupo de los normotensos; la diferencia observada no puede explicarse por el mero efecto del azar.

La salida de R nos informa además que con una confianza del 95% el valor medio de IMC en hipertensos es al menos 3.64 unidades mayor que en normotensos.

Si queremos obtener un intervalo de confianza al 95% para la diferencia en el valor medio de IMC entre hipertensos y normotensos utilizamos la sintaxis anterior sin especificar alternativa; asimismo podemos indicar fácilmente el nivel de confianza deseado:

t.test(IMC~HTA,data=telde, conf=0.99)$conf.int

## [1] 3.335257 5.005155
## attr(,"conf.level")
## [1] 0.99

 

 

Test de Wilcoxon-Mann-Whitney (wilcox.test): ¿Existe asociación entre el nivel de glucosa en sangre y la hipertensión arterial?

De igual modo que para el caso anterior podemos tratar de determinar la posible asociación entre el nivel de glucosa en sangre y la HTA. Los valores medios de glucosa en sangre en hipertensos y normotensos pueden obtenerse como:

aggregate(GLUCB~HTA, data=telde, mean)

##    HTA     GLUCB
## 1 HTA+ 108.78086
## 2 HTA-  93.43768

Gráficamente:

a<- summarize(telde$GLUCB,by=telde$HTA, showSummary = FALSE)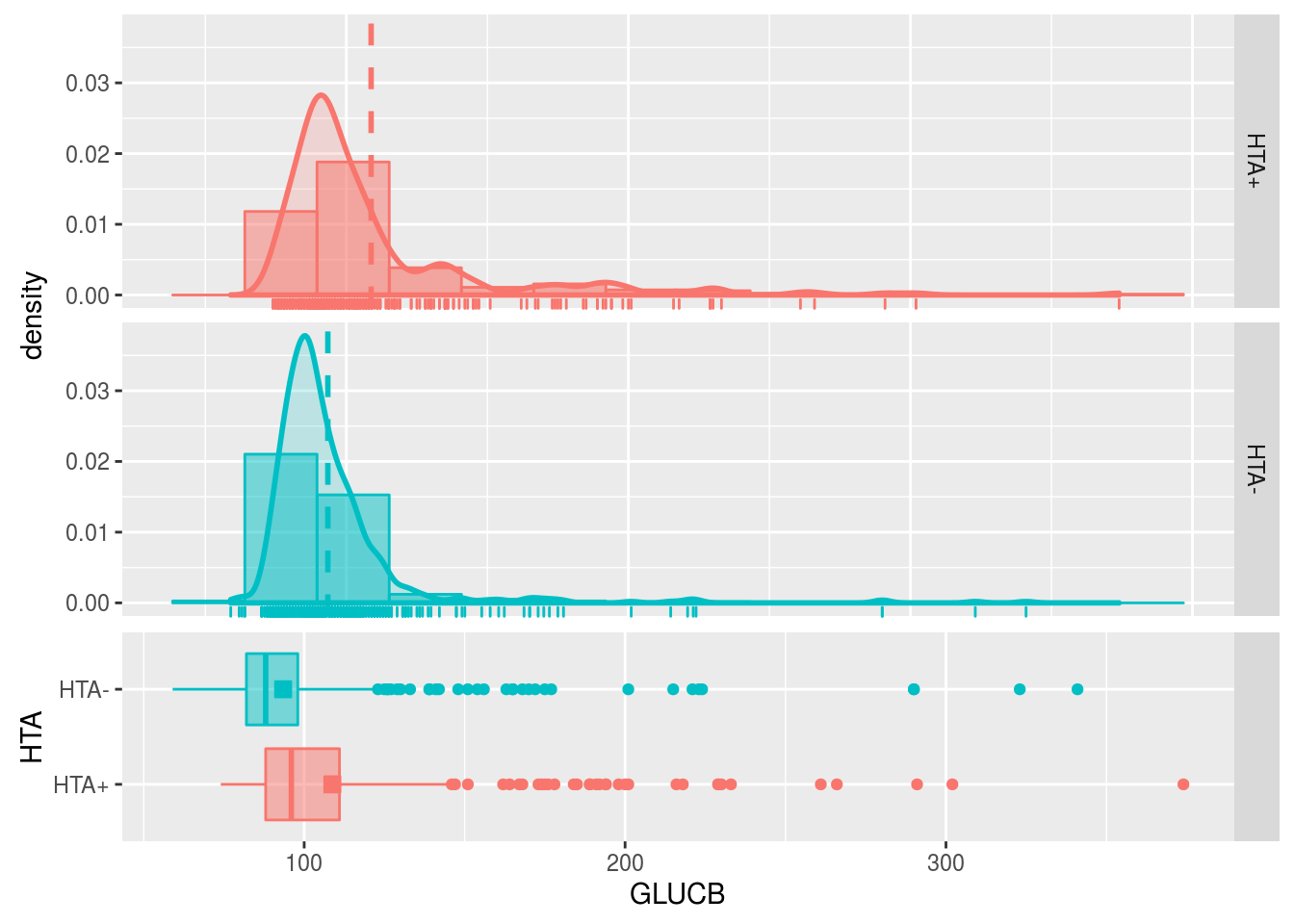

EStos gráficos indican que el nivel de glucosa en sangre tiene una distribución muy asimétrica en ambos grupos. Por tanto compararlos mediante sus valores medios puede ser muy poco adecuado; además la fuerte asimetría implica que la variable bajo estudio (GLUCB) no sigue una distribución normal por lo que el test de la t de Student puede no ser válido.

En este caso resulta más conveniente realizar la comparación mediante el test de Wilcoxon-Mann-Whitney; la hipótesis nula en este test es que los valores de la variable tienden a ser similares en ambos grupos; la hipótesis alternativa es que los valores en uno de los grupos tienden a ser mayores que en el otro. Concretamente, si sospechamos que el nivel de glucosa es mayor en hipertensos, el contraste a realizar es:

wilcox.test(GLUCB~HTA, data=telde,alternative="greater")

## 
##  Wilcoxon rank sum test with continuity correction
## 
## data:  GLUCB by HTA
## W = 152680, p-value < 2.2e-16
## alternative hypothesis: true location shift is greater than 0

El p-valor indica que hay evidencia suficiente para asegurar que efectivamente en el grupo HTA+ el nivel de glucosa es sangre es mayor que en el grupo HTA-.

 

 

Datos emparejados

La siguiente base de datos:

library(foreign)
millac=read.spss("MILLAC.sav", to.data.frame=TRUE)

## Warning in read.spss("MILLAC.sav", to.data.frame = TRUE): MILLAC.sav:
## Unrecognized record type 7, subtype 18 encountered in system file

head(millac)

##   ID          grupo sq  eLDL  vLDL eTG vTG eHDL vHDL eCT vCT elpa vlpa
## 1  1 Entera-Vegetal  1 101.2  89.0  44  90   56   55 166 162 15.0   16
## 2  2 Entera-Vegetal  1 147.4 121.0  73 140   46   45 208 194 19.0   14
## 3  3 Entera-Vegetal  1 118.0  94.8  90  56   46   55 182 161  8.7    7
## 4  4 Entera-Vegetal  1 105.4  91.8  78  96   68   67 189 178  0.6   NA
## 5  5 Entera-Vegetal  1 170.4 133.0  63  60   62   57 245 202  1.4   NA
## 6  6 Entera-Vegetal  1  98.0  70.8  70  61   48   48 160 131  9.6    7
##   eapoa vapoa eapob vapob
## 1   150   157    81    55
## 2   132   147   109    66
## 3   151   156   102    54
## 4   173   181    85    53
## 5   161   130   124    79
## 6   136   119    77    49

corresponde a un estudio sobre los niveles de HDL y LDL observados en niños dependiendo del tipo de leche que consumían. En concreto, el estudio se llevó a cabo mediante un diseño cruzado: los niños se dividieron aleatoriamente en dos grupos; en el primero (sq=1) los niños consumieron leche entera durante 6 meses y leche desnatada (con grasa vegetal) durante los 6 meses siguientes; en el segundo grupo (sq=2), durante los primeros 6 meses se consumió leche desnatada, y los siguientes 6 meses leche entera. Para cada niño se evaluaron los niveles de HDL y LDL al final de cada periodo de 6 meses. En lo que sigue denotamos por eLDL el valor de LDL tras el periodo de consumo de leche entera, y por vLDL el valor de LDL tras el consumo de leche desnatada enriquecida con grasa vegetal.

Los valores medios y desviaciones típicas de los valores de eLDL y vLDL observados han sido:

aggregate(eLDL~grupo,data=millac,function(x) sprintf("%.2f (%.2f)",mean(x),sd(x)))

##            grupo           eLDL
## 1 Entera-Vegetal 111.51 (23.50)
## 2 Vegetal-Entera  99.91 (31.09)

aggregate(vLDL~grupo,data=millac,function(x) sprintf("%.2f (%.2f)",mean(x),sd(x)))

##            grupo          vLDL
## 1 Entera-Vegetal 94.89 (19.95)
## 2 Vegetal-Entera 94.07 (22.83)

Así, los niveles de LDL tras la fase de consumo de leche entera (eLDL) fueron mayores en los niños que comenzaron con leche entera (LDL medio de 111.51) que en los que comenzaron con leche desnatada (LDL medio 99.91). Asimismo, los niveles de LDL tras la fase de consumo de leche desnatada (vLDL) fueron similares en los dos grupos (LDL medio de 94.89 entre los que hicieron la secuencia entera-vegetal, y 94.07 entre los que hicieron la secuencia vegetal-entera).

Gráficamente:

boxplot(eLDL~grupo, data=millac, main="LDL al completar la fase entera", 
        boxwex=0.6,col=c("orange","skyblue"))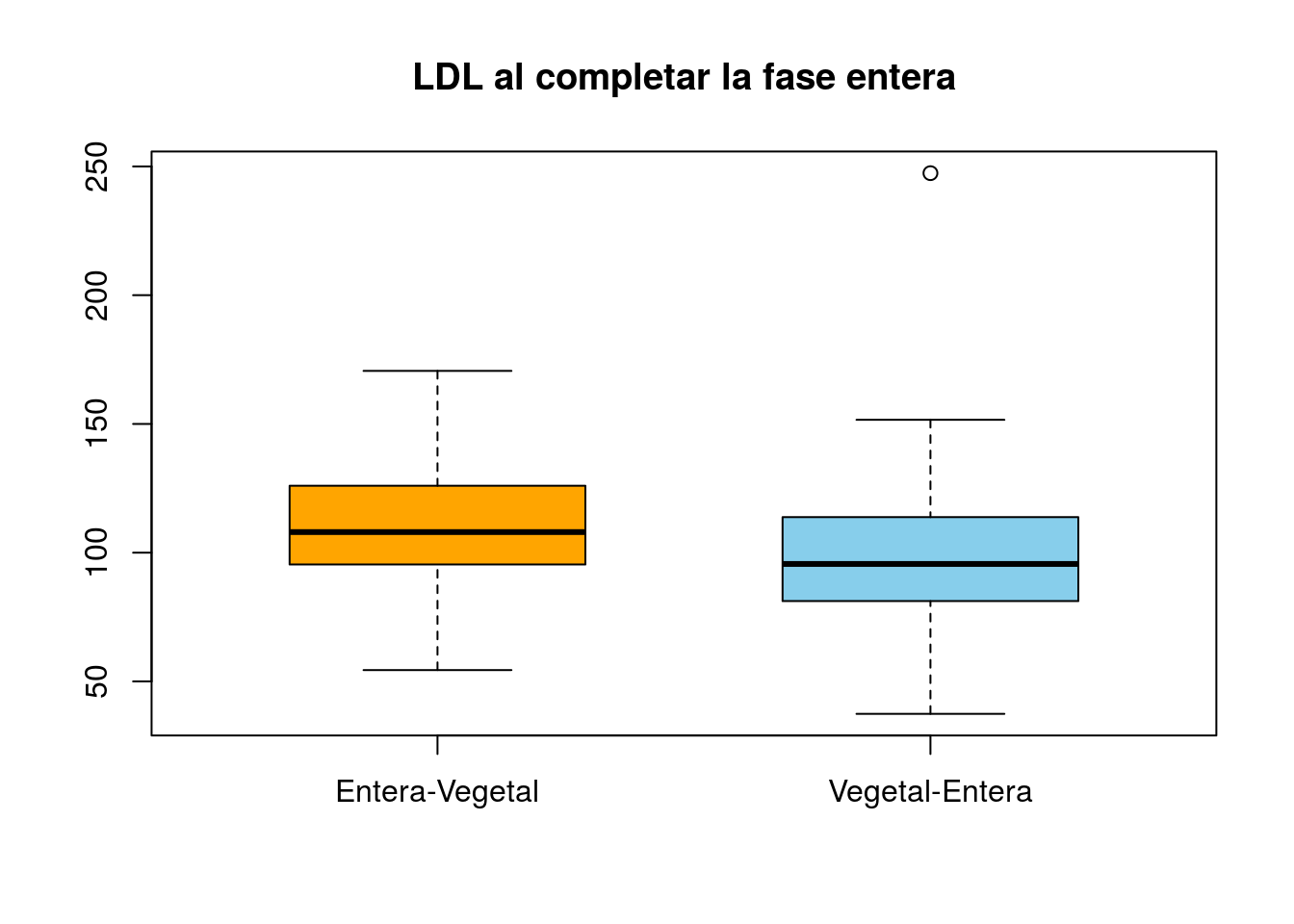

boxplot(vLDL~grupo, data=millac, main="LDL al completar la fase vegetal", 
        boxwex=0.6,col=c("orange","skyblue"))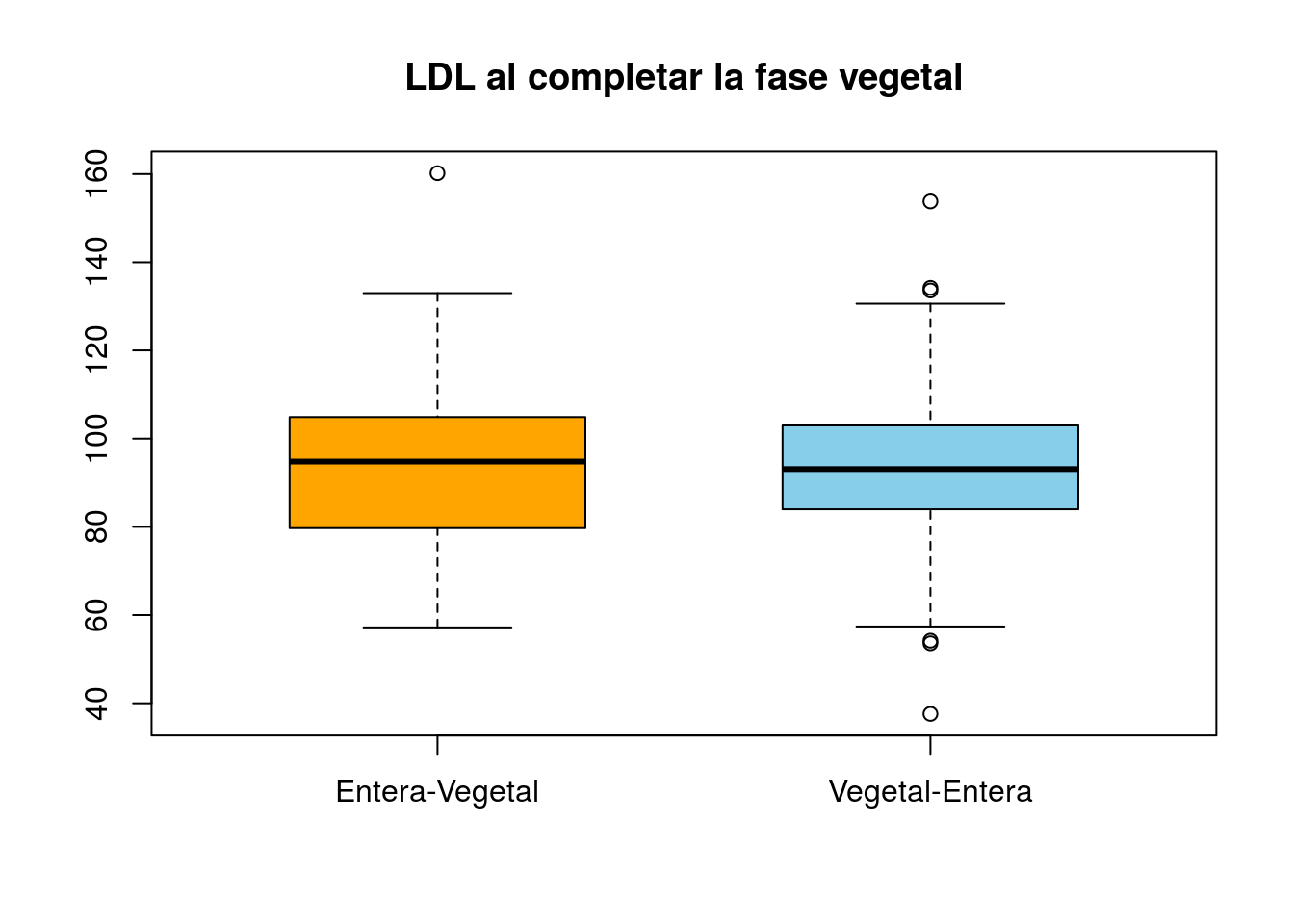

Los niños que han tomado leche en la secuencia “Entera-Vegetal” tuvieron un valor medio de LDL al terminar la fase entera de 111.51 unidades; esos mismos niños, al terminar la fase vegetal mostraron un valor medio de LDL de 94.89 unidades. ¿Es significativa esta diferencia? Es decir ¿puede explicarse por el mero efecto del azar o necesariamente debe atribuirse al efecto de haber cambiado el tipo de leche?

A diferencia de los casos anteriores para hacer esta comparación debe tenerse en cuenta que los datos están emparejados (cada niño se compara consigo mismo). Si suponemos que la variable LDL es aproximadamente normal, podemos aplicar un t.test:

eLDL=subset(millac,sq==1)$eLDL  # Datos del grupo 1 (secuencia entera-vegetal) al final de la fase entera
vLDL=subset(millac,sq==1)$vLDL  # Datos del grupo 1 al final de la fase vegetal
t.test(eLDL,vLDL, paired=TRUE, alternative="greater")

## 
##  Paired t-test
## 
## data:  eLDL and vLDL
## t = 5.2117, df = 46, p-value = 2.153e-06
## alternative hypothesis: true difference in means is greater than 0
## 95 percent confidence interval:
##  11.2359     Inf
## sample estimates:
## mean of the differences 
##                16.57447

lo que indica que existe evidencia suficiente para asegurar que se ha producido una disminución del LDL. La magnitud de dicha dismimución puede estimarse mediante un intervalo de confianza:

t.test(eLDL,vLDL, paired=TRUE, alternative="greater")$conf.int

## [1] 11.2359     Inf
## attr(,"conf.level")
## [1] 0.95

lo que indica que, con un 95% de confianza, que se ha producido un incremento del LDL de al menos 11.236 unidades.

 

 

Por su parte, los niños que hicieron la secuencia inversa (primero leche desnadata-vegetal y luego leche entera), tenían un nivel medio de LDL al terminar la fase vegetal de 94.07, mientras que al terminar la fase entera el LDL había subido a 99.91. Nuevamente nos hacemos la pregunta: ¿es significativa esta diferencia?

Para responderla, al igual que antes, comparamos cada niño consigo mismo a través de un t-test para muestras emparejadas:

eLDL=subset(millac,sq==2)$eLDL  # Datos del grupo 2 (secuencia vegetal-entera) al final de la fase entera
vLDL=subset(millac,sq==2)$vLDL  # Datos del grupo 2 al final de la fase vegetal
t.test(vLDL,eLDL, paired=TRUE, alternative="less")

## 
##  Paired t-test
## 
## data:  vLDL and eLDL
## t = -1.9392, df = 52, p-value = 0.02895
## alternative hypothesis: true difference in means is less than 0
## 95 percent confidence interval:
##        -Inf -0.7803787
## sample estimates:
## mean of the differences 
##               -5.720755

lo que indica que efectivamente se ha producido un incremento significativo del LDL

t.test(eLDL,vLDL, paired=TRUE, alternative="less")$conf.int

## [1]     -Inf 10.66113
## attr(,"conf.level")
## [1] 0.95

Por tanto podemos decir, con un 95% de confianza, que el incremento en LDL ha sido inferior a 10.66 unidades.