Tema 1. Introducción: conceptos y principios básicos de computación científica.

¿Qué es la computación científica?

La computación científica (en inglés scientific computing) es la colección de herramientas, técnicas, procedimientos y desarrollos teóricos que se requieren para resolver problemas más o menos complejos de Ciencias e Ingeniería utilizando ordenadores. Es un campo en rápido crecimiento con aplicaciones en múltiples disciplinas científicas (física, química, ingeniería, ciencias sociales, …) y cuyo objetivo principal es el desarrollo de modelos y simulaciones que permitan comprender (y en muchos casos predecir) el comportamiento de los sistemas naturales.

La computación científica abarca el desarrollo de algoritmos y programas que requieren muchas veces el uso de métodos de análisis numérico, así como de técnicas específicas para el almacenamiento de la información en bases de datos y para su representación gráfica.

¿Por qué necesito esta asignatura?

En Ciencias del Mar se plantean múltiples problemas cuya solución requiere del uso de herramientas de computación científica:

No se espera con esta asignatura que un graduado en Ciencias del Mar se convierta en un programador de alto nivel, pero sí al menos que adquiera el nivel mínimo de conocimientos que le permita comunicarse con el ordenador para realizar tareas de entrada-salida de datos, representación gráfica de la información, desarrollo de procedimientos para la resolución de problemas básicos e implementación de dichos procedimientos en un lenguaje de programación.

Estructuras de datos

En general los modelos que se utilizan en el ámbito de la computación científica deben alimentarse con datos. Los datos pueden ser muy simples: por ejemplo si nuestro problema es sumar dos números \(a\) y \(b\), esos dos valores son todos los datos que necesitamos. En otros casos se requiere más información, y ésta debe organizarse adecuadamente en tablas.

 

Ejemplo 1

Tabla mal organizada.

En el curso del análisis de un tratamiento experimental para recuperar lesiones de cadera en perros, cada perro tratado pasa por una máquina en la que se miden características de tres pasos dados por el perro: dichas características son la fuerza de apoyo, la extensión angular de la articulación de la rodilla y la longitud del paso. La siguiente tabla muestra los datos de estas medidas realizadas en tres perros (Krivi, Linda y Otto):

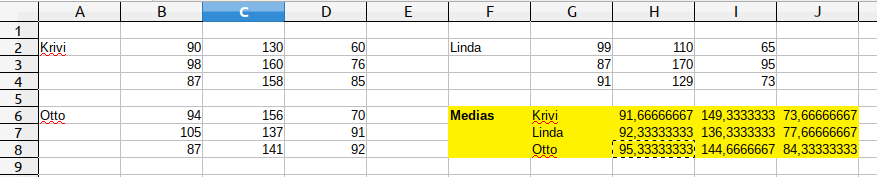
Esta tabla tiene una estructura inadecuada para el tratamiento de los datos:

Los mismos datos en una tabla bien organizada

En realidad, la organización correcta de esta tabla de datos sería la que figura en esta otra tabla:

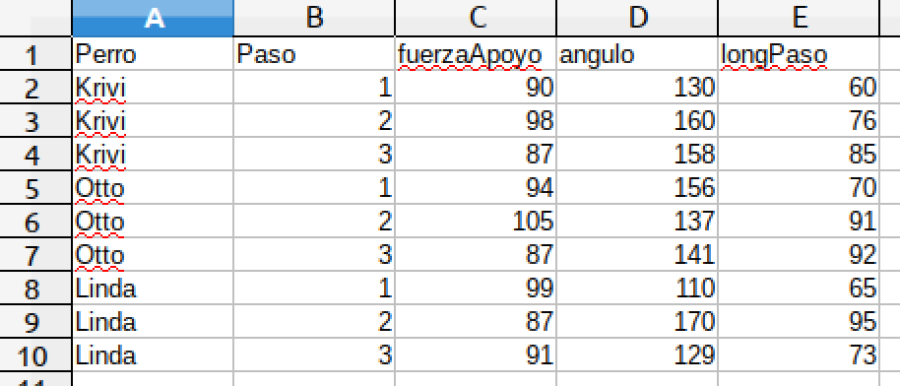
Como vemos, ahora:

De modo adicional, si los nombres de variable no fuesen absolutamente claros, la tabla anterior podría acompañarse de una segunda tabla diccionario, que especifique qué es cada variable:

En un archivo excel (o libreoffice) ambas tablas, la de datos y el diccionario se incluirían en distintas hojas (Ver archivo excel)

 

Ejemplo 2: datos con localización geográfica.

Para representar los datos medidos en esta malla necesitamos tres variables, que determinan para cada nodo, su longitud \(x\), su latitud \(y\) y la temperatura \(t\) medida en dicho punto. Estos datos podrían guardarse en una hoja de cálculo de la forma:

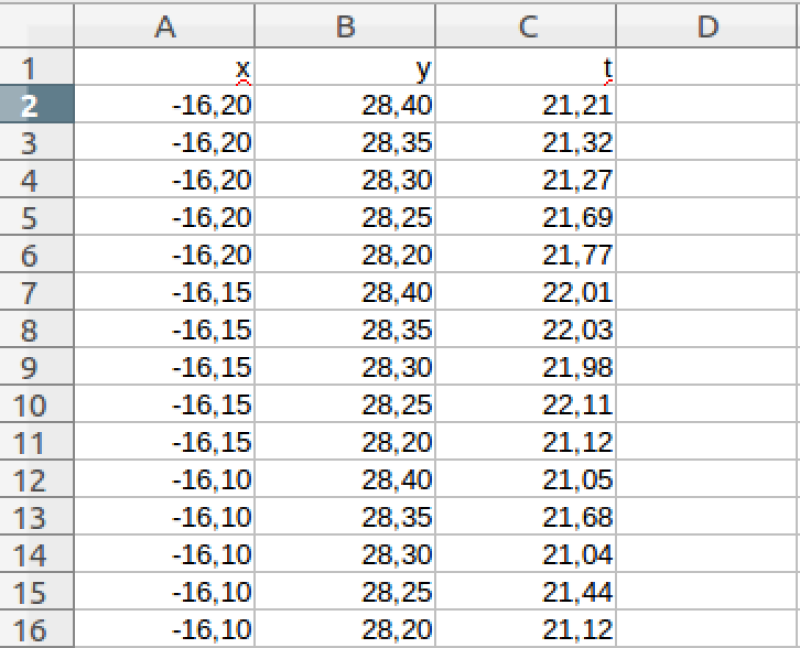
Nótese que, de nuevo, cada columna representa una variable y cada fila una observación \((x,y,t)\). Como en el ejemplo anterior, en esta hoja de cálculo hemos anotado los nombres de cada variable en la cabecera de cada columna.

 

En este caso, para representar estos datos necesitaremos una cuarta variable \(z\) que nos indique la profundidad a la que se ha tomado cada medida. El conjunto de datos sería entonces de la forma:

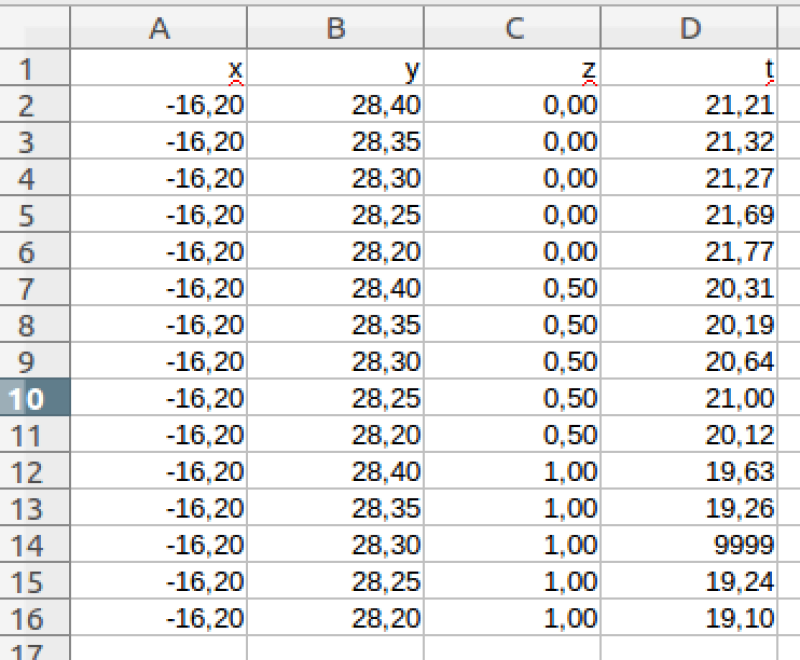
En general, en la generación de conjuntos de datos deberá respetarse el principio de que cada columna es una variable y cada fila una observación. No obstante, existen determinados formatos específicos para el archivo de datos geográficos (HDF o netCDF) que utilizan otras estructuras de datos para evitar tener que repetir, como en este caso, los mismos valores de longitud y latitud a distintas profundidades.

Las bases de datos pueden ser más complejas; por ejemplo, el archivo de datos anterior podría acompañarse de un archivo diccionario adicional que especifique, por ejemplo, el nombre completo de cada variable (“longitud”,“latitud”,“profundidad”,“temperatura”), las unidades en que se miden (grados, metros y grados centigrados) así como otras características de interés.

 

Valores perdidos

Muchas veces, al recopilar datos experimentales hay datos faltantes (“valores perdidos”). Por ejemplo, en una imagen de satélite en la que se mide la clorofila en la superficie del mar, si hay nubes dicha variable no puede medirse y sus valores para las latitudes y longitude cubiertas de nubes quedan “perdidos”. Cuando en una base de datos hay valores perdidos es preciso especificar de qué manera se van a codificar dichos valores. Si nos fijamos en el valor de temperatura de la fila 14 del conjunto de datos anterior, veremos que se ha anotado “9999”. Este suele ser un valor que se utiliza habitualmente para indicar que la variable (en este caso la temperatura) no ha podido medirse. La presencia de posibles valores perdidos ha de ser tenida en cuenta para que el análisis de los datos pueda llevarse a cabo correctamente. Habitualmente, en las tablas “diccionario” se suele añadir el código de valor perdido que se usa para cada variable.

 

Bases de datos multitabla.

En los ejemplos que hemos citado, la estructura de la base de datos se reduce a una simple matriz o tabla de datos. Es frecuente utilizar bases de datos formadas por varias matrices que se relacionan en función de una variable común. Por ejemplo, una base de datos para gestionar las matrículas de la universidad podría contener:

  1. Una tabla con los datos de los alumnos: nombre, apellidos, fecha de nacimiento, nota de entrada en la universidad, etc.
  2. Una tabla con los datos de las asignaturas: clave de identificación, nombre, curso en que se imparte, créditos asignados, etc
  3. Una tabla que especifique para cada alumno las asignaturas cursadas, calificación obtenida en cada convocatoria, … En esta tabla cada alumno se consignaría simplemente mediante su DNI y cada asignatura mediante su clave.

Gráficos

Otra actividad importante que debe contemplarse en el marco de la computación científica es la elaboración de gráficos: gráficos estadísticos, representación de funciones, mapas, … que permitan representar adecuadamente el modelo, sistema o conjunto de datos que se está estudiando. Dada la amplia variedad de gráficos que pueden llegar a necesitarse, resulta conveniente conocer procedimientos gráficos que otorguen al usuario la libertad suficiente para personalizar cada gráfico a su antojo.

Del problema a su solución: algoritmos

Un algoritmo es simplemente la sucesión lógica y ordenada de pasos que se deben dar para resolver un problema. No necesariamente el problema ha de ser de tipo matemático; así, por ejemplo, una receta de cocina es un algoritmo (sucesión de pasos que van desde la adquisición de los ingredientes hasta el plato terminado); el procedimiento para lavar la ropa en la lavadora es también un algoritmo. En el ámbito de la computación científica los algoritmos deben traducirse a algún lenguaje que entienda el ordenador para que pueda llevar a cabo los pasos que lo componen.

De acuerdo con Donald Knuth, un algoritmo bien construído debe cumplir los siguientes requsitos:

  1. Terminar en un número finito de pasos.
  2. Cada paso debe estar descrito de manera precisa, sin ambigüedades.
  3. Entrada/Salida: un algoritmo puede requerir algún o algunos valores de entrada. Asimismo puede producir valores de salida a partir de dichas entradas.
  4. Asimismo las operaciones que requiere cada paso del algoritmo deben ser lo suficientemente básicas como para poder ejecutarse de manera exacta y en un tiempo finito.

¿Cómo construir un algoritmo?

Construir un algoritmo para resolver un problema puede no ser una tarea sencilla. Muchas veces no es inmediato. Podemos sugerir algunos consejos para elaborar nuestros algoritmos:

  1. Análisis del problema: determinar con precisión cuál es el problema y tratar de resolverlo “a mano” utilizando lápiz y papel. Ello nos indicará qué cosas hemos de hacer para llegar a la solución del problema.
  2. Pensar sobre el procedimiento seguido en el punto anterior, identificando qué pasos se han dado y en qué orden; identificando también que datos necesitamos de entrada y qué resultado es el que pretendemos obtener. Cada paso debe ser lo más simple posible.
  3. A partir de la reflexión anterior, escribir un primer boceto del algoritmo, detallando ordenadamente los pasos que lo componen.
  4. Comprobar, ejecutándolo paso a paso, si el algoritmo descrito en el punto 3 realmente resuelve el problema. Si no es el caso, determinar que errores lógicos o conceptuales hemos cometido y corregirlos.

En el diseño de un algoritmo es importante la abstracción, fijándonos en los aspectos relevantes del problema y relegando los aspectos secundarios. Una estrategia que suele ser eficiente es el uso del llamado diseño descendente, consistente en dividir el problema principal (normalmente de solución compleja) en subproblemas o tareas sencillos que puedan resolverse de manera independiente y luego encajarse como las piezas de un puzzle (cada una de estas tareas o subproblemas puede también subdividirse si es necesario). Ello permite la colaboración de varias personas (cada una de ellas se encarga de resolver uno de los subproblemas), permite identificar de manera más fácil donde pueden estar los errores (es más fácil revisar la correcta resolución de los subproblemas sencillos) y permite un más fácil mantenimiento del código que se desarrolle para implementar el algoritmo (si vamos a adaptar el algoritmo a otros problemas similares, o vamos a añadirle o suprimirle pasos para abordar nuevos casos).

Si bien no hay reglas fijas con respecto a en cuántas partes (subproblemas o tareas principales) debe descomponerse un problema, un número conveniente suele ser entre 5 y 9; más tareas pueden hacer el algoritmo excesivamente complejo de entender.

En general siempre es posible construir varios algoritmos distintos para resolver un mismo problema. Por ello se requiere cierta práctica e intuición para elegir el mejor algoritmo, el más rápido o el más eficiente.

Diagramas de Flujo

Los algoritmos pueden representarse gráficamente mediante diagramas de flujo, que ayudan a visualizar ordenadamente la secuencia de tareas que conducen del planteamiento inicial del problema al resultado final que debe obtenerse.

Un diagrama de flujo es un gráfico que contiene los distintos pasos del algoritmo, utilizando distintos símbolos según el tipo de acción que se realice en cada paso. Los símbolos más frecuentes son los siguientes:

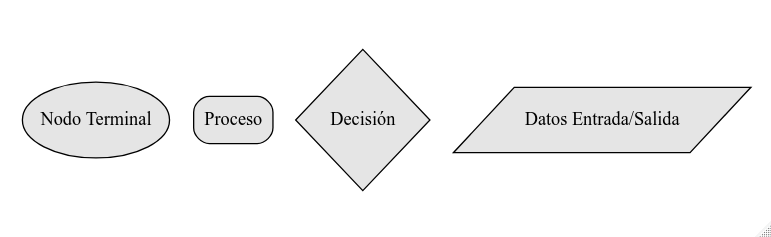
Ejemplo.

Supongamos que nuestro problema es calcular el área de un rectángulo conocidas su base \(B\) y su altura \(A\). El algoritmo para resolver este problema es el siguiente:

  1. Leer la longitud de la base, \(B\).
  2. Leer el valor de la altura, \(A\).
  3. Calcular \(S = B \cdot A\)
  4. Devolver el valor de \(S\)

Gráficamente, en forma de diagrama de flujo:

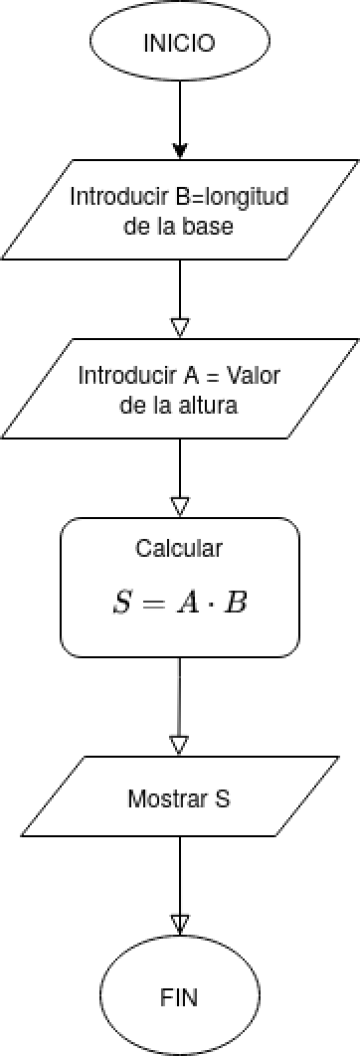
En el algoritmo podríamos añadir una comprobación de que los valores de \(A\) y \(B\) son mayores que 0, ya que en otro caso no estaríamos definiendo correctamente un rectángulo. El diagrama de flujo quedaría entonces de la forma:

 

 

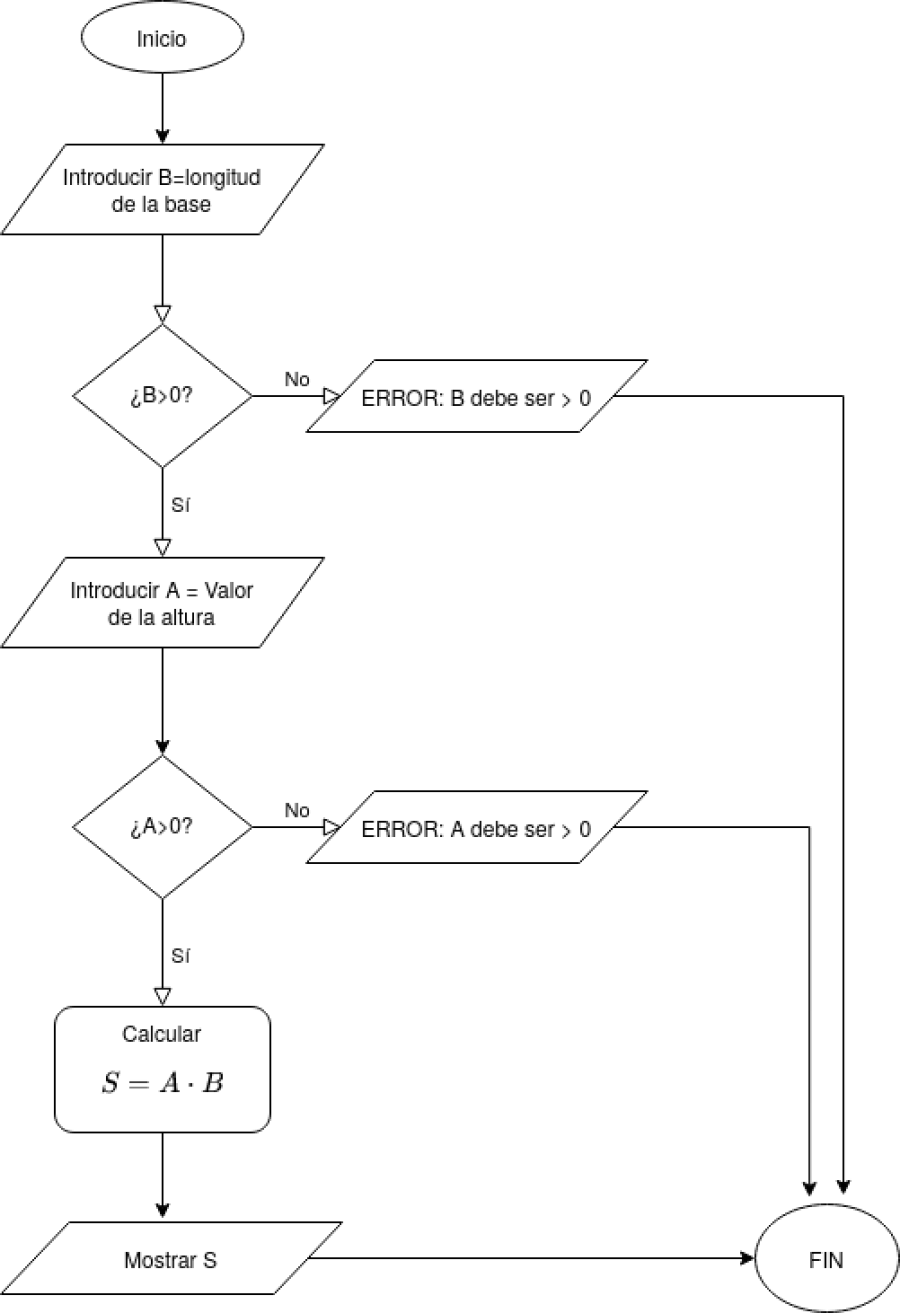
Lenguajes de programación.

Un lenguaje de programación, de acuerdo con la RAE es un conjunto de signos (palabras) y reglas (sintaxis) que permite la comunicación con una computadora. En términos muy generales podemos agrupar los lenguajes de programación en dos grandes clases: los lenguajes máquina o de bajo nivel compuestos por el conjunto de instrucciones y reglas que el procesador del ordenador es capaz de entender y procesar directamente, y los lenguajes de alto nivel, más próximos al lenguaje humano, que de alguna forma deben ser traducidos para que el procesador pueda entenderlos.

En realidad cada procesador entiende exclusivamente el lenguaje máquina para el que ha sido diseñado, cuyo código está compuesto por unos y ceros. Por contra, los lenguajes de alto nivel son de carácter absolutamente general y pueden ser entendidos por cualquier ordenador que disponga de las herramientas necesarias para su traducción a código máquina. Dichas herramientas son, básicamente, los compiladores y los intérpretes:

Para entender la diferencia entre compilador e intérprete podemos imaginar que deseamos leer un libro que se ha editado en ruso, por ejemplo. Compilar el libro sería equivalente a publicar al menos un ejemplar completamente traducido al español, que podemos leer directamente sin ayuda. Interpretar el libro significaría que tenemos un ejemplar en ruso y junto a nosotros hay siempre una persona (el intérprete) que nos va traduciendo frase a frase. Obviamente, si no tenemos intérprete, no podemos hacer nada con el libro.

Los lenguajes Fortran, Cobol, C o C++ son lenguajes que deben ser compilados. Los lenguajes Python, Matlab o R son lenguajes interpretados. Cada uno tiene sus ventajas y sus inconvenientes:

 

Durante este curso utilizaremos los lenguajes (interpretados) Matlab y R. El primero está orientado principalmente al cálculo numérico, mientras que el segundo se orienta fundamentalmente al análisis de datos y a la generación de gráficos.

Como hemos señalado más arriba, la principal desventaja de los lenguajes interpretados es que son de ejecución relativamente lenta en comparación con los compilados. En cualquier caso, dicha “lentitud” no constituye realmente un problema en la mayor parte de aplicaciones prácticas del día a día, que se resuelven con estos lenguajes en un tiempo imperceptible. Sólo si debemos llevar a cabo tareas extremadamente complicadas, que requieran la resolución de múltiples ecuaciones o la lectura de bases de datos enormemente grandes, es cuando la velocidad de ejecución del programa se convierte en un factor relevante. No obstante, como tendremos ocasión de comprobar, tanto Matlab como R incorporan en su sintaxis funciones complejas originalmente programadas en C o en Fortran, que han sido compiladas en dichos lenguajes, y que por tanto se ejecutan muy rápidamente. Es incluso posible utilizar herramientas que hacen posible que el usuario pueda incluir código C o Fortran como parte de un programa que se ejecutará sobre Matlab o R.

 

Por último, debemos señalar que existen otros lenguajes como Maxima (con su interfaz más sofisticada wxMaxima), Mathematica o Maple diseñados específicamente para el cálculo matemático simbólico. Estos lenguajes, que se conocen en inglés como “Computer Algebra Systems” (CAS), son capaces de resolver integrales, derivadas, sistemas de ecuaciones, … de manera simbólica. Si en uno de estos lenguajes planteamos el problema:

\[\int_{a}^{b}x\cdot dx\] nos devolvería como respuesta: \[\frac{b^{2}-a^{2}}{2}\] Los lenguajes que estudiaremos durante este curso están orientados fundamentalmente al cálculo numérico, si bien existen algunos complementos que permiten incorporar ciertas funciones de cálculo simbólico tanto en Matlab, como en R. En cualquier caso, para realizar cálculo simbólico siempre será preferible utilizar alguno de los CAS citados más arriba. También existe la posibilidad de utilizar entornos más sofisticados como Sagemath que permiten integrar en un único espacio de trabajo tareas realizadas con distintos lenguajes.

 

 

Programas

Los lenguajes de programación, como su propio nombre indica, sirven para escribir programas. Un programa es un conjunto ordenado de instrucciones que permite resolver un problema. Dicho de otra forma, un programa es un algoritmo escrito en un lenguaje que puede entender el ordenador.

 

Ejemplo 1


% Script para el cálculo de la superficie de un rectángulo
% ---------------------------------------------------------

% Limpia la pantalla
clc;  

% Informa de lo que vamos a hacer:
disp('Cálculo del área de un rectángulo');
disp('---------------------------------' );

% Pide los valores de base y altura
B = input('Longitud de la base: ');
A = input('Valor de la altura: ');

% Calcula la superficie del rectángulo
S = B*A;

% Muestra la superficie por pantalla
disp(['El valor del área es ', num2str(S)]);

Técnicamente, en matlab este programa recibe el nombre de script (que podemos traducir por guion); es la simple secuencia ordenada de instrucciones para resolver un problema simple, sin definir funciones ni estructuras de programación complejas.

 


% Script para el cálculo de la superficie de un rectángulo
% ---------------------------------------------------------

clc;  % Limpia la pantalla

% Informa de lo que vamos a hacer
disp('Cálculo del área de un rectángulo');
disp('---------------------------------' );

% Pide el valor de la base y comprueba que es mayor que cero:
B = input('Longitud de la base: ');
if B<=0
    fprintf('ERROR: La longitud de la base debe ser un valor positivo\n\n');    
    return
end

% Pide el valor de la altura y comprueba que es mayor que cero:
A = input('Valor de la altura: ');
if A<=0
    fprintf('ERROR: El valor de la altura debe ser positivo\n\n');    
    return
end

% Calcula la superficie del rectángulo:
S = B*A;

% Muestra la superficie en la pantalla:
disp(['El valor del área es ', num2str(S)]);
fprintf('\n\n' );

 

 

Ejemplo 2

Supongamos que queremos encontrar las soluciones de la ecuación:

\[ax^{2}+bx+c=0\] Sabemos que las soluciones se obtienen a partir de la expresión:

\[x=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}\] Concretamente, llamando \(\Delta=b^{2}-4ac\), se tiene que:

\[x_{1}=\frac{-b}{2a}\]

\[x_{1}=\frac{-b-\sqrt{\Delta}}{2a}\,\,\,\,\,\,\,\,\,\,\,x_{2}=\frac{-b+\sqrt{\Delta}}{2a}\]

\[x_{1}=\frac{-b-i\sqrt{-\Delta}}{2a}\,\,\,\,\,\,\,\,\,\,\,x_{2}=\frac{-b+i\sqrt{-\Delta}}{2a}\]  

Hacer un programa que resuelva la ecuación \(ax^{2}+bx+c=0\) consiste en escribir la secuencia de instrucciones que permiten obtener los valores anteriores. El diagrama de flujo correspondiente sería de la forma:

Normalmente en un lenguaje de programación de alto nivel dicha secuencia coincide prácticamente con lo que haríamos si tuviésemos que resolver la ecuación a mano siguiendo los pasos anteriores. A modo de ejemplo, a continuación mostramos como puede resolverse la ecuación de segundo grado utilizando los dos lenguajes de alto nivel, Matlab y R. En ambos casos hemos definido una función (llamada resuelveE2G) que recibe como entrada los coeficientes de la ecuación (\(a\), \(b\) y \(c\)) y devuelve como salida un vector \(x\) que contiene sus soluciones.

 

Programa en Matlab


function [x]=resuelveE2G(a,b,c)
   discrim=b^2-4*a*c;
   if discrim==0
      disp('La ecuación tiene una raíz doble:');
      x=-c/b;
   elseif discrim>0
      disp('La ecuación tiene dos raíces reales:');
      x1=(-b+sqrt(discrim))/(2*a);
      x2=(-b-sqrt(discrim))/(2*a); 
      x=[x1,x2];
   else
      disp('La ecuación tiene dos raíces imaginarias:'); 
      x1=(-b+i*sqrt(-discrim))/(2*a);
      x2=(-b-i*sqrt(-discrim))/(2*a); 
      x=[x1,x2];
end % Fin de la función

 

Programa en R


 resuelveE2G <- function(a,b,c){
   discrim=b^2-4*a*c
   if (discrim==0){
     cat('La ecuación tiene una raíz doble:')
     x=-c/b
   } else if (discrim>0){
     cat('La ecuación tiene dos raíces reales:')
     x1=(-b+sqrt(discrim))/(2*a)
     x2=(-b-sqrt(discrim))/(2*a)
     x=c(x1,x2)
   } else{
     cat('La ecuación tiene dos raíces imaginarias:')
     x1=(-b+1i*sqrt(-discrim))/(2*a)
     x2=(-b-1i*sqrt(-discrim))/(2*a)
     x=c(x1,x2)
   }
   return(x)
   } # Fin de la función

 

Como vemos, el código es casi idéntico en los dos lenguajes. Ambos siguen la misma secuencia lógica de instrucciones, reciben los mismos inputs (los valores de a, b y c), y producen los mismos outputs (un mensaje con las soluciones de la ecuación). Al igual que sucede con los idiomas que utilizamos habitualmente para comunicarnos, cada lenguaje de programación tiene sus propias palabras y sus propias reglas. Como vemos en este ejemplo, hay ligeras diferencias en la sintaxis: en matlab se usa disp para mostrar un texto y en R se usa cat; en matlab se usa elseif todo junto, y en R se separa, else if; para juntar las dos soluciones en un único vector x, en matlab se usa [x1,x2], mientras que en R se escribe c(x1,x2); las líneas de comentario (no ejecutables) empiezan con “%” en matlab y con “#” en R; la propia cabecera del programa, donde se define la función, difiere también entre ambos lenguajes. Si seguimos observando ambos programas podemos encontrar aún más diferencias.

Este pequeño ejemplo nos ilustra sobre las complejidades que podemos esperar encontrar al utilizar un lenguaje de programación: debemos aprender a descomponer un problema en tareas sencillas; aprender a enlazarlas en una secuencia lógica (al iniciar cada tarea deben haberse resuelto las anteriores); y aprender a escribir dicha secuencia utilizando las palabras y la sintaxis propias del lenguaje que utilicemos.

 

Antes de concluir esta sección, veamos cómo ejecutaríamos ambas funciones y cómo los respectivos lenguajes nos devuelven la solución:

 

 

 

¿Qué es Matlab?

Ver la entrada sobre Matlab en la Wikipedia

Web de Matlab

A finales de la década de los 70 del siglo pasado, Cleve Moler, profesor en la universidad de Nuevo Mexico se vio enfrentado al problema de tener que utilizar métodos numéricos para enseñar a sus alumnos como realizar cálculos relacionados con el rendimiento de reacciones químicas. Dichos cálculos implicaban un extenso manejo de sistemas matriciales. Sus alumnos de ingeniería química tenían una formación informática era escasa o nula, por lo que era inviable que usaran el lenguaje de programación por excelencia en aquella época, el Fortran. Por esta razón comenzó el desarrollo de un software que resultara sencillo de manejar para la realización de dichos cálculos, lo que supuso el desarrollo inicial de Matlab, acrónimo de “Matrix Laboratory”. En el año 1984, con otros colaboradores, Moler fundó la empresa The Mathworks, que comenzó a distribuir Matlab de forma comercial.

¿Qué es Octave?

Ver la entrada sobre Octave en la Wikipedia

Web de Octave

Octave es un lenguaje de programación de alto nivel, orientado principalmente al cálculo numérico. Se encuentra vinculado al proyecto GNU, que es un proyecto internacional para el desarrollo de un sistema completo de software libre. Esto significa que una vez que se obtiene el software, se tienen cuatro libertades específicas para usarlo: La libertad de ejecutar el programa como se desee; la libertad de copiar el programa y dárselo a amigos o compañeros de trabajo; la libertad de cambiar el programa como se desee mediante el acceso completo al código fuente; y la libertad de distribuir una versión mejorada, ayudando así a construir la comunidad (texto extraído de la web del proyecto GNU).

Octave fue creado originalmente en 1988 por John W. Eaton (profesor de la universidad de Wisconsin-Madison) para ser utilizado en un curso de diseño de reactores químicos. Del mismo modo que Moler unos años antes, comenzó a desarrollar un software informático simple que pudiesen usar sus alumnos, sin que tuvieran que aprender a programar en Fortran lo que les restaría mucho tiempo para el aprendizaje del diseño de reactores químicos que era el verdadero objetivo del curso. Octave fue el nombre elegido por Eaton para su software, en honor de un antiguo profesor suyo llamado Octave Levenspiel, conocido por ser capaz de resolver rápidamente problemas numéricos en ingeniería química utilizando aproximaciones mediante cálculos elementales. Cuando Eaton comenzó a desarrollar Octave para sus alumnos, se inspiró intencionadamente en Matlab para la sintaxis de su programa, por lo que los dos lenguajes son prácticamente idénticos y altamente compatibles entre sí.

Eaton pronto se dio cuenta de que su programa podía ampliarse y extender su uso fuera de la ingeniería química. El 4 de enero de 1993 lanzó una versión alfa de octave, y un año más tarde, el 17 de febrero de 1994, apareció la versión 1.0. Desde entonces, Octave ha ido creciendo, a la vez que ha procurado mantener una sintaxis compatible con Matlab. Desde la versión 4, Octave cuenta con un entorno de desarrollo también muy similar al de Matlab.

Matlab vs. Octave

En la actualidad Matlab es un software privativo (de pago) mientras que Octave se puede instalar sin coste alguno. El alto grado de compatibilidad entre ambos hace que aquellas personas que no pueden permitirse pagar una licencia de uso de Matlab, puedan aprender a programar en Octave y si en el futuro deben utilizar Matlab, no les va a costar esfuerzo hacer la transición. La compatibilidad entre las sintaxis de ambos programas (Octave y Matlab) es tan alta que un programa escrito para Octave funcionará en Matlab con escasas modificaciones, y viceversa.

En cualquier caso, debemos señalar que Matlab cuenta con diversas ventajas respecto a Octave: es más robusto (Octave depende de muchas librerías de software libre para gráficos, gestión del editor, etc, y la integración de Octave con estas librerías puede fallar en algunos casos; Matlab tampoco está libre de fallos, pero es justo reconocer que en este contexto presenta menos problemas), cuenta con una plataforma llamada Simulink consistente en un entorno de programación visual que facilita determinadas tareas de programación, y cuenta con numerosas librerías (colecciones de programas), denominadas toolboxes, para múltiples tareas (análisis de imágenes, análisis de señales, controladores de dispositivos hardware, …). Octave también cuenta con sus propias librerías (Octave-Forge), si bien aún no alcanzan el nivel de desarrollo de la toolboxes de Matlab.

 

¿Qué es R?

Ver la entrada sobre R en la Wikipedia

Web de R

R es también un lenguaje de programación de alto nivel, orientado principalmente a la estadística y a la generación de gráficos. Al igual que Octave, es también software libre y su gestación tiene características similares a las de Octave. R comenzó a ser desarrollado en 1992 por Robert Gentleman y Ross Ihaka, del departamento de Estadística de la Universidad de Auckland (Nueva Zelanda), con el objetivo de disponer de un lenguaje sencillo (y gratuito) con el que poder enseñar cursos introductorios de estadística en sus clases. El nombre del programa deriva de las iniciales de los nombres de sus dos autores.

La sintaxis de R copia (y es compatible con) la de un lenguaje preexistente, el S, desarrollado entre 1976 y 1980 por John Chambers y Richard Becker en los laboratorios Bell, con objeto de poder abordar con facilidad problemas de tratamiento estadístico de datos sin tener que recurrir constantemente a la programación en Fortran.

En la actualidad R es el software más utilizado para el análisis estadístico. El hecho de ser software libre ha dado lugar a que tenga una amplia base de usuarios y ha permitido además el desarrollo de una ingente cantidad de librerías (más de 10000) que abordan casi cualquier procedimiento estadístico imaginable.

En esta asignatura utilizaremos R como lenguaje para la generación de gráficos. En concreto, utilizaremos la librería ggplot2 que como veremos implementa una gramática específica para la descripción y elaboración de gráficos. Posteriormente, en la asignatura Estadística emplearemos R para el análisis y tratamiento de datos siguiendo este curso de introducción a R.