Problema
Una esfera sólida de radio R cm y densidad \(\rho_e\) gr/cc se sumerge en agua de mar. Suponiendo que \(\rho_e\) es inferior a la densidad del agua del mar, que es aproximadamente de 1,027 gr/cc, se desea determinar a qué profundidad se sumerge la esfera cuando flota en el mar.
Planteamiento
La profundidad buscada coincide con la altura \(h\) (en cm) del casquete esférico sumergido, de acuerdo con la figura siguiente (extraída de Wikipedia):
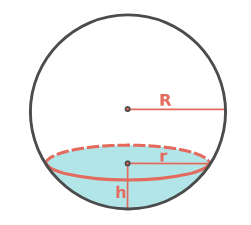
De acuerdo con el principio de Arquímedes: “todo cuerpo sumergido en un líquido experimenta un empuje vertical y hacia arriba igual al peso del volumen de líquido desalojado”. Para que la esfera flote, su peso debe ser compensado por dicho empuje, y por tanto podemos calcular el valor de \(h\) como aquél que hace que el peso del agua desalojada por el casquete esférico coincida con el peso total de las esfera.
El volumen del casquete esférico de altura \(h\) viene dado por la expresión (ver la justificación aquí):
\[V=\frac{1}{3}\pi\cdot h^{2}\left(3R-h\right)\]
Si \(\rho_a\) es la densidad del agua de mar, el peso del agua de mar desalojada por el casquete esférico, y por tanto el empuje hacia arriba experimentado por la esfera, es:
\[Empuje=\rho_a\cdot V=\frac{\rho_a}{3}\pi\cdot h^{2}\left(3R-h\right)\]
La diferencia entre el empuje hacia arriba experimentado por la esfera sumergida una altura \(h\) y su peso es entonces:
\[dif(h)=\frac{\rho_a}{3}\pi\cdot h^{2}\left(3R-h\right)-P_e\]
La esfera flota en el agua cuando su peso se equilibra con el empuje, es decir, cuando la diferencia anterior es cero:
\[dif(h)=\frac{\rho_a}{3}\pi\cdot h^{2}\left(3R-h\right)-P_e=0\]
Por tanto, la altura del casquete sumergido de la esfera se obtiene despejando el valor de \(h\) de esta ecuación. Esta ecuación es cúbica en \(h\) y no tiene una solución explícita que pueda calcularse directamente, por lo que debemos desarrollar un algoritmo para obtenerla.
Algoritmo para la obtención de \(h\)
Para desarrollar nuestro algoritmo debemos tener en cuenta lo siguiente:
Si la densidad de la esfera es mayor que la densidad del agua, la esfera se hunde, por lo que no tiene sentido resolver el problema.
Si la densidad de la esfera es menor que la densidad del agua, podemos empezar probando como posibles valores de \(h\) sus valores extremos: \(h_0=0\) (esto es, toda la esfera está fuera del agua, no tiene ninguna parte sumergida) y \(h_1=2R\) (toda la esfera está bajo el agua).
Si ninguno de estos dos valores es la solución del problema (es decir, ninguno cumple que \(dif(h_i)=0\)), probamos con el valor intermedio \(h_M=\frac{h_0+h_1}{2}\)
Si \(dif(h_M)=0\) quiere decir que \(h_M\) es la solución del problema; en caso de que \(dif(h_M)\neq 0\) ocurre lo siguiente:
Si Signo(dif(\(h_M\)))=Signo(dif(\(h_0\))) entonces el valor de \(h\) que buscamos está entre \(h_M\) y \(h_1\).
Si Signo(dif(\(h_M\))) \(\neq\) Signo(dif(\(h_0\))) entonces el valor de \(h\) que buscamos está entre \(h_0\) y \(h_M\).
En cualquiera de los dos casos repetiríamos el proceso tomando como nueva aproximación de \(h\) el punto medio del intervalo en cuyos extremos la función \(dif(h)\) cambia de signo.
Para que el proceso no se eternice, paramos cuando entre dos aproximaciones sucesivas \(h_0\) y \(h_M\) la diferencia sea menor que un \(\varepsilon\) prefijado.
Todas estas ideas se concretan en el siguiente diagrama de flujo:

En esta hoja de cálculo se muestra como calcular el valor de \(h\) conocidos el diámetro y el peso de la esfera, así como la densidad del líquido en el que se encuentra.
El archivo esfera.m contiene el código matlab de una función que implementa el algoritmo anterior.