El siguiente archivo recoge datos mensuales de temperatura y precipitación medidos en el aeropuerto de Los Rodeos en Tenerife:
TF=read_excel("datos/losRodeosMensual.xlsx")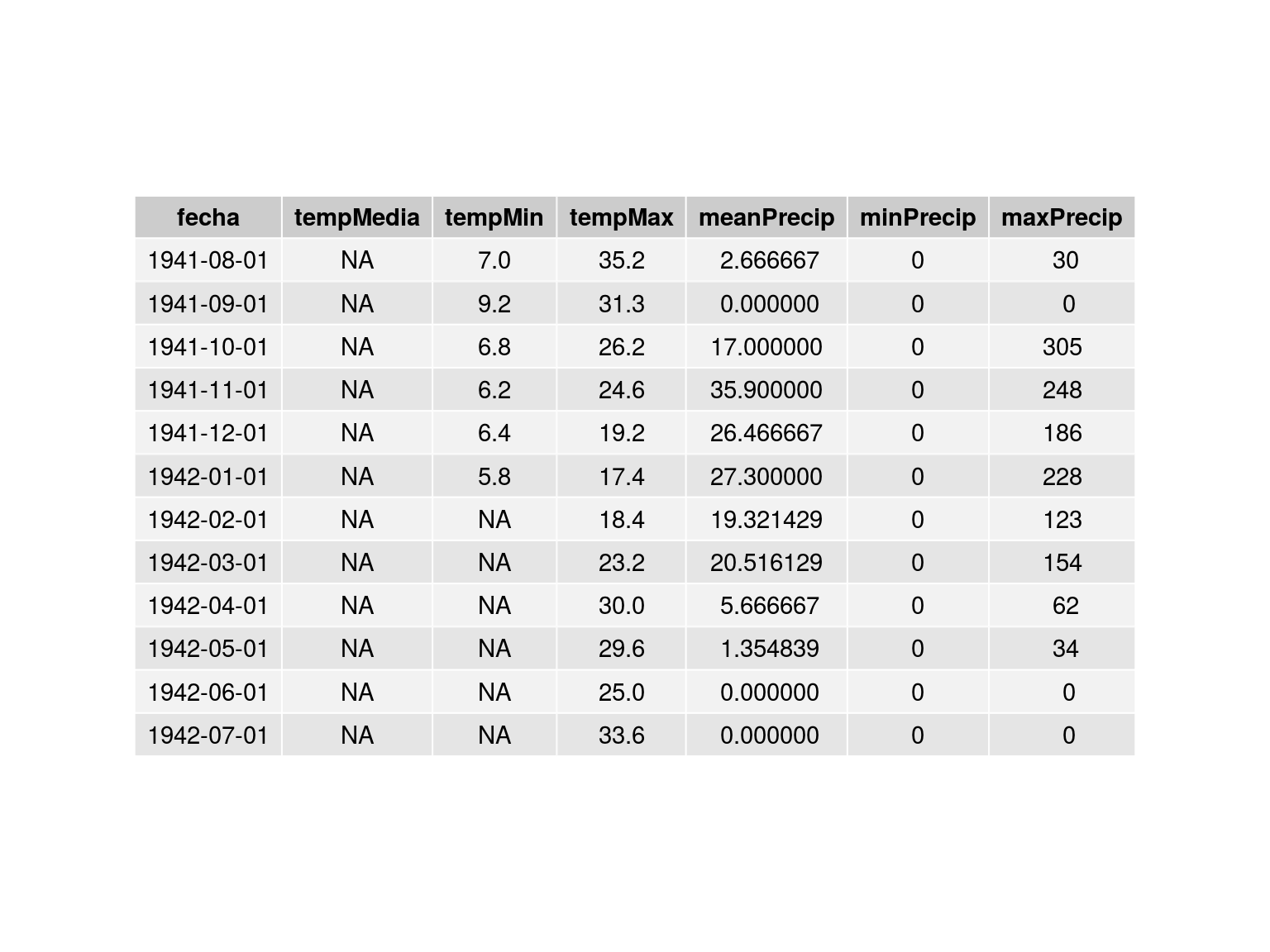
Angelo Santana
23 de octubre de 2017
El siguiente archivo recoge datos mensuales de temperatura y precipitación medidos en el aeropuerto de Los Rodeos en Tenerife:
TF=read_excel("datos/losRodeosMensual.xlsx")
Para que R entienda estos datos como una serie temporal podemos proceder de dos formas:
ts() en la que hay que especificar fecha de inicio y frecuencia de los datos de la serie (el uso de esta función requiere que no falte ningún mes en la serie, aunque los datos de la fila correspondiente sean NA):TF.ts=ts(TF[,-1],start=c(1941,8),freq=12)
zoo del paquete zoo, en la que se puede especificar la variable que recoge la fecha de la toma de datos; esta función permite que los datos estén irregularmente espaciados:library(zoo)
TF.zoo=zoo(TF[,-1], order.by=TF$fecha)
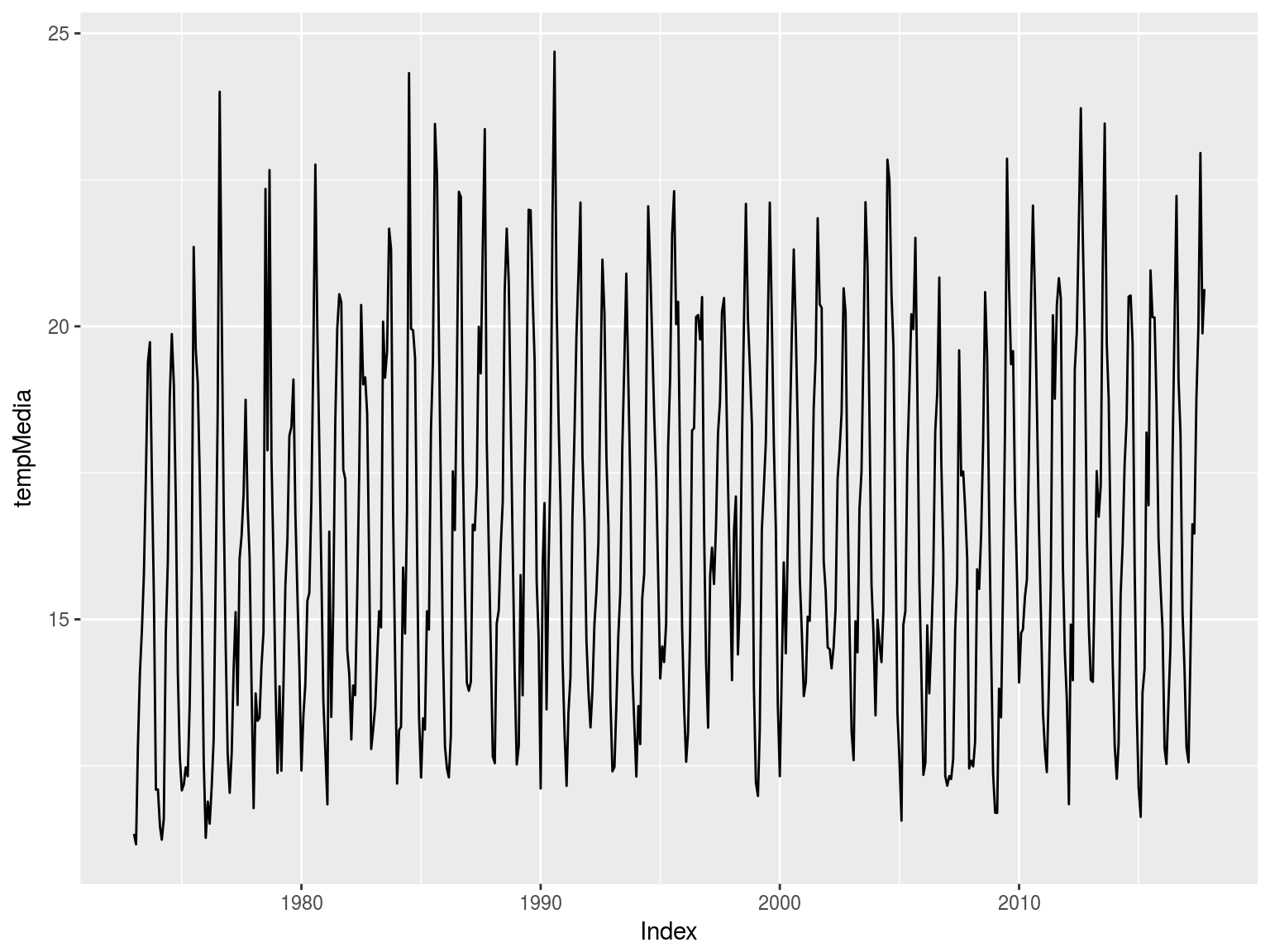
Nos restringimos a los datos a partir de 1973, en que hay un registro casi completo en todas las variables:
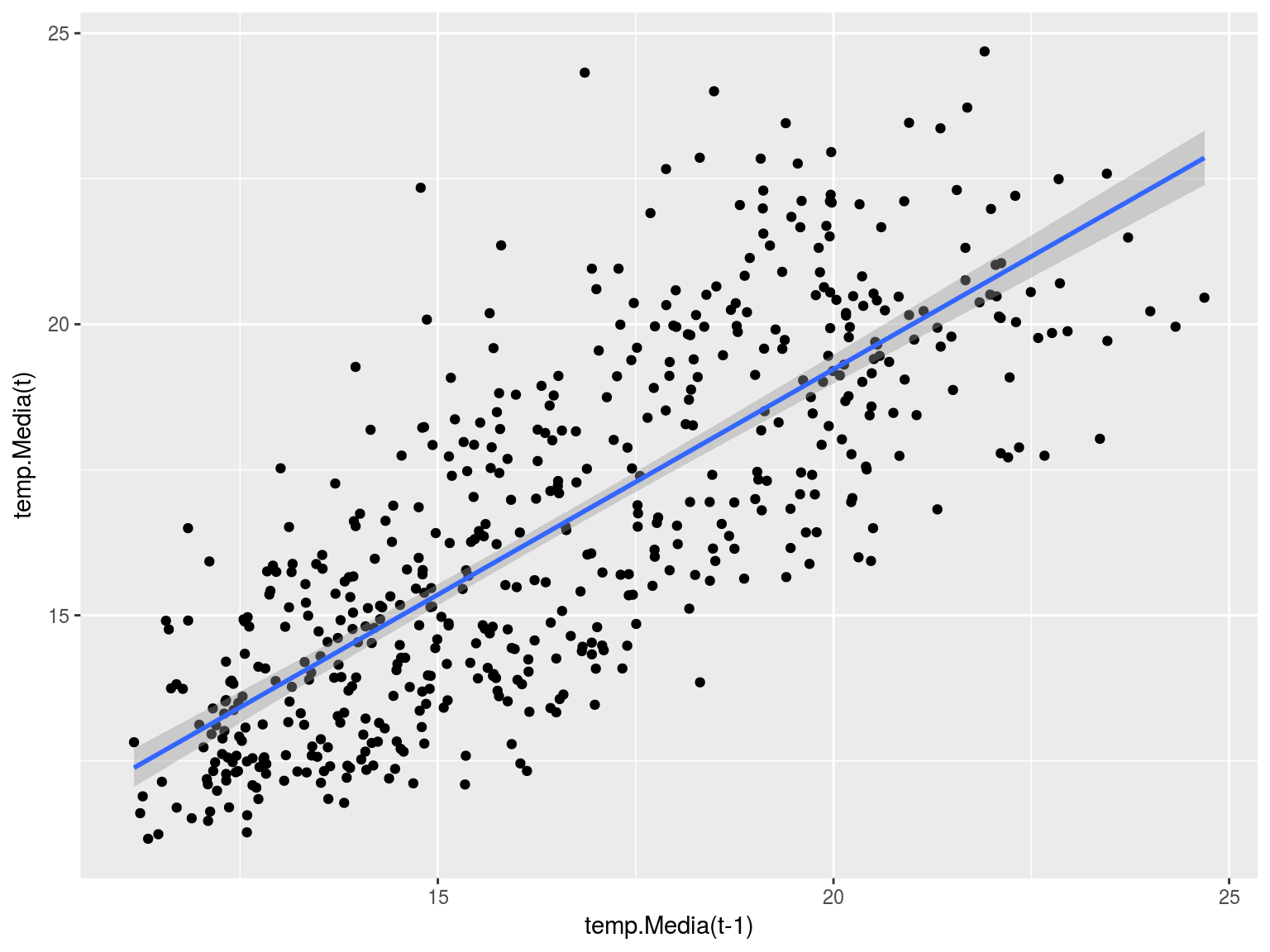
Representamos la temperatura media de un mes frente a la temperatura media del mes anterior:
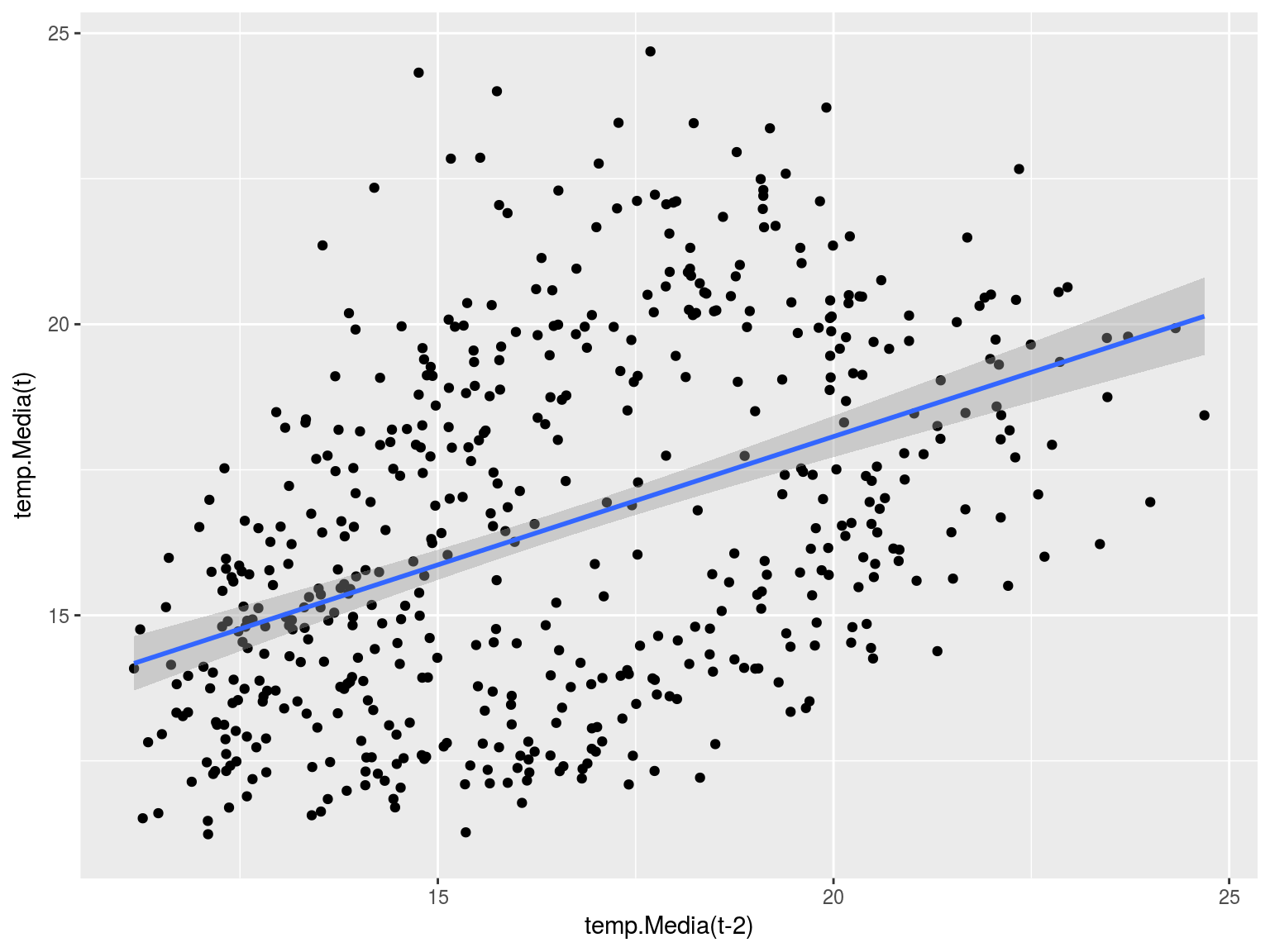
Representamos la temperatura media de un mes frente a la temperatura media de hace dos meses:
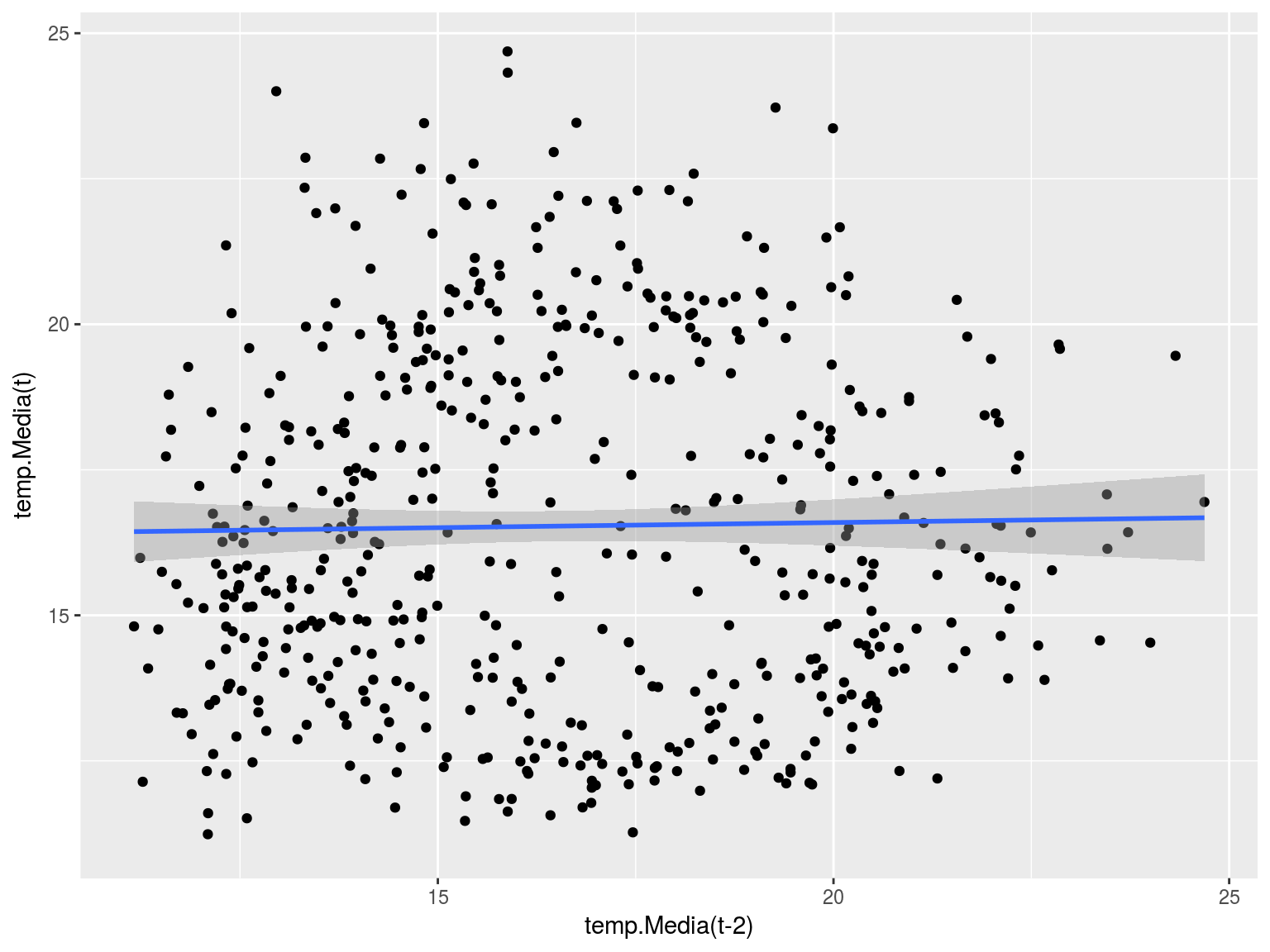
Representamos la temperatura media de un mes frente a la temperatura media de hace tres meses:
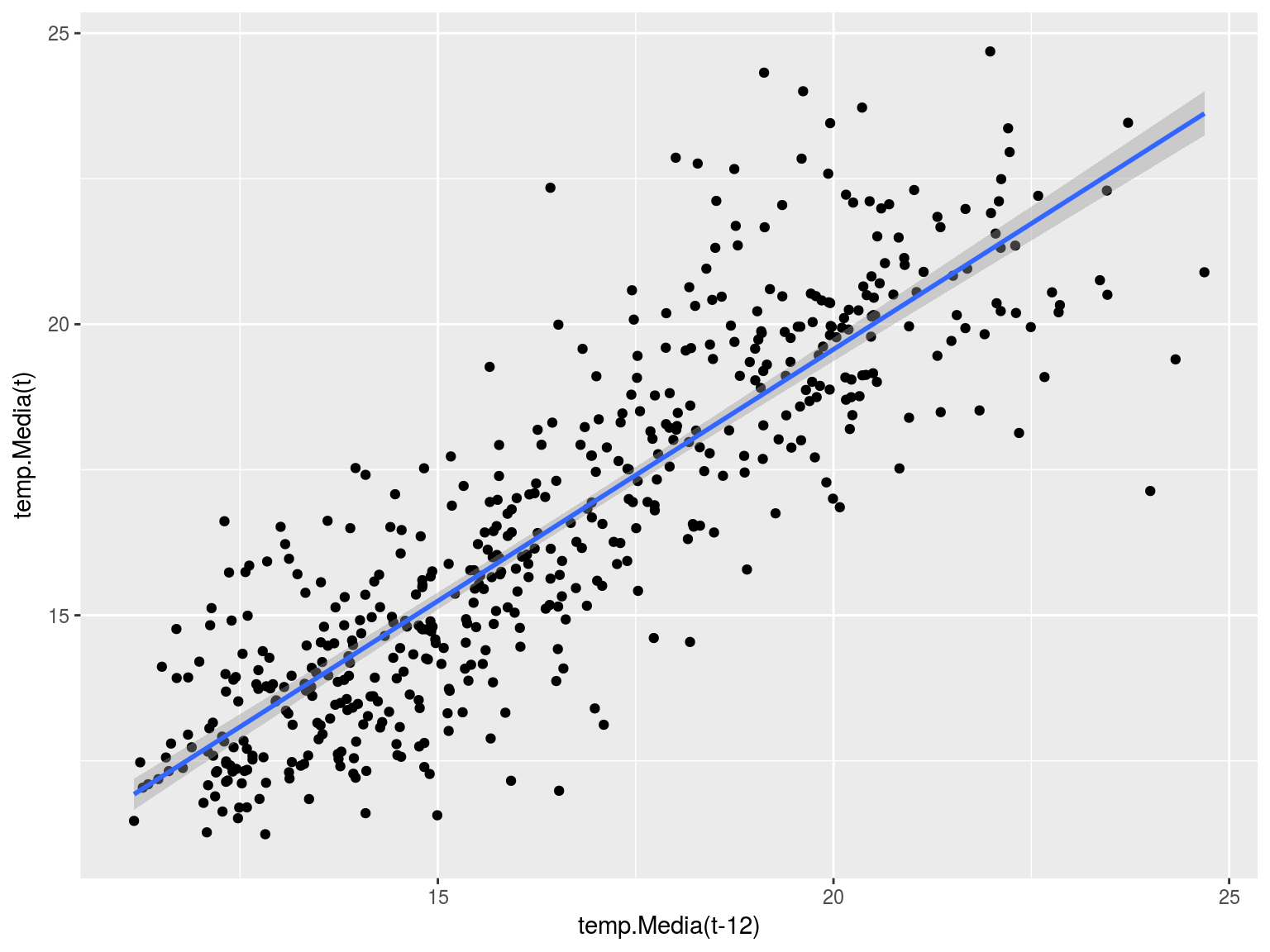
Representamos la temperatura media de un mes frente a la temperatura media de hace un año:
Corresponden a series temporales constantes en media y varianza, y con función de autocorrelación dependiente exclusivamente de la separación entre observaciones y no de cuando se producen éstas.
El patrón de estos modelos se identifica mediante la función de autocorrelación y la función de autocorrelación parcial.
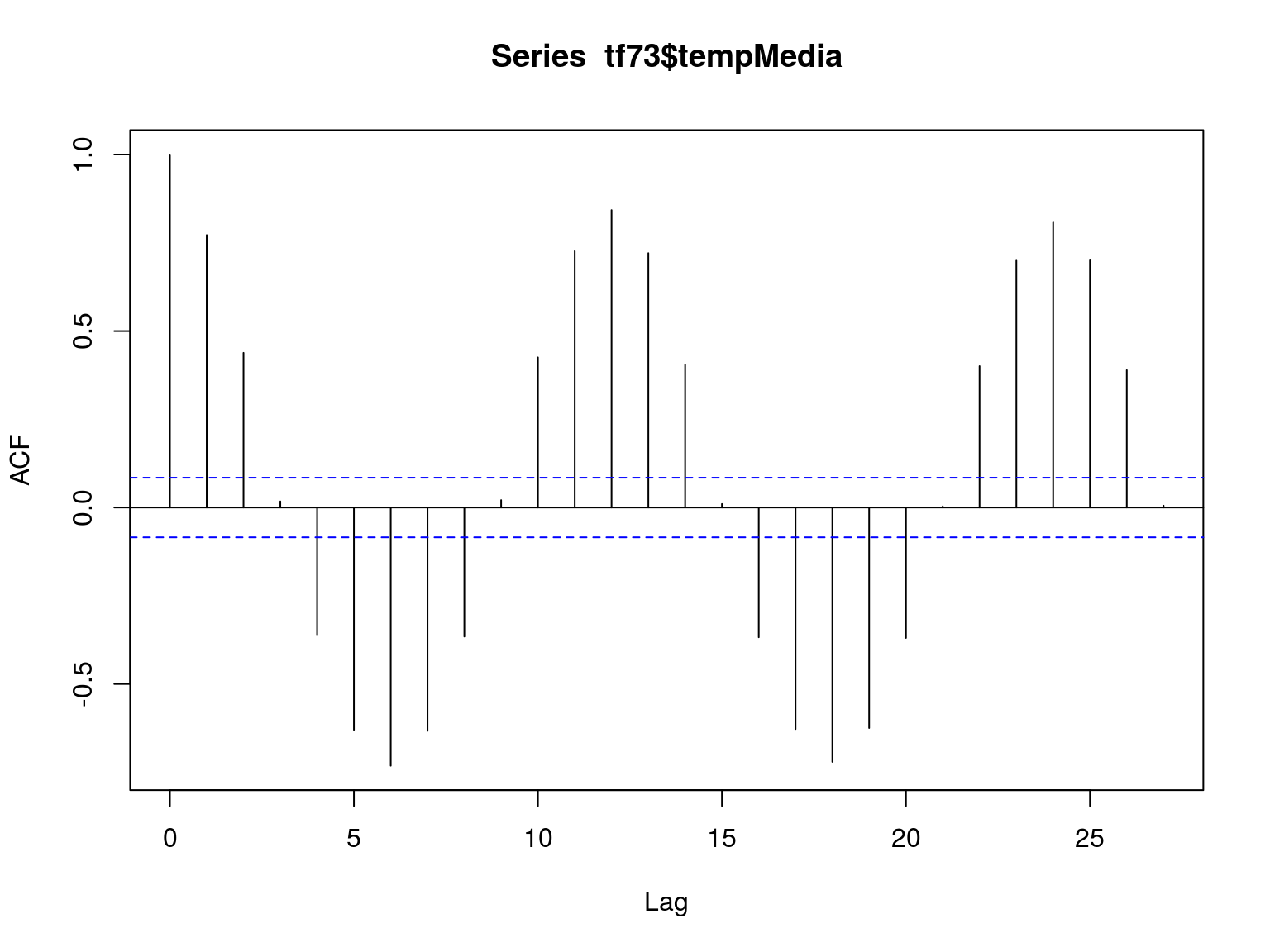
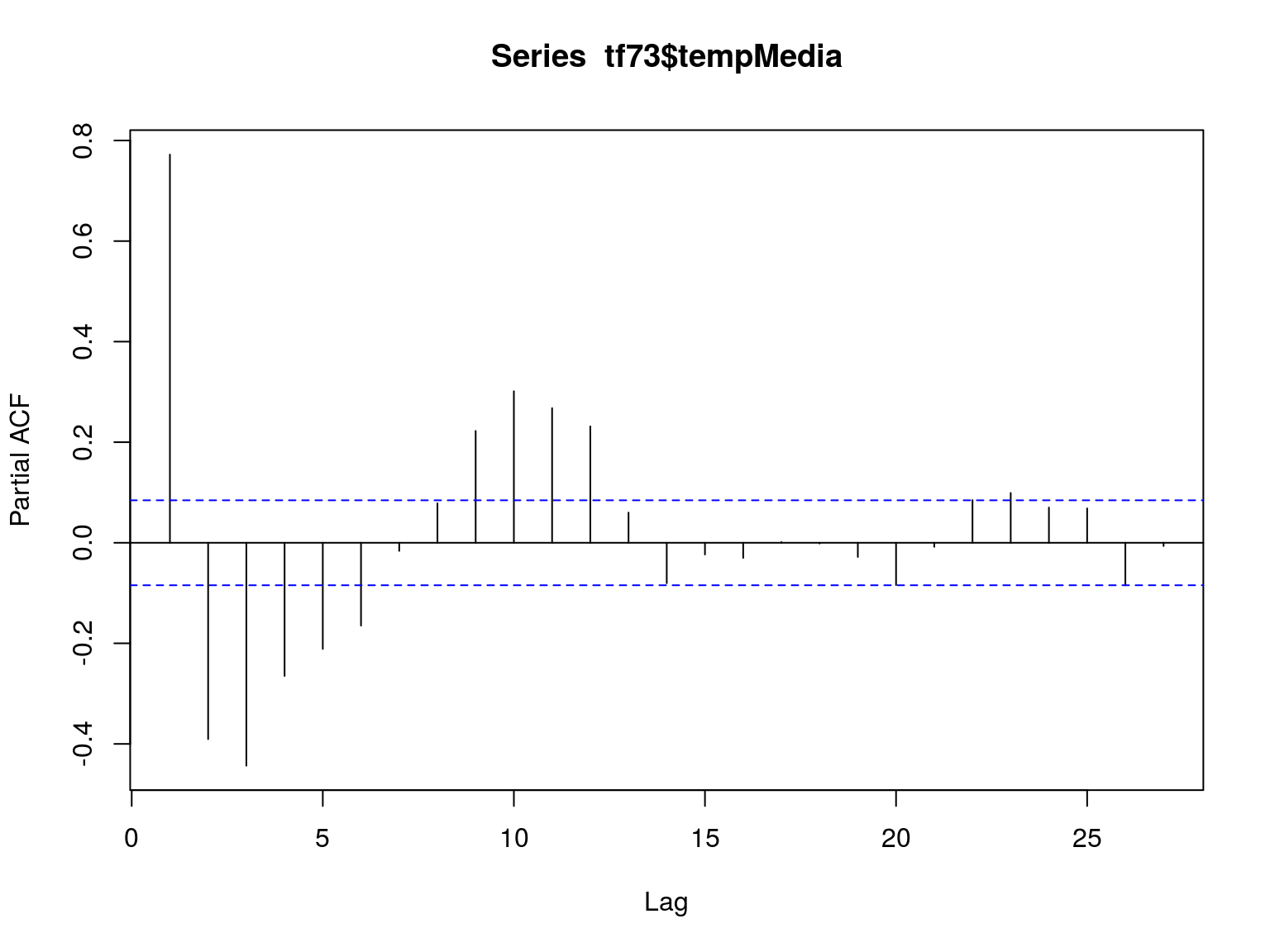
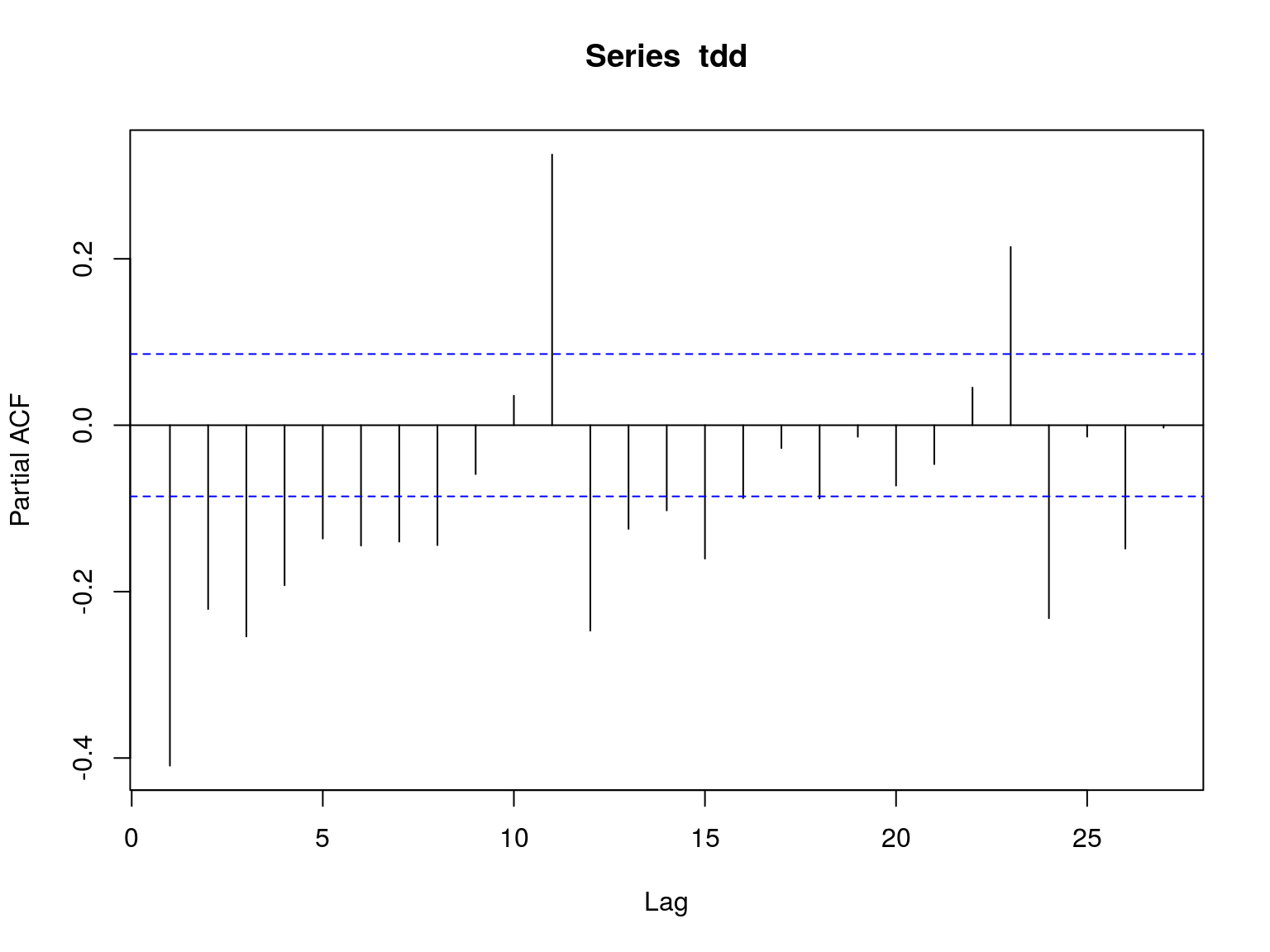
El modelo AR(1) es de la forma:
\[X_{t}=\phi_{1}X_{t-1}+\varepsilon_{t}\]
Básicamente es un modelo de regresión simple en el que el valor de \(X\) en el instante \(t\) depende del valor de la misma variable en el instante \(t-1\).
Las variables \(\varepsilon_t\) se presuponen normales e incorreladas.
El modelo AR(2) es de la forma:
\[X_{t}=\phi_{1}X_{t-1}+\phi_{2}X_{t-2}+\varepsilon_{t}\]
En general, el modelo AR(p) es de la forma:
\[X_{t}=\phi_{1}X_{t-1}+\phi_{2}X_{t-2}+\dots+\phi_{p}X_{t-p}+\varepsilon_{t}\]
El modelo AR(1) podría estimarse por mínimos cuadrados, como cualquier modelo de regresión:
##
## Call:
## lm(formula = tempMedia ~ tempMedia1, data = tf73)
##
## Residuals:
## Min 1Q Median 3Q Max
## -4.0730 -1.4884 -0.2003 1.3217 7.5296
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3.73480 0.45769 8.16 2.41e-15 ***
## tempMedia1 0.77466 0.02727 28.40 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.941 on 535 degrees of freedom
## (1 observation deleted due to missingness)
## Multiple R-squared: 0.6012, Adjusted R-squared: 0.6005
## F-statistic: 806.7 on 1 and 535 DF, p-value: < 2.2e-16o utilizando máxima verosimilitud teniendo en cuenta la autocorrelación en la serie:
arim73=arima(tf73$tempMedia,order=c(1,0,0))
arim73##
## Call:
## arima(x = tf73$tempMedia, order = c(1, 0, 0))
##
## Coefficients:
## ar1 intercept
## 0.7773 16.4983
## s.e. 0.0272 0.3732
##
## sigma^2 estimated as 3.765: log likelihood = -1120.51, aic = 2247.02Calidad del ajuste:
tsdiag(arim73)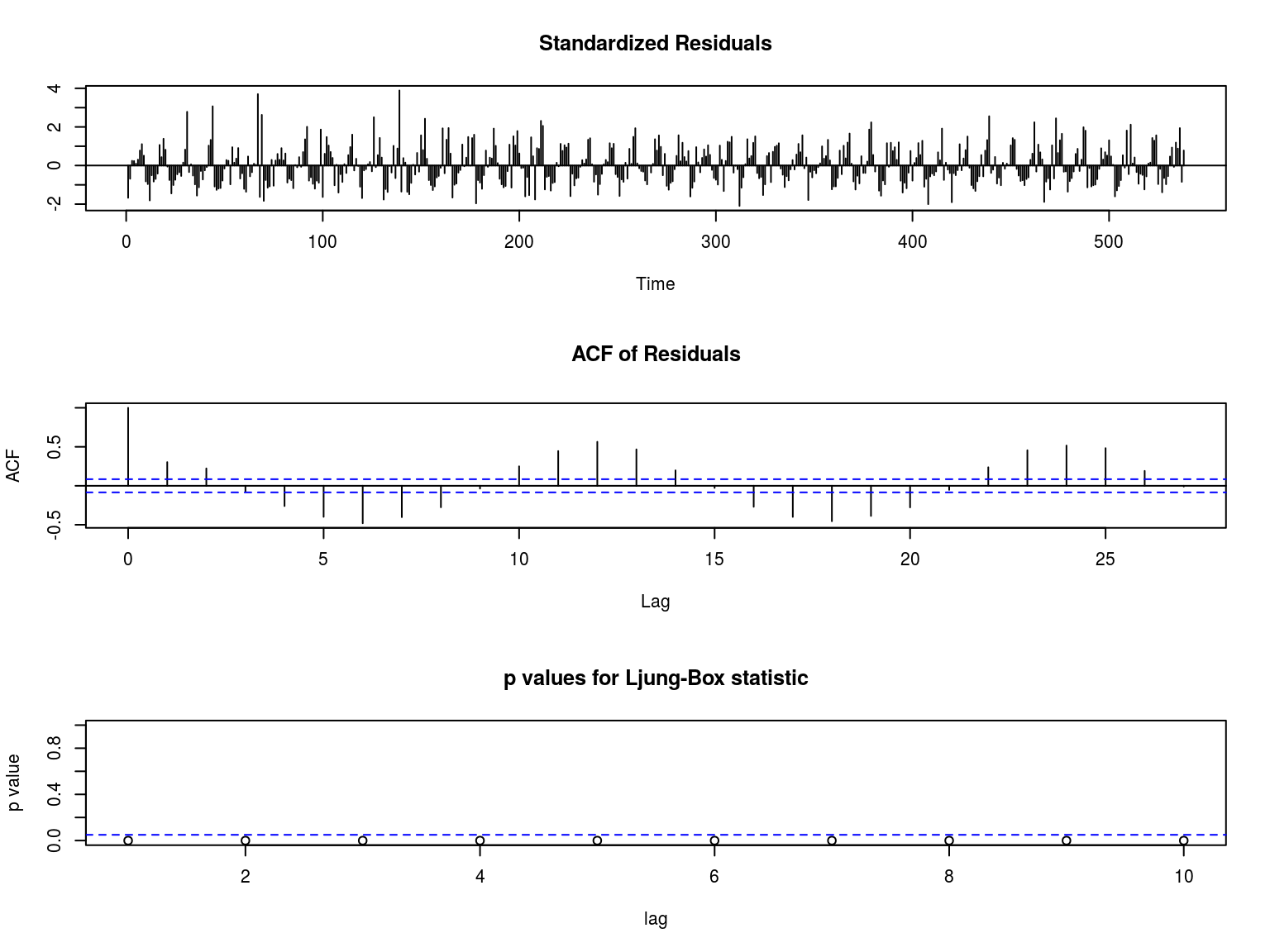
arim73=arima(tf73$tempMedia,order=c(2,1,1))
arim73##
## Call:
## arima(x = tf73$tempMedia, order = c(2, 1, 1))
##
## Coefficients:
## ar1 ar2 ma1
## -0.1125 0.2365 0.3199
## s.e. 0.1460 0.0492 0.1461
##
## sigma^2 estimated as 3.876: log likelihood = -1125.77, aic = 2259.53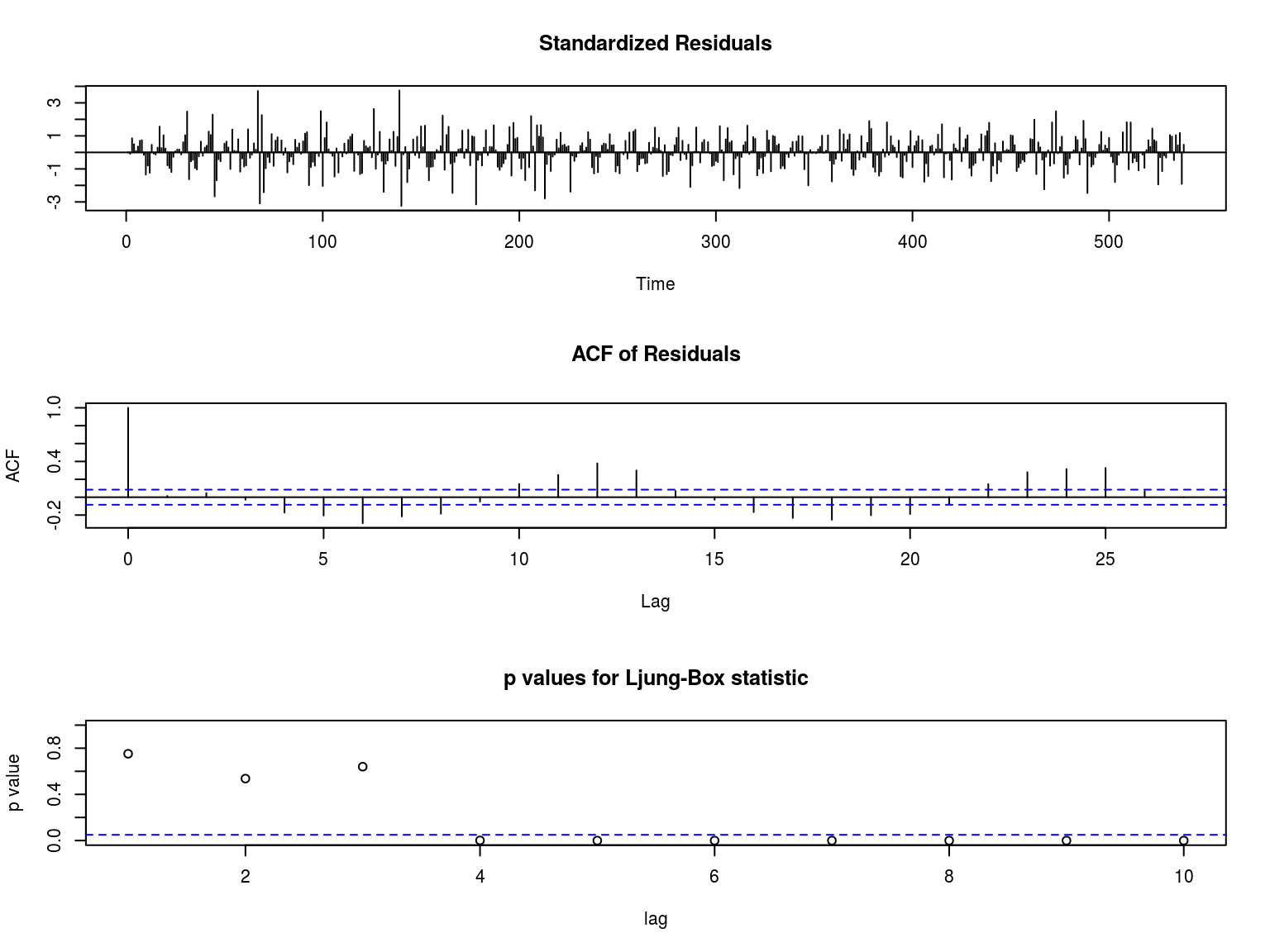
sarim73=arima(tf73$tempMedia, order = c(1,1,1),
seasonal = list(order = c(2, 1, 0), period = 12))
sarim73##
## Call:
## arima(x = tf73$tempMedia, order = c(1, 1, 1), seasonal = list(order = c(2, 1,
## 0), period = 12))
##
## Coefficients:
## ar1 ma1 sar1 sar2
## 0.2016 -0.9339 -0.6237 -0.3362
## s.e. 0.0562 0.0320 0.0430 0.0418
##
## sigma^2 estimated as 1.747: log likelihood = -895.47, aic = 1800.94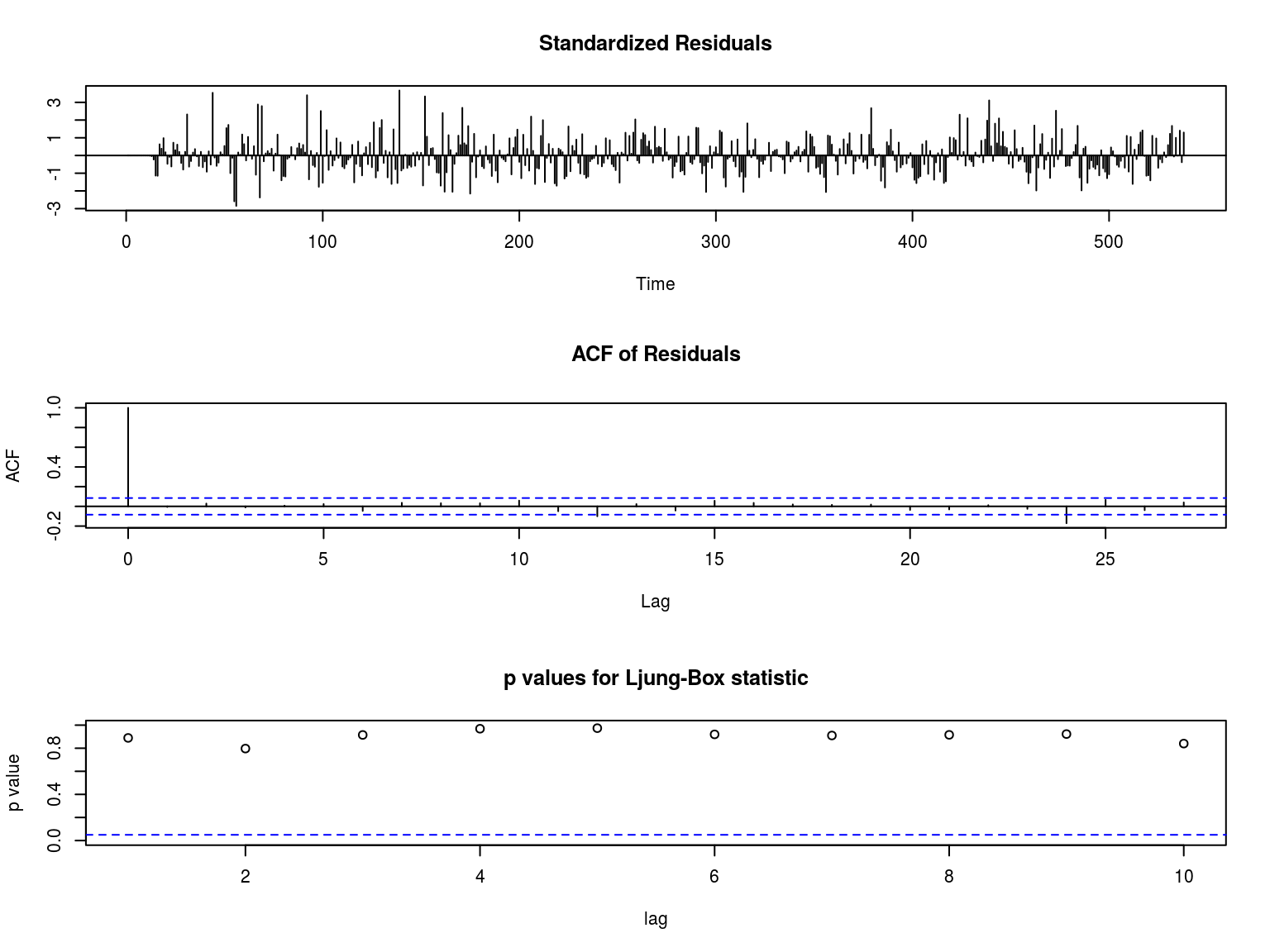
Correlación cruzada entre temperatura y precipitación medias:
TF73=TF.ts[-c(1:377),]
TF73=TF73[-c(539,540),]
ccf(TF73[,2],TF73[,5])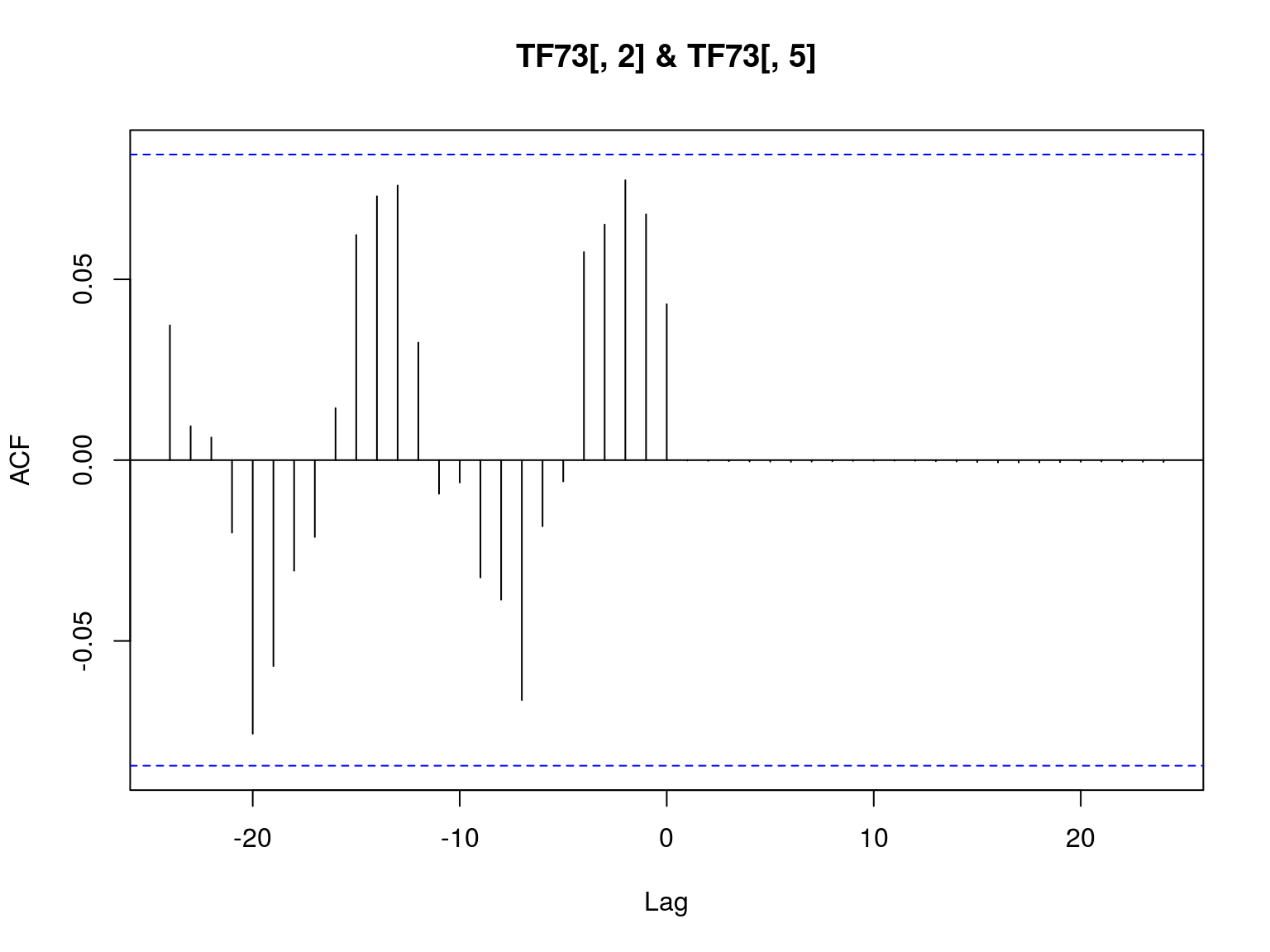
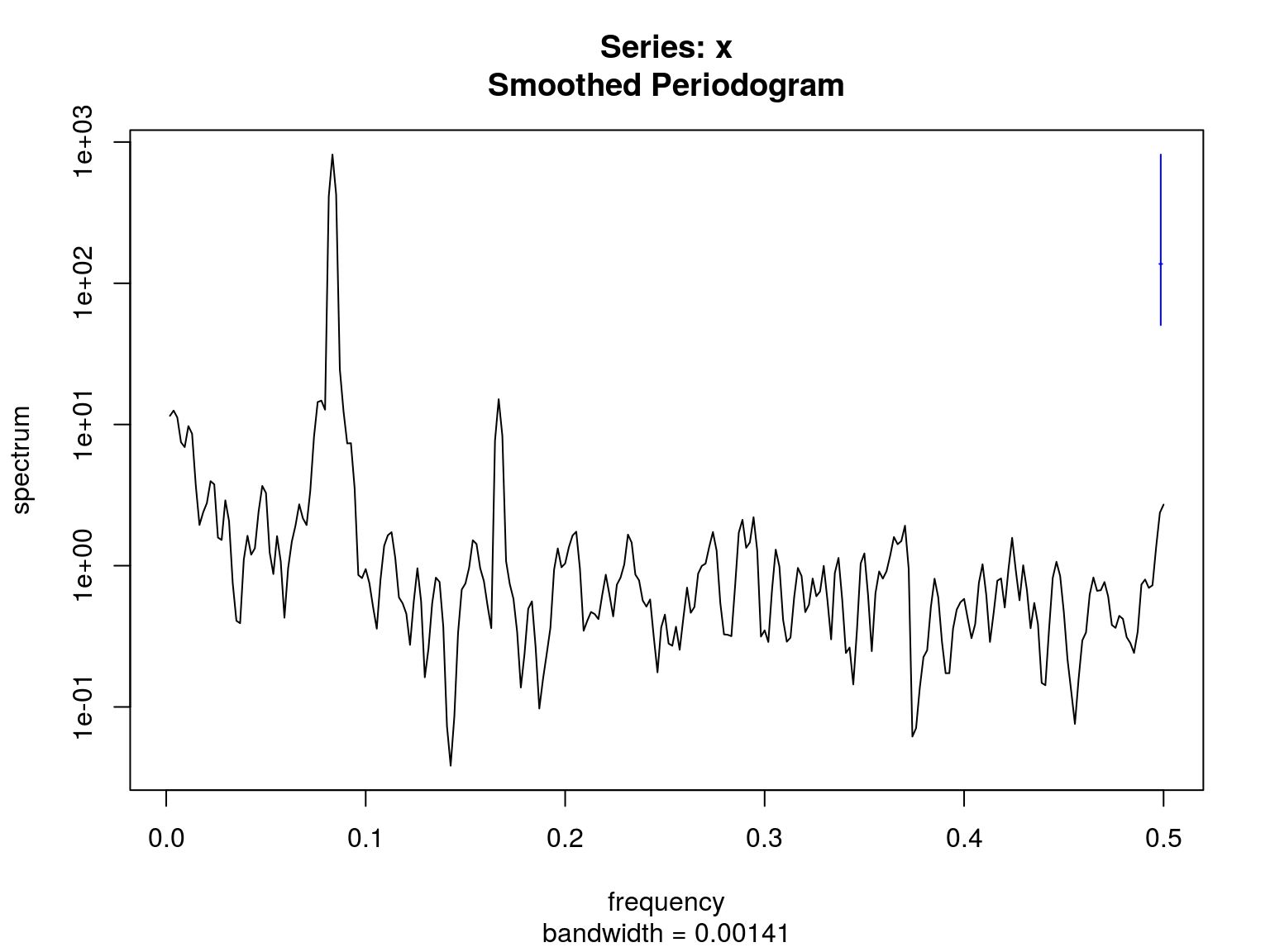
Estudio de los componentes de frecuencia de una serie temporal:
prd=spectrum(TF73[,2])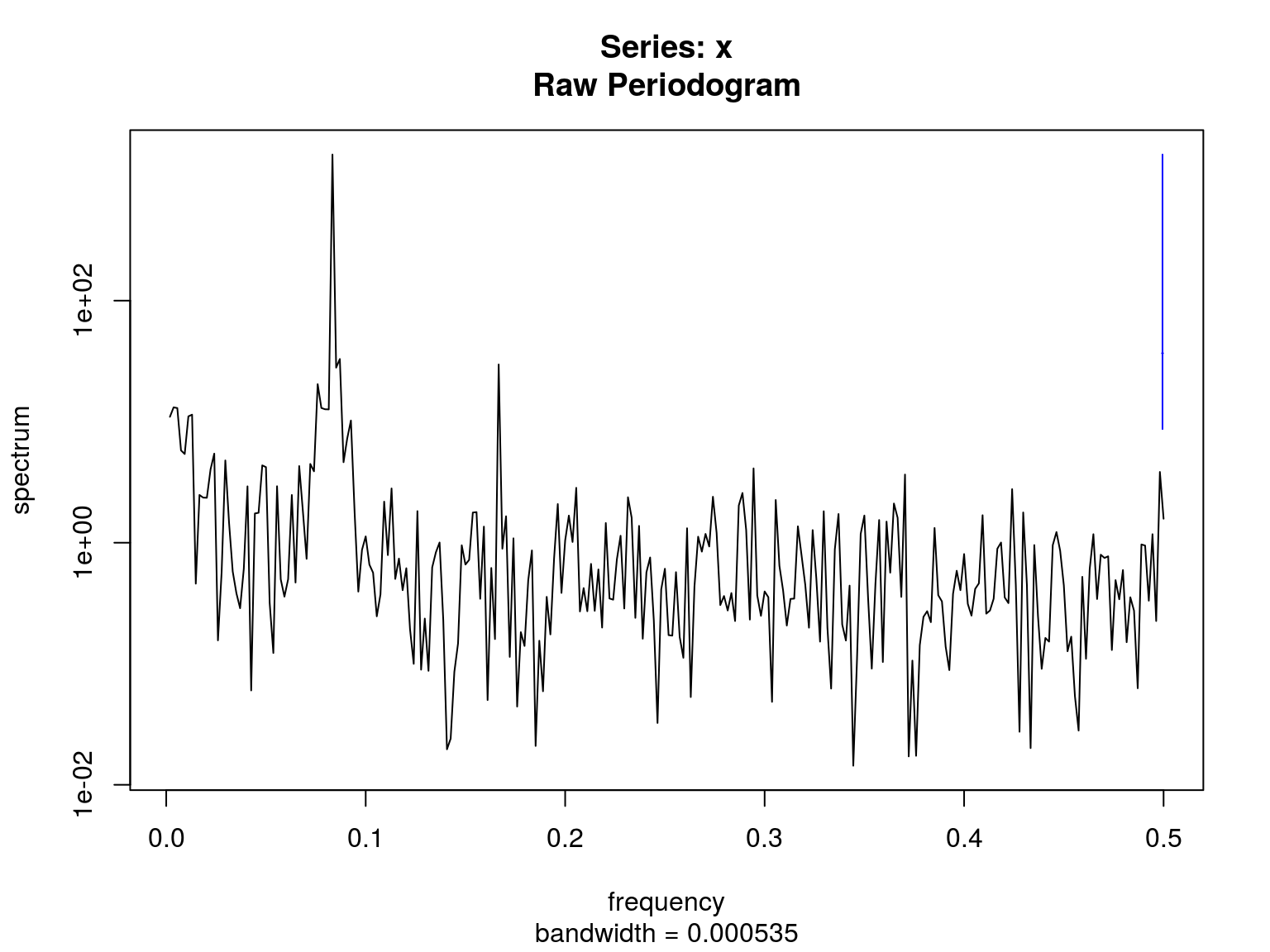
prd$freq[which.max(prd$spec)]## [1] 0.083333331/12## [1] 0.08333333Versión suavizada del espectro: