Introducción

Para este tema utilizaremos los datos del archivo coast.xlsx.

# Lectura de datos
library(readxl)
costa=read_excel("datos/coast.xlsx")
may=subset(costa,month=="may")
nov=subset(costa,month=="nov")

Predicción de la clorofila: Regresión simple

La siguiente tabla nos muestra las correlaciones entre la clorofila y el resto de variables durante el mes de mayo (la clorofila está en la fila 11):

pander(cor(costa[,1:17])[11,])
Table continues below
Temperature pH DO NO2 NO3 NH4 DIN PO4 COD TSM
-0.6959 0.3607 -0.1543 0.4201 0.7974 0.2451 0.4341 0.02255 0.8777 0.1276
Chla As Hg Zn Cd Pb Cu
1 0.6334 -0.3719 -0.1829 -0.3236 -0.1082 -0.1214

Vemos que las correlaciones más altas de la clorofila (en valor absoluto mayores que 0.3) se producen con las variables Temperatura, pH, NO2, NO3, DIN, COD, As y Hg. Podemos representar gráficamente las nubes de puntos correspondientes:

gTemp=ggplot(costa, aes(x=Temperature,y=Chla,col=month)) + geom_point() +
  geom_smooth(method="lm")
gpH=ggplot(costa, aes(x=pH,y=Chla,col=month)) + geom_point() +
  geom_smooth(method="lm")
gNO2=ggplot(costa, aes(x=NO2,y=Chla,col=month)) + geom_point() +
  geom_smooth(method="lm")
gNO3=ggplot(costa, aes(x=NO3,y=Chla,col=month)) + geom_point() +
  geom_smooth(method="lm")
gDIN=ggplot(costa, aes(x=DIN,y=Chla,col=month)) + geom_point() +
  geom_smooth(method="lm")
gCOD=ggplot(costa, aes(x=COD,y=Chla,col=month)) + geom_point() +
  geom_smooth(method="lm")
gAs=ggplot(costa, aes(x=As,y=Chla,col=month)) + geom_point() +
  geom_smooth(method="lm")
gHg=ggplot(costa, aes(x=Hg,y=Chla,col=month)) + geom_point() +
  geom_smooth(method="lm")

grid.arrange(gTemp,gpH,gNO2,gNO3,gDIN,gCOD,gAs,gHg,
             ncol=2,nrow=4)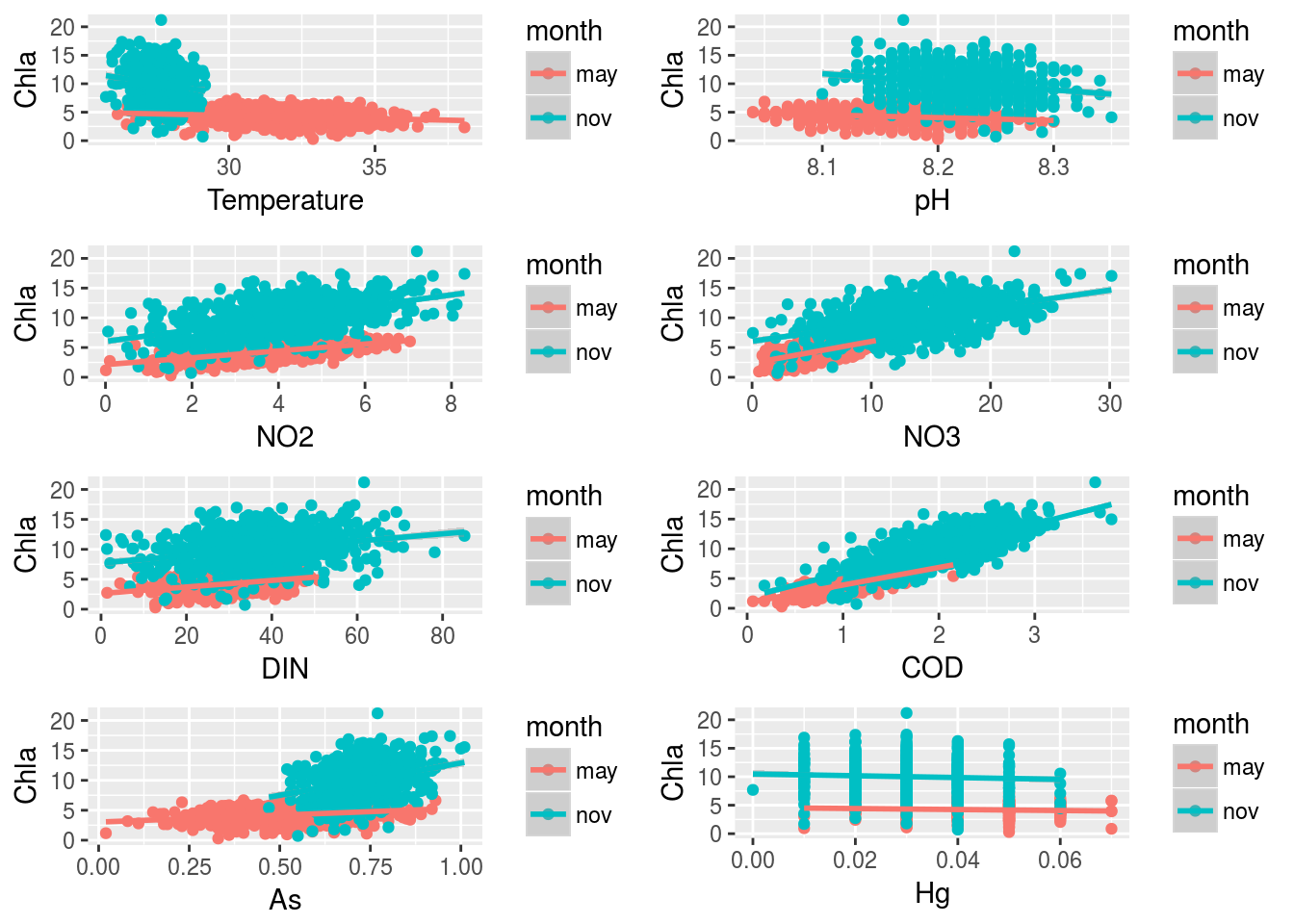

Podemos apreciar que la relación entre las variables cambia según que el mes sea mayo o noviembre; por tanto resulta conveniente ajustar un modelo distinto a cada mes. Podríamos ajustar una regresión simple para cada par de variables:

  • Datos de mayo:
mTemp=lm(Chla~Temperature, data=may)
mpH=lm(Chla~pH, data=may)
mNO2=lm(Chla~NO2, data=may)
mNO3=lm(Chla~NO3, data=may)
mDIN=lm(Chla~DIN, data=may)
mCOD=lm(Chla~COD, data=may)
MAs=lm(Chla~As, data=may)
mHg=lm(Chla~Hg, data=may)
pander(mTemp)
Fitting linear model: Chla ~ Temperature
  Estimate Std. Error t value Pr(>|t|)
Temperature -0.1104 0.02556 -4.32 1.814e-05
(Intercept) 7.742 0.8121 9.534 3.413e-20 
pander(mpH)
Fitting linear model: Chla ~ pH
  Estimate Std. Error t value Pr(>|t|)
pH -4.92 0.9758 -5.042 6.063e-07
(Intercept) 44.39 7.964 5.574 3.718e-08 
pander(mNO2)
Fitting linear model: Chla ~ NO2
  Estimate Std. Error t value Pr(>|t|)
NO2 0.5763 0.0308 18.71 3.135e-62
(Intercept) 2.126 0.1191 17.85 9.147e-58 
pander(mNO3)
Fitting linear model: Chla ~ NO3
  Estimate Std. Error t value Pr(>|t|)
NO3 0.3643 0.0201 18.12 3.542e-59
(Intercept) 2.381 0.1095 21.75 2.405e-78 
pander(mDIN)
Fitting linear model: Chla ~ DIN
  Estimate Std. Error t value Pr(>|t|)
DIN 0.05472 0.00544 10.06 3.833e-22
(Intercept) 2.618 0.1671 15.66 8.41e-47 
pander(mCOD)
Fitting linear model: Chla ~ COD
  Estimate Std. Error t value Pr(>|t|)
COD 2.945 0.1007 29.26 9.043e-119
(Intercept) 0.9668 0.116 8.336 5.011e-16 
pander(MAs)
Fitting linear model: Chla ~ As
  Estimate Std. Error t value Pr(>|t|)
As 2.325 0.3096 7.51 2.076e-13
(Intercept) 3.027 0.1677 18.05 8.585e-59 
pander(mHg)
Fitting linear model: Chla ~ Hg
  Estimate Std. Error t value Pr(>|t|)
Hg -8.59 4.545 -1.89 0.05921
(Intercept) 4.585 0.1888 24.29 5.166e-92
  • Datos de noviembre:
mnTemp=lm(Chla~Temperature, data=nov)
mnpH=lm(Chla~pH, data=nov)
mnNO2=lm(Chla~NO2, data=nov)
mnNO3=lm(Chla~NO3, data=nov)
mnDIN=lm(Chla~DIN, data=nov)
mnCOD=lm(Chla~COD, data=nov)
MnAs=lm(Chla~As, data=nov)
mnHg=lm(Chla~Hg, data=nov)
pander(mnTemp)
Fitting linear model: Chla ~ Temperature
  Estimate Std. Error t value Pr(>|t|)
Temperature -0.7894 0.1937 -4.075 5.193e-05
(Intercept) 31.8 5.348 5.946 4.595e-09 
pander(mnpH)
Fitting linear model: Chla ~ pH
  Estimate Std. Error t value Pr(>|t|)
pH -14.31 2.8 -5.109 4.326e-07
(Intercept) 127.6 23.03 5.543 4.396e-08 
pander(mnNO2)
Fitting linear model: Chla ~ NO2
  Estimate Std. Error t value Pr(>|t|)
NO2 0.9786 0.0675 14.5 3.333e-41
(Intercept) 6.026 0.2931 20.56 5.874e-72 
pander(mnNO3)
Fitting linear model: Chla ~ NO3
  Estimate Std. Error t value Pr(>|t|)
NO3 0.2862 0.0209 13.69 1.8e-37
(Intercept) 6.063 0.3062 19.8 6.352e-68 
pander(mnDIN)
Fitting linear model: Chla ~ DIN
  Estimate Std. Error t value Pr(>|t|)
DIN 0.06069 0.008419 7.209 1.652e-12
(Intercept) 7.732 0.3357 23.03 3.206e-85 
pander(mnCOD)
Fitting linear model: Chla ~ COD
  Estimate Std. Error t value Pr(>|t|)
COD 4.11 0.154 26.69 5.612e-105
(Intercept) 1.846 0.3163 5.836 8.627e-09 
pander(MnAs)
Fitting linear model: Chla ~ As
  Estimate Std. Error t value Pr(>|t|)
As 10.76 1.276 8.429 2.451e-16
(Intercept) 2.13 0.9416 2.262 0.02406 
pander(mnHg)
Fitting linear model: Chla ~ Hg
  Estimate Std. Error t value Pr(>|t|)
Hg -15.7 11.07 -1.419 0.1563
(Intercept) 10.48 0.3541 29.61 1.27e-120

La función summary() muestra un resumen del ajuste del modelo. En particular es interesante el p-valor asociado al estadístico F; este p-valor corresponde al contraste:

\[H_{0}:\beta_{1} =0 H_{1}:\beta_{1} \neq0\]

por lo que un p-valor>0.05 (aceptación de \(H_0\)) quiere decir que la variable analizada no tiene capacidad explicativa/predictiva (de forma lineal) sobre la variable respuesta.

Si quisiéramos calcular intervalos de confianza para los coeficientes del modelo, podemos utilizar la función confint()

summary(mTemp)
## 
## Call:
## lm(formula = Chla ~ Temperature, data = may)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -3.8218 -0.7506 -0.0339  0.8077  2.9556 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  7.74215    0.81206   9.534  < 2e-16 ***
## Temperature -0.11041    0.02556  -4.320 1.81e-05 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.163 on 618 degrees of freedom
## Multiple R-squared:  0.02932,    Adjusted R-squared:  0.02775 
## F-statistic: 18.67 on 1 and 618 DF,  p-value: 1.814e-05
confint(mTemp)
##                  2.5 %      97.5 %
## (Intercept)  6.1474154  9.33689038
## Temperature -0.1605994 -0.06022554

También podemos hacer predicciones con el modelo (por ejemplo para la regresión de la clorofila sobre la temperatura):

nuevasTemperat=data.frame(Temperature=26:40)
nuevasTemperat
##    Temperature
## 1           26
## 2           27
## 3           28
## 4           29
## 5           30
## 6           31
## 7           32
## 8           33
## 9           34
## 10          35
## 11          36
## 12          37
## 13          38
## 14          39
## 15          40
predict(mTemp,newdata=nuevasTemperat)
##        1        2        3        4        5        6        7        8 
## 4.871428 4.761016 4.650603 4.540191 4.429778 4.319366 4.208953 4.098541 
##        9       10       11       12       13       14       15 
## 3.988128 3.877716 3.767303 3.656891 3.546478 3.436066 3.325653

e incluso obtener intervalos de confianza para las predicciones individuales (qué rango de valores podemos esperar para la variable \(y\) dado un valor fijo de \(x\)):

predict(mTemp,newdata=nuevasTemperat, interval="prediction")
##         fit      lwr      upr
## 1  4.871428 2.567825 7.175031
## 2  4.761016 2.463131 7.058901
## 3  4.650603 2.357352 6.943854
## 4  4.540191 2.250483 6.829899
## 5  4.429778 2.142517 6.717039
## 6  4.319366 2.033452 6.605279
## 7  4.208953 1.923286 6.494620
## 8  4.098541 1.812018 6.385064
## 9  3.988128 1.699649 6.276607
## 10 3.877716 1.586182 6.169249
## 11 3.767303 1.471623 6.062984
## 12 3.656891 1.355975 5.957806
## 13 3.546478 1.239248 5.853708
## 14 3.436066 1.121449 5.750682
## 15 3.325653 1.002590 5.648717

o para las predicciones de las medias (en qué rango se mueve el valor medio de las \(y\) para un valor de \(x\) fijo). Estos intervalos son más estrechos que los anteriores:

predict(mTemp,newdata=nuevasTemperat, interval="confidence")
##         fit      lwr      upr
## 1  4.871428 4.569903 5.172953
## 2  4.761016 4.506840 5.015191
## 3  4.650603 4.442444 4.858762
## 4  4.540191 4.375592 4.704789
## 5  4.429778 4.303712 4.555845
## 6  4.319366 4.220724 4.418007
## 7  4.208953 4.116189 4.301717
## 8  4.098541 3.986659 4.210423
## 9  3.988128 3.841611 4.134646
## 10 3.877716 3.689421 4.066010
## 11 3.767303 3.533895 4.000712
## 12 3.656891 3.376638 3.937144
## 13 3.546478 3.218391 3.874566
## 14 3.436066 3.059531 3.812601
## 15 3.325653 2.900267 3.751039

 

Predicción de la clorofila: Regresión múltiple

En general resultará de mayor interés construir un modelo que tenga en cuenta simultáneamente el efecto de varias variables sobre la concentración de clorofila. Si miramos nuevamente las correlaciones de la clorofila con el resto de las variables, separando los datos por meses, tenemos:

  • Correlaciones en mayo:
pander(cor(may[,1:17])[11,])
Table continues below
Temperature pH DO NO2 NO3 NH4 DIN PO4 COD TSM
-0.1712 -0.1988 -0.3646 0.6013 0.589 0.09777 0.3751 0.2481 0.7621 0.2822
Chla As Hg Zn Cd Pb Cu
1 0.2892 -0.07581 0.2253 -0.05337 0.1098 -0.1231
  • Correlaciones en noviembre:
pander(cor(nov[,1:17])[11,])
Table continues below
Temperature pH DO NO2 NO3 NH4 DIN PO4 COD TSM
-0.1618 -0.2013 -0.2842 0.5037 0.4825 0.0438 0.2785 0.1685 0.7318 0.2924
Chla As Hg Zn Cd Pb Cu
1 0.3211 -0.057 0.2372 -0.1032 0.0547 -0.1327

Así, las dos variables con mayor efecto sobre la clorofila tanto en el mes de mayo como en el de noviembre parecen ser COD y NO2. Podemos visualizar la asociación global entre estas variables mediante la siguiente función, que nos permite hacer un gráfico tridimensional:

  • Para los datos de mayo:
library(rgl)
with(may,plot3d(COD,NO2,Chla))

 

  • Para los de noviembre:
with(nov,plot3d(COD,NO2,Chla))

Estos modelos pueden ajustarse mediante:

mMay=lm(Chla~COD+NO2,data=may)
mNov=lm(Chla~COD+NO2,data=nov)
pander(mMay)
Fitting linear model: Chla ~ COD + NO2
  Estimate Std. Error t value Pr(>|t|)
COD 2.447 0.1246 19.64 4.736e-67
NO2 0.1987 0.0309 6.43 2.55e-10
(Intercept) 0.7923 0.1156 6.854 1.747e-11 
pander(mNov)
Fitting linear model: Chla ~ COD + NO2
  Estimate Std. Error t value Pr(>|t|)
COD 3.682 0.1837 20.05 3.262e-69
NO2 0.2635 0.06353 4.147 3.834e-05
(Intercept) 1.623 0.3168 5.122 4.043e-07

En este caso la aplicación de la función summary(), por ejemplo, a los datos del mes de mayo:

summary(mMay)
## 
## Call:
## lm(formula = Chla ~ COD + NO2, data = may)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -2.80131 -0.51683  0.03332  0.51218  1.80807 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   0.7923     0.1156   6.854 1.75e-11 ***
## COD           2.4467     0.1246  19.635  < 2e-16 ***
## NO2           0.1987     0.0309   6.430 2.55e-10 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.7405 on 617 degrees of freedom
## Multiple R-squared:  0.6071, Adjusted R-squared:  0.6058 
## F-statistic: 476.7 on 2 and 617 DF,  p-value: < 2.2e-16

nos muestra el p-valor asociado al contraste:

\[\begin{cases} H_{0}: & \beta_{1}=\beta_{2}=0\\ H_{1}: & \beta_{1}\neq0\,\,\,ó\,\,\,\beta_{2}\neq0 \end{cases}\]

En este caso concluimos que puede rechazarse \(H_0\), y por tanto que alguna de las dos variables (o ambas) \(X_i\) (esto es, COD y NO2) tienen capacidad explicativa/predictiva sobre la respuesta (Chla).

Se pueden obtener intervalos de confianza para los coeficientes y para las predicciones exactamente igual que hemos hecho para regresión simple:

newCODNO2=data.frame(COD=seq(0,4,by=0.5),NO2=seq(0,8,by=1))
confint(mMay)
##                 2.5 %    97.5 %
## (Intercept) 0.5652833 1.0193203
## COD         2.2020084 2.6914229
## NO2         0.1380004 0.2593476
predicciones=predict(mMay,newdata=newCODNO2,interval="prediction")
predicciones
##          fit        lwr       upr
## 1  0.7923018 -0.6794362  2.264040
## 2  2.2143336  0.7527202  3.675947
## 3  3.6363654  2.1784780  5.094253
## 4  5.0583973  3.5977882  6.519006
## 5  6.4804291  5.0106867  7.950172
## 6  7.9024609  6.4172917  9.387630
## 7  9.3244928  7.8177966 10.831189
## 8 10.7465246  9.2124580 12.280591
## 9 12.1685564 10.6015823 13.735531

Por claridad podemos mostrar los valores de COD y NO2 junto con las predicciones obtenidas por el modelo para dichos valores:

cbind(newCODNO2,predicciones)
##   COD NO2        fit        lwr       upr
## 1 0.0   0  0.7923018 -0.6794362  2.264040
## 2 0.5   1  2.2143336  0.7527202  3.675947
## 3 1.0   2  3.6363654  2.1784780  5.094253
## 4 1.5   3  5.0583973  3.5977882  6.519006
## 5 2.0   4  6.4804291  5.0106867  7.950172
## 6 2.5   5  7.9024609  6.4172917  9.387630
## 7 3.0   6  9.3244928  7.8177966 10.831189
## 8 3.5   7 10.7465246  9.2124580 12.280591
## 9 4.0   8 12.1685564 10.6015823 13.735531

 

Calidad del ajuste de la regresión

 

A partir de ahora, para simplificar, nos quedaremos sólo con los datos del mes de mayo.

Las siguientes gráficas presentan los valores observados frente a los valores ajustados por los distintos modelos (los valores ajustados son las predicciones del modelo para los valores de las \(X_i\) observados)

compara1=data.frame(observed=mCOD$model$Chla,fitted=fitted(mCOD))
ggplot(compara1,aes(x=observed,y=fitted)) + geom_point() + ylim(-3,8) +
  geom_abline(intercept=0,slope=1,col="red") + ggtitle("Predicting Chla from COD")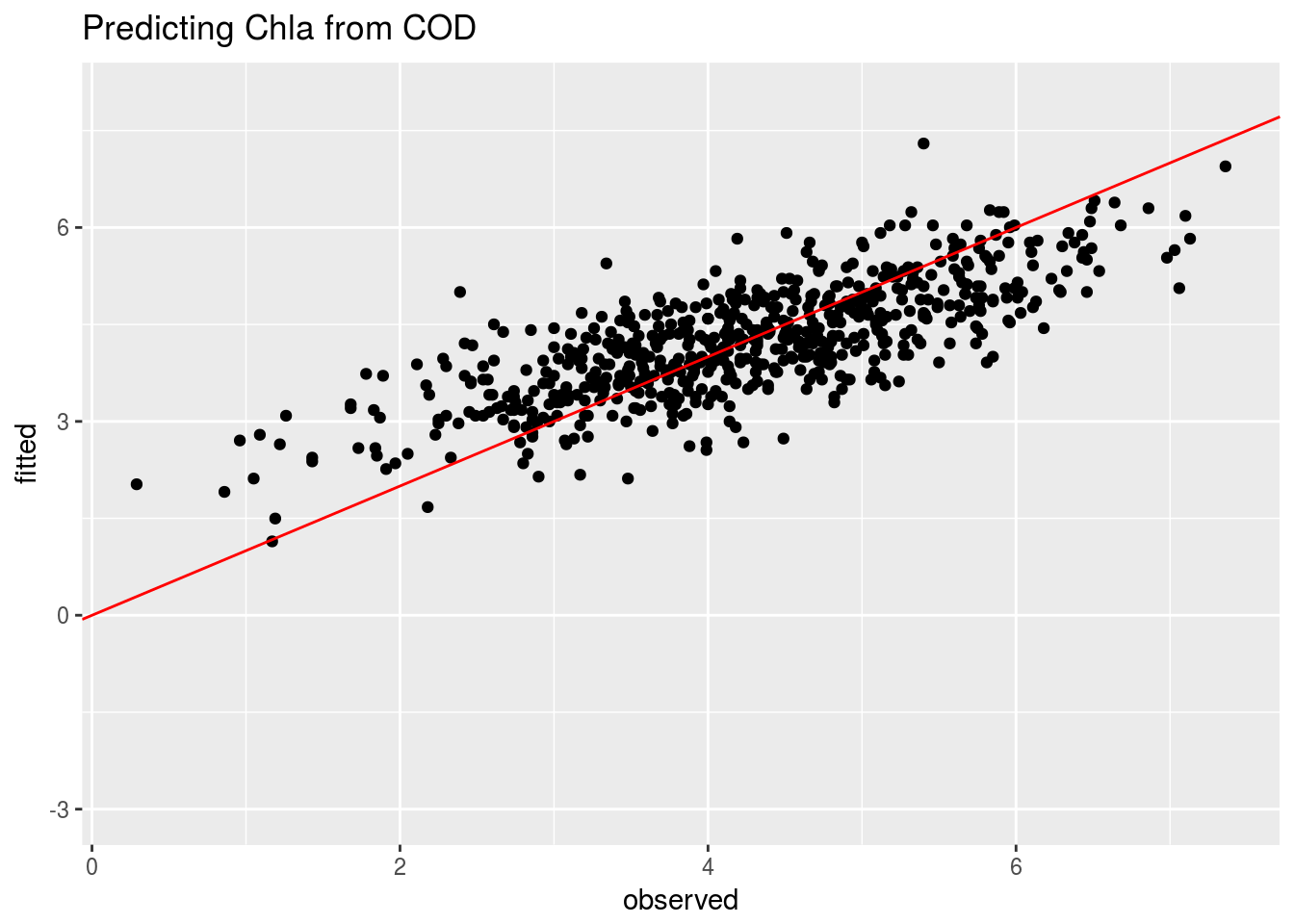

compara2=data.frame(observed=mNO2$model$Chla,fitted=fitted(mNO2))
ggplot(compara2,aes(x=observed,y=fitted)) + geom_point() + ylim(-3,8) +
  geom_abline(intercept=0,slope=1,col="red") + ggtitle("Predicting Chla from NO2")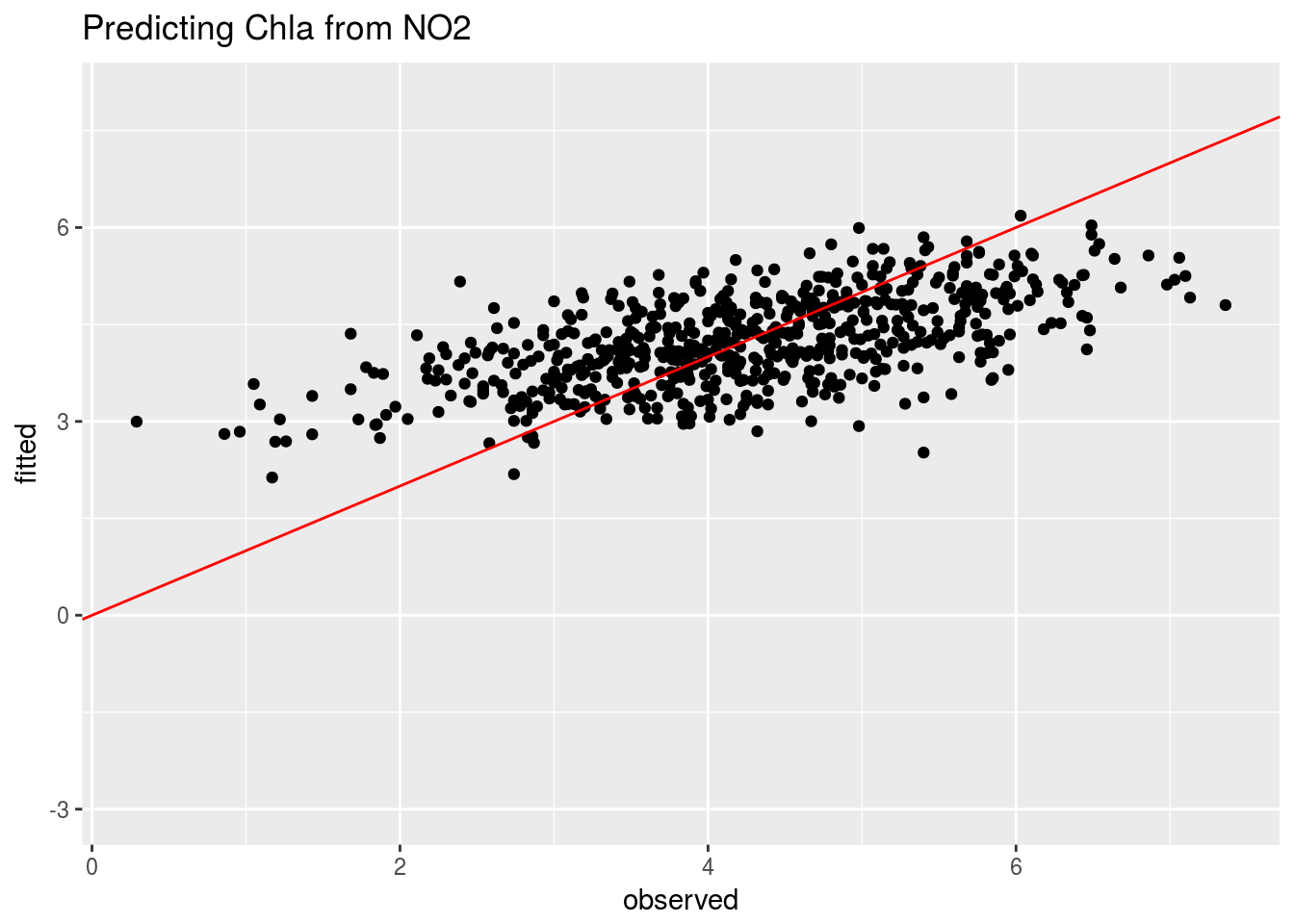

compara3=data.frame(observed=mMay$model$Chla,fitted=fitted(mMay))
ggplot(compara3,aes(x=observed,y=fitted)) + geom_point() + ylim(-3,8) +
  geom_abline(intercept=0,slope=1,col="red") + ggtitle("Predicting Chla from COD and NO2")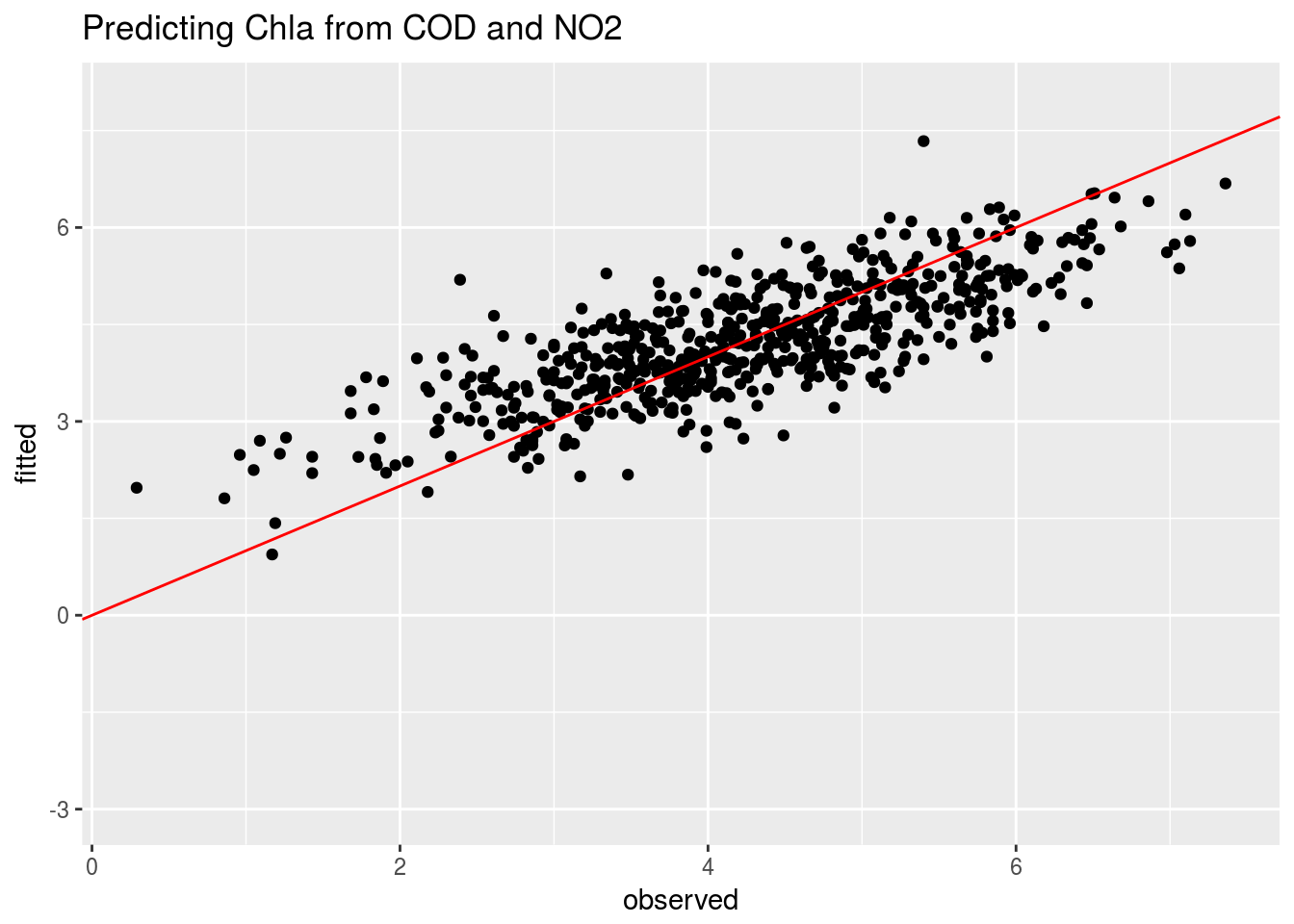

Podemos apreciar visualmente que el ajuste peor es el conseguido con el NO2; mejora bastante con el COD; y no parece demasiado claro si considerar las dos variables NO2 y COD simultáneamente introduce alguna mejora sustantiva en el ajuste.

Para valorar el ajuste de los modelos se puede utilizar el coeficiente de determinación (si solo hay una variable predictiva) o el coeficiente de determinación ajustado (si hay más de una variable predictiva). Para entender estos coeficientes, conviene revisar el concepto de descomposición de la variabilidad en los modelos lineales:

 

Descomposición de la variabilidad.

La variabilidad total presente en la variable respuesta puede descomponerse en la parte explicada por las variables explicativas, más la variabilidad residual:

VARIABILIDAD TOTAL = VARIABILIDAD EXPLICADA + VARIABILIDAD RESIDUAL

donde:

VARIABILIDAD TOTAL: VT = \(\sum_{i=1}^{n}\left(y_{i}-\overline{y}\right)^{2}\)

VARIABILIDAD EXPLICADA: VE = \(\sum_{i=1}^{n}\left(\hat{y}_{i}-\overline{y}\right)^{2}\)

VARIABILIDAD RESIDUAL: VR = \(\sum_{i=1}^{n}\left(y_{i}-\hat{y}_{i}\right)^{2}\)

 

Es decir:

\[\sum_{i=1}^{n}\left(y_{i}-\overline{y}\right)^{2}=\sum_{i=1}^{n}\left(\hat{y}_{i}-\overline{y}\right)^{2}+\sum_{i=1}^{n}\left(y_{i}-\hat{y}_{i}\right)^{2}\]

 

A partir de esta descomposición es posible definir coeficientes para medir la calidad de ajuste del modelo (coeficientes de determinación y de determinación corregido), y construir un contraste (conocido como análisis de la varianza del modelo) que permite decidir si las variables explicativas realmente son explicativas; dicho de otra forma, permite decidir si la variabilidad explicada por dichas variables representa una proporción significativa de la variabilidad total presente en el modelo.

 

Coeficiente de determinación \(R^2\)

Este coeficiente mide simplemente la proporción de la variabilidad en la variable respuesta que es explicada (o está determinada) por las variables explicativas. Cuanto más se aproxime su valor a 1, mejor es el modelo; cuanto más se aproxime a cero tanto peor:

\[R^2=\frac{VE}{VT}\]

 

Coeficiente de determinación corregido (o ajustado) \(\tilde{R}^2\)

El coeficiente de determinación que se acaba de definir presenta el problema práctico de que su valor se va aproximando a 1 a medida que se añaden variables explicativas \(X_i\) al modelo, aunque la aportación de cada una sea irrelevante. Interesa por ello redefinir el coeficiente de determinación de forma que se vea “penalizado” si su valor aumenta por introducir muchas variables que no expliquen nada en lugar de pocas variables que expliquen mucho. Para ello observemos en primer lugar que el coeficiente de determinación \(R^2\) puede expresarse como: \[R^{2}=\frac{VE}{VT}=1-\frac{VR}{VT}\]

Para penalizar el exceso de variables explicativas, el coeficiente de determinación corregido se define de manera similar mediante:

\[\tilde{R}^{2}=1-\frac{VR/\left(n-p\right)}{VT/\left(n-1\right)}=1-\frac{n-1}{n-p}\frac{VR}{VT}\]

De esta forma, el término \(\frac{n-1}{n-p}\) es mayor que 1 (tanto mayor cuanto mayor sea el número de variables explicativas \(p\)). Dicho término multiplica a la proporción de varianza no explicada \(\frac{VR}{VT}\), por lo cual su efecto es “inflar” la variabilidad no explicada y por tanto reducir la variabilidad explicada artificialmente por un exceso de variables. Si después de estos ajustes el coeficiente de determinación así obtenido es próximo a 1, ello significaría que aún penalizando la introducción de variables, la varibilidad explicada es alta, y por tanto las variables consideradas puede considerarse que tienen buena capacidad explicativa o predictiva de la variable respuesta.

 

 

En los tres modelos que hemos ajustado más arriba podemos obtener el valor del coeficiente de determinación ajustado mediante la función summary aplicada al modelo:

summary(mCOD)
## 
## Call:
## lm(formula = Chla ~ COD, data = may)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -2.61204 -0.54368 -0.00059  0.53182  1.99905 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   0.9668     0.1160   8.336 5.01e-16 ***
## COD           2.9455     0.1007  29.261  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.7642 on 618 degrees of freedom
## Multiple R-squared:  0.5808, Adjusted R-squared:  0.5801 
## F-statistic: 856.2 on 1 and 618 DF,  p-value: < 2.2e-16
summary(mNO2)
## 
## Call:
## lm(formula = Chla ~ NO2, data = may)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -2.77301 -0.61085 -0.00634  0.66472  2.88204 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   2.1261     0.1191   17.85   <2e-16 ***
## NO2           0.5763     0.0308   18.71   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.9431 on 618 degrees of freedom
## Multiple R-squared:  0.3616, Adjusted R-squared:  0.3606 
## F-statistic: 350.1 on 1 and 618 DF,  p-value: < 2.2e-16
summary(mMay)
## 
## Call:
## lm(formula = Chla ~ COD + NO2, data = may)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -2.80131 -0.51683  0.03332  0.51218  1.80807 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   0.7923     0.1156   6.854 1.75e-11 ***
## COD           2.4467     0.1246  19.635  < 2e-16 ***
## NO2           0.1987     0.0309   6.430 2.55e-10 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.7405 on 617 degrees of freedom
## Multiple R-squared:  0.6071, Adjusted R-squared:  0.6058 
## F-statistic: 476.7 on 2 and 617 DF,  p-value: < 2.2e-16

o si queremos extraer directamente el coeficiente:

summary(mCOD)$adj.r.squared
## [1] 0.580108
summary(mNO2)$adj.r.squared
## [1] 0.3605832
summary(mMay)$adj.r.squared
## [1] 0.6058435

Vemos que efectivamente el peor resultado se obtiene sólo con el NO2 (0.36); el valor mejora si se utiliza sólo el COD (0.58); y mejora un poquito más en el modelo en que se utilizan ambas variables, NO2 y COD (0.6058).

La pregunta obvia es ¿La mejora en \(R`2\) que se consigue utilizando dos variables en vez de una, ¿justifica de verdad el uso de un modelo más complicado? Esta pregunta podemos plantearla de otra manera: si para predecir la clorofila utilizamos el COD solamente, ¿mejora de manera significativa la calidad de las predicciones si se añade el valor del NO2? Piénsese, por ejemplo, que en un contexto aplicado medir dos variables puede resultar más costoso que medir solo una; y si la predicción no mejora, en realidad posiblemente no haga falta medir la segunda variable.

Para responder a esta pregunta podemos utilizar la estrategia que ya hemos utilizado en el análisis de la varianza: comparar la variabilidad explicada con el modelo de dos variables frente a la variabilidad explicada por el modelo de una única variable. Si la diferencia no es significativa, ello quiere decir que ambos modelos tienen la misma capacidad explicativa, por lo que resulta adecuado quedarse con el más simple; si la diferencia entre ambos modelos es significativa, nos quedaremos con aquel que presente una menor suma de cuadrados residual, que será habitualmente el modelo con las dos variables.

En nuestro caso, si comparamos el modelo que contiene las dos variables con el que contiene sólo el NO2, la diferencia es significativa, y resulta mejor modelo el que contiene las dos variables, esto es, no se puede prescindir del CO2:

anova(mMay,mNO2)
## Analysis of Variance Table
## 
## Model 1: Chla ~ COD + NO2
## Model 2: Chla ~ NO2
##   Res.Df    RSS Df Sum of Sq      F    Pr(>F)    
## 1    617 338.29                                  
## 2    618 549.67 -1   -211.39 385.55 < 2.2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

 

Ahora, si comparamos el modelo de dos variables con el que tiene sólo al COD como variable explicativa, resulta:

anova(mMay,mCOD)
## Analysis of Variance Table
## 
## Model 1: Chla ~ COD + NO2
## Model 2: Chla ~ COD
##   Res.Df    RSS Df Sum of Sq      F   Pr(>F)    
## 1    617 338.29                                 
## 2    618 360.96 -1   -22.672 41.351 2.55e-10 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Nótese que las variabilidades residuales de ambos modelos (RSS) son mucho más parecidas que en el caso anterior (338.29 vs. 360.96), la diferencia es también significativa, lo que significa que si en el modelo se ha incluído ya el COD, el NO2 aporta información adicional que no puede despreciarse.

 

Detección de outliers

La función plot() aplicada al modelo ajustado permite hacer un diagnóstico de posibles outliers:

layout(matrix(c(1,2,3,4),2,2))
plot(mMay)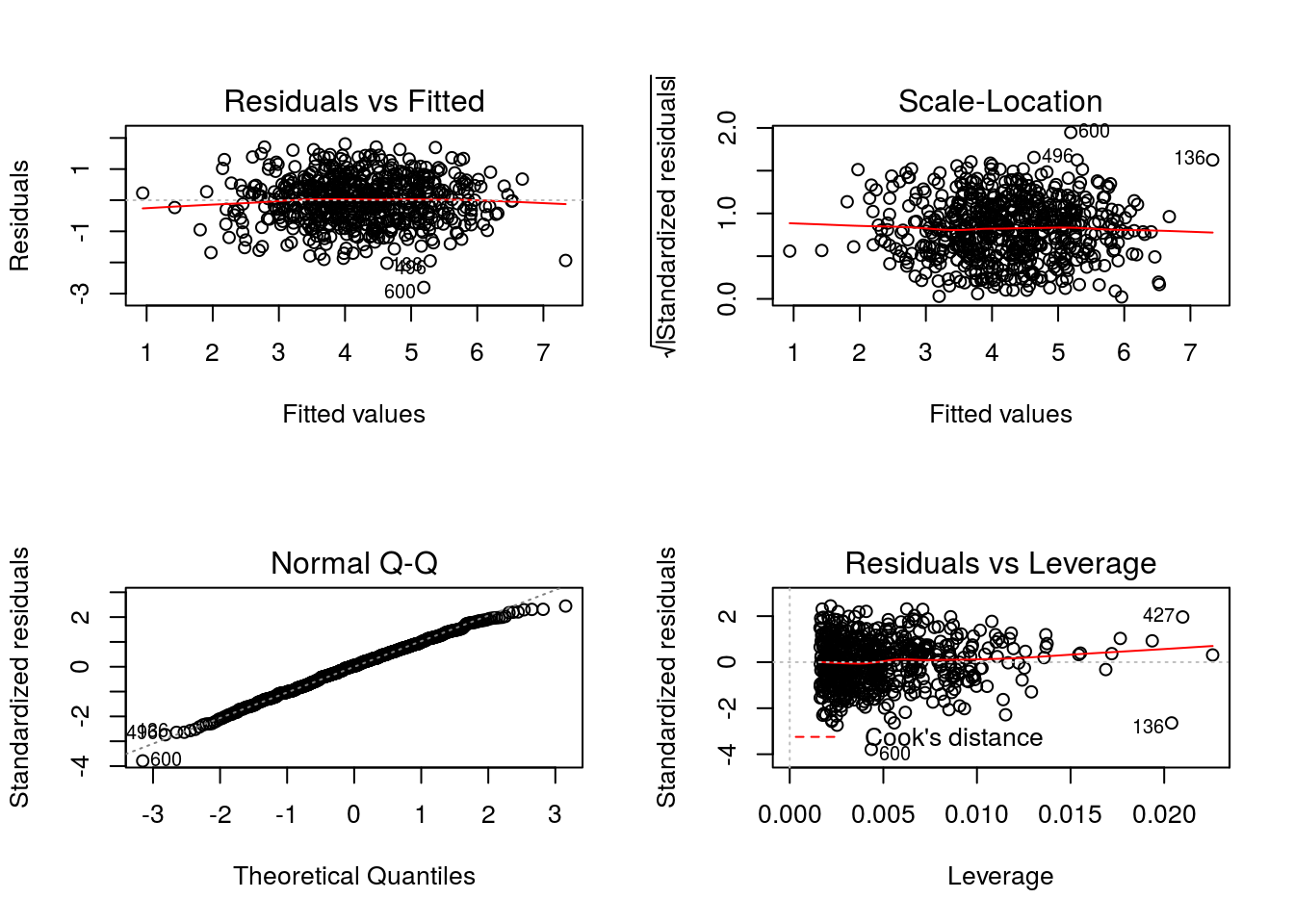

Selección del mejor modelo

 

Podemos preguntarnos ahora: ¿mejorará la capacidad predictiva del modelo si incluímos una tercera variable?. Observando de nuevo la tabla de correlaciones, las siguientes variables más correladas con la clorofila son el NO3 y el DIN. Podemos construir entonces los modelos:

mMayNO3=lm(Chla~COD+NO2+NO3,data=may)
mMayDIN=lm(Chla~COD+NO2+DIN,data=may)
summary(mMayNO3)$adj.r.squared
## [1] 0.6860601
summary(mMayDIN)$adj.r.squared
## [1] 0.6483958

Vemos los valores observados frente a las predicciones:

compara4=data.frame(observed=mMayNO3$model$Chla,fitted=fitted(mMayNO3))
ggplot(compara4,aes(x=observed,y=fitted)) + geom_point() + ylim(-3,8) +
  geom_abline(intercept=0,slope=1,col="red") + ggtitle("Predicting Chla from COD, NO2 and NO3")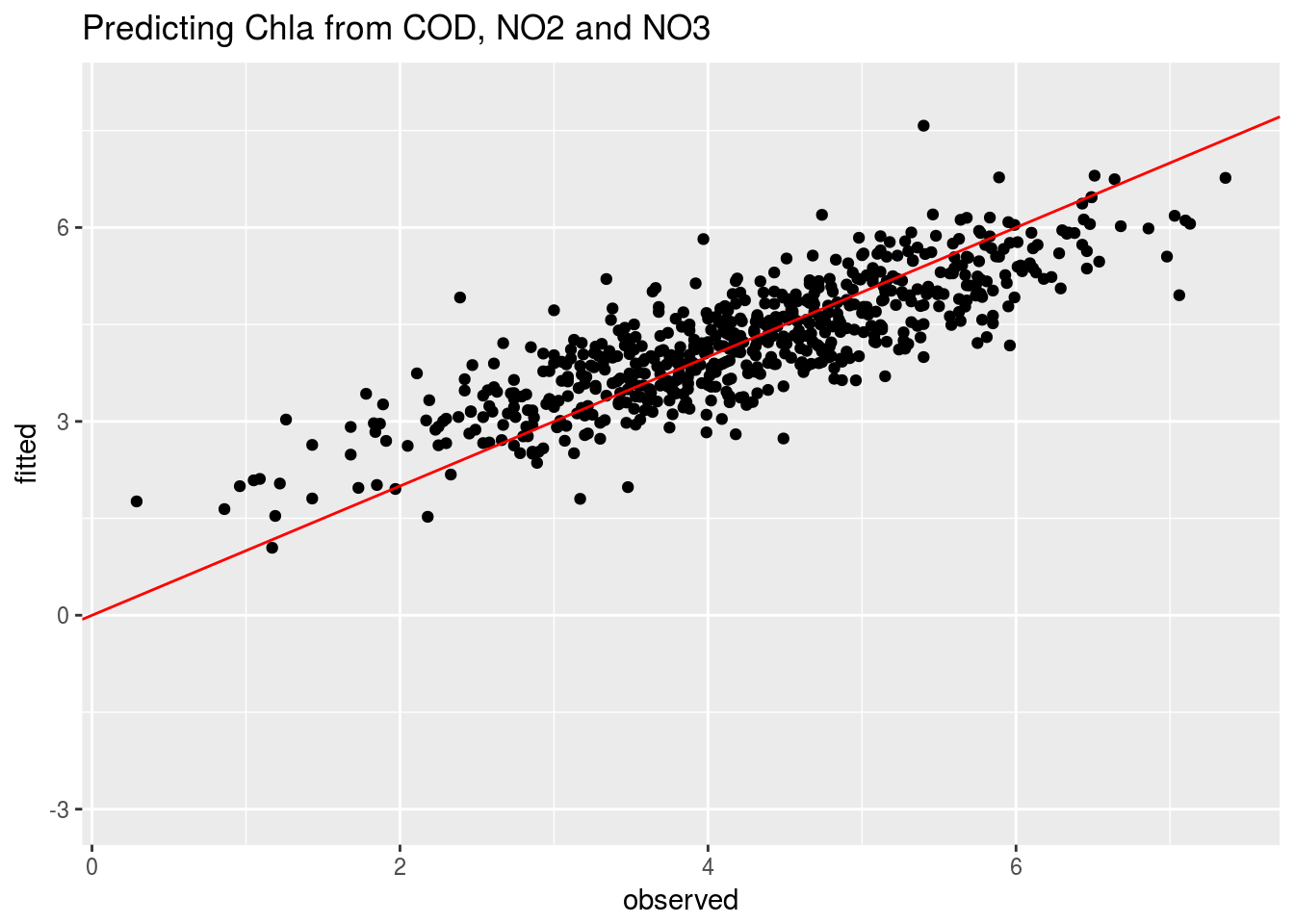

compara5=data.frame(observed=mMayDIN$model$Chla,fitted=fitted(mMayDIN))
ggplot(compara5,aes(x=observed,y=fitted)) + geom_point() + ylim(-3,8) +
  geom_abline(intercept=0,slope=1,col="red") + ggtitle("Predicting Chla from COD, NO2 and DIN")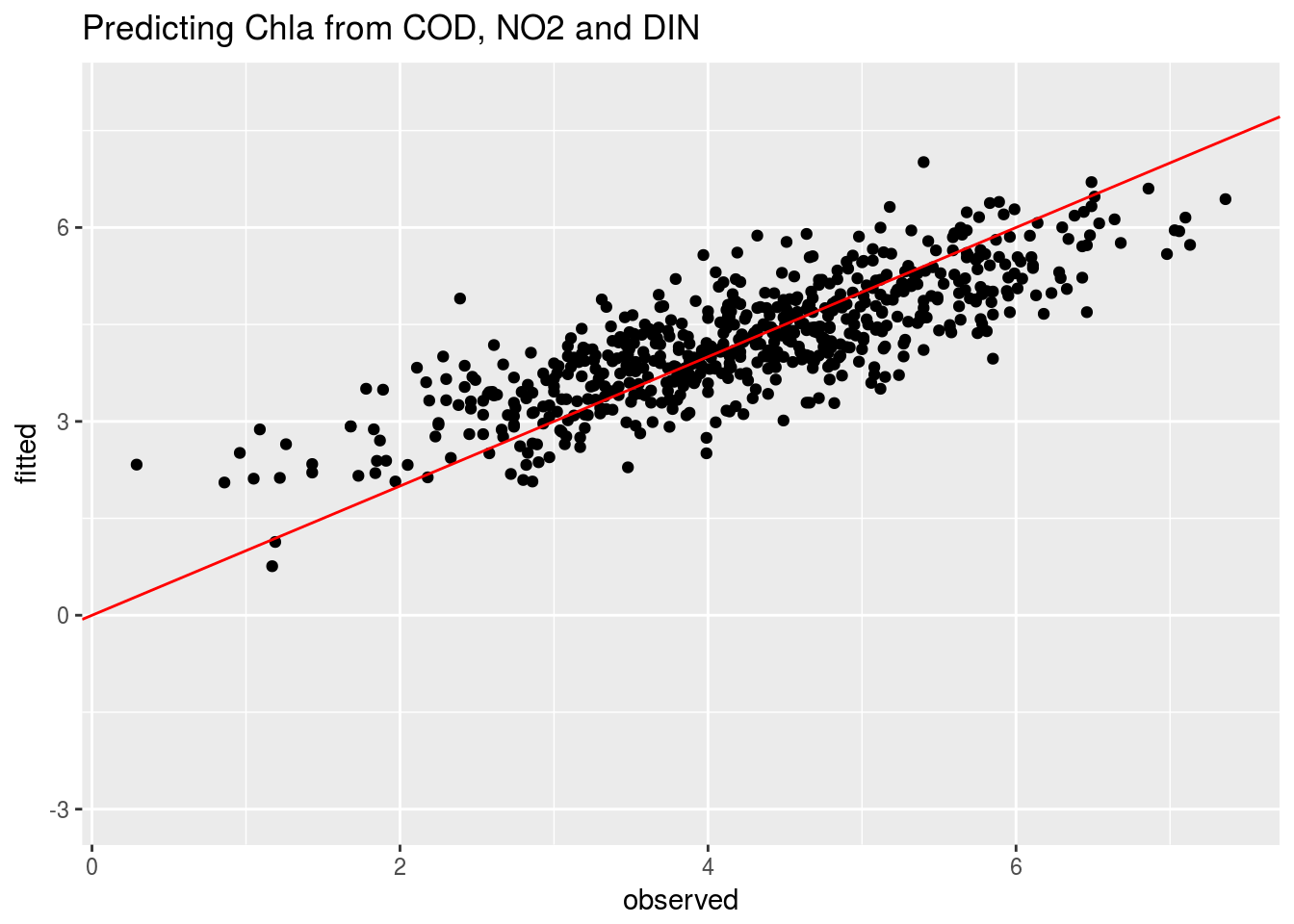

Determinamos si existen diferencias significativas entre estos modelos y el modelo de dos variables:

anova(mMayNO3,mMay)
## Analysis of Variance Table
## 
## Model 1: Chla ~ COD + NO2 + NO3
## Model 2: Chla ~ COD + NO2
##   Res.Df    RSS Df Sum of Sq      F    Pr(>F)    
## 1    616 269.00                                  
## 2    617 338.29 -1   -69.283 158.65 < 2.2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
anova(mMayDIN,mMay)
## Analysis of Variance Table
## 
## Model 1: Chla ~ COD + NO2 + DIN
## Model 2: Chla ~ COD + NO2
##   Res.Df    RSS Df Sum of Sq      F    Pr(>F)    
## 1    616 301.28                                  
## 2    617 338.29 -1    -37.01 75.671 < 2.2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

En ambos casos se consigue una reducción significativa de la variabilidad; como la reducción es mayor con el modelo que contiene NO3, nos podríamos quedar con ése, aunque surge la cuestión ¿mejorará la capacidad explicativa si se incluyen las cuatro variables?

mMay4=lm(Chla~COD+NO2+NO3+DIN,data=may)
compara6=data.frame(observed=mMay4$model$Chla,fitted=fitted(mMay4))
ggplot(compara5,aes(x=observed,y=fitted)) + geom_point() + ylim(-3,8) +
  geom_abline(intercept=0,slope=1,col="red") + ggtitle("Predicting Chla from COD, NO2, NO3 and DIN")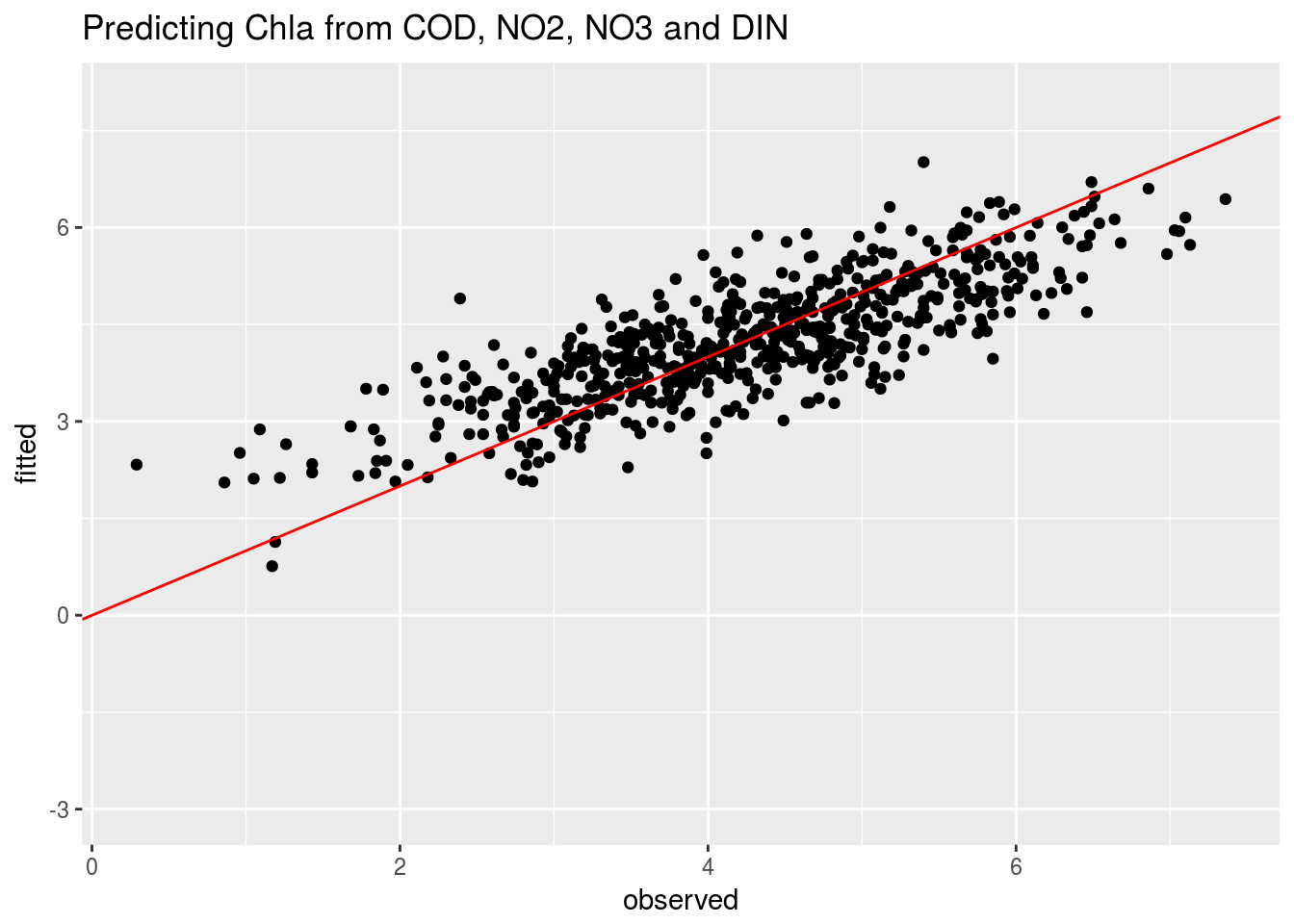

summary(mMay4)
## 
## Call:
## lm(formula = Chla ~ COD + NO2 + NO3 + DIN, data = may)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -2.23485 -0.38547 -0.01811  0.41707  1.61428 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  1.081513   0.117922   9.171  < 2e-16 ***
## COD          2.433315   0.105456  23.074  < 2e-16 ***
## NO2          0.264150   0.050851   5.195 2.79e-07 ***
## NO3          0.254634   0.018748  13.582  < 2e-16 ***
## DIN         -0.061174   0.006153  -9.942  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.6139 on 615 degrees of freedom
## Multiple R-squared:  0.7308, Adjusted R-squared:  0.7291 
## F-statistic: 417.5 on 4 and 615 DF,  p-value: < 2.2e-16
anova(mMay4,mMayNO3)
## Analysis of Variance Table
## 
## Model 1: Chla ~ COD + NO2 + NO3 + DIN
## Model 2: Chla ~ COD + NO2 + NO3
##   Res.Df    RSS Df Sum of Sq      F    Pr(>F)    
## 1    615 231.76                                  
## 2    616 269.00 -1   -37.245 98.834 < 2.2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
anova(mMay4,mMayDIN)
## Analysis of Variance Table
## 
## Model 1: Chla ~ COD + NO2 + NO3 + DIN
## Model 2: Chla ~ COD + NO2 + DIN
##   Res.Df    RSS Df Sum of Sq      F    Pr(>F)    
## 1    615 231.76                                  
## 2    616 301.28 -1   -69.518 184.48 < 2.2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Por tanto, el modelo mejora con cuatro variables.

No obstante, al margen de la capacidad predictiva de los modelos, muchas veces estamos interesados en su capacidad explicativa, esto es, en que el modelo sea útil para determinar como (y cuanto) es el efecto de cada variable X sobre la respuesta Y. Obsérvese en el ajuste de los últimos modelos como el efecto del NO2 ha ido cambiando (0.26 en un caso, -0.10 en otro y 0.57 en el tercero). ¿Cuál es el efecto real del NO2 sobre la clorofila? ¿Por qué el valor del coeficiente de esta variable en la regresión va cambiando según las distintas variables que la acompañan?. Nos encontramos aquí con un problema que se denomina multicolinealidad

pander(mMay4)
Fitting linear model: Chla ~ COD + NO2 + NO3 + DIN
  Estimate Std. Error t value Pr(>|t|)
COD 2.433 0.1055 23.07 2.443e-85
NO2 0.2642 0.05085 5.195 2.794e-07
NO3 0.2546 0.01875 13.58 6.166e-37
DIN -0.06117 0.006153 -9.942 1.072e-21
(Intercept) 1.082 0.1179 9.171 6.96e-19 
pander(mMayNO3)
Fitting linear model: Chla ~ COD + NO2 + NO3
  Estimate Std. Error t value Pr(>|t|)
COD 2.608 0.1119 23.3 1.444e-86
NO2 -0.1096 0.03687 -2.972 0.003078
NO3 0.2542 0.02018 12.6 1.565e-32
(Intercept) 0.4471 0.1067 4.188 3.221e-05 
pander(mMayDIN)
Fitting linear model: Chla ~ COD + NO2 + DIN
  Estimate Std. Error t value Pr(>|t|)
COD 2.273 0.1194 19.04 6.836e-64
NO2 0.5717 0.05187 11.02 6.573e-26
DIN -0.06098 0.00701 -8.699 3.045e-17
(Intercept) 1.425 0.1312 10.86 2.862e-25

Medidas de multicolinealidad

  • Presencia de correlaciones altas entre variables explicativas \(X_i\)

  • Factor de Inflación de la varianza, VIF \(\ge\) 10. El VIF de la variable \(X_i\) se define como:

\[VIF_i=\frac{1}{1-{R_i^2}}\]

siendo \({R_i^2}\) el coeficiente de determinación del modelo lineal en el que la variable \(X_i\) es la variable respuesta y el resto de variables \(X_j,\) \(j=1,2,\dots,p\), \(j\neq i\) son las variables explicativas.

  • Número de Condición (\(K\)) de la matriz de varianzas-covarianzas de variables explicativas (Un valor \(K \ge 30\) indica la presencia de alta colinealidad entre las variables)
library(car)
vif(mMay4)
##      COD      NO2      NO3      DIN 
## 1.701049 6.433799 2.099983 4.064835
kappa(costa[,c("COD","NO2","NO3","DIN")])
## [1] 66.66841
cor(costa[,c("COD","NO2","NO3","DIN")])
##           COD       NO2       NO3       DIN
## COD 1.0000000 0.5007984 0.6918162 0.5268604
## NO2 0.5007984 1.0000000 0.5327271 0.8453534
## NO3 0.6918162 0.5327271 1.0000000 0.6195060
## DIN 0.5268604 0.8453534 0.6195060 1.0000000

Selección de variables

Stepwise regression:

library(MASS)
step <- step(mMay, direction="both")
## Start:  AIC=-369.61
## Chla ~ COD + NO2
## 
##        Df Sum of Sq    RSS     AIC
## <none>              338.29 -369.61
## - NO2   1    22.672 360.96 -331.39
## - COD   1   211.386 549.67  -70.64
summary(step) # display results 
## 
## Call:
## lm(formula = Chla ~ COD + NO2, data = may)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -2.80131 -0.51683  0.03332  0.51218  1.80807 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   0.7923     0.1156   6.854 1.75e-11 ***
## COD           2.4467     0.1246  19.635  < 2e-16 ***
## NO2           0.1987     0.0309   6.430 2.55e-10 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.7405 on 617 degrees of freedom
## Multiple R-squared:  0.6071, Adjusted R-squared:  0.6058 
## F-statistic: 476.7 on 2 and 617 DF,  p-value: < 2.2e-16

 

Todas las posibles regresiones

La librería leaps nos permite encontrar el mejor (o los k mejores) modelos con una variable, con dos variables, con tres variables, etc.

Por ejemplo, para que busque los mejores modelos con hasta 7 variables como máximo:

# All Subsets Regression
library(leaps)
regsubsets.out <-
    regsubsets(Chla~Temperature+pH+DO+NO2+NO3+NH4+DIN+PO4+COD+TSM+As+Hg+Zn+Cd+Pb+Cu,
               data = may,
               nbest = 2,       # 2 best modela for each number of predictors
               nvmax = 7,    # NULL for no limit on number of variables
               force.in = NULL, force.out = NULL,
               method = "exhaustive")

summary.out <- summary(regsubsets.out)
as.data.frame(summary.out$outmat)
##          Temperature pH DO NO2 NO3 NH4 DIN PO4 COD TSM As Hg Zn Cd Pb Cu
## 1  ( 1 )                                         *                      
## 1  ( 2 )                     *                                          
## 2  ( 1 )                         *               *                      
## 2  ( 2 )                                         *                  *   
## 3  ( 1 )                         *           *   *                      
## 3  ( 2 )                         *   *           *                      
## 4  ( 1 )                         *   *       *   *                      
## 4  ( 2 )                         *       *   *   *                      
## 5  ( 1 )                         *   *       *   *   *                  
## 5  ( 2 )                         *   *   *   *   *                      
## 6  ( 1 )              *          *   *       *   *   *                  
## 6  ( 2 )                         *   *   *   *   *   *                  
## 7  ( 1 )              *          *   *   *   *   *   *                  
## 7  ( 2 )              *          *   *       *   *   *                 *

El modelo con mejor \(R^2\) ajustado se obtiene mediante:

which.max(summary.out$adjr2)
## [1] 13
summary.out$which[13,]
## (Intercept) Temperature          pH          DO         NO2         NO3 
##        TRUE       FALSE        TRUE       FALSE       FALSE        TRUE 
##         NH4         DIN         PO4         COD         TSM          As 
##        TRUE        TRUE        TRUE        TRUE        TRUE       FALSE 
##          Hg          Zn          Cd          Pb          Cu 
##       FALSE       FALSE       FALSE       FALSE       FALSE

En este caso, el modelo con mayor \(R^2\) ajustada es el que incluye las variables siguientes:

best.Model=lm(Chla~pH+NO3+NH4+DIN+PO4+COD+TSM, data=costa)
summary(best.Model)
## 
## Call:
## lm(formula = Chla ~ pH + NO3 + NH4 + DIN + PO4 + COD + TSM, data = costa)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -4.0479 -0.7406 -0.0321  0.6217  4.7435 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 37.877441   6.536898   5.794 8.70e-09 ***
## pH          -4.590934   0.800068  -5.738 1.20e-08 ***
## NO3          0.319685   0.011204  28.534  < 2e-16 ***
## NH4         -0.076160   0.014424  -5.280 1.53e-07 ***
## DIN         -0.002009   0.011153  -0.180    0.857    
## PO4         -4.603366   0.288474 -15.958  < 2e-16 ***
## COD          3.736585   0.081803  45.678  < 2e-16 ***
## TSM          0.072844   0.008521   8.548  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.201 on 1232 degrees of freedom
## Multiple R-squared:  0.8924, Adjusted R-squared:  0.8918 
## F-statistic:  1460 on 7 and 1232 DF,  p-value: < 2.2e-16

lo que no significa que todas las variables deban quedarse en el modelo (vemos que hay variables no significativas). Si aplicamos ahora un método stepwise:

final.Model=step(best.Model,direction="both")
## Start:  AIC=462.5
## Chla ~ pH + NO3 + NH4 + DIN + PO4 + COD + TSM
## 
##        Df Sum of Sq    RSS     AIC
## - DIN   1      0.05 1777.5  460.53
## <none>              1777.5  462.50
## - NH4   1     40.22 1817.7  488.25
## - pH    1     47.51 1825.0  493.21
## - TSM   1    105.43 1882.9  531.95
## - PO4   1    367.39 2144.9  693.48
## - NO3   1   1174.64 2952.1 1089.59
## - COD   1   3010.30 4787.8 1689.18
## 
## Step:  AIC=460.53
## Chla ~ pH + NO3 + NH4 + PO4 + COD + TSM
## 
##        Df Sum of Sq    RSS     AIC
## <none>              1777.5  460.53
## + DIN   1      0.05 1777.5  462.50
## - pH    1     52.38 1829.9  494.55
## - TSM   1    108.79 1886.3  532.20
## - NH4   1    287.08 2064.6  644.18
## - PO4   1    383.33 2160.8  700.68
## - NO3   1   1713.63 3491.1 1295.55
## - COD   1   3116.12 4893.6 1714.30
summary(final.Model)
## 
## Call:
## lm(formula = Chla ~ pH + NO3 + NH4 + PO4 + COD + TSM, data = costa)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -4.0325 -0.7368 -0.0358  0.6262  4.7467 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 37.499262   6.188125   6.060 1.81e-09 ***
## pH          -4.542700   0.753626  -6.028 2.19e-09 ***
## NO3          0.318544   0.009239  34.477  < 2e-16 ***
## NH4         -0.078556   0.005567 -14.112  < 2e-16 ***
## PO4         -4.613413   0.282920 -16.306  < 2e-16 ***
## COD          3.733813   0.080310  46.492  < 2e-16 ***
## TSM          0.072541   0.008350   8.687  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 1.201 on 1233 degrees of freedom
## Multiple R-squared:  0.8924, Adjusted R-squared:  0.8919 
## F-statistic:  1704 on 6 and 1233 DF,  p-value: < 2.2e-16
anova(final.Model,best.Model)
## Analysis of Variance Table
## 
## Model 1: Chla ~ pH + NO3 + NH4 + PO4 + COD + TSM
## Model 2: Chla ~ pH + NO3 + NH4 + DIN + PO4 + COD + TSM
##   Res.Df    RSS Df Sum of Sq      F Pr(>F)
## 1   1233 1777.5                           
## 2   1232 1777.5  1   0.04681 0.0324 0.8571

Otras librerías para encontrar el mejor modelo: bestglm