# Lectura de datos
library(readxl)
costa=read_excel("datos/coast.xlsx")

Exploración de datos.

Antes de ajustar ningún modelo, conviene explorar los datos para detectar particularidades, outliers, etc.

Diferencias entre noviembre y mayo

La siguiente gráfica muestra las posibles diferencias entre los meses del año para las distintas variables del archivo.

library(ggplot2)
library(gridExtra)
costa$obs=1:nrow(costa)
costa=data.frame(costa)
costaRes=reshape(costa,idvar="obs",varying=list(1:17), timevar="variable",
                 times=names(costa)[1:17],v.names="value",direction="long")
vbles=names(costa)[1:17]
plots=lapply(1:17,function(k) {
  ggplot(subset(costaRes,variable==vbles[k]),
         aes(x=month,y=value,fill=month)) + geom_boxplot() +
    guides(fill=FALSE) + ylab(vbles[k])
    
})
grid.arrange(grobs=plots[1:6],nrow=3,ncol=2)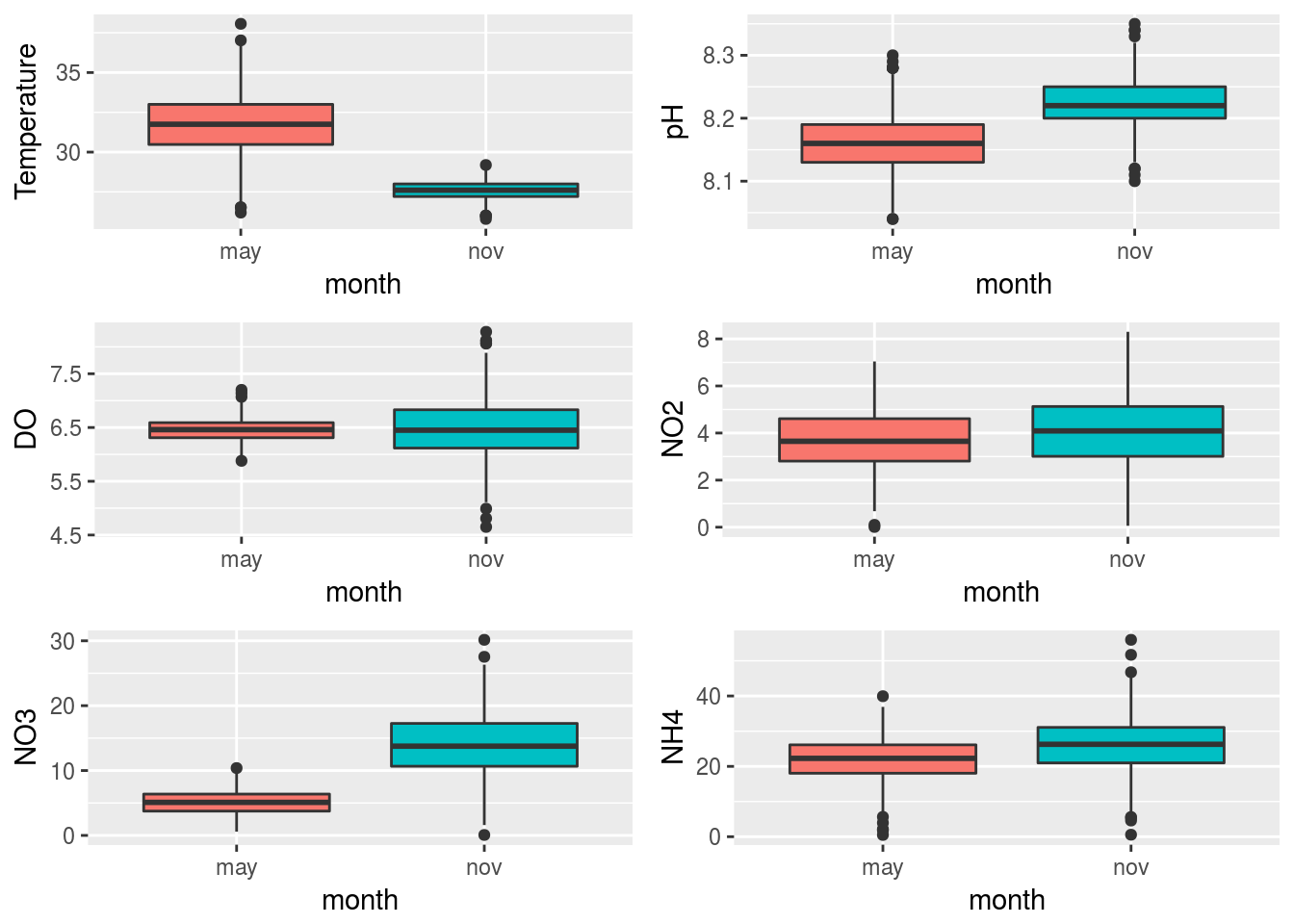

grid.arrange(grobs=plots[7:12],nrow=3,ncol=2)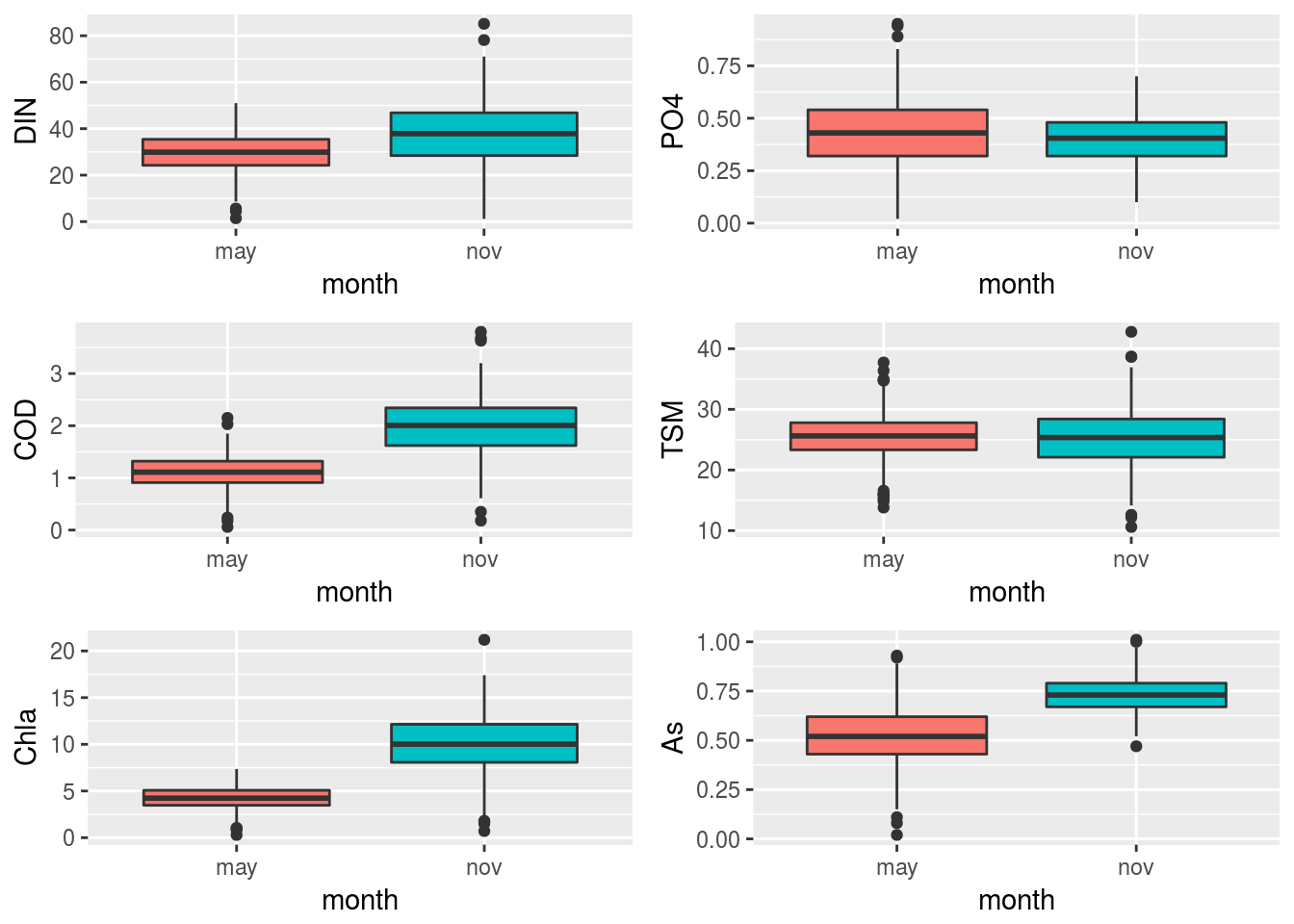

grid.arrange(grobs=plots[13:17],nrow=3,ncol=2)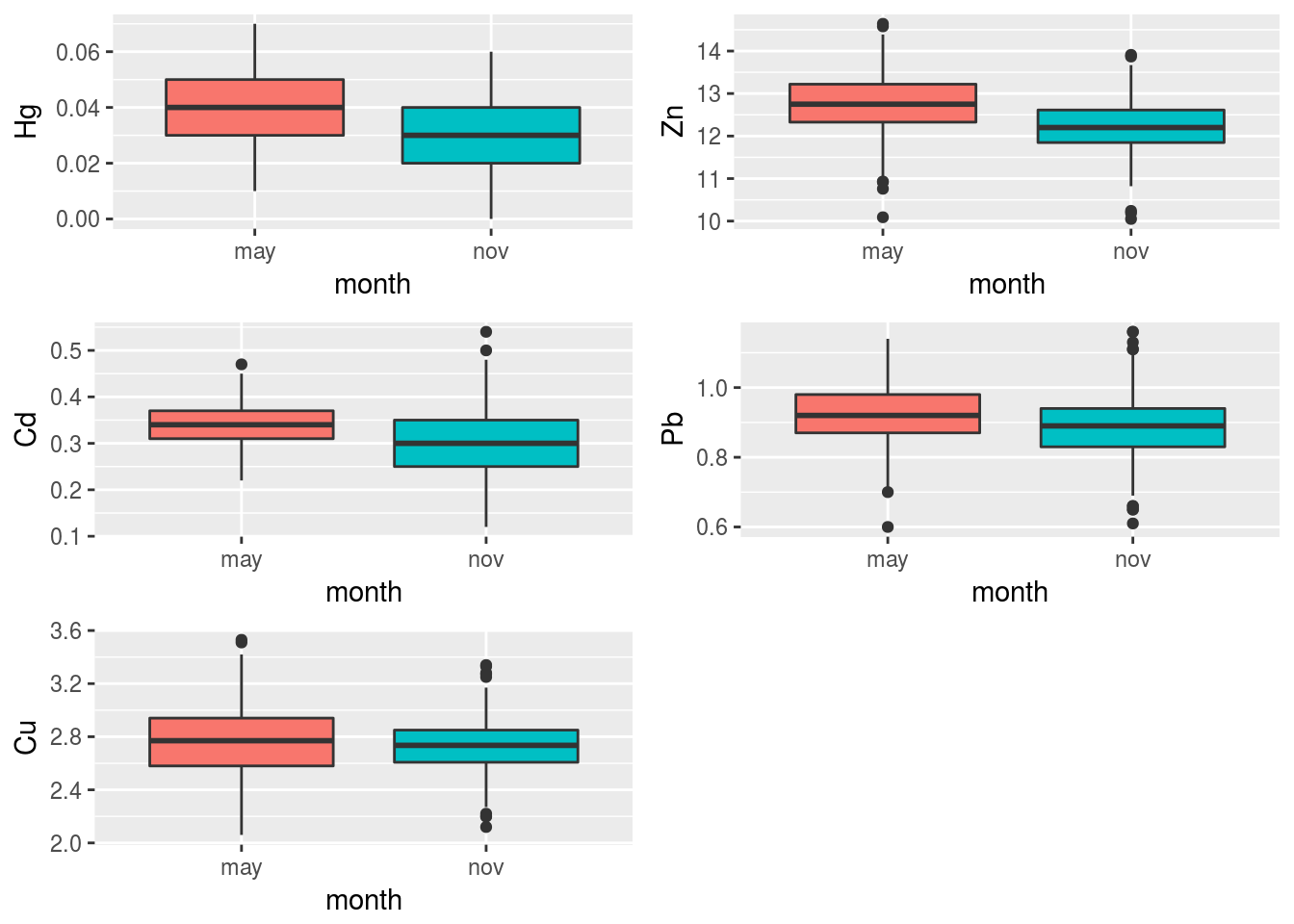

Puede apreciarse que prácticamente todas las variables manifiestan comportamientos diferentes en los dos meses de observación. Por tanto, en el análisis conjunto de las mismas habrá de tenerse el mes en cuenta.

 

Asociación Temperatura - Clorofila

El siguiente gráfico muestra, a modo de ejemplo, como varía la clorofila en función de la temperatura. Cada uno de los meses se ha señalado en un color distinto:

# Gráfica con el plot básico de R
plot(Chla~Temperature,costa,col=factor(month))
legend("topright",title="Month",c("May","November"),col=c(1,2),pch=1)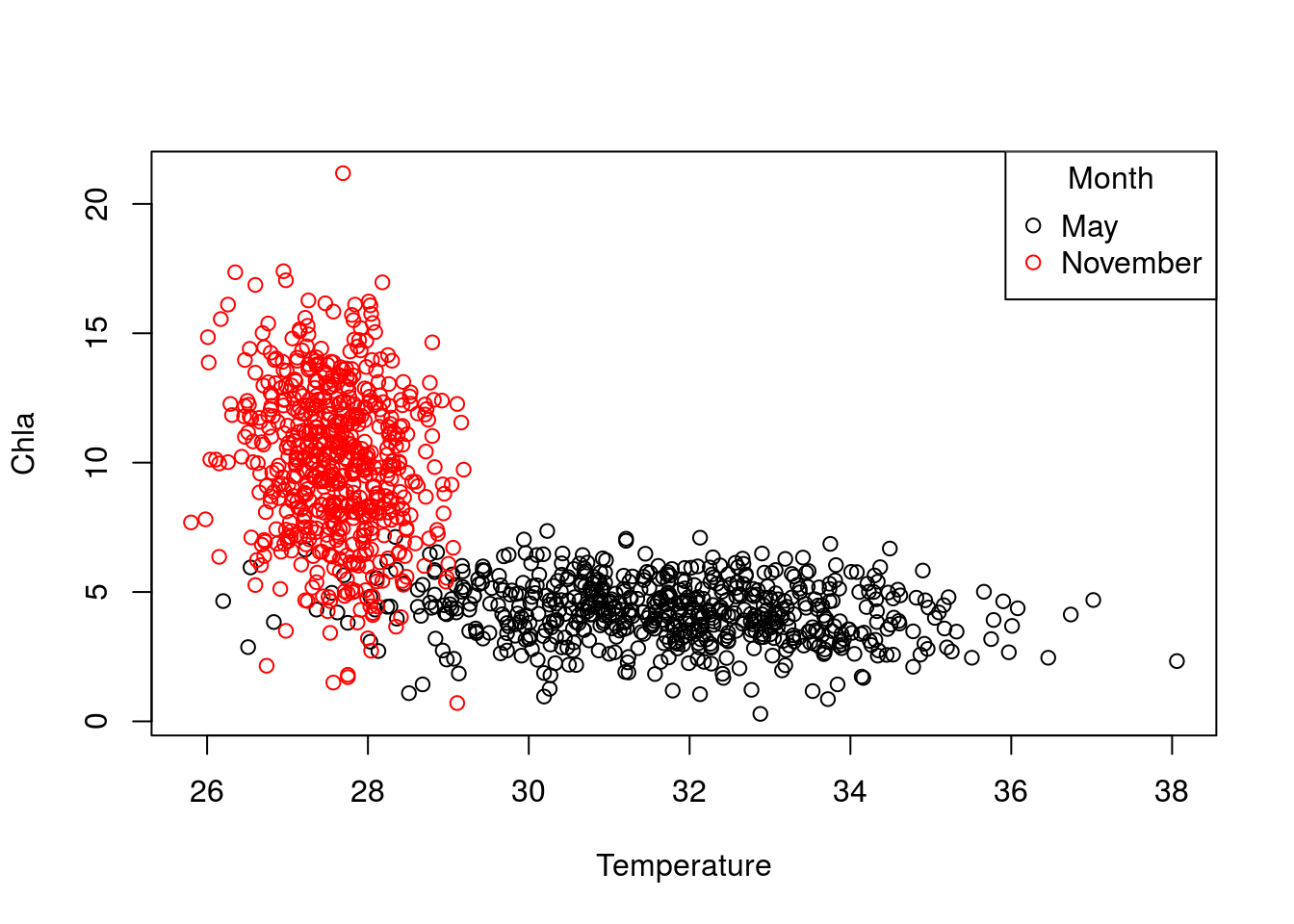

# Misma gráfica con ggplot
ggplot(costa,aes(x=Temperature,y=Chla, col=month)) + geom_point()

Si calculásemos la correlación entre ambas variables sin tener en cuenta el mes obtenemos un valor de correlación relativamente alto:

with(costa,cor(Temperature,Chla))

## [1] -0.6958878

lo que significaría la existencia de una fuerte asociación entre clorofila y temperatura.

Sin embargo, la correlación entre ambas variables cada mes es sensiblemente inferior:

may=subset(costa,month=="may")
nov=subset(costa,month=="nov")
with(may,cor(Temperature,Chla))

## [1] -0.1712265

with(nov,cor(Temperature,Chla))

## [1] -0.1617771

Esto significa que la correlación detectada inicialmente entre clorofila y temperatura en realidad se debía al efecto del mes (en noviembre hay más clorofila que en mayo, sin que un incremento de temperatura en un mes concreto signifique una variación notable de la clorofila). Podemos ver estos efectos dibujando las correspondientes rectas de regresión:

# Con los gráficos básicos de R
plot(Chla~Temperature,costa,col=factor(month))
legend("topright",title="Month",c("May","November"),col=c(1,2),pch=1)
rectaGlobal=lm(Chla~Temperature,costa)
rectaNov=lm(Chla~Temperature,nov)
rectaMay=lm(Chla~Temperature,may)
abline(rectaGlobal,col=4,lwd=3)
abline(rectaMay,col=1,lwd=2)
abline(rectaNov,col=2,lwd=2)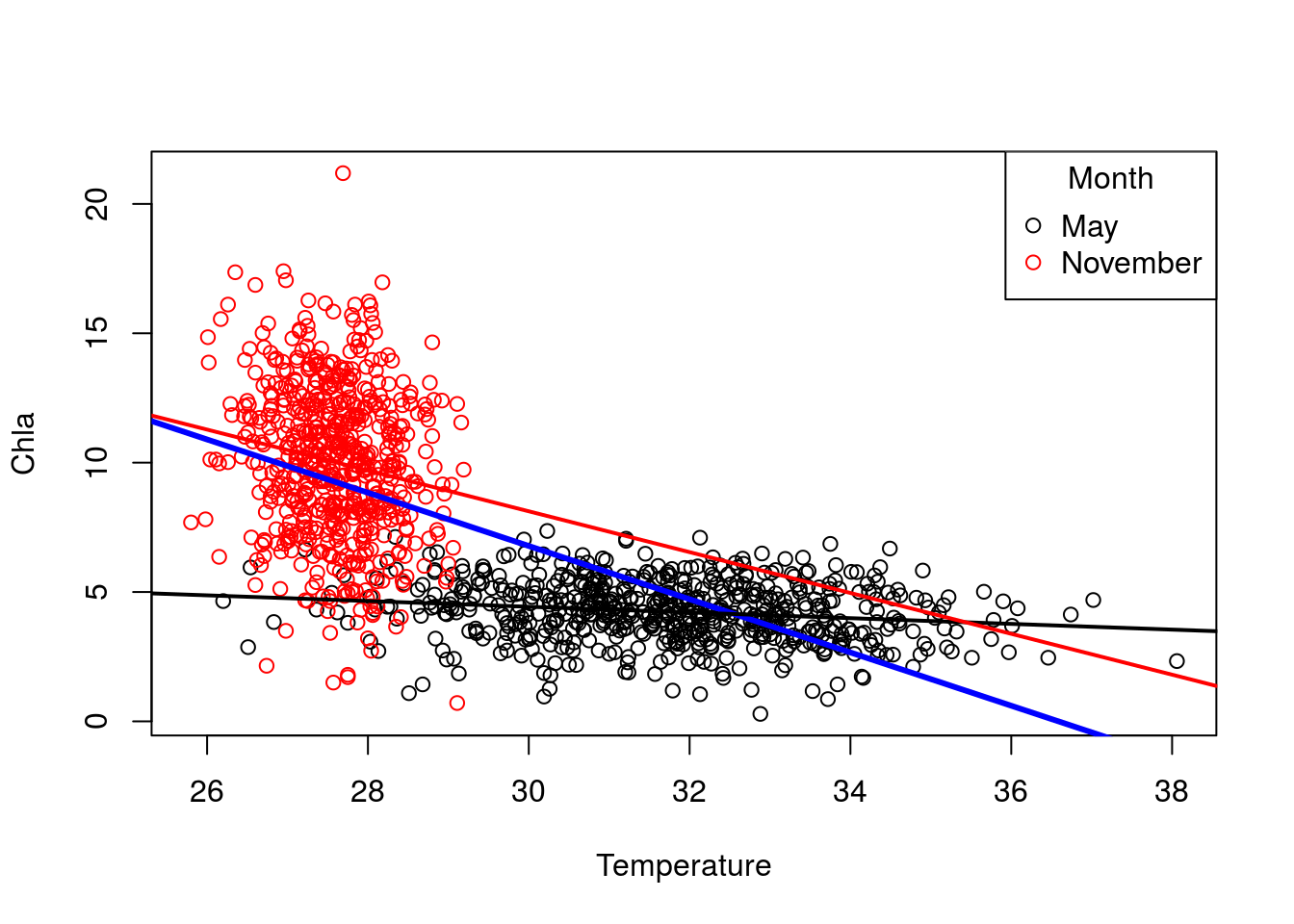

# Con ggplot
ggplot(costa,aes(x=Temperature,y=Chla)) + 
  geom_point(aes(colour=month)) +
  geom_smooth(method="lm", aes(color="all data"), size=1.5) + 
  geom_smooth(method="lm",aes(color=month)) +
  scale_colour_manual(name="month",values=1:3) + 
  guides(colour = guide_legend(override.aes = list(alpha = 0)))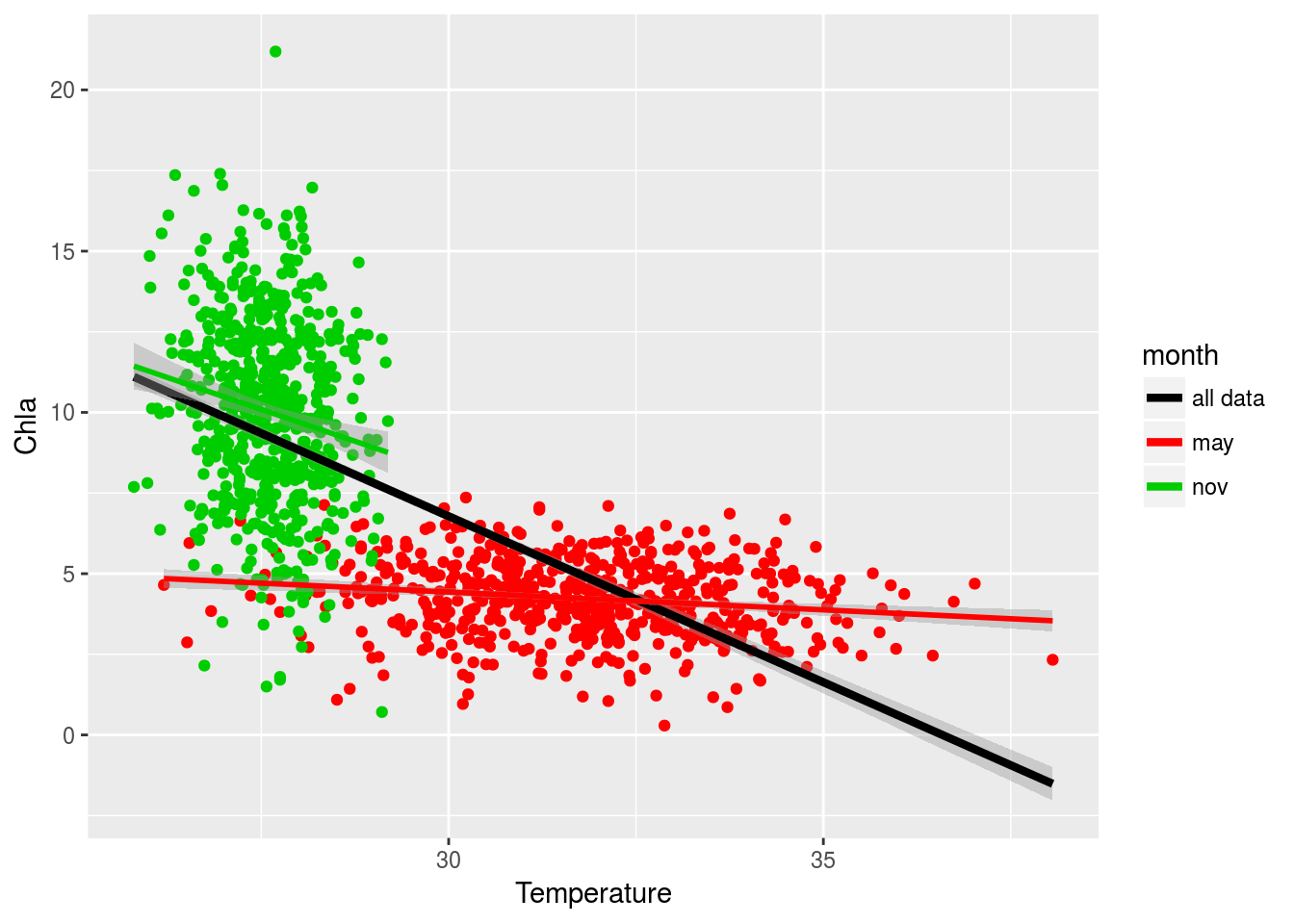

 

Asociación DIN - NO2

Evaluamos ahora la asociación entre Nitrógeno disuelto (DIN) y dióxido de nitrógeno:

ggplot(costa,aes(x=NO2,y=DIN)) + 
  geom_point(aes(colour=month,shape=month)) +
  geom_smooth(method="lm", size=1.5) + 
  geom_smooth(method="lm",aes(color=month))

En este caso las dos rectas son muy parecidas:

Para los datos de mayo:

lm(DIN~NO2,may)

## 
## Call:
## lm(formula = DIN ~ NO2, data = may)
## 
## Coefficients:
## (Intercept)          NO2  
##       8.824        5.677

Para los datos de noviembre:

lm(DIN~NO2,nov)

## 
## Call:
## lm(formula = DIN ~ NO2, data = nov)
## 
## Coefficients:
## (Intercept)          NO2  
##       6.210        7.693

Por tanto cabe hacerse la pregunta de si la diferencia observada entre ambas rectas obedece a que la relación entre las variables cambia de mayo a noviembre, o si se debe simplemente al azar del muestreo, y en realidad el comportamiento ambos meses es análogo y se debería ajustar un único modelo.

 

 

Diferencias entre localizaciones.

Los datos han sido muestreados en 10 localizaciones distintas. Los siguientes gráficos nos informan del comportamiento de cada variable en las distintas localizaciones:

costaRes$location=factor(costaRes$location)
plots=lapply(1:17,function(k) {
  ggplot(subset(costaRes,variable==vbles[k]),
         aes(x=location,y=value,fill=location)) + geom_boxplot() +
    guides(fill=FALSE) + ylab(vbles[k])
    
})
grid.arrange(grobs=plots[1:6],nrow=3,ncol=2)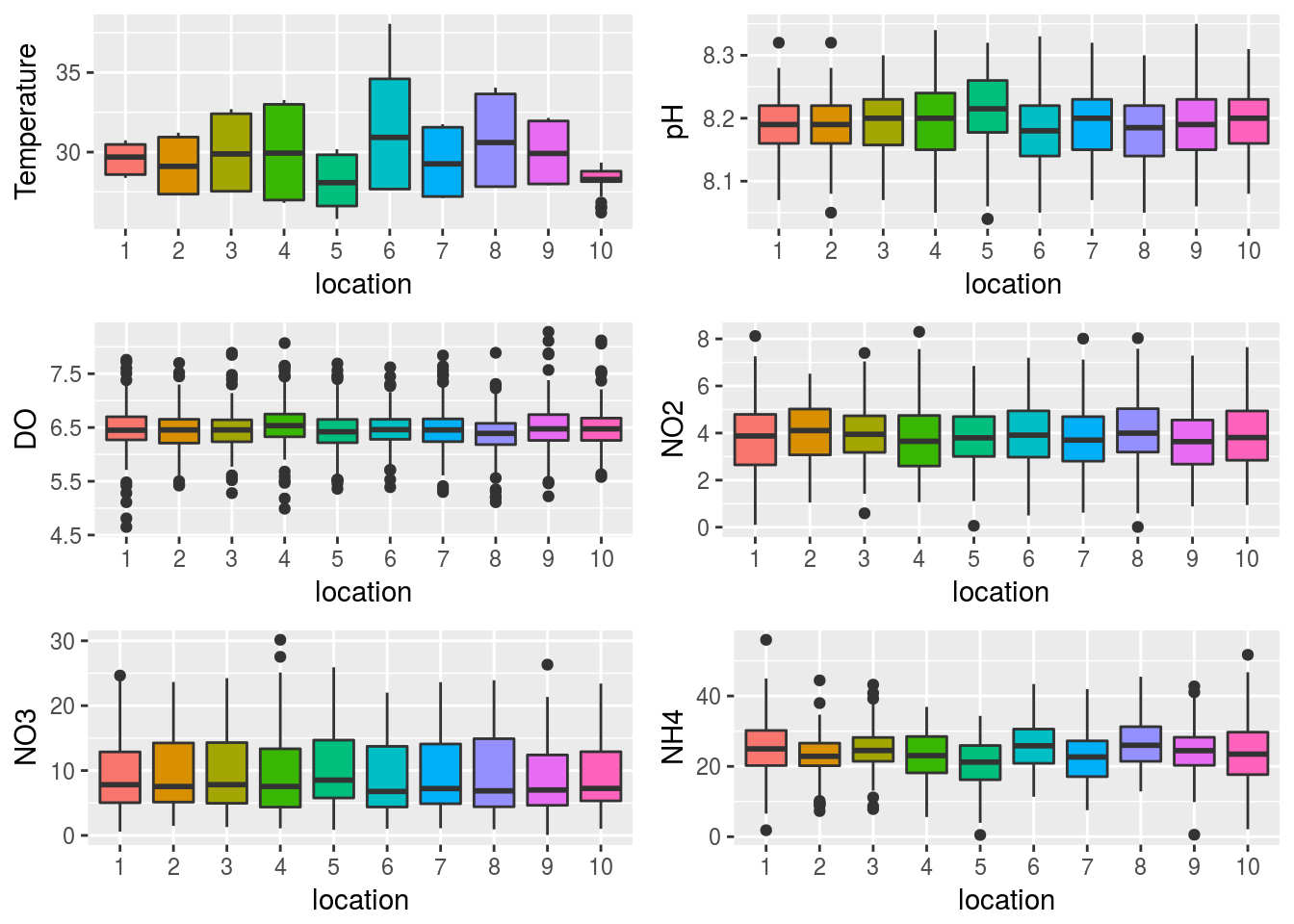

grid.arrange(grobs=plots[7:12],nrow=3,ncol=2)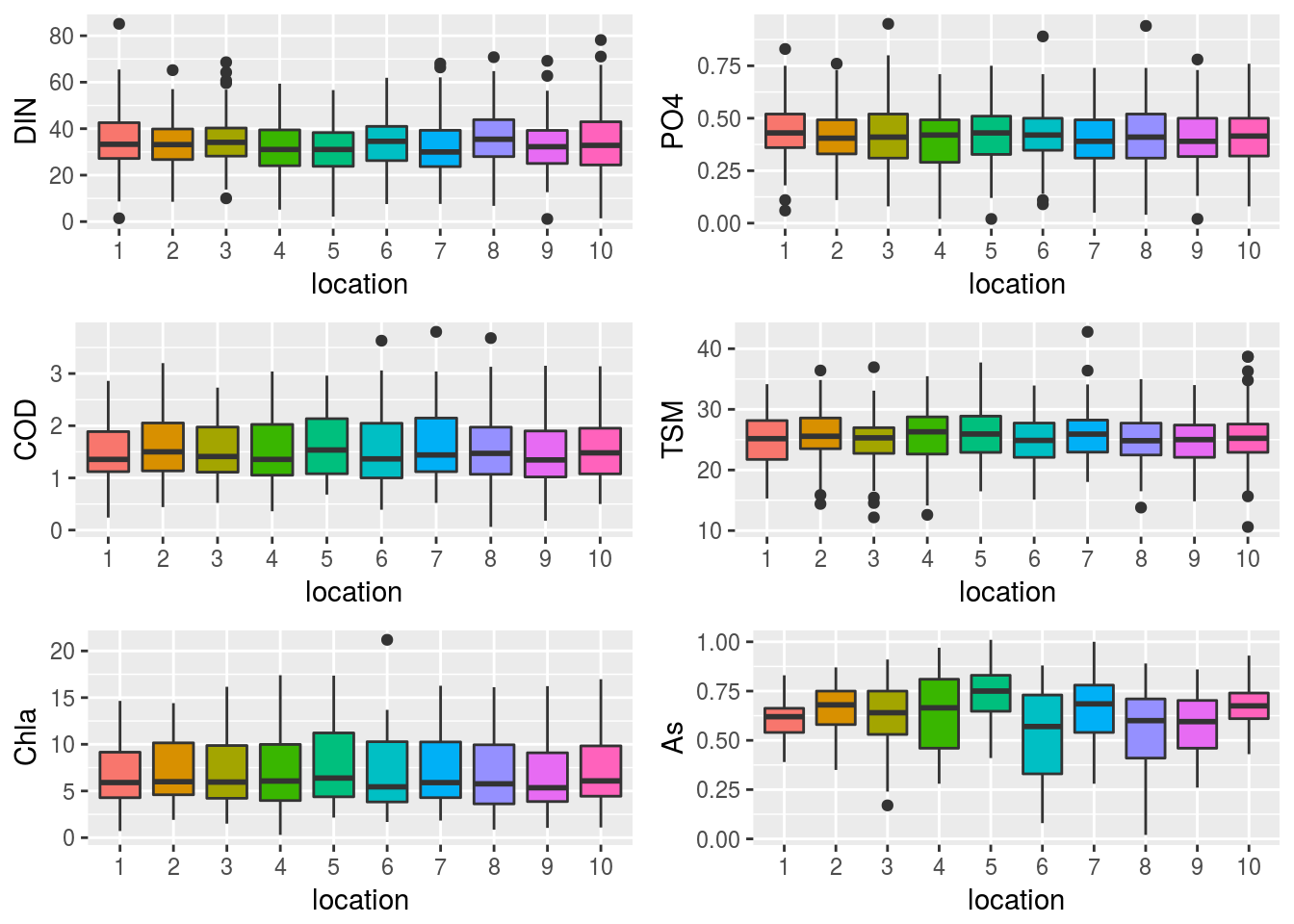

grid.arrange(grobs=plots[13:17],nrow=3,ncol=2)

Fijémonos con detalle en la primera de estas gráficas (la correspondiente a la temperatura):

costa$location=factor(costa$location)
ggplot(costa,aes(x=location,y=Temperature,fill=location)) +geom_boxplot()+guides(fill=FALSE)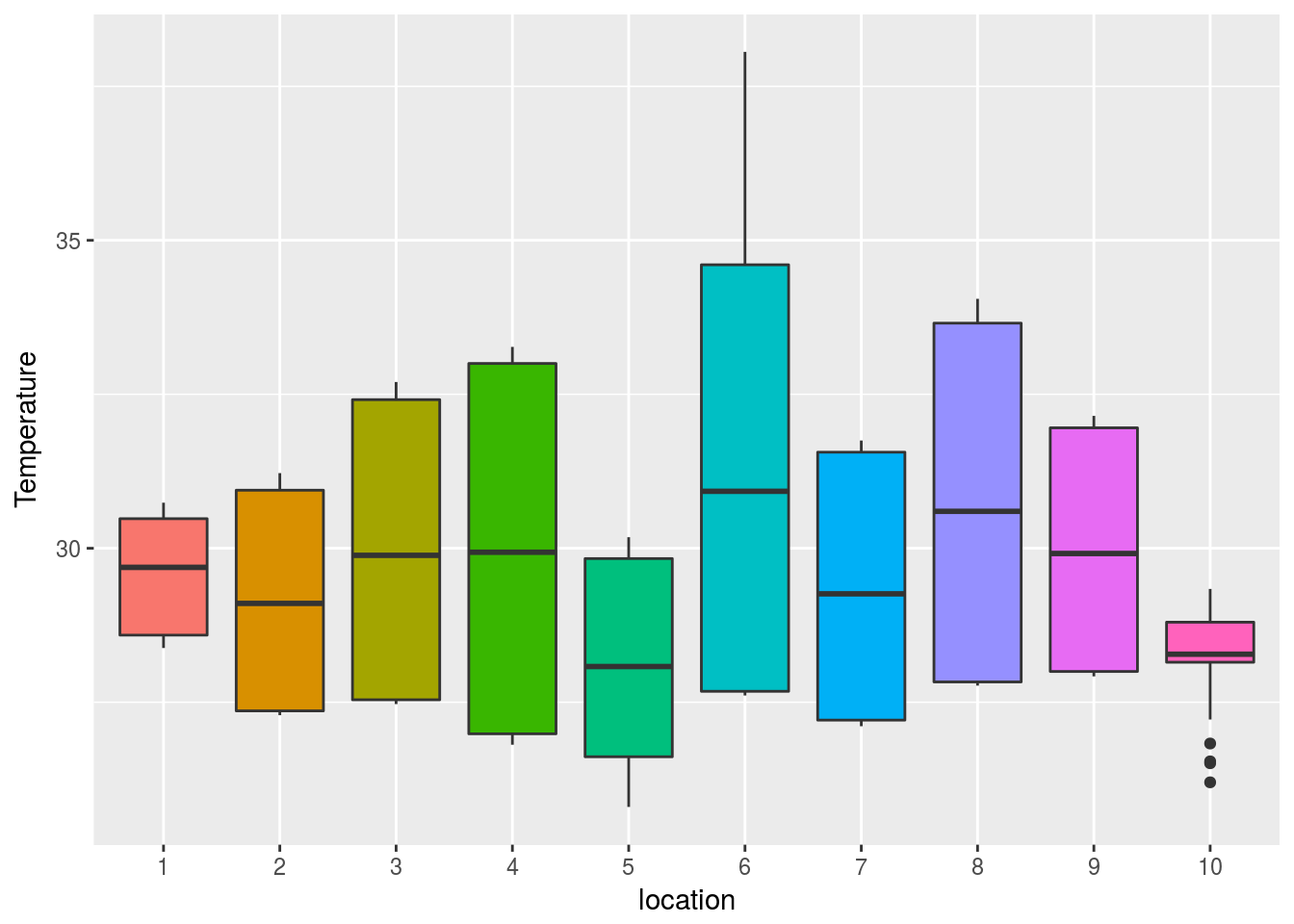

El gráfico indica que aparentemente las localizaciones 5 y 10 presentan una temperatura más baja que el resto. La tabla siguiente nos proporciona los valores medios (y sus correspondientes desviaciones típicas) de la temperatura en cada sitio:

library(pander)
pander(aggregate(Temperature~location,costa,
                 function(x) sprintf("%.2f (%.2f)",mean(x),sd(x))))

location	Temperature
1	29.57 (0.94)
2	29.17 (1.81)
3	29.98 (2.45)
4	29.98 (3.02)
5	28.17 (1.66)
6	31.29 (3.67)
7	29.36 (2.17)
8	30.74 (2.92)
9	29.98 (1.99)
10	28.38 (0.55)

Al igual que en el caso anterior podemos preguntarnos si las diferencias que se aprecian entre los valores medios de temperatura se deben a que existen diferencias reales en temperatura entre los distintos lugares, o si simplemente dichas diferencias pueden atribuirse al azar del muestreo.

 

 

Efecto combinado de localización y temperatura.

Los gráficos que mostramos a continuación revelan el comportamiento conjunto de cada variable frente a la localización y el mes del año en que se ha evaluado:

plots=lapply(1:17,function(k) {
  ggplot(subset(costaRes,variable==vbles[k]),
         aes(x=location,y=value,fill=month)) + 
    geom_boxplot() + ylab(vbles[k]) + ggtitle(vbles[k])
})
for (k in 1:17) print(plots[[k]])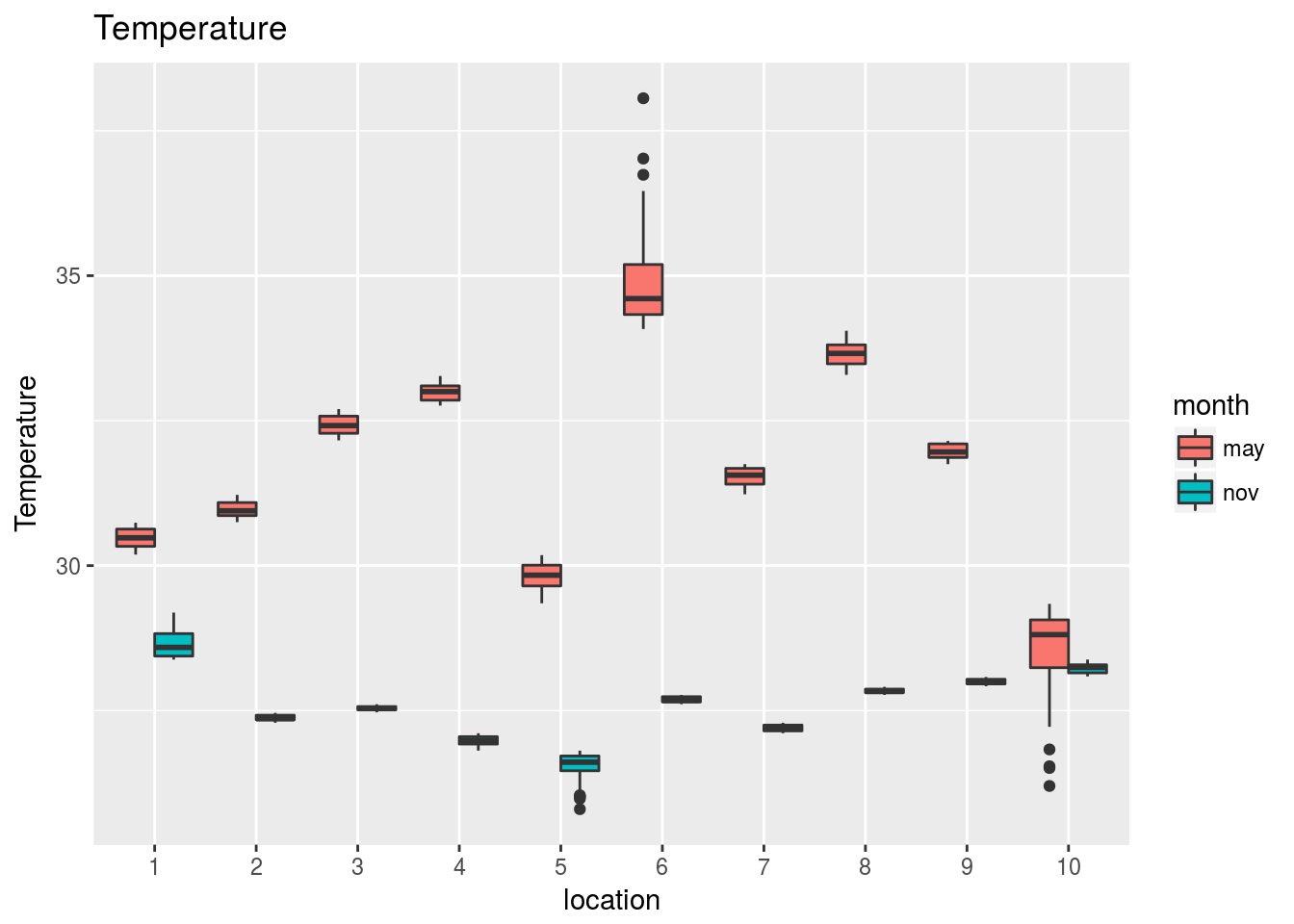

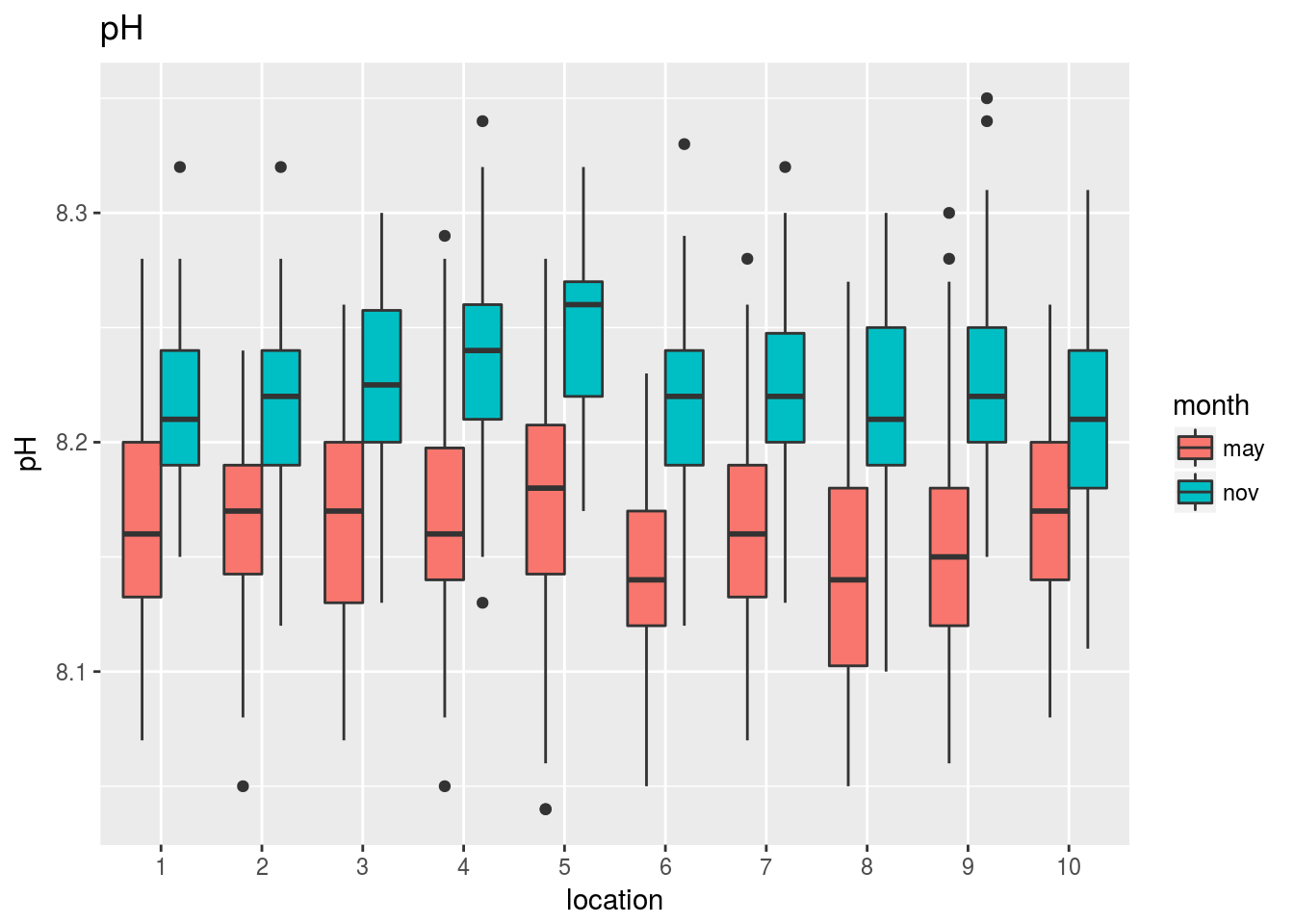
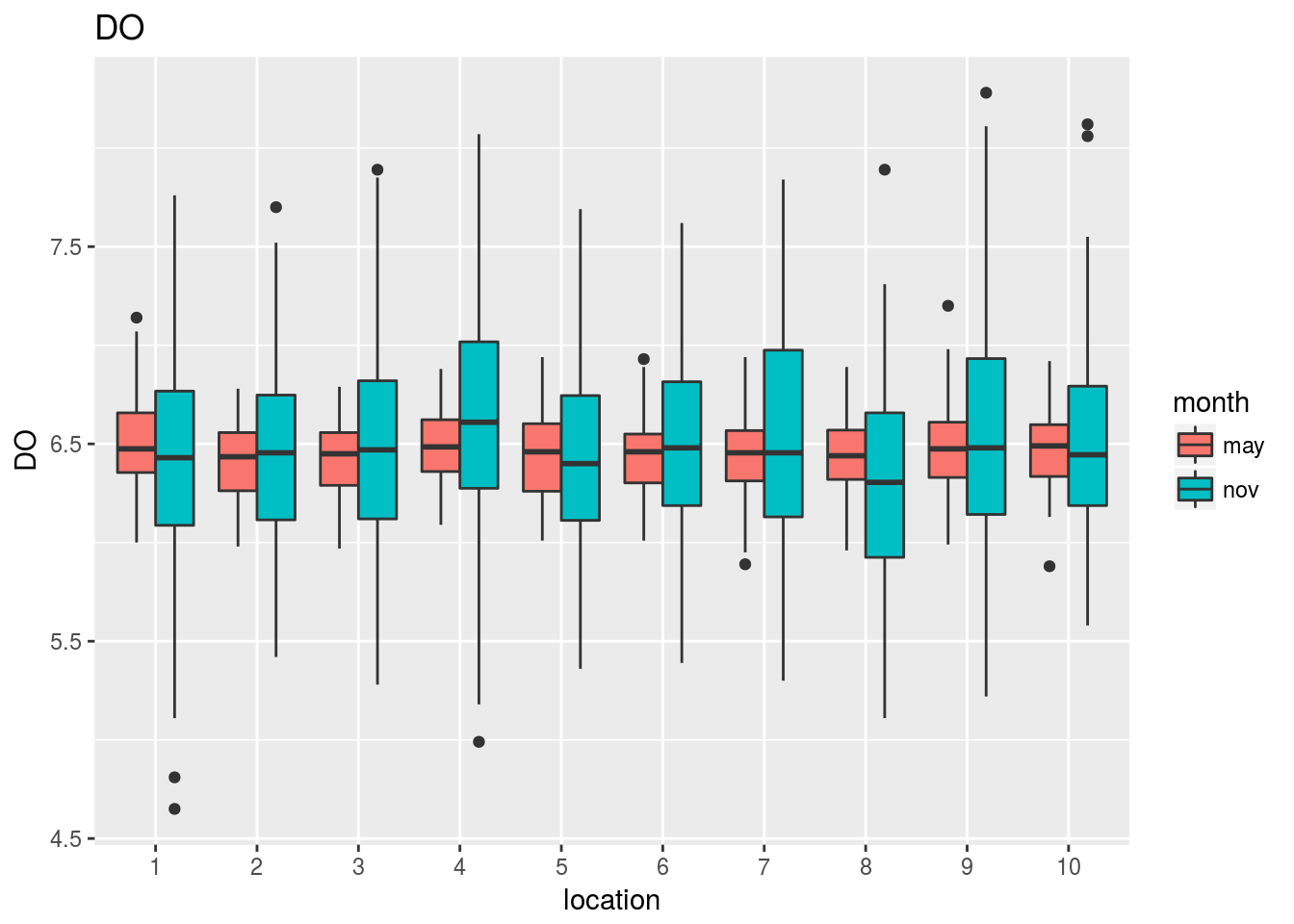
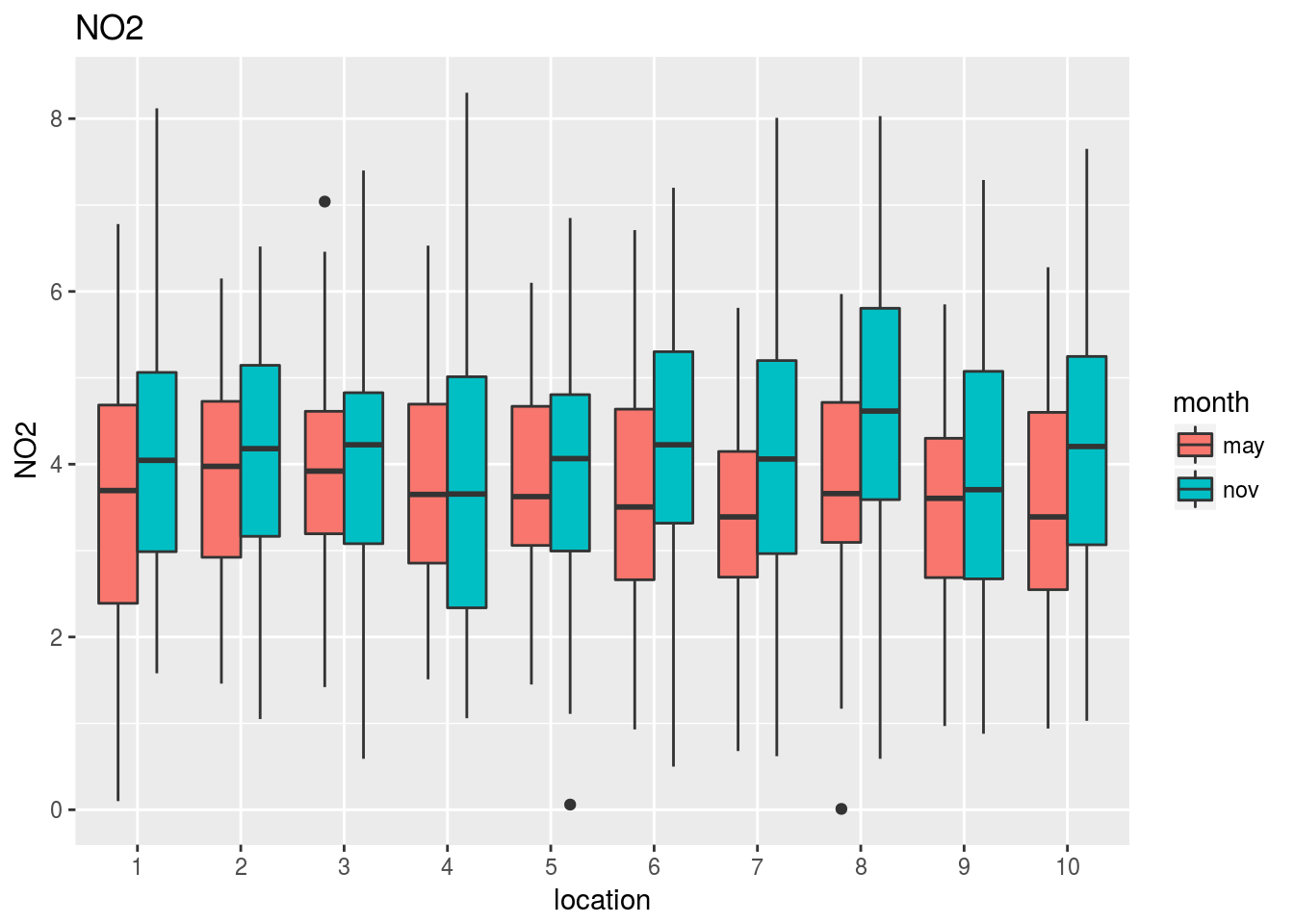
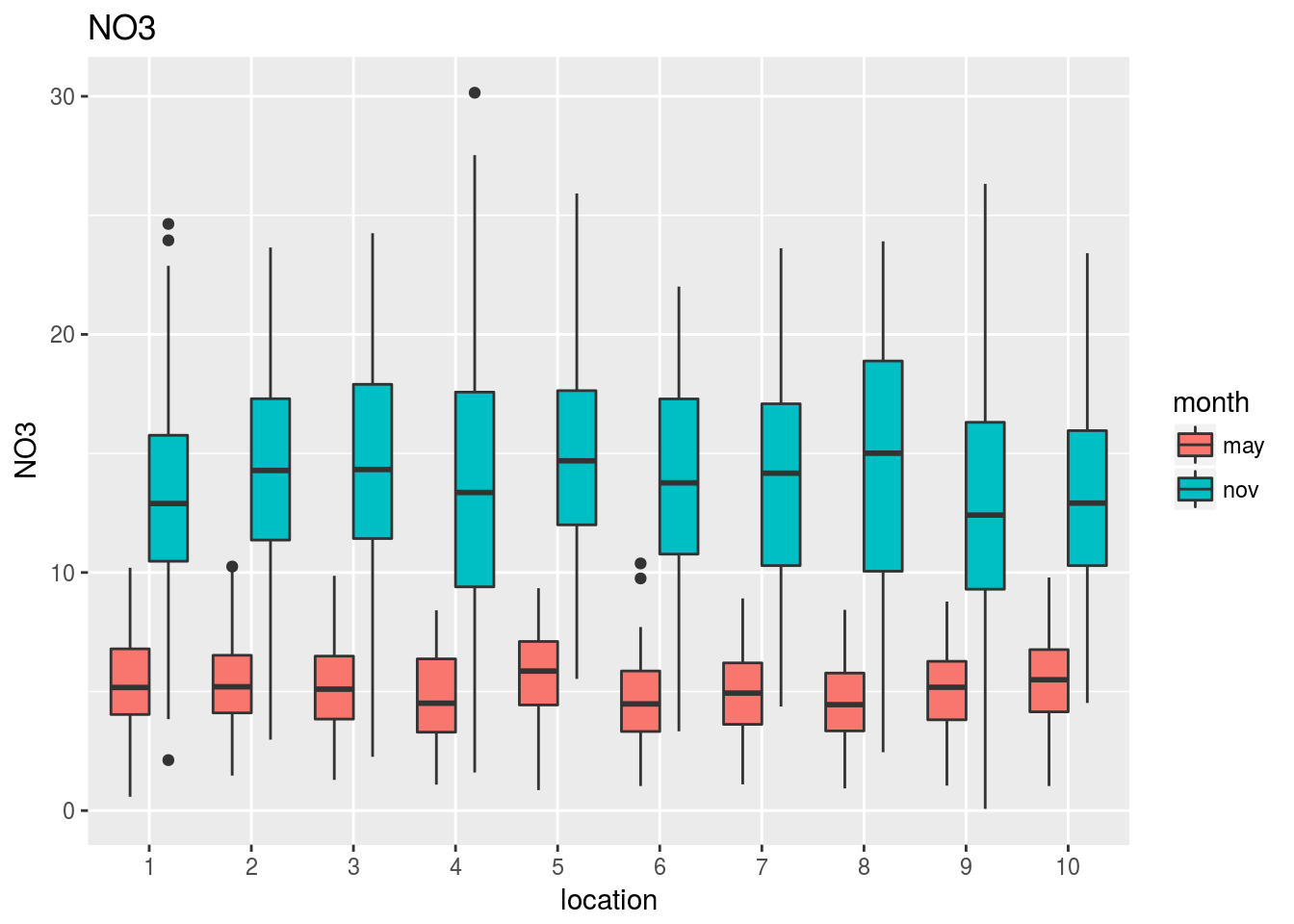
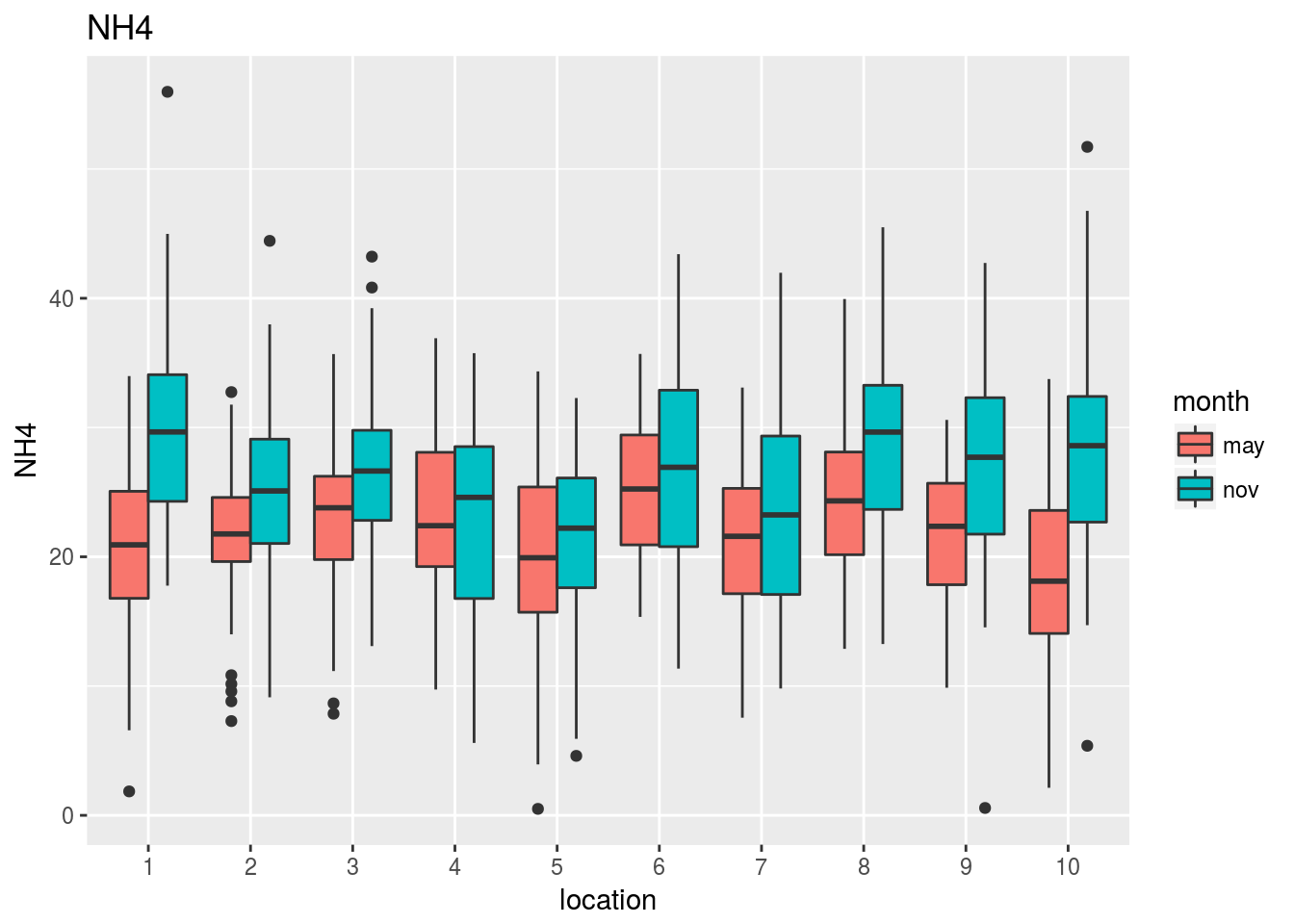
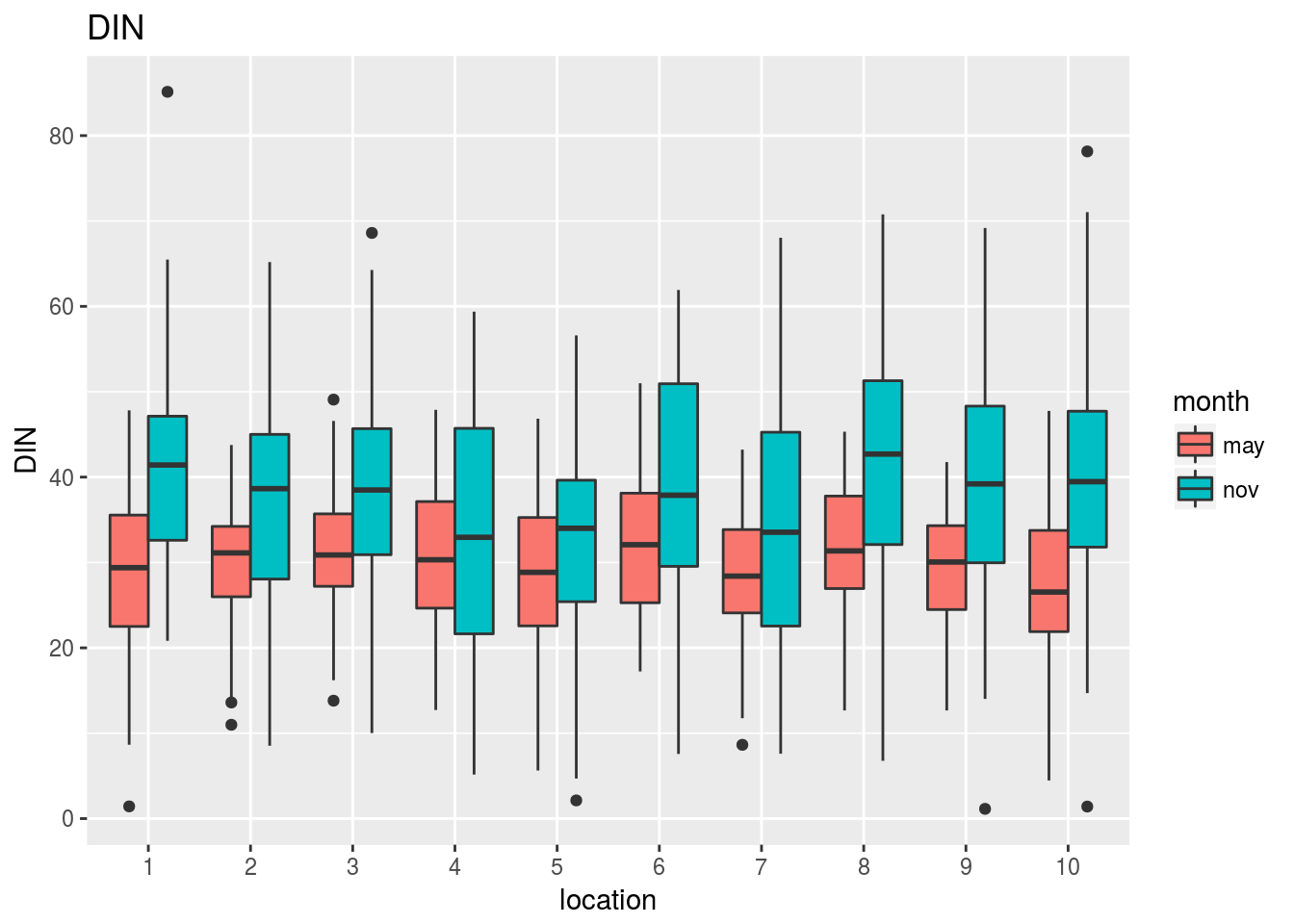
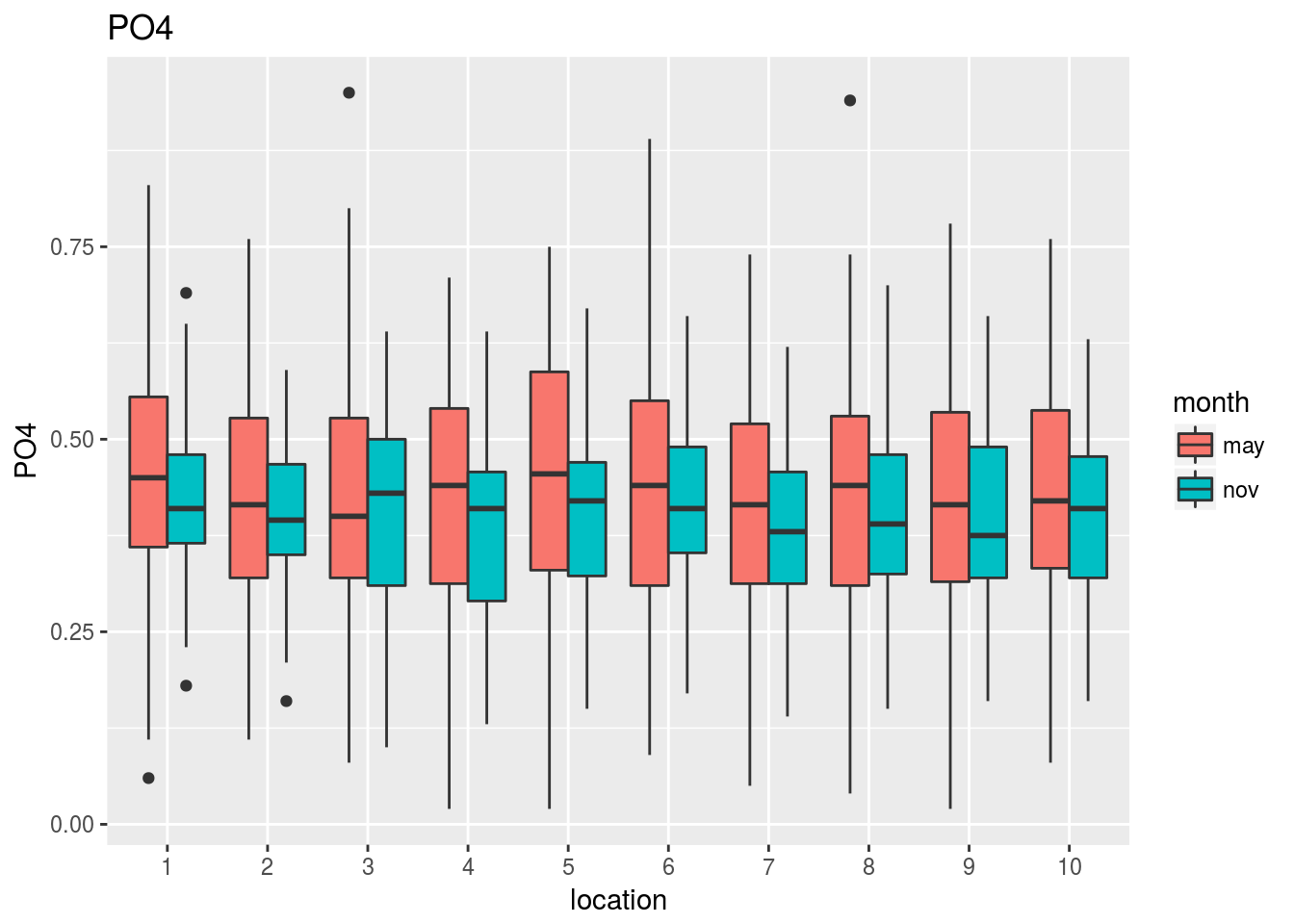
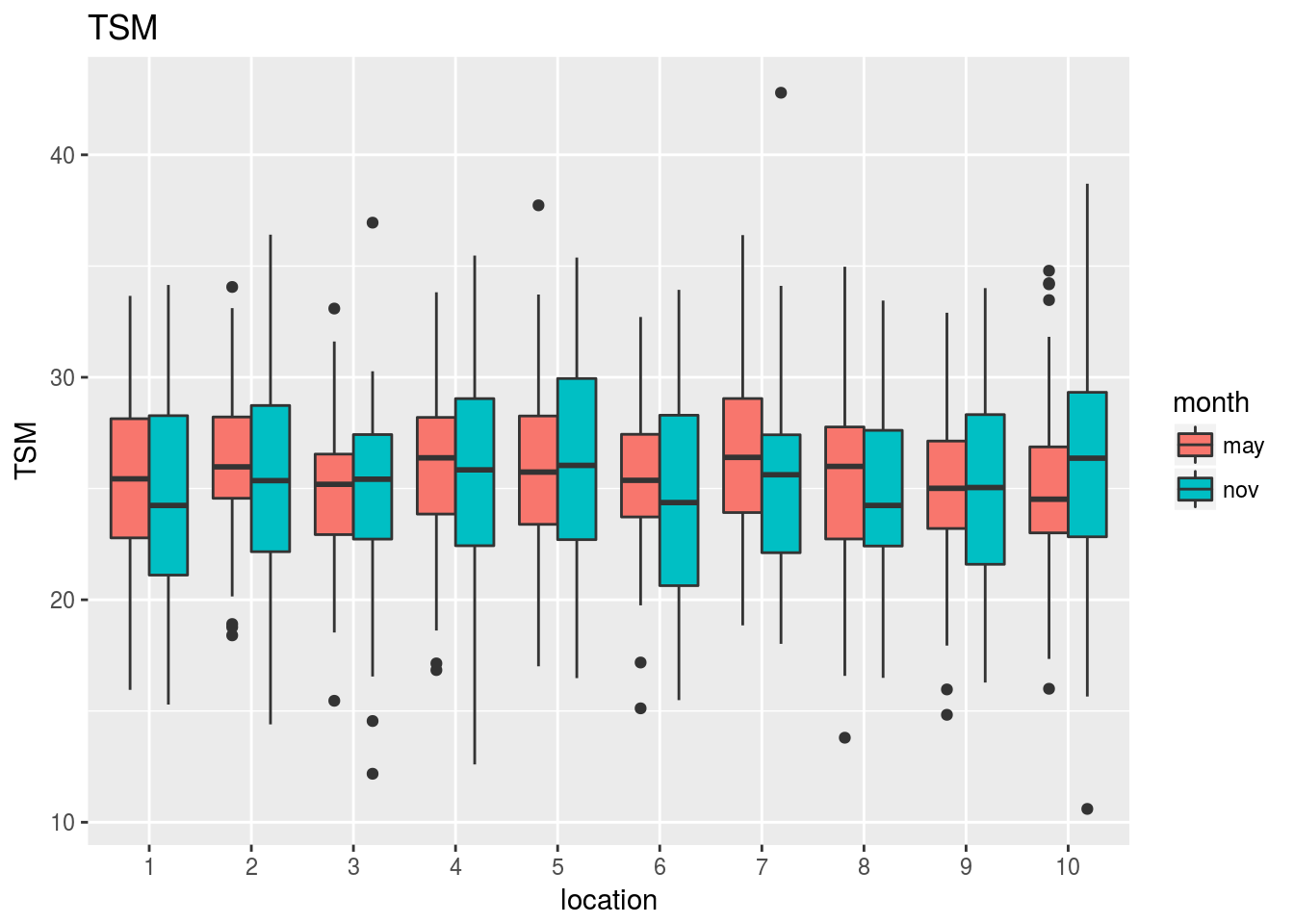
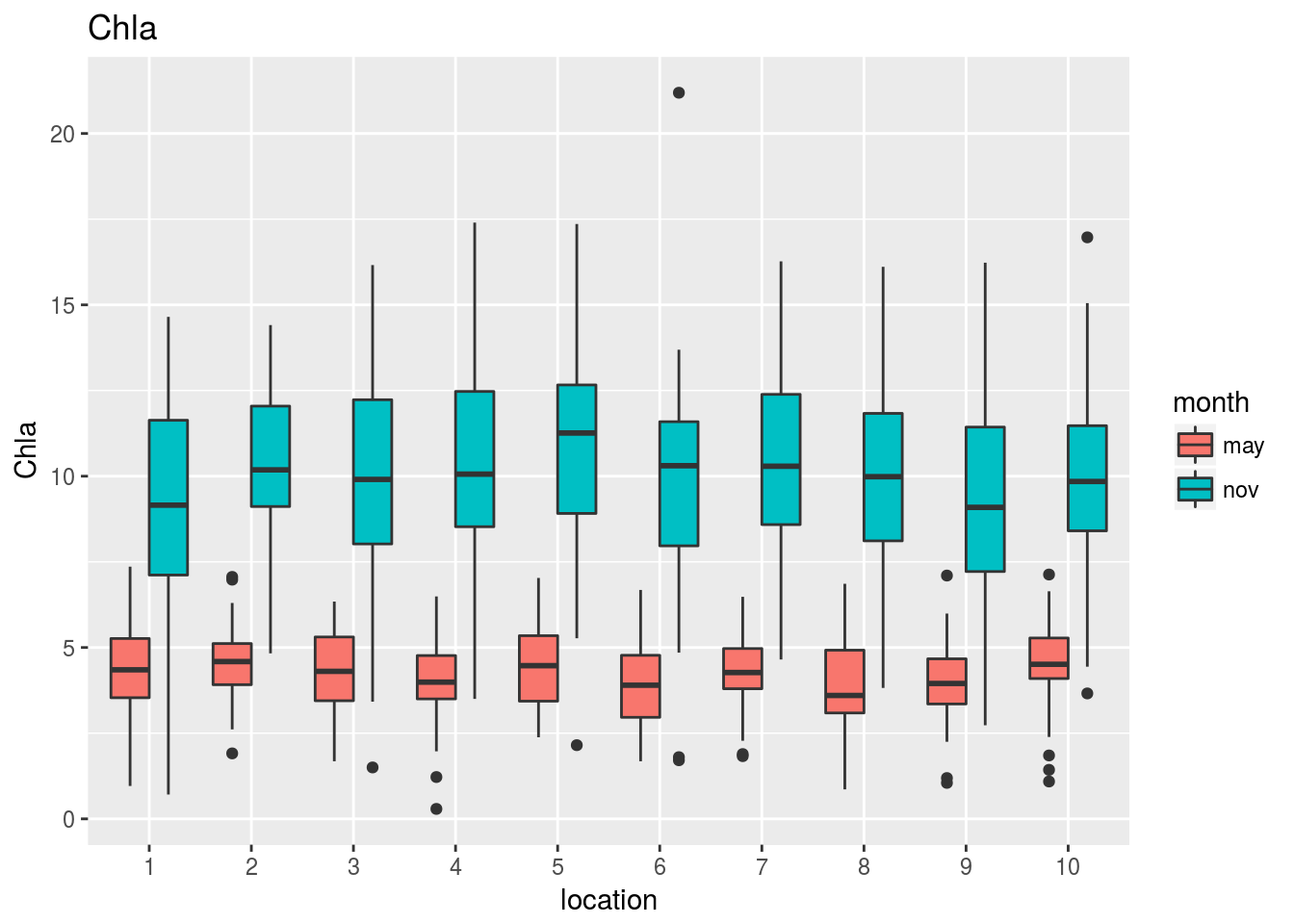
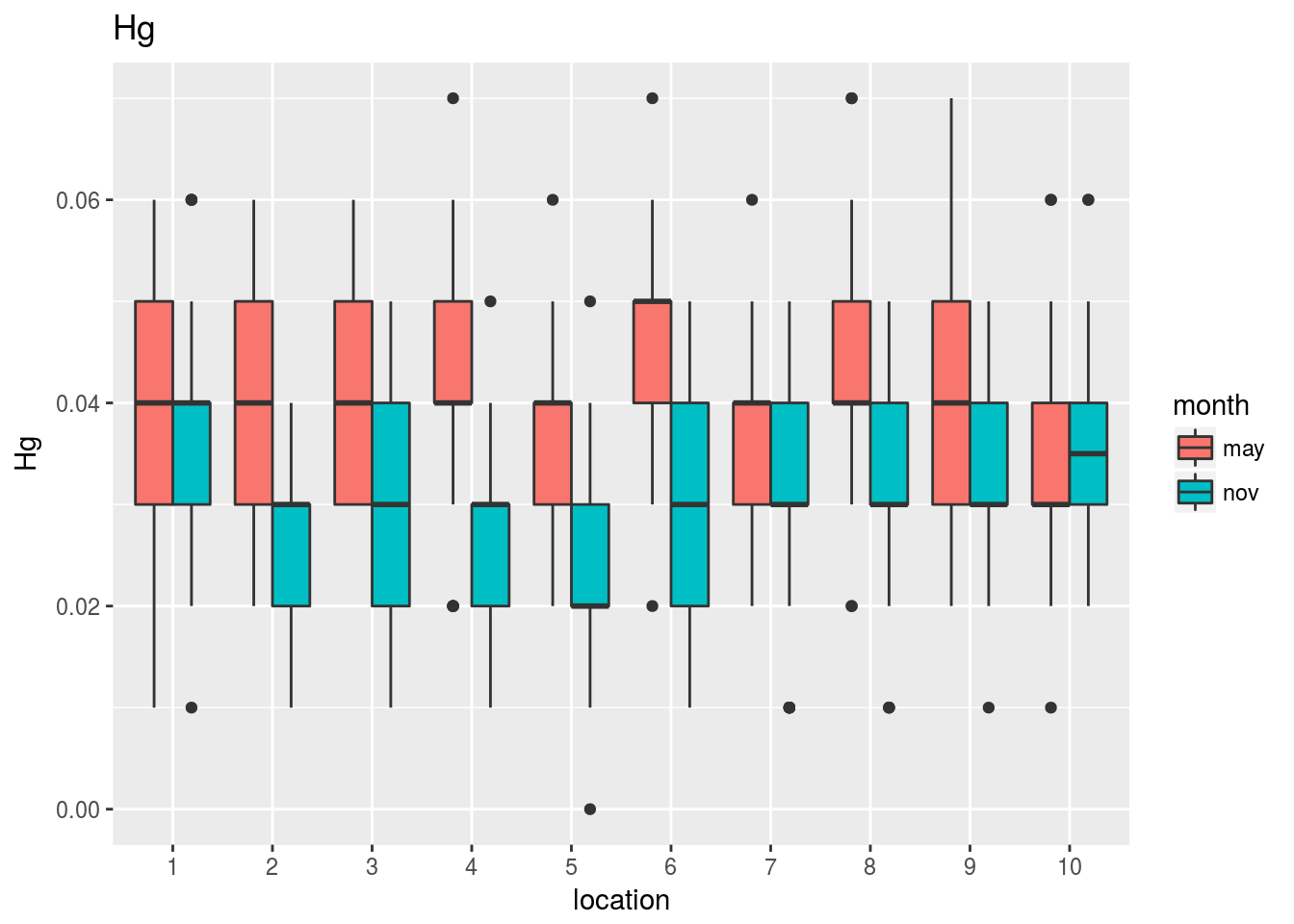
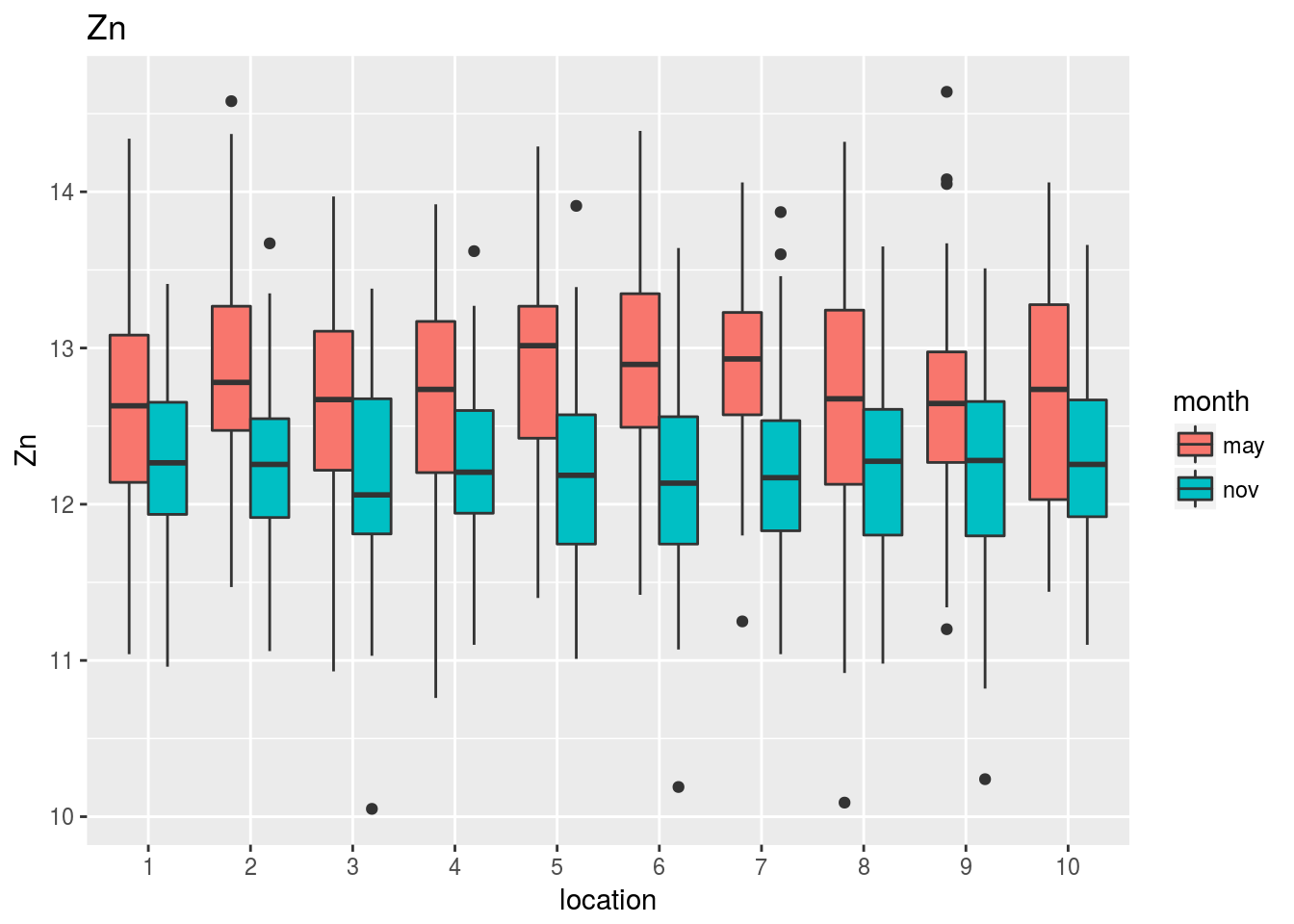
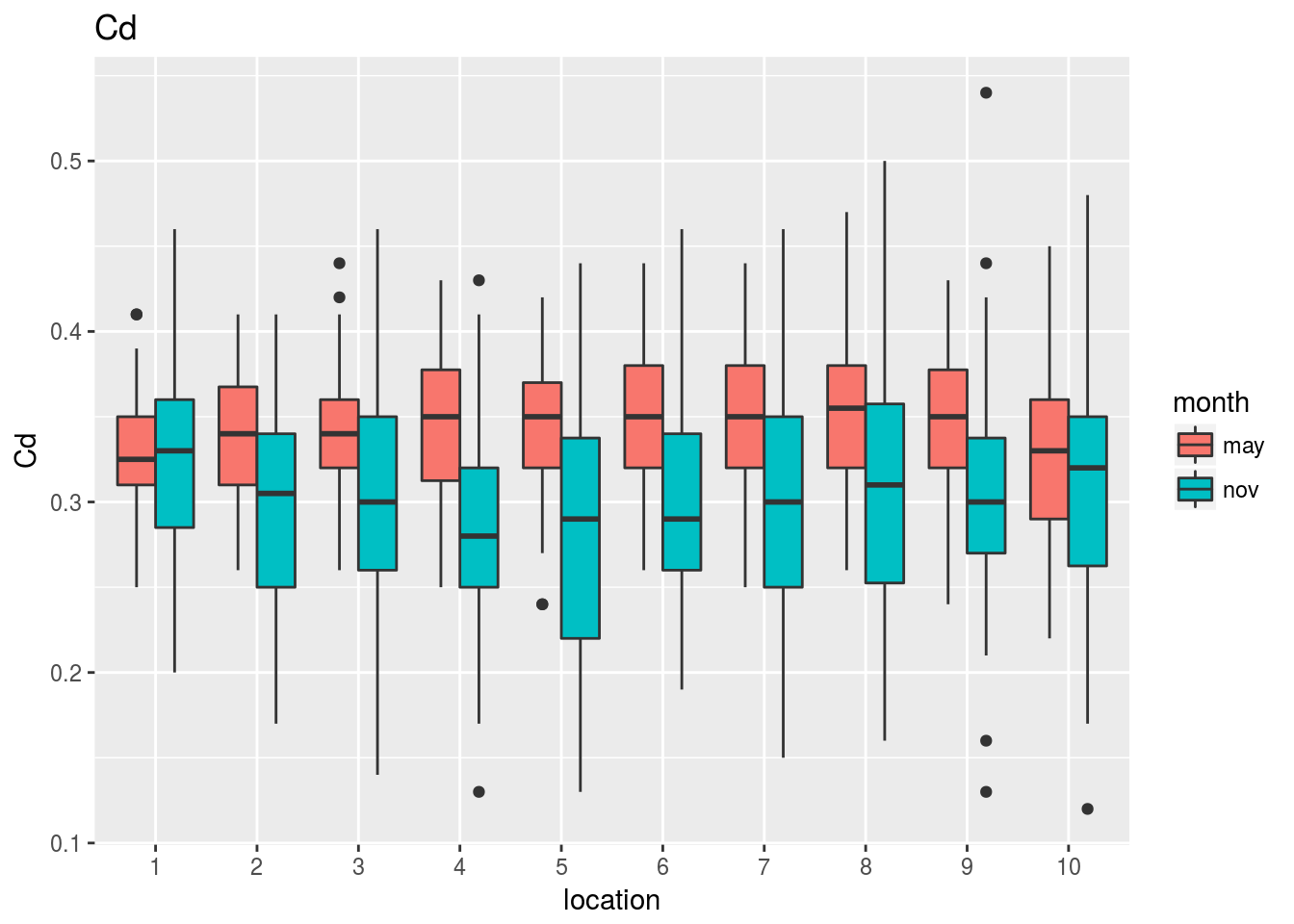
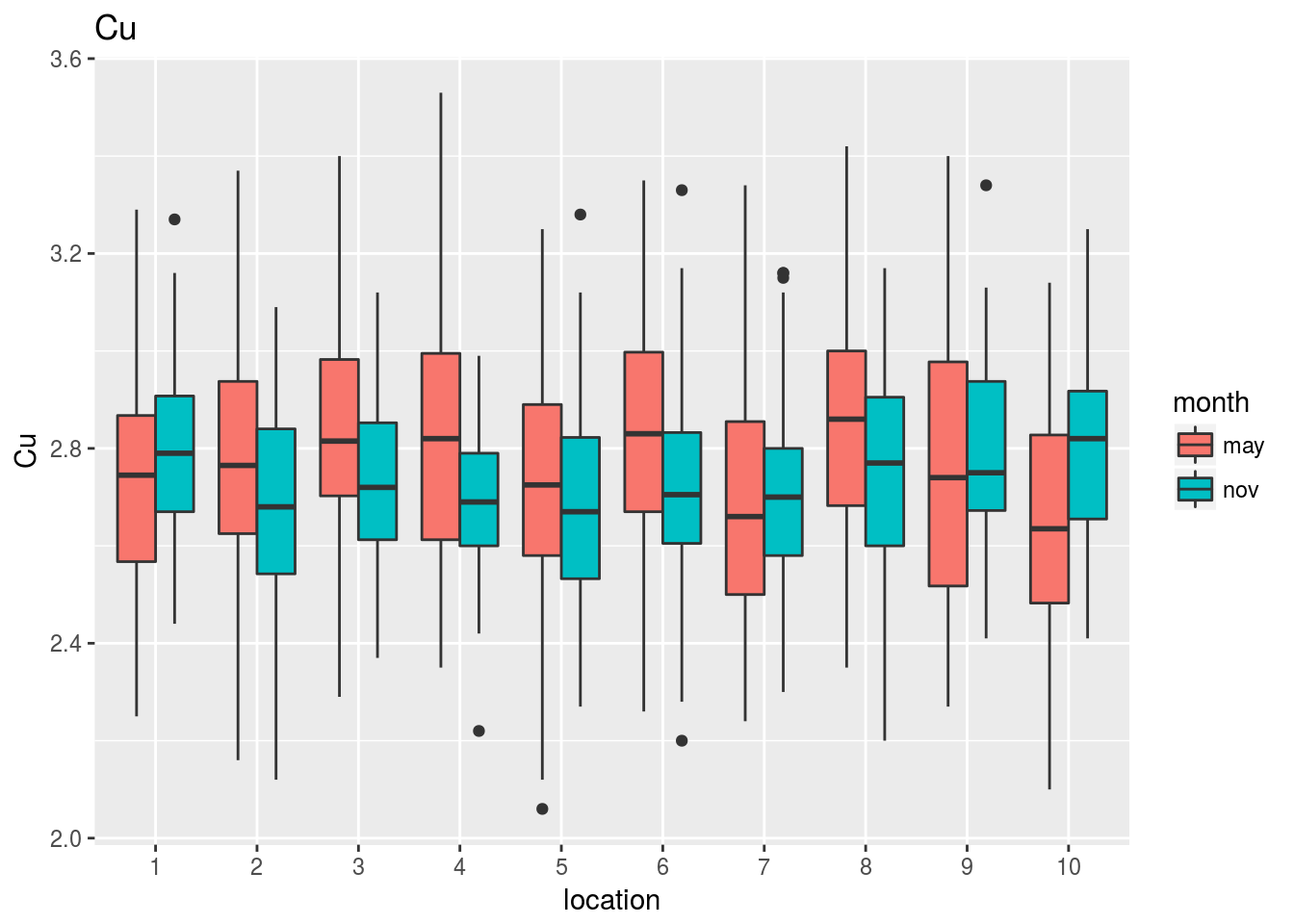
Observando estos gráficos vemos, por ejemplo, que:

• La clorofila mantiene aproximadamente la misma diferencia entre mayo y noviembre cualquiera que sea la localización que se considere. En noviembre la concentración es siempre mayor que en mayo, y no parece haber diferencias en concentración entre localizaciones.

• El PO4 no muestra diferencias notables entre noviembre y mayo ni, aparentemente tampoco entre estaciones.

• La temperatura o el As muestran cambios tanto en la diferencia entre mayo y noviembre como en las diferencias entre estaciones.

• En el Pb no parece haber grandes diferencias entre mayo y noviembre, aunque sí parece que hay algunas localizaciones con mayores niveles de Pb que otras.

 

 

Predicción de la clorofila.

La siguiente tabla nos muestra las correlaciones entre la clorofila y el resto de variables durante el mes de mayo (la clorofila está en la fila 11):

pander(cor(may[,1:17])[11,])

Table continues below

Temperature	pH	DO	NO2	NO3	NH4	DIN	PO4	COD	TSM
-0.1712	-0.1988	-0.3646	0.6013	0.589	0.09777	0.3751	0.2481	0.7621	0.2822

Chla	As	Hg	Zn	Cd	Pb	Cu
1	0.2892	-0.07581	0.2253	-0.05337	0.1098	-0.1231

Asimismo las correlaciones durante el mes de noviembre son

pander(cor(nov[,1:17])[11,])

Table continues below

Temperature	pH	DO	NO2	NO3	NH4	DIN	PO4	COD	TSM
-0.1618	-0.2013	-0.2842	0.5037	0.4825	0.0438	0.2785	0.1685	0.7318	0.2924

Chla	As	Hg	Zn	Cd	Pb	Cu
1	0.3211	-0.057	0.2372	-0.1032	0.0547	-0.1327

Vemos que en ambos meses las correlaciones más altas de la clorofila (mayores que 0.3) se producen con las variables DO, NO2, NO3, DIN y COD. La siguiente función calcula el modelo de regresión para predecir el nivel de clorofila a partir de estas variables durante el mes de mayo:

lm(Chla~DO+NO2+NO3+DIN+COD, data=may)

## 
## Call:
## lm(formula = Chla ~ DO + NO2 + NO3 + DIN + COD, data = may)
## 
## Coefficients:
## (Intercept)           DO          NO2          NO3          DIN  
##     2.15892     -0.15585      0.26820      0.24840     -0.06251  
##         COD  
##     2.41981

Lo mismo durante el mes de noviembre:

lm(Chla~DO+NO2+NO3+DIN+COD, data=nov)

## 
## Call:
## lm(formula = Chla ~ DO + NO2 + NO3 + DIN + COD, data = nov)
## 
## Coefficients:
## (Intercept)           DO          NO2          NO3          DIN  
##      3.2815      -0.2515       0.6206       0.1928      -0.1069  
##         COD  
##      3.6175

Obviamente los valores son distintos: ¿efecto del azar en el muestreo o diferencias significativas entre meses?

La siguiente función nos permite hacer un gráfico tridimensional de la relación de la clorofila con otras dos variables:

library(rgl)
with(may,plot3d(COD,NO2,Chla))

 

Si hubiésemos decidido incluir en el modelo aquellas variables con dan con la clorofila una correlación mayor que 0.25, deberíamos incluir también PO4, TSM y As. En tal caso, los modelos ajustados habrían sido:

lm(Chla~DO+NO2+NO3+DIN+COD+PO4+TSM+As, data=may)

## 
## Call:
## lm(formula = Chla ~ DO + NO2 + NO3 + DIN + COD + PO4 + TSM + 
##     As, data = may)
## 
## Coefficients:
## (Intercept)           DO          NO2          NO3          DIN  
##     0.21484      0.04846      0.25775      0.36422     -0.05421  
##         COD          PO4          TSM           As  
##     2.46472     -2.25512      0.03759     -0.42333

lm(Chla~DO+NO2+NO3+DIN+COD+PO4+TSM+As, data=nov)

## 
## Call:
## lm(formula = Chla ~ DO + NO2 + NO3 + DIN + COD + PO4 + TSM + 
##     As, data = nov)
## 
## Coefficients:
## (Intercept)           DO          NO2          NO3          DIN  
##     0.84065     -0.02439      0.50971      0.31505     -0.08178  
##         COD          PO4          TSM           As  
##     3.62315     -9.00244      0.09521     -0.01337

Nuevamente tenemos valores estimados distintos en ambos modelos, y además los valores estimados en cada variable son distintos de los que se estimaron cuando usamos menos variables. Podemos plantearnos la cuestión ¿Cuál es el mejor modelo para predecir la clorofila? ¿Sobra alguna de las variables que hemos considerado? ¿Habría que añadir alguna de las variables que hemos dejado fuera?

 

 

Una visión global de todos los problemas anteriores.

De modo resumido, los problemas anteriores parecen presentar problemas bastante diferentes:

• Dada una variable continua (e.g. la temperatura) y una o varias variables categóricas (el mes, la localización) ¿existen diferencias en el valor medio de la variable continua según los distintos niveles de las variables categóricas? Este problema se conoce habitualmente como de análisis de la varianza

• Dadas dos variables continuas (e.g. DIN frente a NO2) y una variable categórica (el mes), ¿la relación entre DIN y NO2 es fija o cambia con el mes? . Podríamos incluso extender la pregunta: ¿cambia con la localización? ¿cambia según la combinación de mes y localización? Estos problemas se conocen como de análisis de la covarianza.

• Dadas una variable continua (respuesta), y otra (o varias) variables continuas (explicativas) ¿Cuál es el modelo lineal que mejor permite predecir la respuesta en función de las variables explicativas? ¿Como seleccionar las mejores variables explicativas? Estos problemas entran dentro del marco de la regresión lineal

 

Aunque todos estos problemas parecen tener una naturaleza muy diferente, desde el punto de vista teórico se encuadran dentro del mismo marco conceptual: el modelo lineal

 

 

 

Definición

Un vector de variables aleatorias \(\mathbf{Y}= \left(y_1,y_2,\dots, y_n\right)'\) sigue un modelo lineal si:

\[\mathbf{Y} \cong \mathbf{N_n} \left(\mathbf{X} \beta, \mathbf{I_n}\sigma \right)\]

donde:

• \(\mathbf{X}=\left(\begin{array}{ccccc} 1 & x_{11} & x_{21} & \ldots & x_{p1}\\ 1 & x_{12} & x_{22} & \vdots & x_{p2}\\ 1 & \vdots & \vdots & \ddots\\ 1 & x_{1n} & x_{2n} & \ldots & x_{pn} \end{array}\right)\) es una matriz de dimensión \(n\times p\), cuya columna \(j\)-ésima (j>2) contiene los valores observados en la variable \(X_j\).

 

• \(\beta=\left(\begin{array}{c} \beta_{0}\\ \beta_{1}\\ \vdots\\ \beta_{p} \end{array}\right)\) es un vector de parámetros \(p\)-dimensional.

 

• \(\mathbf{I_{n}}\) es la matriz identidad de orden \(n\).

 

De manera alternativa y equivalente, el modelo lineal puede expresarse como: \[\mathbf{Y=}\beta_{0}+\beta_{1}X_{1}+\beta_{2}X_{2}+\dots+\beta_{p}X_{p}+\varepsilon,\,\,\,\,\,\,\varepsilon\approx N \left(0,\sigma\right)\]

siendo las \(X_j\) las columnas de la matrix \(\mathbf{X}\) anterior.

 

la variable \(\mathbf{Y}\) se conoce habitualmente como variable respuesta y las variables \(\mathbf{X}\) como variables explicativas o predictoras.

 

---

 

Bajo esta definición general se engloban los modelos clásicos de:

• Regresión: La variable \(\mathbf{Y}\) y las \(\mathbf{X}\) son continuas

• Análisis de la varianza: La variable \(\mathbf{Y}\) es continua y las \(\mathbf{X}\) son categóricas.

• Análisis de la covarianza: La variable \(\mathbf{Y}\) es continua y entre las \(\mathbf{X}\) hay variables categóricas y variables continuas

 

---

 

Cuando en este modelo la distribución normal se cambia por otra distribución y la relación entre la \(\mathbf{Y}\) y las \(\mathbf{X}\) es lineal a través de una función de enlace \(f\), nos encontramos ante los modelos lineales generalizados:

• Regresión logística Binaria: La variable \(\mathbf{Y}\) es dicotómica y las \(X_i\) pueden ser categóricas y/o continuas. La distribución de \(\mathbf{Y}\) es binomial, \[\mathbf{Y} \cong \mathbf{B} \left(N,f(\mathbf{X} \beta)\right)\]

• Regresión de Poisson: La variable \(\mathbf{Y}\) es una variable de recuento y las \(X_i\) pueden ser categóricas y/o continuas. La distribución de \(\mathbf{Y}\) es de Poisson, \[\mathbf{Y} \cong \mathbf{P} \left(f(\mathbf{X} \beta)\right)\]

 

 

Cuando la relación entre la \(\mathbf{Y}\) y las \(\mathbf{X}\) es de la forma: \[Y=f_{1} \left(X_{1}\right)+f_{2}\left(X_{2}\right)+\dots f_{p}\left(X_{p}\right)+\varepsilon\] nos encontramos ante los modelos aditivos generalizados (GAM).

 

 

Estimación del modelo lineal

El modelo lineal para predecir (o explicar) la variable respuesta \(\mathbf{Y}\) en función de la matriz de variables explicativas \(\mathbf{X}\) puede estimarse por dos métodos:

• Mínimos cuadrados: Este método puede aplicarse siempre y consiste en encontrar los valores de los parámetros \(\beta_i\) que minimizan la distancia entre los valores observados y los predichos.

• Máxima verosimilitud: Este método sólo es de aplicación cuando las observaciones son independientes y las distancias de los puntos al modelo (residuos) siguen una distribución normal. Cuando estas condiciones se cumplen, el método de máxima verosimilitud y el de mínimos cuadrados producen los mismos estimadores.

Sólo en el caso de que los residuos del modelo sean normales e independientes puede llevarse a cabo adecuadamente la inferencia clásica sobre los parámetros del modelo.

Los estimadores de los parámetros, utilizando cualquiera de los dos métodos anteriores, se obtienen mediante:

\[ \hat{\beta} = \left(X^{t}X\right)^{-1}X^{t}Y\]

\[\hat{\sigma}^{2}=\frac{1}{n-p}\sum_{i=1}^{n}\left(y_{i}-\hat{y_{i}}\right)^{2}=\frac{1}{n-p}\sum_{i=1}^{n}\left(y_{i}-X_{i}\hat{\beta}\right)^{2}=\frac{1}{n-p}\left(\mathbf{Y-X}\hat{\beta}\right)^{t}\left(\mathbf{Y-X}\hat{\beta}\right)\]

La matriz de covarianzas de los estimadores de \(\beta_i\) es:

\[\textrm{Var}\left(\hat{\beta}\right)=\hat{\sigma}^{2}\left(X^{t}X\right)^{-1}\]

La raiz cuadrada de la diagonal de esta matriz nos proporciona los errores estándar de los \(\beta_i\), que permiten construir contrastes e intervalos de confianza para estos parámetros. Concretamente, si llamamos \(\hat{\sigma}_{\beta_{i}}\) al error estándar del parámetro \(\beta_i\), puede obtenerse un intervalo de confianza a nivel \(1-\alpha\) para dicho parámetro mediante: \[\left[\hat{\beta}_{i}\pm t_{n-p,1-\alpha/2}\hat{\sigma}_{\beta_{i}}\right]\]