bootstrap
Angelo Santana
25 de septiembre de 2017
# Lectura de datos
library(readxl)
costa=read_excel("datos/coast.xlsx")
algae=read_excel("datos/algae.xlsx")Bootstrap para la construcción de intervalos de confianza
La idea detrás del método bootstrap es replicar el comportamiento de la distribución de los datos disponibles; para ello se lleva a cabo un muestreo con reemplazamiento sobre dichos datos.
A continuación se muestra el histograma de los valores de pH registrados en el archivo algae.xlsx, al que se le ha superpuesto una estimación de la función de densidad correspondiente a dichos datos así como la densidad de una distribución normal con la media y desviación típica de esta variable:
library(ggplot2)
rangePH=seq(min(algae$mxPH,na.rm=TRUE),max(algae$mxPH,na.rm=TRUE),length=200)
normalCurve=dnorm(rangePH,mean=mean(algae$mxPH,na.rm=TRUE),sd=sd(algae$mxPH,na.rm=TRUE))
normalDensity=data.frame(rangePH,normalCurve)
ggplot(algae,aes(x=mxPH)) +
geom_histogram(aes(y=..density..),fill="cyan3") + # Histograma en frecuencias relativas
geom_density(col="red4", size=1.2, alpha=0.1) + # Densidad estimada
geom_line(data=normalDensity, aes(x=rangePH,y=normalCurve),
col="blue4",linetype=2, size=1.2) + # Densidad bajo la hipótesis de normalidad
scale_colour_manual("",breaks=c("Empirical Density","Normal Density"),
values=c("red4","blue4"))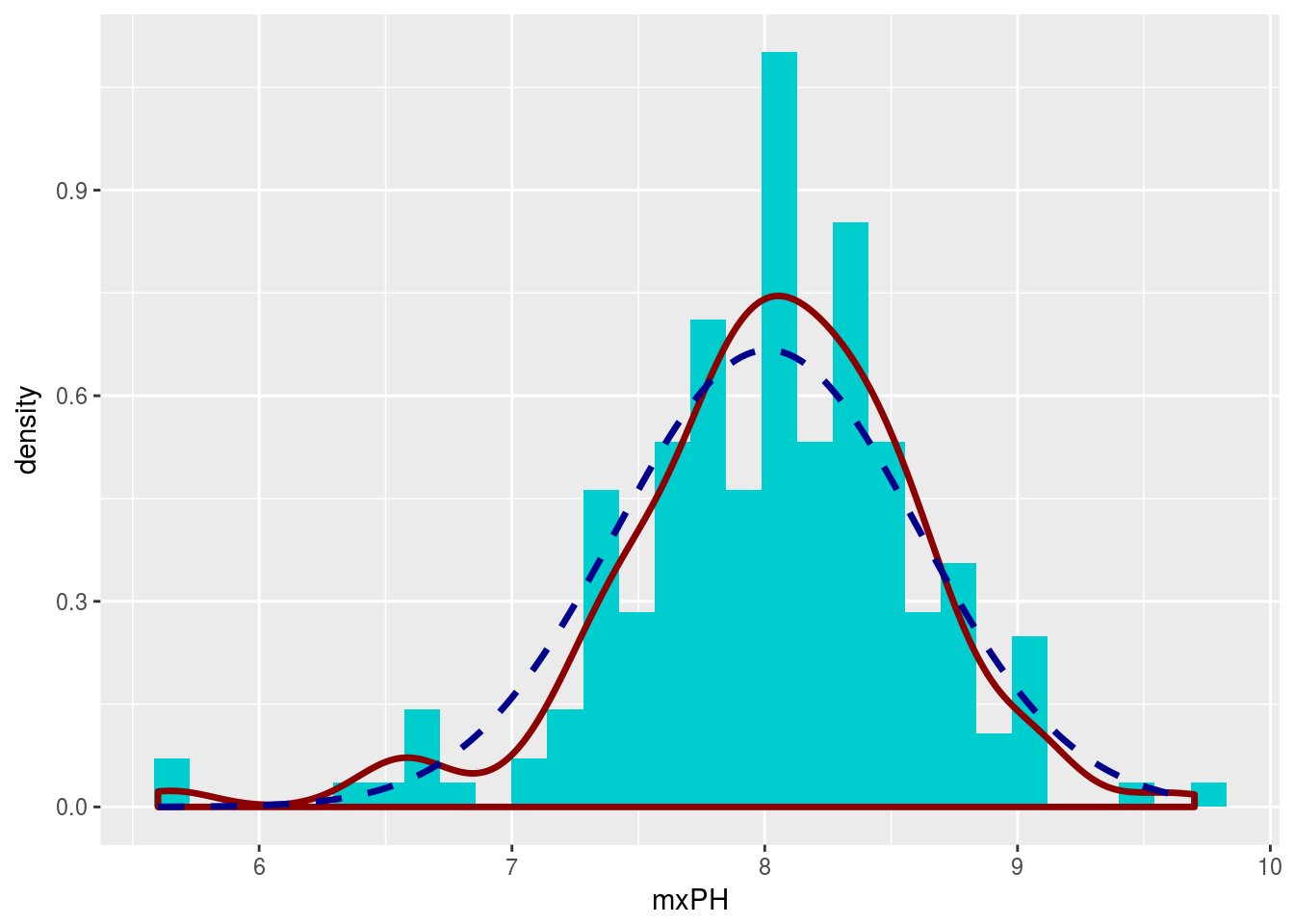
Como puede apreciarse, la densidad empírica y la normal son diferentes; de hecho si llevamos a cabo un test de Shapiro-Wilk para contrastar la normalidad de esta variable, comprobamos que no puede aceptarse la hipótesis de normalidad:
shapiro.test(algae$mxPH)##
## Shapiro-Wilk normality test
##
## data: algae$mxPH
## W = 0.96247, p-value = 3.865e-05Si los datos fuesen normales, sería adecuado el intervalo calculado por el procedimiento de la t de Student:
t.test(algae$mxPH)$conf.int## [1] 7.928095 8.095372
## attr(,"conf.level")
## [1] 0.95En ausencia de normalidad podemos utilizar un algoritmo bootstrap para obtener B estimaciones de la media, basadas en B muestras obtenidas por remuestreo sobre la muestra original:
mediaBootstrap=function(x){ # Esta función realiza el remuestreo y calcula la media
muestra.Boot=sample(na.omit(x),replace=TRUE)
return(mean(muestra.Boot))
}
B=2000
medias=replicate(B,mediaBootstrap(algae$mxPH))
ggplot(data.frame(medias=medias),aes(x=medias)) + geom_histogram()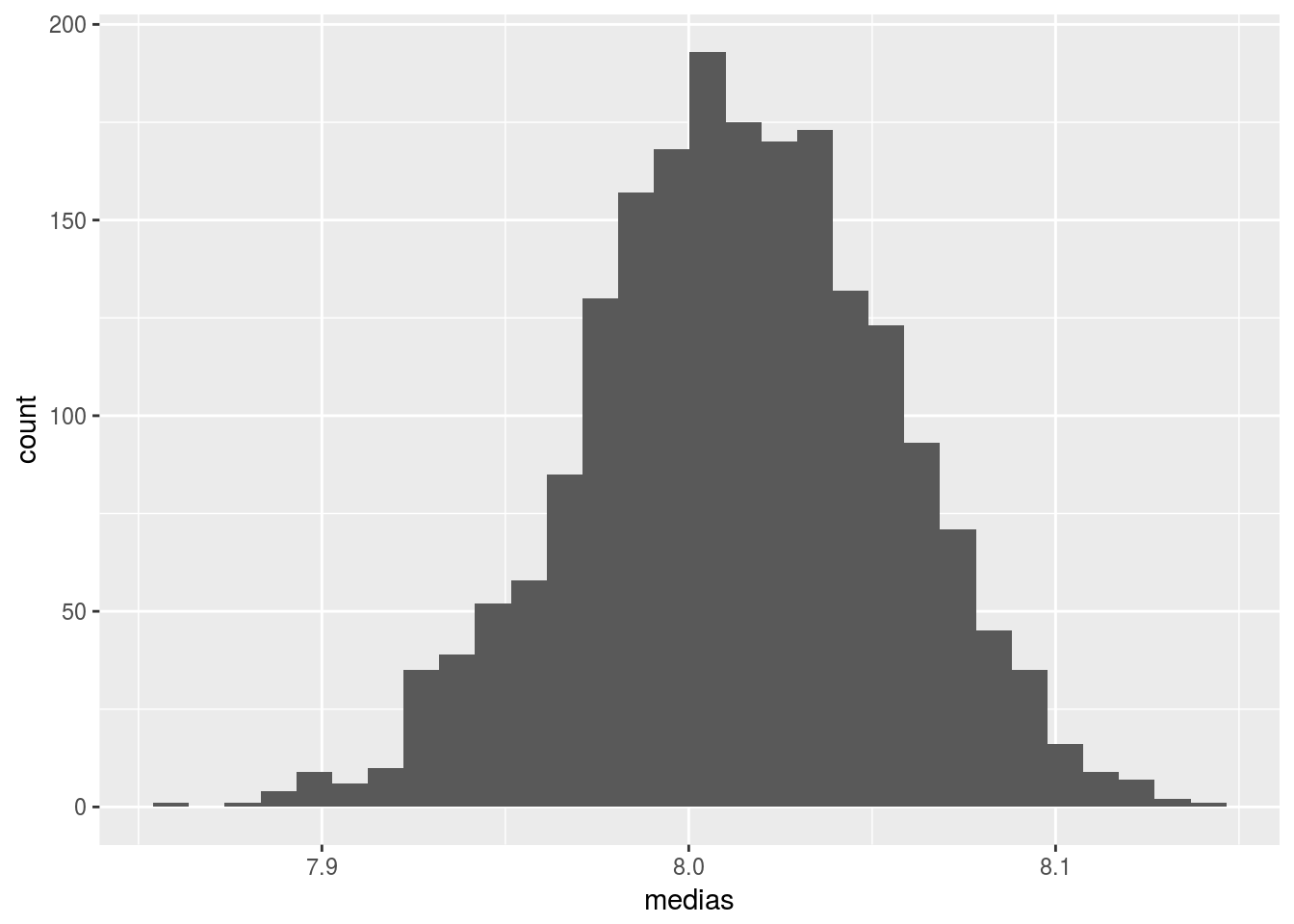
Obtenemos los percentiles 2.5 y 97.5:
extremos=quantile(medias,probs=c(0.025,0.975))
extremos## 2.5% 97.5%
## 7.929019 8.093795Podemos hacer un último ajuste para forzar a que el centro del intervalo boostrap coincida con la media de la muestra original que, como vemos, no son iguales:
mean(medias)## [1] 8.012919mean(algae$mxPH,na.rm=TRUE)## [1] 8.011734El ajuste sería el siguiente:
medias=medias-mean(medias)+mean(algae$mxPH,na.rm=TRUE)
mean(medias)## [1] 8.011734y el intervalo de confianza bootstrap definitivo:
boot.interval=quantile(medias,probs=c(0.025,0.975))
boot.interval## 2.5% 97.5%
## 7.927834 8.092609Podemos compararlo con el que calculamos inicialmente con el t-test:
t.test(algae$mxPH)$conf.int## [1] 7.928095 8.095372
## attr(,"conf.level")
## [1] 0.95Como vemos, ambos intervalos son muy parecidos; ello se debe fundamentalmente a dos razones:
A que en este caso, la distribución de mxPH aunque no es normal, tampoco se aleja mucho de la normalidad (en particular de la simetría).
A que el tamaño de la muestra es grande (n=200) y el teorema central del límite garantiza que la distribución de la media muestral será aproximadamente normal aunque la variable cuya media se está calculando no lo sea.
En R el paquete boot permite “acelerar” el cálculo de los estimadores bootstrap, aunque su uso no se diferencia mucho de lo que hemos hecho más arriba; esta función ofrece además cuatro estimadores bootstrap distintos (el que hemos calculado arriba es el bootstrap percentil):
library(boot)
boot.mean=function(x,indices)
mean(x[indices],na.rm=TRUE)
mx=boot(algae$mxPH,boot.mean,2000)
boot.ci(mx)## BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
## Based on 2000 bootstrap replicates
##
## CALL :
## boot.ci(boot.out = mx)
##
## Intervals :
## Level Normal Basic
## 95% ( 7.930, 8.095 ) ( 7.930, 8.096 )
##
## Level Percentile BCa
## 95% ( 7.927, 8.093 ) ( 7.925, 8.092 )
## Calculations and Intervals on Original Scale
Contrastes de hipótesis. Contraste sobre una media
La metodología bootstrap puede utilizarse también para llevar a cabo contrastes de hipótesis. Para ello deberemos replicar la distribución empírica del estadístico de contraste bajo el supuesto de que la hipótesis nula sea cierta, obteniendo B observaciones de dicho estadístico. Dependiendo de la dirección de la hipótesis nula:
Podemos comprobar si el valor observado del estadístico de contraste cae dentro del intervalo de los valores esperables cuando \(H_0\) es cierta, en cuyo caso aceptamos dicha hipótesis; en caso contrario se rechazaría.
También podemos calcular el p-valor del contraste como la proporción de valores bootstrap más extremos que el valor observado del estadístico de contraste; si este p-valor es grande (mayor que \(\alpha\), el nivel de significación que hayamos elegido, habitualmente 0.05), aceptamos \(H_0\) pues el valor observado no es demasiado extremo cuando \(H_0\) es cierta; en caso contrario rechazamos \(H_0\)
Ejemplo
Queremos determinar si existe evidencia suficiente de que el valor medio (poblacional) de \(O_2\) es mayor que 8.5 \(\mu\)gr/litro. El contraste a llevar a cabo es de la forma:
\[\begin{cases} H_{0}: & \mu\le8.5\\ H_{1} & \mu>8.5 \end{cases}\]
Los datos disponibles indican que el valor medio observado de oxígeno disuelto es:
mean(algae$mnO2,na.rm=TRUE)## [1] 9.117778con una desviación típica
sd(algae$mnO2,na.rm=TRUE)## [1] 2.391253Si la distribución de esta variable fuese normal, el resultado del contraste sería el siguiente:
t.test(algae$mnO2,mu=8.5,alternative="greater")##
## One Sample t-test
##
## data: algae$mnO2
## t = 3.6353, df = 197, p-value = 0.0001772
## alternative hypothesis: true mean is greater than 8.5
## 95 percent confidence interval:
## 8.836932 Inf
## sample estimates:
## mean of x
## 9.117778lo que significa que los datos contienen evidencia suficiente para asegurar (con una significación o riesgo de error tipo I de 0.05) que el valor medio polbacional de \(O_2\) efectivamente supera los 8.5 \(\mu\)gr/litro.
Ahora bien, la gráfica de los datos apunta a que en este caso tampoco es creíble la normalidad:
library(ggplot2)
rangePH=seq(min(algae$mnO2,na.rm=TRUE),max(algae$mnO2,na.rm=TRUE),length=200)
normalCurve=dnorm(rangePH,mean=mean(algae$mnO2,na.rm=TRUE),sd=sd(algae$mnO2,na.rm=TRUE))
normalDensity=data.frame(rangePH,normalCurve)
ggplot(algae,aes(x=mnO2)) +
geom_histogram(aes(y=..density..),fill="cyan3") + # Histograma en frecuencias relativas
geom_density(col="red4", size=1.2, alpha=0.1) + # Densidad estimada
geom_line(data=normalDensity, aes(x=rangePH,y=normalCurve),
col="blue4",linetype=2, size=1.2) + # Densidad bajo la hipótesis de normalidad
scale_colour_manual("",breaks=c("Empirical Density","Normal Density"),
values=c("red4","blue4"))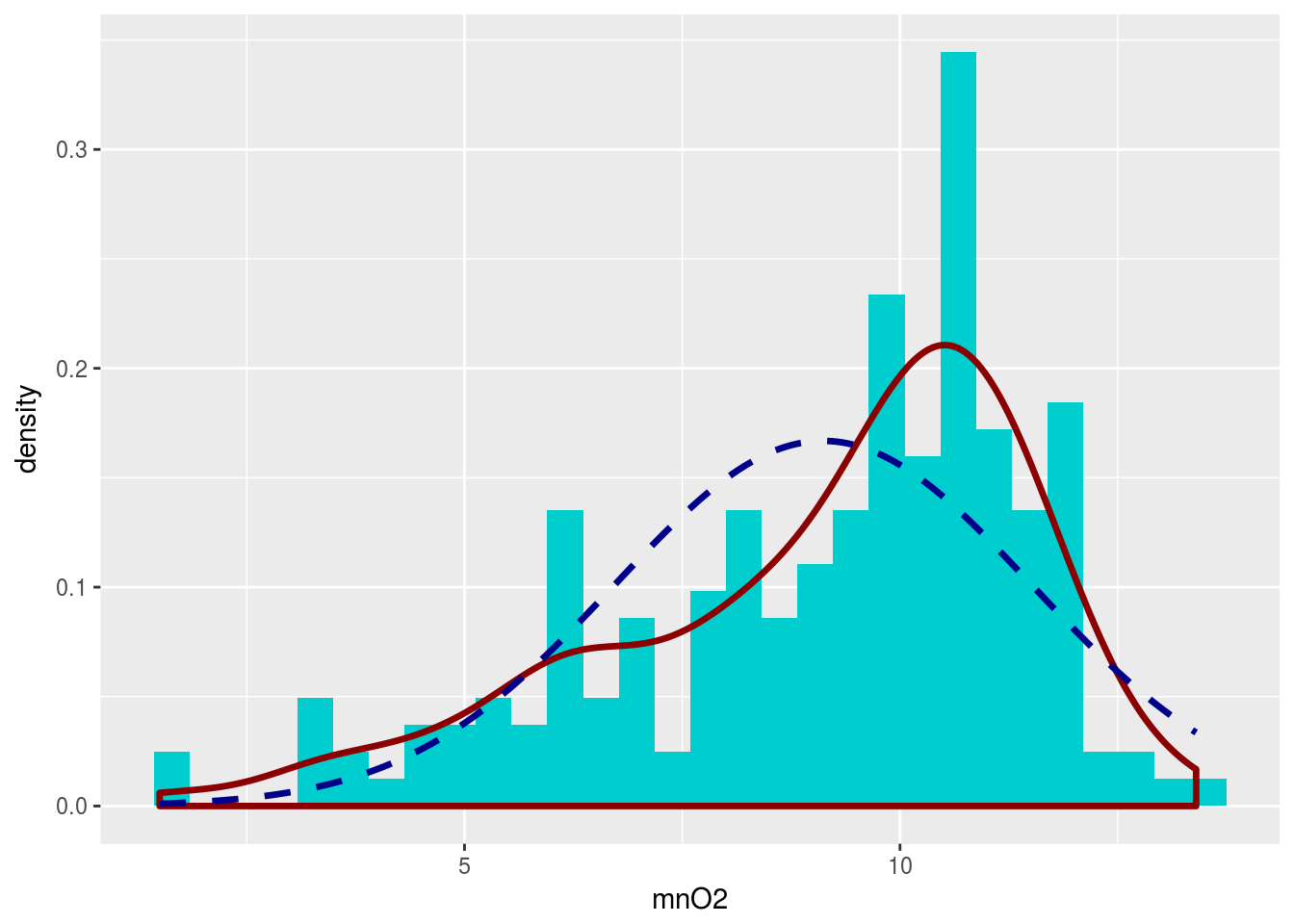
El estadístico de contraste utilizado en el t-test es de la forma:
\[\frac{\overline{X}-\mu_{0}}{s_{x}/\sqrt{n}}\]
siendo \(\mu_0\) la media poblacional supuesta (en nuestro ejemplo 8.5), \(\overline{X}\) la media de la muestra, \(s_x\) su desviación típica y \(n\) el tamaño de la muestra. Cuando la variable de partida (la concentración de \(O_2\) en este caso) es normal, este estadístico sigue una distribución t de Student y las tablas de dicha distribución permiten determinar si el valor observado es o no demasiado extremo. Cuando no es normal (como parece en este caso), la referencia de la t de Student puede no ser adecuada. El método bootstrap procedería del siguiente modo:
Calcular la media muestral \(\overline{X}\) de los datos.
Calcular el valor \(t_{exp}=\frac{\overline{X}-\mu_{0}}{s_{x}/\sqrt{n}}\) a partir de los datos disponibles.
Extraer con reemplazamiento una muestra de tamaño \(n\) a partir de la muestra original. Calcular \(\overline{Y}\) la media de la muestra bootstrap
Dado que la muestra original funciona como “población”, calcular el valor del estadístico \(t\) en la muestra bootstrap: \[t_{b}=\frac{\overline{Y}-\overline{X}}{s_{y}/\sqrt{n}}\]
Repetir los pasos 3-4, B veces (siendo B algún valor entre 100 y 10000), guardando en cada iteración el valor \(t_b\) obtenido; de esta forma obtenemos una aproximación bootstrap de la distribución de \(t\)
Calcular el p-valor del test. Como en este caso la hipótesis nula es que \(\mu\le 8.5\), lo que no es esperable es que la diferencia \(\mu-8.5\) sea muy grande; en otras palabras, si \(H_0\) es cierta, los valores extremos son los valores grandes del estadístico \(t\). Dado que el valor observado es \(t_{exp}\), podemos calcular la probabilidad de observar un valor más extremo que éste contando cuántos de los valores \(t_b\) obtenidos por remuestreo son mayores que \(t_{exp}\). Sea \(N_{ext}\) el número de dichos valores; el p-valor es entonces \(p=N_{ext}/B\)
Si \(p\ge\alpha\), se acepta \(H_0\); en caso contrario, se rechaza.
Este algoritmo se puede implementar fácilmente en R:
# step 1:
x=na.omit(algae$mnO2)
mX=mean(x)
# step 2:
t.exp=(mX-8.5)/(sd(x)/sqrt(length(x)))
# steps 3-4:
tb=function(x){
y=sample(x,replace=TRUE)
return((mean(y)-mX)/(sd(y)/sqrt(length(y))))
}
# step 5
B=5000
distribT=replicate(B,tb(x))
# step 6:
N.extreme=sum(distribT>t.exp) # o también length(which(distribT>t.exp))
p.value=N.extreme/B
sprintf("p-value = %.4f",p.value)## [1] "p-value = 0.0008"Por tanto, rechazamos que \(\mu\le8.5\)
Contrastes de hipótesis. Contraste sobre dos medias
library(plyr)
temp=seq(min(costa$Temperature),max(costa$Temperature),length=100)
normalDens<-ddply(costa,"month", function(df){
data.frame(temp=temp,
normalCurve=dnorm(temp,mean(df$Temperature),sd(df$Temperature)))
})
ggplot(costa,aes(x=Temperature,fill=month)) + geom_histogram(aes(y=..density..), alpha=0.4) +
facet_grid(month~. ) +
geom_density(alpha=0,aes(col=month), size=1.3) +
geom_line(data=normalDens, aes(x=temp,y=normalCurve,fill=month),
col="grey20",linetype=2, size=1.2)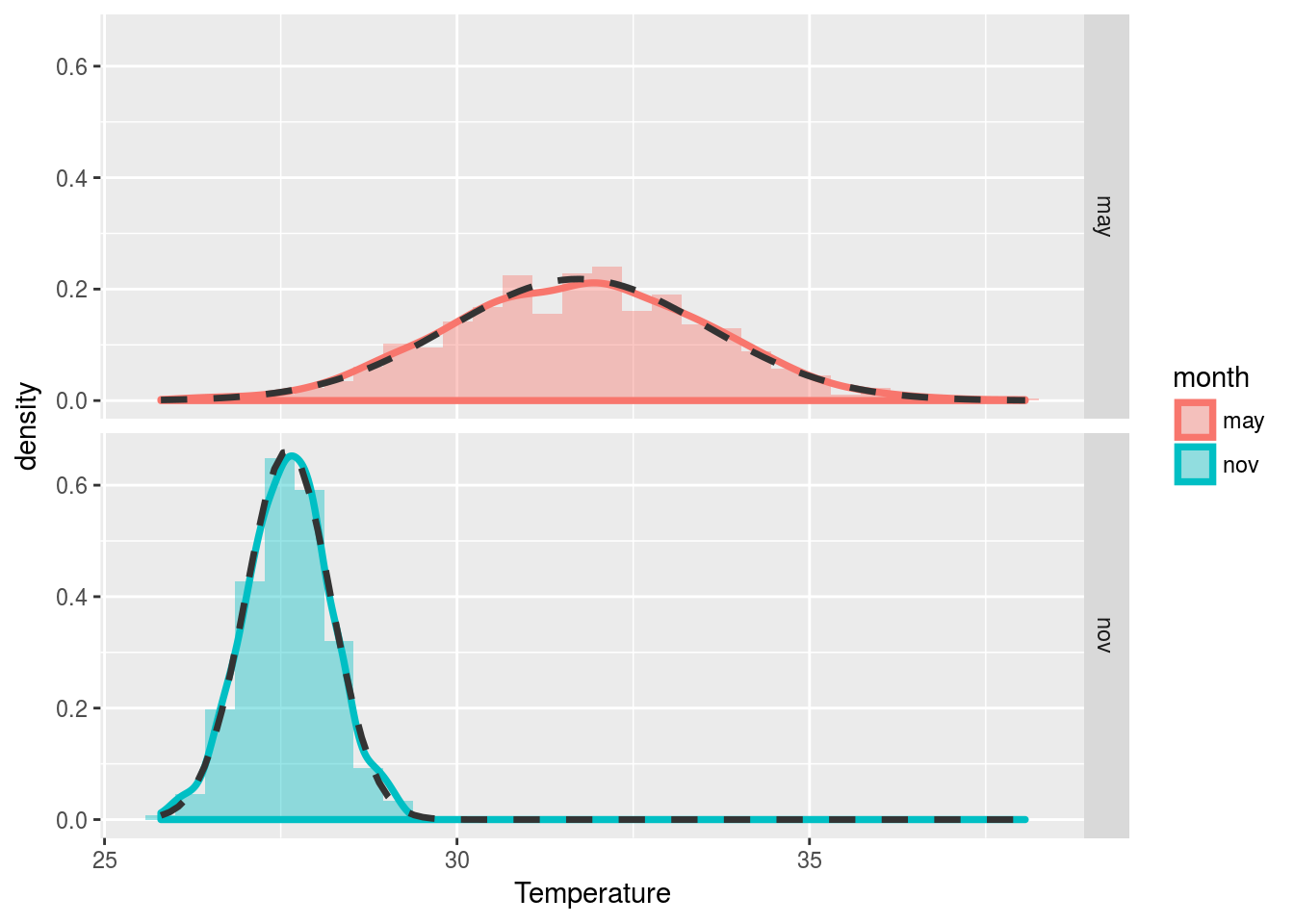
La hipótesis nula especifica que las medias son iguales. Hacemos remuestreo bootstrap bajo esta hipótesis:
tempMay=costa$Temperature[costa$month=="may"]
tempNov=costa$Temperature[costa$month=="nov"]
t.exp=t.test(Temperature~month,costa)$statistic
globalMean=mean(costa$Temperature,na.rm = TRUE)
# Se fuerza a que las dos distribuciones tengan la misma media (H0)
tempMay=tempMay-mean(tempMay)+globalMean
tempNov=tempNov-mean(tempNov)+globalMean
simDifMedias=function(x,y){
m1=sample(x,size=length(x),replace=TRUE)
m2=sample(y,size=length(y),replace=TRUE)
t.test(m1,m2)$statistic
}
B=2000
distribT=replicate(B,simDifMedias(tempMay,tempNov))
quantile(distribT,probs=c(0.025,0.975))## 2.5% 97.5%
## -2.000773 1.955477p.h0 <- sum(abs(distribT) > abs(t.exp)) / B #
p.h0## [1] 0
Bootstrap para Regresion
library(MASS)
datos=data.frame(mvrnorm(123,mu=c(0,0),Sigma=cbind(c(1,0.87),c(0.87,1))))
names(datos)=c("x","y")
datos$x=12+3*datos$x
datos$y=34+5*datos$y
plot(datos)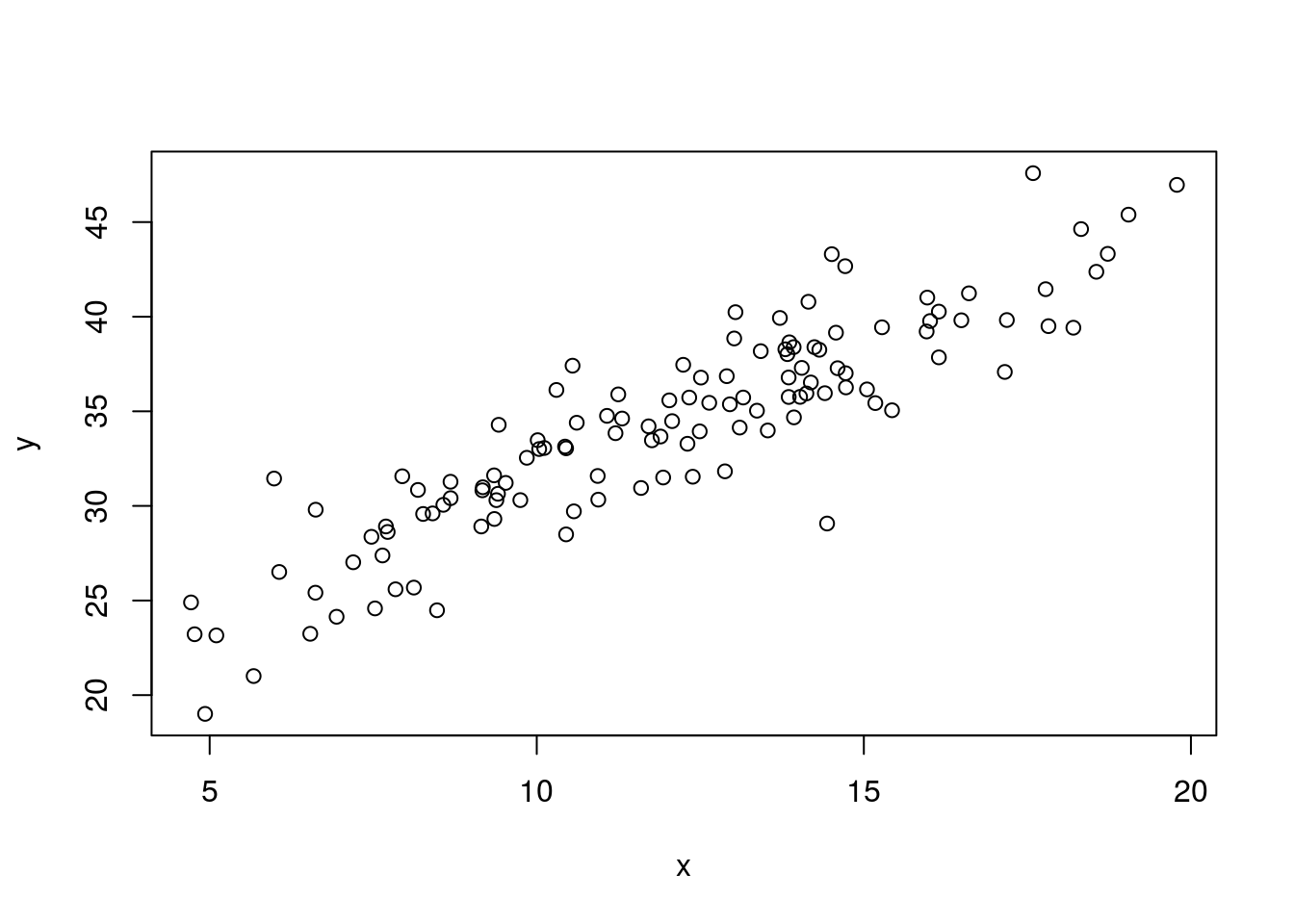
cor(datos)## x y
## x 1.0000000 0.8987603
## y 0.8987603 1.0000000lm(y~x,datos)##
## Call:
## lm(formula = y ~ x, data = datos)
##
## Coefficients:
## (Intercept) x
## 17.332 1.405confint(lm(y~x,datos))## 2.5 % 97.5 %
## (Intercept) 15.796694 18.866428
## x 1.281656 1.528372Intervalo bootstrap para la pendiente de la regresión
simreg=function(){
nn=sample(1:nrow(datos),replace=TRUE)
lm(y~x,datos[nn,])$coefficients[2]
}
cfx=replicate(2000,simreg())
hist(cfx)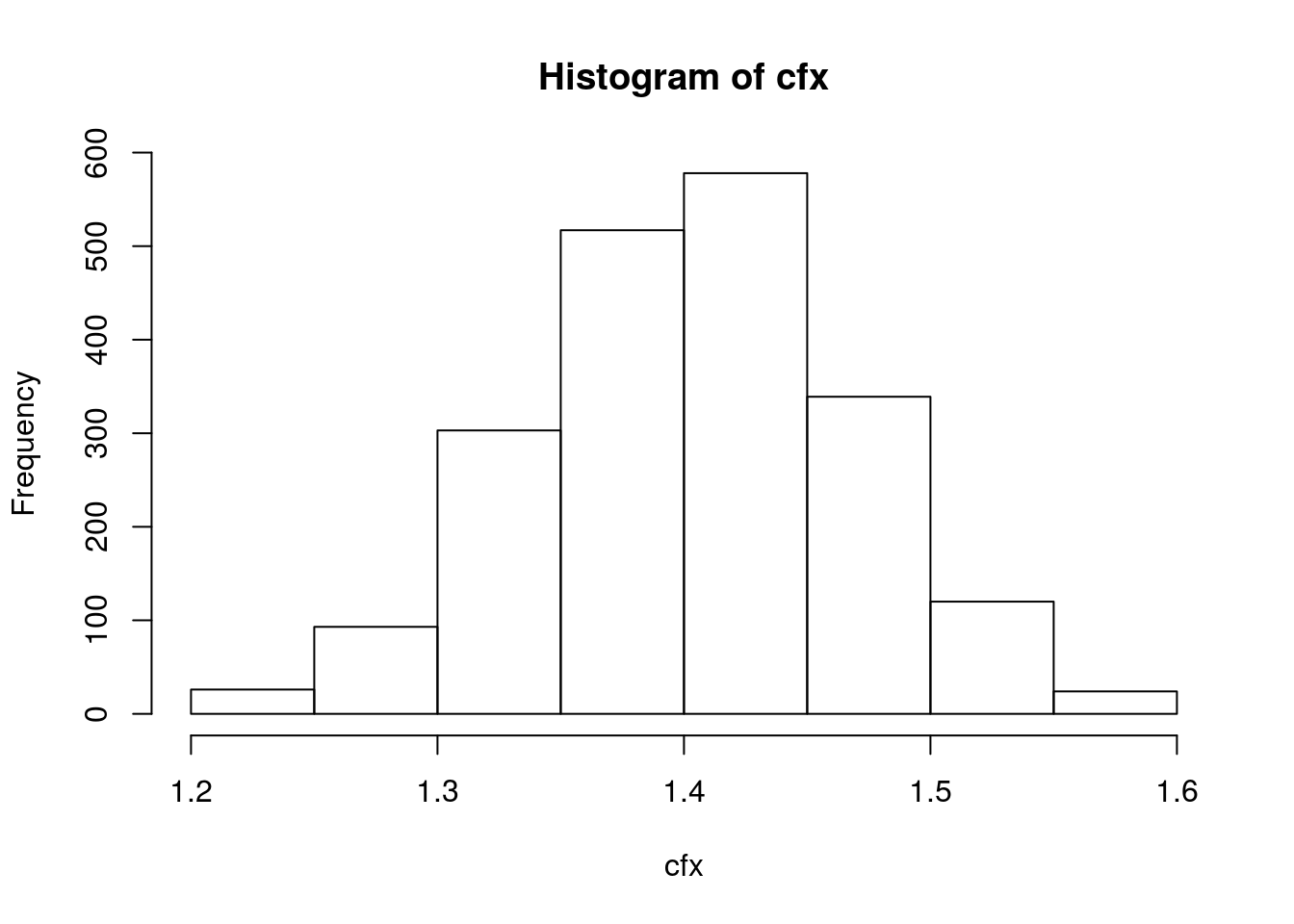
quantile(cfx,probs=c(0.025,0.975))## 2.5% 97.5%
## 1.271806 1.529036