Modelos lineales generalizados: Regresión
logística
Angelo Santana
MEDIDAS DE ASOCIACIÓN ENTRE VARIABLES CUALITATIVAS
Probabilidad
condicionada e independencia de sucesos
Para un suceso \(A\) tal que \(Pr\left( A \right) > 0\), la
probabilidad de otro suceso \(B\)
condicionada por \(A\) se define
por:
\[Pr\left(\textrm{B}\left|\textrm{A}\right.\right)=\frac{Pr\left(\textrm{A}\cap\textrm{B}\right)}{Pr\left(\textrm{A}\right)}\]
Dos sucesos \(A\) y \(B\) se dicen
independientes si:
\[Pr\left(\textrm{B}\left|A\right.\right)=Pr\left(B\right)\]
En caso contrario \(A\) y \(B\) están asociados. ¿Cómo medir la fuerza
de la asociación?
PROBABILIDAD: Ejemplo
En los últimos años se han detectado problemas de piel en los
delfines. Se ha realizado una campaña y se han capturado 1030 delfines.
Se sospecha que la presencia de cierto contaminante en el agua puede
estar asociada con la presencia de lesiones en la piel de los
delfines:

Para cada delfín se ha anotado si el contaminante está presente o no
en su hábitat natural. La tabla siguiente muestra los datos
disponibles:
|
|
LP
|
|
|
Contaminacion
|
Total (1030)
|
Sí (128)
|
No (902)
|
p (Chi-Square)
|
|
Sí
|
324 (31.46%)
|
83 (64.84%)
|
241 (26.72%)
|
<0.0001
|
|
No
|
706 (68.54%)
|
45 (35.16%)
|
661 (73.28%)
|
|
De esta tabla deducimos:
\[
Pr\left(LP\right)=\frac{128}{1030}=0.124 \;\;\;\;\;\;\;
Pr\left(C\right)=\frac{324}{1030}=0.314 \]
\[Pr\left(\textrm{LP}\left|\textrm{C}\right.\right)=\frac{N\left(\mathrm{LP}\cap\mathrm{C}\right)}{N\left(\mathrm{C}\right)}=\frac{83}{83+241}=\frac{83}{324}=0.256\]
\[Pr\left(\textrm{C}\left|\textrm{LP}\right.\right)=\frac{N\left(\mathrm{LP}\cap\mathrm{C}\right)}{N\left(\mathrm{LP}\right)}=\frac{83}{83+45}=\frac{83}{128}=0.648\]
Asociación entre eventos: Riesgo Relativo (RR)
La asociación entre dos sucesos puede
medirse mediante el riesgo
relativo, definido como:
\[RR=\frac{P\left(B\left|A\right.\right)}{P\left(B\left|A^{c}\right.\right)}\]
(\(A^c\) es el suceso contrario de
\(A\))
Nótese que:
RR = 1 : No hay asociación
RR > 1 : La ocurrencia de A incrementa la probabilidad de B.
(riesgo)
RR < 1 : La ocurrencia de A disminuye la probabilidad de B.
(protección)
Asociación entre eventos: Riesgo Relativo (RR)
El RR como medida de asociación no es una
medida simétrica: no es lo mismo el riesgo relativo de B
según la presencia/ausencia de A que el riesgo relativo de A según la
presencia/ausencia de B.
Veamos un ejemplo:
Asociación entre eventos: Riesgo Relativo (RR)
|
|
Contaminacion
|
|
|
LP
|
Total (1030)
|
Sí (324)
|
No (706)
|
p (Chi-Square)
|
|
Sí
|
128 (12.43%)
|
83 (25.62%)
|
45 (6.37%)
|
<0.0001
|
|
No
|
902 (87.57%)
|
241 (74.38%)
|
661 (93.63%)
|
|
\[P\left(LP\left|C\right.\right)=0.2562
\;\;\;\;\;\;\;\;\;\;\;
P\left(LP\left|{C}^c\right.\right)=0.0637\]
El riesgo relativo de padecer lesiones de la piel (LP)
cuando el delfín está expuesto a Contaminacion (C) es
entonces:
\[
RR=\frac{P\left(LP\left|C\right.\right)}{P\left(LP\left|{C}^{c}\right.\right)}=\frac{0.2562}{0.0637}=4.02\]
El riesgo de padecer LP es 4 veces más alto entre los delfines
expuestos al contaminante.
Asociación entre eventos: Riesgo Relativo (RR)
|
|
Contaminacion
|
|
|
LP
|
Total (1030)
|
Sí (324)
|
No (706)
|
p (Chi-Square)
|
|
Sí
|
128 (12.43%)
|
83 (25.62%)
|
45 (6.37%)
|
<0.0001
|
|
No
|
902 (87.57%)
|
241 (74.38%)
|
661 (93.63%)
|
|
\[P\left(C\left|LP\right.\right)=0.6484
\;\;\;\;\;\;\;\;\;\;\;
P\left(C\left|{LP}^c\right.\right)=0.2672\]
El riesgo relativo de que el hábitat esté contaminado cuando el
delfín presenta lesiones en la piel (LP) es entonces:
\[
RR=\frac{P\left(C\left|LP\right.\right)}{P\left(C\left|{LP}^{c}\right.\right)}=\frac{0.6484}{0.2672}=2.43\]
El riesgo de vivir en una zona contaminada es 2.43 veces más alto
entre los delfines que tienen lesiones de piel.
Asociación entre eventos: Riesgo Relativo (RR)
El riesgo relativo no debe utilizarse como
medida de asociación en estudios de Caso-Control.
Supongamos que el estudio anterior se hubiese realizado como un
estudio de casos y controles, siendo los casos los sujetos con LP y los
controles los sujetos sin LP. En un estudio de esta clase, tanto el
número de casos (128) como el número de controles (902) son elegidos
arbitrariamente por el investigador.
Supongamos que el investigador hubiese decidido elegir 4000 casos; si
la proporción de sujetos que proceden de zona con contaminación entre
los que tienen LP hubiese sido la misma que la ya observada ello
significaría que de los 4000 casos, 2594 (el 64.84%) provendrían de
hábitats contaminados y 1406 (el 35.16%) de hábitats sin contaminación.
La tabla resultante en este caso sería de la forma:
Asociación entre eventos: Riesgo Relativo (RR)
|
Presencia
|
Total
|
Lesiones Piel Sí
|
Lesiones Piel No
|
|
Contaminación
|
n=4902
|
n=4000
|
n=902
|
|
Sí
|
2835
|
2594
|
241
|
|
No
|
2067
|
1406
|
661
|
Entonces:
\[P\left(LP\left|C\right.\right)=\frac{2594}{2835}=0.9150
\;\;\;\;\;\;\;
P\left(LP\left|{C}^c\right.\right)=\frac{1406}{2067}=0.6802\]
El riesgo relativo de LP cuando hay C es entonces:
\[
RR=\frac{P\left(LP\left|C\right.\right)}{P\left(LP\left|{C}^{c}\right.\right)}=\frac{0.9150}{0.6802}=1.34\]
Así pues, el riesgo se ha reducido casi a la mitad, ¡solo por haber
aumentado el tamaño de la muestra!
Asociación entre eventos: Odds-Ratio (OR)
Definición de odd (ventaja): mide cuanto más
probable es la ocurrencia de un suceso B frente a la no ocurrencia del
mismo suceso: \[odd(B)=\frac{P\left(B\right)}{P\left(B^C\right)}\]
Definición de odds-ratio: evalúa el cociente de
las odds (ventajas) de \(B\) según que ocurra o no un segundo suceso
\(A\): \[OR=\frac{odd(B\left|A\right.)}{odd(B\left|A^C\right.)}=\frac{P\left(B\left|A\right.\right)\left/P\left(B^{C}\left|A\right.\right)\right.}{P\left(B\left|A^{C}\right.\right)\left/P\left(B^{C}\left|A^{C}\right.\right)\right.}=\frac{P\left(B\left|A\right.\right)\cdot
P\left(B^{C}\left|A^{C}\right.\right)}{P\left(B^{C}\left|A\right.\right)\cdot
P\left(B\left|A^{C}\right.\right)}\]
Una OR>1 significa que \(A\)
favorece la ocurrencia de \(B\) (\(A\) es factor de riesgo para \(B\))
Una OR<1 significa que \(A\)
dificulta la ocurrencia de \(B\) (\(A\) es factor de protección frente
a \(B\))
Una OR=1 significa que \(A\) no
favorece ni dificulta la ocurrencia de \(B\) (No hay asociación entre ambos
sucesos)
Asociación entre eventos: Odds-Ratio (OR)
Los datos para el cálculo de la OR se suelen presentar en una tabla
como la siguiente:

Nótese que los sucesos \(B\)
y \(A\) ocupan, respectivamente, la
primera fila y la primera columna de esta tabla
La odds-ratio se calcula entonces como el producto de la diagonal
principal dividido entre el producto de la diagonal inversa:
\[OR=\frac{P\left(B\left|A\right.\right)\cdot
P\left(B^{C}\left|A^{C}\right.\right)}{P\left(B^{C}\left|A\right.\right)\cdot
P\left(B\left|A^{C}\right.\right)}\]
Asociación entre eventos: Odds-Ratio (OR)
Se puede probar que la OR es una medida de asociación simétrica:
\[OR=\frac{odd(B\left|A\right.)}{odd(B\left|A^{C}\right.)}=\frac{P\left(B\left|A\right.\right)\cdot
P\left(B^{C}\left|A^{C}\right.\right)}{P\left(B^{C}\left|A\right.\right)\cdot
P\left(B\left|A^{C}\right.\right)}=\] \[=\frac{P\left(A\left|B\right.\right)\cdot
P\left(A^{C}\left|B^{C}\right.\right)}{P\left(A^{C}\left|B\right.\right)\cdot
P\left(A\left|B^{C}\right.\right)}=\frac{odd(A\left|B\right.)}{odd(A\left|B^{C}\right.)}\]
La validez de este resultado se deduce del Teorema de
Bayes: Sea \(A_{1},A_{2},\ldots,A_{n}\) un sistema
completo de sucesos y sea B un suceso arbitrario tal que \(B\cap A_{j}\ne\emptyset\).
Entonces:
\[P\left(A_{j}\left|B\right.\right)=\frac{{P\left(B\left|A_{j}\right.\right)P\left({A_{j}}\right)}}{{\sum\limits
_{i=1}^{n}{P\left(B\left|A_{i}\right.\right)P\left({A_{i}}\right)}}}\]
Asociación entre eventos: Odds-Ratio (OR)
|
|
LP
|
|
|
Contaminacion
|
Total (1030)
|
Sí (128)
|
No (902)
|
p (Chi-Square)
|
|
Sí
|
324 (31.46%)
|
83 (64.84%)
|
241 (26.72%)
|
<0.0001
|
|
No
|
706 (68.54%)
|
45 (35.16%)
|
661 (73.28%)
|
|
\[OR=\frac{P\left(C\left|LP\right.\right)/P\left(C^{c}\left|LP\right.\right)}{P\left(C\left|LP^{c}\right.\right)/P\left(C^{c}\left|LP^{c}\right.\right)}\]
\[ =
\frac{0.6484/0.3516}{0.2672/0.7328}=\frac{1.844}{0.3646}=5.06\]
Asociación entre eventos: Odds-Ratio (OR)
|
|
Contaminacion
|
|
|
LP
|
Total (1030)
|
Sí (324)
|
No (706)
|
p (Chi-Square)
|
|
Sí
|
128 (12.43%)
|
83 (25.62%)
|
45 (6.37%)
|
<0.0001
|
|
No
|
902 (87.57%)
|
241 (74.38%)
|
661 (93.63%)
|
|
\[OR=\frac{P\left(LP\left|C\right.\right)/P\left(LP^{c}\left|C\right.\right)}{P\left(LP\left|C^{c}\right.\right)/P\left(LP^{c}\left|C^{c}\right.\right)}\]
\[ =
\frac{0.2562/0.7438}{0.0637/0.9363}=\frac{0.3444}{0.068}=5.06\]
ESTUDIOS OBSERVACIONALES: El problema de los factores de
confusión.

ESTUDIOS OBSERVACIONALES: El problema de los factores de
confusión.
Consideremos ahora otras variables en nuestro estudio:
|
|
LP
|
|
|
Peso
|
Total (1030)
|
Sí (128)
|
No (902)
|
p (t-test)
|
|
peso
|
540.00 (440.00; 620.00)
|
405.00 (330.00; 470.00)
|
560.00 (460.00; 620.00)
|
<0.0001
|
|
|
LP
|
|
|
Contaminacion
|
Total (1030)
|
Sí (128)
|
No (902)
|
p (Chi-Square)
|
|
Sí
|
324 (31.46%)
|
83 (64.84%)
|
241 (26.72%)
|
<0.0001
|
|
No
|
706 (68.54%)
|
45 (35.16%)
|
661 (73.28%)
|
|
|
|
LP
|
|
|
Edad
|
Total (1030)
|
Sí (128)
|
No (902)
|
p (Chi-Square)
|
|
Juvenil
|
330 (32.04%)
|
103 (80.47%)
|
227 (25.17%)
|
<0.0001
|
|
Adulto
|
700 (67.96%)
|
25 (19.53%)
|
675 (74.83%)
|
|
ESTUDIOS OBSERVACIONALES: El problema de los factores de
confusión.
¿Es la contaminación la causa de las lesiones en la
piel?
ESTUDIOS OBSERVACIONALES: El problema de los factores de
confusión.
¿Es la contaminación la causa de las lesiones en la
piel?
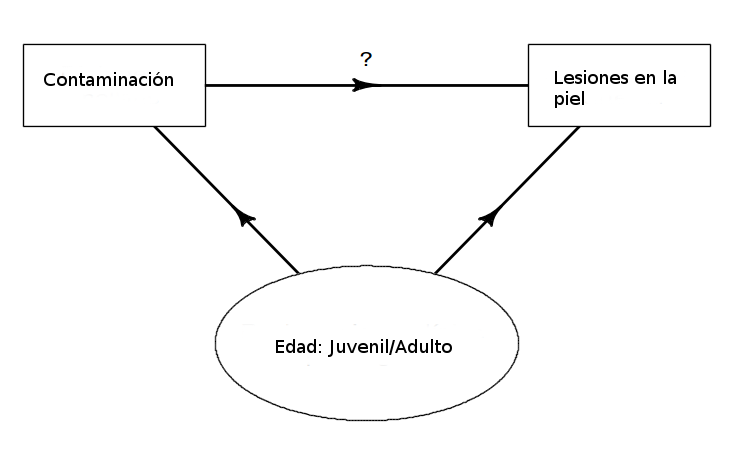
diabetes-HTA
¿o hay un efecto confusor de la edad del delfín?
Las zonas contaminadas están más próximas a la costa; asimismo, los
delfines jóvenes se mantienen más cerca de la costa que los delfines
adultos; podría ocurrir que los delfines jóvenes sean más propensos a
infecciones que causan lesiones en la piel, y como éstos están más cerca
de la costa, donde hay más contaminación, ello da lugar a que aparezca
una asociación entre contaminación y lesiones epidérmicas.
Distribución de probabilidad binomial
Consideremos un experimento aleatorio en el cuál solo son
posibles dos resultados excluyentes; por ejemplo,
seleccionar al azar a un delfín de una población y determinar si ese
delfín tiene o no lesiones en la piel .
Sea \(\pi\) la probabilidad de
ocurrencia de cierto suceso de interés; por ejemplo, que
el delfín tenga lesiones en la piel
.
Supongamos que el experimento se repite \(n\) veces en las mismas condiciones, de tal
forma que los sucesivos resultados sean independientes; por ejemplo,
se evalúan \(n\)
delfines elegidos al azar en la misma población .
Sea \(X\) = “número de
ocurrencias del suceso de interés”; por ejemplo, el
número de delfines con lesiones cutáneas entre
los \(n\) .
\(X\) es, por definición, una
variable aleatoria con distribución de probabilidad
binomial de parámetros \(n\) y \(\pi\).
Distribución de probabilidad binomial
- Para denotar las variables aleatorias binomiales de parámetros \(n\) y \(\pi\) utilizaremos la notación:
\[ X\cong B\left(n,\pi\right)
\]
\[P\left(X=k\right)=\binom{n}{k}\pi^{k}\left(1-\pi\right)^{n-k}\]
Distribución de probabilidad binomial
Ejemplo
La prevalencia \(\pi\) de
lesiones de piel en nuestra población de delfines es del 12.4% (128
casos en una muestra de 1030 delfines).
Si se elige una muestra de tamaño \(n\) de esta población y se define la
variable aleatoria:
\(X\) = “Número de delfines con
lesiones cutáneas”
entonces \(X\cong
B\left(n,0.124\right)\).
Ya hemos visto que la contaminación se asocia con la presencia de
lesiones en la piel. Esta asociación se traduce en que el parámetro de
la distribución binomial cambia según que los sujetos vivan en una zona
con o sin contaminación.
Regresión logística.
|
|
Contaminacion
|
|
|
LP
|
Total (1030)
|
Sí (324)
|
No (706)
|
p (Chi-Square)
|
|
Sí
|
128 (12.43%)
|
83 (25.62%)
|
45 (6.37%)
|
<0.0001
|
|
No
|
902 (87.57%)
|
241 (74.38%)
|
661 (93.63%)
|
|
La variable Contaminacion determina dos hábitats:
Hábitat 0 \(\cong\) {Contaminacion=No} y
Hábitat 1 \(\cong\) {Contaminacion=Sí}
Si se eligiera una muestra aleatoria de tamaño \(n_i\) en el hábitat \(i\), el número de delfines con lesiones
cutáneas en esa muestra sería una variable aleatoria binomial de
parámetros \(n_i\) y \(\pi\left(i\right)\), \(i=0,1\). Concretamente:
En el hábitat 0 (no contaminado): \(X\cong
B\left(n,\pi\left(0\right)=0.0637\right)\).
En el hábitat 1 (contaminado): \(X\cong
B\left(n,\pi\left(1\right)=0.2562\right)\).
Regresión logística.
- Si consideramos la variable
\[I_{Contam}=\begin{cases}
0 & Contaminacion=No\\
1 & Contaminacion=Sí
\end{cases}\]
El modelo de regresión logística asume que la función \(\pi\left(i\right)\) es de la forma:
\[\pi\left(I_{Contam}\right)=Pr\left(LP\left|I_{Contam}\right.\right)=\frac{\exp\left(\beta_{0}+\beta_{1}\cdot
I_{Contam}\right)}{1+\exp\left(\beta_{0}+\beta_{1}\cdot
I_{Contam}\right)}\]
En este caso se obtienen: \(\beta_0\) = -2.68709, \(\beta_1\) = 1.62114
De forma que:
\(\pi\left(I_{Contam}=1\right)=\frac{\exp\left(-2.68709+1.62114
\right)}{1+\exp\left(-2.68709+1.62114\right)} \approx
0.2562\)
\(\pi\left(I_{Contam}=0\right)=\frac{\exp\left(-2.68709
\right)}{1+\exp\left(-2.68709\right)} \approx 0.0637\)
Estimación de la regresión logística con R
logist <- glm(LP~Contaminacion,data=delfines,family=binomial)
summary(logist)
##
## Call:
## glm(formula = LP ~ Contaminacion, family = binomial, data = delfines)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -0.7693 -0.3629 -0.3629 -0.3629 2.3465
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -2.6871 0.1541 -17.442 < 2e-16 ***
## ContaminacionSí 1.6211 0.1998 8.113 4.96e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 773.22 on 1029 degrees of freedom
## Residual deviance: 703.56 on 1028 degrees of freedom
## AIC: 707.56
##
## Number of Fisher Scoring iterations: 5
Interpretación de los coeficientes de la regresión logística
\[Pr\left(LP\left|I_{Contam}\right.\right)=\frac{\exp\left(\beta_{0}+\beta_{1}\cdot
I_{Contam}\right)}{1+\exp\left(\beta_{0}+\beta_{1}\cdot
I_{Contam}\right)}\]
puede probarse sin mucha dificultad que:
\[OR=\frac{\Pr\left(LP\left|Contam\right.\right)\left/\Pr\left(LP^{c}\left|Contam\right.\right)\right.}{\Pr\left(LP\left|Contam^{c}\right.\right)\left/\Pr\left(LP^{c}\left|Contam^{c}\right.\right)\right.}=\exp\left(\beta_{1}\right)=e^{\beta_{1}}\]
\[e^{\beta_{1}} = e^{1.62114} =
5.0589\]
Regresión logística: OR e intervalo de confianza con R
## (Intercept) ContaminacionSí
## 0.06807867 5.05882895
## 2.5 % 97.5 %
## (Intercept) 0.04963516 0.09092621
## ContaminacionSí 3.43664865 7.53453814
Distribución binomial con el parámetro \(\pi\) dependiente de varios factores
Cuando consideramos conjuntamente la presencia o no de contaminación
y el grupo de edad a que pertenece el delfín, obtenemos la siguiente
tabla para los totales y proporciones de delfines con lesiones
cutáneas:
| No |
539 (98.00) |
122 (78.21) |
136 (90.67) |
105 (60.34) |
| Sí |
11 (2.00) |
34 (21.79) |
14 (9.33) |
69 (39.66) |
Regresión logística multivariante
- Consideramos ahora que la probabilidad de que un delfin tenga
lesiones cutáneas depende no sólo de la presencia de contaminación sino
también del grupo de Edad (Adulto=0, Juvenil=1):
\[\pi\left(I_{Contam},I_{Edad}\right)=\Pr\left(LP\left|I_{Contam},I_{Edad}\right.\right)=\frac{\exp\left(\beta_{0}+\beta_{1}I_{Contam}+\beta_{2}I_{Edad}\right)}{1+\exp\left(\beta_{0}+\beta_{1}I_{Contam}+\beta_{2}I_{Edad}\right)}\]
Estimación con R
logist <- glm(LP~Contaminacion+Edad,data=delfines,family=binomial)
summary(logist)
##
## Call:
## glm(formula = LP ~ Contaminacion + Edad, family = binomial, data = delfines)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.0360 -0.3854 -0.2293 -0.2293 2.7026
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -3.6258 0.2238 -16.204 < 2e-16 ***
## ContaminacionSí 1.0630 0.2163 4.915 8.86e-07 ***
## EdadJuvenil 2.2208 0.2429 9.144 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 773.22 on 1029 degrees of freedom
## Residual deviance: 600.68 on 1027 degrees of freedom
## AIC: 606.68
##
## Number of Fisher Scoring iterations: 6
Estimación con R
Predicción
logist <- glm(LP~Contaminacion+Edad,data=delfines,family=binomial)
dtf=data.frame(Contaminacion=factor(c("No","No","Sí","Sí")),
Edad=factor(c("Adulto","Juvenil","Adulto","Juvenil")))
cbind(dtf,predic=predict(logist,newdata=dtf, type="response"))
## Contaminacion Edad predic
## 1 No Adulto 0.02593608
## 2 No Juvenil 0.19702022
## 3 Sí Adulto 0.07156769
## 4 Sí Juvenil 0.41531521
Estimación con R
OR:
## (Intercept) ContaminacionSí EdadJuvenil
## 0.02662668 2.89500851 9.21487079
Intervalos de confianza
para las OR:
## 2.5 % 97.5 %
## (Intercept) 0.01673201 0.04033425
## ContaminacionSí 1.90056305 4.44332512
## EdadJuvenil 5.80800938 15.10193864
Regresión logística multivariante: Odds-ratios ajustadas
En regresión logística multivariante, el efecto de cada variable
ha de interpretarse bajo el supuesto de que el resto de variables que
intervienen en el modelo no cambian de valor.
Así la OR de 2.895 entre LP y
Contaminacion en este modelo significa que:
cuando se comparan dos individuos
adultos : el que viva en un hábitat contaminado
tiene un riesgo 2.895 veces mayor de padecer LP que el que vive en un
hábitat limpio.
cuando se comparan dos individuos
juveniles : el que viva en un hábitat
contaminado tiene un riesgo 2.895 veces mayor de padecer LP que el que
vive en un hábitat limpio.
Diremos entonces que 2.895 es la odds-ratio entre LP y
Contaminación ajustada por Edad
Nótese que la OR entre LP y Contaminación sin ajustar era 5.06; la
disminución a 2.895 significa que parte de la asociación entre LP y
Contaminación se explica por la edad.
Regresión logística multivariante: Odds-ratios ajustadas
Diremos entonces que 9.214 es la odds-ratio entre LP y Edad
ajustada por la presencia de contaminación
Regresión logística multivariante: asociación con variables
continuas
- ¿Cuál es el efecto del peso sobre la probabilidad de padecer
Lesiones en la Piel?
\[\pi\left(\textrm{peso}\right)=\Pr\left(LP\left|\textrm{peso}\right.\right)=\frac{\exp\left(\beta_{0}+\beta_{1}\textrm{peso}\right)}{1+\exp\left(\beta_{0}+\beta_{1}\textrm{peso}\right)}\]
En este caso se obtienen: \(\beta_0\) = 2.17443, \(\beta_1\) = -0.0087
La OR entre LP y peso es entonces \(e^{\beta_{1}}=e^{-0.0087}=0.99134\)
Esta OR representa la disminución (pues es menor que 1) en el
riesgo de padecer lesiones en la piel por cada kg adicional de peso del
delfín.
Podemos calcular la disminución de riesgo que se produce en un
delfín que pese 80 kg más que otro:
\[e^{80 \beta_{1}}=e^{-0.696} = 0.4985756
\]
Por tanto, por cada 80 kg de incremento de peso, el riesgo de
padecer lesiones en la piel se reduce a la mitad.
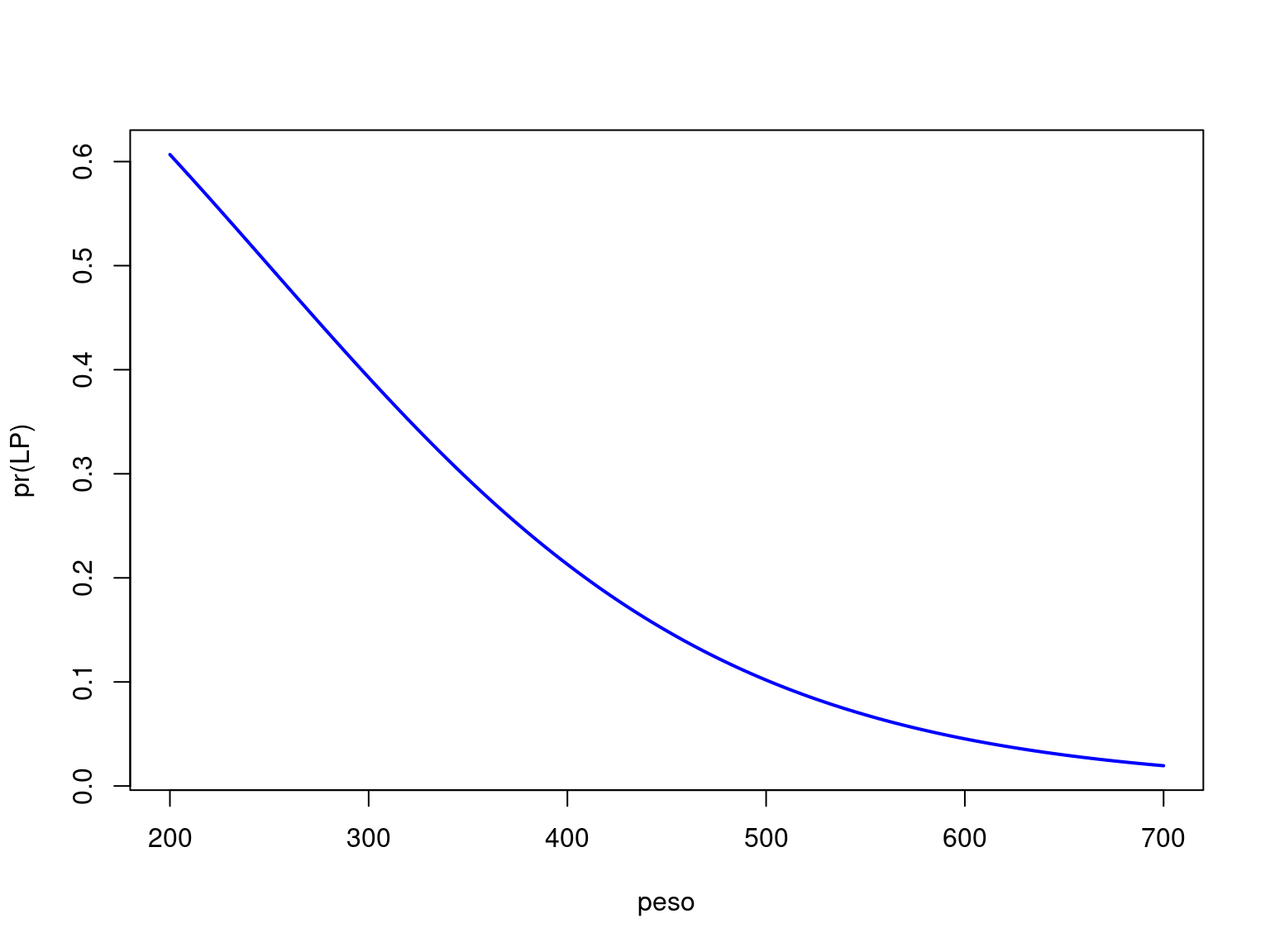
Regresión logística multivariante
- Podemos visualizar el efecto del peso sobre el riesgo de padecer
lesiones en la piel:
mg <- glm(LP ~ peso, data=delfines, family=binomial)
peso=seq(200,700,length=200)
pLP=predict(mg,newdata=data.frame(peso=peso),type="response")
plot(pLP~peso, ylab="pr(LP)", type="l", col="blue",lwd=2)
Regresión logística multivariante
Podemos usar la regresión logística para ajustar el efecto del peso
sobre el riesgo de padecer lesiones en la piel según el tipo de hábitat
(contaminado o no) donde viva el delfín:
\[\pi\left(I_{Contam},\textrm{peso}\right)=\Pr\left(LP\left|I_{Contam},\textrm{peso}\right.\right)=\]
\[\frac{\exp\left(\beta_{0}+\beta_{1}I_{Contam}+\beta_{2}\textrm{peso}\right)}{1+\exp\left(\beta_{0}+\beta_{1}I_{Contam}+\beta_{2}\textrm{peso}\right)}\]
En este caso: \(\beta_0\) =
1.05744, \(\beta_1\) = 0.94434, \(\beta_2\) = -0.00725
La OR de padecer lesiones en la piel cuando el hábitat está
contaminado, ajustada por el peso del delfín, es entonces:
\[ e^{\beta_1} = e^{0.94434} = 2.57112
\]
- Esto es, para un peso fijo, el vivir en un hábitat contaminado
incrementa en 2.57 veces el riesgo de padecer lesiones en la piel, con
respecto a vivir en un hábitat limpio.
mg <- glm(LP ~ Contaminacion + peso, data=delfines, family=binomial)
summary(mg)
##
## Call:
## glm(formula = LP ~ Contaminacion + peso, family = binomial, data = delfines)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.4838 -0.4896 -0.3111 -0.2258 2.7909
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 1.0574439 0.4741222 2.230 0.0257 *
## ContaminacionSí 0.9443353 0.2200621 4.291 1.78e-05 ***
## peso -0.0072522 0.0009333 -7.771 7.81e-15 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 773.22 on 1029 degrees of freedom
## Residual deviance: 637.21 on 1027 degrees of freedom
## AIC: 643.21
##
## Number of Fisher Scoring iterations: 5
Odds-Ratio
## (Intercept) ContaminacionSí peso
## 2.879003 2.571104 0.992774
## Waiting for profiling to be done...
## 2.5 % 97.5 %
## (Intercept) 1.1344205 7.3000662
## ContaminacionSí 1.6737438 3.9726820
## peso 0.9909244 0.9945626
- Representamos ahora gráficamente la relación entre la
probabilidad de padecer lesiones en la piel y
el peso según que el animal viva en un
hábitat contaminado o limpio:
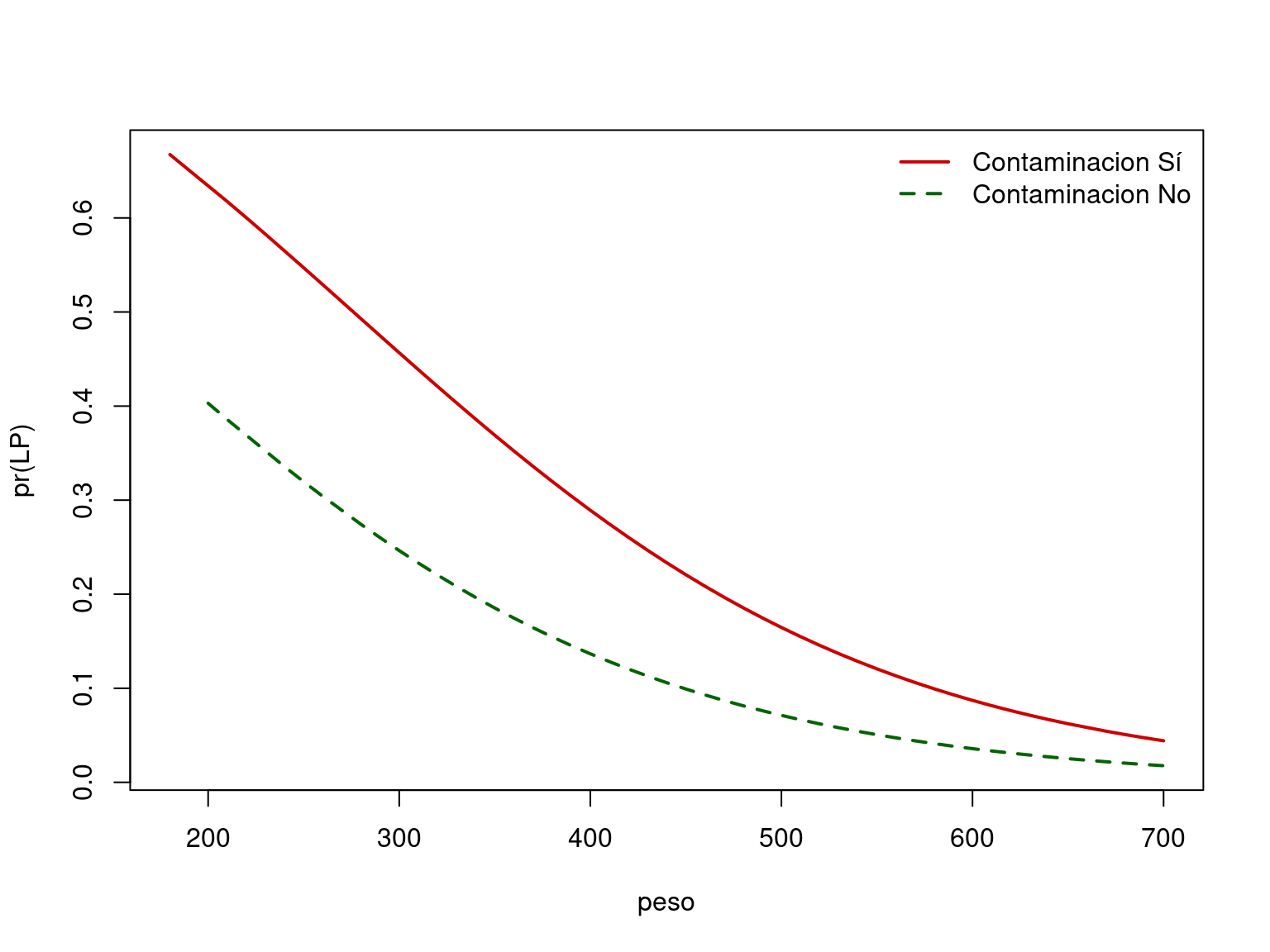
- El gráfico muestra que cualquiera que sea el valor del peso, el
riesgo de padecer LP es mayor entre los delfines que viven en hábitats
contaminados. Puede apreciarse además que la diferencia entre los
riesgos va disminuyendo a medida que aumenta el peso.
El código utilizado para generar el gráfico anterior fue:
mg <- glm(LP ~ Contaminacion + peso, data=delfines, family=binomial)
delfines$pLP=mg$fitted # Añadimos las predicciones a la base de datos
delfines=delfines[order(delfines$peso), ] # Ordenamos por peso
si.Contaminacion=subset(delfines,Contaminacion=="Sí") # habitat contaminado
no.Contaminacion=subset(delfines,Contaminacion=="No") # habitat no contaminado
plot(pLP~peso,delfines, type="n", xlab="peso", ylab="pr(LP)") # Gráfico en blanco
lines(no.Contaminacion$peso,no.Contaminacion$pLP,type="l",col="darkgreen",lwd=2,lty=2)
lines(si.Contaminacion$peso,si.Contaminacion$pLP,type="l",col="red3",lwd=2,lty=1)
legend("topright", c("Contaminacion Sí","Contaminacion No"),
lty=c(1,2), col=c("red3","darkgreen"), lwd=2, bty="n")
Regresión logística multivariante
- Por último estudiamos la asociación de la presencia de lesiones en
la piel con la contaminación ajustando simultáneamente por Edad y
Peso:
\[\pi\left(I_{Contam},I_{Edad},\textrm{peso}\right)=\Pr\left(LP\left|I_{Contam},I_{Edad},\textrm{peso}\right.\right)=\]
\[=\frac{\exp\left(\beta_{0}+\beta_{1}I_{Contam}+\beta_{2}I_{Edad}+\beta_{3}\textrm{peso}\right)}{1+\exp\left(\beta_{0}+\beta_{1}I_{Contam}+\beta_{2}I_{Edad}+\beta_{3}\textrm{peso}\right)}\]
mg2 <- glm(LP~Contaminacion+Edad+peso,data=delfines,family=binomial)
summary(mg2)
##
## Call:
## glm(formula = LP ~ Contaminacion + Edad + peso, family = binomial,
## data = delfines)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.7904 -0.4269 -0.1931 -0.1226 3.1551
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 0.431514 0.516648 0.835 0.4036
## ContaminacionSí 0.486373 0.234574 2.073 0.0381 *
## EdadJuvenil 2.371529 0.255720 9.274 < 2e-16 ***
## peso -0.008310 0.001056 -7.873 3.47e-15 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 773.22 on 1029 degrees of freedom
## Residual deviance: 528.87 on 1026 degrees of freedom
## AIC: 536.87
##
## Number of Fisher Scoring iterations: 6
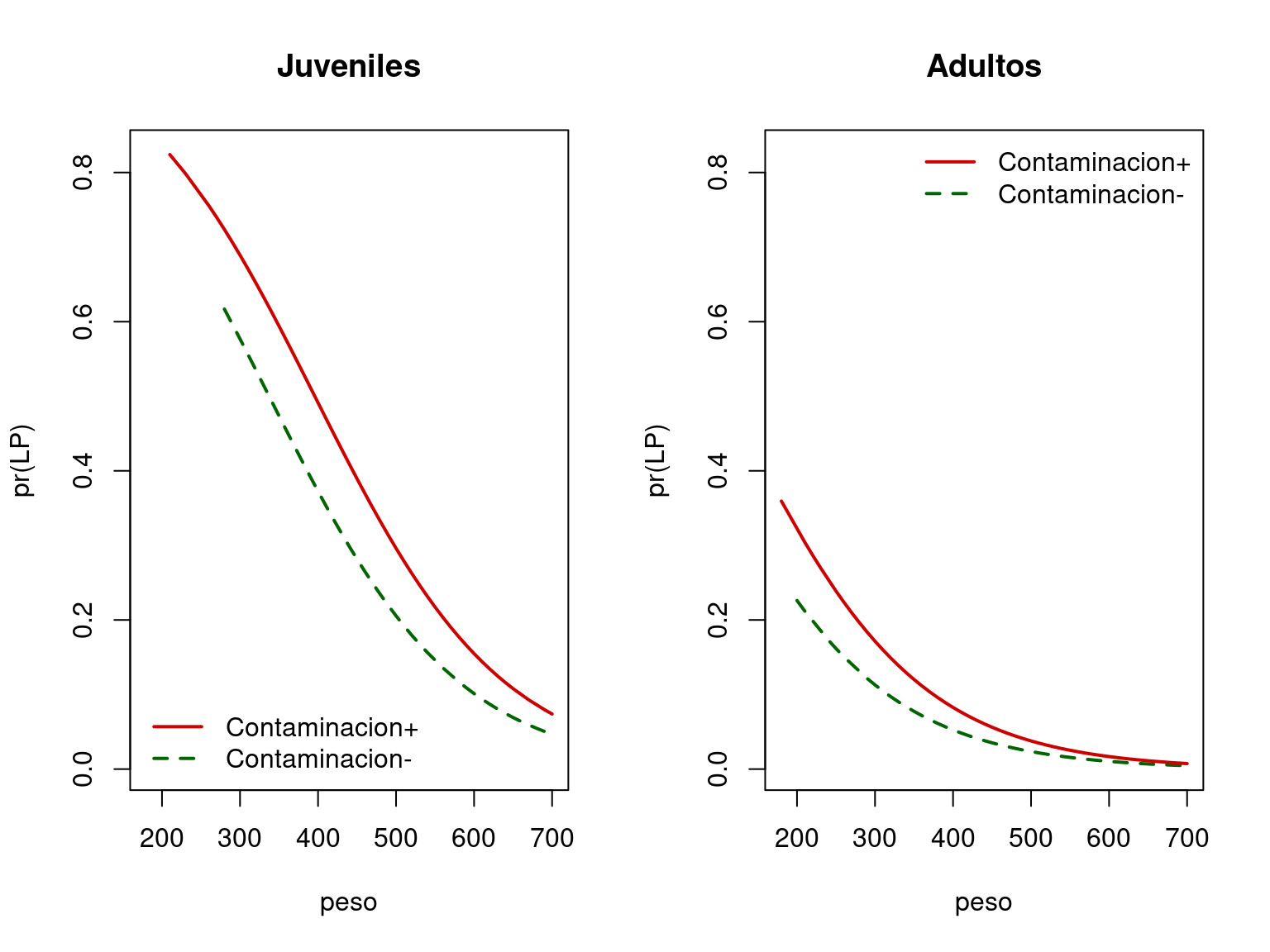
- Entre los juveniles, el riesgo de LP disminuye con el peso, si bien
dicho riesgo es siempre mayor donde hay contaminación. En el caso de los
adultos, el riesgo de padecer LP también disminuye a medida que aumenta
el peso, pero el efecto de la contaminación sólo se deja sentir en los
animales más pequeños; En los delfines adultos grandes no hay más riesgo
de lesiones por vivir en hábitats contaminados.
El código utilizado para generar el gráfico anterior fue:
delfines$pLP=mg2$fitted # Añadimos las predicciones a la base de datos
delfines=delfines[order(delfines$peso), ] # Ordenamos por peso
par(mfrow=c(1,2))
# Juveniles
delfinesEdad=subset(delfines,Edad=="Juvenil")
si.Contaminacion=subset(delfinesEdad,Contaminacion=="Sí") # Juveniles en region contaminada
no.Contaminacion=subset(delfinesEdad,Contaminacion=="No") # Juveniles en region limpia
plot(pLP~peso,delfines, type="n", xlab="peso", ylab="pr(LP)",
main="Juveniles")
lines(no.Contaminacion$peso,no.Contaminacion$pLP,type="l",col="darkgreen",lwd=2,lty=2)
lines(si.Contaminacion$peso,si.Contaminacion$pLP,type="l",col="red3",lwd=2,lty=1)
legend("bottomleft", c("Contaminacion+","Contaminacion-"),
lty=c(1,2), col=c("red3","darkgreen"), lwd=2, bty="n")
# Adultos
delfinesEdad=subset(delfines,Edad=="Adulto")
si.Contaminacion=subset(delfinesEdad,Contaminacion=="Sí") # Adultos en region contaminada
no.Contaminacion=subset(delfinesEdad,Contaminacion=="No") # Adultos en region limpia
plot(pLP~peso,delfines, type="n", xlab="peso", ylab="pr(LP)",
main="Adultos")
lines(no.Contaminacion$peso,no.Contaminacion$pLP,type="l",col="darkgreen",lwd=2,lty=2)
lines(si.Contaminacion$peso,si.Contaminacion$pLP,type="l",col="red3",lwd=2,lty=1)
legend("topright", c("Contaminacion+","Contaminacion-"),
lty=c(1,2), col=c("red3","darkgreen"), lwd=2, bty="n")
Regresión logística multivariante
- Resumen de la estimación del modelo:
| (Intercept) |
0.432 (0.517) |
0.404 |
1.540 (0.557,4.233) |
| ContaminacionSí |
0.486 (0.235) |
0.038 |
1.626 (1.027,2.581) |
| EdadJuvenil |
2.372 (0.256) |
< .001 |
10.714 (6.594,18.027) |
| peso |
-0.008 (0.001) |
< .001 |
0.992 (0.990,0.994) |







