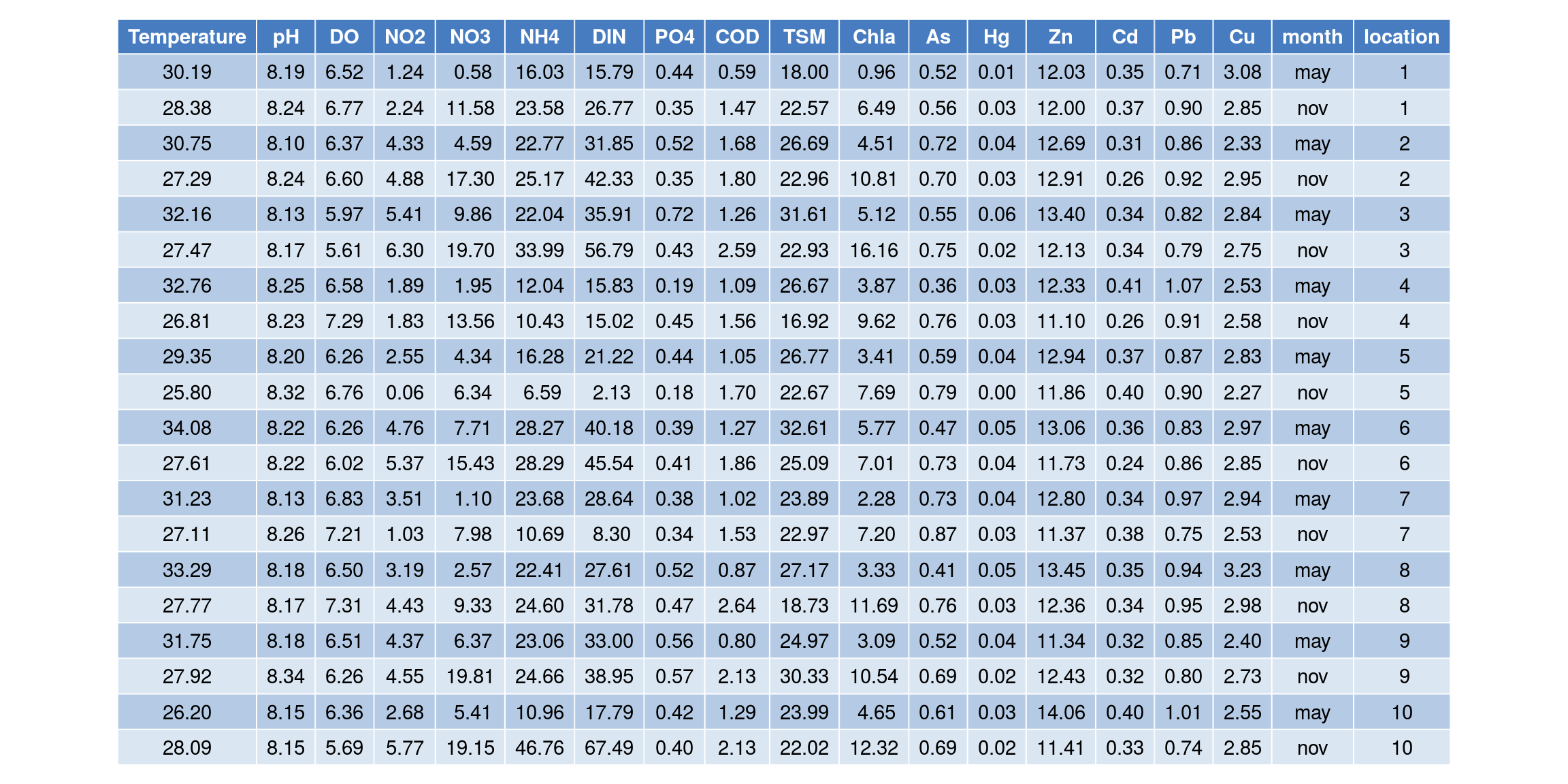
Se dispone de una muestra de observaciones de variables ambientales medidas en 10 localizaciones situadas a lo largo de la costa durante dos periodos de tiempo (mayo y noviembre). A continuación se muestran algunos datos de dicha muestra:
Angelo Santana
20 de octubre de 2017
Se dispone de una muestra de observaciones de variables ambientales medidas en 10 localizaciones situadas a lo largo de la costa durante dos periodos de tiempo (mayo y noviembre). A continuación se muestran algunos datos de dicha muestra:

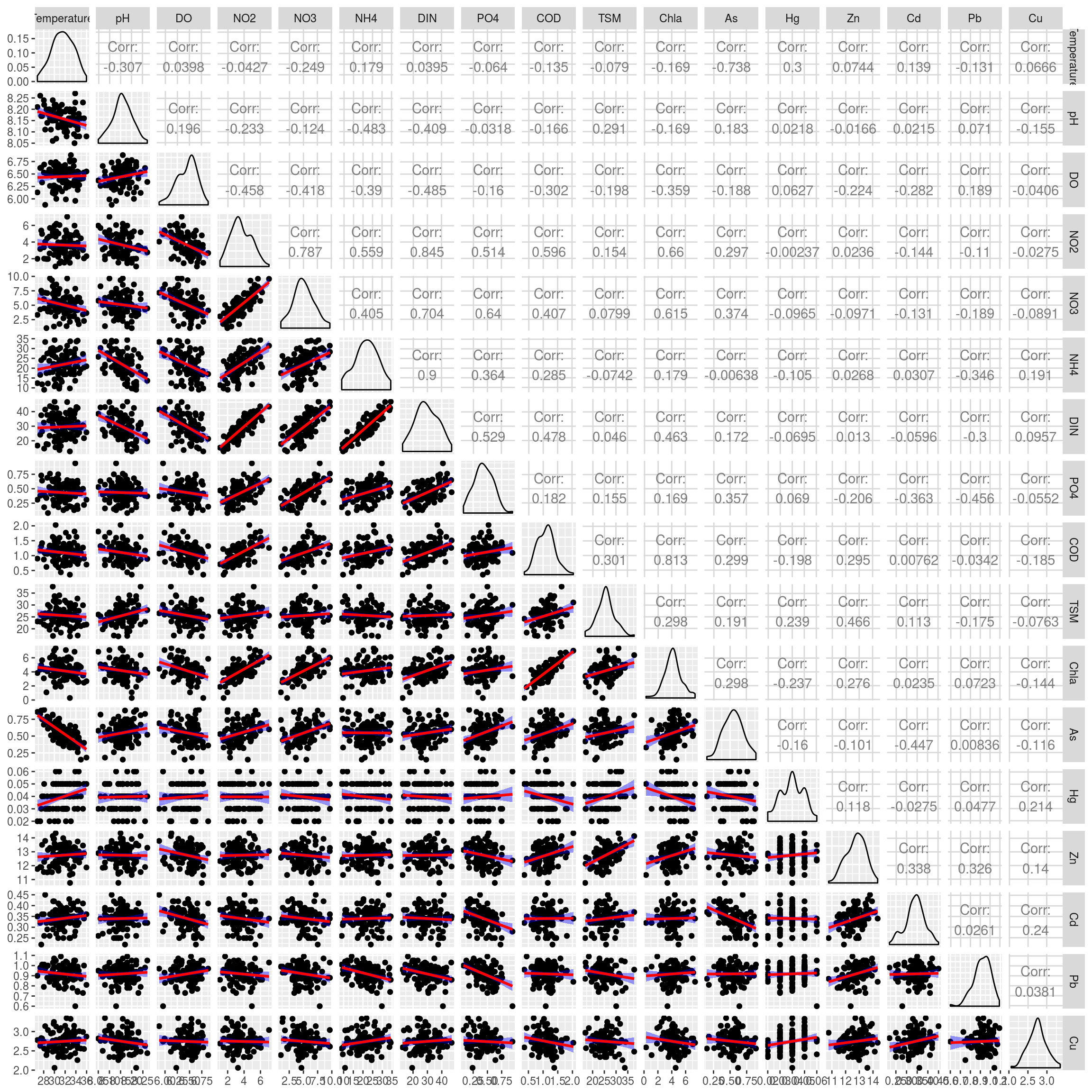
El gráfico anterior muestra la existencia de correlaciones (en algunos casos relativamente altas) entre las variables, lo que significa que muchas variables comparten información.
Nos preguntamos entonces si es posible simplificar la estructura de este conjunto de datos, tratando de localizar factores comunes a las variables que permitan visualizar de manera sencilla la relaciones entre ellas (y con otras posibles variables, como la posición espacial de cada estación).
La técnica de las componentes principales persigue precisamente el objetivo de reducir la dimensionalidad del conjunto de datos observados, transformando el conjunto original de variables en otro conjunto de variables incorreladas entre sí (las componentes principales), y ordenadas de tal forma que la primera componente principal recoge la máxima variabilidad posible en la muestra; la segunda componente es aquella que siendo incorrelada con la primera recoge la siguiente mayor variabilidad posible; y así sucesivamente.
Las componentes principales se conocen también como funciones ortogonales empíricas.
Para entender la idea geométrica que está detrás de las componentes principales consideremos el siguiente ejemplo: se han medido temperatura y concentración de un compuesto químico en una zona, con los datos siguientes:
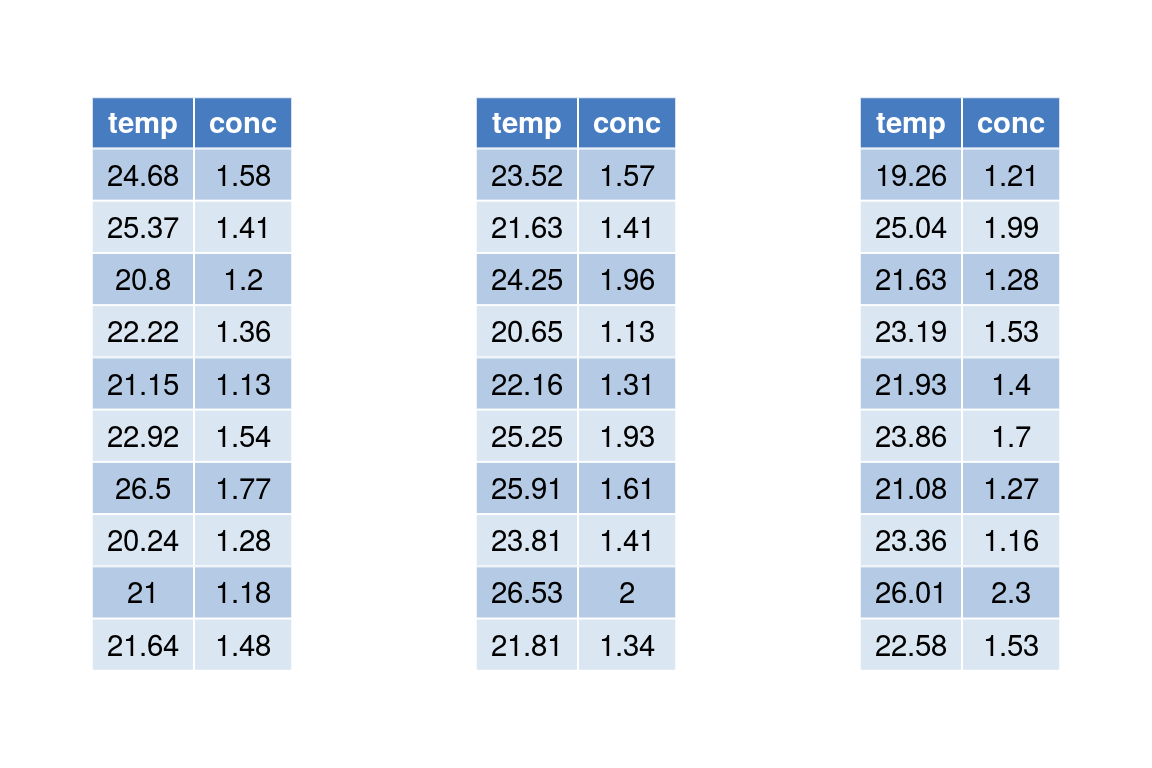
Si los representamos gráficamente vemos que están más o menos alineados a lo largo de una recta:
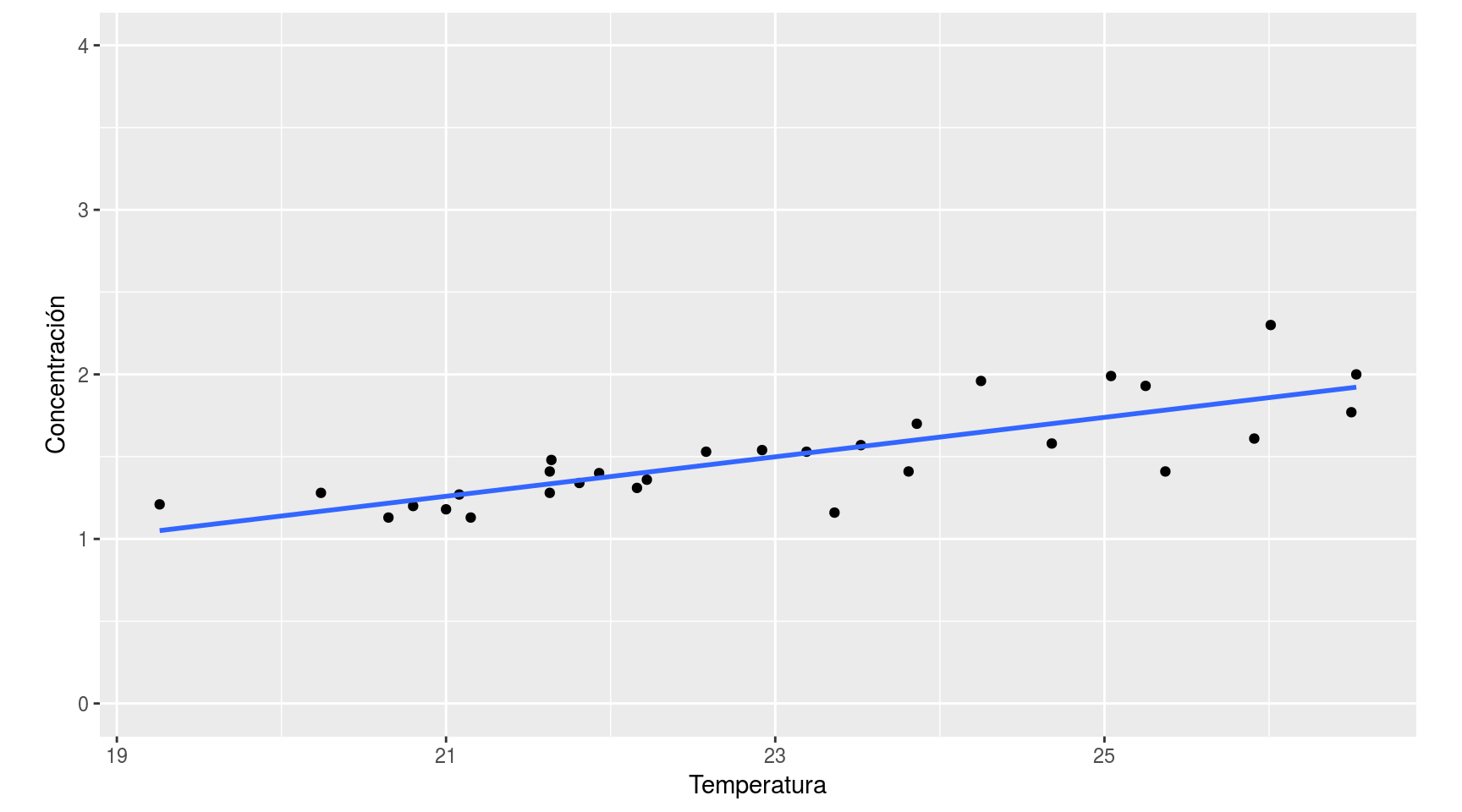
Para situar la posición un punto en este plano, debemos dar sus coordenadas (x,y). Así, por ejemplo, para localizar el punto P señalado en la gráfica siguiente debemos dar sus dos coordenadas (24.25, 1.96):
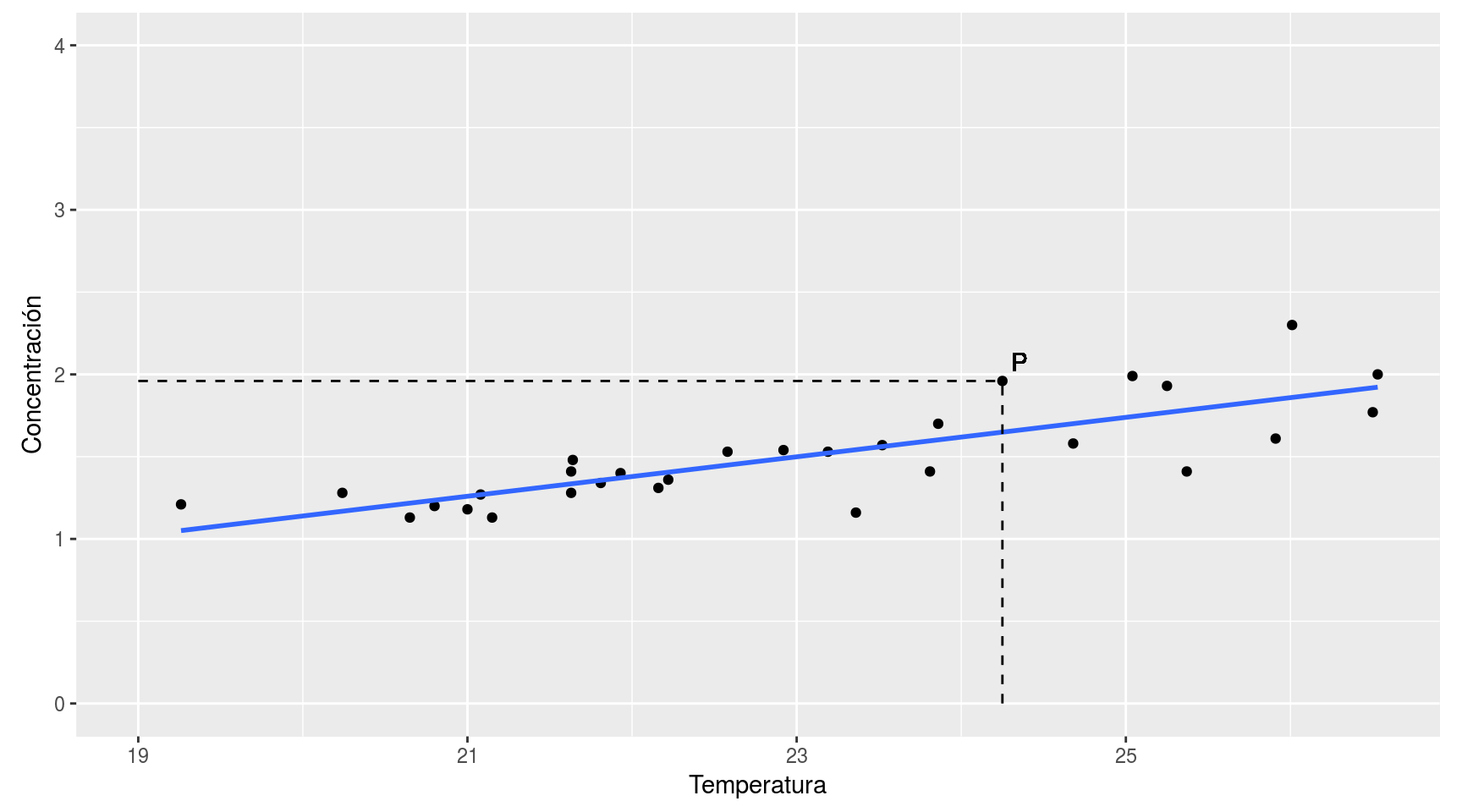
En lugar de dar las dos coordenadas, podemos dar una posición aproximada del punto simplemente por referencia a la recta de regresión: marcamos un origen en la recta de regresión (por ejemplo el centro de la nube de puntos) y damos la posición del punto P como la distancia desde ese centro hasta la posición del cuadradito rojo (que es el punto de la recta más cercano a P). De esta forma, en lugar de dar dos coordenadas para localizar dicho punto, damos simplemente una (la longitud del segmento marcado en rojo, que mide 1.3 unidades).
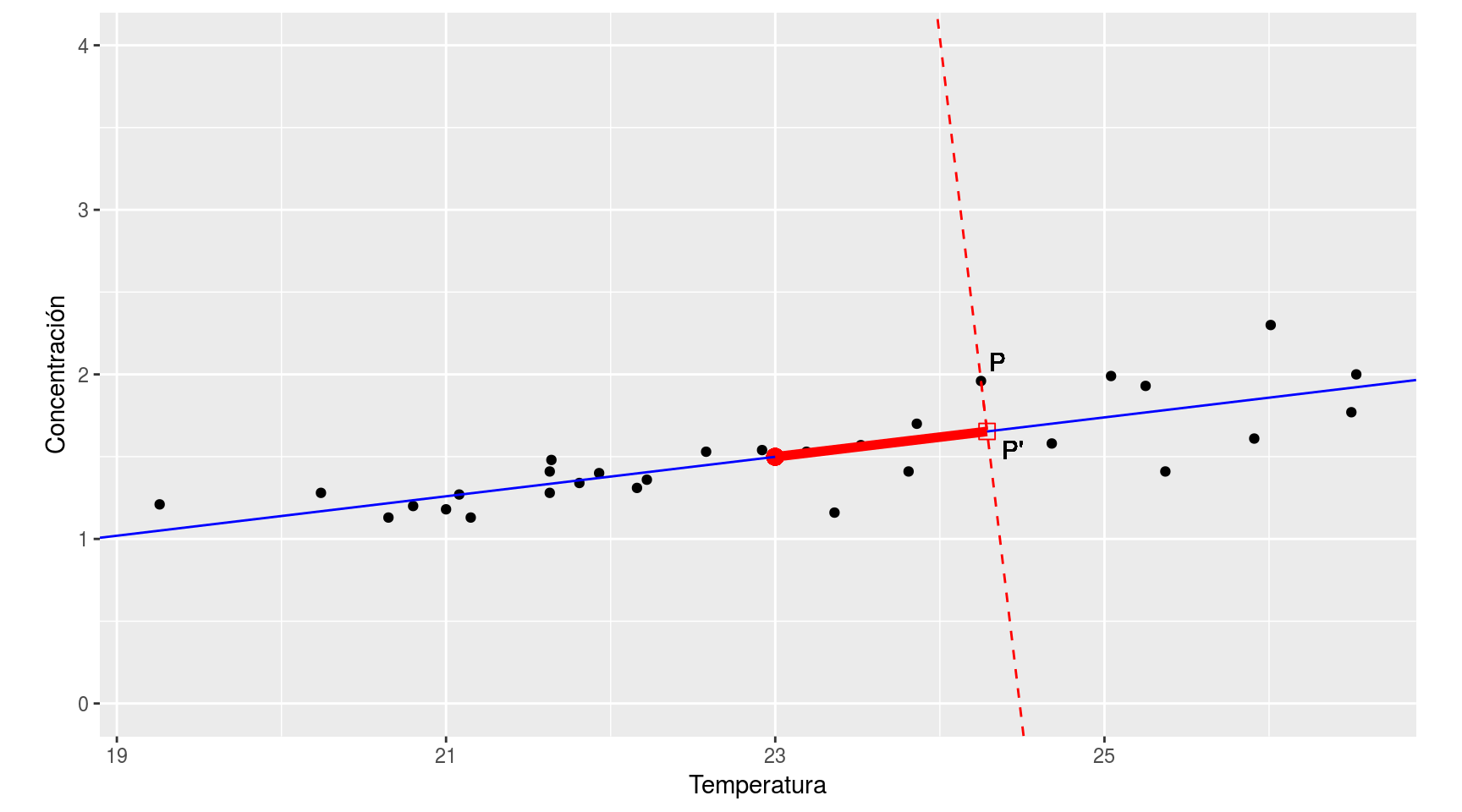
Obviamente, así no localizamos exactamente P, pero damos una posición muy aproximada, P’; hemos perdido precisión (P no se localiza exactamente, sino aproximadamente), pero hemos ganado simplicidad (sólo hemos de dar una coordenada, no dos).
De una manera más algebraica, hemos pasado de describir los puntos (las observaciones) en un espacio bidimensional (dado por las coordenadas de Temperatura y Concentración) a describirlos en un espacio unidimensional, la posición sobre la recta de regresión.
La primera componente principal es, por definición, el eje a lo largo del cuál se produce la mayor variabilidad en la nube de puntos. En este ejemplo, es de esperar que dicha componente sea muy similar a la recta de regresión (no tienen por qué coincidir).
La segunda componente principal es, por definición, la dirección que, siendo perpendicular a la primera, aglutina la siguiente mayor variabilidad en la nube de puntos. En este caso, como estamos en un plano, no hay más que una posible dirección perpendicular.
Las componentes principales, serían por tanto unos nuevos ejes coordenados, agrupados a lo largo de las sucesivas direcciones de mayor variabilidad de la nube de puntos:
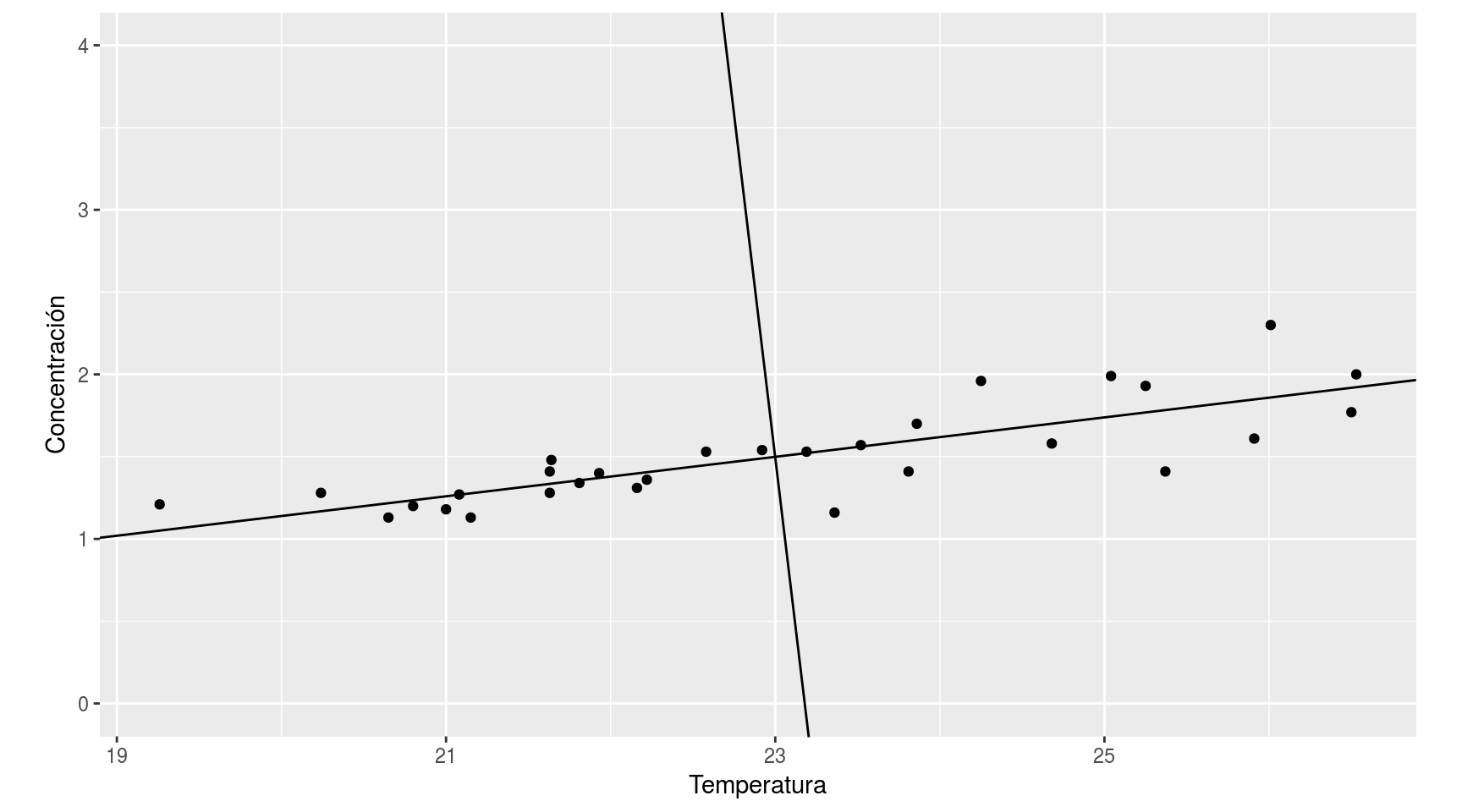
La reducción de la dimensionalidad se consigue cuando se puede prescindir de algún eje porque en torno a él hay muy poca variabilidad, como en este caso, que podemos pasar de dos variables a una (aunque se pierde algo de información)
Sólo se conseguirá reducir la dimensionalidad si entre las variables observadas hay correlaciones relativamente altas que producen que los puntos se alineen a lo largo de ejes definidos.
Si los puntos están dispersos al azar en el espacio, las componentes principales no sirven para conseguir una reducción de dimensionalidad efectiva.
Dadas las variables \(X_1, X_2, \dots, X_p\), con matriz de covarianzas:
\[\text{var}(\textbf{X}) = \Sigma = \left(\begin{array}{cccc}\sigma^2_1 & \sigma_{12} & \dots &\sigma_{1p}\\ \sigma_{21} & \sigma^2_2 & \dots &\sigma_{2p}\\ \vdots & \vdots & \ddots & \vdots \\ \sigma_{p1} & \sigma_{p2} & \dots & \sigma^2_p\end{array}\right)\] queremos encontrar unas nuevas variables \(Y_1, Y_2, \dots, Y_p\) (las componentes principales), que sean combinaciones lineales de las \(X_i\):
\[\begin{array}{lll} Y_1 & = & e_{11}X_1 + e_{12}X_2 + \dots + e_{1p}X_p \\ Y_2 & = & e_{21}X_1 + e_{22}X_2 + \dots + e_{2p}X_p \\ & & \vdots \\ Y_p & = & e_{p1}X_1 + e_{p2}X_2 + \dots +e_{pp}X_p\end{array}\]
y que cumplan dos condiciones:
\(Var\left(Y_1\right) \ge Var\left(Y_2\right) \ge \dots Var\left(Y_p\right)\)
\(Cov\left(Y_i,Y_j\right)=0 \;\; \forall i,j\) (las componentes principales son incorreladas dos a dos)
Si llamamos: \[\mathbf{e}_i = \left(\begin{array}{c} e_{i1}\\ e_{i2}\\ \vdots \\ e_{ip}\end{array}\right)\]
tenemos que:
\[\text{var}(Y_i) = \sum_{k=1}^{p}\sum_{l=1}^{p}e_{ik}e_{il}\sigma_{kl} = \mathbf{e}'_i\Sigma\mathbf{e}_i\] \[\text{cov}(Y_i, Y_j) = \sum_{k=1}^{p}\sum_{l=1}^{p}e_{ik}e_{jl}\sigma_{kl} = \mathbf{e}'_i\Sigma\mathbf{e}_j\]
Por tanto, para calcular la primera componente principal hemos de hallar los valores de \(e_{11}, e_{12}, \dots, e_{1p}\) que maximicen:
\[\text{var}(Y_1) = \sum_{k=1}^{p}\sum_{l=1}^{p}e_{1k}e_{1l}\sigma_{kl} = \mathbf{e}'_1\Sigma\mathbf{e}_1\]
Para que este problema tenga solución única hemos de imponer la restricción adicional de que el vector \(e_1\) sea unitario, esto es: \[\mathbf{e}'_1\mathbf{e}_1 = \sum_{j=1}^{p}e^2_{1j} = 1\]
Asimismo, para calcular la segunda componente principal, hemos de hallar los valores de \(e_{21}, e_{22}, \dots, e_{2p}\) que maximicen:
\[\text{var}(Y_2) = \sum_{k=1}^{p}\sum_{l=1}^{p}e_{2k}e_{2l}\sigma_{kl} = \mathbf{e}'_2\Sigma\mathbf{e}_2\]
sujeto a la restricción de que \(e_2\) sea un vector unitario: \[\mathbf{e}'_2\mathbf{e}_2 = \sum_{j=1}^{p}e^2_{2j} = 1\] y que \(Y_2\) esté incorrelada con \(Y_i\): \[\text{cov}(Y_1, Y_2) = \sum_{k=1}^{p}\sum_{l=1}^{p}e_{1k}e_{2l}\sigma_{kl} = \mathbf{e}'_1\Sigma\mathbf{e}_2 = 0\]
En general, para calcular la \(i\)-ésima componente principal, hemos de encontrar los valores \(e_{i1}, e_{i2}, \dots, e_{ip}\) que maximicen: \[\text{var}(Y_i) = \sum_{k=1}^{p}\sum_{l=1}^{p}e_{ik}e_{il}\sigma_{kl} = \mathbf{e}'_i\Sigma\mathbf{e}_i\]
sujeto a la restricción de que \(e_i\) sea un vector unitario: \[\mathbf{e}'_i\mathbf{e}_i = \sum_{j=1}^{p}e^2_{ij} = 1\]
y tal que \(Y_i\) esté incorrelada con las componentes anteriores: \[\text{cov}(Y_j, Y_i) = \sum_{k=1}^{p}\sum_{l=1}^{p}e_{jk}e_{il}\sigma_{kl} = \mathbf{e}'_j\Sigma\mathbf{e}_i = 0, \;\;\; j=1,2,\dots, j-1\]
El problema de encontrar los vectores \(e_i\) de acuerdo con las condiciones anteriores se resuelve mediante el método de los multiplicadores de Lagrange (ver, por ejemplo, http://halweb.uc3m.es/esp/Personal/personas/jmmarin/esp/AMult/tema3am.pdf).
La solución a este problema consiste en calcular los autovalores y autovectores de la matriz de covarianzas \(\Sigma\).
Si se ordenan los autovalores de forma que \(\lambda_1 \ge \lambda_2 \ge \dots \ge \lambda_p\), los autovectores correspondientes nos proporcionan las coordenadas de las componentes principales \(e_1, e_2, \dots, e_p\) y además \(Var\left(Y_i\right)=\lambda_i\)
Volvamos a nuestro ejemplo anterior.
La matriz de covarianzas de los datos de temperatura y concentración es:
cov(data)## temp conc
## temp 4.0011926 0.47964759
## conc 0.4796476 0.08958172Sus autovalores y autovectores pueden calcularse fácilmente mediante:
eigen(cov(data))## eigen() decomposition
## $values
## [1] 4.05914904 0.03162533
##
## $vectors
## [,1] [,2]
## [1,] -0.9927789 0.1199587
## [2,] -0.1199587 -0.9927789
Los términos etiquetados como values corresponden a las varianzas de cada componente principal.
Los términos etiquetados como vectors son los autovectores (expresados en forma de columnas) que especifican los coeficientes de las componentes principales:
\[ PC1 = -0.9927789\; temp -0.1199587\; conc\] \[ PC2 = 0.1199587\; temp -0.9927789\; conc\]
La pendiente de una recta en la dirección de la primera componente principal se obtiene simplemente dividiendo la segunda componente del vector por la primera:
\[ \frac{-0.12}{-0.9928}=0.1208\] La recta de regresión de la concentración sobre la temperatura es:
##
## Call:
## lm(formula = conc ~ temp, data = data)
##
## Coefficients:
## (Intercept) temp
## -1.2581 0.1199Así pues, vemos que la pendiente de la regresión (0.1199) y la pendiente de la primera componente principal (0.1208) son muy parecidas, como cabía esperar.
Gráficamente resultan indistinguibles:
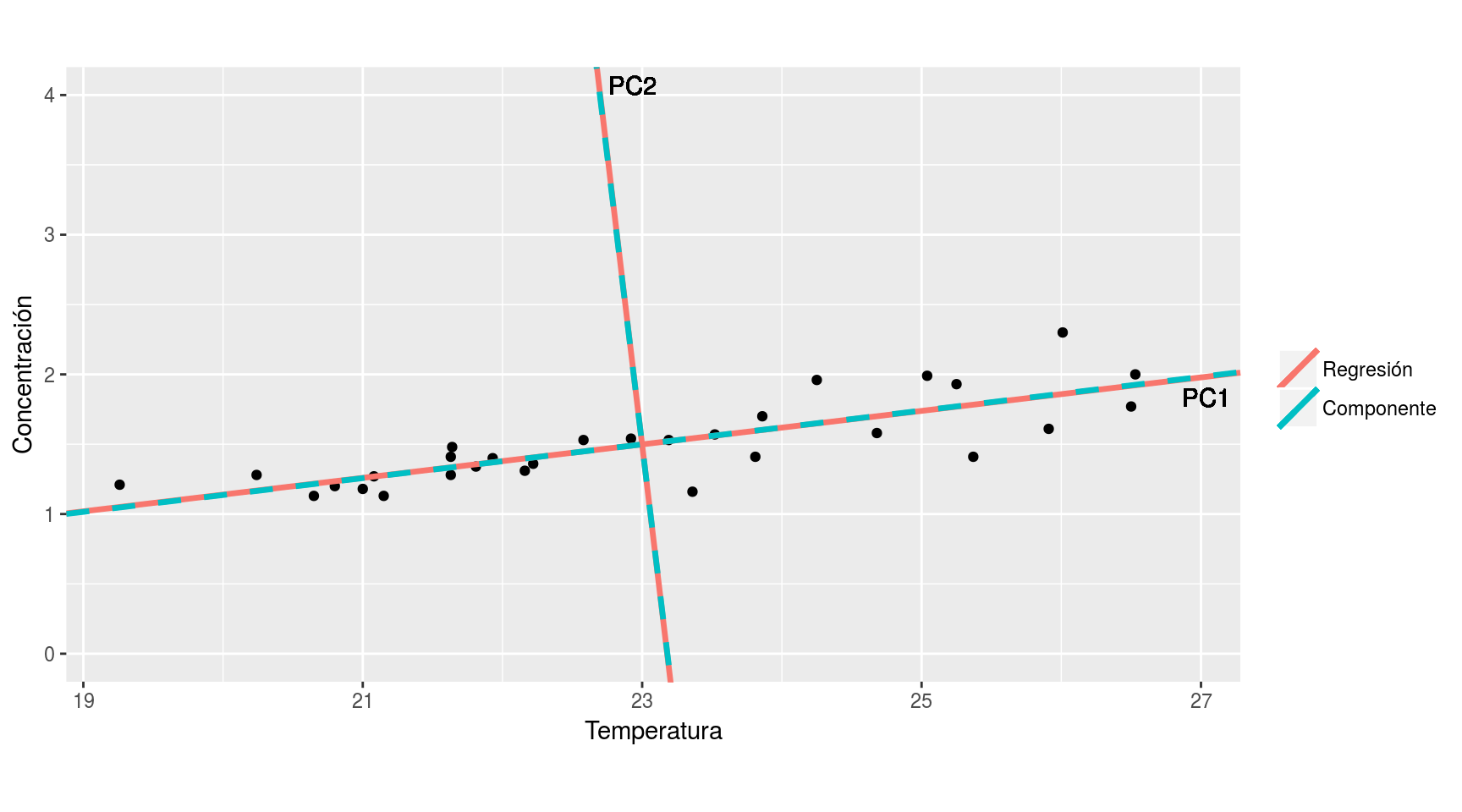
Volvamos a la expresión de las componentes principales:
\[ PC1 = -0.9927789\; temp -0.1199587\; conc\]
\[ PC2 = 0.1199587\; temp -0.9927789\; conc\]
Utilizando estas ecuaciones podemos obtener las coordenadas de los puntos observados con respecto al sistema de ejes dado por las componentes principales:
CP=as.matrix(data) %*% eigen(cov(data))$vectors
CP## [,1] [,2]
## [1,] -24.69132 1.3919892
## [2,] -25.35594 1.6435331
## [3,] -20.79375 1.3038056
## [4,] -22.22269 1.3153023
## [5,] -21.13283 1.4152856
## [6,] -22.93923 1.2205731
## [7,] -26.52097 1.4216860
## [8,] -20.24739 1.1572064
## [9,] -20.98991 1.3476529
## [10,] -21.66127 1.1265928
## [11,] -23.53849 1.2627650
## [12,] -21.64295 1.1948877
## [13,] -24.31001 0.9631510
## [14,] -20.63644 1.3553063
## [15,] -22.15713 1.3577437
## [16,] -25.29919 1.1128930
## [17,] -25.91603 1.5097550
## [18,] -23.80721 1.4563976
## [19,] -26.57834 1.1969456
## [20,] -21.81325 1.2859748
## [21,] -19.26607 1.1091414
## [22,] -25.09790 1.0281350
## [23,] -21.62735 1.3239490
## [24,] -23.20608 1.2628898
## [25,] -21.93958 1.2408031
## [26,] -23.89163 1.1744896
## [27,] -21.08013 1.2678995
## [28,] -23.33047 1.6506109
## [29,] -26.09808 0.8367334
## [30,] -22.60048 1.1897150y representarlos gráficamente con respecto a ese sistema:
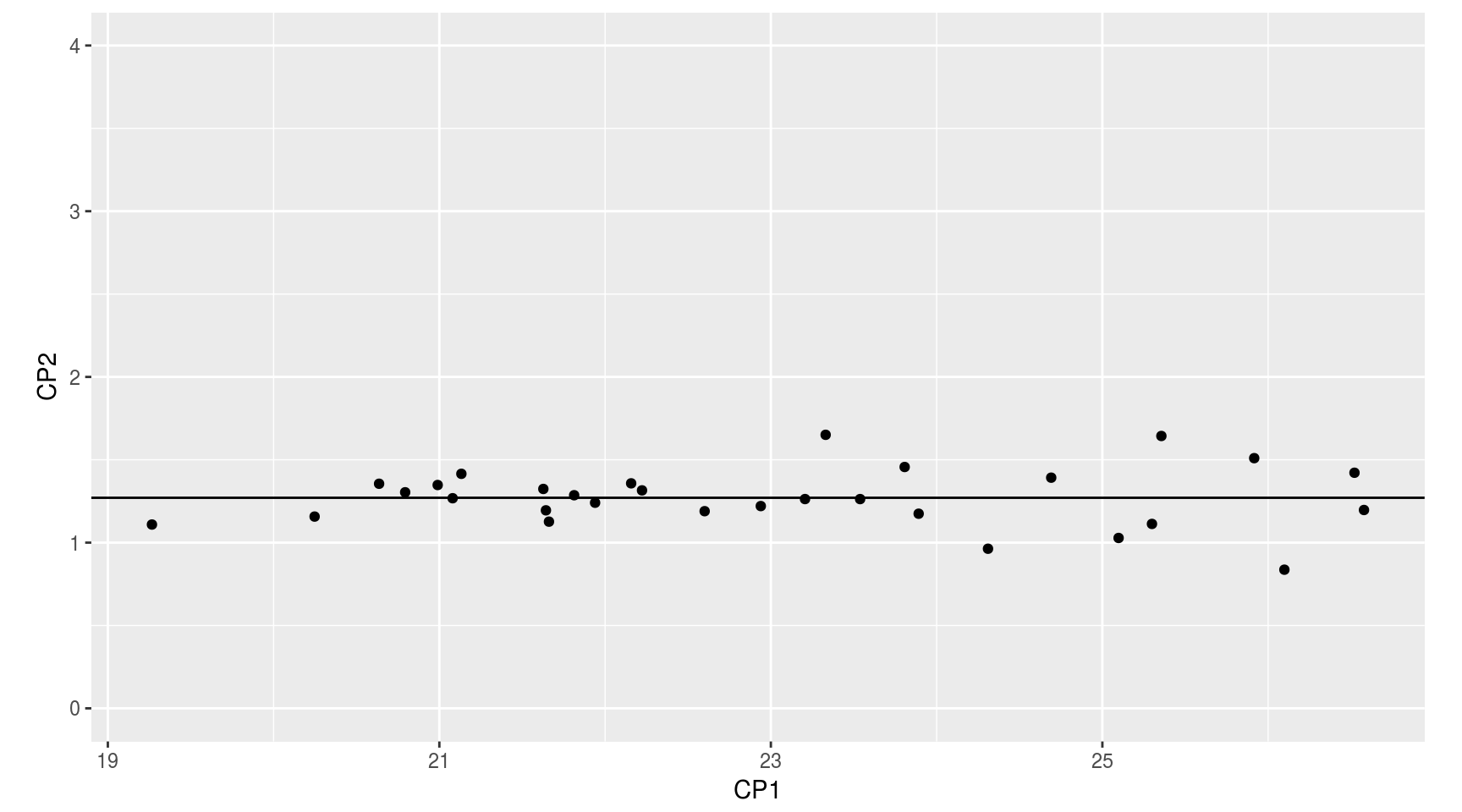
Nótese que, tal como hemos procedido, el origen de los ejes transformados (las componentes principales) coincide con el origen de los ejes originales (el punto (0,0) es el mismo en ambos sistemas de referencia). Desde el punto de vista de la interpretación es aconsejable situar el origen en el centro de la nube de puntos.
Para situar el origen en el centro de la nube de puntos, basta restar a cada variable su media:
data2=apply(data,2,scale,center=TRUE,scale=FALSE)Las componentes principales de los datos recentrados de esta forma coinciden con las componentes originales (lógicamente ya que recentrar los datos no altera la posición relativa de los mismos ni su variabilidad):
## Standard deviations (1, .., p=2):
## [1] 2.0147330 0.1778351
##
## Rotation (n x k) = (2 x 2):
## PC1 PC2
## temp -0.9927789 -0.1199587
## conc -0.1199587 0.9927789Las coordenadas de los puntos con respecto al sistema de referencia dado por las componentes principales centradas en el punto medio de la nube de puntos son ahora:
CP2=as.matrix(data2) %*% eigen(cov(data))$vectors
CP2## [,1] [,2]
## [1,] -1.67824703 0.121195440
## [2,] -2.34287149 0.372739330
## [3,] 2.21931934 0.033011796
## [4,] 0.79037993 0.044508479
## [5,] 1.88024384 0.144491851
## [6,] 0.07384215 -0.050220655
## [7,] -3.50789676 0.150892223
## [8,] 2.76567882 -0.113587368
## [9,] 2.02316274 0.076859107
## [10,] 1.35179665 -0.144201014
## [11,] -0.52542394 -0.008028823
## [12,] 1.37012154 -0.075906078
## [13,] -1.29693641 -0.307642763
## [14,] 2.37663328 0.084512518
## [15,] 0.85594460 0.086949903
## [16,] -2.28611653 -0.157900731
## [17,] -2.90296383 0.238961232
## [18,] -0.79413643 0.185603812
## [19,] -3.56527062 -0.073848161
## [20,] 1.19981845 0.015181004
## [21,] 3.74699924 -0.161652337
## [22,] -2.08483049 -0.242658784
## [23,] 1.38571617 0.053155177
## [24,] -0.19300856 -0.007904027
## [25,] 1.07348746 -0.029990690
## [26,] -0.87856339 -0.096304132
## [27,] 1.93294414 -0.002894300
## [28,] -0.31739626 0.379817135
## [29,] -3.08501319 -0.434060333
## [30,] 0.41258656 -0.081078812Gráficamente:
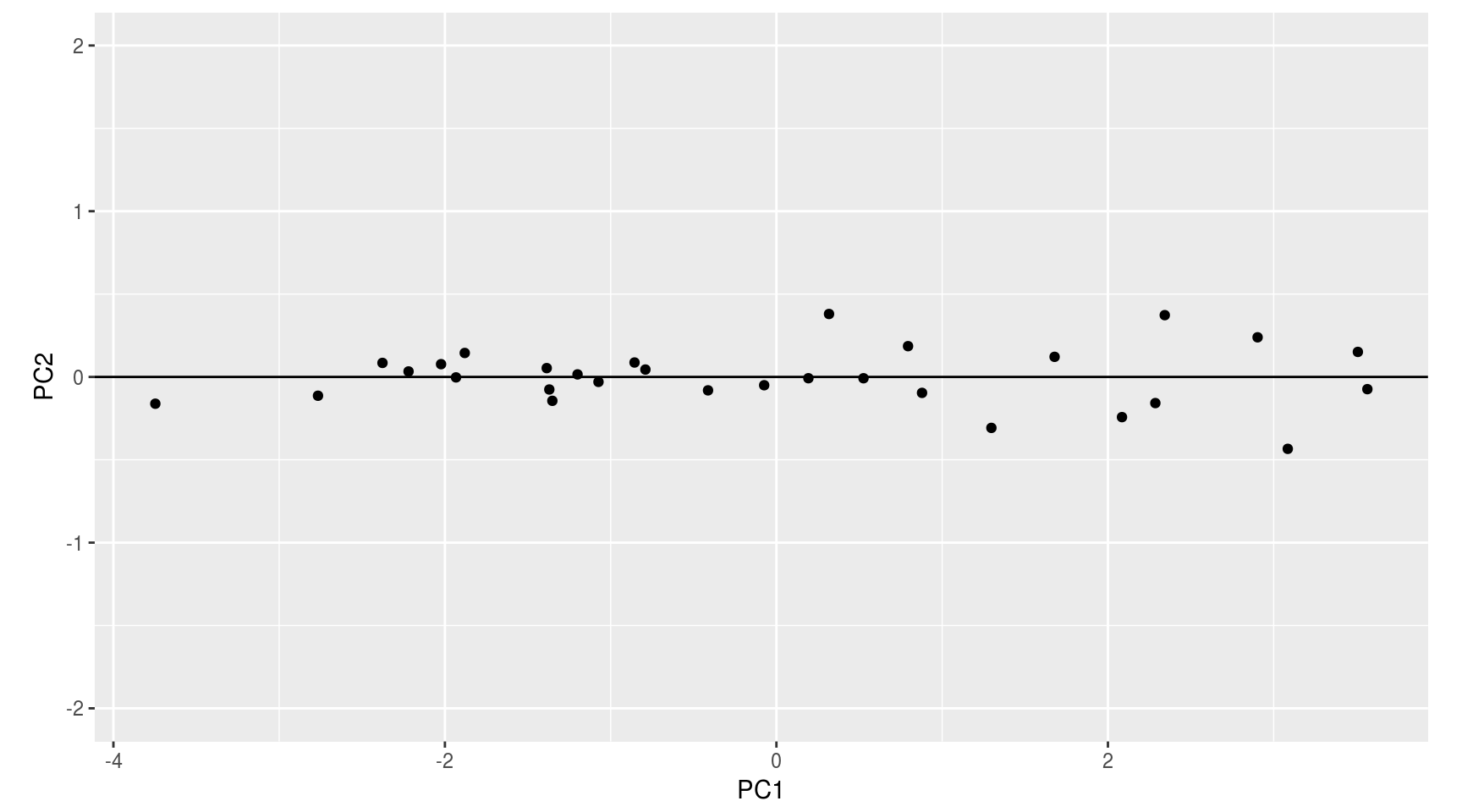
prcomp()En R las componentes principales pueden calcularse usando la función prcomp():
## Standard deviations (1, .., p=2):
## [1] 2.0147330 0.1778351
##
## Rotation (n x k) = (2 x 2):
## PC1 PC2
## temp -0.9927789 -0.1199587
## conc -0.1199587 0.9927789Nótese que la salida por defecto muestra las desviaciones típicas en la dirección de cada componente, que coinciden con las raíces cuadradas de las varianzas:
sqrt(eigen(cov(data))$values)## [1] 2.0147330 0.1778351La función summary() aplicada al resultado anterior nos da algo más de información:
summary(PC)## Importance of components:
## PC1 PC2
## Standard deviation 2.0147 0.17784
## Proportion of Variance 0.9923 0.00773
## Cumulative Proportion 0.9923 1.00000En la primera componente principal se concentra el 99.23% de la variabilidad total presente en la nube de puntos.
Gráficamente:
plot(PC)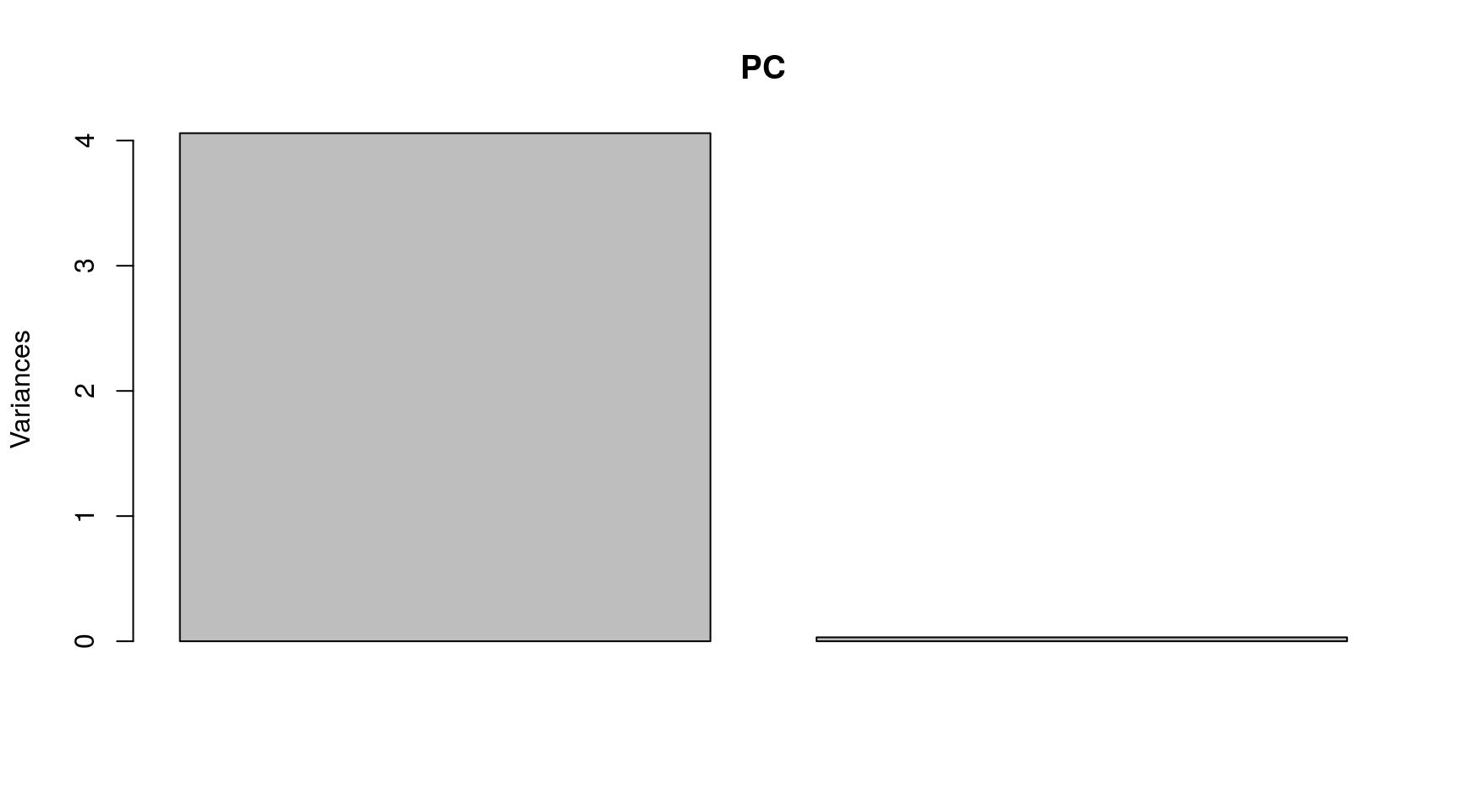
La función prcomp() proporciona también las coordenadas de los puntos respecto al sistema de referencia dado por las componentes principales y centrado en el centro (promedio) de la nube de puntos.
PC$x## PC1 PC2
## [1,] -1.67824703 -0.121195440
## [2,] -2.34287149 -0.372739330
## [3,] 2.21931934 -0.033011796
## [4,] 0.79037993 -0.044508479
## [5,] 1.88024384 -0.144491851
## [6,] 0.07384215 0.050220655
## [7,] -3.50789676 -0.150892223
## [8,] 2.76567882 0.113587368
## [9,] 2.02316274 -0.076859107
## [10,] 1.35179665 0.144201014
## [11,] -0.52542394 0.008028823
## [12,] 1.37012154 0.075906078
## [13,] -1.29693641 0.307642763
## [14,] 2.37663328 -0.084512518
## [15,] 0.85594460 -0.086949903
## [16,] -2.28611653 0.157900731
## [17,] -2.90296383 -0.238961232
## [18,] -0.79413643 -0.185603812
## [19,] -3.56527062 0.073848161
## [20,] 1.19981845 -0.015181004
## [21,] 3.74699924 0.161652337
## [22,] -2.08483049 0.242658784
## [23,] 1.38571617 -0.053155177
## [24,] -0.19300856 0.007904027
## [25,] 1.07348746 0.029990690
## [26,] -0.87856339 0.096304132
## [27,] 1.93294414 0.002894300
## [28,] -0.31739626 -0.379817135
## [29,] -3.08501319 0.434060333
## [30,] 0.41258656 0.081078812Por último, la función biplot() muestra en un único gráfico los puntos observados y las variables que componen las componentes principales, lo que puede ayudar a su interpretación:
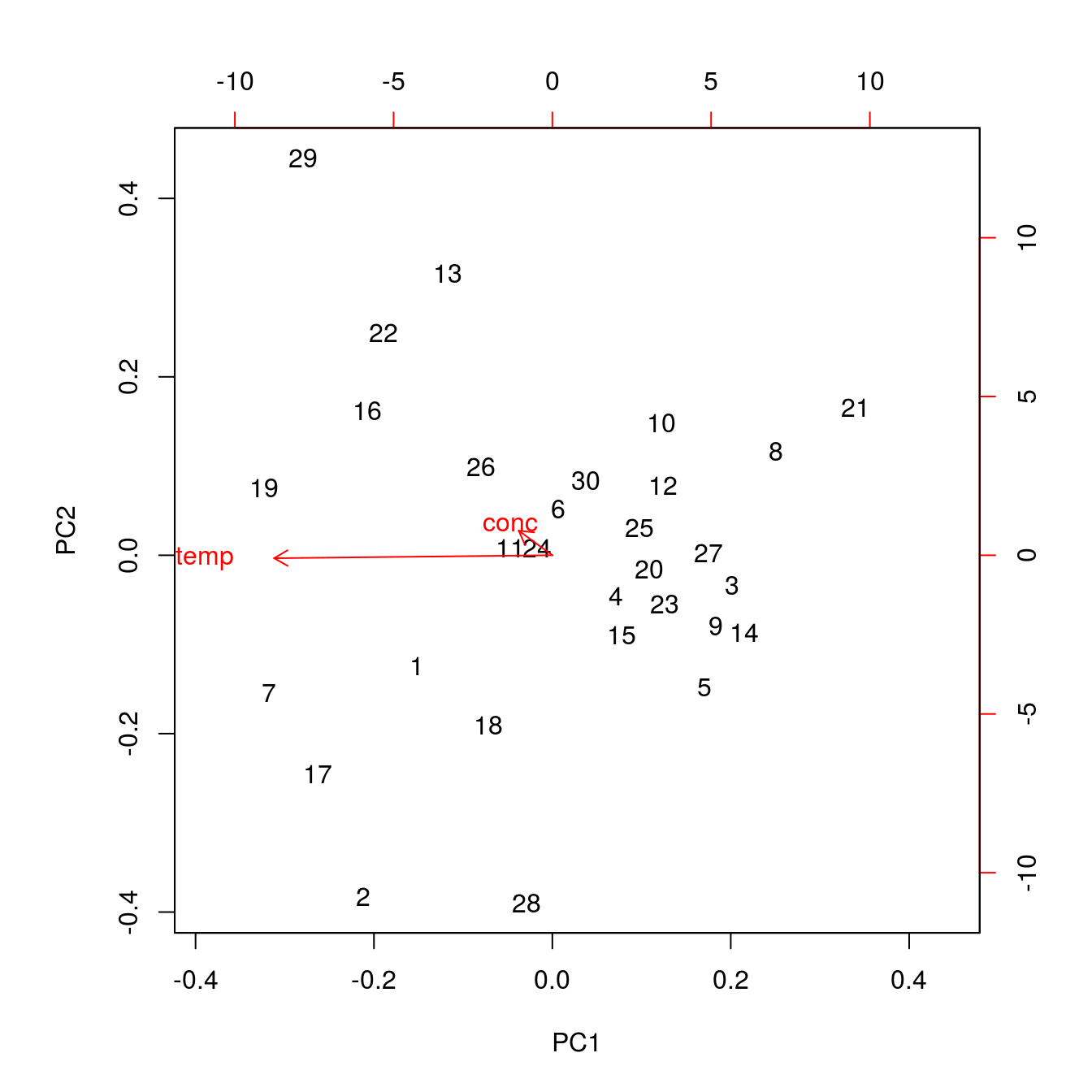
Se puede mejorar la presentación con la función ggbiplot(), del paquete homónimo (https://github.com/vqv/ggbiplot)
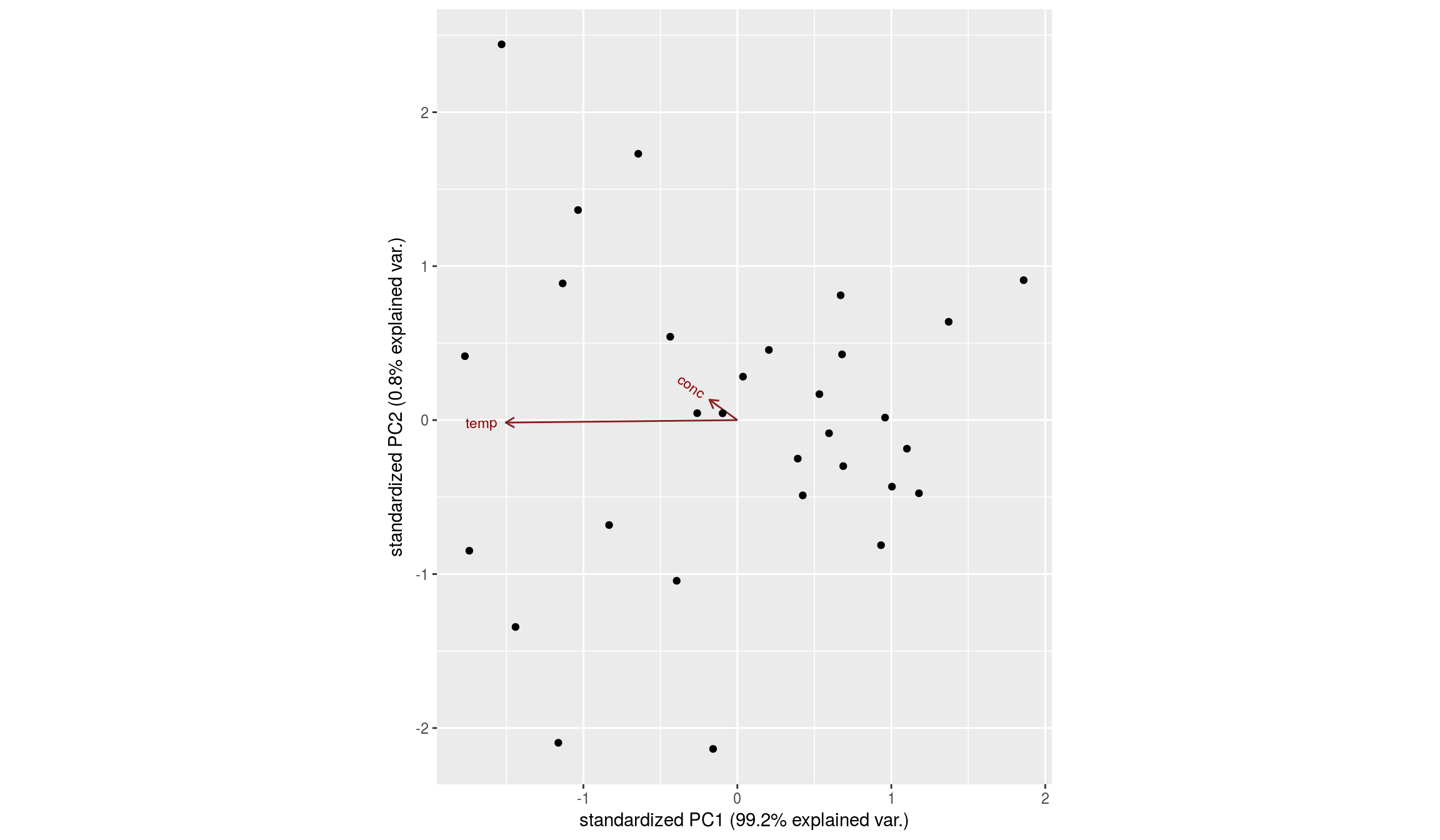
Veamos ahora la aplicación de las componentes principales a los datos de variables ambientales medidas a lo largo de la costa:
mayPC=prcomp(may[,1:17])
mayPC## Standard deviations (1, .., p=17):
## [1] 10.127873984 3.920210045 2.635802136 1.563565591 0.958603137
## [6] 0.828762837 0.547145851 0.292447331 0.245041391 0.169526897
## [11] 0.164497199 0.100040793 0.086173786 0.059964734 0.040346970
## [16] 0.027792275 0.007870373
##
## Rotation (n x k) = (17 x 17):
## PC1 PC2 PC3 PC4
## Temperature 0.0377046436 0.0494612915 -0.4052414026 0.9089618838
## pH -0.0018959054 -0.0015846516 -0.0011857021 -0.0047674263
## DO -0.0096681690 0.0081428322 -0.0162049478 -0.0066491994
## NO2 0.0973329899 -0.0766536536 0.1954097053 0.1292819064
## NO3 0.1050314540 -0.1279697870 0.4703663419 0.1880678618
## NH4 0.5918152641 0.2276702516 -0.5484984026 -0.2793610656
## DIN 0.7911186354 -0.1176568076 0.3386908358 0.1207406226
## PO4 0.0073895523 -0.0101006979 0.0200644049 0.0093007795
## COD 0.0127950656 -0.0201876988 0.0383458757 0.0055437362
## TSM 0.0195373192 -0.9429109164 -0.3070046440 -0.0883065450
## Chla 0.0345344809 -0.1231408193 0.2483881271 0.1370281876
## As 0.0010796357 -0.0069828079 0.0265001080 -0.0472657457
## Hg 0.0000296842 -0.0005034164 -0.0003020573 0.0026970239
## Zn -0.0063859734 -0.0685272378 -0.0368219826 -0.0046967811
## Cd -0.0006640443 0.0002038733 -0.0043049243 0.0002167222
## Pb -0.0028076831 0.0003128224 0.0060034512 0.0063136266
## Cu 0.0043640522 0.0075158013 -0.0242835773 0.0046709635
## PC5 PC6 PC7 PC8
## Temperature -3.195079e-02 -0.009032649 -0.0035620912 -0.0262561986
## pH -6.115763e-03 -0.006587117 -0.0156590763 0.0131397493
## DO 3.102422e-02 -0.043307920 -0.0224185652 -0.0593308515
## NO2 2.696320e-01 -0.133383521 0.0620165437 0.8562565199
## NO3 -8.124428e-01 0.181708936 -0.0003853336 0.1213277625
## NH4 -2.389276e-01 0.303537234 -0.1169235909 0.2195394844
## DIN 2.403636e-01 -0.266096901 0.1062394163 -0.2868894879
## PO4 -5.198042e-02 -0.037114102 -0.0119742161 0.0727917300
## COD 1.369368e-01 0.150188080 -0.0506965357 0.1610221183
## TSM -5.383604e-02 -0.040966311 -0.0603131118 0.0107815691
## Chla 3.465799e-01 0.767613268 -0.3851801165 -0.0817726428
## As 1.830618e-02 -0.008289512 -0.0257162859 0.1026140598
## Hg -3.924747e-04 -0.003113765 0.0056565789 -0.0007725476
## Zn 7.378890e-02 0.410751284 0.9011260044 -0.0301803479
## Cd 1.141733e-05 0.015672344 0.0068883872 -0.0023905013
## Pb 9.286792e-03 0.018467222 0.0403449456 0.0113500847
## Cu 4.190234e-03 0.004874082 0.0363853562 0.2600261362
## PC9 PC10 PC11 PC12
## Temperature 0.0137155585 0.013768528 0.028062918 -0.0198516232
## pH -0.0093092348 -0.007911795 0.020321619 0.0974315105
## DO 0.0065176669 -0.920620492 0.357101942 0.0513268136
## NO2 0.1723088865 -0.130134384 -0.223578923 -0.0100323508
## NO3 0.0277727081 -0.040966997 0.021888012 0.0606517247
## NH4 0.0595562867 -0.044542089 -0.046516390 -0.0095261084
## DIN -0.0663665427 0.039290003 0.050135417 0.0058274584
## PO4 0.0539316221 0.078561992 0.399083630 -0.6798242217
## COD 0.2893082451 0.289310102 0.731054263 0.4600470415
## TSM 0.0003080821 -0.002889073 -0.003540069 0.0091626202
## Chla -0.0829207334 -0.067566331 -0.113901839 -0.1123442643
## As 0.0316678553 0.089770186 0.213339088 -0.5138944651
## Hg -0.0072023831 -0.009389939 0.002821260 0.0001378378
## Zn 0.0243692696 -0.030616568 0.012368516 -0.0508619305
## Cd -0.0207860538 0.061127294 -0.038639120 0.1373859180
## Pb -0.0081446225 -0.136022983 -0.107135284 0.0595616876
## Cu -0.9303971139 0.065542948 0.225375365 0.0892646896
## PC13 PC14 PC15 PC16
## Temperature -0.047165131 0.005521104 -0.005469424 -0.006601339
## pH -0.067844818 -0.040173930 -0.925864546 0.354054360
## DO -0.019783150 0.100865581 -0.007283330 -0.064945487
## NO2 0.059780539 0.043983346 -0.002442504 0.002895749
## NO3 -0.034530933 0.015081297 0.011596088 -0.003740532
## NH4 0.011099249 0.002353195 0.003026762 0.002778390
## DIN -0.014514777 -0.008479154 -0.005697853 -0.002816596
## PO4 0.554074185 -0.208007733 -0.095064895 -0.003516682
## COD -0.050781527 -0.081586537 0.072369520 0.012816437
## TSM -0.002046603 -0.004568180 0.005052127 -0.001142571
## Chla 0.035631001 0.011286257 -0.016490189 0.007029796
## As -0.788660917 0.096920279 -0.062763767 -0.177224361
## Hg -0.006298127 -0.011909923 0.019992769 -0.020883090
## Zn 0.001613111 0.043395904 -0.020744452 0.013786832
## Cd 0.143731603 0.047424050 -0.348370707 -0.911468049
## Pb -0.184744893 -0.960180302 0.027022312 -0.084090317
## Cu -0.003564353 -0.016019441 0.032802426 0.015452989
## PC17
## Temperature -0.0027007294
## pH 0.0248891837
## DO -0.0097763398
## NO2 0.0013317624
## NO3 -0.0006928348
## NH4 0.0026074453
## DIN -0.0022528541
## PO4 0.0028987969
## COD 0.0011230009
## TSM -0.0003375714
## Chla 0.0042273093
## As -0.0053842001
## Hg 0.9993921085
## Zn -0.0027573049
## Cd -0.0100848708
## Pb -0.0161204701
## Cu -0.0072889453summary(mayPC)## Importance of components:
## PC1 PC2 PC3 PC4 PC5 PC6
## Standard deviation 10.1279 3.9202 2.63580 1.56357 0.9586 0.82876
## Proportion of Variance 0.7923 0.1187 0.05366 0.01888 0.0071 0.00531
## Cumulative Proportion 0.7923 0.9110 0.96466 0.98355 0.9907 0.99595
## PC7 PC8 PC9 PC10 PC11 PC12
## Standard deviation 0.54715 0.29245 0.24504 0.16953 0.16450 0.10004
## Proportion of Variance 0.00231 0.00066 0.00046 0.00022 0.00021 0.00008
## Cumulative Proportion 0.99826 0.99892 0.99939 0.99961 0.99982 0.99990
## PC13 PC14 PC15 PC16 PC17
## Standard deviation 0.08617 0.05996 0.04035 0.02779 0.00787
## Proportion of Variance 0.00006 0.00003 0.00001 0.00001 0.00000
## Cumulative Proportion 0.99995 0.99998 0.99999 1.00000 1.00000Con 2 componentes recogemos el 91% de la variabilidad en los datos y con 3 componentes el 96.5%.
Gráficamente:
plot(mayPC)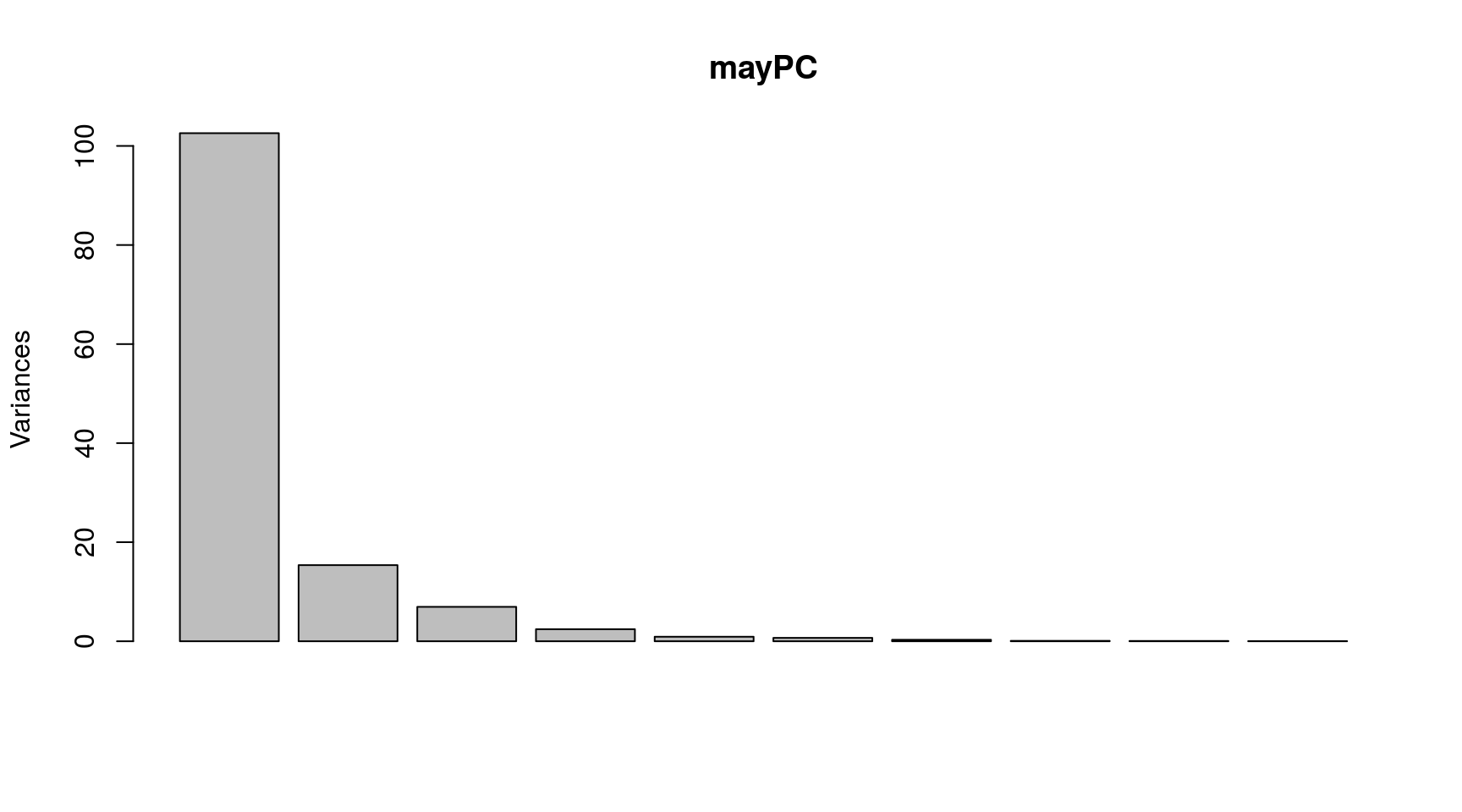
Podemos ver las coordenadas de los puntos respecto a las componentes principales
head(mayPC$x)## PC1 PC2 PC3 PC4 PC5 PC6
## [1,] -15.527534 8.619087 -1.8690163 -2.336380 0.3171959 -1.1899597
## [2,] -18.021334 -1.538813 -0.8857441 -1.322336 -0.8609959 -1.5872505
## [3,] 4.596975 3.284975 0.2605533 -1.936944 -0.5638501 -0.2146216
## [4,] -3.270559 -0.806144 -0.9930682 -1.928164 -0.5034174 1.5164027
## [5,] 8.227151 -5.957258 0.8624052 -1.225362 1.4757712 2.1656847
## [6,] -16.183880 4.894091 -0.4774078 -1.492710 -1.3401406 -0.7893206
## PC7 PC8 PC9 PC10 PC11
## [1,] 0.19894035 0.2748093 -0.18823137 0.30648582 0.11609590
## [2,] 0.04488376 -0.5729049 -0.07268862 0.19760652 0.32146625
## [3,] -0.36906427 0.3518057 0.27672870 -0.14231182 0.11355224
## [4,] -0.38991790 -0.1354737 0.03149421 -0.08323958 0.01987632
## [5,] 0.29236538 -0.3963799 0.01094414 0.26424589 0.23786566
## [6,] 0.98446485 -0.1479414 -0.04372229 0.35579467 0.32182891
## PC12 PC13 PC14 PC15 PC16
## [1,] -0.1332296899 0.185549515 0.130341137 -0.011833698 0.034531947
## [2,] 0.0470453474 0.031511478 -0.006831779 -0.011431290 -0.032369318
## [3,] 0.0001561318 0.002113765 0.013970568 0.008528950 -0.009553553
## [4,] 0.0463416566 -0.067194201 0.074697138 -0.022140507 -0.009238032
## [5,] -0.0665087396 0.001601523 0.046015037 -0.016624613 0.038011749
## [6,] -0.0218466644 -0.080025573 0.030487207 0.005139331 -0.026023702
## PC17
## [1,] -0.019286864
## [2,] 0.006965164
## [3,] -0.001774867
## [4,] -0.008899477
## [5,] 0.019069130
## [6,] 0.009289002Representamos la nube de puntos respecto a las dos primeras componentes principales:
ggplot(data.frame(mayPC$x),aes(x=PC1,y=PC2)) + geom_point()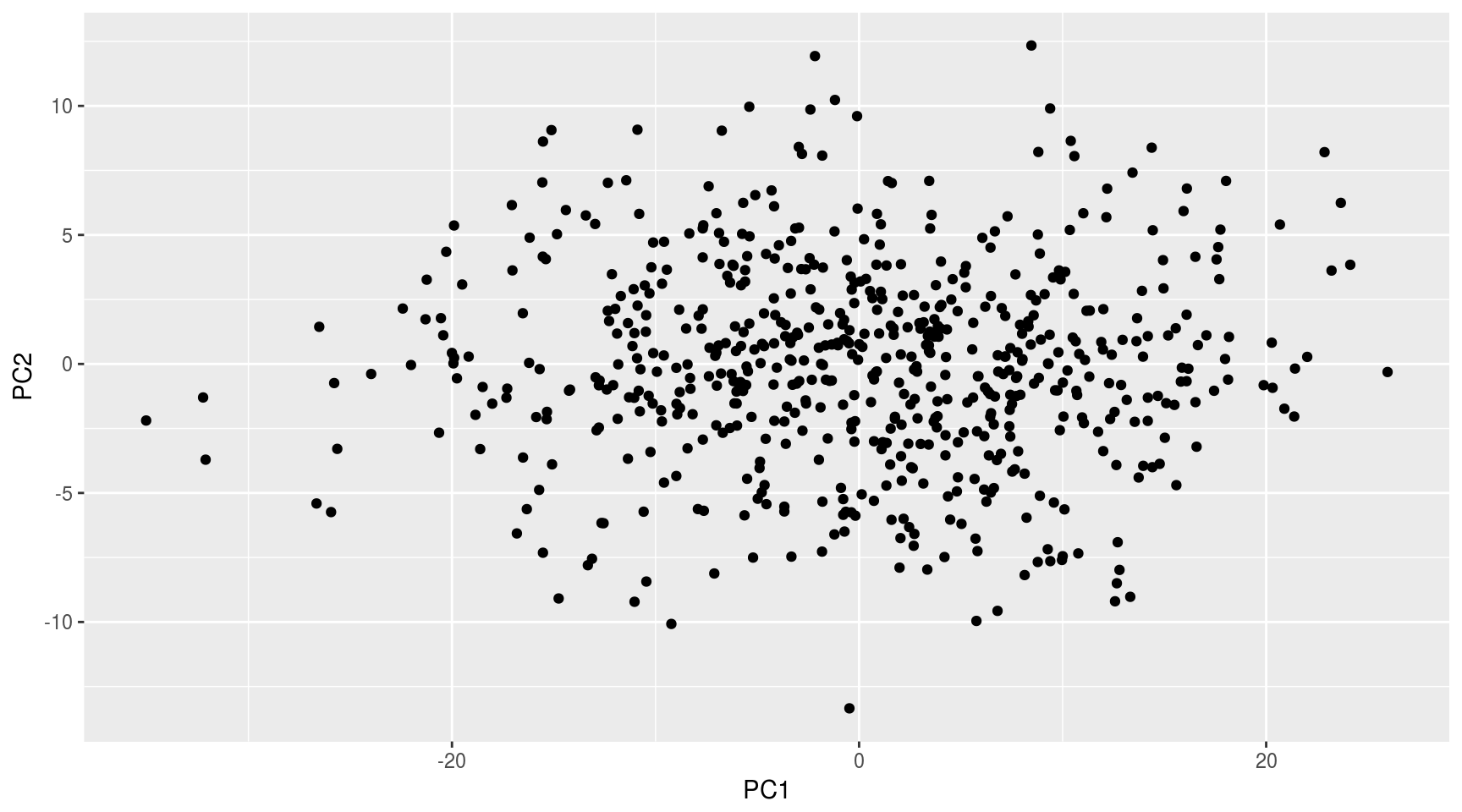
Si damos color a los puntos según la localización de la estación de medida:
mayPCcoords=data.frame(mayPC$x,location=factor(may$location))
ggplot(data.frame(mayPCcoords),aes(x=PC1,y=PC2,color=location)) + geom_point()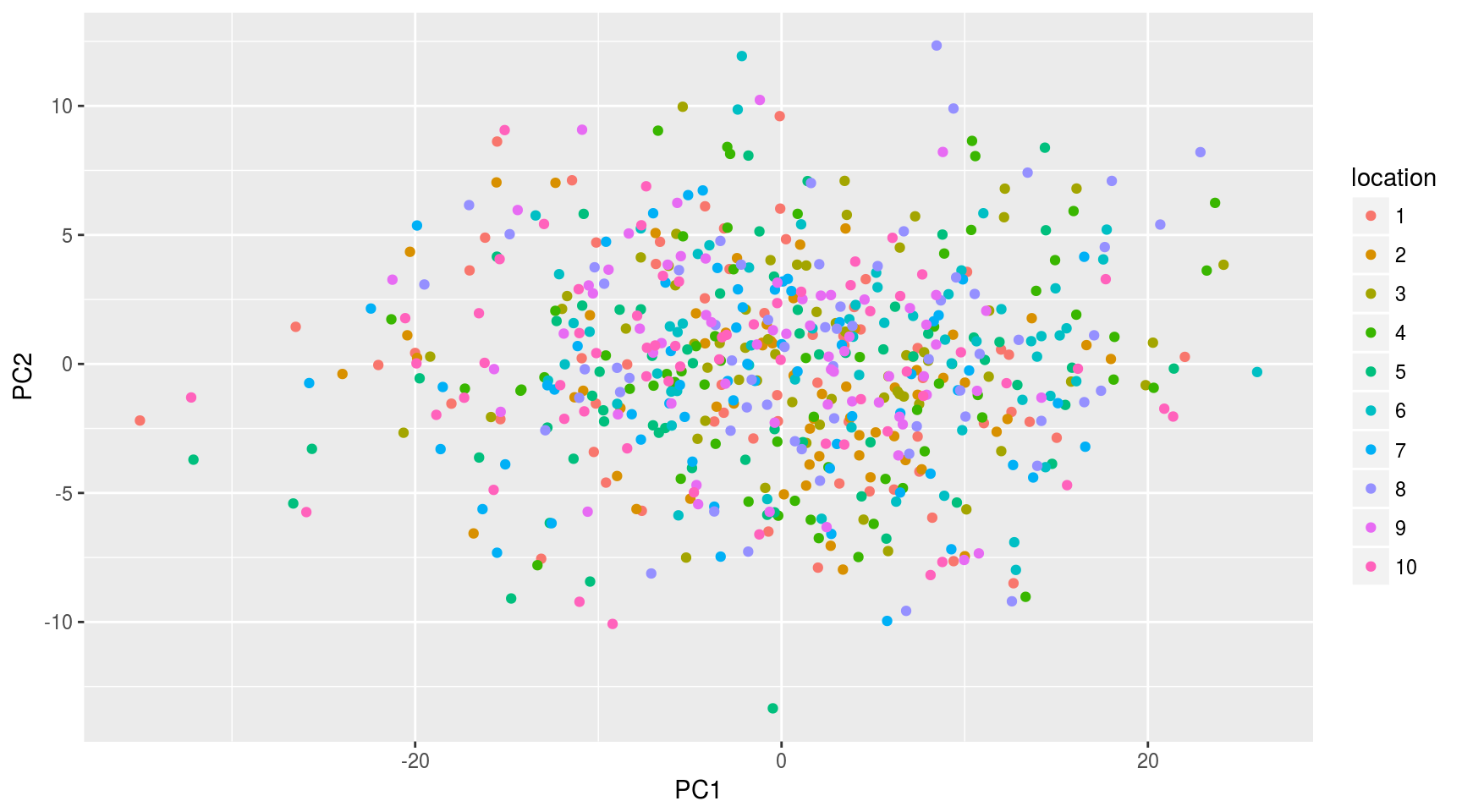
Un biplot nos puede ayudar a interpretar (o no) las dos primeras componentes principales:
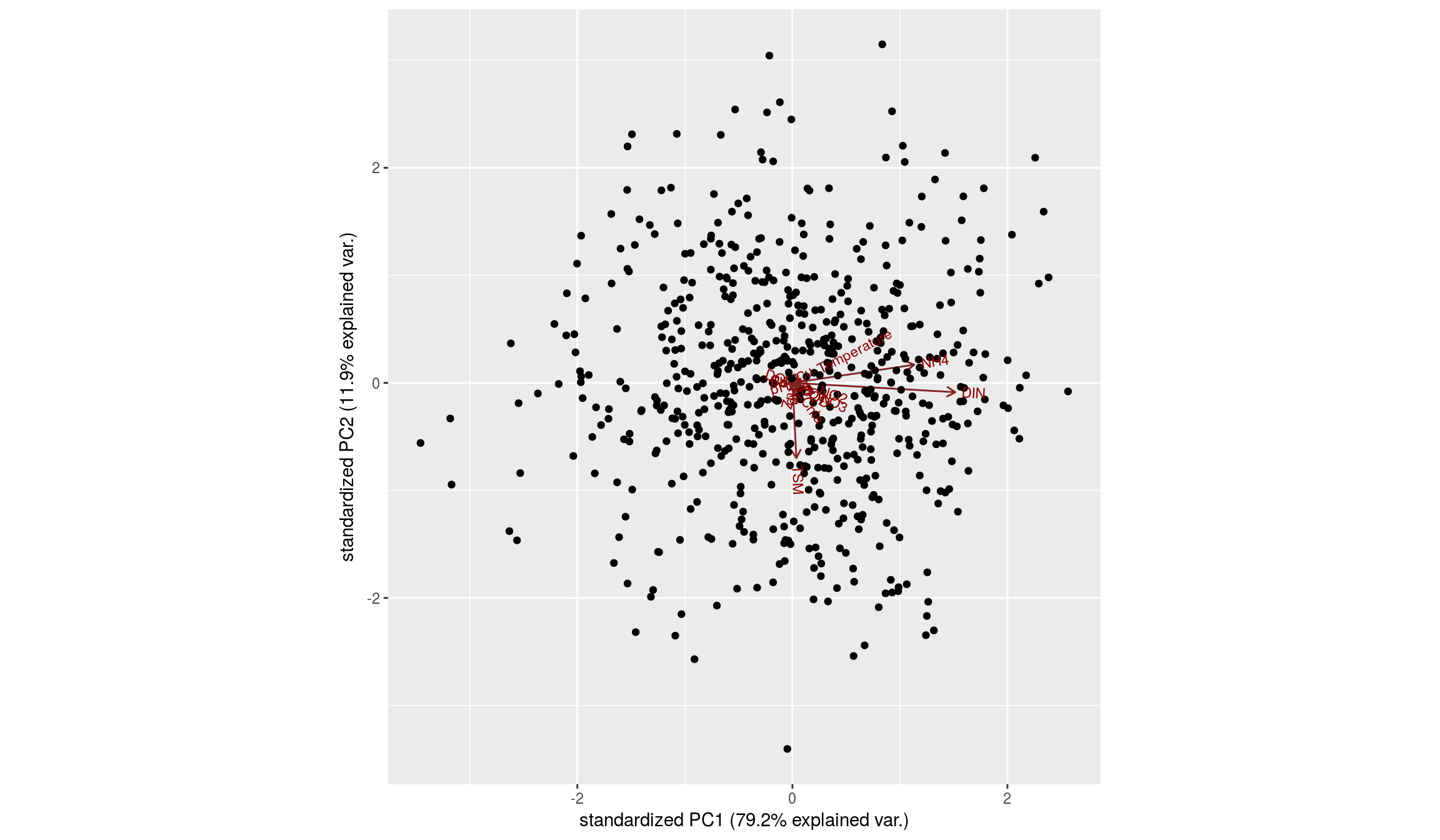
Puede ocurrir que las variables de entrada se midan en escalas tan diferentes que la variabilidad recogida por el modelo obedezca más a la escala de medida que a la propia variabilidad intrínseca de la variable.
Por ello resulta conveniente calcular las componentes principales estandarizando todos las variables de entrada de forma que su importancia relativa no obedezca a las unidades de medida.
Vemos que en nuestro caso efectivamente hay grandes diferencias de escala entre las variables:
colMeans(may[,1:17])## Temperature pH DO NO2 NO3 NH4
## 31.72333871 8.16088710 6.45451613 3.66741935 5.10106452 22.00580645
## DIN PO4 COD TSM Chla As
## 29.64235484 0.42825806 1.11111290 25.63129032 4.23950000 0.52148387
## Hg Zn Cd Pb Cu
## 0.04020968 12.73511290 0.34277419 0.92043548 2.76725806El análisis con las variables estandarizadas se obtiene mediante:
mayPC=prcomp(may[,1:17],scale. = TRUE)
summary(mayPC)## Importance of components:
## PC1 PC2 PC3 PC4 PC5 PC6 PC7
## Standard deviation 2.2297 1.5569 1.392 1.18913 1.0932 0.97783 0.91440
## Proportion of Variance 0.2924 0.1426 0.114 0.08318 0.0703 0.05624 0.04918
## Cumulative Proportion 0.2924 0.4350 0.549 0.63220 0.7025 0.75875 0.80793
## PC8 PC9 PC10 PC11 PC12 PC13
## Standard deviation 0.87737 0.76093 0.6825 0.66856 0.6185 0.52131
## Proportion of Variance 0.04528 0.03406 0.0274 0.02629 0.0225 0.01599
## Cumulative Proportion 0.85321 0.88727 0.9147 0.94097 0.9635 0.97946
## PC14 PC15 PC16 PC17
## Standard deviation 0.38549 0.34690 0.27247 0.07783
## Proportion of Variance 0.00874 0.00708 0.00437 0.00036
## Cumulative Proportion 0.98820 0.99528 0.99964 1.00000Ahora necesitamos 3 variables para llegar a explicar un 54.9% de variabilidad. Esto significa que en el análisis anterior la escala de medida de cada variable tuvo un impacto indeseado.
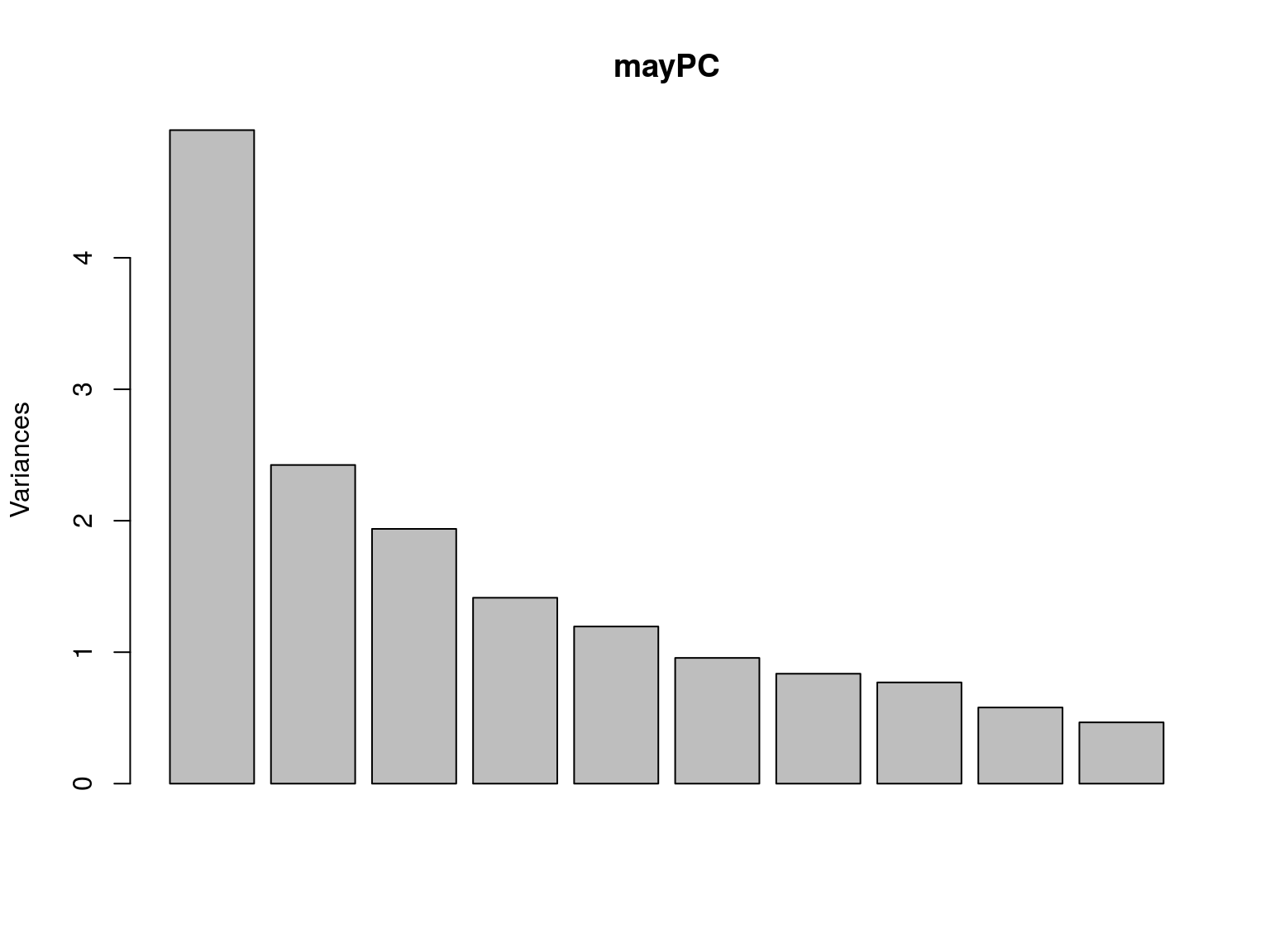
Obtenemos de nuevo el biplot:
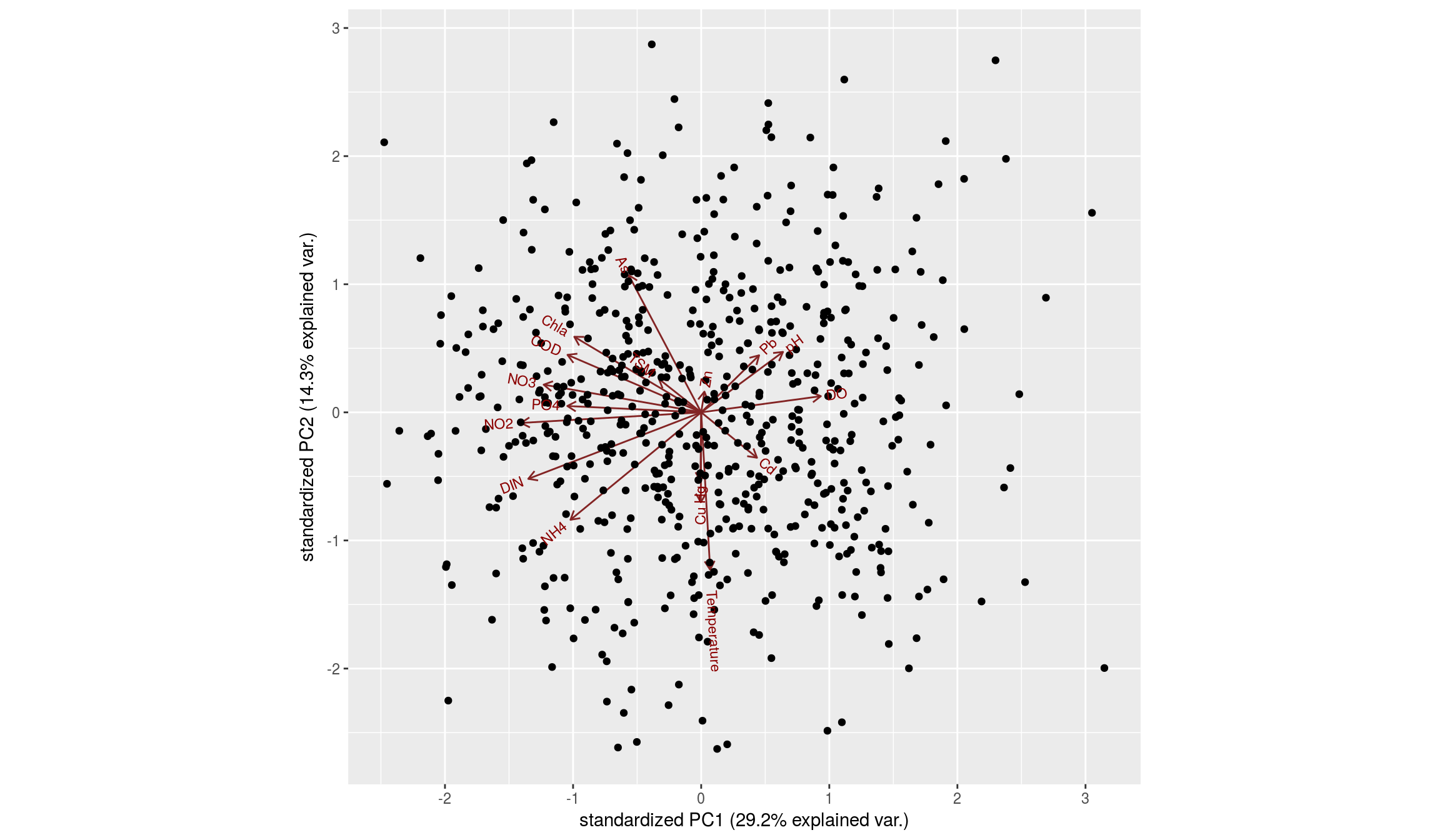
Biplot para las componentes 2 y 3:
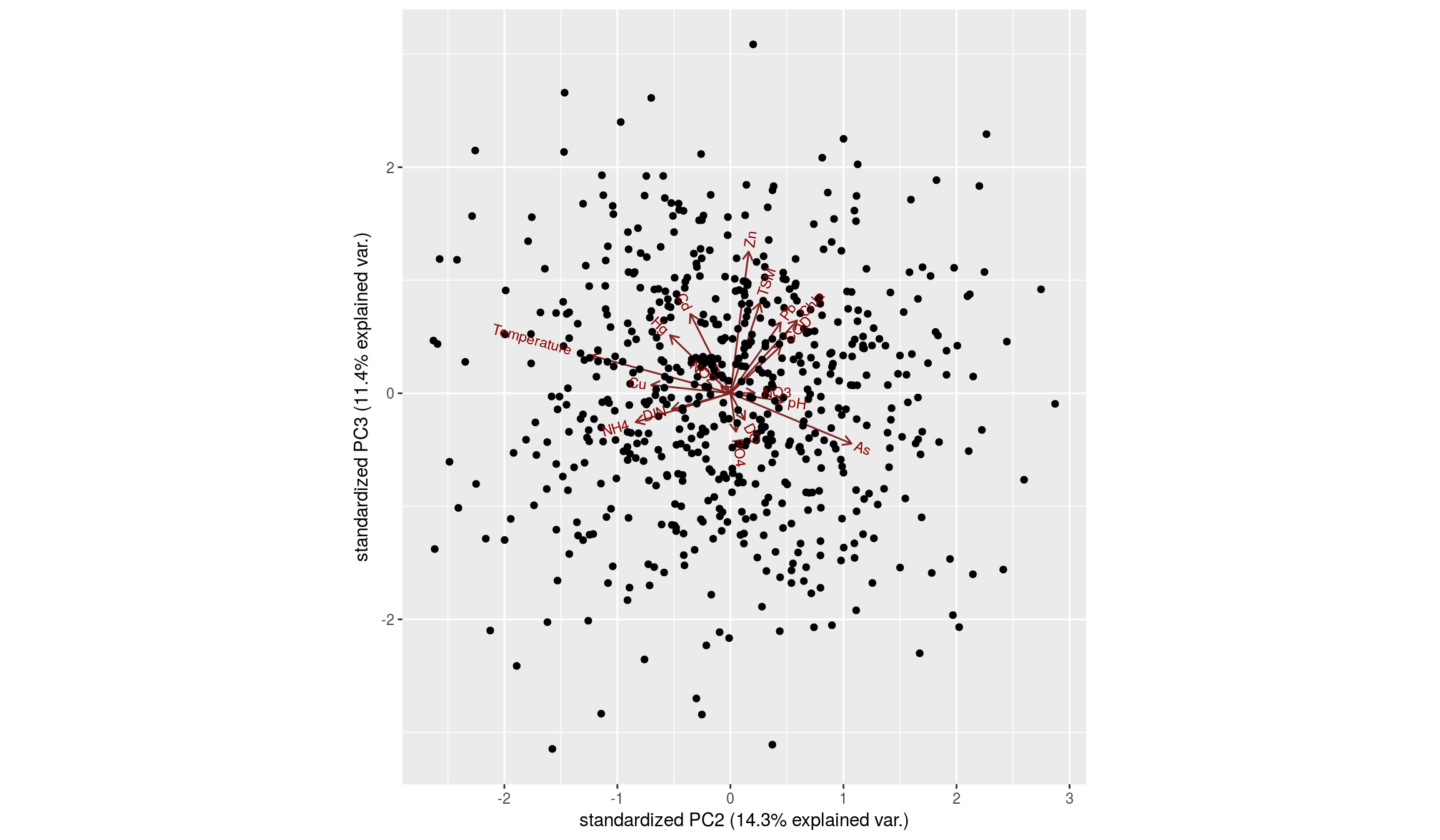
Representamos de nuevo nube de puntos respecto a las dos primeras componentes principales:
mayPCcoords=data.frame(mayPC$x,location=factor(may$location))
ggplot(data.frame(mayPCcoords),aes(x=PC1,y=PC2,color=location)) + geom_point()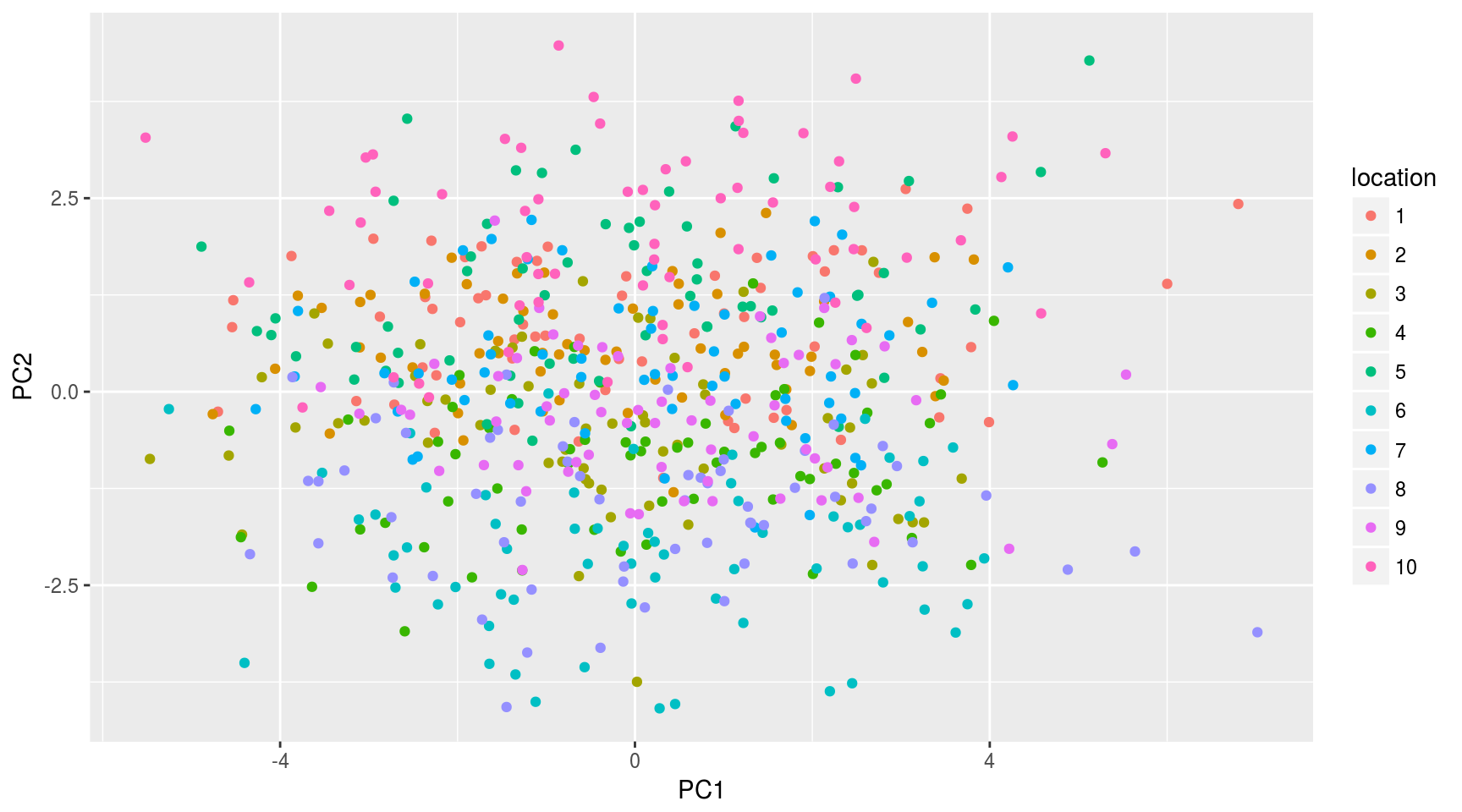
Ahora sí se aprecian agrupaciones entre observaciones dentro de la misma localización.
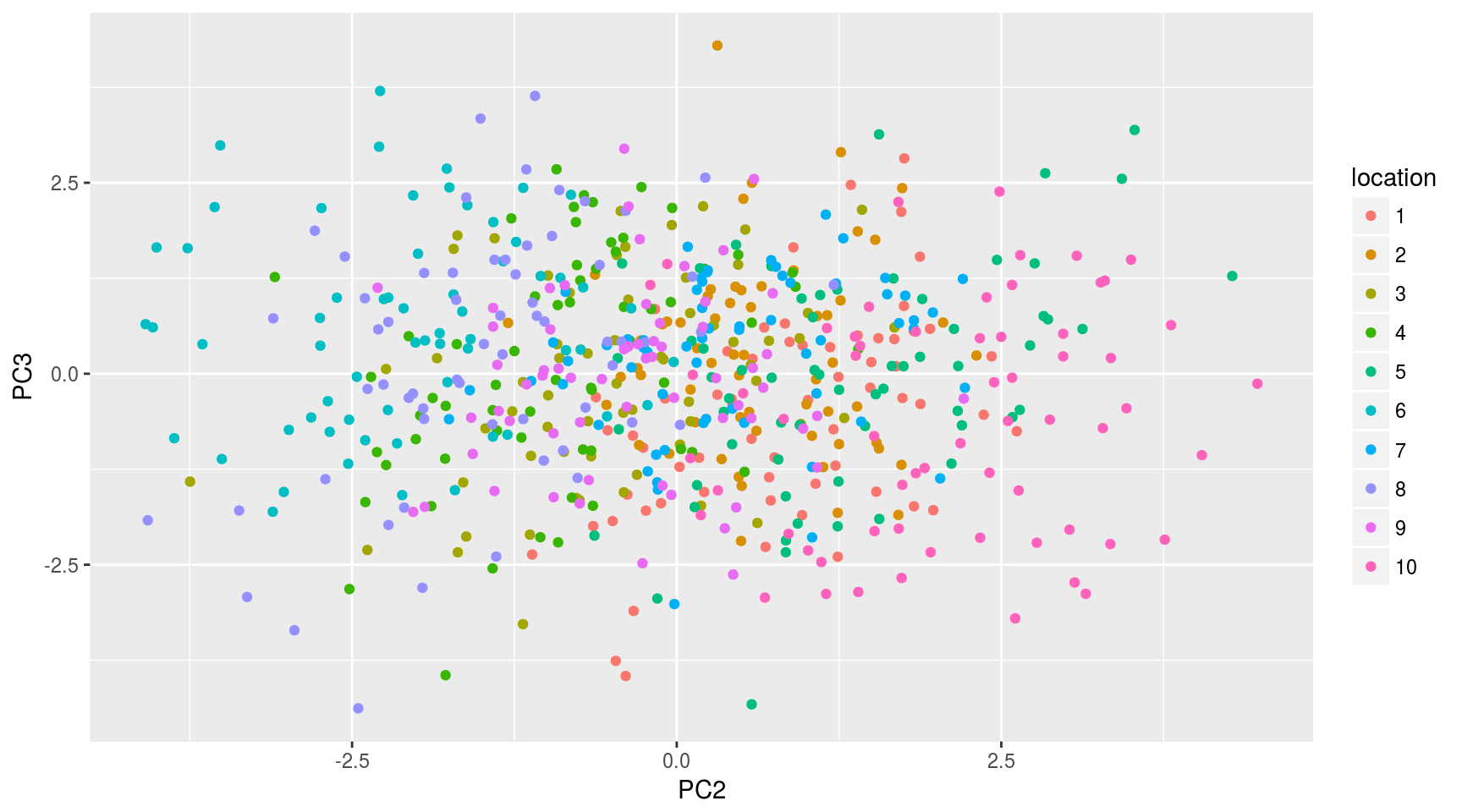
Respecto a la segunda y tercera componentes:
ggplot(data.frame(mayPCcoords),aes(x=PC2,y=PC3,color=location)) + geom_point()