Modelos lineales
Definición
Un vector de variables aleatorias \(\mathbf{Y}= \left(y_1,y_2,\dots, y_n\right)'\) sigue un modelo lineal si:
\[\mathbf{Y} \cong \mathbf{N_n} \left(\mathbf{X} \beta, \mathbf{I_n}\sigma \right)\]
donde:
- \(\mathbf{X}=\left(\begin{array}{ccccc} 1 & x_{11} & x_{21} & \ldots & x_{p1}\\ 1 & x_{12} & x_{22} & \vdots & x_{p2}\\ 1 & \vdots & \vdots & \ddots\\ 1 & x_{1n} & x_{2n} & \ldots & x_{pn} \end{array}\right)\) es una matriz de dimensión \(n\times p\), cuya columna \(j\)-ésima (j>2) contiene los valores observados en la variable \(X_j\).
- \(\beta=\left(\begin{array}{c} \beta_{0}\\ \beta_{1}\\ \vdots\\ \beta_{p} \end{array}\right)\) es un vector de parámetros \(p\)-dimensional.
- \(\mathbf{I_{n}}\) es la matriz identidad de orden \(n\).
De manera alternativa y equivalente, el modelo lineal puede expresarse como: \[\mathbf{Y=}\beta_{0}+\beta_{1}X_{1}+\beta_{2}X_{2}+\dots+\beta_{p}X_{p}+\varepsilon,\,\,\,\,\,\,\varepsilon\approx N \left(0,\sigma\right)\]
siendo las \(X_j\) las columnas de la matrix \(\mathbf{X}\) anterior.
la variable \(\mathbf{Y}\) se conoce habitualmente como variable respuesta y las variables \(\mathbf{X}\) como variables explicativas o predictoras.
Bajo esta definición general se engloban los modelos clásicos de:
Regresión: La variable \(\mathbf{Y}\) y las \(\mathbf{X}\) son continuas
Análisis de la varianza: La variable \(\mathbf{Y}\) es continua y las \(\mathbf{X}\) son categóricas.
Análisis de la covarianza: La variable \(\mathbf{Y}\) es continua y entre las \(\mathbf{X}\) hay variables categóricas y variables continuas
Cuando en este modelo la distribución normal se cambia por otra distribución y la relación entre la \(\mathbf{Y}\) y las \(\mathbf{X}\) es lineal a través de una función de enlace \(f\), nos encontramos ante los modelos lineales generalizados:
Regresión logística Binaria: La variable \(\mathbf{Y}\) es dicotómica y las \(X_i\) pueden ser categóricas y/o continuas. La distribución de \(\mathbf{Y}\) es binomial, \[\mathbf{Y} \cong \mathbf{B} \left(N,f(\mathbf{X} \beta)\right)\]
Regresión de Poisson: La variable \(\mathbf{Y}\) es una variable de recuento y las \(X_i\) pueden ser categóricas y/o continuas. La distribución de \(\mathbf{Y}\) es de Poisson, \[\mathbf{Y} \cong \mathbf{P} \left(f(\mathbf{X} \beta)\right)\]
Cuando la relación entre la \(\mathbf{Y}\) y las \(\mathbf{X}\) es de la forma: \[Y=f_{1} \left(X_{1}\right)+f_{2}\left(X_{2}\right)+\dots f_{p}\left(X_{p}\right)+\varepsilon\] nos encontramos ante los modelos aditivos generalizados (GAM).
Algunos ejemplos nos ayudaran a entender el significado y aplicación de estos modelos.
Ejemplo 1: Ecología reproductiva del cangrejo de herradura
Info sobre esta especie, Más info

cangrejo
Durante la temporada de desove, las hembras de esta especie migran a la costa para realizar la puesta, con un macho enganchado en su cola. Cavan en la arena, donde depositan los huevos que son fertilizados externamente, tanto por el macho enganchado a la hembra como por otros machos que se reúnen alrededor de la pareja. Estos otros machos reciben el nombre de satélites. El archivo crabs.txt contiene datos de un estudio realizado sobre esta especie en el golfo de Mexico. Las variables contenidas en el archivo son:
- Crab: Número de identificación de la hembra.
- y: Número de machos satélite.
- Weight: Peso
- Width: Anchura del caparazón
- Color: color del caparazón, de 1 a 4. El color se relaciona con la edad, siendo 1 el color más claro, correspondiente a ejemplares más jóvenes y 4 el color más oscuro.
- Spine: Estado de las espinas laterales del cangrejo: 1: buen estado en ambos lados, 2: Un lado en buen estado, el otro dañado, 3: ambos lados dañados.
El siguiente código R nos permite acceder a los datos, y mostrar los valores registrados para los 6 primeros ejemplares:
library(RCurl)
miCsv=getURL("https://dl.dropboxusercontent.com/u/7610774/GSRP/Crabs.txt")
cangrejos=read.table(textConnection(miCsv),header=TRUE)
head(cangrejos)## crab y weight width color spine
## 1 [1,] 8 3.05 28.3 2 3
## 2 [2,] 0 1.55 22.5 3 3
## 3 [3,] 9 2.30 26.0 1 1
## 4 [4,] 0 2.10 24.8 3 3
## 5 [5,] 4 2.60 26.0 3 3
## 6 [6,] 0 2.10 23.8 2 3
Ejemplo 2: Long-term changes in deep-water fish populations in the northeast Atlantic: a deeper reaching effect of fisheries?

“Moofushi Kandu fish” by Bruno de Giusti - Own work. Licensed under CC BY-SA 2.5 it via Commons - https://commons.wikimedia.org/wiki/File:Moofushi_Kandu_fish.jpg#/media/File:Moofushi_Kandu_fish.jpg
En este artículo se estudia el efecto de las pesquerías en el Atlántico nororiental sobre las poblaciones de peces de aguas profundas. Para ello los autores dispusieron de datos de campañas realizadas desde 1997 a 1989 y desde 1997 a 2002, a profundidades de 800 a 4800 metros. Durante este tiempo, la abundancia de peces decreció de manera significativa a todas las profundidades de 800 a 2500 metros, en particular a profundidades mayores que las habituales en pesca comercial (aproximadamente 1600 metros). Los datos se encuentran disponibles en este archivo, y puede accederse directamente a ellos con R mediante:
miCsv=getURL("https://dl.dropboxusercontent.com/u/7610774/GSRP/fishing.csv")
pesca=read.table(textConnection(miCsv),header=TRUE,sep=",")
head(pesca)## X site totabund density meandepth year period sweptarea
## 1 1 1 76 0.002070281 804 1978 1977-1989 36710.00
## 2 2 2 161 0.003519799 808 2001 2000-2002 45741.25
## 3 3 3 39 0.000980515 809 2001 2000-2002 39775.00
## 4 4 4 410 0.008039216 848 1979 1977-1989 51000.00
## 5 5 5 177 0.005933375 853 2002 2000-2002 29831.25
## 6 6 6 695 0.021800501 960 1980 1977-1989 31880.00
Descripción de los datos
Descripción univariante: resumen general, tablas y gráficos
La descripción univariante de datos tiene como objetivo mostrar las características relevantes de cada una de las variables medidas en la muestra.
Resumen general:
summary(cangrejos)## crab y weight width
## [1,] : 1 Min. : 0.000 Min. :1.200 Min. :21.0
## [10,] : 1 1st Qu.: 0.000 1st Qu.:2.000 1st Qu.:24.9
## [100,] : 1 Median : 2.000 Median :2.350 Median :26.1
## [101,] : 1 Mean : 2.919 Mean :2.437 Mean :26.3
## [102,] : 1 3rd Qu.: 5.000 3rd Qu.:2.850 3rd Qu.:27.7
## [103,] : 1 Max. :15.000 Max. :5.200 Max. :33.5
## (Other):167
## color spine
## Min. :1.000 Min. :1.000
## 1st Qu.:2.000 1st Qu.:2.000
## Median :2.000 Median :3.000
## Mean :2.439 Mean :2.486
## 3rd Qu.:3.000 3rd Qu.:3.000
## Max. :4.000 Max. :3.000
##
Tablas para las variables discretas:
attach(cangrejos)
table(y)## y
## 0 1 2 3 4 5 6 7 8 9 10 11 12 14 15
## 62 16 9 19 19 15 13 4 6 3 3 1 1 1 1table(color)## color
## 1 2 3 4
## 12 95 44 22table(spine)## spine
## 1 2 3
## 37 15 121
Diagramas de barras: una imagen vale más que mil palabras.
barplot(table(y),main="Número de satélites",col="cyan")
barplot(table(color),main="Color del Caparazón",col="pink")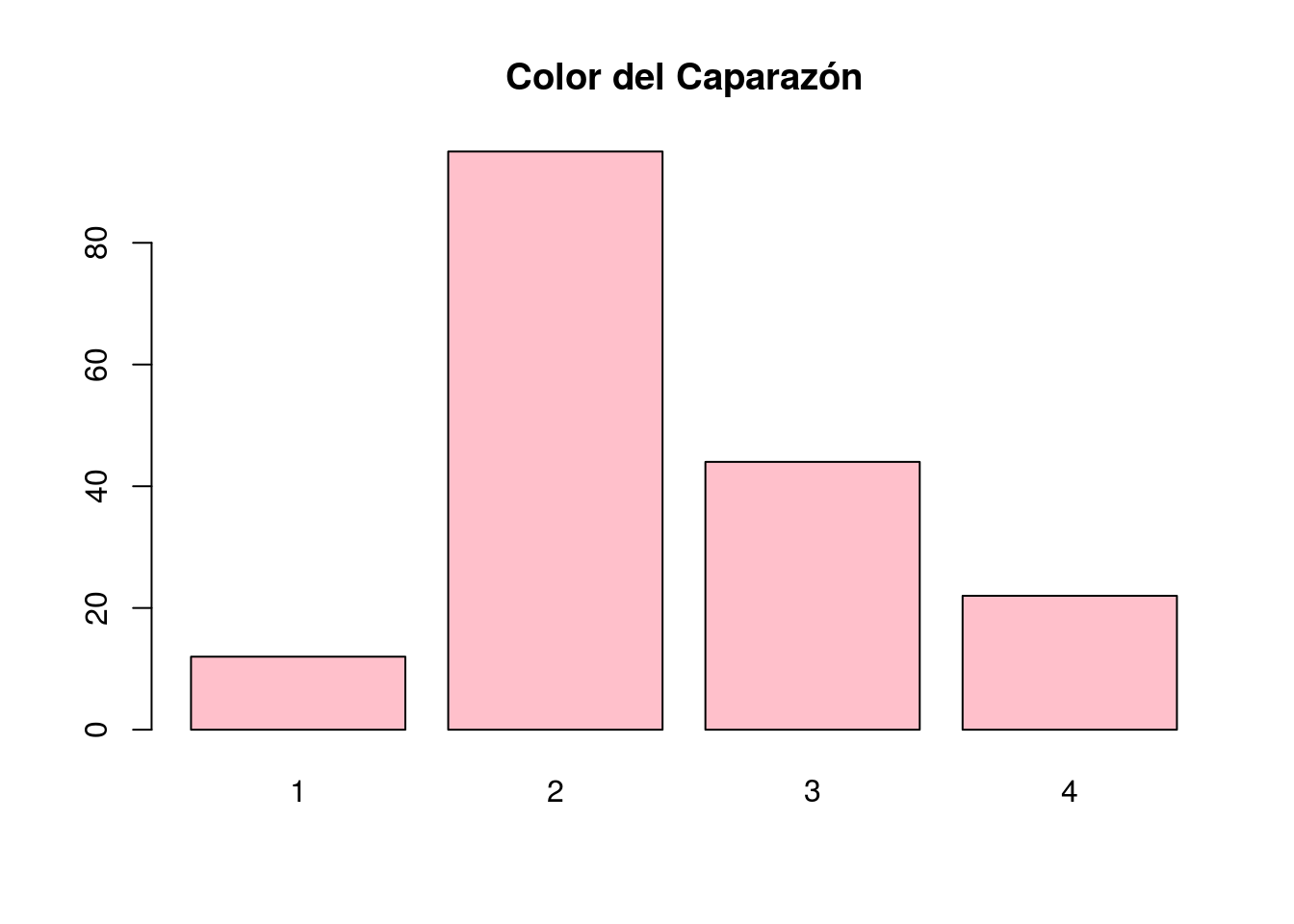
barplot(table(spine),main="Estado de las espinas",col=c("green","yellow","red"))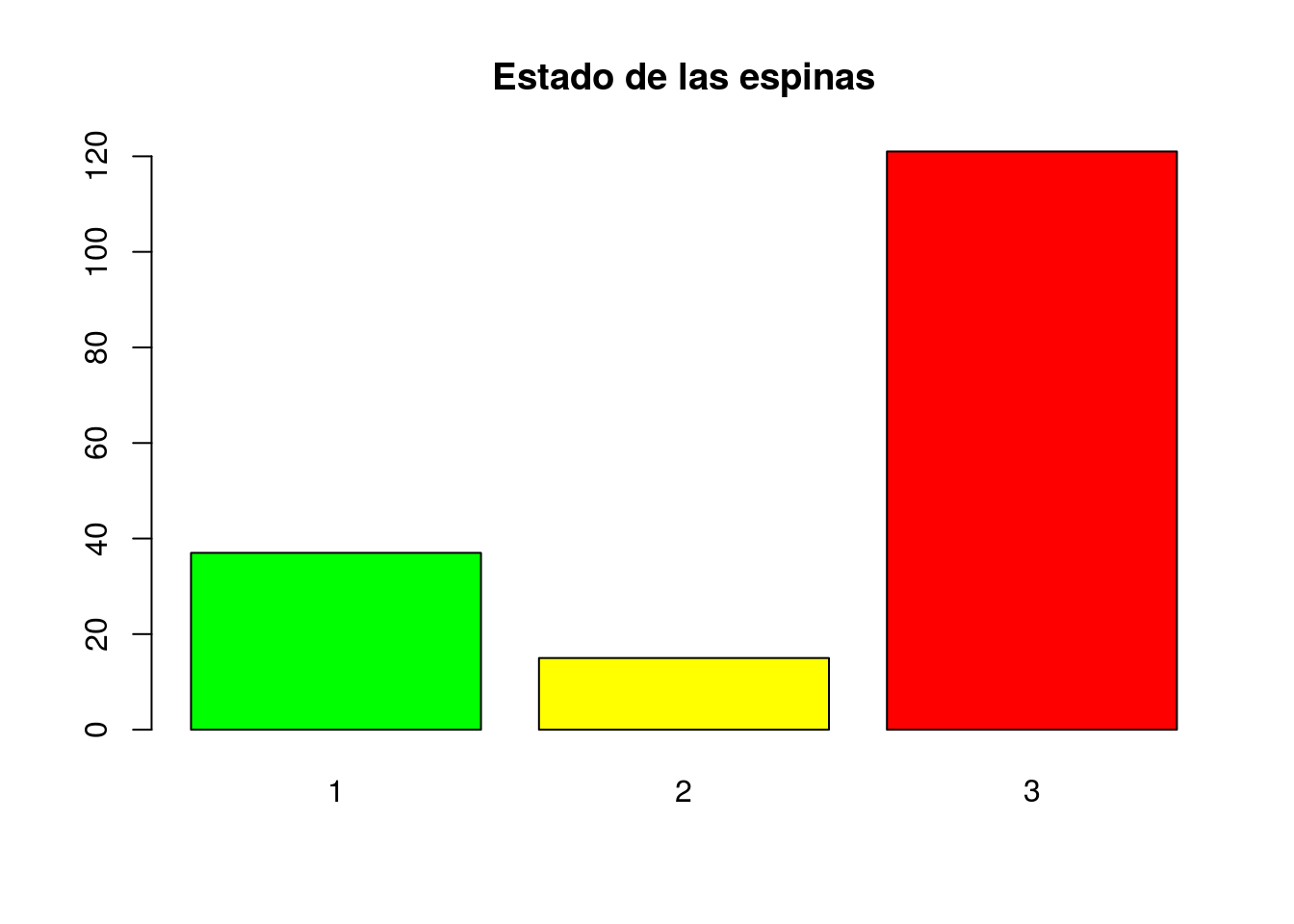
Repetimos los últimos gráficos, jugando con las etiquetas y los colores para darles más interés e interpretabilidad:
Asignación de etiquetas a valores
Aquí una carta de algunos de los colores disponibles en R.
spine=factor(spine,levels=c(1,2,3),labels=c("Bueno","Un lado malo","Dos lados mal"))
table(spine)## spine
## Bueno Un lado malo Dos lados mal
## 37 15 121barplot(table(spine),main="Estado de las espinas laterales",col=c("green","yellow","red"))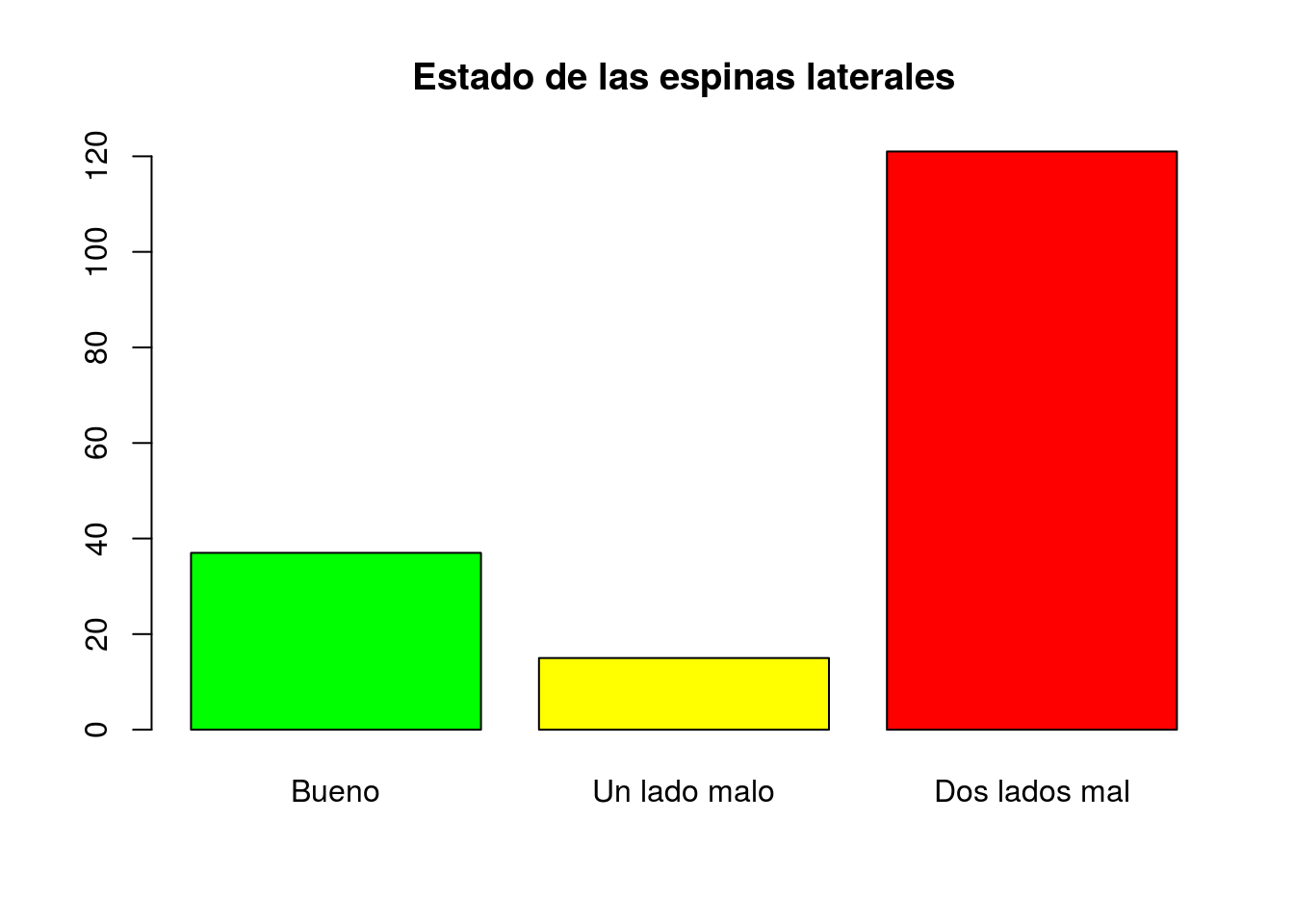
color=factor(color,levels=c(1,2,3,4),labels=c("claro","medio","medio-oscuro","oscuro"))
table(color)## color
## claro medio medio-oscuro oscuro
## 12 95 44 22barplot(table(color),main="Estado de las espinas laterales",
col=c("lightgoldenrod1","goldenrod2","darkorange3","chocolate4"))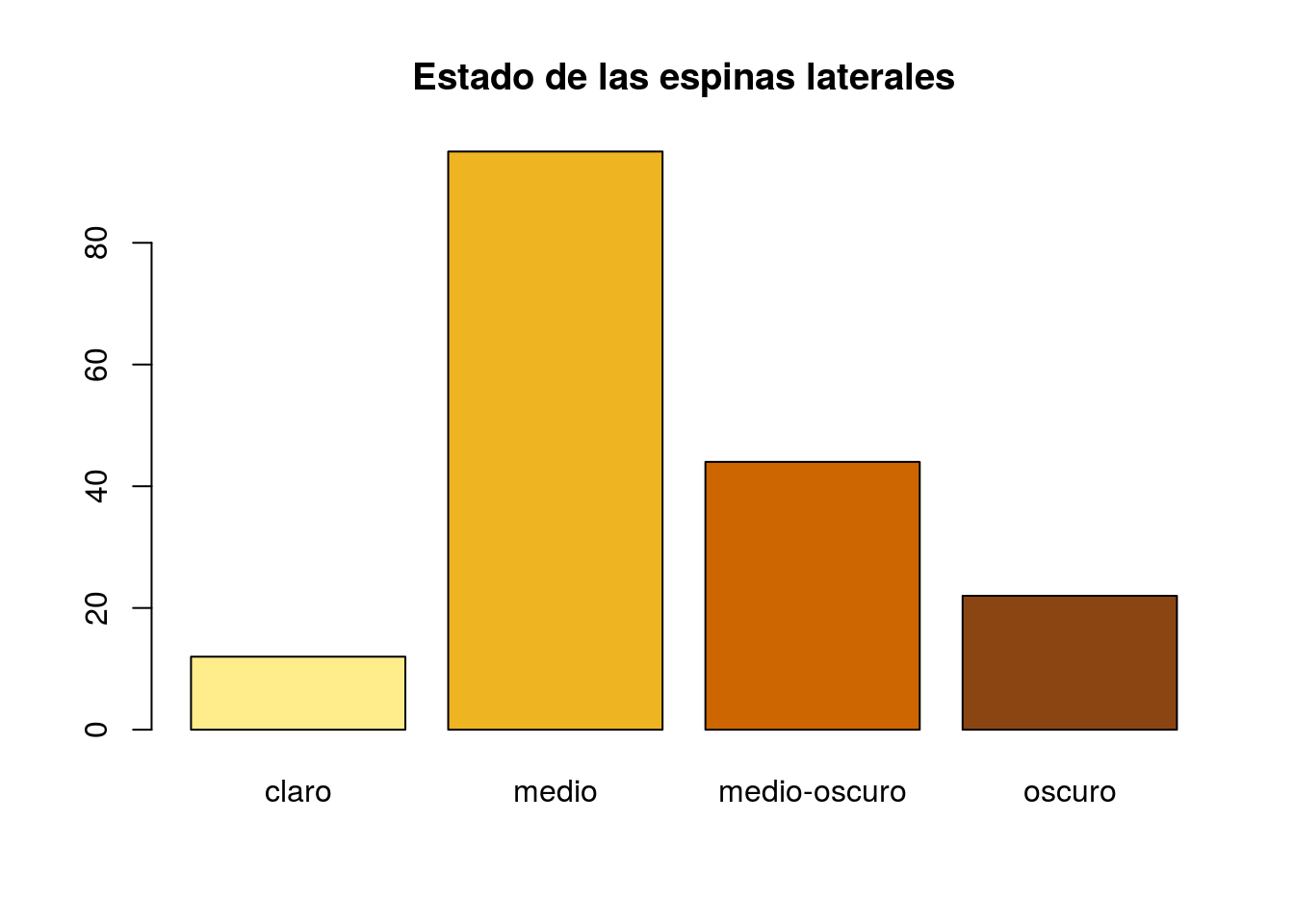
Histogramas para variables continuas
hist(width,main="anchura del caparazon",col="olivedrab1")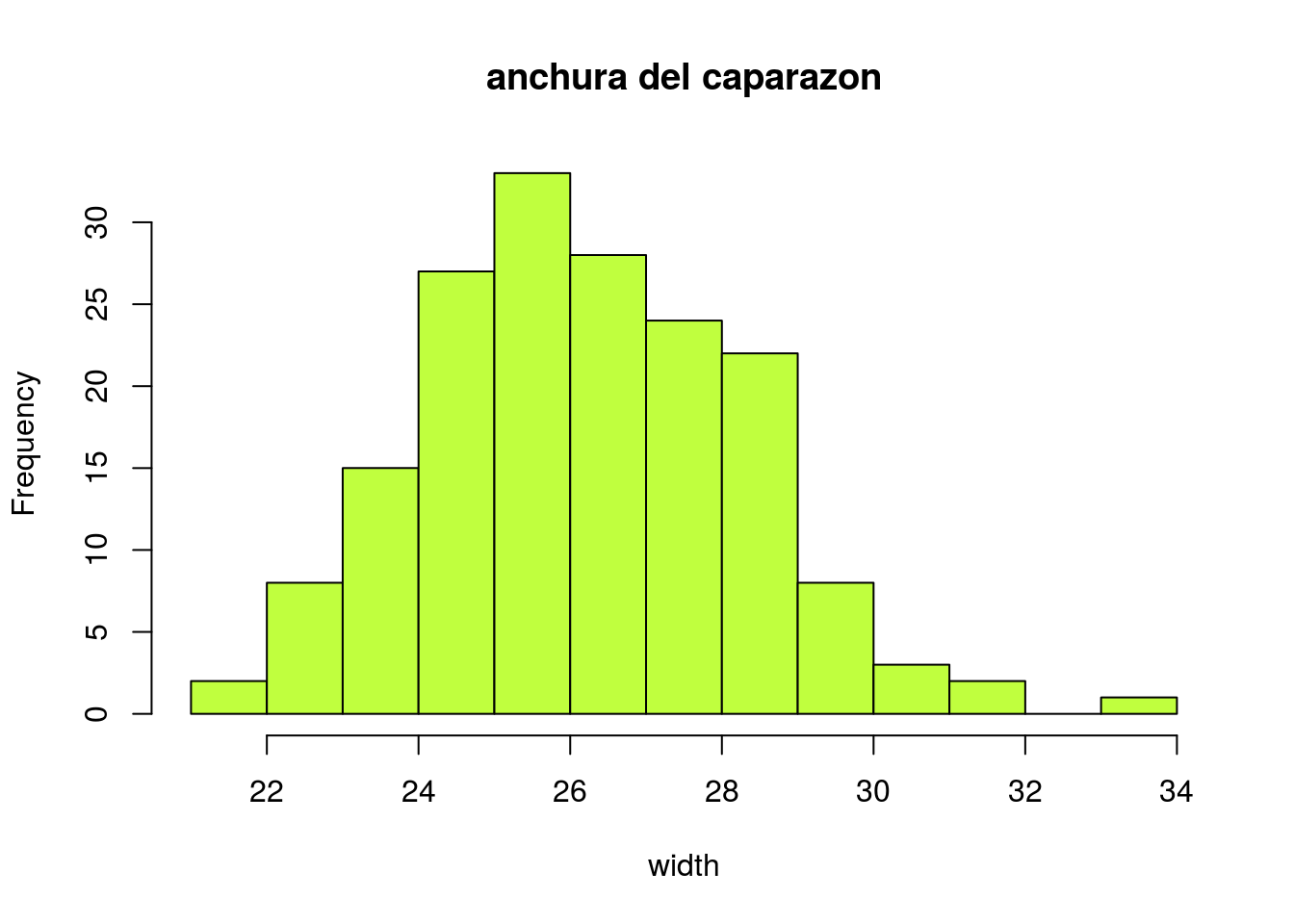
hist(weight,main="Peso",col="turquoise")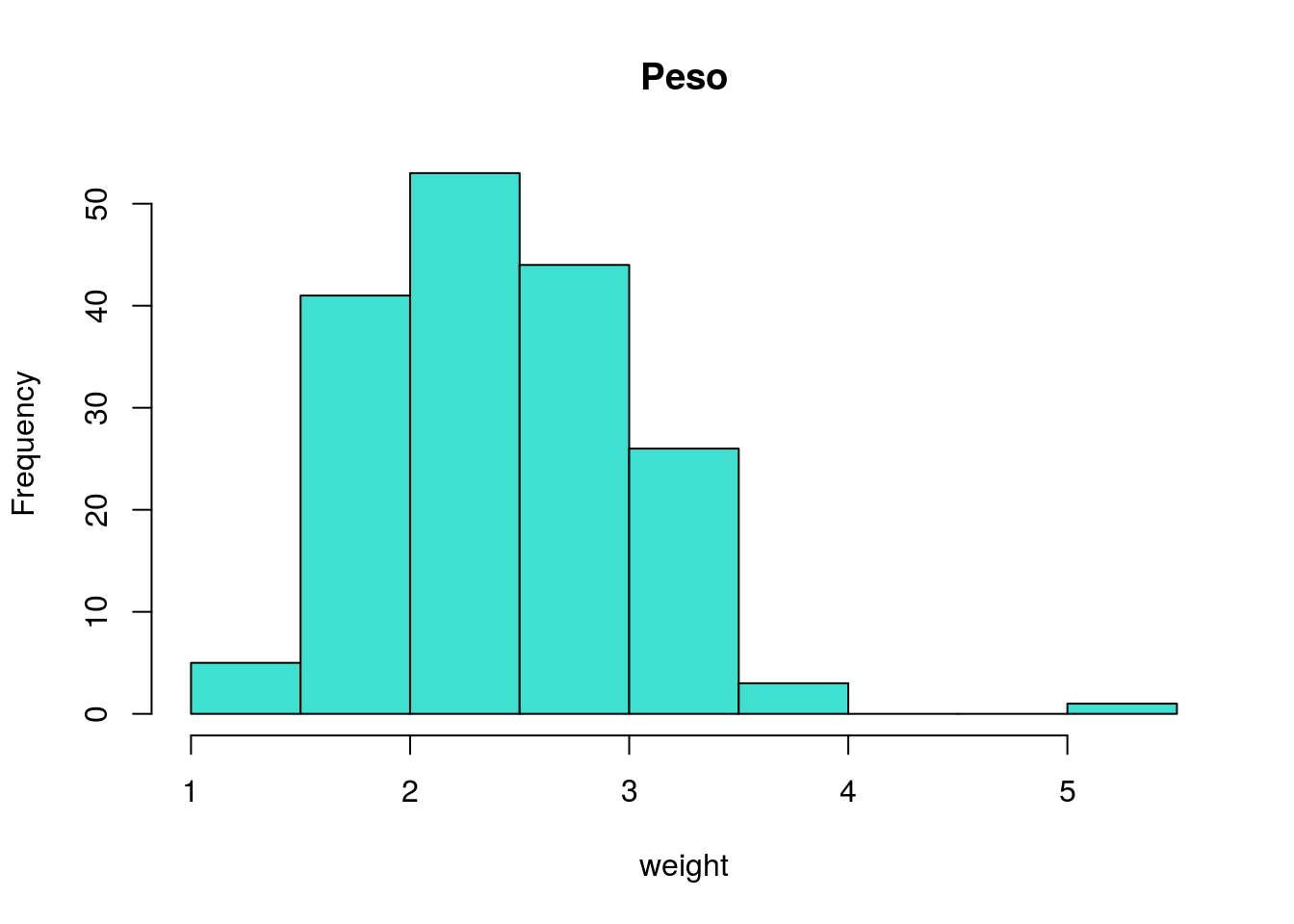
Descripción numérica.
Las variables continuas se suelen resumir en media \(\pm\) desviación típica (en caso de seguir distribución normal), o en mediana y percentiles 5 y 95 en caso de seguir otra distribución. La normalidad puede contrastarse mediante el test de Shapiro-Wilk. Aplicamos este test a las dos variables continuas presentes en la muestra:
shapiro.test(width)##
## Shapiro-Wilk normality test
##
## data: width
## W = 0.99122, p-value = 0.3707shapiro.test(weight)##
## Shapiro-Wilk normality test
##
## data: weight
## W = 0.96471, p-value = 0.0002272En un test de hipótesis, un p-valor mayor o igual que el nivel de significación elegido a priori (habitualmente el 5%) conduce a aceptar la hipótesis “nula” (en este caso que la variable sigue una distribución normal). En caso contrario dicha hipótesis debe rechazarse, ya que un p-valor pequeño indica que los datos disponibles no son compatibles (es muy improbable que puedan haberse producido) con dicha hipótesis. En este caso, podemos aceptar la normalidad de la variable anchura, pero no del peso. La anchura puede resumirse entonces en media:
mean(width)## [1] 26.29884y desviación típica:
sd(width)## [1] 2.109061
Si observamos atentamente el histograma anterior, vemos que hay un cangrejo cuyo peso se aparta notablemente de los demás (pesa 5.2 kg). Si quitamos este cangrejo, podemos aceptar la normalidad del resto:
shapiro.test(weight[-which(weight>5)])##
## Shapiro-Wilk normality test
##
## data: weight[-which(weight > 5)]
## W = 0.98631, p-value = 0.0915No obstante, a falta de argumentos para eliminar este cangrejo de la muestra (¿es un cangrejo realmente anómalo?), la variable peso debe resumirse en mediana:
median(weight)## [1] 2.35y percentiles:
quantile(weight,probs=c(0.05,0.95))## 5% 95%
## 1.600 3.275
La variable “Número de satélites” puede describirse también en mediana y percentiles, ya que es una variable numérica discreta:
median(y)## [1] 2quantile(y,probs=c(0.05,0.95))## 5% 95%
## 0 9
En cuanto a las variables “Color” y “Estado de las espinas” el único resumen con sentido son las tablas mostradas más arriba (cuántos cangrejos hay de cada color, y cuantos tienen las espinas laterales en buen o mal estado).
Descripción bivariante de los datos
La descripción bivariante, por su parte, pretende hacer visibles las posibles relaciones que existen entre las variables tomadas de dos en dos.
Gráficos
Variable continua frente a variable continua: nube de puntos
Gráfico básico
plot(width,weight,xlab="Anchura del caparazón (cm)",
ylab="Peso (kg)",main="Morfología del cangrejo de herradura")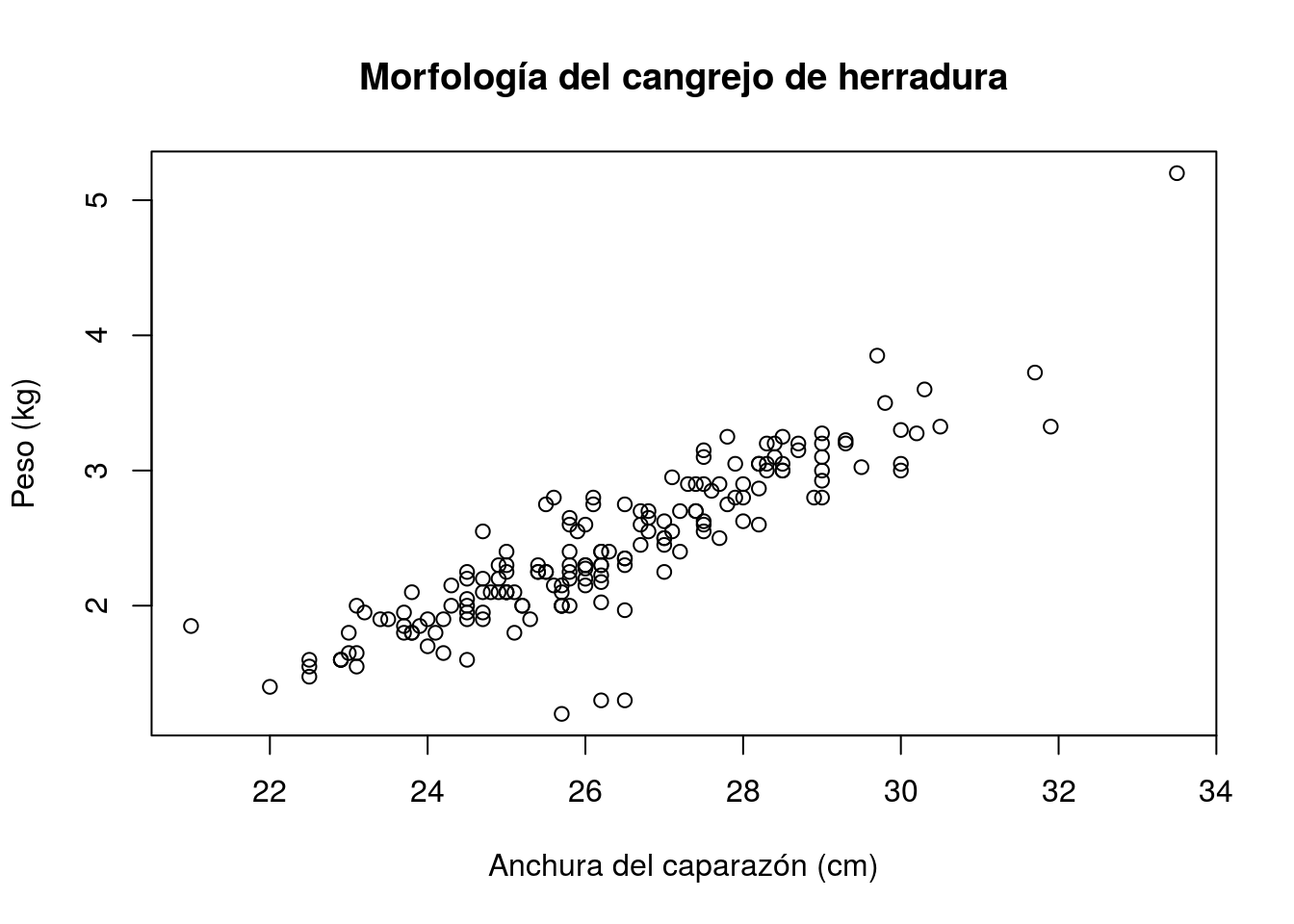
Gráfico un poco más sofisticado, con colores que representan el color del caparazón:
colores=c("lightgoldenrod1","goldenrod2","darkorange3","chocolate4")
plot(width,weight,xlab="Anchura del caparazón (cm)",
ylab="Peso (kg)",main="Morfología del cangrejo de herradura",
pch=16,col=colores[as.integer(color)])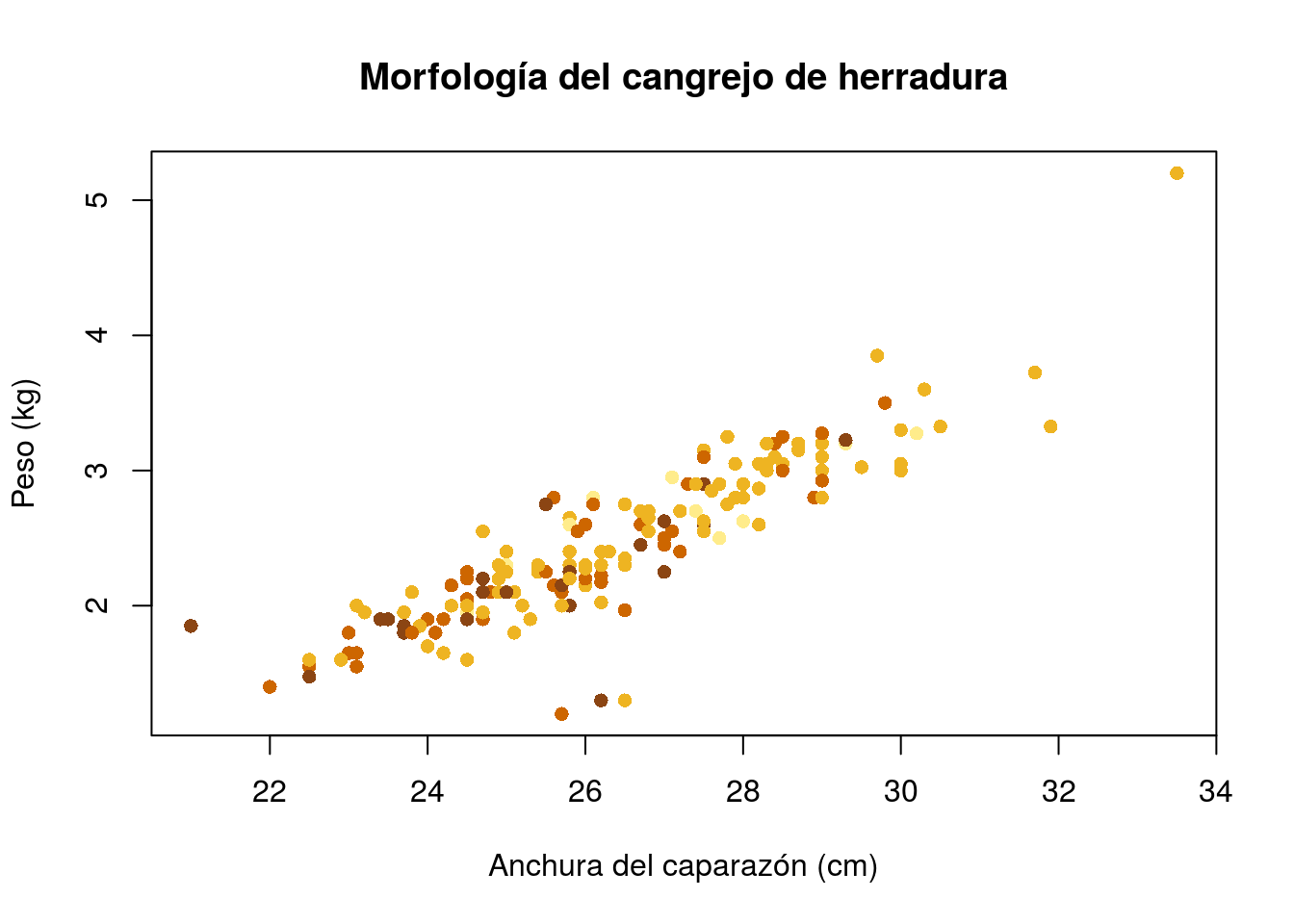
Descripción numérica
Cuando, como en el gráfico anterior, se aprecia asociación lineal entre variables, ésta se describe mediante el coeficiente de correlación cuyo valor oscila entre -1 y 1. Los valores positivos indican ajuste a una recta de pendiente positiva (creciente) y los negativos a una recta decreciente. Los valores extremos (-1 y 1) representan ajustes perfectos a rectas (decreciente o creciente respectivamente), mientras que valores próximos a 0 representan un ajuste muy pobre a una recta. En R, el coeficiente de correlación se calcula mediante:
cor(width,weight)## [1] 0.8868715y puede acompañarse de un intervalo de confianza que indica la precisión con que se ha estimado dicha correlación:
cor.test(width,weight)##
## Pearson's product-moment correlation
##
## data: width and weight
## t = 25.102, df = 171, p-value < 2.2e-16
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## 0.8501665 0.9149979
## sample estimates:
## cor
## 0.8868715El p-valor mostrado en la salida anterior permite contrastar la hipótesis de que en la población la correlación entre estas variables no es nula. Un p-valor tan pequeño como el indicado indica que hay evidencia suficiente en los datos de una fuerte asociación lineal entre las variables. Si el p-valor hubiese sido un valor mayor que 0.05, habríamos concluido que dicha asociación no es significativa (lo que significa que puede haberse debido al azar, inherente a todo proceso de muestreo).
Variable continua frente a variable discreta: boxplot
Estos gráficos permiten visualizar los valores medianos, primer y tercer cuartil, así como los valores extremos de una variable en distintos grupos:
boxplot(width~color,xlab="Color",ylab="Anchura del caparazon (cm)",
col=c("lightgoldenrod1","goldenrod2","darkorange3","chocolate4"))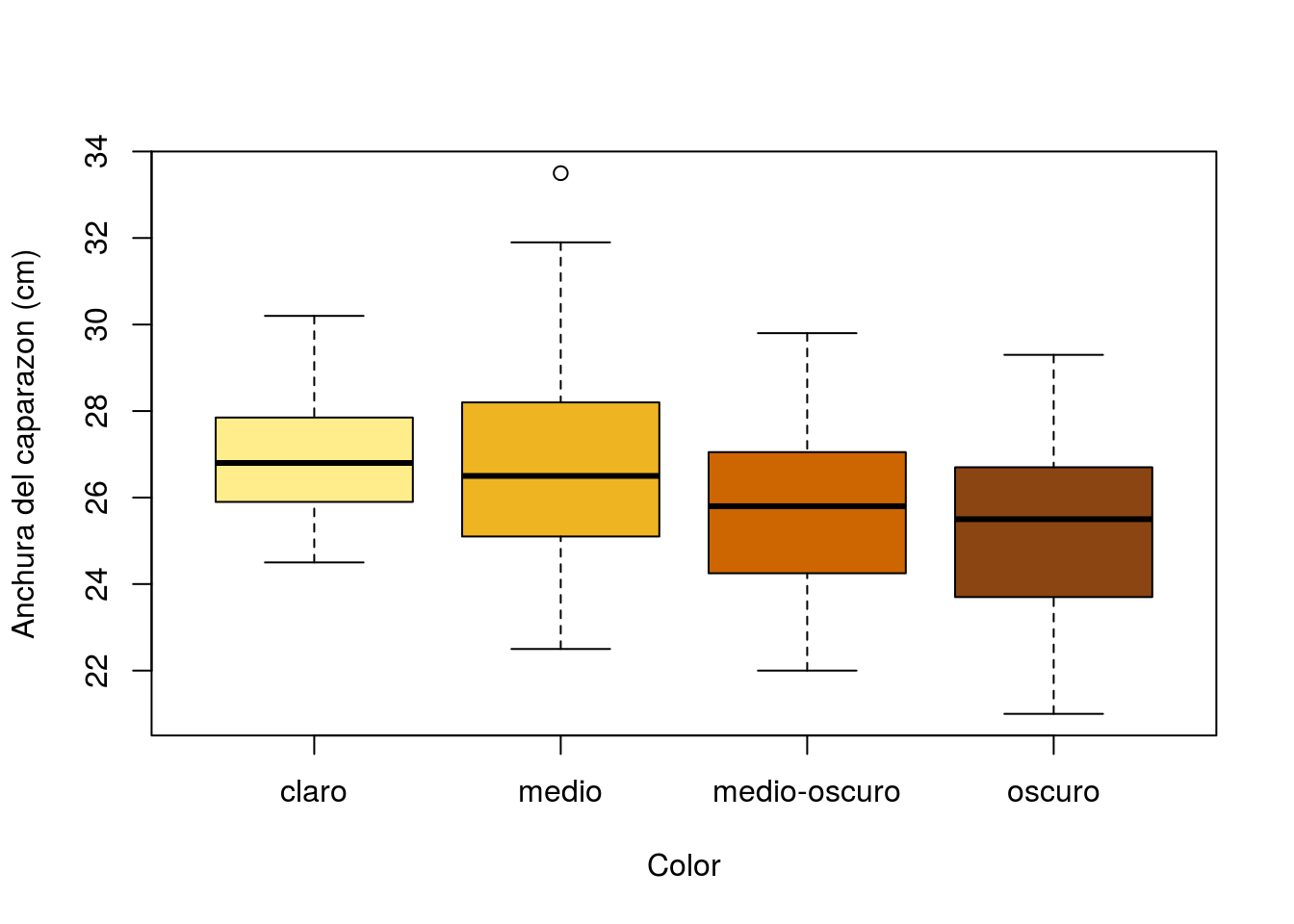
boxplot(weight~color,xlab="Color",ylab="Peso (kg)",
col=c("lightgoldenrod1","goldenrod2","darkorange3","chocolate4"))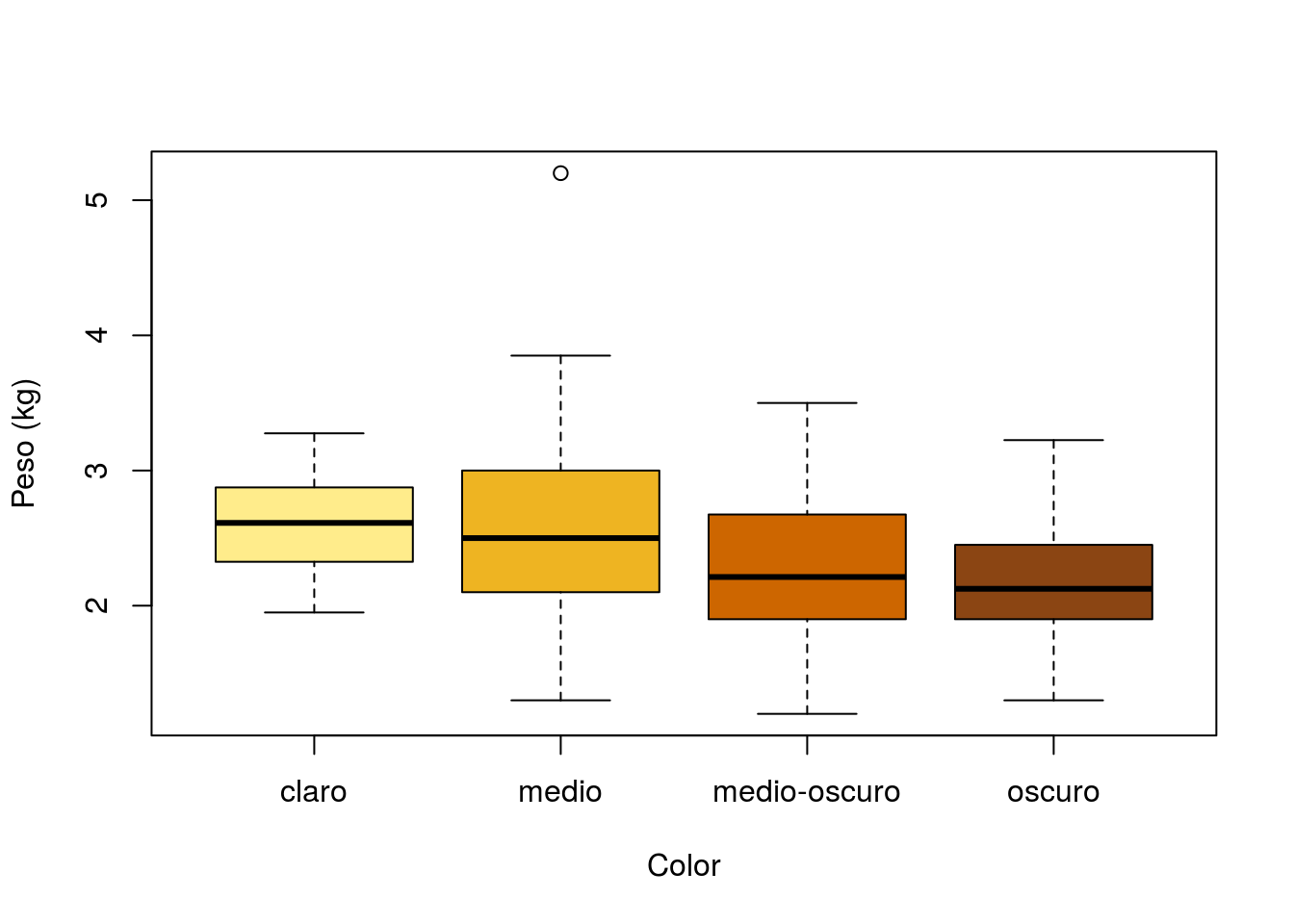
boxplot(width~spine,xlab="Estado de las espinas",ylab="Anchura del caparazon",
col=c("olivedrab2","yellow1","tomato"))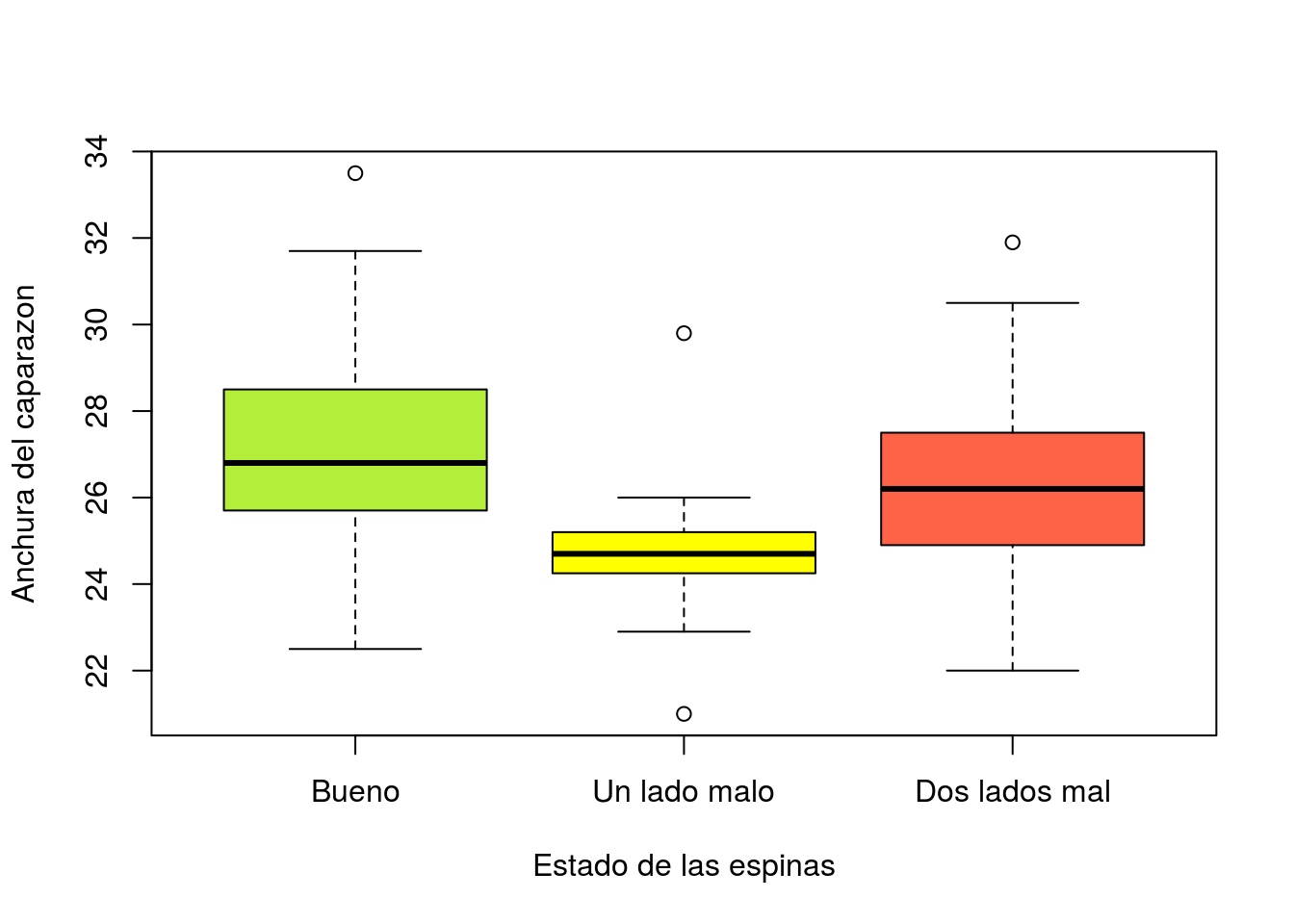
boxplot(weight~spine,xlab="Estado de las espinas",ylab="Peso",
col=c("olivedrab2","yellow1","tomato"))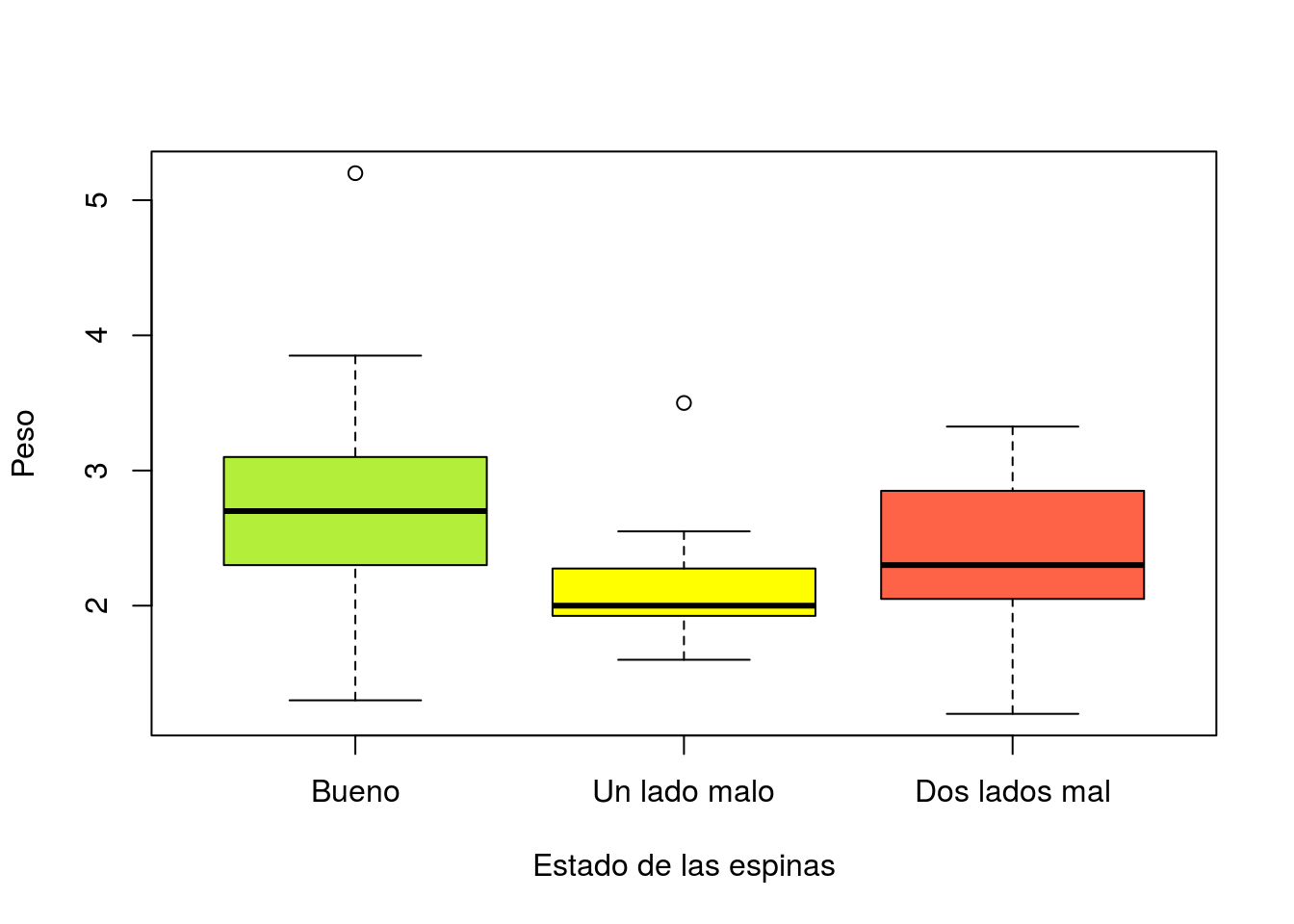
Los valores numéricos correspondientes pueden obtenerse mediante la función aggregate:
aggregate(width~color,data=cangrejos,summary)## color width.Min. width.1st Qu. width.Median width.Mean width.3rd Qu.
## 1 1 24.50 25.95 26.80 26.97 27.78
## 2 2 22.50 25.10 26.50 26.70 28.20
## 3 3 22.00 24.28 25.80 25.75 27.02
## 4 4 21.00 23.90 25.50 25.28 26.58
## width.Max.
## 1 30.20
## 2 33.50
## 3 29.80
## 4 29.30aggregate(weight~color,data=cangrejos,summary)## color weight.Min. weight.1st Qu. weight.Median weight.Mean
## 1 1 1.950 2.338 2.612 2.629
## 2 2 1.300 2.100 2.500 2.538
## 3 3 1.200 1.900 2.213 2.299
## 4 4 1.300 1.900 2.125 2.174
## weight.3rd Qu. weight.Max.
## 1 2.837 3.275
## 2 3.000 5.200
## 3 2.638 3.500
## 4 2.400 3.225Si sólo quisiéramos mostrar la media y desviación típica en cada grupo:
aggregate(width~color,data=cangrejos,function(x){c(media=mean(x), sd=sd(x))})## color width.media width.sd
## 1 1 26.966667 1.676757
## 2 2 26.704211 2.162343
## 3 3 25.750000 1.946673
## 4 4 25.281818 1.886200aggregate(weight~color,data=cangrejos,function(x){c(media=mean(x), sd=sd(x))})## color weight.media weight.sd
## 1 1 2.6291667 0.3877138
## 2 2 2.5378105 0.6072106
## 3 3 2.2992500 0.5472630
## 4 4 2.1738636 0.4531292
Variable cualitativa vs. variable cualitativa: mosaico
Para evaluar la asociación entre variables cualitativas, los datos pueden mostrarse en una tabla cruzada:
table(color,spine)## spine
## color Bueno Un lado malo Dos lados mal
## claro 9 2 1
## medio 24 8 63
## medio-oscuro 3 4 37
## oscuro 1 1 20prop.table(table(color,spine),1)## spine
## color Bueno Un lado malo Dos lados mal
## claro 0.75000000 0.16666667 0.08333333
## medio 0.25263158 0.08421053 0.66315789
## medio-oscuro 0.06818182 0.09090909 0.84090909
## oscuro 0.04545455 0.04545455 0.90909091y representarse gráficamente en un mosaico:
library(vcd)## Loading required package: gridmosaic(table(color,spine))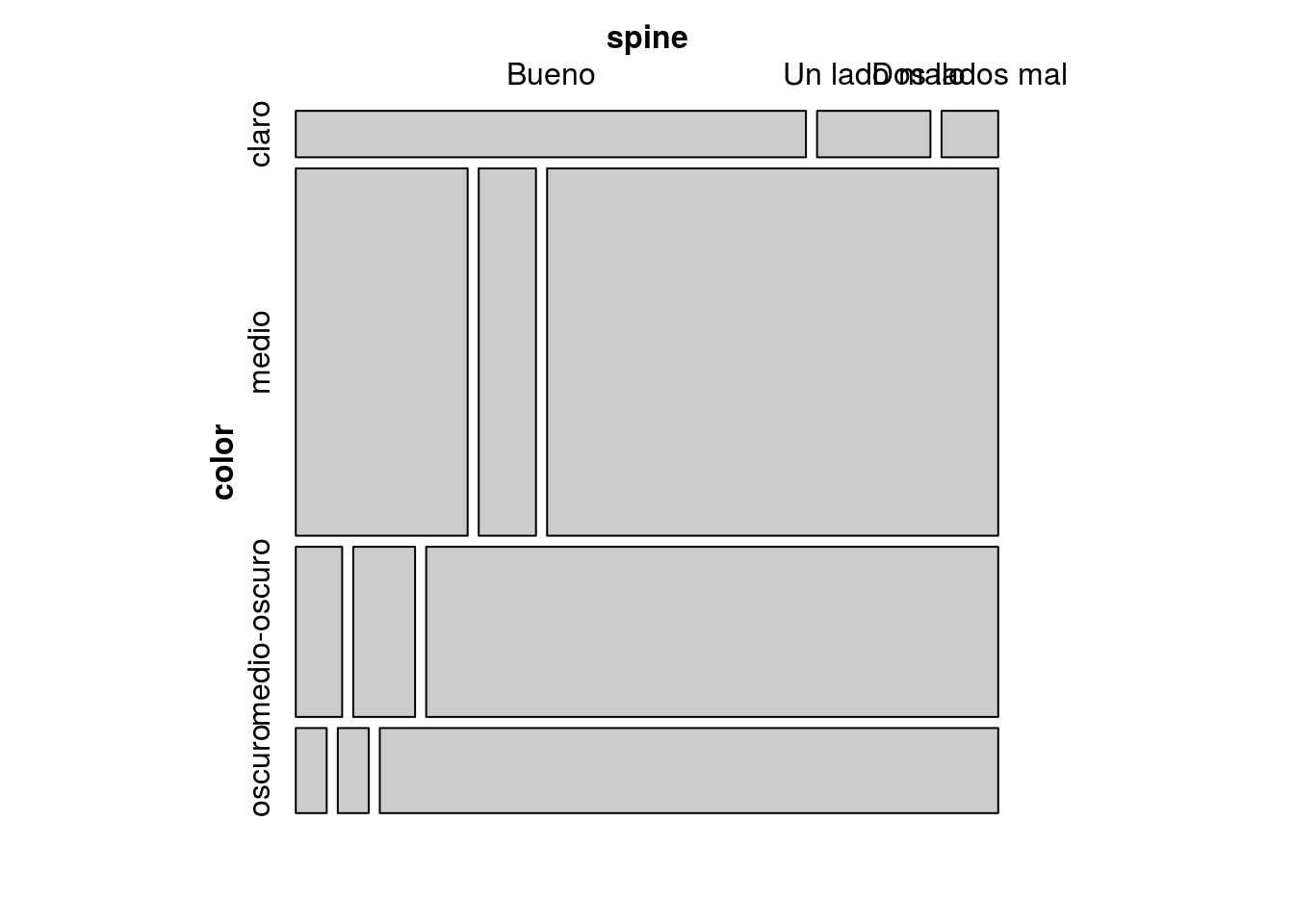
mosaic(table(color,spine),highlighting="spine", highlighting_fill=c("olivedrab2","yellow1","tomato"))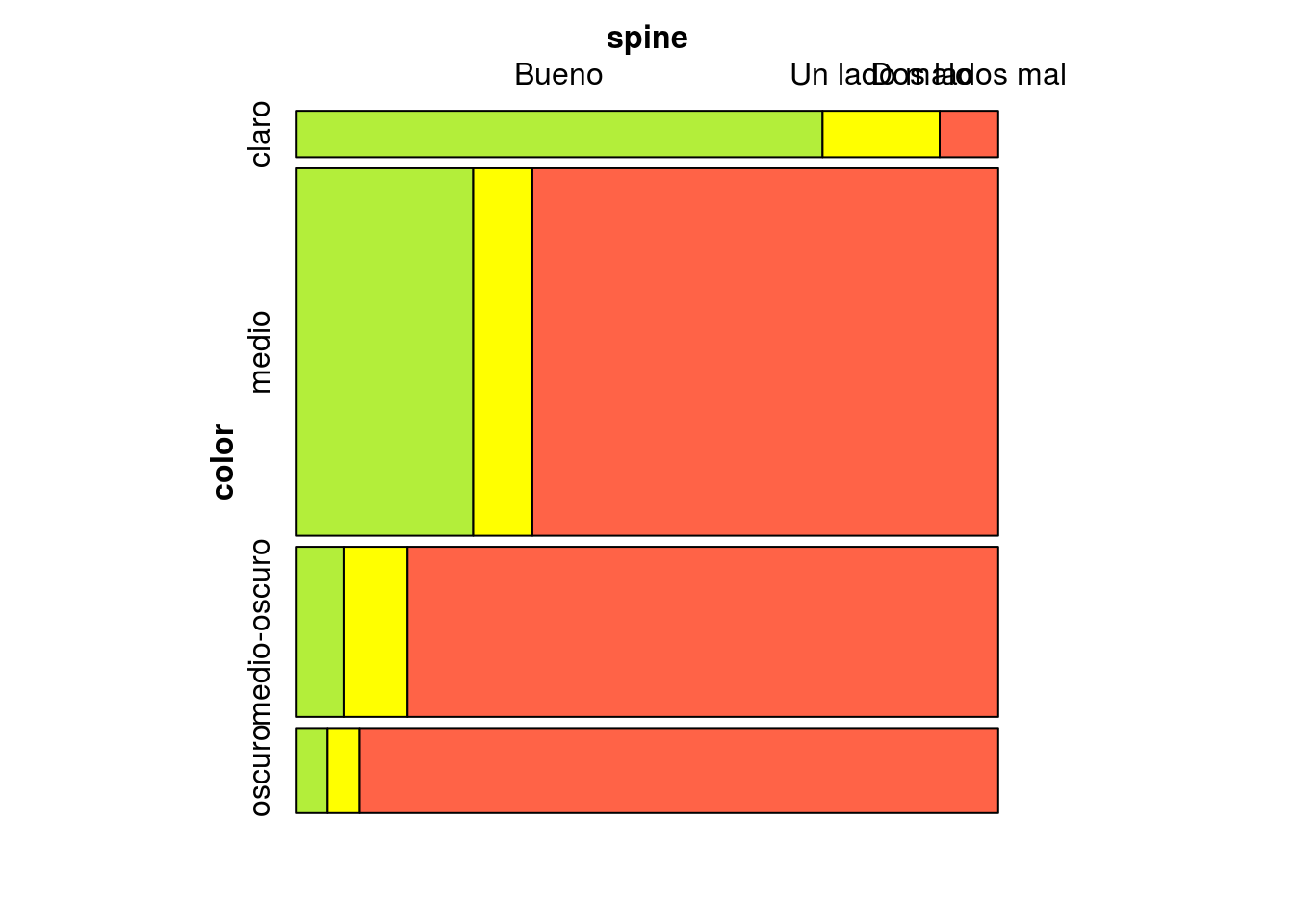
mosaic(table(color,spine),highlighting="color",
highlighting_fill=c("lightgoldenrod1","goldenrod2","darkorange3","chocolate4"),
highlighting_direction="bottom")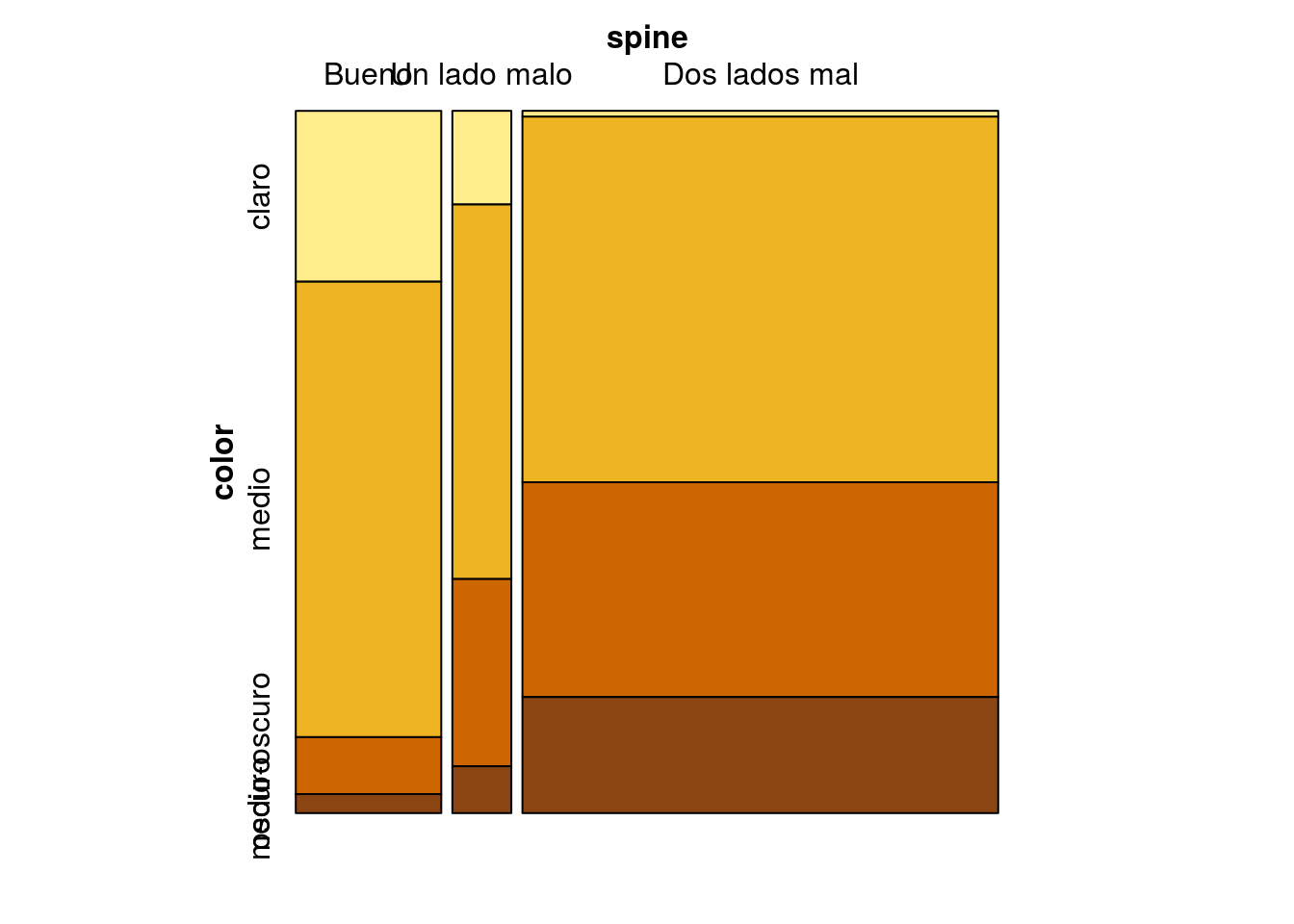
Desde el punto de vista de la inferencia, la asociación entre variables cualitativas se puede llevar a cabo mediante un test de la chi-cuadrado:
chisq.test(table(color,spine))## Warning in chisq.test(table(color, spine)): Chi-squared approximation may
## be incorrect##
## Pearson's Chi-squared test
##
## data: table(color, spine)
## X-squared = 34.745, df = 6, p-value = 4.83e-06Nótese que en este caso el programa informa de que la aproximación puede ser incorrecta; ello es debido a que la validez de la prueba chi-cuadrado exige que al menos el 80% de las casillas de la tabla tengan una frecuencia esperada mayor que 5, y que ninguna frecuencia esperada sea menor que 1; las frecuencias esperadas en este caso son:
chisq.test(table(color,spine))$expected## Warning in chisq.test(table(color, spine)): Chi-squared approximation may
## be incorrect## spine
## color Bueno Un lado malo Dos lados mal
## claro 2.566474 1.040462 8.393064
## medio 20.317919 8.236994 66.445087
## medio-oscuro 9.410405 3.815029 30.774566
## oscuro 4.705202 1.907514 15.387283Entre las 12 casillas de esta tabla sólo hay 7 con frecuencias mayores que 5; pero 7 de 12 son sólo el 58% de las casillas, por lo que es obvio que no se cumple una de las condiciones de validez. En este caso, el p-valor puede calcularse mediante un método Montecarlo (simulación):
chisq.test(table(color,spine), simulate.p.value = TRUE)##
## Pearson's Chi-squared test with simulated p-value (based on 2000
## replicates)
##
## data: table(color, spine)
## X-squared = 34.745, df = NA, p-value = 0.0004998En este caso el p-valor menor que el 5% indica la presencia de una asociación significativa (esto es, no producida por azar) entre el color del cangrejo y el estado de las espinas. Tanto las tablas anteriores como los gráficos indican que la asociación se produce porque a medida que el cangrejo es más oscuro, aumenta la frecuencia con que presenta daños en las espinas de ambos lados. Posiblemente ello sea debido al efecto de la edad: los cangrejos más viejos son más oscuros y han tenido más tiempo para sufrir incidencias en las espinas.
Ejercicio
Describir los datos del archivo de las pesquerias en el Atlantico nororiental.
Ajuste de modelos lineales.
Estimación del modelo lineal
El modelo lineal para predecir (o explicar) la variable respuesta \(\mathbf{Y}\) en función de la matriz de variables explicativas \(\mathbf{X}\) puede estimarse por dos métodos:
Mínimos cuadrados: Este método puede aplicarse siempre y consiste en encontrar los valores de los parámetros \(\beta_i\) que minimizan la distancia entre los valores observados y los predichos.
Máxima verosimilitud: Este método sólo es de aplicación cuando las observaciones son independientes y las distancias de los puntos al modelo (residuos) siguen una distribución normal. Cuando estas condiciones se cumplen, el método de máxima verosimilitud y el de mínimos cuadrados producen los mismos estimadores.
Sólo en el caso de que los residuos del modelo sean normales e independientes puede llevarse a cabo adecuadamente la inferencia clásica sobre los parámetros del modelo.
Los estimadores de los parámetros, utilizando cualquiera de los dos métodos anteriores, se obtienen mediante:
\[ \hat{\beta} = \left(X^{t}X\right)^{-1}X^{t}Y\]
\[\hat{\sigma}^{2}=\frac{1}{n-p}\sum_{i=1}^{n}\left(y_{i}-\hat{y_{i}}\right)^{2}=\frac{1}{n-p}\sum_{i=1}^{n}\left(y_{i}-X_{i}\hat{\beta}\right)^{2}=\frac{1}{n-p}\left(\mathbf{Y-X}\hat{\beta}\right)^{t}\left(\mathbf{Y-X}\hat{\beta}\right)\]
La matriz de covarianzas de los estimadores de \(\beta_i\) es:
\[\textrm{Var}\left(\hat{\beta}\right)=\hat{\sigma}^{2}\left(X^{t}X\right)^{-1}\]
La raiz cuadrada de la diagonal de esta matriz nos proporciona los errores estándar de los \(\beta_i\), que permiten construir contrastes e intervalos de confianza para estos parámetros. Concretamente, si llamamos \(\hat{\sigma}_{\beta_{i}}\) al error estándar del parámetro \(\beta_i\), puede obtenerse un intervalo de confianza a nivel \(1-\alpha\) para dicho parámetro mediante: \[\left[\hat{\beta}_{i}\pm t_{n-p,1-\alpha/2}\hat{\sigma}_{\beta_{i}}\right]\]
Descomposición de la variabilidad.
La variabilidad total presente en la variable respuesta puede descomponerse en la parte explicada por las variables explicativas, más la variabilidad residual:
VARIABILIDAD TOTAL = VARIABILIDAD EXPLICADA + VARIABILIDAD RESIDUAL
donde:
VARIABILIDAD TOTAL: VT = \(\sum_{i=1}^{n}\left(y_{i}-\overline{y}\right)^{2}\)
VARIABILIDAD EXPLICADA: VE = \(\sum_{i=1}^{n}\left(\hat{y}_{i}-\overline{y}\right)^{2}\)
VARIABILIDAD RESIDUAL: VR = \(\sum_{i=1}^{n}\left(y_{i}-\hat{y}_{i}\right)^{2}\)
Es decir:
\[\sum_{i=1}^{n}\left(y_{i}-\overline{y}\right)^{2}=\sum_{i=1}^{n}\left(\hat{y}_{i}-\overline{y}\right)^{2}+\sum_{i=1}^{n}\left(y_{i}-\hat{y}_{i}\right)^{2}\]
A partir de esta descomposición es posible definir coeficientes para medir la calidad de ajuste del modelo (coeficientes de determinación y de determinación corregido), y construir un contraste (conocido como análisis de la varianza del modelo) que permite decidir si las variables explicativas realmente son explicativas; dicho de otra forma, permite decidir si la variabilidad explicada por dichas variables representa una proporción significativa de la variabilidad total presente en el modelo.
Coeficiente de determinación \(R^2\)
Este coeficiente mide simplemente la proporción de la variabilidad en la variable respuesta que es explicada (o está determinada) por las variables explicativas. Cuanto más se aproxime su valor a 1, mejor es el modelo; cuanto más se aproxime a cero tanto peor:
\[R^2=\frac{VE}{VT}\]
Coeficiente de determinación corregido (o ajustado) \(\tilde{R}^2\)
El coeficiente de determinación que se acaba de definir presenta el problema práctico de que su valor se va aproximando a 1 a medida que se añaden variables explicativas \(X_i\) al modelo, aunque la aportación de cada una sea irrelevante. Interesa por ello redefinir el coeficiente de determinación de forma que se vea “penalizado” si su valor aumenta por introducir muchas variables que no expliquen nada en lugar de pocas variables que expliquen mucho. Para ello observemos en primer lugar que el coeficiente de determinación \(R^2\) puede expresarse como: \[R^{2}=\frac{VE}{VT}=1-\frac{VR}{VT}\]
Para penalizar el exceso de variables explicativas, el coeficiente de determinación corregido se define de manera similar mediante:
\[\tilde{R}^{2}=1-\frac{VR/\left(n-p\right)}{VT/\left(n-1\right)}=1-\frac{n-1}{n-p}\frac{VR}{VT}\]
De esta forma, el término \(\frac{n-1}{n-p}\) es mayor que 1 (tanto mayor cuanto mayor sea el número de variables explicativas \(p\)). Dicho término multiplica a la proporción de varianza no explicada \(\frac{VR}{VT}\), por lo cual su efecto es “inflar” la variabilidad no explicada y por tanto reducir la variabilidad explicada artificialmente por un exceso de variables. Si después de estos ajustes el coeficiente de determinación así obtenido es próximo a 1, ello significaría que aún penalizando la introducción de variables, la varibilidad explicada es alta, y por tanto las variables consideradas puede considerarse que tienen buena capacidad explicativa o predictiva de la variable respuesta.
Análisis de la varianza del modelo lineal
Se denomina así al contraste:
\[H_0:\beta_{1}=\beta_{2}=\dots=\beta_{p}=0\]
que de forma matricial puede expresarse como:
\[H_0:\left(\begin{array}{ccccc} 0 & 0 & 0 & \ldots & 0\\ 0 & 1 & 0 & \ldots & 0\\ 0 & 0 & 1 & \ldots & 0\\ \vdots & \vdots & \vdots & \ddots & \vdots\\ 0 & 0 & 0 & \ldots & 1 \end{array}\right)\left(\begin{array}{c} \beta_{0}\\ \beta_{1}\\ \beta_{2}\\ \vdots\\ \beta_{p} \end{array}\right)=\left(\begin{array}{c} 0\\ 0\\ 0\\ \vdots\\ 0 \end{array}\right)\]
Este contraste tiene como objetivo decidir si, consideradas conjuntamente, las variables \(X_i\) tienen capacidad explicativa/predictiva sobre la variable respuesta \(\mathbf{Y}\). En caso de acepar la hipótesis nula, ello significaría que el posible efecto de las \(X_i\) sobre la \(\mathbf{Y}\) puede atribuirse simplemente al azar; en caso de rechazarla, ello implicaría que las \(X_i\) (todas o algunas de estas variables) tienen realmente efecto sobre la \(\mathbf{Y}\), mas alla de lo que cabría esperar por azar.
Este es un contraste lineal de la forma:
\[H_0:\mathbf{A\beta}=0\]
Cuando \(H_0\) es cierta el test estadístico:
\[F=\frac{1}{q\hat{\sigma}^{2}}\hat{\beta}^{t}\mathbf{A}^{t}\left(\mathbf{A}\left(\mathbf{X}^{t}\mathbf{X}\right)^{-1}\mathbf{A}^{t}\right)^{-1}\mathbf{A\hat{\beta}}\]
(siendo \(q\) el número de filas de la matriz \(\mathbf{A}\)) sigue una distribución \(F\) de Fisher con \(q\) y \(n-p\) grados de libertad. El p-valor del contraste es
\[p-valor=P\left(F_{q,n-p}>F_{obs}\right)=1-P\left(F_{q,n-p} \le F_{obs}\right)\]
siendo \(F_{obs}\) el valor observado del test estadístico \(F\).
En el caso particular del contraste que hemos planteado inicialmente, la matriz \(\mathbf{A}\) es: \[\mathbf{A=}\left(\begin{array}{ccccc} 1 & 0 & 0 & \ldots & 0\\ 0 & 1 & 0 & \ldots & 0\\ 0 & 0 & 1 & \ldots & 0\\ \vdots & \vdots & \vdots & \ddots & \vdots\\ 0 & 0 & 0 & \ldots & 1 \end{array}\right)\] en cuyo caso puede probarse que:
\[F_{obs}=\frac{VE/(p-1)}{VR/(n-p)}\]
lo que nos indica que este contraste está, en definitiva, comparando la variabilidad explicada por el modelo con la variabilidad residual (tras ajustar por el número de casos y por el número de variables); sólo si la variabilidad explicada es significativamente mayor que la residual es cuando el valor de \(F_obs\) resultaría lo suficientemente grande para rechazar \(H_0\).
Nótese que este test simplemente decide si hay o no efecto de las \(X_i\) sobre la \(\mathbf{Y}\). No nos dice nada sobre la intensidad de dicho efecto, que deberá cuantificarse en términos del coeficiente de determinación.
Predicción
Una vez ajustado un modelo lineal, puede utilizarse para realizar predicciones sobre los valores de la variable respuesta \(Y\). Hay dos tipos de predicciones que se pueden realizar:
Predicción del valor medio de \(Y\) dado el valor de \(X\).
Predicción del valor individual de \(Y\) dado el valor de \(X\).
En ambos casos la predicción es análoga; si \(X=x_0\) el valor predicho es:
\[\hat{Y} = X\hat{\beta} = x_0\hat{\beta}\]
Aunque el valor predicho sea el mismo, el error estándar difiere entre ambas predicciones. De manera intuitiva, es obvio que el valor medio tiene menor dispersión que los valores individuales y, en efecto, así ocurre. La varianza de la predicción del valor medio dado que \(X=x_0\) es:
\[Var\left(\left.\hat{y}\right|X=x_{0}\right)=\hat{\sigma}^{2}x_{0}\left(X^{t}X\right)^{-1}x_{0}^{t} \]
y la varianza de la predicción del valor individual dado que \(X=x_0\) es:
\[Var\left(\left.\widetilde{y}\right|X=x_{0}\right)=\hat{\sigma}^{2}\left(1+x_{0}\left(X^{t}X\right)^{-1}x_{0}^{t}\right)\]
Los errores estándar son, respectivamente, las raíces cuadradas de estas varianzas. Llamando:
\[ \hat{y}_0 = x_0 \hat{\beta}\]
podemos construir intervalos de confianza para las predicciones mediante:
- Intervalo de confianza a nivel \(1-\alpha\) para la predicción del valor medio de \(Y\) cuando \(X=x_0\):
\[\left[\hat{y}_{0}\pm t_{n-p,1-\alpha/2}\hat{\sigma}\sqrt{x_{0}\left(X^{t}X\right)^{-1}x_{0}^{t}}\right]\]
- Intervalo de confianza a nivel \(1-\alpha\) para la predicción del valor individual de \(Y\) cuando \(X=x_0\):
\[\left[\hat{y}_{0}\pm t_{n-p,1-\alpha/2}\hat{\sigma}\sqrt{1+x_{0}\left(X^{t}X\right)^{-1}x_{0}^{t}}\right]\]
Estimación con R
Regresión lineal
Veamos en primer lugar como ajustamos un modelo de regresión lineal con R para explicar el peso de los cangrejos en función de la anchura de su caparazón. En este caso la variable \(Y\) es el peso y la \(X\) es la anchura del caparazón. El modelo de regresión es de la forma:
\[Y =\beta_0 +\beta_1 X + \varepsilon,\;\;\;\;\; \varepsilon \approx N\left(0,\sigma_\varepsilon\right)\]
recta=lm(weight~width,data=cangrejos)
summary(recta)##
## Call:
## lm(formula = weight ~ width, data = cangrejos)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.18600 -0.11615 -0.00513 0.15076 1.01550
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -3.944019 0.255027 -15.46 <2e-16 ***
## width 0.242642 0.009666 25.10 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.2674 on 171 degrees of freedom
## Multiple R-squared: 0.7865, Adjusted R-squared: 0.7853
## F-statistic: 630.1 on 1 and 171 DF, p-value: < 2.2e-16En esta salida vemos:
Los valores estimados de los coeficientes del modelo: \(\hat{\beta}_0 =\) -3.944, \(\hat{\beta}_1 =\) 0.2426
Los errores estándar de estos estimadores: \(\hat{\sigma}_{\beta_0}\) = 0.255, \(\hat{\sigma}_{\beta_1}\) = 0.0097.
Los correspondientes p-valores de los contrastes de los coeficientes individuales; el primer p-valor corresponde al contraste de la hipótesis \(H_0: \beta_0=0\) y el segundo al contraste de \(H_0: \beta_1=0\). En ambos casos los p-valores son casi cero, lo que indica que puede aceptarse que ambos coeficientes son no nulos.
El valor estimado del error estándar residual: \(\hat{\sigma}_\varepsilon\) = 0.2674
El coeficiente de determinación \(R^2\) = 0.7865
El coeficiente de determinación \(\tilde{R}^2\) = 0.7853
El contraste de la regresión (o análisis de la varianza de la regresión); el valor de \(F_{obs}\) es 630.1 y su p-valor (prácticamente cero) permite rechazar la hipótesis de que \(\beta_0\) y \(\beta_1\) sean simultáneamente nulos (\(H_0:\beta_0=\beta_1=0\)).
La siguiente función permite obtener fácilmente intervalos de confianza al 95% para los valores de los coeficientes del modelo:
confint(recta)## 2.5 % 97.5 %
## (Intercept) -4.4474244 -3.440613
## width 0.2235614 0.261723y mediante la función predict podemos predecir el valor de la variable respuesta (el peso) para un cangrejo con un ancho de caparazón de 30 centímetros; si queremos añadir a dicha predicción un intervalo de confianza al 95% bastaría con ejecutar:
predict(recta,newdata=data.frame(width=30), interval="prediction")## fit lwr upr
## 1 3.335247 2.801256 3.869238mientras que si deseamos obtener el intervalo de confianza para el peso medio de todos los cangrejos con un caparazón de ancho 30 cm utilizaríamos:
predict(recta,newdata=data.frame(width=30), interval="confidence")## fit lwr upr
## 1 3.335247 3.254023 3.416472Por último, la función abline permite superponer a la nube de puntos la recta de regresión ajustada:
plot(width,weight,xlab="Anchura del caparazón (cm)",
ylab="Peso (kg)",main="Morfología del cangrejo de herradura")
abline(recta)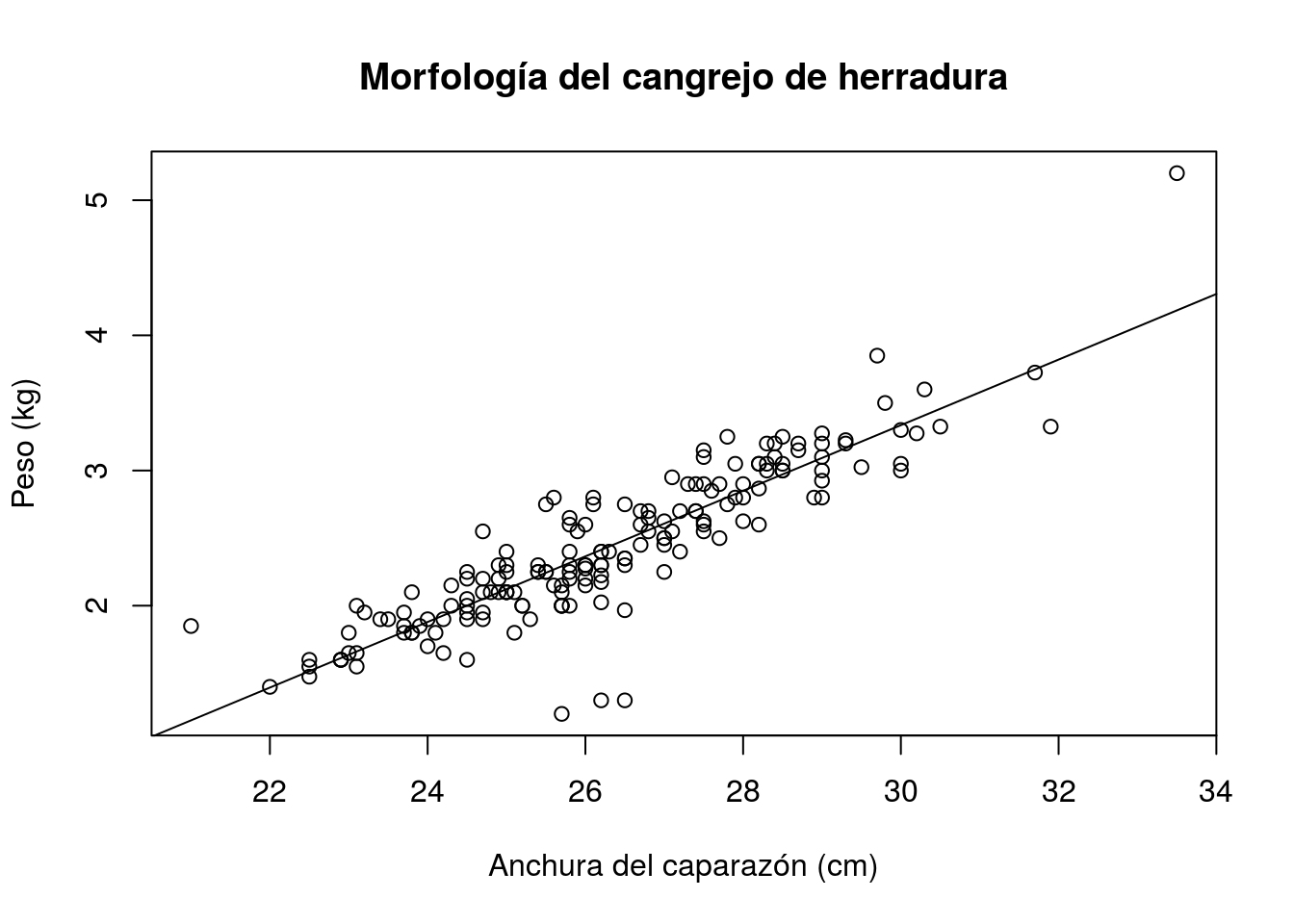
Análisis de la varianza.
Supongamos ahora que nuestro objetivo es decidir si existen diferencias significativas en la anchura media del caparazón según el color del mismo. Al calcular las medias según color:
aggregate(width~color,data=cangrejos,mean)## color width
## 1 1 26.96667
## 2 2 26.70421
## 3 3 25.75000
## 4 4 25.28182vemos que hay pequeñas diferencias entre los valores medios. La pregunta que nos hacemos aquí es si estas diferencias son lo suficientemente pequeñas como para ser atribuidas al mero efecto del azar o si, por el contrario, aún siendo pequeñas, estas diferencias (o algunas de ellas) no pueden atribuírse al azar y por tanto debe concluirse que cangrejos de color distinto tienen tamaños distintos.
Si llamamos \(\mu_i\) a la talla media para el color \(i\), el contraste que nos planteamos aquí es:
\[\begin{cases} H_{0}: & \mu_{1}=\mu_{2}=\mu_{3}=\mu_{4}\\ H_{1}: & \exists\mu_{i}\neq\mu_{j} \end{cases} \]
Si definimos las variables:
\[X_{i}=\begin{cases} 0 & \textrm{Si el cangrejo NO es de color i }\\ 1 & \textrm{Si el cangrejo es de color i } \end{cases} \]
podemos llevar a cabo nuestro análisis mediante el modelo lineal:
\[Y=\beta_1 + \beta_2 X_2 + \beta_3 X_3 +\beta_4 X_4 + \varepsilon \; \;\;\;\varepsilon\approx N\left(0,\sigma_{\varepsilon}\right)\]
donde:
\[\mu_{1} = \beta_{1} \\ \mu_{2} = \beta_{1}+\beta_{2} \\ \mu_{3} = \beta_{1}+\beta_{3} \\ \mu_{4} = \beta_{1}+\beta_{4}\]
Para ajustar este modelo debemos definir las variables \(X_2\), \(X_3\) y \(X_4\). R permite crearlas de manera sencilla mediante model.matrix:
X=model.matrix(~factor(color))
head(X)## (Intercept) factor(color)medio factor(color)medio-oscuro
## 1 1 1 0
## 2 1 0 1
## 3 1 0 0
## 4 1 0 1
## 5 1 0 1
## 6 1 1 0
## factor(color)oscuro
## 1 0
## 2 0
## 3 0
## 4 0
## 5 0
## 6 0El ajuste del modelo lineal sería entonces:
modAnova=lm(width~X[,2]+X[,3]+X[,4])
summary(modAnova)##
## Call:
## lm(formula = width ~ X[, 2] + X[, 3] + X[, 4])
##
## Residuals:
## Min 1Q Median 3Q Max
## -4.282 -1.550 -0.050 1.418 6.796
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 26.9667 0.5909 45.636 <2e-16 ***
## X[, 2] -0.2625 0.6271 -0.419 0.6761
## X[, 3] -1.2167 0.6666 -1.825 0.0698 .
## X[, 4] -1.6848 0.7346 -2.294 0.0230 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.047 on 169 degrees of freedom
## Multiple R-squared: 0.07447, Adjusted R-squared: 0.05804
## F-statistic: 4.532 on 3 and 169 DF, p-value: 0.004392Obviamente, tener que definir las variables indicadoras \(X_i\) puede resultar tedioso. En realidad R nos ahorra este trabajo, ya que el modelo anterior puede estimarse de modo mucho más simple mediante:
modAnova=lm(width~factor(color))
summary(modAnova)##
## Call:
## lm(formula = width ~ factor(color))
##
## Residuals:
## Min 1Q Median 3Q Max
## -4.282 -1.550 -0.050 1.418 6.796
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 26.9667 0.5909 45.636 <2e-16 ***
## factor(color)medio -0.2625 0.6271 -0.419 0.6761
## factor(color)medio-oscuro -1.2167 0.6666 -1.825 0.0698 .
## factor(color)oscuro -1.6848 0.7346 -2.294 0.0230 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.047 on 169 degrees of freedom
## Multiple R-squared: 0.07447, Adjusted R-squared: 0.05804
## F-statistic: 4.532 on 3 and 169 DF, p-value: 0.004392y que como vemos produce exactamente el mismo resultado. Para cambiar la categoría de referencia se puede utilizar la función relevel:
color=relevel(color,ref="oscuro")
modAnova2=lm(width~factor(color))
summary(modAnova2)##
## Call:
## lm(formula = width ~ factor(color))
##
## Residuals:
## Min 1Q Median 3Q Max
## -4.282 -1.550 -0.050 1.418 6.796
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 25.2818 0.4364 57.931 < 2e-16 ***
## factor(color)claro 1.6848 0.7346 2.294 0.02305 *
## factor(color)medio 1.4224 0.4843 2.937 0.00378 **
## factor(color)medio-oscuro 0.4682 0.5345 0.876 0.38231
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.047 on 169 degrees of freedom
## Multiple R-squared: 0.07447, Adjusted R-squared: 0.05804
## F-statistic: 4.532 on 3 and 169 DF, p-value: 0.004392Las estimadores de los coeficientes son \(\hat{\beta}_1\)=26.9667, \(\hat{\beta}_2\)=-0.2625, \(\hat{\beta}_3\)=-1.2167 y \(\hat{\beta}_4\)=-1.6848, respectivamente, y podemos comprobar que la anchura media de caparazón en cada grupo coincide con la suma de coeficientes correspondiente en el modelo:
\(\overline{y}_{1} = \hat{\beta}_{1}\) = 26.9667
\(\overline{y}_{2} = \hat{\beta}_{1}+\hat{\beta}_{2}\) =26.7042
\(\overline{y}_{3} = \hat{\beta}_{1}+\hat{\beta}_{3}\) =25.75
\(\overline{y}_{4} = \hat{\beta}_{1}+\hat{\beta}_{4}\) = 25.2819
El valor de \(F_{obs}\) para el análisis de la varianza de nuestro modelo es 4.532, y el p-valor correspondiente es 0.00439. Un valor tan pequeño indica que existe evidencia suficiente para rechazar la hipótesis nula: \[H_0: \beta_2=\beta_3=\beta_4=0\] esto es, los \(\beta_i\) no pueden ser nulos simultáneamente, lo que implica que las diferencias detectadas entre algunas de las medias no pueden ser atribuidas al azar.
Si volvemos al resultado de la estimación inicial del modelo y observamos los p-valores correspondientes a los contrastes individuales \(H_0:\beta_i=0\), vemos que el único contraste significativo (con p-valor<0.05) es el que corresponde al \(\beta_4=\mu[4]-\mu[1]\). Como este valor resulta significativamente distinto de cero, ello quiere decir que la media en el grupo 4 (color más oscuro) es diferente que en el grupo 1 (color más claro). Los otros dos contrastes han resultado no significativos, lo que indica que las diferencias entre los grupos 1 y 2 y entre los grupos 1 y 3 no son significativas. Como en el grupo 4 la anchura del caparazón es menor que en el grupo 1 concluimos que con la edad (recordemos que los cangrejos más oscuros son los más viejos) disminuye la anchura del caparazón. Desde el punto de vista biológico esto tiene sentido si asumimos (puesto que los cangrejos no se encogen) que los cangrejos de mayor tamaño mueren antes, y solo llegan a mayor edad los más pequeños.
El planteamiendo tradicional del modelo de análisis de la varianza aplicado a la comparación de medias entre grupos consiste simplemente en construir la llamada “tabla del análisis de la varianza”, en la que se consignan las variabilidades explicadas, residuales y totales, los grados de libertad (los valores \(q\) y \(n-p\) que hemos visto más arriba; en este caso \(q=p-1\)), el valor de la \(F_{obs}\) y su p-valor:
| Df | Sum Sq | Mean Sq | F value | Pr(>F) | |
|---|---|---|---|---|---|
| factor(color) | 3 | 56.97206 | 18.990686 | 4.532398 | 0.0043919 |
| Residuals | 169 | 708.10771 | 4.189986 |
En R esta tabla es muy fácil de obtener:
anova(lm(width~factor(color),data=cangrejos))## Analysis of Variance Table
##
## Response: width
## Df Sum Sq Mean Sq F value Pr(>F)
## factor(color) 3 56.97 18.991 4.5324 0.004392 **
## Residuals 169 708.11 4.190
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1o también:
oneway.test(width~factor(color),data=cangrejos,var.equal=TRUE)##
## One-way analysis of means
##
## data: width and factor(color)
## F = 4.5324, num df = 3, denom df = 169, p-value = 0.004392(Esta última opción permite realizar el análisis de la varianza si se incumple la hipótesis de homoscedasticidad, esto es, que el error estándar residual \(\sigma_\varepsilon\) sea el mismo en todos los grupos)
Si, como en este caso, existe evidencia suficiente para rechazar la hipótesis nula, el problema que se plantea a continuación es localizar qué grupos son los que presentan medias diferentes. Debido al problema de contrastes múltiples debe utilizarse el procedimiento adecuado para localizar dichos grupos. Procedimientos habituales para ello son el de Bonferroni, Scheffe o Tukey.
Análisis de la covarianza.
Supongamos ahora que nuestro objetivo es decidir si la relación entre peso y talla es la misma en los tres grupos definidos por el estado de las espinas laterales.
library(car)
scatterplot(weight~width|spine,reg.line=lm,smooth=FALSE)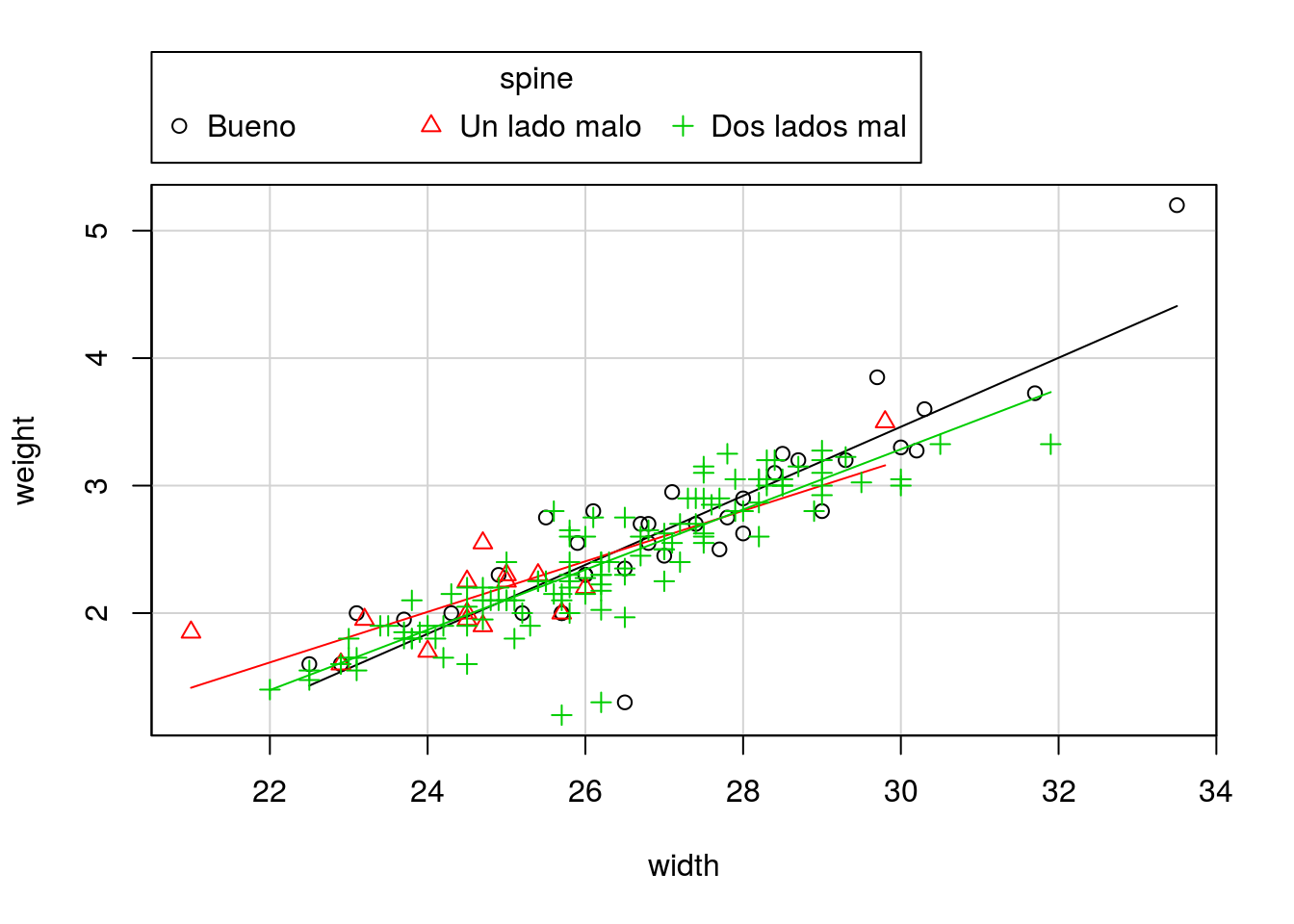
La siguiente sintaxis ajusta un modelo con pendiente común para los tres grupos:
ancova1=lm(weight~width+spine)
summary(ancova1)##
## Call:
## lm(formula = weight ~ width + spine)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.23016 -0.10828 0.01016 0.13356 0.96350
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -3.92955 0.27506 -14.286 <2e-16 ***
## width 0.24376 0.01002 24.335 <2e-16 ***
## spineUn lado malo 0.05544 0.08475 0.654 0.514
## spineDos lados mal -0.06969 0.05065 -1.376 0.171
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.2656 on 169 degrees of freedom
## Multiple R-squared: 0.7918, Adjusted R-squared: 0.7881
## F-statistic: 214.2 on 3 and 169 DF, p-value: < 2.2e-16Esta otra sintaxis ajusta una pendiente distinta a cada grupo:
ancova2=lm(weight~width*spine)
summary(ancova2)##
## Call:
## lm(formula = weight ~ width * spine)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.21372 -0.11963 0.00676 0.14984 0.79156
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -4.65914 0.49664 -9.381 <2e-16 ***
## width 0.27067 0.01825 14.833 <2e-16 ***
## spineUn lado malo 1.91050 1.05774 1.806 0.0727 .
## spineDos lados mal 0.86047 0.59602 1.444 0.1507
## width:spineUn lado malo -0.07243 0.04186 -1.730 0.0854 .
## width:spineDos lados mal -0.03455 0.02213 -1.561 0.1204
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.2641 on 167 degrees of freedom
## Multiple R-squared: 0.7966, Adjusted R-squared: 0.7906
## F-statistic: 130.8 on 5 and 167 DF, p-value: < 2.2e-16Para comparar un modelo con otro contrastamos si la variabilidad explicada por el primero difiere de forma significativa de la variabilidad explicada por el segundo:
anova(ancova1,ancova2)## Analysis of Variance Table
##
## Model 1: weight ~ width + spine
## Model 2: weight ~ width * spine
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 169 11.926
## 2 167 11.646 2 0.27946 2.0036 0.1381El p-valor obtenido indica que no hay diferencias entre ambos modelos, por lo que en aplicación del principio de la navaja de Ockham (entre dos modelos equivalentes es preferible el más parsimonioso), nos quedamos con el más sencillo (el primero).
Podemos ajustar un modelo que no incluya una ordenada distinta para cada grupo (es decir, un único modelo de regresión para todos los grupos):
modregre=lm(weight~width)
summary(modregre)##
## Call:
## lm(formula = weight ~ width)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1.18600 -0.11615 -0.00513 0.15076 1.01550
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -3.944019 0.255027 -15.46 <2e-16 ***
## width 0.242642 0.009666 25.10 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.2674 on 171 degrees of freedom
## Multiple R-squared: 0.7865, Adjusted R-squared: 0.7853
## F-statistic: 630.1 on 1 and 171 DF, p-value: < 2.2e-16y compararlo con el modelo ANCOVA:
anova(ancova1, modregre)## Analysis of Variance Table
##
## Model 1: weight ~ width + spine
## Model 2: weight ~ width
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 169 11.926
## 2 171 12.225 -2 -0.29887 2.1177 0.1235Como vemos no hay diferencias significativas en la capacidad explicativa de ambos modelos; como el modelo de regresión es el más simple, es el preferido y concluimos que el estado de las espinas laterales no produce modificación entre la relación entre anchura y peso.
Regresión de Poisson
Una variable \(Y\) sigue una distribución de probabilidad de Poisson cuando \[P\left(Y=k\right)=\frac{\lambda^{k}}{k!}e^{-\lambda},\,\,\,\,\,k\ge0\] Aquí el valor \(\lambda\) representa el valor medio de la variable \(Y\).
El modelo de regresión de Poisson se aplica cuando la variable \(Y\) es una variable de recuento que depende de unas variables explicativas \(X_i\), de tal modo que el valor de \(Y\) para un conjunto de valores de \(X_i\) puede aproximarse mediante una distribución de Poisson de parámetro \(\lambda(\mathbf{X})=exp(\beta_0+\beta_1 X_1 + \dots + \beta_p X_p)\).
Para interpretar los parámetros de este modelo basta tener en cuenta que de acuerdo con la descripción anterior:
\[log\left(\lambda(\mathbf{X})\right)=\beta_0+\beta_1 X_1 + \dots + \beta_p X_p\]
por lo que si los valores de todas las \(X_i\) se mantienen fijos, salvo el valor de \(X_j\), que se incrementa en una unidad, entonces:
\[\log\left(\frac{\lambda\left(X_{1},\dots,X_{j}+1,\dots,X_{p}\right)}{\lambda\left(X_{1},\dots,X_{j},\dots,X_{p}\right)}\right)=\log\left(\lambda\left(X_{1},\dots,X_{j}+1,\dots,X_{p}\right)\right)-\log\left(\lambda\left(X_{1},\dots,X_{j},\dots,X_{p}\right)\right)=\]
\[=\beta_{j}\left(X_{j}+1\right)-\beta_{j}X_{j}=\beta_{j} \]
o lo que es lo mismo: \[\frac{\lambda\left(X_{1},\dots,X_{j}+1,\dots,X_{p}\right)}{\lambda\left(X_{1},\dots,X_{j},\dots,X_{p}\right)}=e^{\beta_{j}}\]
Por tanto \(e^{\beta_j}\) representa el incremento proporcional en el valor de \(Y\) por cada unidad de incremento en el valor de \(X_j\). Por ejemplo, si \(\beta_j=1.388\) se tiene que \(e^{1.388}=4\). Ello significa que por cada unidad que se incrementa el valor de \(X_j\) se cuadruplica el valor de \(Y\) (siempre y cuando se mantengan fijos los valores del resto de las variables).
Estimación del modelo de Poisson
Ajustamos ahora un modelo de regresión de Poisson para predecir el número de satélites macho en función del peso del cangrejo hembra:
modPois=glm(y~weight,family=poisson(link=log))
summary(modPois)##
## Call:
## glm(formula = y ~ weight, family = poisson(link = log))
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.9307 -1.9981 -0.5627 0.9298 4.9992
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -0.42841 0.17893 -2.394 0.0167 *
## weight 0.58930 0.06502 9.064 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for poisson family taken to be 1)
##
## Null deviance: 632.79 on 172 degrees of freedom
## Residual deviance: 560.87 on 171 degrees of freedom
## AIC: 920.16
##
## Number of Fisher Scoring iterations: 5Calculamos los valores de \(e^{\beta_i}\):
exp(coef(modPois))## (Intercept) weight
## 0.6515473 1.8027335exp(confint(modPois))## Waiting for profiling to be done...## 2.5 % 97.5 %
## (Intercept) 0.4597023 0.9268994
## weight 1.5835992 2.0431615Por tanto, por cada kg de peso adicional del cangrejo hembra, el número medio de satélites macho se multiplica por un número entre 1.58 y 2.04.
Gráficamente:
plot(y~weight)
abline(exp(coef(modPois)))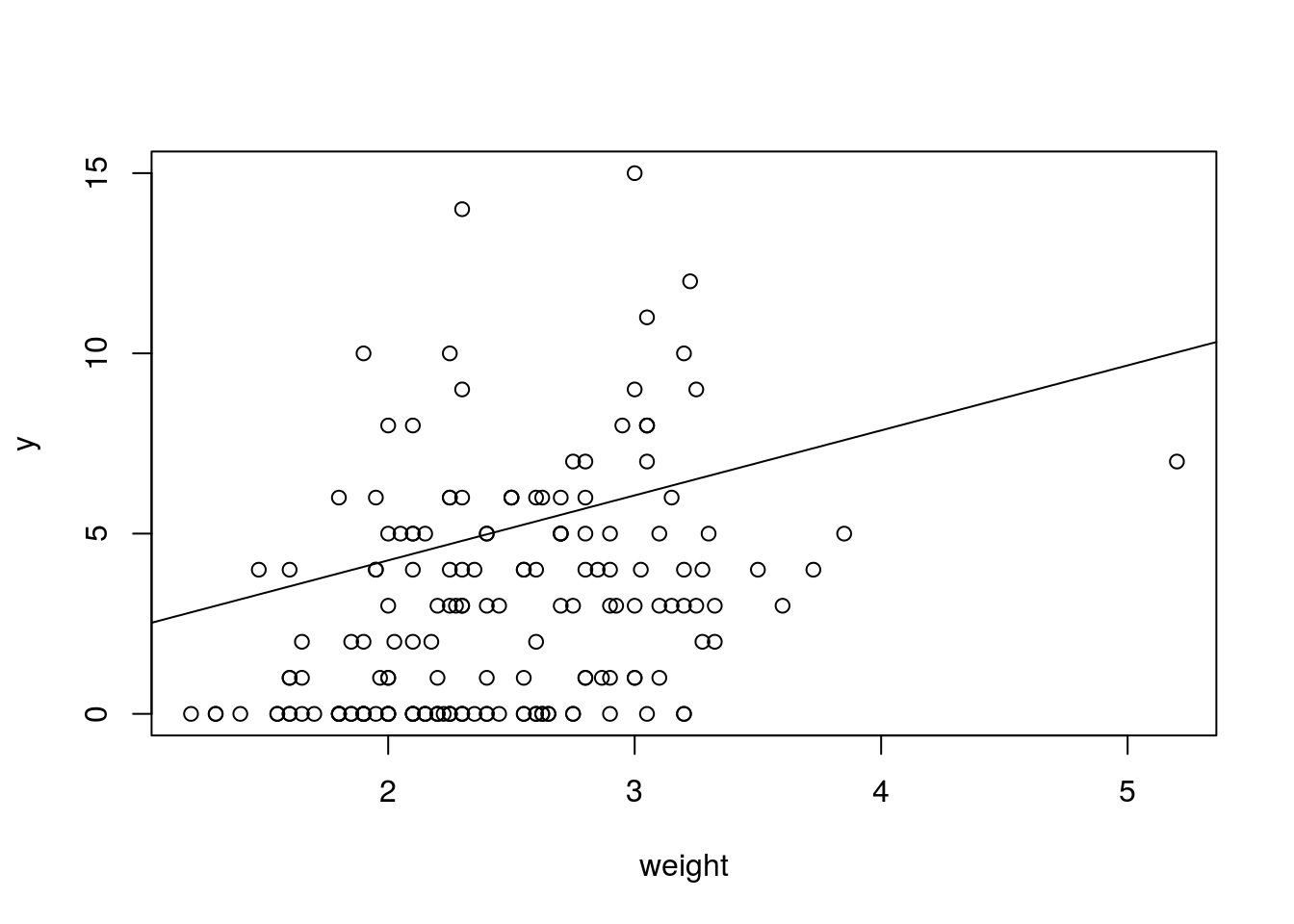
© 2016 Angelo Santana, Departamento de Matemáticas ULPGC