Gráficos simples: la función `plot`

En Matlab/Octave es muy sencillo generar gráficos de funciones. Supongamos que queremos dibujar la función:

\[f(x) = 4x^3 +10x^2+6\] en el intervalo \(\left[-3,1\right]\). Para ello comenzamos por definir la función; podemos hacerlo creando el archivo f.m con el código de la función:

function y=f(x)
  y=4*x.^3+10*x.^2+6;
end

o de manera equivalente, teniendo en cuenta que en este caso la función es sencilla y se puede definir en una linea, podemos definirla directamente como una función anónima:

>> f = @(x) 4*x.^3+10*x.^2+6;

Ahora construimos una malla sobre el intervalo \(\left[-3,1\right]\). Esto significa que vamos a definir una colección de puntos equiespaciados en este intervalo; si entre punto y punto dejamos una distancia de 0.1 unidades, el vector de puntos de la malla se obtiene mediante:

>> x=[-3 : 0.1 : 1];

De manera alternativa podemos usar la función linspace(a,b,n) que crea una malla de n puntos equiespaciados entre a y b. Por ejemplo, si queremos crear una malla de 50 puntos entre -3 y 1 ejecutaríamos el siguiente comando:

>> x=linspace(-3,1,50);

Por último utilizamos la función plot() indicando cuáles son los valores x y f(x) que describen el recorrido de la función:

>> plot(x,f(x))

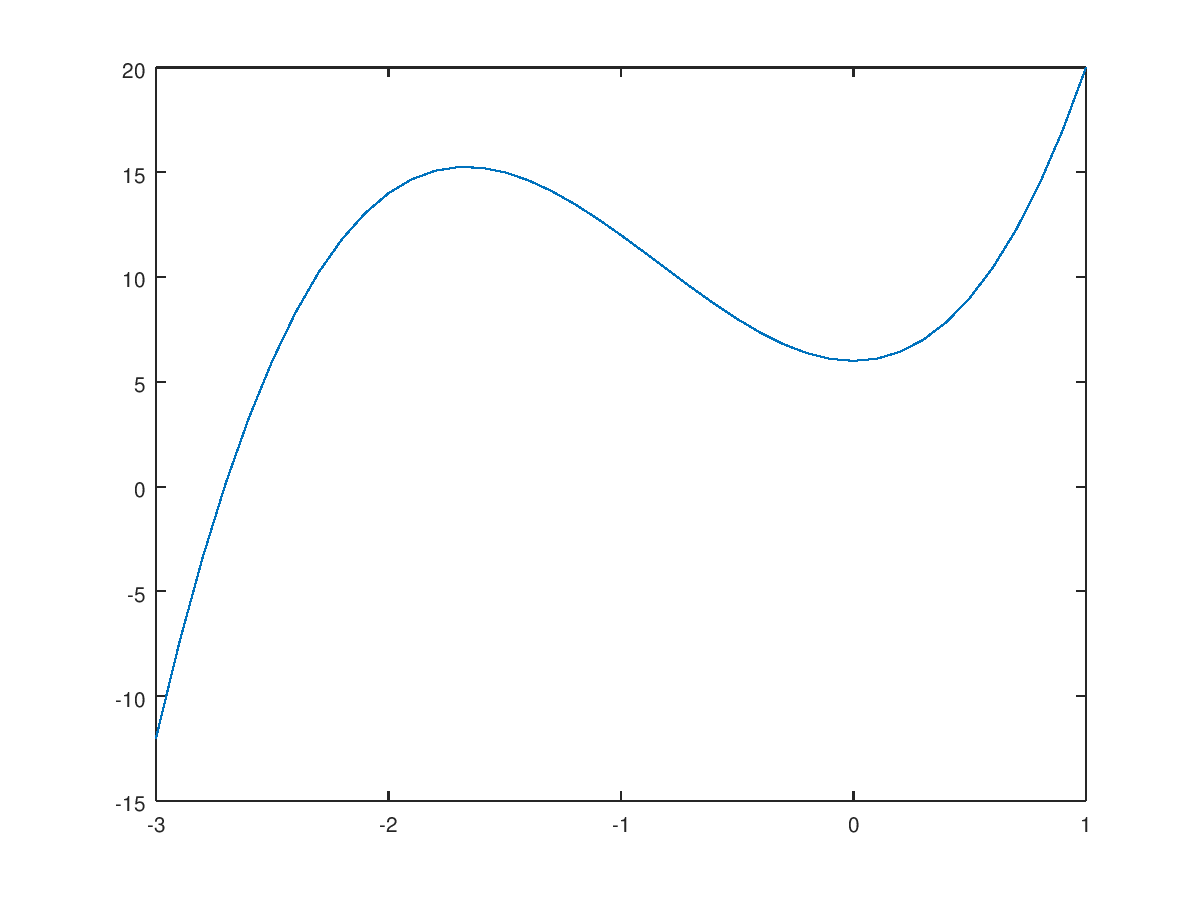
Por cierto, que Matlab/Octave cuentan con una función para definir polinomios. La función que hemos dibujado en el ejemplo anterior, \(f(x) = 4x^3 +10x^2+6\) es un polinomio de tercer grado cuyos coeficientes, de mayor a menor grado son [4, 10, 0, 6]. La función polyval(coefs,x) calcula los valores de un polinomio con coeficientes coefs sobre una malla x. Por tanto, obtenemos el mismo resultado de antes si utilizamos la sintaxis:

>> f=polyval([4, 10, 0, 6],x);
 plot(x, f)

y así nos ahorramos tener que definir la función f(x).

Como modificar el estilo de un gráfico.

En Matlab/Octave existen múltiples opciones para modificar el estilo de un gráfico. En general estas opciones se especifican añadiendo dentro de la llamada a la función plot() las propiedades del gráfico que se quieren modificar y a continuación de cada propiedad el valor que se quiere dar a la misma. A continuación se listan las propiedades que se pueden modificar y sus posibles valores:

Color: color de linea. Posibles valores: “red”, “green”, “blue”, “yellow”, “magenta”, “cyan”, “white”, “black”. Los colores se pueden acortar a su primera letra (“r”,“g”,“b”,“y”,“m”,“c”,“w”,“b”). También se puede especificar un color distinto mediante un vector [r g b] donde r, g y b son valores reales entre 0 y 1 que especifican, respectivamente, las proporciones de rojo, verde y azul en la construcción del nuevo color.
LineStyle: estilo de línea. Posibles valores: “-” (linea continua), “–” (linea discontinua), “:” (linea de puntos), “-.” (linea discontinua de guiones y puntos), “none” (sin linea)
LineWidth: Ancho de linea
Marker: Símbolo para el punto. Posibles valores: “none” (ningún punto), “o”, “+”,“*“,”.”, “x”, “s” (square, cuadrado), “d” (diamond, rombo), “^”, “v”, “<”, “>”, “p” (estrella de 5 puntas), “h” (estrella de 6 puntas).
MarkerEdgeColor: Color del borde del punto. Posibles valores: los mismos que para el color de linea.
MarkerFaceColor: Color del interior del punto.
MarkerSize: Tamaño del punto. Por ejemplo, si en el gráfico anterior se desea que solamente se dibujen los puntos de la función correspondientes a los valores x de la malla, que dichos puntos sean círculos, que su tamaño sea 4 y que su color sea rojo:

Ejemplo:

El siguiente código dibuja la misma función \(f(x)\) anterior utilizando ahora un círculo para los puntos de la malla, que se dibujan a tamaño 4 y de color azul, y se unen con una linea de color rojo. Obsérvese que la sintaxis comienza con el plot seguida de la sucesión de propiedades y valores; éstas se pueden poner en cualquier orden, si bien detrás de cada propiedad debe ir su valor:

plot(x, f, "marker", "o", "markerEdgeColor", "b", ... 
     "markersize", 4, "color","red")

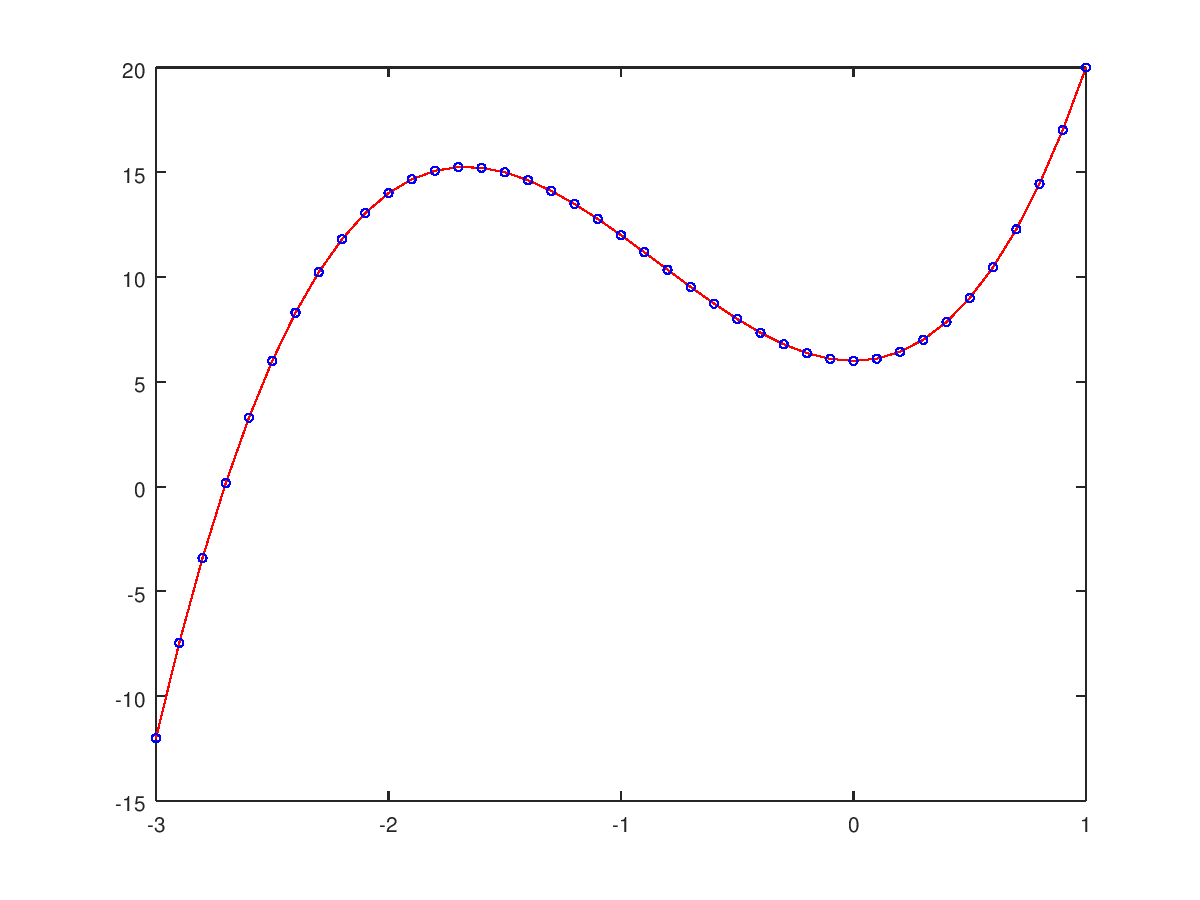
Si se quieren unir los puntos con lineas discontinuas de anchura 3, haciendo los puntos más grandes (tamaño 6), la sintaxis a seguir sería:

plot(x, f, "marker", "o", "markerEdgeColor", "b", ... 
     "markersize", 6, "linewidth", 3, "linestyle", ... 
     "--", "color","red")

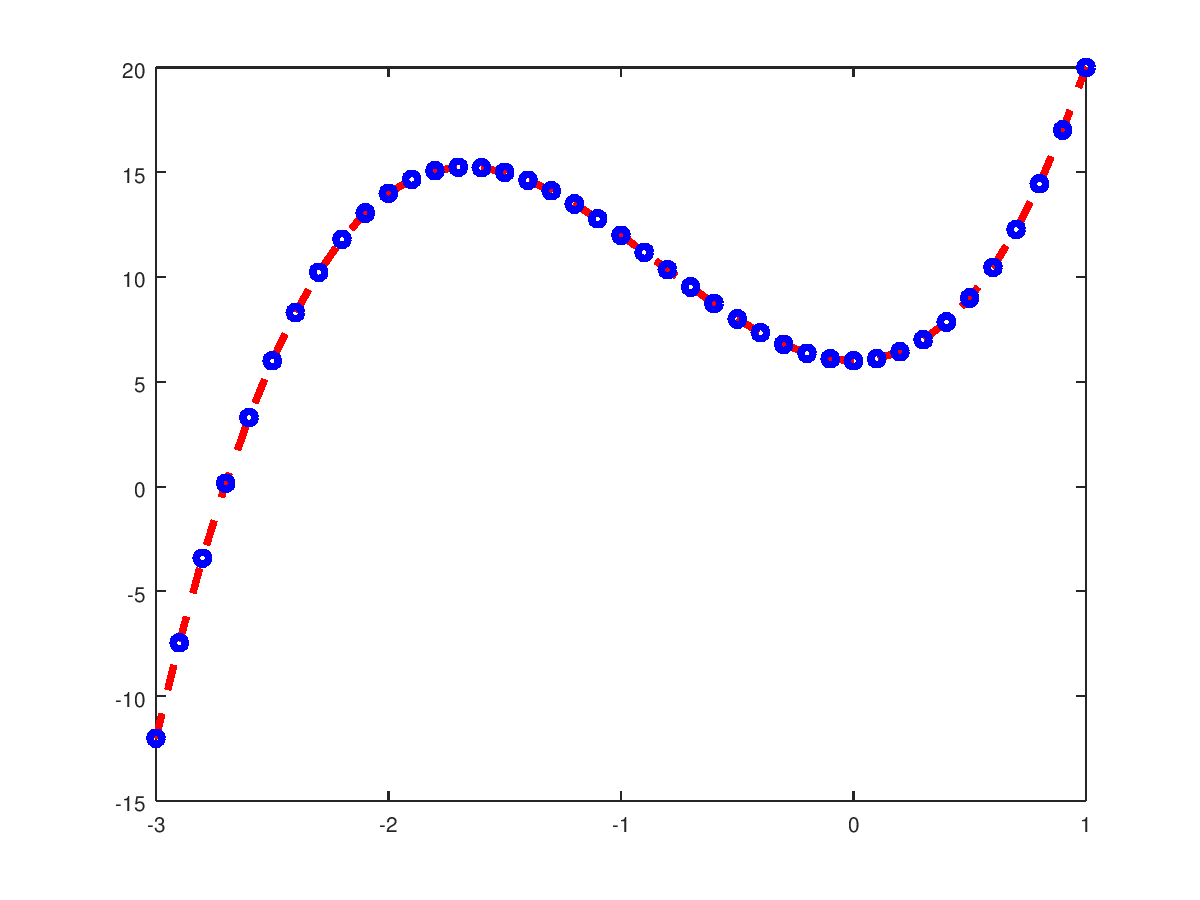
Estilo de linea y puntos resumido: se puede especificar el tipo de punto, el tipo de linea y su color mediante una cadena de caracteres en la que se concatenen los identificadores de los valores elegidos para estas tres propiedades; los identificadores pueden ir en cualquier orden y no necesariamente tienen que estar los tres. Por ejemplo, la siguiente sintaxis especifica que los puntos se representan con el símbolo x, se unen con una linea discontinua y se dibuja todo de color verde:

>> plot(x, f, "x--g")

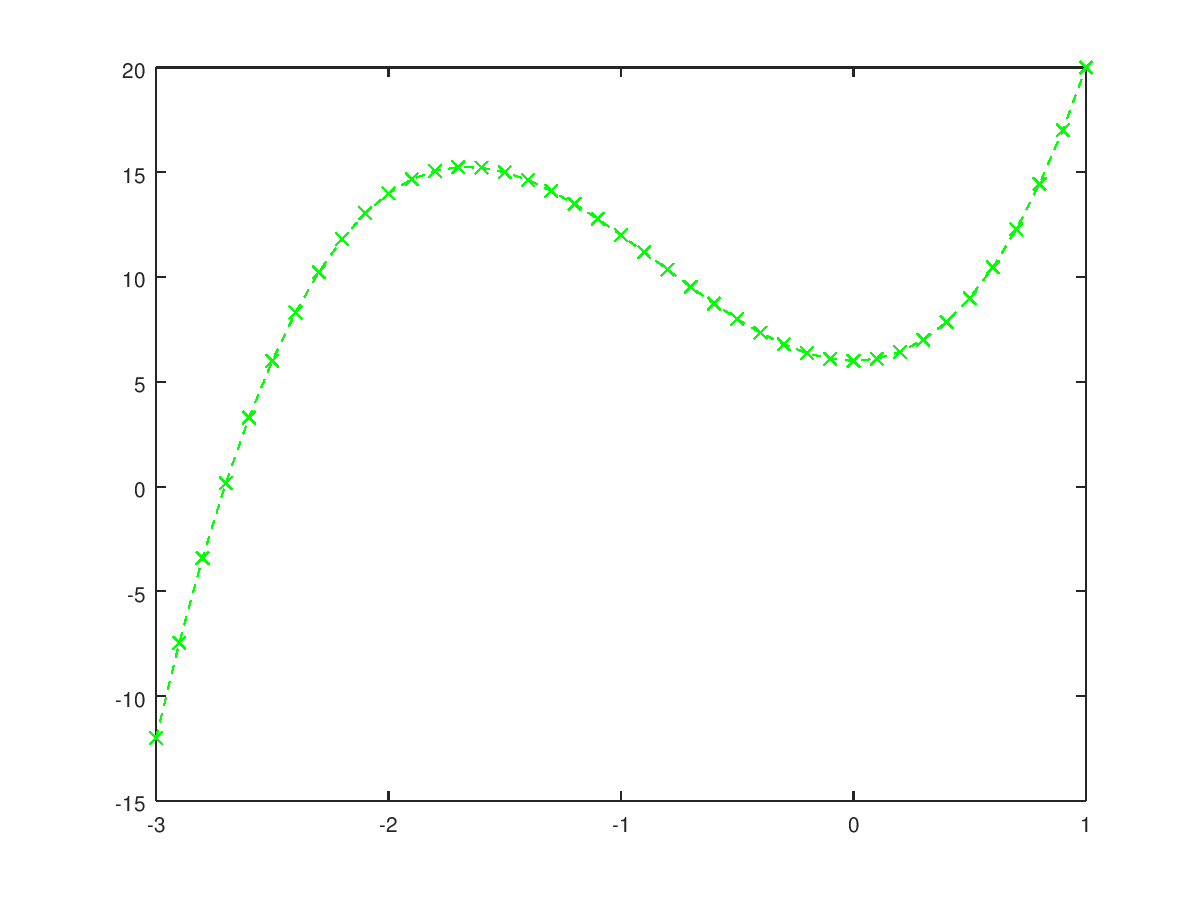
Si especificamos solo el tipo de punto y el color, no se dibuja la linea:

>> plot(x, f, "or")

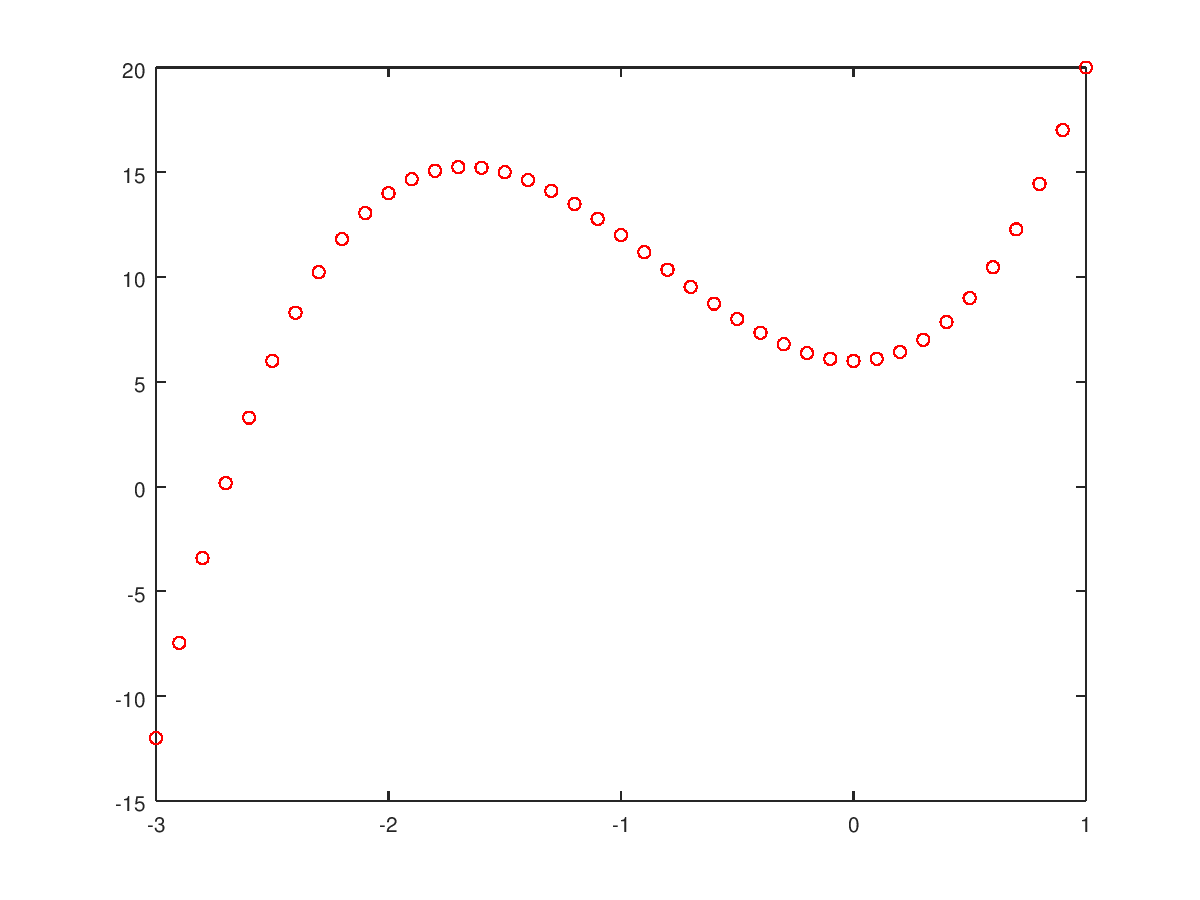
Ejes, títulos, etc: También podemos modificar los ejes (etiquetas, tamaño de letra, grosor de la linea de los ejes, límites de los ejes …) y poner un título al gráfico. Para ello primero se crea el gráfico tal como acabamos de hacer y luego se van añadiendo títulos para los ejes, para el gráfico, límites en cada eje, etc:

x=[-3 : 0.1 : 1];
f=polyval([4, 10, 0, 6],x);
plot(x, f, "o-r")
xlabel("Eje x")
ylabel("f(x)")
xlim([-4,2])
ylim([-20,20])
title("Gráfica de la función f(x)=4x^3+10x^2+6")
legend("f(x","location","southeast")

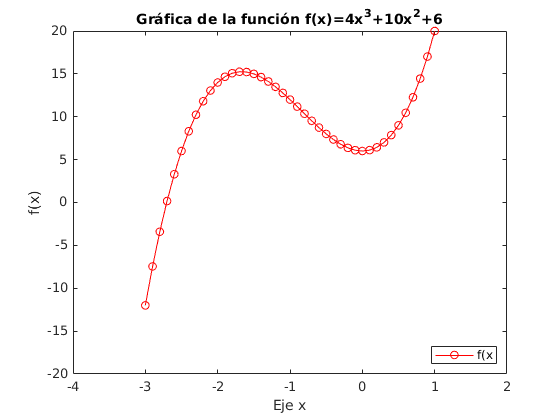
Es posible controlar también el tamaño de letra para los ejes, títulos, etc mediante la función set(gca, ...) (la palabra gca es un acrónimo de get current axis). Además podemos añadir texto en los ejes o en cualquier lugar del gráfico mediante la función text. Veamos a modo de ejemplo el resultado de la siguiente sintaxis:

plot(x, f, "o-", "markersize", 4, "linewidth", 2, ...
     "color","red")
set(gca, "xlabel", ...
    text("string", "x", "fontsize", 15), ...
    "xlim",[-4,2], "fontsize",10)
set(gca, "ylabel", ...
    text("string", "f(x)", "fontsize", 15), ... 
    "ylim",[-20,20], "fontsize", 10, "ytick",[-20:5:20])
set(gca, "title", ...
    text("string","Polinomio de grado 3","fontsize", 22))
text(-3,-15,"Gráfica de la función f(x)", "fontsize", 18)
grid on

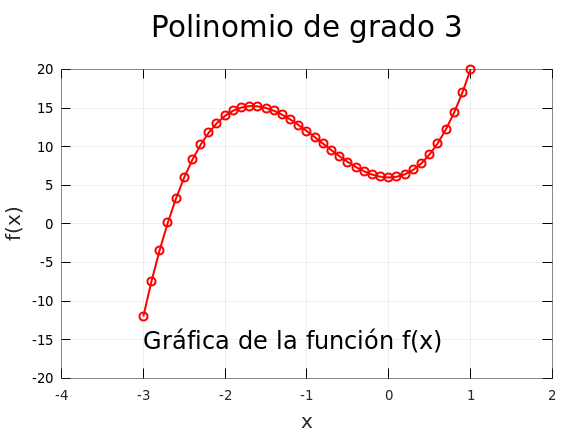
La función `fplot()`

Esta función permite dibujar funciones definidas por el usuario (o ya existentes) de manera muy simple, indicando el recorrido de la función y el número de puntos que se quieren emplear para hacer la gráfica. Por ejemplo, para dibujar la función coseno (cos) entre \(-2\pi\) y \(pi\), utilizando 50 puntos, podemos utilizar la sintaxis:

>> fplot("cos", [-2*pi, pi], 50)

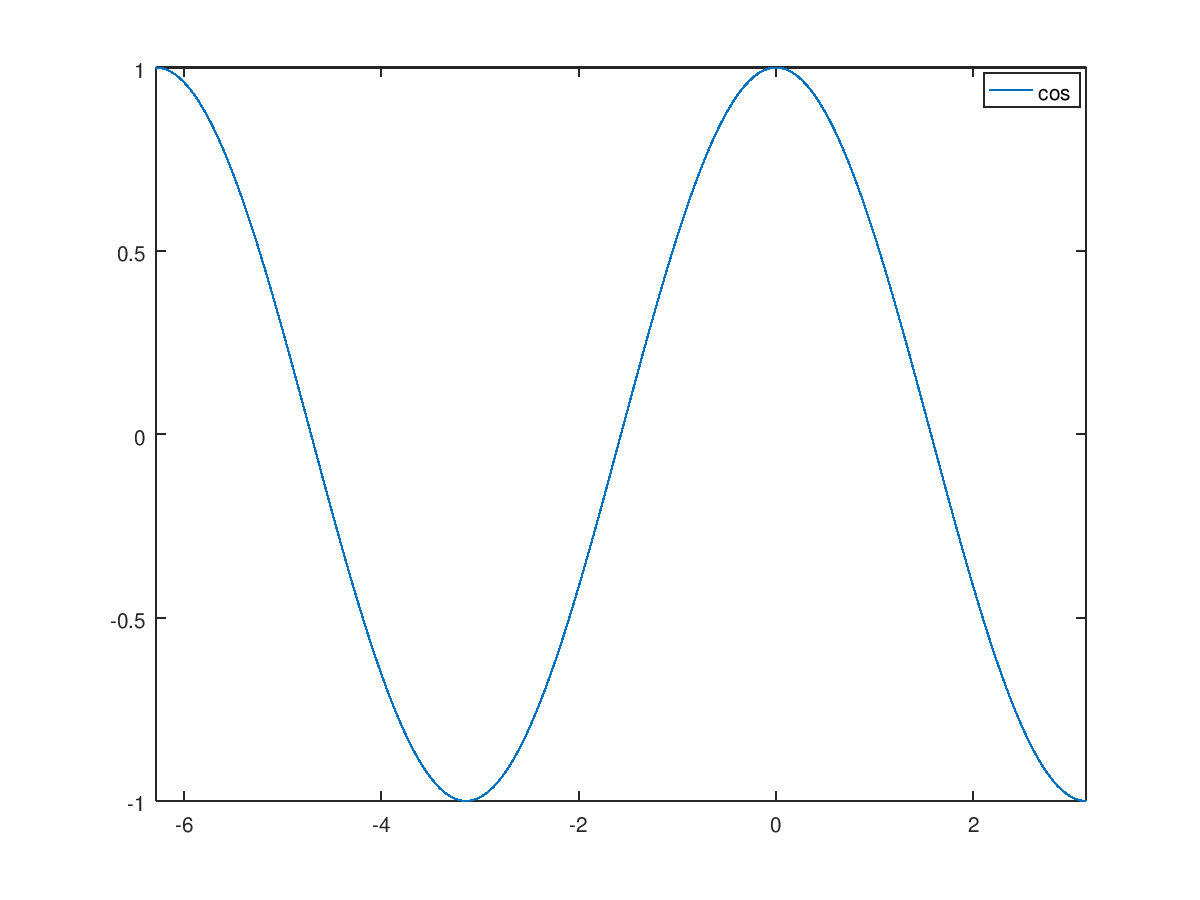
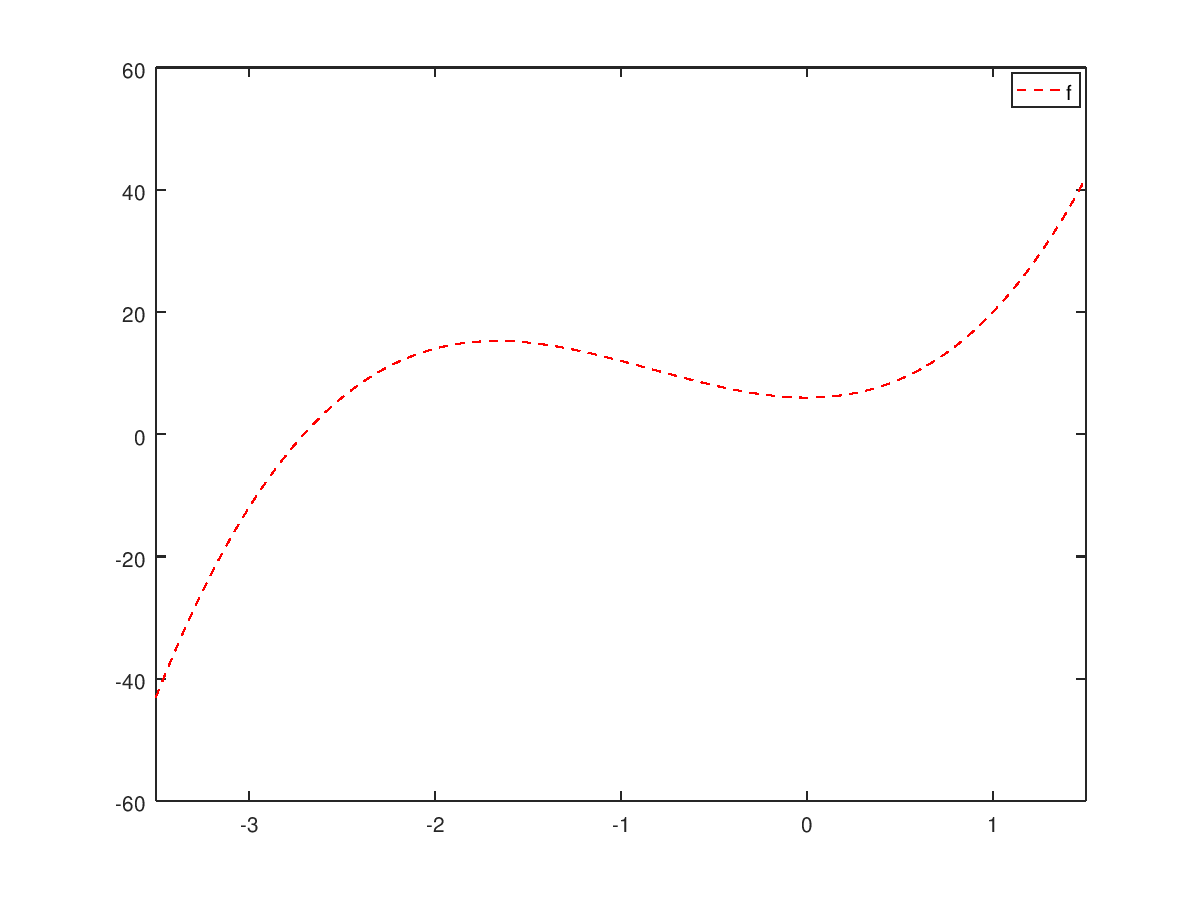
También podemos dibujar el polinomio que ya definimos más arriba, utilizando la función “f” que hemos creado:

>> fplot("f", [-3.5, 1.5], 50, "--r")

Superposición de varias funciones en un mismo gráfico.

Supongamos que queremos superponer en un mismo gráfico la representación de las siguientes funciones entre \(-\pi\) y \(2\pi\):

\[f_1(x)=sin(x) \;\;\;\;\;\;\;\;\; f_2(x)=sin(x+\frac{\pi}{5})\;\;\;\;\;\;\;\;\; f_3(x)=sin(x-\frac{\pi}{5})\] En primer lugar debemos definir las funciones \(f_2(x)\) y \(f_3(x)\):

>> f2 = @(x) sin(x+pi/5);
 f3 = @(x) sin(x-pi/5);

y ahora podemos representarlas con una única llamada a la función plot. Nótese que al final añadimos el comando legend para indicar que coloque en la esquina superior derecha (noreste) una leyenda especificando qué gráfica corresponde a cada función:

x=[-pi:0.1:2*pi];
plot(x,sin(x),"+-b",x,f2(x),"o--r",x,f3(x),"*-.c");
set(gca, "xlim",[-pi,2*pi]);
legend ({"f_1", "f_2", "f_3"}, "location", "northeast");

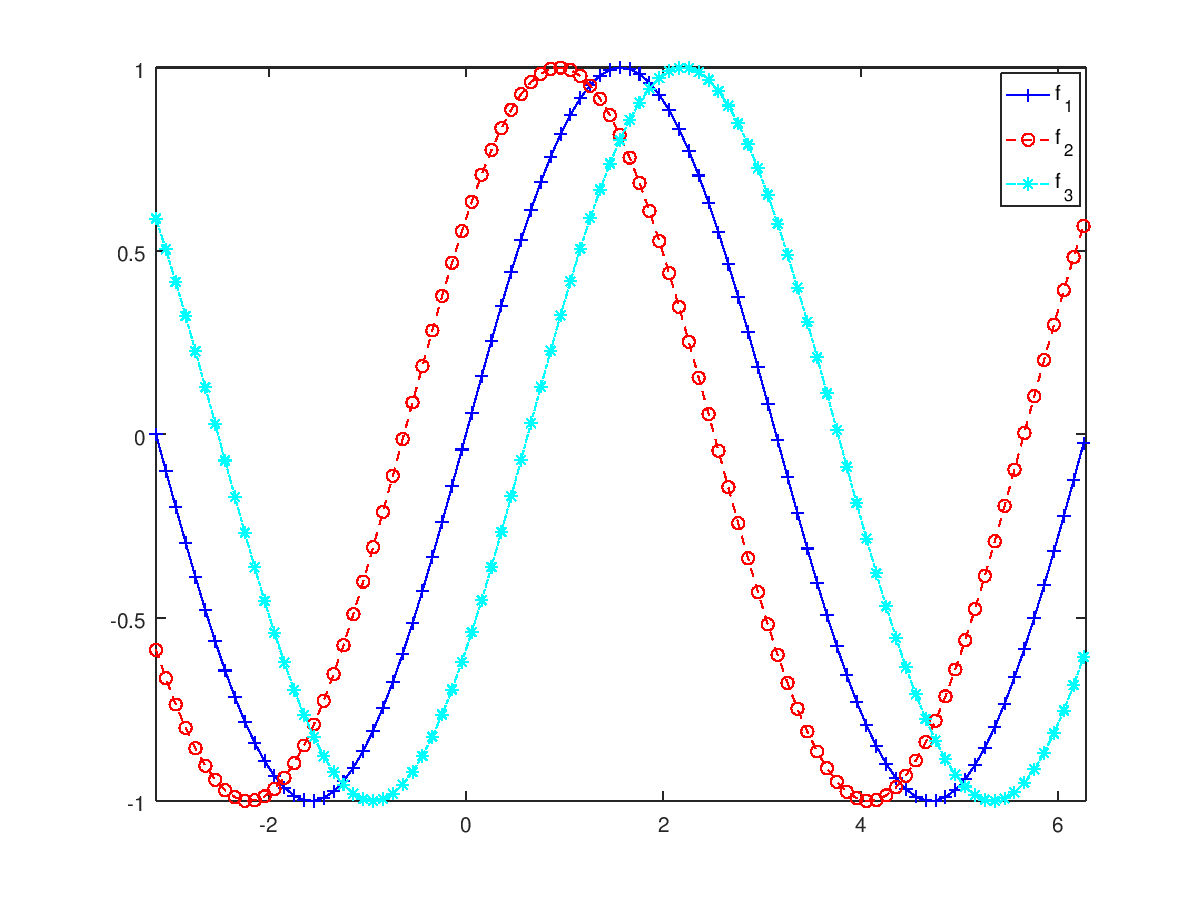
Nótese que a continuación de cada par x, f(x) se incluyen las propiedades de esa función; en este caso hemos usado la versión abreviada del estilo de linea, pero podríamos usar la versión completa e ir especificando propiedades (markerSize, markerEdgeColor, lineWidth, …) distintas para cada gráfica.

Otra manera de superponer dos o más funciones en un mismo gráfico consiste en dibujar la primera función seguida del comando hold on. A continuación se escribe el código para el resto de las funciones y se termina con hold off. El siguiente ejemplo aclara como se realiza el proceso:

plot(x,sin(x),"+-b")
hold on
plot(x,f2(x),"o--r")
plot(x,f3(x),"*-.c")
hold off
set(gca, "xlim",[-pi,2*pi])
legend ({"f_1", "f_2", "f_3"}, "location", "northeast");

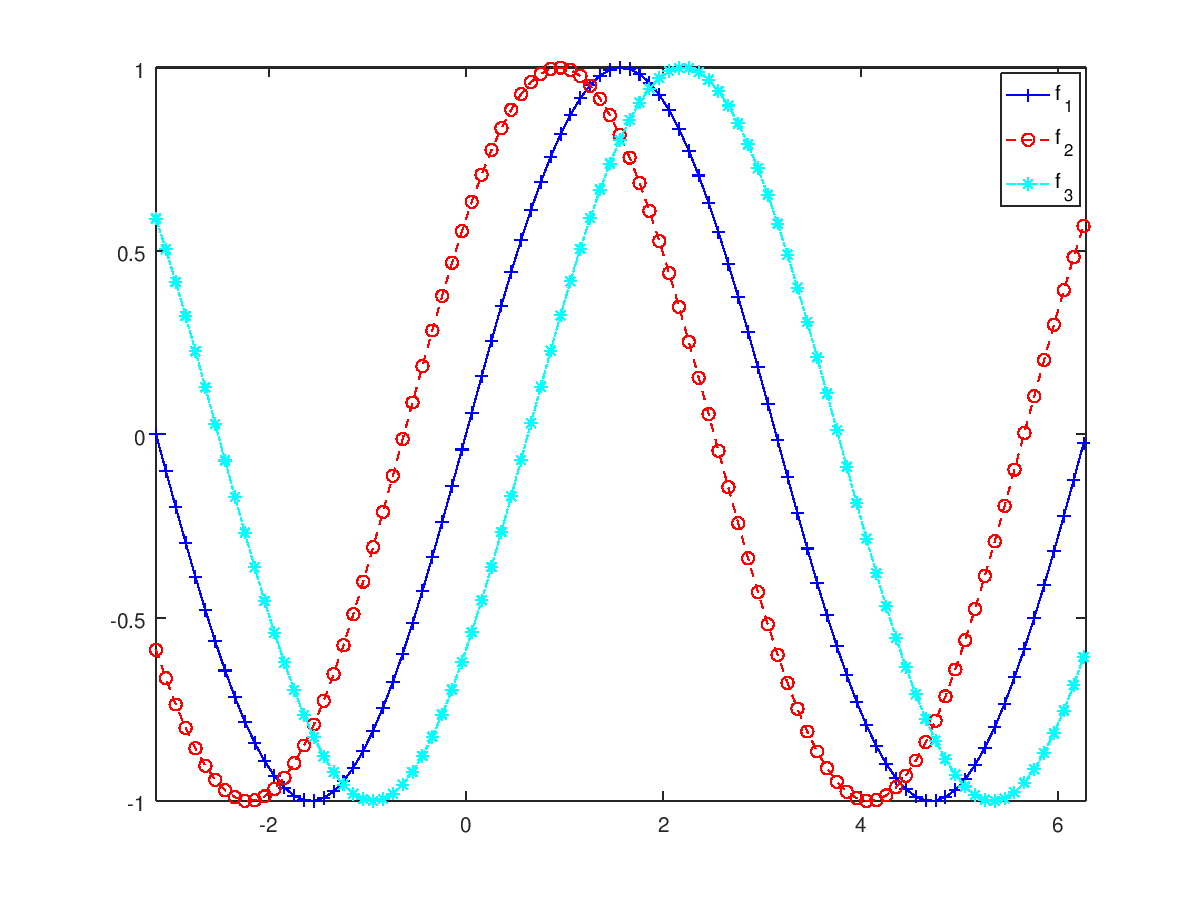
Pueden combinarse también varias gráficas en la misma figura utilizando fplot() en lugar de plot().

Borrado de un gráfico

La función clf borra el gráfico actual, dejando la ventana de gráficos en blanco.

Guardar gráficos

Una vez que hemos generado un gráfico, podemos guardarlo en un archivo png, jpg, pdf o eps (postscript) entre otros formatos, mediante la sintaxis:

>> print("miGrafico.png", "-dpng");
 print("miGrafico.jpg", "-djpg");
 print("miGrafico.pdf", "-dpdf");
 print("miGrafico.eps", "-deps");

Tecleando help print en la consola veremos más opciones para guardar (o imprimir) gráficos.

Gráficos 3D

Matlab/Octave ofrecen también la posibilidad de dibujar superficies 3D. Supongamos que queremos dibujar la función:

\[f(x,y) = x^2 - y^2, \;\;\;x\in [-2,2], \; y \in [-2,2]\] Comenzamos definiendo el dominio de la función:

>> x = [-2:0.1:2]; 
 y = x;

Ahora generamos la malla \(\left(x,y\right)\) sobre la que se va a dibujar la superficie \(f(x,y)\):

>> [X Y] = meshgrid(x,y);

Ahora calculamos los valores \(z = f(x,y) = x^2 - y^2\) para todos los puntos de esta malla:

>> Z = X.^2 - Y.^2;

Por último usamos la función surf() para dibujar la superficie \(f(x,y)\):

>> surf(X, Y, Z)

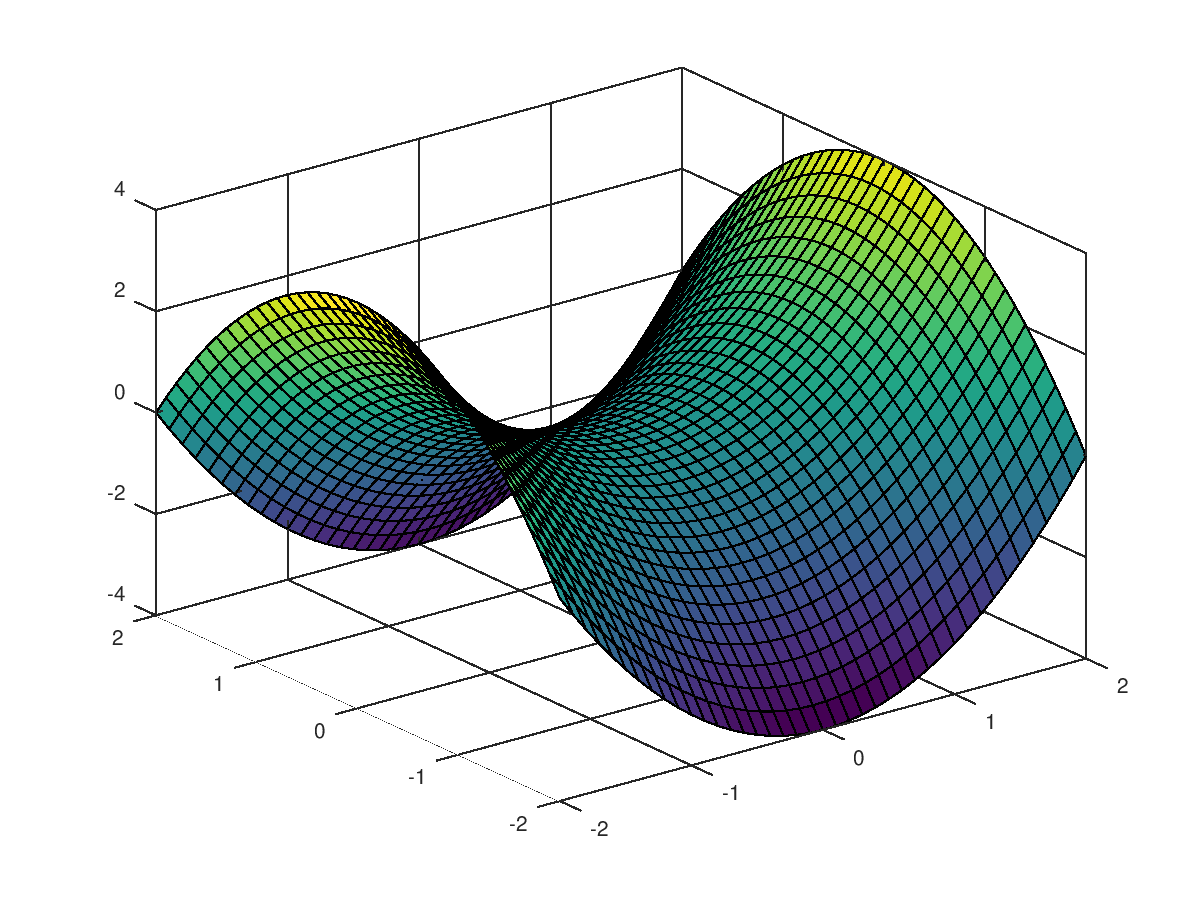
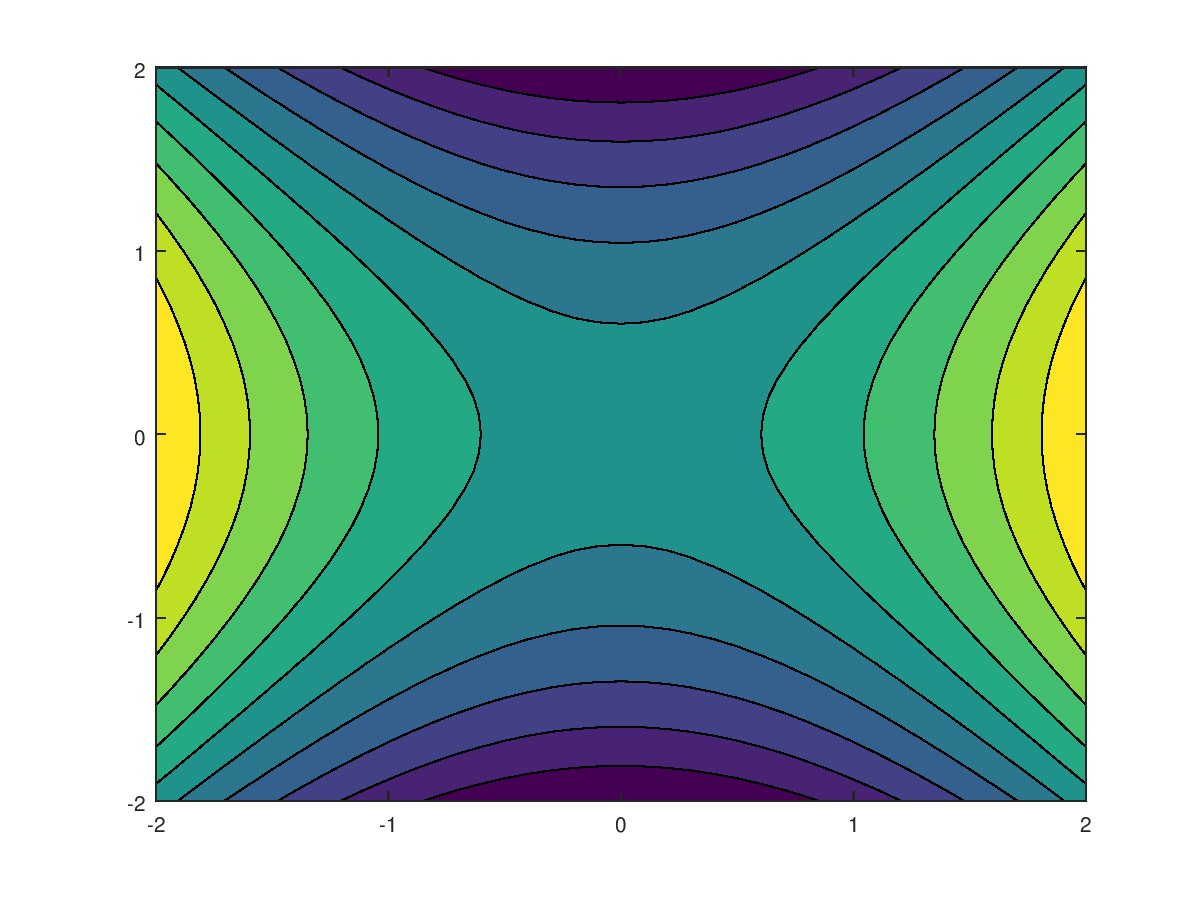
La función contourf() traza las curvas de nivel correspondientes a la figura anterior:

>> contourf(X, Y, Z)

Se puede consultar la ayuda de Matlab (o cualquiera de los numerosos tutoriales que hay en linea) para ver las opciones existentes para modificar los gráficos 3D: modificaciones en los ejes, colores, orientación, punto de vista, …

8. Gráficos

Gráficos simples: la función plot