Definición de funciones en Matlab

Una función es una colección de operaciones cuyo objetivo es realizar una tarea particular. En general una función puede recibir uno o varios valores de entrada (input1, input2, …) y producir como salida uno o varios valores (output1, output2, …). También es posible que la función no reciba ninguna entrada o no produzca ninguna salida.

La sintaxis para definir una función en Matlab/Octave es la siguiente:

function [output1, output2, ...] = nombreFuncion(input1, input2, ...)
  < Hacer cosas (cuerpo de la función) >
end

Opcionalmente a continuación de la primera linea de una función y antes de su cuerpo podemos insertar una o varias lineas de comentario (precedidas por el símbolo %) que expliquen de manera sucinta qué hace la función. El texto de este comentario servirá como ayuda sobre el funcionamiento de la función y aparecerá en la ventana de comandos si el usuario teclea help seguido del nombre de la función.

Ejemplo: Construir una función con el nombre rango que reciba como entrada un vector de longitud arbitraria \(n\) y devuelva como salida un vector formado por los valores mínimo y máximo de dicho vector

function y = rango(x)
  % Esta función calcula los valores mínimo y máximo de un vector o matriz x
  y = [min(x) max(x)];
end

En este ejemplo la función tiene una única salida (y) y una única entrada (x). Por defecto, Matlab/Octave asume que tanto y como x pueden ser vectores o matrices. Como hemos añadido una linea de comentario, ésta se muestra si el usuario pide ayuda sobre la función:

>> help rango

Esta función calcula los valores mínimo y máximo de un vector o matriz x

Ejecutemos ahora esta función, creando en primer lugar un vector de valores aleatorios:

>> v=rand(1,6)

v =

   0.991870   0.777889   0.593820   0.031225   0.947793   0.351061

y ahora utilizando la función rango() para encontrar sus valores mínimo y máximo:

>> rango(v)

ans =

   0.031225   0.991870

Como vemos, Matlab devuelve un vector con el mínimo y el máximo del vector v.

Alternativamente, esta función podría programarse del modo siguiente:

function [minx, maxx] = minmax(x)
  maxx = max(x);
  minx = min(x);
end

Nótese que en este caso, la función devuelve explícitamente un vector con dos términos, el mínimo y el máximo respectivamente. Al ejecutar esta función obtenemos como resultado:

>> minmax(v)

ans =  0.031225

¿Qué ha ocurrido aquí? Pues que, por defecto, cuando la salida de una función explícitamente declara varios términos distintos, al ejecutarla sin asignar su resultado a ninguna variable se muestra solamente el primero de sus valores de salida (en este ejemplo, el mínimo). Si queremos obtener todos los valores que proporciona la función la llamada a la misma debe realizarse del modo siguiente:

>> [minV, maxV]=minmax(v)

minV =  0.031225
maxV =  0.99187

esto es, asignando la salida de la función explícitamente a un vector de dimensión coincidente con la forma en que se ha definido la función; podemos ahora utilizar cada uno de los términos de este vector de salida:

>> minV

minV =  0.031225

>> maxV

maxV =  0.99187

Importante: para que una función devuelva un valor o valores, las variables que se han declarado como salida en la propia definición de la función, deben calcularse explícitamente en el cuerpo de la función. Así, en la función rango la salida es la variable y, que se calcula explícitamente en el cuerpo de la función. Asimismo en el cuerpo de la función minmax se calculan explícitamente las variables maxx y minx utilizadas en su definición. Si alguna de estas variables no se calculase en el cuerpo de la función, el valor de dicha variable se devolvería como un vector nulo. Obsérvese lo que ocurre si definimos la función como:

function [minx, maxx] = minmax2(x)
  maxx = max(x);
  minimo = min(x);
end

Si nos damos cuenta, tal como la hemos declarado, la función debe devolver minx y maxx. Pero en el cuerpo de esta función no se calcula la variable minx. ¿Qué ocurre al ejecutarla?:

• Si la ejecutamos sin asignar su resultado a ninguna variable:

>> minmax2(v)

no se produce ninguna salida, pues el primer valor que devuelve dicha función es minx y esta variable no se ha calculado.

• Si la ejecutamos asignando su resultado al vector [minV, maxV]:

>> [minV, maxV]=minmax2(v);

warning: minmax2: some elements in list of return values are undefined
warning: called from
    minmax2 at line 4 column 1

>> minV
 minV = [](0x0)

>> maxV
 maxV =  0.99187

Guardar una función

En Matlab/Octave es posible declarar una función en la ventana de comandos. No obstante, esto entraña varias dificultades:

• Si la función es medianamente larga o compleja, es difícil escribirla pues la ventana de comandos no permite la edición de manera sencilla (por ejemplo, no es posible volver a la línea anterior si nos hemos equivocado en una letra)

• La función sólo estará activa mientras dure nuestra sesión. Si la función hace alguna tarea interesante (o complicada) conviene tenerla archivada para poder utilizarla en otras ocasiones.

Por ello la mejor manera de programar funciones es utilizando la ventana de edición, que además ofrece ventajas como distintos colores según que se incluyan comentarios, funciones propias de matlab, etc, o indentación, que hace más claras las distintas partes de la función.

Una vez hayamos terminado de editar la función, debe guardarse en un archivo con el mismo nombre de la función y con la extensión .m. Matlab busca siempre los archivos .m en nuestro directorio home y en los directorios definidos por defecto para que Matlab busque dichos archivos. Se puede saber cuáles son dichos directorios ejecutando el comando path.

Resulta conveniente disponer de una carpeta específica para los archivos .m (por una mera cuestión de organización y de facilidad para encontrarlos). Para incluir dicha carpeta dentro de aquellas en las que Matlab busca por defecto los archivos .m se utiliza el comando:

>> addpath ruta

donde ruta es la dirección de dicha carpeta (por ejemplo c:\Documents and settings\usuario\mis archivos\misFunciones).

function x = resuelveEc2G(a,b,c)
    discrim=b^2-4*a*c;
    x1=(-b-sqrt(discrim))/(2*a);
    x2=(-b+sqrt(discrim))/(2*a);
    x=[x1;x2];
end

>> resuelveEc2G(1, -1, -6)

ans =

  -2
   3

>> resuelveEc2G(1,2,5)

ans =

  -1 - 2i
  -1 + 2i

Buenas prácticas de programación de funciones

Es una buena práctica de programación no acumular demasiadas tareas en una función. Si debemos realizar varias tareas independientes es mejor separarlas en varias funciones simples y usar una “función principal” que las vaya llamando en el orden adecuado. Ello hace más fácil detectar y corregir posibles fallos en la programación y permite reutilizar la misma función (simple) en varios contextos.

Por ejemplo, supongamos que queremos pedir al usuario que introduzca por pantalla los valores de los coeficientes de la ecuación de segundo grado, para a continuación resolverla y dibujar la parábola resultante entre los puntos de corte. Podemos descomponer este trabajo en tres funciones distintas:

• Una función que pida los valores de los coeficientes y compruebe que los valores son válidos (en este caso, que \(a\neq 0\), porque si fuese \(a=0\) no tendríamos una ecuación de segundo grado).

• Una segunda función que resuelva la ecuación.

• Una función que represente la parábola y los puntos de corte.

La función que resuelve la ecuación ya la hemos construido antes. Para pedir al usuario que introduzca los valores de los coeficientes podemos usar la siguiente función:

function [a,b,c,error]=pideCoeficientesEc2G()
      % Esta función solicita los coeficientes de una
      % ecuación de segundo grado 
      clc; % Limpia la pantalla
      disp('=============================================');
      disp('programa para resolver ecuaciones de 2º grado'); 
      disp('=============================================');
      disp(' ');
      % Introducción de los coeficientes desde teclado:
      disp('Introduzca los coeficientes de la ecuación'); 
      disp(' ');
      a = input('Valor del coeficiente a: ');
      b = input('Valor del coeficiente b: ');
      c = input('Valor del coeficiente c: ');
      if a==0
          error=true;
          disp('ERROR: El valor del coeficiente "a" no puede ser 0')
      else
          error=false;
      end 
end

Asimismo, la siguiente función se encargaría de representar la parábola con los puntos de corte:

function dibujaParabola(coefs,raices)
% Esta función dibuja una parábola y muestra
% sus puntos de corte con el eje X
   % Se asignan las raíces a las variables x1 y x2:
    x1=min(raices);
    x2=max(raices);       
    % Se fijan los límites de la gráfica de forma
    % que contengan las raices y quede margen a
    % los lados. Si hay una raíz única se fija 
    % un margen de 2 unidades
    if x1==x2
        margen=2;
    else
        margen=(x2-x1)/4;
    limInf=x1-margen;
    limSup=x2+margen;
    % Se calculan los valores de la parábola entre
    % los dos límites elegidos
    x=linspace(limInf, limSup, 200);
    y=coefs(1)*x.^2+coefs(2)*x+coefs(3);
    % Se dibuja la parábola
    plot(x,y);
    % Se centran los ejes en el origen de coordenadas
    ax = gca; 
    ax.XAxisLocation = 'origin'; 
    ax.YAxisLocation = 'origin';
    box off
end

Por último, la “función principal” siguiente se encargaría de integrar las tres funciones anteriores: la que pide los datos, la que soluciona la ecuación y la que dibuja la parábola cuando las raíces son reales:

function ec2G()
    [a,b,c,error]=pideCoeficientesEc2G();
    if ~error
        raices=resuelveEc2G(a,b,c);
        disp('Las raices de la ecuación son:');
        disp(raices);
        if imag(raices(1))==0
            % Solo se dibuja la parábola si 
            % las raices son reales
            dibujaParabola([a,b,c],raices);
        end
    end
end

>> ec2G()

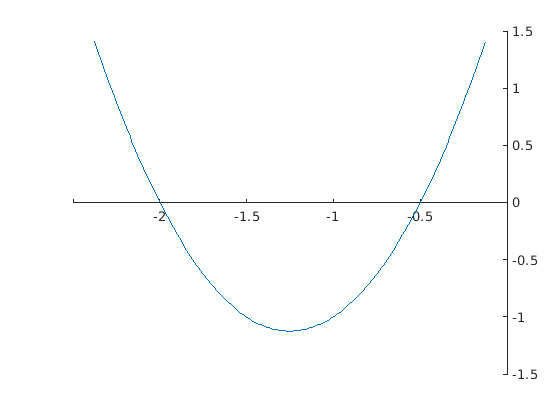
Cuando ejecutamos la función, nos pide los valores de los coeficientes y a continuación nos muestra la solución (o un mensaje de error) y la gráfica en su caso:

=============================================
programa para resolver ecuaciones de 2º grado
=============================================

Introduzca coeficientes de la ecuación

Valor del coeficiente a: 2
Valor del coeficiente b: 5
Valor del coeficiente c: 2

ans =

   -2.0000
   -0.5000

Identificadores de funciones (function handles)

En matlab un identificador de función es un tipo de dato cuyo nombre se asocia de manera unívoca con una función. En la práctica ello permitirá usar funciones en algunos contextos en los que normalmente se usan variables (por ejemplo, cuando el argumento de una función sea otra función, o cuando se quiere crear una función sencilla dentro de un script).

A modo de ejemplo, supongamos que hemos creado la función cuadrado, encargada simplemente de elevar al cuadrado un valor o todos los valores de un vector:

function x2 = cuadrado(x)
    x2=x.^2;
end

Crear un identificador de función consiste en asignarle a esta función un nombre de variable; para ello el nombre de la función debe ir precedido por el símbolo @ ; el siguiente ejemplo asigna el identificador f a la función cuadrado.

>> addpath programas;
 f=@cuadrado;

A partir de ahora la variable f se comportará como si fuera la función original:

>> addpath programas
 f = @cuadrado;
 a = 2;
 b = f(a)

b =  4

Más información aquí

>> integral(cuadrado,1,3)

>> Not enough input arguments.
 
 Error in cuadrado (line 2)
     x2=x.^2;

>> integral(f,1,3)

>> ans =
 
     8.6667

>> integral(@cuadrado,1,3)

>> ans =
 
     8.6667

>> g = @(x) 2*(x.^2)*exp(-x);

>> g(1)

ans =  0.73576

>> g(2)

ans =  1.0827

>> g([1 2 3])

ans =

   0.73576   1.08268   0.89617

Ejercicios

1. Construye una función llamada C2F que convierta grados Celsius en Fahrenheit.

2. Construye una función llamada F2C que convierta grados Fahrenheit en Celsius.

3. Construye una función llamada distancia que calcule la distancia euclídea entre dos vectores u y v

4. Construye una función que simule el lanzamiento de n dados y devuelva los valores obtenidos y su suma.

5. Construye una función que reciba como entrada una matriz A y devuelva como salida el vector formado por las medias aritméticas de las columnas de A

6. Construye una función que reciba como entrada una matriz A y devuelva como salida un vector formado por los módulos de cada fila de A (el módulo de una fila es la raíz cuadrada de la suma de los cuadrados de los términos de esa fila)