Aproximación de funciones: Interpolación.
Ejamplo: Estimación de área de playas

En los proyectos de conservación de playas se debe hacer un seguimiento de la línea de costa para determinar los posibles avances o retrocesos. Ello requiere calcular la superficie de arena que tiene la playa en cada momento. En la fotografía se muestra la playa de Maspalomas en la actualidad. ¿Cómo podemos calcular la superficie de arena en esta playa? ¿Como podemos automatizar el proceso para poder ver la evolución de esta playa si se toman 4 fotografías diarias (una cada 6 horas)?
La idea básica para llevar a cabo esta tarea parte de disponer de una colección de puntos que tracen el contorno de la playa, a partir de los cuales se pueda llevar a cabo la estimación del área de la playa, uniendo dichos puntos mediante rectas o curvas:

Interpolación
Supongamos que de una función continua \(f\left(x\right)\) se conocen sus valores en tres puntos próximos \(x_{1}\), \(x_{2}\) y \(x_{3}\), siendo \(x_{1}<x_{2}<x_{3}\). Llamemos \(y_1= f\left(x_{1}\right)\), \(y_2=f\left(x_{2}\right)\) e \(y_3=f\left(x_{3}\right)\). Interpolar los valores de \(f(x)\) entre \(x_1\) y \(x_3\) consiste en encontrar una función continua \(g(x)\) “parecida” a \(f(x)\) y que coincida con ésta en los puntos \(x_1\), \(x_2\) y \(x_3\). Es obvio que hay muchas funciones \(g(x)\) que coinciden con \(f(x)\) en estos puntos. Los métodos de interpolación tienen como objetivo encontrar funciones \(g(x)\) cuya aproximación a \(f(x)\) cumpla ciertas condiciones: por ejemplo, que \(g(x)\) sea “suave”, o que no tenga muchas oscilaciones.
Interpolación lineal
La interpolación más sencilla y más inmediata es la interpolación lineal: se aproxima \(f(x)\) por un segmento recto entre \(x_1\) y \(x_2\), y por otro segmento recto entre \(x_2\) y \(x_3\). Esta interpolación en la mayoría de los casos presentará un punto anguloso en \(x_2\). A modo de ejemplo, si las coordenadas de los puntos son \(P_1=(x_1,y_1)\), \(P_2=(x_2,y_2)\) y \(P_3=(x_3,y_3)\), el resultado la la interpolación lineal sería:
Recta \(P_1P_2\): \[\frac{x-x_{1}}{x_{2}-x_{1}}=\frac{y-y_{1}}{y_{2}-y_{1}}\Rightarrow y=y_{1}+\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\left(x-x_{1}\right)\]
Recta \(P_2P_3\):
\[\frac{x-x_{2}}{x_{3}-x_{2}}=\frac{y-y_{2}}{y_{3}-y_{2}}\Rightarrow y=y_{2}+\frac{y_{3}-y_{2}}{x_{3}-x_{2}}\left(x-x_{3}\right)\]
Gráficamente:
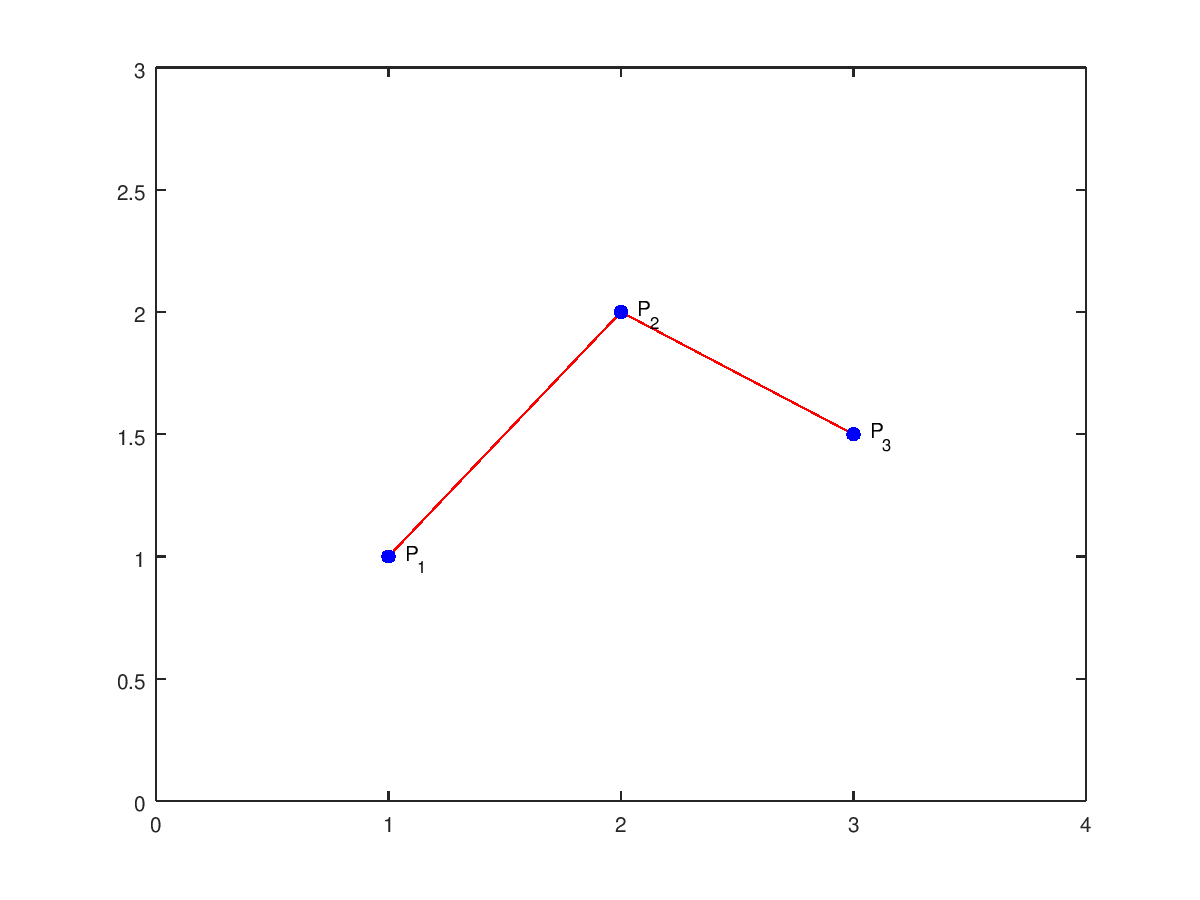
Dados dos puntos \(P_1\) y \(P_2\) el siguiente código matlab permite interpolar valores de \(x\) entre \(P_1\) y \(P_2\):
function y=interpola1(x,P1,P2)
if x<P1(1)|x>P2(1)
y=NaN;
disp('Error: el valor de X está fuera del segmento P1-P2');
else
b=(P2(2)-P1(2))/(P2(1)-P1(1));
a=P1(2)-b*P1(1);
y=a+b*x;
end
endAsí, si los puntos son \(P_1=(1,1)\), \(P_2=(2,2)\) y \(P_3=\left(3,\frac{3}{2}\right)\) y queremos interpolar el valor \(x=1.5\), como este valor de \(x\) está entre \(P_1\) y \(P_2\):
>> P1=[1 1];
P2=[2 2];
interpola1(1.5,P1,P2)ans = 1.5000Si quisiéramos interpolar el valor \(x=2.5\), como este valor de \(x\) está entre \(P_2\) y \(P_3\):
>> P2=[2 2];
P3=[3 1.5];
interpola1(2.5,P2,P3)ans = 1.7500
No es difícil construir una nueva función tal que dado un valor de \(x\), y dada una matriz de puntos \(P\) (una matriz \(n\times 2\), cada una de cuyas filas corresponde a un punto), nos devuelva el valor interpolado de \(x\), buscando primero entre qué puntos se encuentra \(x\):
function y=interpola(x,P)
n=size(P,1); % Número de filas (puntos) en P
P=sortrows(P); % Se ordena P por el primer valor de cada fila
if x<P(1,1)|x>P(n,1)
y=[];
disp('Error: el valor de x se encuentra fuera del rango de puntos');
else
k=1;
while ~(x>=P(k,1)&x<=P(k+1,1))
k=k+1;
end
y=interpola1(x,P(k,:),P(k+1,:));
end
endPara usar esta función:
>> P=[1 1; 2 2; 3 1.5];
interpola(2.8, P)ans = 1.6000
Interpolación lineal en matlab/octave
Matlab cuenta con una función específica para hacer interpolación lineal, la función interp1. Su sintaxis es interp(x,v,xq), donde x es el vector de coordenadas \(x\) de los puntos \(P_1, P_2, P_3, ...\), e y es el vector de coordenadas \(y\). xq es el vector de valores de \(x\) en los que se desea interpolar.
En nuestro ejemplo anterior, para interpolar en valor \(x=2.8\) entre los puntos \(P_1=(1,1), P_2=(2,2), P_3=(3,1.5)\) ejecutaríamos el comando siguiente:
>> x=[1 2 3]; % coordenadas x de los puntos
y=[1 2 1.5]; % coordenadas y de los puntos
interp1(x,y,2.8)ans = 1.6000Si queremos interpolar varios valores de \(x\) simultáneamente:
>> interp1(x,y,[1.1,1.6,2.2,2.7])ans =
1.1000 1.6000 1.9000 1.6500
Ejemplo: Usamos interpolación lineal para aproximar la función \(sen(x)\) entre 0 y \(2\pi\) partiendo de sus valores en \(0,\frac{\pi}{4},\frac{\pi}{2}, \frac{3\pi}{4}, \pi, \frac{5\pi}{4}, \frac{3\pi}{2}, \frac{7\pi}{4}, 2\pi\)
>> x = 0: pi/4: 2*pi;
y = sin(x);Interpolamos sobre una malla más fina: (puntos entre 0 y \(2\pi\), separados \(pi/16\)):
>> xq = 0: pi/16: 2*pi;Hacemos la interpolación y mostramos el resultado:
>> vq1 = interp1(x,y,xq);
plot(x,y,'o',xq,vq1,':.');
xlim([0 2*pi]);
title('Interpolación lineal');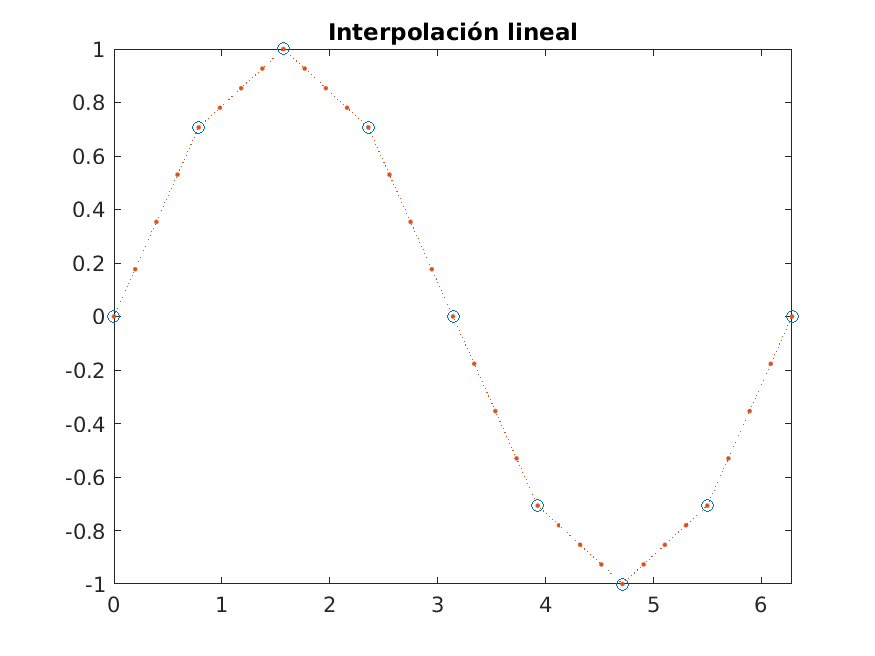
Los valores interpolados son:
>> vq1vq1 =
Columns 1 through 8:
0.00000 0.17678 0.35355 0.53033 0.70711 0.78033 0.85355 0.92678
Columns 9 through 16:
1.00000 0.92678 0.85355 0.78033 0.70711 0.53033 0.35355 0.17678
Columns 17 through 24:
0.00000 -0.17678 -0.35355 -0.53033 -0.70711 -0.78033 -0.85355 -0.92678
Columns 25 through 32:
-1.00000 -0.92678 -0.85355 -0.78033 -0.70711 -0.53033 -0.35355 -0.17678
Column 33:
-0.00000
Interpolación polinomial
Podemos llevar a cabo también una interpolación polinomial, esto es, buscar un polinomio que pase por los tres puntos. El caso más sencillo consiste en buscar un polinomio de grado 2 de la forma \(p(x)=ax^2 + bx + c\). Para que este polinomio pase por los tres puntos indicados debe ocurrir que los tres puntos estén sobre la parábola, esto es:
\[\left\{ \begin{array}{cc} y_{1}= & ax_{1}^{2}+bx_{1}+c\\ y_{2}= & ax_{2}^{2}+bx_{2}+c\\ y_{3}= & ax_{3}^{2}+bx_{3}+c \end{array}\right.\]
lo cual es equivalente a resolver:
\[\left(\begin{array}{ccc} x_{1}^{2} & x_{1} & 1\\ x_{2}^{2} & x_{2} & 1\\ x_{3}^{2} & x_{3} & 1 \end{array}\right)\left(\begin{array}{c} a\\ b\\ c \end{array}\right)=\left(\begin{array}{c} y_{1}\\ y_{2}\\ y_{3} \end{array}\right)\]
Por tanto, los coeficientes \((a,b,c)\) del polinomio interpolador de segundo grado se obtienen a partir de:
\[\left(\begin{array}{c} a\\ b\\ c \end{array}\right)=\left(\begin{array}{ccc} x_{1}^{2} & x_{1} & 1\\ x_{2}^{2} & x_{2} & 1\\ x_{3}^{2} & x_{3} & 1 \end{array}\right)^{-1}\left(\begin{array}{c} y_{1}\\ y_{2}\\ y_{3} \end{array}\right)\]
Para los puntos del ejemplo anterior, \(P_1=(1,1)\), \(P_2=(2,2)\) y \(P_3=\left(2,\frac{3}{2}\right)\), la ecuación matricial es:
\[\left(\begin{array}{c} a\\ b\\ c \end{array}\right)=\left(\begin{array}{ccc} x_{1}^{2} & x_{1} & 1\\ x_{2}^{2} & x_{2} & 1\\ x_{3}^{2} & x_{3} & 1 \end{array}\right)^{-1}\left(\begin{array}{c} y_{1}\\ y_{2}\\ y_{3} \end{array}\right)=\left(\begin{array}{ccc} 1 & 1 & 1\\ 4 & 2 & 1\\ 9 & 3 & 1 \end{array}\right)^{-1}\left(\begin{array}{c} 1\\ 2\\ \frac{3}{2} \end{array}\right)=\left(\begin{array}{c} -0.75\\ 3.25\\ -1.5 \end{array}\right)\]
Este resultado puede obtenerse fácilmente en octave mediante:
>> A=[ 1 1 1; 4 2 1; 9 3 1];
b=[1 2 1.5]';
A\bans =
-0.75000
3.25000
-1.50000Por tanto el polinomio interpolador es:
\[p(x)=-0.75x^2+3.25x-1.5\] Gráficamente:
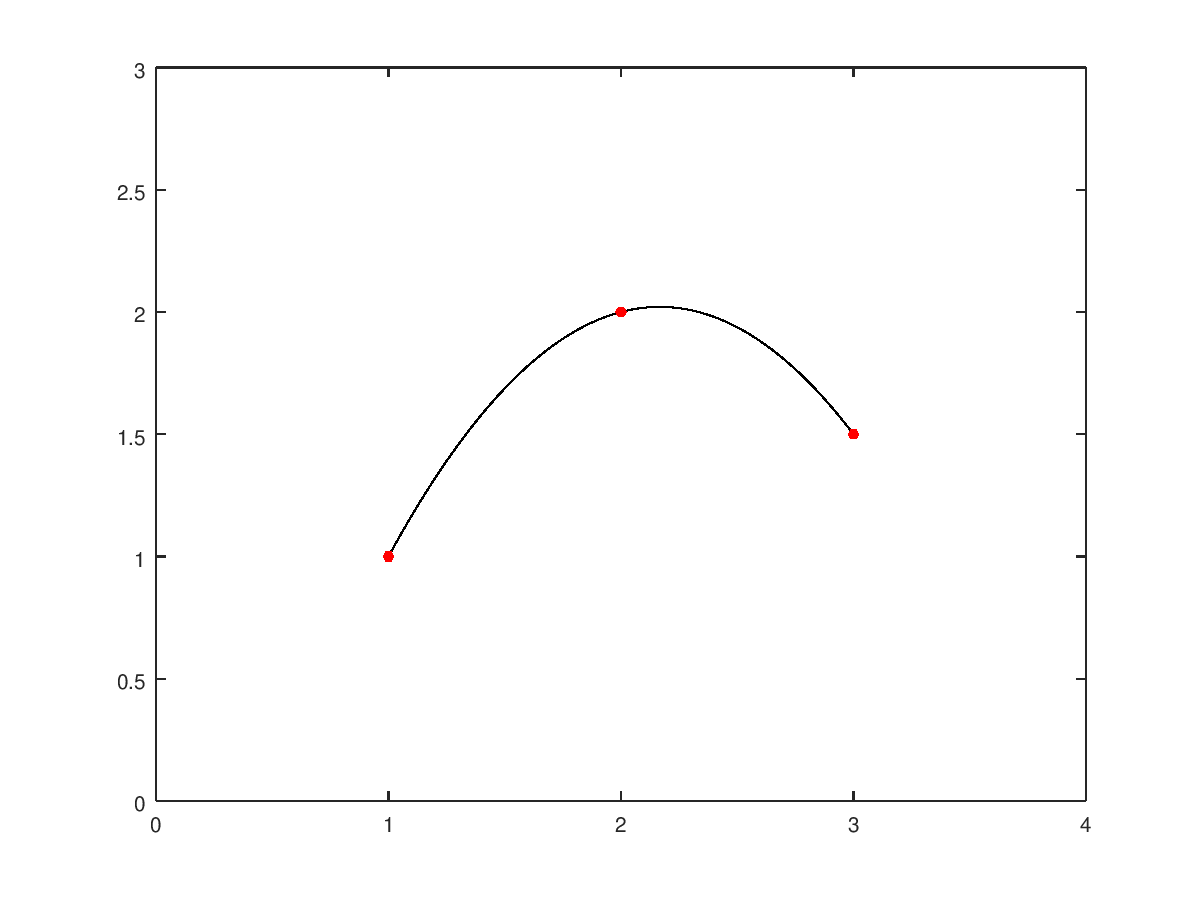
La interpolación polinomial en general no da buen resultado cuando se trata de interpolar sobre una base formada por muchos puntos. Si disponemos de \(n\) puntos podemos ajustar un polinomio de grado \(n-1\) que pase por todos ellos, mediante un procedimiento análogo al que hemos hecho para ajustar la parábola anterior. Sin embargo a media que \(n\) crece, el polinomio tiene más oscilaciones, lo que lo convierte en una herramienta poco apropiada para interpolar. La interpolación mediante splines que veremos a continuación constituye una estrategia más efectiva, pues permite interpolar una función de forma suave (sin oscilaciones) entre un número de puntos todo lo grande que deseemos.
Interpolación spline: tres puntos
La interpolación de \(f\left(x\right)\) mediante splines cúbicos consiste en encontrar dos polinomios cúbicos:
\[P\left(x\right) =ax^{3}+bx^{2}+cx+d\]
\[Q\left(x\right) =px^{3}+qx^{2}+rx+s\]
tales que:
\(P\left(x\right)\) pase por \(\left(x_{1},y_{1}\right)\) y \(\left(x_{2},y_{2}\right)\), y \(Q\left(x\right)\) pase por \(\left(x_{2},y_{2}\right)\) y \(\left(x_{3},y_{3}\right)\)
El “empalme” entre las dos funciones sea “suave” (sin aristas). Para ello debe ocurrir que:
\[P'\left(x_{2}\right)=Q'\left(x_{2}\right)\]
y que:
\[P''\left(x_{2}\right)=Q''\left(x_{2}\right)\].
- Como condición de regularidad se exige que \(P''\left(x_{1}\right)=0\) y que \(Q''\left(x_{3}\right)=0\).
Así pues, para determinar los polinomios \(P(x)\) y \(Q(x)\), comenzamos por imponer la primera condición, que se traduce en que:
\[P\left(x_{1}\right)=y_{1} \Rightarrow ax_{1}^{3}+bx_{1}^{2}+cx_{1}+d=y_{1}\] \[P\left(x_{2}\right)=y_{2} \Rightarrow ax_{2}^{3}+bx_{2}^{2}+cx_{2}+d=y_{2}\] \[Q\left(x_{2}\right)=y_{2} \Rightarrow px_{2}^{3}+qx_{2}^{2}+rx_{2}+s=y_{2}\] \[Q\left(x_{3}\right)=y_{3} \Rightarrow px_{3}^{3}+qx_{3}^{2}+rx_{3}+s=y_{3}\]
De la segunda condición:
\[P'\left(x_{2}\right)=Q'\left(x_{2}\right) \Rightarrow3ax_{2}^{2}+2bx_{2}+c=3px_{2}^{2}+2qx_{2}+r\] \[P''\left(x_{2}\right)=Q''\left(x_{2}\right) \Rightarrow6ax_{2}+2b=6px_{2}+2q\]
Por último, imponemos las condiciones relativas a las derivadas segundas en los extremos \(x_{1}\) y \(x_{3}\):
\[P''\left(x_{1}\right) =0\Rightarrow6ax_{1}+2b=0\]
\[Q''\left(x_{3}\right) =0\Rightarrow6px_{3}+2q=0\]
Tenemos de esta forma 8 ecuaciones con 8 incógnitas que podemos organizar en forma matricial del siguiente modo:
\[\left(\begin{array}{cccccccc} x_{1}^{3} & x_{1}^{2} & x_{1} & 1 & 0 & 0 & 0 & 0\\ x_{2}^{3} & x_{2}^{2} & x_{2} & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & x_{2}^{3} & x_{2}^{2} & x_{2} & 1\\ 0 & 0 & 0 & 0 & x_{3}^{3} & x_{3}^{2} & x_{3} & 1\\ 3x_{2}^{2} & 2x_{2} & 1 & 0 & -3x_{2}^{2} & -2x_{2} & -1 & 0\\ 6x_{2} & 2 & 0 & 0 & -6x_{2} & -2 & 0 & 0\\ 6x_{1} & 2 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 6x_{3} & 2 & 0 & 0 \end{array}\right)\left(\begin{array}{c} a\\ b\\ c\\ d\\ p\\ q\\ r\\ s \end{array}\right)=\left(\begin{array}{c} y_{1}\\ y_{2}\\ y_{2}\\ y_{3}\\ 0\\ 0\\ 0\\ 0 \end{array}\right)\]
El problema de encontrar los polinomios interpoladores se reduce entonces simplemente a resolver este sistema.
El siguiente código muestra la implementación en Octave/Matlab:
function [P,Q]=ajustaSpline(x,y)
x1=x(1);
x2=x(2);
x3=x(3);
y1=y(1);
y2=y(2);
y3=y(3);
A=[x1^3 x1^2 x1 1 0 0 0 0;
x2^3 x2^2 x2 1 0 0 0 0;
0 0 0 0 x2^3 x2^2 x2 1;
0 0 0 0 x3^3 x3^2 x3 1;
3*x2^2 2*x2 1 0 -3*x2^2 -2*x2 -1 0;
6*x2 2 0 0 -6*x2 -2 0 0;
6*x1 2 0 0 0 0 0 0;
0 0 0 0 6*x3 2 0 0];
b=[y1;y2;y2;y3;0;0;0;0];
pq=transpose(A\b);
P=pq(1:4);
Q=pq(5:8);
end %functionEl spline ajustado a los puntos anteriores es entonces:
>> [P Q] = ajustaSpline([1 2 3],[1 2 1.5])P =
-3.7500e-01 1.1250e+00 2.5000e-01 1.1842e-15
Q =
0.37500 -3.37500 9.25000 -6.00000Gráficamente:
P =
-3.7500e-01 1.1250e+00 2.5000e-01 1.1842e-15
Q =
0.37500 -3.37500 9.25000 -6.00000
Interpolación spline: Caso general
En la práctica muchas veces se encuentra el problema de ajustar una función “suave” \(f(x)\) que pase por un conjunto de puntos observados, como en la figura siguiente:

Dados \(n+1\) puntos \((x_0,y_0)\), \((x_1,y_1)\), \((x_2,y_2), \dots,\) \((x_n,y_n)\), el procedimiento general de interpolación mediante splines consiste en unir todos los puntos mediante \(n\) splines cúbicos \(S_i,\; i=0,\dots, n-1\) de tal forma que \(S_i\) es el spline (polinomio de orden 2) entre \((x_{i},y_{i})\) y \((x_{i+1},y_{i+1})\). Conceptualmente el procedimiento es análogo al que acabamos de mostrar: es preciso construir una sucesión de polinomios de tal forma que las derivadas primera y segunda de cada dos polinomios sucesivos coincidan en cada punto, lo que garantiza la continuidad y la suavidad del ajuste.
Cada spline \(S_i(x)\) puede expresarse como:
\[\begin{equation} S_{i}\left(x\right)=a_{i}\left(x-x_{i}\right)^{3}+b_i\left(x-x_{i}\right)^{2}+c_{i}\left(x-x_{i}\right)+d_{i},\,\,\,\,x\in\left[x_{i},x_{i+1}\right] \end{equation}\]
La primera y segunda derivadas de esta función son:
\[\begin{equation} S'_{i}\left(x\right)=3a_{i}\left(x-x_{i}\right)^{2}+2b_i\left(x-x_{i}\right)+c_{i} \end{equation}\]
\[\begin{equation} S''_{i}\left(x\right)=6a_{i}\left(x-x_{i}\right)+2b_i \end{equation}\]
Las condiciones para que los sucesivos segmentos se unan de forma suave pueden especificarse como:
- \(S_i(x_i)=y_i\) para \(i=0,\dots, n-1\)
- \(S_i(x_{i+1})=S_{i+1}(x_{i+1})=y_{i+1}\) para \(i=0,\dots, n-1\)
- \(S'_{i}(x_{i+1})=S'_{i+1}(x_{i+1})\) para \(i=0,\dots, n-1\)
- \(S''_{i}(x_{i+1})=S''_{i+1}(x_{i+1})\) para \(i=0,\dots, n-1\)
Estas condiciones dan lugar a un sistema de ecuaciones que puede resolverse recursivamente y obtener de manera simple los coeficientes \(a_i\), \(b_i\), \(c_i\) y \(d_i\) para todos los splines. El resultado sería el mostrado en la imagen:

Interpolación spline en matlab.
La función interp1 de matlab permite también ajustar splines. La manera de indicarlo es especificar 'spline' como opción en la llamada a esta función.
Así, para interpolar los puntos del ejemplo anterior mediante splines cúbicos utilizaríamos la siguiente sintaxis:
>> x=[1 3 5 7 9 11];
y=[1 2 1.5, 1 3 5];
xq=1:0.25:11;
vq2 = interp1(x,y,xq,'spline');
plot(x,y,'o',xq,vq2,':.');
xlim([0 11]);
title('Interpolación mediante splines cúbicos ');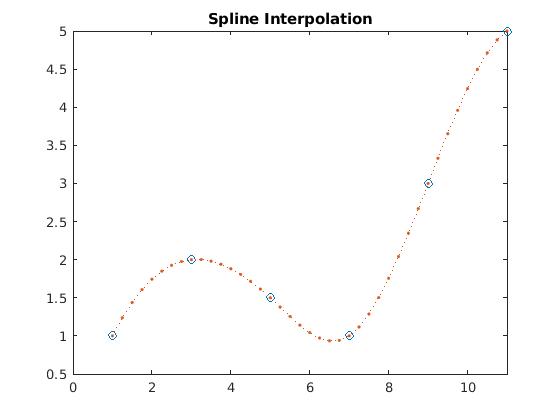
Los primeros valores interpolados se muestran en la tabla siguiente:
>> puntos=[xq',vq2'];
puntos(1:10,:)ans =
1.0000 1.0000
1.2500 1.2378
1.5000 1.4398
1.7500 1.6079
2.0000 1.7437
2.2500 1.8491
2.5000 1.9258
2.7500 1.9755
3.0000 2.0000
3.2500 2.0011Ejemplo: Interpolación con fechas
>> x = (datetime(2016,1,1):hours(4):datetime(2016,1,2))';
x.Format = 'MMM dd, HH:mm';
T = [31 25 24 41 43 33 31]';
datosTemp = table(x,T,'VariableNames',{'Hora','Temperatura'})>> datosTemp =
7×2 table
Time Temperature
_____________ ___________
Jan 01, 00:00 31
Jan 01, 04:00 25
Jan 01, 08:00 24
Jan 01, 12:00 41
Jan 01, 16:00 43
Jan 01, 20:00 33
Jan 02, 00:00 31 >> plot(datosTemp.Hora, datosTemp.Temperatura, 'o')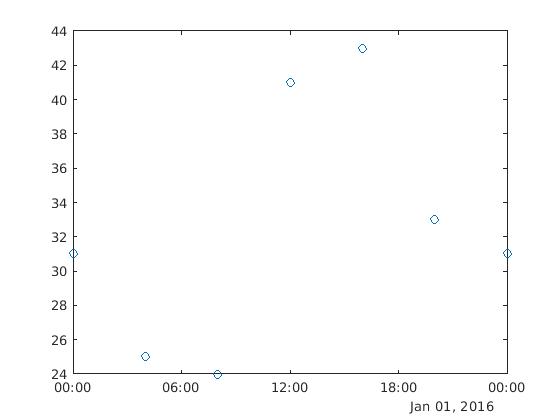 Ahora predecimos la temperatura durante cada minuto del día:
Ahora predecimos la temperatura durante cada minuto del día:
>> xq = (datetime(2016,1,1):minutes(1):datetime(2016,1,2))';
V = interp1(datosTemp.Hora, datosTemp.Temperatura, xq, 'spline');y la representamos gráficamente:
>> hold on
plot(xq,V,'r')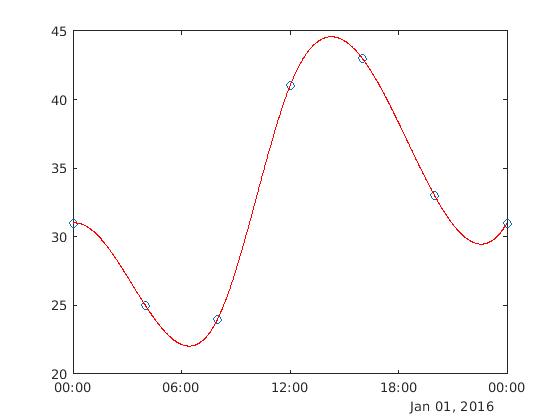
Los valores interpolados son:
>> datosInterp=table(xq,V,'VariableNames',{'Minuto','Temperatura'});
datosInterp(1:10,:)>> ans =
10×2 table
Minuto Temperatura
___________ ___________
01-Jan-2016 31
01-Jan-2016 31.003
01-Jan-2016 31.005
01-Jan-2016 31.007
01-Jan-2016 31.008
01-Jan-2016 31.01
01-Jan-2016 31.01
01-Jan-2016 31.011
01-Jan-2016 31.011
01-Jan-2016 31.01
Ejemplo: Cálculo del área de la playa
Los datos de los puntos elegidos como frontera en la playa de Maspalomas pueden descargarse en este enlace y en este otro enlace, correspondientes respectivamente a las lineas de costa y frontera interior de la playa.
El programa matlab para calcular el área encerrada en esta región es el siguiente:
>> % Leo los datos de los puntos de la linea de costa de la playa de Maspalomas
costa=csvread("maspaCosta.csv")
% Leo los datos de los puntos del límite interior de la playa de Maspalomas
interior=csvread("maspaInte.csv")
% Dibujo los puntos:
figure("name","Puntos del contorno de la Playa de Maspalomas")
plot(costa(:,1),costa(:,2),"or")
hold on
plot(interior(:,1),interior(:,2),"ob")
hold off
% Rango de valores de x
xmin=min(costa(:,1))
xmax=max(costa(:,1))
% Interpolación lineal
% ---------------------
% Defino el rango de valores de x sobre los que se va a interpolar
x_interp=0:0.01:3.2;
% Calculo los valores de y interpolados para la linea de costa
y_lin=interp1(costa(:,1),costa(:,2),x_interp);
% Los dibujo:
figure("name","Interpolación lineal")
plot(costa(:,1),costa(:,2),"ob",x_interp,y_lin,".r")
% Calculo los valores de y interpolados para el límite interior de la playa
y_lin2=interp1(interior(:,1),interior(:,2),x_interp);
% Los dibujo:
hold on; % Para añadirlos al gráfico anterior
plot(interior(:,1),interior(:,2),"ob",x_interp,y_lin2,".r")
hold off
% Interpolación spline
% --------------------
% Calculo los valores de y interpolados para la linea de costa
y_spl=interp1(costa(:,1),costa(:,2),x_interp, 'spline');
% Los dibujo:
figure("name","Interpolación Spline")
plot(costa(:,1),costa(:,2),"ob",x_interp,y_spl,".r")
% Calculo los valores de y interpolados para el límite interior de la playa
y_spl2=interp1(interior(:,1),interior(:,2),x_interp, 'spline');
% Los dibujo:
hold on; % Para añadirlos al gráfico anterior
plot(interior(:,1),interior(:,2),"ob",x_interp,y_spl2,".r")
hold off
% Cálculo de la superficie de la playa
% ------------------------------------
% Función que define la linea de costa por interpolación spline
funCosta=@(x) interp1(costa(:,1),costa(:,2),x,"spline")
% Función que define la linea interior por interpolación spline
funInterior=@(x) interp1(interior(:,1),interior(:,2),x,"spline")
% Gráfico de las áreas bajo cada linea
hold on
% Area bajo la linea interior
area(x_interp,funInterior(x_interp))
% Area bajo la linea de costa
area(x_interp,funCosta(x_interp))
hold off
% Se calcula el área bajo la linea interior y se le resta el área bajo la
% costa
areaBajoCosta=integral(funCosta,0,xmax)
areaBajoInterior=integral(funInterior,0,xmax)
areaPlaya=areaBajoInterior-areaBajoCosta