Método de Newton-Raphson

Es otro método que se utiliza para calcular los ceros de una función real de variable real. Aunque no sea siempre el mejor método para un problema dado, su simplicidad formal y su rapidez de convergencia hacen que, con frecuencia, sea el primer algoritmo a considerar para esta tarea.

El método de Newton-Raphson se basa en el desarrollo de Taylor de la función cuya raíz se quiere calcular. Consideremos la ecuación \(f(x)=0\), y supongamos que posee una y sólo una solución \(\alpha\in\left[a,b\right]\). Partiendo de un punto \(x_{0}\) suficientemente cercano a dicha raíz, podemos escribir:

\[f\left(\alpha\right)=f(x_{0})+\left(\alpha-x_{0}\right)f^{\prime}(x_{0})+\frac{\left(\alpha-x_{0}\right)^{2}}{2}f^{\prime\prime}(x_{0}+\theta h)\]

con \(0<\theta<1\), \(h=\alpha-x_0\).

Suponiendo que \(f^{\prime}(x)\) no se anula en \([a,b]\), y que la diferencia \(\alpha-x_{0}\) es muy pequeña, el método de Newton-Raphson consiste en despreciar el sumando en \(\left(\alpha-x_{0}\right)^{2}\) del desarrollo anterior, quedándonos con la aproximación:

\[f\left(\alpha\right)\cong f(x_{0})+\left(\alpha-x_{0}\right)f^{\prime}(x_{0})\] Como \(\alpha\) es la solución de la ecuación \(f\left(x\right)=0\), se tiene que \(f(\alpha)\)=0 y por tanto, de la expresión anterior se sigue que:

\[f(x_{0})+\left(\alpha-x_{0}\right)f^{\prime}(x_{0})\cong 0\]

y despejando \(\alpha\) resulta:

\[\alpha\cong x_{0}-\frac{f(x_{0})}{f^{\prime}(x_{0})}=x_1\]

Así pues, si se parte de un valor \(x_0\) próximo a \(\alpha\), el valor \(x_1\) obtenido de esta forma proporciona un valor también próximo a la raíz \(\alpha\). Bajo determinadas condiciones (las veremos en un momento) ocurre que \(x_1\) está más próximo a \(\alpha\) que \(x_0\). En tales condiciones, como \(x_1\) es un valor más cercano a la solución \(\alpha\) que \(x_0\), podemos repetir el razonamiento anterior para acercarnos aún más a \(\alpha\), partiendo ahora de \(x_1\). Ello nos conduce a una segunda aproximación:

\[x_{2}=x_{1}-\frac{f(x_{1})}{f^{\prime}(x_{1})}\]

De la misma manera podemos obtener una nueva (y mejor) aproximación \(x_3\) a partir de \(x_2\) mediante:

\[x_{3}=x_{2}-\frac{f(x_{2})}{f^{\prime}(x_{2})}\]

El proceso puede seguir repitiéndose sucesivamente hasta encontrar un \(x_k\) lo suficientemente próximo a la raíz \(\alpha\).

Obviamente, para que este algoritmo funcione tienen que ocurrir dos cosas:

• Se debe partir de una aproximación inicial \(x_0\) de la solución \(\alpha\). El método, como hemos visto, parte de suponer que se puede despreciar el sumando en \((\alpha-x_{0})^{2}\) del desarrollo de Taylor de la función. Pero si la aproximación inicial está lejos de la solución, al despreciar el valor \((\alpha-x_{0})^{2}\) podemos estar cometiendo un error muy grande y el método de Newton termina por alejarnos de la solución en lugar de acercarnos a ella. En la práctica el valor inicial para aplicar el método de Newton-Raphson puede obtenerse tras ejecutar algunas iteraciones del método de bisección.

• Deben darse las condiciones para que en cada iteración el valor \(x_i\) esté mas cerca de \(\alpha\) que el de la iteración anterior \(i-1\). Para entender cuales son tales condiciones observemos que la ecuación:

\[y=f(x_{0})+\left(x-x_{0}\right)f^{\prime}(x_{0})\]

corresponde s la recta tangente a \(f(x)\) en \(x_0\). Por tanto la solución \(x_1\) de la ecuación:

\[f(x_{0})+\left(x-x_{0}\right)f^{\prime}(x_{0}) = 0\]

es el punto de corte de la recta anterior con el eje de abcisas. La siguiente imagen (extraida de la entrada sobre el método de Newton en la Wikipedia) ilustra el funcionamiento del método:

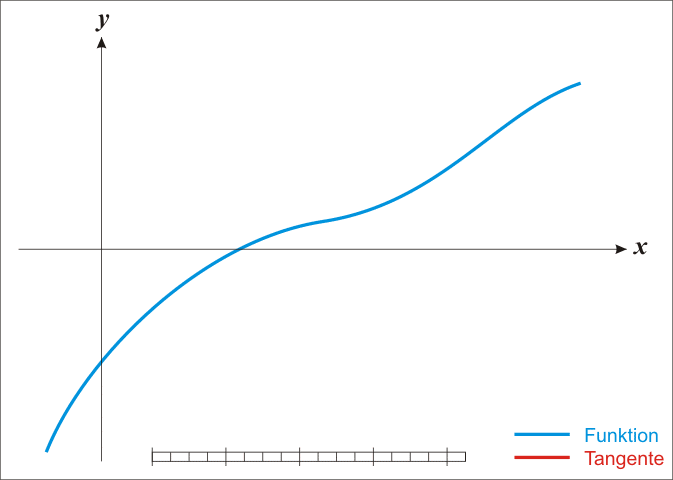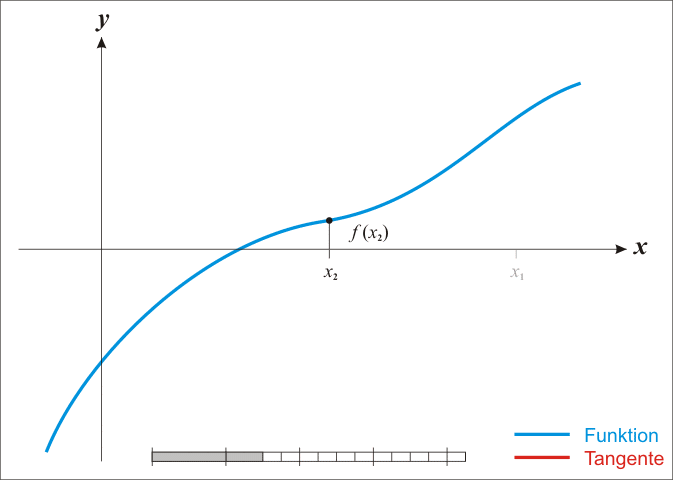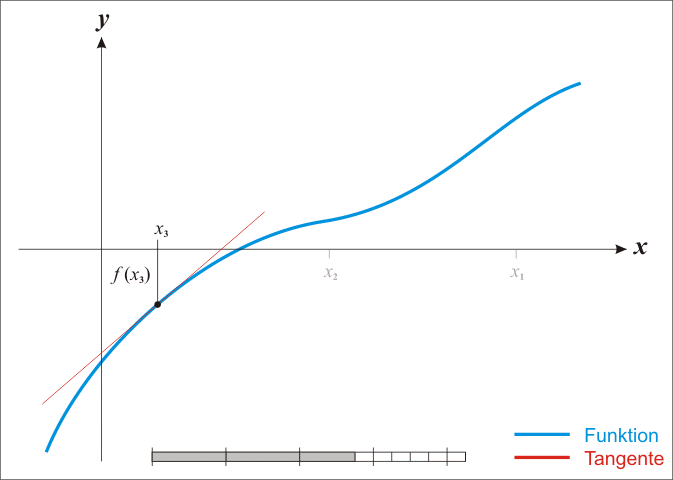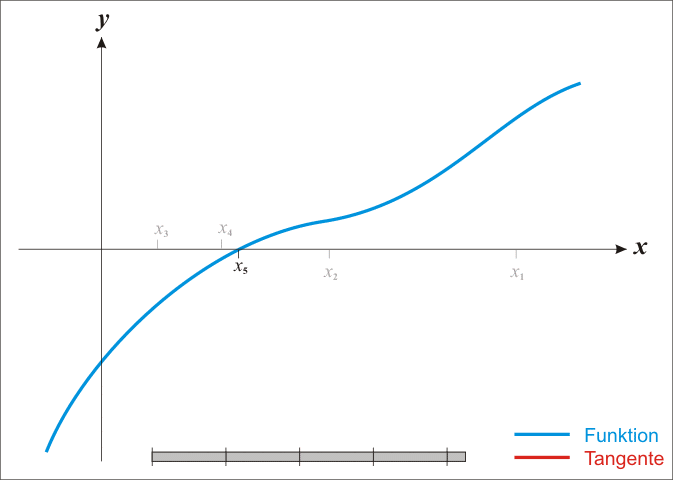
Así pues, para que el método de Newton-Raphson converja, la función \(f(x)\) debe ser derivable en el intervalo considerado, y en dicho intervalo no debe tener puntos de inflexión, ni máximos ni mínimos. En la siguiente figura podemos apreciar, como aún partiendo de un punto cercano a la raíz buscada, en un caso el método converge y en el otro caso no:

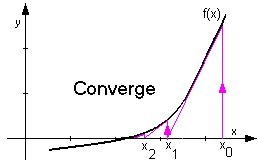
El siguiente teorema muestra condiciones suficientes para la convergencia del método de Newton:

Teorema: (Condiciones de convergencia para el método de Newton-Raphson). Supongamos que \(f\in C^{2}([a,b])\) (f admite primera y segunda derivadas) y verifica:

1. \(f(a)f(b)<0\), es decir, \(f(x)\) tiene una raíz en \((a,b)\).

2. \(f^{\prime}(x)\neq0\;\;\;\; x\in\left[a,b\right]\). En otras palabras, la raíz es única.

3. \(f^{\prime\prime}(x)\neq0\;\;\;\; x\in\left[a,b\right]\). Esto es, la función es cóncava o convexa, pero no tiene puntos de inflexión en el intervalo.

Entonces, existe una única raíz \(\alpha\) de \(f\) en \([a,b]\) y, la sucesión \(\{x_{n}\}\) generada por el método de Newton converge hacia \(\alpha\), para cualquier valor inicial \(x_{0}\in [a,b]\) que cumpla que:

\[f(x_{0})f^{\prime\prime}(x_{0})\geq0\].

Ejemplo: La función \(f(x)=x^{2}-x-\frac{1}{2}\) tiene una y sólo una raíz en \([-0.5,0]\). Comprobar si se cumplen las condiciones del teorema anterior. En caso afirmativo hallar la solución para las condiciones iniciales \(x_0=-\frac{1}{2}\), \(x_0=-\frac{2}{5}\) y \(x_0=-0.3\)

Algoritmo para el método de Newton-Raphson

La siguiente figura sintetiza el diagrama de flujo para el algoritmo de Newton-Raphson:

Implementación del método de Newton-Raphson.

Para implementar el método de bisección, los argumentos de entrada deben ser:

• La función \(f\) cuya raíz se quiere hallar.

• La derivada \(f'\) de dicha función.

• La aproximación inicial \(x_0\) a la solución

• La tolerancia o error con que deseamos obtener la raíz.

La llamada a la función podría ser de la forma:

>> newtonRaphson(f, fprima, x0, tol)

y debería obtenerse como resultado una raíz de \(f(x)\) próxima a \(x_0\). La implementación del algoritmo anterior puede llevarse a cabo de la forma siguiente (nótese que las lineas de comentario al inicio de la función son las que se mostrarán como ayuda si el usuario ejecuta help biseccion):

function [raiz, niter]=newtonRaphson(f,fprima,x0,tol,nmaxiter=10000)
% Resolución de la ecuación f(x)=0 mediante el algoritmo de Newton-Raphson.
% Argumentos:
% f: es la función cuya raiz se desea calcular (deberá definirse 
%      como función anónima, previamente o en la llamada a esta funcion).
% fprima: derivada de la función f, definida también como función anónima
% x0: Aproximación inicial de la solución.
% tol (tolerancia): Si abs(x1-x0)<tol el algoritmo se detiene.  
% nmaxiter: número máximo de iteraciones. Si se alcanza este valor sin encontrar
% la solución el algoritmo se detiene.
   if f(x0)==0
       raiz=x0;
   else
     niter=1;  
     do       
       fp=fprima(x0);
       if fp==0
         disp('ERROR: la derivada se anula y el método no puede proseguir')
         x1=[];
         break; % Se fuerza la salida del bucle do
       else
         delta=f(x0)/fprima(x0);
         x1=x0-delta;
         x0=x1;
         niter=niter+1;
        end%if
     until f(x1)==0 | abs(delta)<tol | niter>nmaxiter;
     raiz=x1;
     if niter>nmaxiter
       disp("Se ha alcanzado el número máximo de iteraciones sin lograr la convergencia");
       raiz=[];
      end% if niter... 
    end%if
end%function

Ejemplos de aplicación

>> f=@(x) exp(x)-x.^2;
 fp=@(x) exp(x)-2.*x;
 [a,niter]=newtonRaphson(f,fp,-1,0.00001)

a = -0.70347
niter =  5

Si partimos de una aproximación inicial peor el algoritmo converge pero necesita más iteraciones:

>> [a,niter]=newtonRaphson(f,fp,10,0.00001)

a = -0.70347
niter =  17

Si partimos de una aproximación aún más mala y fijamos el máximo de iteraciones en 1000, el algoritmo se detiene antes de llegar a la solución:

>> [a,niter]=newtonRaphson(f,fp,5000,0.00001,1000)

Se ha alcanzado el número máximo de iteraciones sin lograr la convergencia
a = [](0x0)
niter =  1001

Método de la secante

Es una variante del método de Newton-Raphson en la que el cálculo de la derivada en \(x_k\) se sustituye por una aproximación. Recordemos que la definición de derivada es:

\[f'\left(x\right)=\underset{\Delta\rightarrow0}{lim}\frac{f\left(x\right)-f\left(x-\Delta\right)}{\Delta}\] Cuando se dan las condiciones de convergencia del método de Newton ocurre que \(x_k-x_{k-1}\rightarrow 0\). En tal caso, llamando \(\Delta=x_k-x_{k-1}\), la derivada en \(x_k\) puede expresarse como:

\[f'\left(x_{k}\right)=\underset{x_{k-1}\rightarrow x_{k}}{lim}\frac{f\left(x_{k}\right)-f\left(x_{k-1}\right)}{x_{k}-x_{k-1}}\]

y cuando \(x_k\) y \(x_{k-1}\) están muy próximos entre sí:

\[f'\left(x_{k}\right)\cong\frac{f\left(x_{k}\right)-f\left(x_{k-1}\right)}{x_{k}-x_{k-1}}\]

El método de la secante es análogo al método de Newton-Raphson, salvo que en cada iteración la derivada se sustituye por esta aproximación, esto es:

\[x_{k+1}=x_{k}-\frac{f(x_{k})}{f^{\prime}(x_{k})}=x_{k}-\frac{f(x_{k})}{\frac{f\left(x_{k}\right)-f\left(x_{k-1}\right)}{x_{k}-x_{k-1}}}=x_{k}-\frac{\left(x_{k}-x_{k-1}\right)f\left(x_{k}\right)}{f\left(x_{k}\right)-f\left(x_{k-1}\right)}=\frac{x_{k-1}f\left(x_{k}\right)-x_{k}f\left(x_{k-1)}\right)}{f\left(x_{k}\right)-f\left(x_{k-1}\right)}\] Obviamente para poner en marcha el método hacen falta dos aproximaciones iniciales de la solución \(x_0\) y \(x_1\). Podemos entonces sintetizar el algoritmo de la secante como:

Dado que se está utilizando una aproximación de la derivada, este algoritmo converge más lentamente que el de Newton-Raphson. Modificando el programa que hicimos anteriormente para el algoritmo de bisección, podemos construir la siguiente función para aplicar el algoritmo de la secante:  

function [raiz, niter]=secante(f,x0,x1,tol,nmaxiter=10000)
% Resolución de la ecuación f(x)=0 mediante el algoritmo de Newton-Raphson.
% Argumentos:
% f: es la función cuya raiz se desea calcular (deberá definirse 
%      como función anónima, previamente o en la llamada a esta funcion).
% x0: Aproximación inicial de la solución.
% x1: Otra aproximación inicial de la solución.
% tol (tolerancia): Si abs(x1-x0)<tol el algoritmo se detiene.  
% nmaxiter: número máximo de iteraciones. Si se alcanza este valor sin encontrar
% la solución el algoritmo se detiene.
   if f(x0)==0
       raiz=x0;
   elseif f(x1)==0
       raiz=x1;
   else
     niter=1;  
     do       
       denom=f(x1)-f(x0);
       if denom==0
         disp('ERROR: la aproximacion de la derivada se anula y el método no puede proseguir')
         x1=[];
         break; % Se fuerza la salida del bucle do
       else
         delta=x1-x0;
         x1_anterior=x1;
         x1=(x0*f(x1)-x1*f(x0))/denom;
         x0=x1_anterior;
         niter=niter+1;
        end%if
     until f(x1)==0 | abs(delta)<tol | niter>nmaxiter;
     raiz=x1;
     if niter>nmaxiter
       disp("Se ha alcanzado el número máximo de iteraciones sin lograr la convergencia");
       raiz=[];
      end% if niter... 
    end%if
end%function

Ejemplo

>> f=@(x) exp(x)-x.^2;
 [raiz,numiter]=secante(f,-1,0,0.00001)

raiz = -0.70347
numiter =  8

En matlab, la función fzero() utiliza el algoritmo de bisección cuando se proporciona un intervalo [a,b] donde buscar la solución, o el algoritmo de la secante cuando se proporciona una solución inicial x0.