Planteamiento del problema

Se plantea encontrar la solución \(x\) de la ecuación:

\[f(x)=0\]

Los valores \(x\) que cumplen esta condición se denominan raíces de \(f(x)\). No siempre es posible encontrar de forma analítica las raíces de \(f(x)\), de ahí que se recurra a métodos numéricos para resolver el problema de forma aproximada, utilizando normalmente como instrumento el ordenador. En realidad, se considera que \(\alpha \in \mathbb{C}\) es raíz de \(f(x)\) si se cumple que \(|f(\alpha)| < \varepsilon\), siendo \(\varepsilon\) una tolerancia predeterminada.

 

Separación de raíces.

Muchoa métodos numéricos para resolver \(f(x) = 0\) parten inicialmente del conocimiento de un cierto intervalo \([a_i, b_i]\) donde la ecuación admite una solución y sólo una.

La separación de raíces consiste precisamente en obtener intervalos \([a_i, b_i]\) donde la función tenga una y sólo una raíz (por tanto separada del resto de raíces, de ahí el nombre del método), y se realiza, en general, a partir de consideraciones gráficas:

1. Podemos dibujar \(y = f(x)\) y observar intervalos donde puede existir una y sólo una raíz. Esto puede hacerse con la ayuda del ordenador.

2. Si la función puede expresarse como diferencia de dos funciones, esto es, si \(f (x) = f_1(x) − f_2(x)\) el problema \(f(x)=0\) se puede plantear como la obtención de los valores de \(x\) tales que \(f_1(x) = f_2(x)\). De esta forma, si llamamos \(y_1 = f_1(x)\) e \(y_2 = f_2(x)\), y estas funciones se pueden representar fácilmente, basta con encontrar los puntos de corte de ambas curvas.

 

Ejemplos:

1. Hallar las raíces de \(f(x)=x^3-3x^2-x+2\)

Dibujamos la curva:

>> function y=f(x)
   y=x.^3-3*x.^2-x+2;
 end
 fplot("f",[-2,4],1000);
 set(gca,"ylim",[-10,10]);
 hold on
 line ([-2 4], [0 0], "linestyle", "-", "color", "black");
 hold off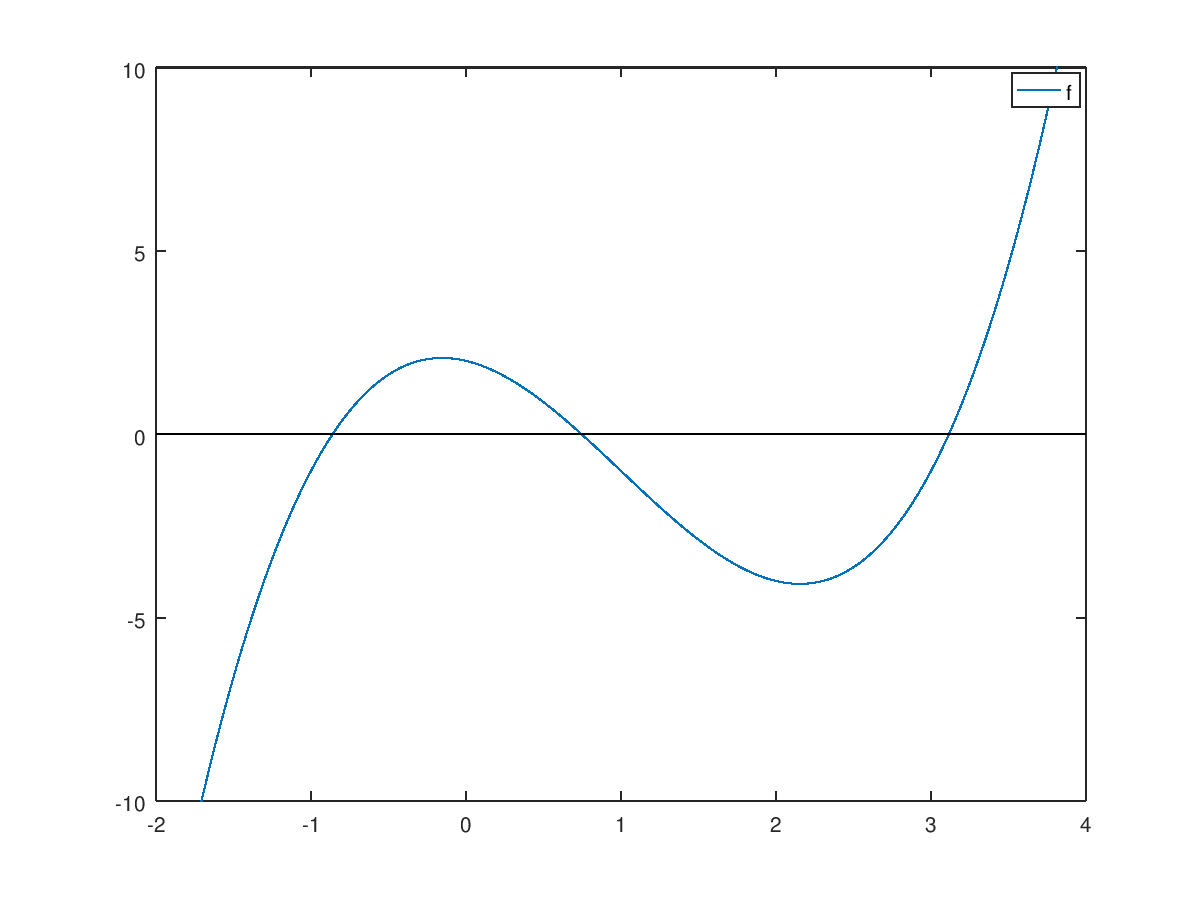

El gráfico muestra que hay una raíz entre -2 y 0, otra entre 0 y 2 y otra entre 2 y 4.

 

2. Hallar las raíces de \(f(x)=tan(x)-x\) en \(0\le x\le 2\pi\)

Dibujamos \(y_1=tan(x)\) e \(y_2=x\):

>> function y=y1(x)
   y=tan(x);
 end
 function y=y2(x)
    y=x;
 end
 fplot("y1",[0,2*pi],1000);
 set(gca,"ylim",[-10,10]);
 hold on
 fplot("y2",[0,2*pi],1000,"color","r");
 line ([0 2*pi], [0 0], "linestyle", "-", "color", "black");
 hold off
 legend ({"y1", "y2"}, "location", "northeast");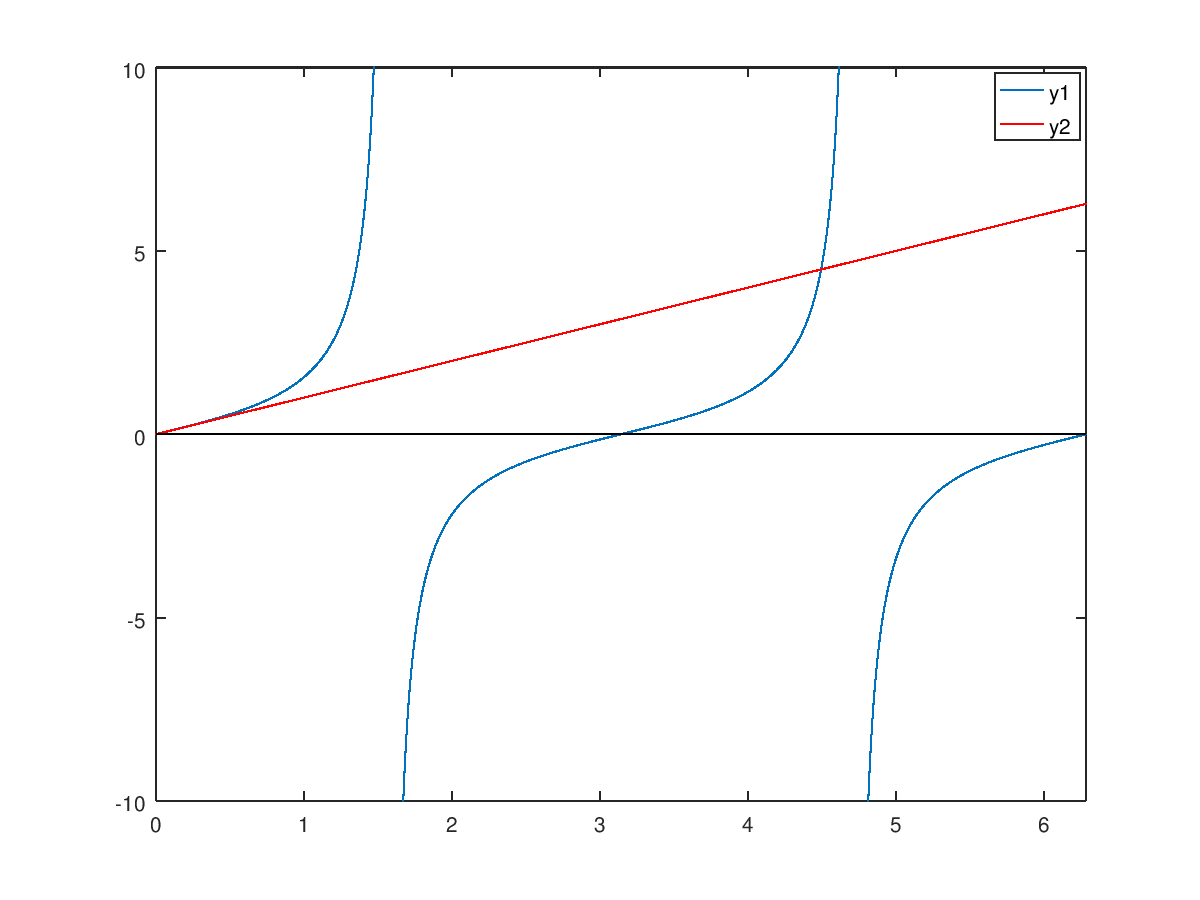

Como vemos, en el intervalo \([0, 2\pi]\) las curvas \(y_1\) e \(y_2\) se cortan en dos puntos; uno es \(x=0\) y el otro está entre \(\pi\) y \(3\pi/2\).

 

 

Para encontrar los intervalos en los que buscar las raíces de una función \(f(x)\) es útil el siguiente resultado, basado en los teoremas de Rolle y Bolzano:

• Si \(f(a)\cdot f(b) < 0\), entonces existe un número impar de raíces en el intervalo \((a, b)\). Además, si \(f'(x) \neq 0\) en \((a, b)\), entonces la raíz es única. (Nota: Esta última condición es suficiente pero no necesaria, ya que podría existir un punto de inflexión).

• Si \(f(a)\cdot f(b) > 0\), entonces existe un número par de raíces en \((a, b)\), eventualmente ninguna. Además, si \(f'(x) \neq 0\) en \((a, b)\), entonces no existe \(\alpha \in (a, b)\) tal que \(f(\alpha) = 0\).

 

Ejercicio: separar las raíces de la ecuación \(f(x) = x^3 − 5x + 3 = 0\) en \([−3, 2]\) (Pista: dar valores a \(f(x)\) en \(x=-3,-2,-1,0,1,2\)).

 

 

Método de bisección.

Sea \(f(x)\) una función continua en \([a,b]\) que satisface \(f(a)f(b)<0\). Entonces \(f(x)\) tiene, necesariamente, al menos un cero en \((a,b)\). Supongamos por simplicidad que este cero es único, y llamémosle \(\alpha\) (por tanto \(f(\alpha)=0\)).

La estrategia del método de bisección consiste en dividir en dos partes iguales el intervalo dado y seleccionar el subintervalo donde \(f(x)\) experimenta un cambio de signo, repitiendo este proceso las veces que sea necesario hasta encontrar la raíz de \(f(x)\) o hasta que el intervalo sea más estrecho que un valor \(\varepsilon\) prefijado.

De esta forma el método va eligiendo siempre el intervalo que contiene la solución de \(f(x)=0\). Dado que la amplitud de intervalo se va reduciendo cada vez a la mitad, el procedimiento converge necesariamente al valor \(\alpha\), puesto que la longitud de los subintervalos tiende a cero cuando \(k\) tiende a infinito.

Concretamente, dado que en cada paso la longitud del intervalo donde se encuentra la raíz se divide por dos, si la longitud inicial es \(b-a\), tras \(k\) pasos del algoritmo (\(k\) divisiones sucesivas) la longitud del intervalo será \(\frac{b-a}{2^k}\). Si llamamos \(m^{(k)}\) al punto medio de dicho intervalo, se tiene que si se elige dicho valor \(m^{(k)}\) como aproximación de \(\alpha\), el error de aproximación cometido es:

\[|e^{(k)}|=|m^{(k)}-\alpha|<\frac{1}{2}\frac{b-a}{2^k}=\left(\frac{1}{2}\right)^{k+1}\left(b-a\right)\]  

Para garantizar que \(|e^{(k)}|<\varepsilon\), para una tolerancia dada \(\varepsilon\), basta con llevar a cabo \(k_{min}\) iteraciones, siendo \(k_{min}\) el menor entero que satisface la desigualdad: \(k>\frac{\ln\left(\frac{b-a}{\epsilon}\right)}{\ln\left(2\right)}-1\)

 

La siguiente figura sintetiza el diagrama de flujo para el algoritmo de bisección:

 

Implementación del método de bisección.

Para implementar el método de bisección, los argumentos de entrada deben ser:

• La función \(f\) cuya raíz se quiere hallar.

• Los extremos \(a, b\) del intervalo donde está la raíz.

• La tolerancia o error con que deseamos obtener la raíz.

La llamada a la función podría ser entonces algo así como:

>> biseccion(f, a, b, tol)

y debería obtenerse como resultado la raíz en el intervalo \((a,b)\). La implementación del algoritmo anterior puede llevarse a cabo de la forma siguiente (nótese que las lineas de comentario al inicio de la función son las que se mostrarán como ayuda si el usuario ejecuta help biseccion):

function raiz=biseccion(f,a,b,tol)
% Resolución de la ecuación f(x)=0 mediante el algoritmo de bisección.
% Argumentos:
% f: es la función cuya raiz se desea calcular (deberá definirse 
%      como función anónima, previamente o en la llamada a esta funcion).
% a: Extremo inferior del intervalo inicial
% b: Extremo superior del intervalo inicial
% tol (tolerancia): si |b-a|<tol el algoritmo se detiene y devuelve el punto
%                  medio de (a,b) como solución.    
  if f(a)*f(b)>0 accion="error";
    elseif f(a)*f(b)==0 accion="a o b son soluciones";
    else accion="biseccion";      
  end
  raiz=[];
  switch accion
    case "error"
      disp ('ERROR: Debe introducir otro intervalo')
    case "a o b son soluciones"      
      if f(a)==0 raiz = a; end %if
      if f(b)==0 raiz=[raiz, b]; end %if
    case "biseccion"
      m=(a+b)/2;
      while f(m)~=0 && abs(b-a)>tol
        if f(m)*f(b)<0 a=m; else b=m; end%if;
              m=(a+b)/2;
          end% while
          raiz=m;
    end% switch
end% function

 

 

 

Nota sobre las funciones como argumentos de otras funciones:

Recuérdese que para poder pasar una función como argumento de otra función, en octave/matlab pueden utilizarse las funciones anónimas o los manipuladores de funciones (function handlers).

Una función anónima se construye de la forma:

>> @(argumentos) expresión

Por ejemplo, si la función es \(f(x)=x^2-1\), puede definirse mediante:

>> f=@(x) x^2-1;
 f(2)

ans =  3

De esta forma, si queremos utilizar la anterior función bisección() para encontrar una raíz de \(x^2-1\) entre 0 y 2, procederíamos del modo siguiente:

>> f=@(x) x^2-1;
 biseccion(f,0,2,0.00001)

ans =  1

También podemos definir la función f directamente en la llamada a biseccion():

>> biseccion(@(x) x^2-1,0,2,0.00001)

ans =  1

 

Cuando la función cuya raíz queremos calcular existe ya en octave/matlab podemos pasarla como argumento a bisección() de la forma que mostramos en el siguiente ejemplo. Supongamos que queremos hallar la raíz de la función cos(x) entre \(\frac{\pi}{2}\) y \(\frac{3\pi}{2}\):

>> biseccion(@cos,pi/2,3*pi/2,0.00001)

ans =  1.5708

 

 

La función fzero

En matlab, la función fzero es capaz de encontrar las raíces de una ecuación. Para ello utiliza una combinación del método de bisección con otros métodos. Por defecto la tolerancia (error) admitida por el método es \(2.2 \cdot 10 ^{-16}\). Este error se puede modificar mediante la opción “TolX”.

Por ejemplo, supongamos que queremos hallar una raíz de la función:

\[f(x) = x^2-e^x\]

Podemos comprobar fácilmente que: \[f(0) = 0 -1 < 0\] \[f(-1) = 1-\frac{1}{e} >0\] Por tanto esta función tiene una raíz en el intervalo [-1,0]. Usando nuestro programa de bisección, la raíz resultante es:

>> f =@(x) x^2-exp(x);
 biseccion(f,-1,0,0.00001)

ans = -0.70346

Para utilizar la función fzero debemos indicar la función cuyos ceros queremos hallar, y pasarle un vector con los extremos del intervalo donde se encuentra la raíz:

>> fzero(f,[-1,0])

ans = -0.70347

La función fzero puede funcionar también si le pasamos un único valor en lugar de un intervalo; en ese caso, fzero trata de encontrar la raíz más próxima al valor indicado:

>> fzero(f,-1)

ans = -0.70347

 

La función roots

Cuando la función \(f(x)\) es un polinomio, la función roots proporciona sus raíces. Por ejemplo, si \[f(x) = 2x^4-3x^2 +6x-1\]

>> coefPolin = [2 0 -3 6 -1];
 roots(coefPolin)

ans =

  -1.81722 + 0.00000i
   0.81709 + 0.91407i
   0.81709 - 0.91407i
   0.18305 + 0.00000i