class: center, middle, inverse, title-slide # Estadística y Procesos Estocásticos <br> Tema 2: Variables Aleatorias ### <br><br><br><br><br><br><br>Grado en Ingeniería en Tecnologías de la Telecomunicación --- background-image: url(http://www.dma.ulpgc.es/profesores/personal/asp/descargas/azar.jpg) background-size: cover background-position: 15% 45% class: inverse, top, left # 9. Variables Aleatorias con Octave/Matlab. --- background-image: url(http://www.dma.ulpgc.es/profesores/personal/stat/webEyPE/imagenes/darkGaussianBlur.jpg) background-size: cover class: inverse, center, middle # Distribuciones de Probabilidad en octave/matlab --- # Distribuciones de Probabilidad en octave/matlab El programa octave (o matlab) dispone de múltiples funciones para calcular valores de las funciones de densidad o distribución de muchas variables aleatorias de uso común, así como para calcular sus cuantiles o para generar valores aleatorios de dichas distribuciones. -- En general todas estas funciones comparten un término común (por ejemplo .red[ __bino__] para la distribución binomial), seguido de la terminación: * .red[ __pdf__] (_probability density function_) para la función de densidad de probabilidad. -- * .red[ __cdf__] (_cumulative density function_) para la función de distribución de probabilidad. -- * .red[ __inv__] para el cálculo de los cuantiles (valores inversos de la función de distribución). -- * .red[ __rnd__] (_random_) para la generación de valores aleatorios con dicha distribución. --- # Distribuciones de Probabilidad en octave/matlab Esta tabla resume las funciones de uso más común: <table> <thead> <tr> <th style="text-align:left;"> Distribución </th> <th style="text-align:left;"> Func. Densidad </th> <th style="text-align:left;"> Func. Distribución </th> <th style="text-align:left;"> Cuantiles </th> </tr> </thead> <tbody> <tr> <td style="text-align:left;"> Binomial </td> <td style="text-align:left;"> binopdf </td> <td style="text-align:left;"> binocdf </td> <td style="text-align:left;"> binoinv </td> </tr> <tr> <td style="text-align:left;"> Exponential </td> <td style="text-align:left;"> exppdf </td> <td style="text-align:left;"> expcdf </td> <td style="text-align:left;"> expinv </td> </tr> <tr> <td style="text-align:left;"> Gamma </td> <td style="text-align:left;"> gampdf </td> <td style="text-align:left;"> gamcdf </td> <td style="text-align:left;"> gaminv </td> </tr> <tr> <td style="text-align:left;"> Normal </td> <td style="text-align:left;"> normpdf </td> <td style="text-align:left;"> normcdf </td> <td style="text-align:left;"> norminv </td> </tr> <tr> <td style="text-align:left;"> Poisson </td> <td style="text-align:left;"> poisspdf </td> <td style="text-align:left;"> poisscdf </td> <td style="text-align:left;"> poissinv </td> </tr> <tr> <td style="text-align:left;"> Uniform </td> <td style="text-align:left;"> unifpdf </td> <td style="text-align:left;"> unifcdf </td> <td style="text-align:left;"> unifinv </td> </tr> <tr> <td style="text-align:left;"> Weibull </td> <td style="text-align:left;"> wblpdf </td> <td style="text-align:left;"> wblcdf </td> <td style="text-align:left;"> wblinv </td> </tr> </tbody> </table> --- # Distribuciones de Probabilidad en octave/matlab: .blue[Binomial] .pull-left[ * `\(\large{X\approx B(8,0.6): P(X=4)}\)` ```octave binopdf(4,8,0.6) ``` ``` >> ans = 0.23224 ``` <br> * `\(\large{X\approx B(8,0.6): P(X\le 4)}\)` ```octave binocdf(4,8,0.6) ``` ``` >> ans = 0.40591 ``` ] -- .pull-right[ * `\(\large{X\approx B(8,0.6)}\)`: Percentil 25 ```octave binoinv(0.25,8,0.6) ``` ``` >> ans = 4 ``` <br> * `\(\large{X\approx B(8,0.6)}\)`: Percentil 50 ```octave binoinv(0.5,8,0.6) ``` ``` >> ans = 5 ``` ] --- # Distribuciones de Probabilidad en octave/matlab: .blue[Poisson] .pull-left[ * `\(\large{X\approx P(5): P(X=3)}\)` ```octave poisspdf(3,5) ``` ``` >> ans = 0.14037 ``` <br> * `\(\large{X\approx P(5): P(X\le 3)}\)` ```octave poisscdf(3,5) ``` ``` >> ans = 0.26503 ``` ] -- .pull-right[ * `\(\large{X\approx P(5)}\)`: Percentil 20 ```octave poissinv(0.2,5) ``` ``` >> ans = 3 ``` <br> * `\(\large{X\approx P(5)}\)`: Percentil 75 ```octave poissinv(0.75,5) ``` ``` >> ans = 6 ``` ] --- # Distribuciones de Probabilidad en octave/matlab: .blue[Uniforme] .pull-left[ * `\(\large{X\approx U(1,5): f(3)}\)` ```octave unifpdf(3,1,5) ``` ``` >> ans = 0.25000 ``` <br> * `\(\large{X\approx U(1,5): F(3)=P(X\le 3)}\)` ```octave unifcdf(3,1,5) ``` ``` >> ans = 0.50000 ``` ] -- .pull-right[ * `\(\large{X\approx U(1,5)}\)`: Percentil 30 ```octave unifinv(0.3,1,5) ``` ``` >> ans = 2.2000 ``` <br> * `\(\large{X\approx U(1,5)}\)`: Percentil 90 ```octave unifinv(0.9,1,5) ``` ``` >> ans = 4.6000 ``` ] --- # Distribuciones de Probabilidad en octave/matlab: .blue[Exponencial] .pull-left[ * `\(\large{X\approx exp(3): f(1)}\)` ```octave exppdf(1,1/3) ``` ``` >> ans = 0.14936 ``` <br> * `\(\large{X\approx exp(3): F(1) = P(X\le 1)}\)` ```octave expcdf(1,1/3) ``` ``` >> ans = 0.95021 ``` ] -- .pull-right[ * `\(\large{X\approx exp(3)}\)`: Percentil 10 ```octave expinv(0.10,1/3) ``` ``` >> ans = 0.035120 ``` <br> * `\(\large{X\approx exp(3)}\)`: percentil 95 ```octave expcdf(0.95,1/3) ``` ``` >> ans = 0.94216 ``` ] --- # Distribuciones de Probabilidad en octave/matlab: .blue[Weibull] .pull-left[ * `\(\large{X\approx Weibull(\mu=30,\kappa=2)}\)` <br>&nbsp;&nbsp;&nbsp; Densidad: `\(f(20)\)` ```octave wblpdf(20,30,2) ``` ``` >> ans = 0.028497 ``` <br> * `\(\large{X\approx Weibull(\mu=30,\kappa=2)}\)`: <br>&nbsp;&nbsp;&nbsp; `\(\large{F(20)=P(X\le 20)}\)` ```octave wblcdf(20,30,2) ``` ``` >> ans = 0.35882 ``` ] -- .pull-right[ * `\(\large{X\approx Weibull(\mu=30,\kappa=2)}\)`: Percentil 5 ```octave wblinv(0.05,30,2) ``` ``` >> ans = 6.7944 ``` <br> * `\(\large{X\approx Weibull(\mu=30,\kappa=2)}\)`: <br>&nbsp;&nbsp;&nbsp; Percentil 80 ```octave wblinv(0.80,30,2) ``` ``` >> ans = 38.059 ``` ] --- # Distribuciones de Probabilidad en octave/matlab: .blue[Normal] .pull-left[ * `\(\large{X\approx N(0,1): f(1.5)}\)` ```octave normpdf(1.5,0,1) ``` ``` >> ans = 0.12952 ``` <br> * `\(\large{X\approx N(0,1):}\)` <br> &nbsp;&nbsp; `\(\large{F(1.5)=P(X\le 1.5)}\)` ```octave normcdf(1.5,0,1) ``` ``` >> ans = 0.93319 ``` ] -- .pull-right[ * `\(\large{X\approx N(0,1)}\)`: Percentil 2.5 ```octave norminv(0.025,0,1) ``` ``` >> ans = -1.9600 ``` <br> * `\(\large{X\approx N(0,1)}\)`: Percentil 97.5 ```octave norminv(0.975,0,1) ``` ``` >> ans = 1.9600 ``` ] --- background-image: url(http://www.dma.ulpgc.es/profesores/personal/stat/webEyPE/imagenes/darkGaussianBlur.jpg) background-size: cover class: inverse, center, middle # Simulación de variables aleatorias --- ## Simulación de variables aleatorias Una de las propiedades más interesantes de la distribución uniforme es que sirve de base para .red[ __simular__] variables aleatorias que tengan otras distribuciones de probabilidad. -- El fundamento teórico para ello lo proporciona el siguiente: .resalta[ __Teorema:__ Sea `\(F\left(x\right)\)` una función de distribución acumulativa continua y estrictamente creciente y sea `\(U\approx U\left[0,1\right]\)`. Entonces, la variable aleatoria `\(X=F^{-1}\left(U\right)\)` tiene a `\(F\left(x\right)\)` como función de distribución. ] -- <br> De esta forma, .red[ _si disponemos de algún mecanismo para simular valores con distribución uniforme_], podemos utilizarlo para simular valores de otras distribuciones. --- ### Simulación de valores con distribución `\(\Large{U[0,1]}\)` usando la calculadora. La mayoría de las calculadoras científicas ofrecen la posibilidad de generar valores aleatorios con distribución uniforme en `\([0,1]\)`. -- .pull-left[ .center[] ] .pull-right[ <br><br><br> Habitualmente ello se consigue simplemente pulsando las teclas .red[SHIFT RAN#] ] --- ### Simulación de valores con distribución `\(\Large{U[a,b]}\)` en octave/matlab El programa .red[octave/matlab] dispone de la función .blue[ __unifrnd__] para generar valores aleatorios con distribución uniforme en `\((0,1)\)`. -- Concretamente, la sintaxis .blue[ __unifrnd(a,b,[m n])__] indica a octave que debe generar una matriz de dimensión `\(m\times n\)` cuyos valores son aleatorios con distribución `\(U[a,b]\)` -- Por ejemplo, para generar un vector con 10 valores aleatorios de dicha distribución escribimos: ```octave unifrnd(0,1,[1 10]) ``` ``` >> ans = >> >> Columns 1 through 6: >> >> 9.5688e-01 5.6842e-01 4.1837e-05 1.1109e-01 7.1739e-01 6.5120e-01 >> >> Columns 7 through 10: >> >> 4.9737e-01 6.0888e-01 1.7069e-01 4.6358e-01 ``` --- ### Simulación de variables aleatorias con distribución no uniforme. .blue[Ejemplo:] Se desea simular `\(n\)` valores de una variable aleatoria `\(X\)` con función de distribución: .pull-left[ `$$\large{F\left(x\right)=x^{4}\,:\,0\leq x\leq1}$$` <br> La función de densidad en este caso es: `$$\large{f(x)=4x^3, \;\; 0\le x\le 1}$$` ] .pull-right[ <img src="tema2-6_Octave_Simulacion_de_VA_files/figure-html/unnamed-chunk-27-1.png" style="display: block; margin: auto;" /> ] -- Esta función de densidad nos indica que una simulación correcta debe producir más valores entre 0.75 y 1 (región más probable) que entre 0 y 0.25 (región poco probable). --- ### Simulación de variables aleatorias con distribución no uniforme. .blue[Ejemplo:] El procedimiento a seguir para simular esta variable aleatoria es el siguiente: -- .blue[ __[1]__] Calculamos la función inversa `\(F^{-1}(u)\)`: -- Para ello tengamos en cuenta que si `\(u=F\left(x\right)\Rightarrow x=F^{-1}\left(u\right)\)`. Entonces: -- `$$F\left(x\right)=x^{4}\Rightarrow u=x^{4}\Rightarrow x=u^{1/4}\Rightarrow F^{-1}\left(u\right)=u^{1/4}$$` -- <br> .blue[ __[2]__] Simulamos `\(n\)` valores `\(u_1, u_2, \dots, u_n\)` con distribución uniforme en `\([0,1]\)` -- <br> .blue[ __[3]__] Calculamos los `\(n\)` valores `\(x_1, x_2, \dots, x_n\)` mediante `\(x_i=F^{-1}(u_i)=u_i^{1/4}\)`. Los valores `\(x_1, x_2, \dots, x_n\)` así obtenidos tienen la distribución `\(F(x)\)` --- ### Simulación de variables aleatorias con calculadora. .blue[Ejemplo:] Para simular `\(n\)` valores de la distribución `\(F(x)\)` anterior utilizando la calculadora: .pull-left[ .center[  ] ] .pull-right[ <br> 1. Obtenemos un número aleatorio uniforme en `\([0,1]\)` pulsando las teclas .red[SHIFT RAN#] 2. Lo convertimos en un valor de la distribución `\(F(x)\)` mediante `\(x=F^{-1}(u)=u^{1/4}\)` 3. Repetimos los pasos 1 y 2 anteriores `\(n\)` veces. ] --- ### Simulación de variables aleatorias con octave/matlab. .blue[Ejemplo:] ``` ## warning: print.m: fig2dev binary is not available. ## Some output formats are not available. ## warning: called from ## __print_parse_opts__ at line 388 column 9 ## print at line 316 column 8 ``` ```r n=1000; U=unifrnd(0,1,[1,n]); X=U.^(1/4); hist(X); ylabel("Frecuencia"); title("Histograma de valores de X"); ``` -- .pull-left[ ``` X 1 0.8555638 2 0.9021367 3 0.8547001 4 0.7019274 5 0.6116102 6 0.9297767 7 0.9000007 8 0.9789969 9 0.8605193 10 0.9568471 ``` `\(\vdots \;\;\;\;\;\;\;\;\;\;\;\; \vdots\)` ] .pull-right[ 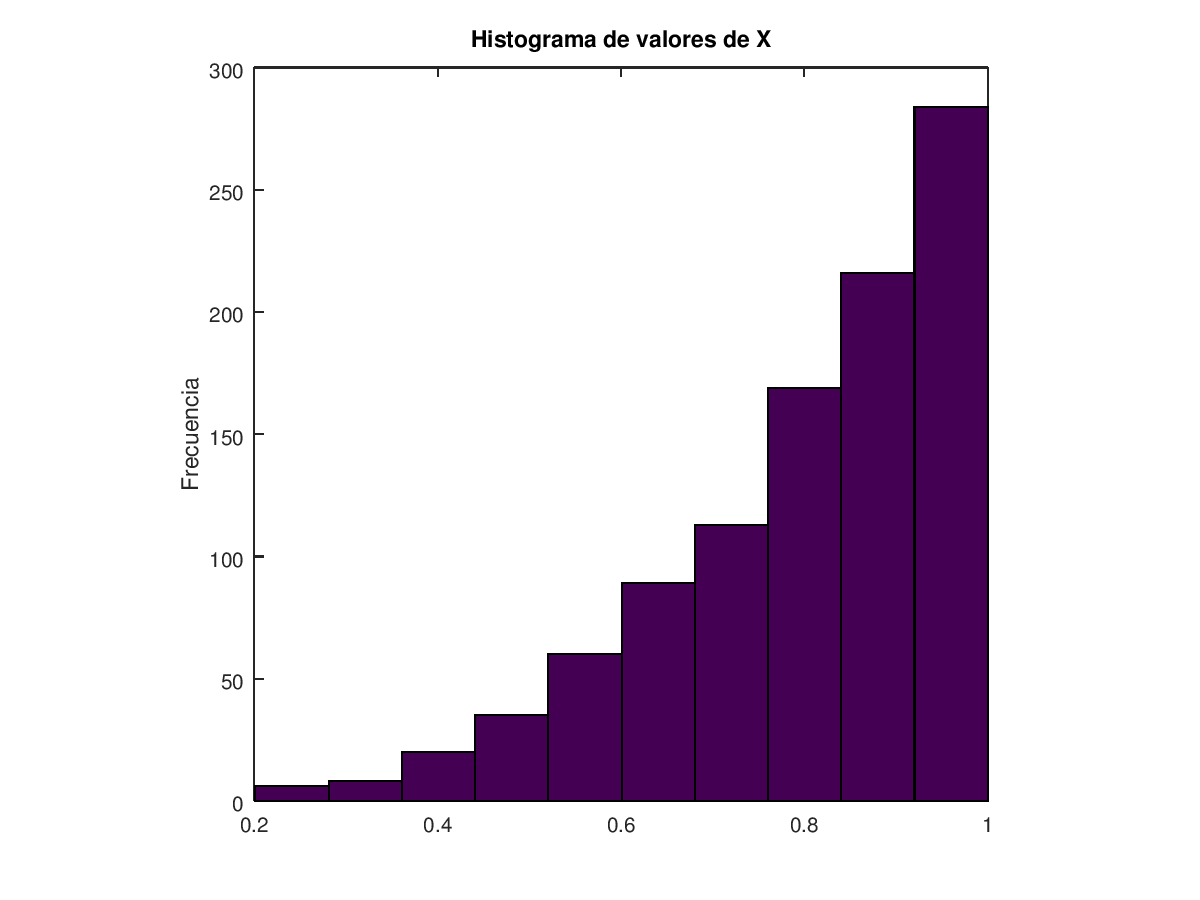 ]