Estadística y Procesos Estocásticos Tema 2: Variables Aleatorias

class: center, middle, inverse, title-slide

# Estadística y Procesos Estocásticos <br> Tema 2: Variables Aleatorias
### <br><br><br><br><br><br><br>Grado en Ingeniería en Tecnologías de la Telecomunicación

---

background-image: url(http://www.dma.ulpgc.es/profesores/personal/asp/descargas/azar.jpg)
background-size: cover
background-position: 15% 45%
class: inverse, top, left

# 5. Características de las distribuciones de probabilidad
---

### Características de las distribuciones de probabilidad

En esta sección describiremos una serie de medidas que tienen como objetivo .red[ __resumir__] las características principales de la distribución de una variable aleatoria:

.pull-left[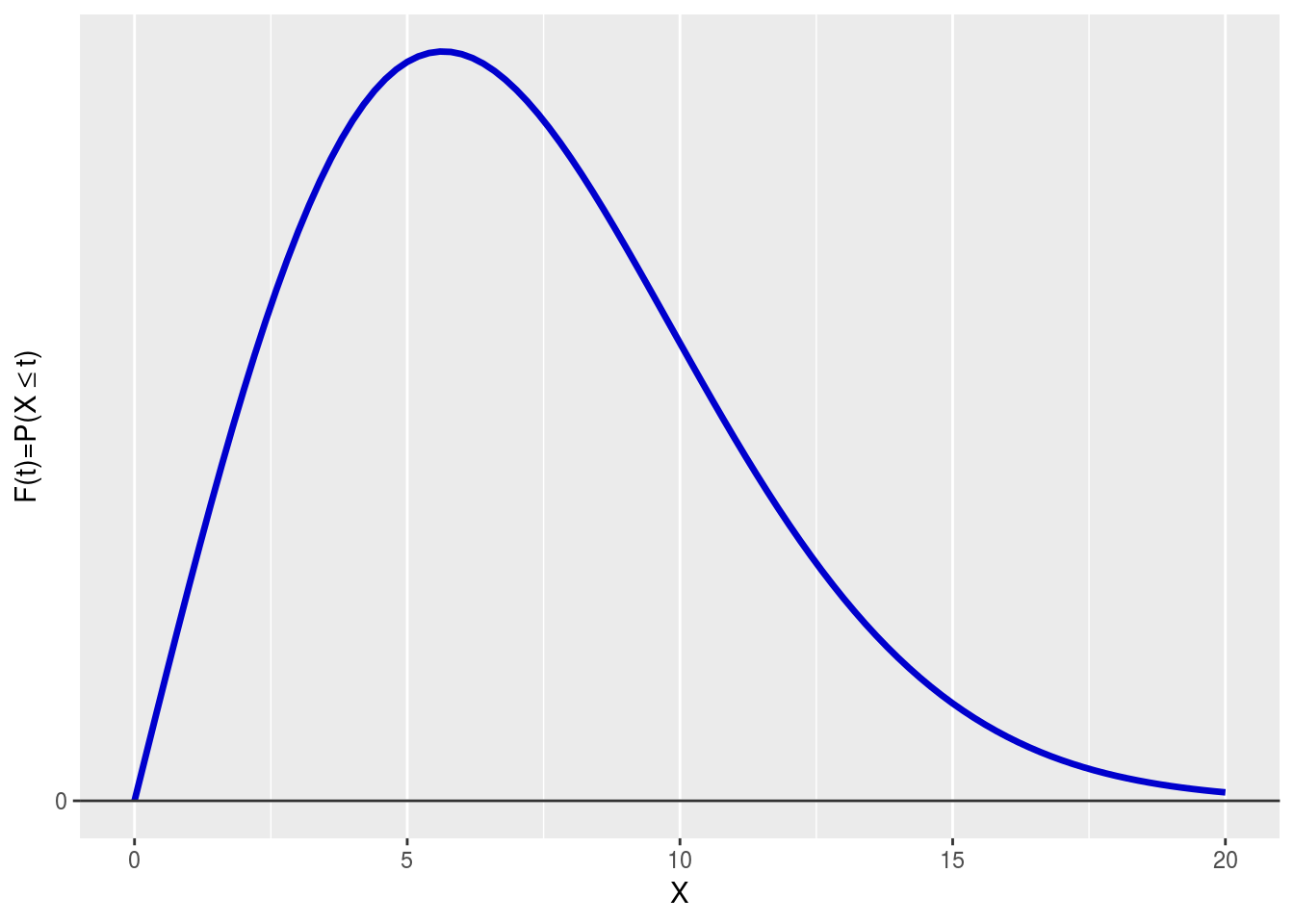

![](tema2-2_Caracteristicas_VA_files/figure-html/unnamed-chunk-1-1.png)

]

.pull-right[

<br>

* .red[Valor central:] esperanza.

* .red[Dispersión:] varianza y desviación típica.

* .red[Forma:] asimetría y apuntamiento.

* .red[Posición:] cuantiles.

]

---
background-image: url(http://www.dma.ulpgc.es/profesores/personal/stat/webEyPE/imagenes/darkGaussianBlur.jpg)
background-size: cover
class: inverse, center, middle

# Valor central: Esperanza

---

## Esperanza matemática

__Objetivo:__ Resumir la variable aleatoria `$X$` en un valor .red[ __central__] representativo de la totalidad de su distribución de probabilidad.

.pull-left[

#### .blue[Ejemplo:]

<table>
 <thead>
  <tr>
   <th style="text-align:right;"> X </th>
   <th style="text-align:right;"> Probabilidad </th>
  </tr>
 </thead>
<tbody>
  <tr>
   <td style="text-align:right;"> 1 </td>
   <td style="text-align:right;"> 0.15 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 2 </td>
   <td style="text-align:right;"> 0.25 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 3 </td>
   <td style="text-align:right;"> 0.40 </td>
  </tr>
  <tr>
   <td style="text-align:right;"> 4 </td>
   <td style="text-align:right;"> 0.20 </td>
  </tr>
</tbody>
</table>
]

.pull-right[

<img src="tema2-2_Caracteristicas_VA_files/figure-html/unnamed-chunk-3-1.png" style="display: block; margin: auto;" />
]

---

## Esperanza matemática

__Objetivo:__ Resumir la variable aleatoria `$X$` en un valor .red[ __central__] representativo de la totalidad de su distribución de probabilidad.

.pull-left[

#### .blue[Ejemplo:]

.pull-right[

<img src="tema2-2_Caracteristicas_VA_files/figure-html/unnamed-chunk-5-1.png" style="display: block; margin: auto;" />
]

Usando la analogía entre probabilidad y masa, la .red[ __esperanza__] `$\large{\mu=E[X]}$` de una variable aleatoria se corresponde con el .red[ __centro de gravedad__ ] de su distribu- ción de probabilidad:

`$$\large{E\left[X\right]=1\cdot0.15+2\cdot0.25+3\cdot0.4+4\cdot0.2=2.65}$$`

---

### Esperanza matemática

Sea `$X$` una variable aleatoria __discreta__. Se define la esperanza de `$X$` como:

.resalta[

`$$\Large{E\left[X\right]=\sum\nolimits _{t}t\cdot\Pr\left(X=t\right)}$$`
]
---

.large[ .blue[Ejemplo:]] suma de resultados de dos lanzamientos sucesivos de un dado
<br>

.pull-left[
<table class="table" style="font-size: 13px; margin-left: auto; margin-right: auto;">
 <thead>
  <tr>
   <th style="text-align:center;"> X </th>
   <th style="text-align:center;"> Probabilidad </th>
  </tr>
 </thead>
<tbody>
  <tr>
   <td style="text-align:center;"> 2 </td>
   <td style="text-align:center;"> 1/36 </td>
  </tr>
  <tr>
   <td style="text-align:center;"> 3 </td>
   <td style="text-align:center;"> 2/36 </td>
  </tr>
  <tr>
   <td style="text-align:center;"> 4 </td>
   <td style="text-align:center;"> 3/36 </td>
  </tr>
  <tr>
   <td style="text-align:center;"> 5 </td>
   <td style="text-align:center;"> 4/36 </td>
  </tr>
  <tr>
   <td style="text-align:center;"> 6 </td>
   <td style="text-align:center;"> 5/36 </td>
  </tr>
  <tr>
   <td style="text-align:center;"> 7 </td>
   <td style="text-align:center;"> 6/36 </td>
  </tr>
  <tr>
   <td style="text-align:center;"> 8 </td>
   <td style="text-align:center;"> 5/36 </td>
  </tr>
  <tr>
   <td style="text-align:center;"> 9 </td>
   <td style="text-align:center;"> 4/36 </td>
  </tr>
  <tr>
   <td style="text-align:center;"> 10 </td>
   <td style="text-align:center;"> 3/36 </td>
  </tr>
  <tr>
   <td style="text-align:center;"> 11 </td>
   <td style="text-align:center;"> 2/36 </td>
  </tr>
  <tr>
   <td style="text-align:center;"> 12 </td>
   <td style="text-align:center;"> 1/36 </td>
  </tr>
</tbody>
</table>
]

.pull-right[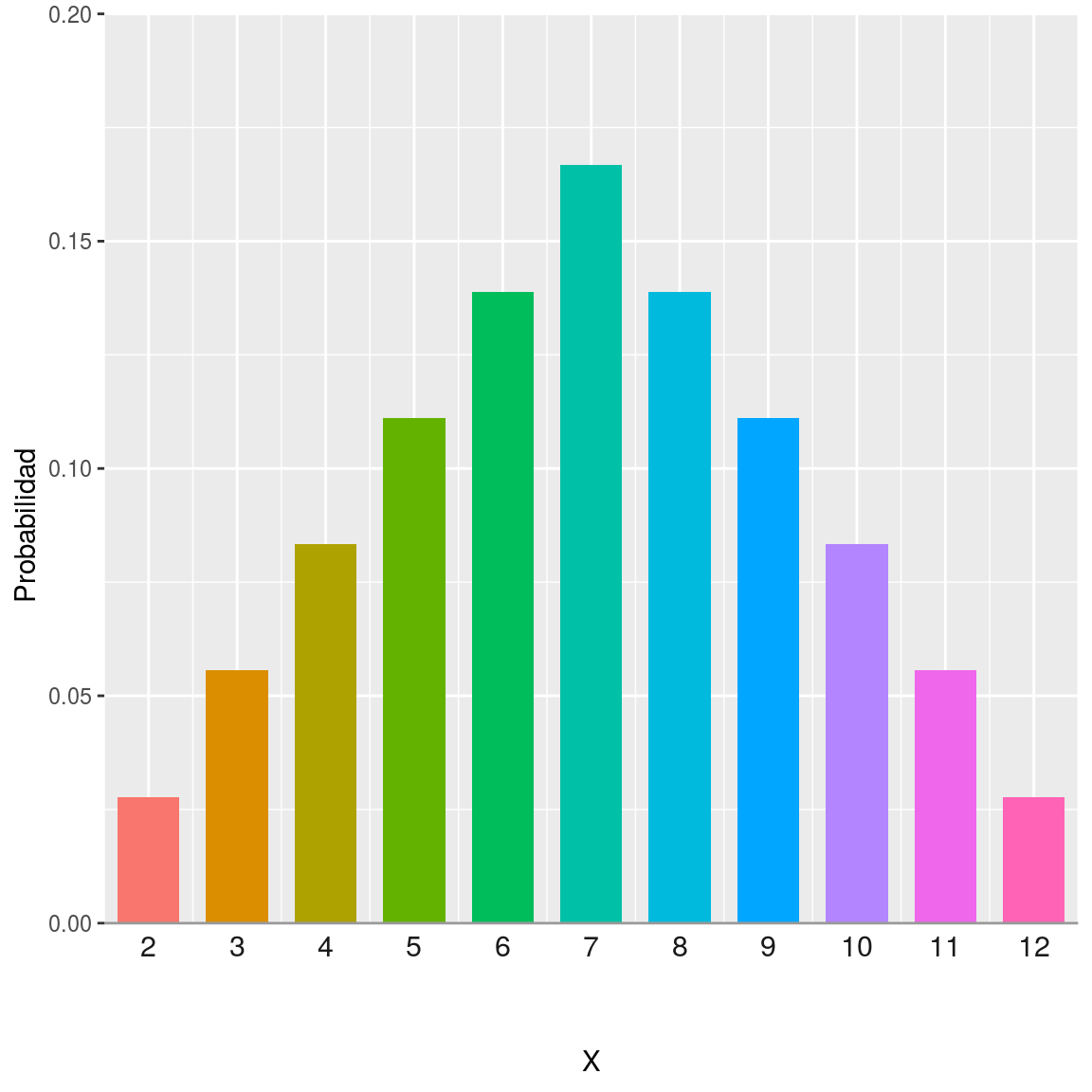
![](tema2-2_Caracteristicas_VA_files/figure-html/unnamed-chunk-7-1.png)

]
---

.large[.blue[Ejemplo:]] suma de resultados de dos lanzamientos sucesivos de un dado
<br>

.pull-right[
![](tema2-2_Caracteristicas_VA_files/figure-html/unnamed-chunk-9-1.png)

]

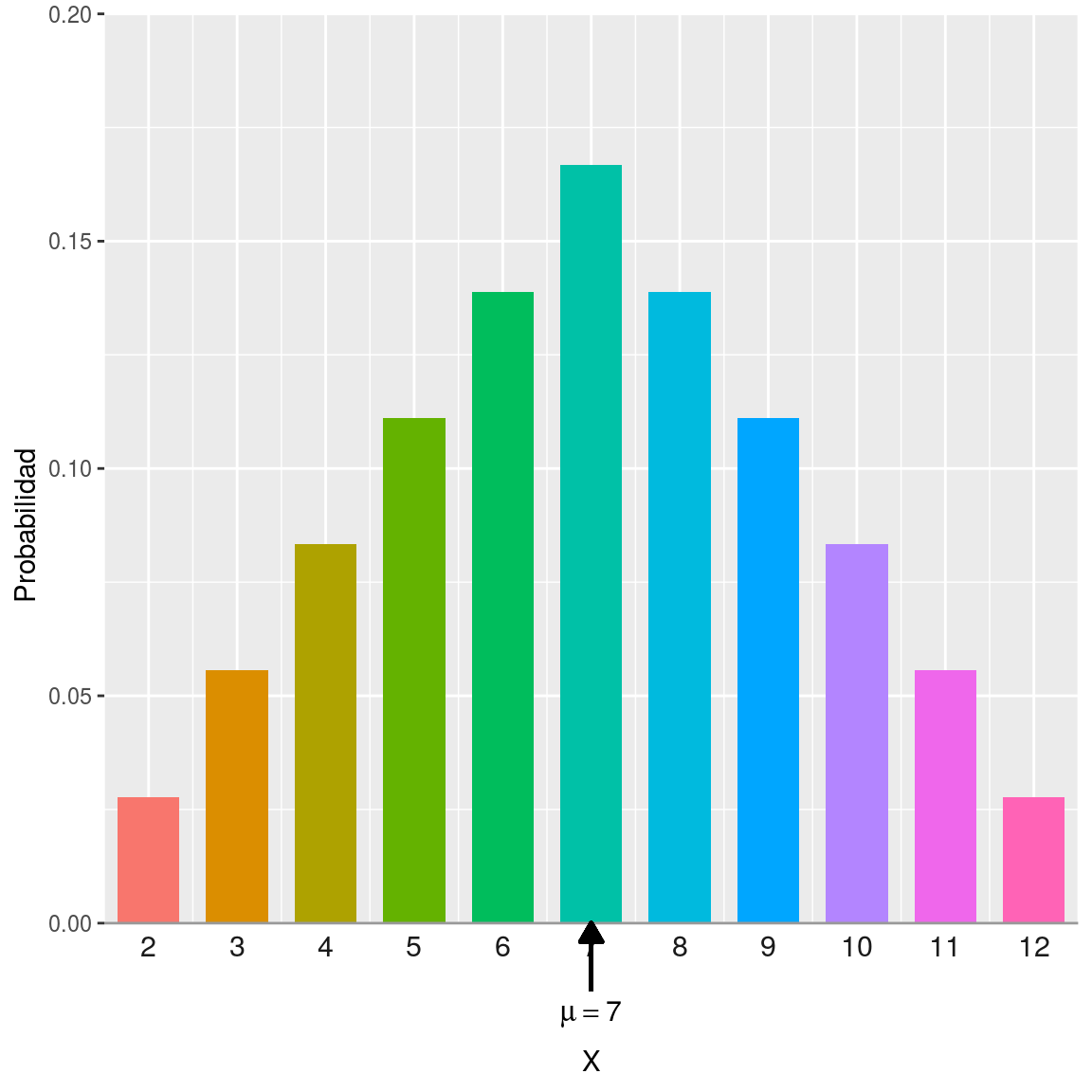`$$E\left[X\right]=2\cdot\frac{1}{36}+3\cdot\frac{2}{36}+4\cdot\frac{3}{36}+5\cdot\frac{4}{36}+6\cdot\frac{5}{36}+$$`

`$$+7\cdot\frac{6}{36}+8\cdot\frac{5}{36}+9\cdot\frac{4}{36}+10\cdot\frac{3}{36}+11\cdot\frac{2}{36}+12\cdot\frac{1}{36}=7$$`

---
### Esperanza matemática

Sea `$X$` una variable aleatoria __continua__. Se define la esperanza de `$X$` como:

.resalta[

`$$\Large{E\left[X\right]=\int_{-\infty}^{\infty}tf\left(t\right)dt}$$`
]

---

### .blue[Ejemplo]

* El __lugar__ en una carretera en que se produce la avería de un coche.

.pull-left[

]

.pull-right[
<br><br>
`$$f\left(x\right)=\frac{1}{6}\,\,\,0\leq x\leq6$$`]
---

### .blue[Ejemplo]

* El __lugar__ en una carretera en que se produce la avería de un coche.

.pull-left[

<img src="tema2-2_Caracteristicas_VA_files/figure-html/unnamed-chunk-11-1.png" style="display: block; margin: auto;" />
]

.pull-right[
<br><br>
`$$f\left(x\right)=\frac{1}{6}\,\,\,0\leq x\leq6$$`]

`$$E\left[X\right]=\int_{0}^{6}t\frac{1}{6}dt=\left.\frac{t^{2}}{2\cdot6}\right]_{0}^{6}=\frac{6^{2}}{2\cdot6}=3$$`

---

### Esperanza Matemática

Sea `$X$` una variable aleatoria y consideremos la función `$\large{g:\mathbb{R\rightarrow R}}$`. La esperanza matemática de la variable aleatoria `$\bf{g\left(X\right)}$` se define como:

* Si `$X$` es discreta:

.resalta[

`$$\large{E\left[g\left(X\right)\right]=\sum\nolimits _{t}g\left(t\right)\cdot\Pr\left(X=t\right)}$$`
]

<br>

* Si `$X$` es continua y tiene función de densidad `$f\left(t\right)$`

.resalta[

`$$\large{E\left[g\left(X\right)\right]=\int\limits _{-\infty}^{\infty}g\left(t\right)\cdot f\left(t\right)\cdot dt}$$`
]

---

### .blue[Ejemplo:]

Una empresa de software ha desarrollado un programa para generar fondos de pantalla animados. Uno de los modelos de fondo consiste en la generación de círculos de radio y color aleatorios que se van moviendo al azar por la pantalla. El radio `$X$` de cada círculo es una variable aleatoria que toma valores entre 1 y 5 cm con función de densidad:

`$$f\left(x\right)=\begin{cases}
\lambda x\left(1-x\right)\left(x-5\right) & 1\le x\le5\\
0 & \textrm{en otro caso}
\end{cases}$$`

1. Calcula la probabilidad de que el programa genere un círculo de radio mayor que 3 cm.

2. Calcula `$E[X]$` (valor esperado del radio de un círculo generado al azar por el programa)

3. Calcula el valor esperado de la superficie de un círculo generado al azar por el programa

---

### .blue[Ejemplo:]

<br>

En primer lugar hemos de calcular el valor de `$\lambda$` de tal forma que la probabilidad total de que el radio de un círculo elegido al azar esté entre 1 y 5 cm. sea 1:

`$$\int_{1}^{5}f\left(x\right)dx=1\Rightarrow\int_{1}^{5}\lambda x\left(1-x\right)\left(x-5\right)dx=1\Rightarrow\lambda\int_{1}^{5}\left(-x^{3}+6x^{2}-5x\right)dx=1$$`

`$$\Rightarrow\lambda\left[-\frac{x^{4}}{4}+\frac{6x^{3}}{3}-\frac{5x^{2}}{2}\right]_{1}^{5}=1\Rightarrow\lambda\left[\frac{375}{12}-\left(-\frac{9}{12}\right)\right]=1\Rightarrow\lambda\cdot32=1\Rightarrow\lambda=\frac{1}{32}$$`

---

### .blue[Ejemplo:]

Podemos utilizar .red[octave/matlab] para dibujar la función de densidad:

```octave
x=1:0.01:5
plot(x,(1/32).*x.*(1-x).*(x-5), "linewidth",3)
```

.center[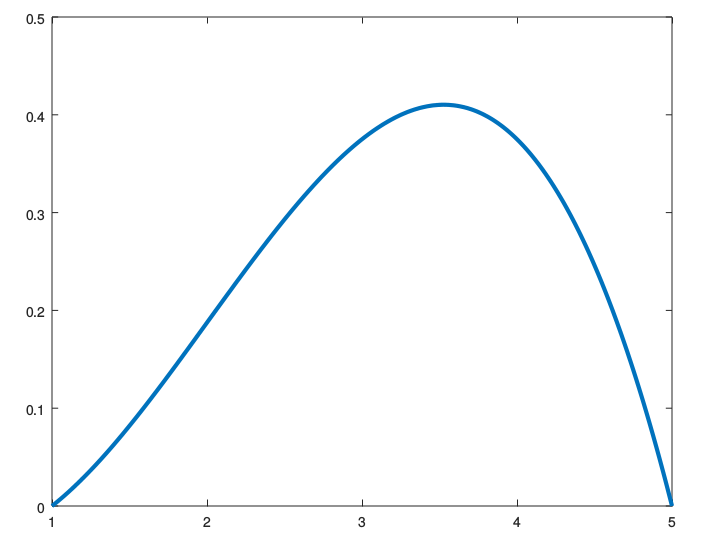

![:scale 50%](imagenes/densidad.png)

]

---

### .blue[Ejemplo:]

1. Calcula la probabilidad de que el programa genere un círculo de radio mayor que 3 cm.

`$$P\left(X>3\right)=P\left(3\le X\le5\right)=\int_{3}^{5}\frac{1}{32}x\left(1-x\right)\left(x-5\right)dx=$$`

`$$=\frac{1}{32}\left[-\frac{x^{4}}{4}+\frac{6x^{3}}{3}-\frac{5x^{2}}{2}\right]_{3}^{5}=\frac{1}{32}\left[\frac{375}{12}-\frac{135}{12}\right]=\frac{20}{32}=\frac{5}{8}=0.625$$`

---

### .blue[Ejemplo:]

Gráficamente:

`$$f\left(x\right)=\begin{cases}
\frac{1}{32} x\left(1-x\right)\left(x-5\right) & 1\le x\le5\\
0 & \textrm{en otro caso}
\end{cases}$$`

---

### .blue[Ejemplo:]

`2.` Calcula `$E[X]$` (valor esperado del radio de un círculo generado al azar por el programa)

Se tiene:

`$$E\left[X\right]=\int_{1}^{5}xf\left(x\right)dx=\int_{1}^{5}\frac{1}{32}x^{2}\left(1-x\right)\left(x-5\right)dx=\frac{1}{32}\int_{1}^{5}\left(-x^{4}+6x^{3}-5x^{2}\right)dx=$$`

`$$=\frac{1}{32}\left[-\frac{x^{5}}{5}+\frac{6x^{4}}{4}-\frac{5x^{3}}{3}\right]_{1}^{5}=\frac{49}{15}=3.26667\,\,cm$$`
<img src="tema2-2_Caracteristicas_VA_files/figure-html/unnamed-chunk-14-1.png" style="display: block; margin: auto;" />

---

### .blue[Ejemplo:]

`3.` Calcula el valor esperado de la superficie de un círculo generado al azar por el programa

La superficie de un círculo de radio `$r$` es `$Sup(r)=\pi r^2$`; por tanto, como el radio es aleatorio, la superficie será también un valor aleatorio función del valor del radio; la superficie esperada del círculo es entonces:

`$$E\left[Sup(X)\right]=\int_{1}^{5}\pi x^{2}f\left(x\right)dx=\int_{1}^{5}\frac{\pi}{32}x^{3}\left(1-x\right)\left(x-5\right)dx=\frac{\pi}{32}\int_{1}^{5}\left(-x^{5}+6x^{4}-5x^{3}\right)dx$$`
--

`$$=\frac{\pi}{32}\left[-\frac{x^{6}}{6}+\frac{6x^{5}}{5}-\frac{5x^{4}}{4}\right]_{1}^{5}=35.81416\,\,cm^2$$`

---

### Primera propiedad de linealidad de la esperanza

Sea `$\lambda$` una constante y `$X$` una variable aleatoria. Entonces

.resalta[
`$$\large{E\left[\lambda\cdot X\right]=\lambda\cdot E\left[X\right]}$$`
]
--

<br>

.blue[ _Demostración_]. (caso discreto)
 
`$$E\left[\lambda X\right]=\sum_{t}\lambda t\cdot\Pr\left(X=t\right)=\lambda\sum_{t}t\cdot\Pr\left(X=t\right)=\lambda E\left[X\right]$$`

.blue[ _Demostración_]. (caso continuo)
 
`$$E\left[\lambda X\right]=\int_{t}\lambda t\cdot f\left(t\right)=\lambda\int_{t}t\cdot f\left(t\right)=\lambda E\left[X\right]$$`
---
background-image: url(http://www.dma.ulpgc.es/profesores/personal/stat/webEyPE/imagenes/darkGaussianBlur.jpg)
background-size: cover
class: inverse, center, middle

# Dispersion: Varianza y Desviación típica

---

## Dispersión de variables aleatorias (Varianza)

Para una variable aleatoria `$X$` con esperanza `$\mu$`, la varianza `$\sigma^2$` se define como:

.resalta[
`$$\sigma^2=\textrm{var}\left(X\right)=E\left[\left(X-\mu\right)^{2}\right]$$`
]
--

---

## Dispersión de variables aleatorias (Varianza)

Para una variable aleatoria `$X$` con esperanza `$\mu$`, la varianza `$\sigma^2$` se define como:

.resalta[
`$$\sigma^2=\textrm{var}\left(X\right)=E\left[\left(X-\mu\right)^{2}\right]$$`
]

<br>

Por tanto:

* Cuanto mayor sea la varianza __más dispersos__ (alejados del centro de gravedad o esperanza) se encuentran los  valores que puede tomar la variable aleatoria.

* Una menor varianza supone una __mayor concentración__ de la distribución alrededor de su centro de gravedad.

---

.large[.blue[Ejemplo:]] suma de resultados de dos lanzamientos sucesivos de un dado
<br>

.pull-left[
<table class="table" style="font-size: 11px; margin-left: auto; margin-right: auto;">
 <thead>
  <tr>
   <th style="text-align:center;"> X </th>
   <th style="text-align:center;"> Probabilidad </th>
  </tr>
 </thead>
<tbody>
  <tr>
   <td style="text-align:center;"> 2 </td>
   <td style="text-align:center;"> 1/36 </td>
  </tr>
  <tr>
   <td style="text-align:center;"> 3 </td>
   <td style="text-align:center;"> 2/36 </td>
  </tr>
  <tr>
   <td style="text-align:center;"> 4 </td>
   <td style="text-align:center;"> 3/36 </td>
  </tr>
  <tr>
   <td style="text-align:center;"> 5 </td>
   <td style="text-align:center;"> 4/36 </td>
  </tr>
  <tr>
   <td style="text-align:center;"> 6 </td>
   <td style="text-align:center;"> 5/36 </td>
  </tr>
  <tr>
   <td style="text-align:center;"> 7 </td>
   <td style="text-align:center;"> 6/36 </td>
  </tr>
  <tr>
   <td style="text-align:center;"> 8 </td>
   <td style="text-align:center;"> 5/36 </td>
  </tr>
  <tr>
   <td style="text-align:center;"> 9 </td>
   <td style="text-align:center;"> 4/36 </td>
  </tr>
  <tr>
   <td style="text-align:center;"> 10 </td>
   <td style="text-align:center;"> 3/36 </td>
  </tr>
  <tr>
   <td style="text-align:center;"> 11 </td>
   <td style="text-align:center;"> 2/36 </td>
  </tr>
  <tr>
   <td style="text-align:center;"> 12 </td>
   <td style="text-align:center;"> 1/36 </td>
  </tr>
</tbody>
</table>
]

.pull-right[
![](tema2-2_Caracteristicas_VA_files/figure-html/unnamed-chunk-17-1.png)
]

`$$Var\left(X\right)=E\left[\left(X-\mu\right)^{2}\right]=\sum_{k=2}^{12}\left(x-\mu\right)^{2}P\left(X=x\right)=$$`
--

`$$=\left(2-7\right)^{2}\frac{1}{36}+\left(3-7\right)^{2}\frac{2}{36}+\left(4-7\right)^{2}\frac{3}{36}+\left(5-7\right)^{2}\frac{4}{36}+\left(6-7\right)^{2}\frac{5}{36}+\left(7-7\right)^{2}\frac{6}{36}+$$`

$$+\left(8-7\right)^{2}\frac{5}{36}+\left(9-7\right)^{2}\frac{4}{36}+\left(10-7\right)^{2}\frac{3}{36}+\left(11-7\right)^{2}\frac{2}{36}+\left(12-7\right)^{2}\frac{1}{36}=5.833 $$

---
.large[.blue[Ejemplo:]] Lugar de una carretera en que se produce la avería de un coche.
<br>
.pull-left[

<img src="tema2-2_Caracteristicas_VA_files/figure-html/unnamed-chunk-18-1.png" style="display: block; margin: auto;" />
]

.pull-right[
<br><br>
`$$f\left(x\right)=\frac{1}{6}\,\,\,0\leq x\leq6$$`]

`$$Var\left(X\right)=E\left[\left(X-\mu\right)^{2}\right]=\int_{0}^{6}(x-\mu)^{2}f\left(x\right)dx=\int_{0}^{6}\left(x-3\right)^{2}\frac{1}{6}dx=$$`
--

`$$=\frac{1}{6}\left[\frac{\left(x-3\right)^{3}}{3}\right]_{0}^{6}=\frac{1}{6}\left[\frac{\left(6-3\right)^{3}}{3}-\frac{\left(0-3\right)^{3}}{3}\right]=\frac{1}{6}\left(3^{2}+3^{2}\right)=3$$`
---

.large[.blue[Ejemplo:]] Cálculo de esperanzas y varianzas con .red[octave/matlab]

* El siguiente código en .red[octave/matlab] permite calcular la esperanza y la varianza en el problema del lanzamiento de dos dados; para ello simplemente definimos los valores de `$\large{X}$` y las probabilidades `$\large{p}$` y utilizamos el producto escalar:

```octave
x=2:1:12  
p=[1,2,3,4,5,6,5,4,3,2,1]/36  
mu=x*p'  
var=((x-mu).^ 2)*p' 
```

* Asimismo, para calcular la esperanza y varianza en el problema de la carretera, definimos la función de densidad y utilizamos la función .red[quad] que permite el cálculo de integrales definidas:

```r
function y=f(x)  
  y=(1/6);  
endfunction  
mu=quad(@(x) x.*f(x),0,6)  
var=quad(@(x) ((x-mu).^2).*f(x),0,6)
```

---

<br>

## Desviación Típica

La desviación típica se define como:

.resalta[

`$$\large{\sigma=\textrm{sd}\left(X\right)=\sqrt{\textrm{var}\left(X\right)}}$$`
]

<br>

Como medida de dispersión, `$\sigma$` tiene la ventaja de que se mide en la misma escala (mismas unidades de medida) que la variable `$X$`.

---
### Interpretación de la Varianza: Desigualdad de Chebyshev

.pull-left[
.center[
![](imagenes/Chebyshev.jpg)
]
.center[ [Pafnuty Chebyshev (1821-1894)](https://en.wikipedia.org/wiki/Pafnuty_Chebyshev)]
<br>
]

.pull-right[
<div class=resalta>$$\large{P\left(\left|X-\mu\right|\le k\sigma\right)\ge1-\frac{1}{k^{2}}}$$</div><br> Esta desigualdad indica que la probabilidad de que la variable _X_ tome valores entre su esperanza `$\mu$` y _k_ veces su desviación típica `$\sigma$` es al menos `$1-1/k^2$`. En particular:

]

Así, conocidas `$\mu$` y `$\sigma$` esta desigualdad nos da una idea del rango en que se mueven los valores más probables de la variable aleatoria `$X$`.

[Demostración de la desigualdad de Chebyshev](Demostraciones.html#Chebyshev)
---

### Propiedades de la Varianza

.resalta[
`$$\large{\textrm{var}\left(\lambda X\right)=\lambda^{2}\textrm{var}\left(X\right)}$$`
]

<br>

.blue[ _Demostración_]: Llamando `$\mu=E\left[X\right]$`, por la propiedad de linealidad de la esperanza, se tiene que `$E\left[\lambda X\right]=\lambda\mu$`. Utilizando entonces la definición de varianza:

`$$\textrm{var}\left(\lambda X\right)=E\left[\left(\lambda X-E[\lambda X]\right)^{2}\right]=
E\left[\left(\lambda X-\lambda\mu\right)^{2}\right] =$$`

$$ =E\left[\lambda^{2}\left(X-\mu\right)^{2}\right]=\lambda^{2}E\left[\left(X-\mu\right)^{2}\right]=$$
--

`$$=\lambda^{2}\textrm{var}\left(X\right)$$`
---

### Propiedades de la Varianza

.resalta[
`$$\large{\textrm{var}\left(X\right)=E\left[X^{2}\right]-E\left[X\right]^{2}}=E[X^2]-\mu^2$$`
]

<br>

.blue[ _Demostración_]:

`$$\textrm{var}\left(X\right)=E\left[\left(X-\mu\right)^{2}\right]=E\left[X^{2}-2\mu X+\mu^{2}\right]$$`

* En el caso discreto:

`$$E\left[X^{2}-2\mu X+\mu^{2}\right]=\sum_{x}\left(x^{2}-2\mu x+\mu^{2}\right)P\left(X=x\right)=$$`

`$$=\sum_{x}x^{2}P\left(X=x\right)-2\mu\sum_{x}xP\left(X=x\right)+\mu^{2}\sum_{x}P\left(X=x\right)=$$`

`$$E\left[X^{2}\right]-2\mu^{2}+\mu^{2}=E\left[X^{2}\right]-\mu^{2}$$`

---
### Propiedades de la Varianza

.resalta[
`$$\large{\textrm{var}\left(X\right)=E\left[X^{2}\right]-E\left[X\right]^{2}}=E[X^2]-\mu^2$$`
]

<br>

.blue[ _Demostración_]:

`$$\textrm{var}\left(X\right)=E\left[\left(X-\mu\right)^{2}\right]=E\left[X^{2}-2\mu X+\mu^{2}\right]$$`

* En el caso continuo:

`$$E\left[X^{2}-2\mu X+\mu^{2}\right]=\int_{x}\left(x^{2}-2\mu x+\mu^{2}\right)f\left(x\right)dx=$$`

`$$=\int_{x}x^{2}f\left(x\right)dx-2\mu\int_{x}xf\left(x\right)dx+\mu^{2}\int_{x}f\left(x\right)dx$$`

`$$=E\left[X^{2}\right]-2\mu E\left[X\right]+\mu^{2}=E\left[X^{2}\right]-\mu^{2}$$`

---

### .blue[Ejemplo:]

Recordemos que en el problema del programa generador de círculos de radio aleatorio, el radio `$X$` de cada círculo es una variable aleatoria con función de densidad:

`$$f\left(x\right)=\begin{cases}
\frac{1}{32} x\left(1-x\right)\left(x-5\right) & 1\le x\le5\\
0 & \textrm{en otro caso}
\end{cases}$$`

Entonces:

`$$E\left[X^{2}\right]=\int_{1}^{5}x^{2}f\left(x\right)dx=\int_{1}^{5}\frac{1}{32}x^{3}\left(1-x\right)\left(x-5\right)dx=\frac{1}{32}\int_{1}^{5}\left(-x^{5}+6x^{4}-5x^{3}\right)dx$$`

`$$=\frac{1}{32}\left[-\frac{x^{6}}{6}+\frac{6x^{5}}{5}-\frac{5x^{4}}{4}\right]_{1}^{5}=\frac{1}{32}\left[5^{4}\left(-\frac{5^{2}}{6}+6-\frac{5}{4}\right)-\left(-\frac{1}{6}+\frac{6}{5}-\frac{5}{4}\right)\right]=$$`

`$$=\frac{1}{32}\left[5^{4}\left(\frac{-250+360-75}{60}\right)-\left(\frac{-10+72-75}{60}\right)\right]=
\frac{21888}{32\cdot60}=\frac{684}{60}=\frac{57}{5}=11.4$$`

Por tanto:

`$$Var(X)=E[X^2]-E[X]^2 = \frac{57}{5}-\left(\frac{49}{15}\right)^{2}=\frac{45\cdot57-49^{2}}{225}=\frac{164}{225}=0.7289$$`

---

### .blue[Ejemplo:]

<br>

El cálculo anterior puede llevarse a cabo fácilmente utilizando .red[octave/matlab]:

```r
function y=f(x)  
  y=(1/32).*x.*(1-x).*(x-5);  
endfunction  
mu=quad(@(x) x.*f(x),1,5)  
var=quad(@(x) ((x-mu).^2).*f(x),1,5)
```

---
background-image: url(http://www.dma.ulpgc.es/profesores/personal/stat/webEyPE/imagenes/darkGaussianBlur.jpg)
background-size: cover
class: inverse, center, middle

# Forma: Asimetría y Apuntamiento

---

## Momentos

Sea `$X$` una variable aleatoria. Se define el momento de orden `$k$` respecto al origen (o simplemente .red[ __momento de orden k__]) como:

.resalta[
`$$\large{\mu_{k}=E\left[X^{k}\right]}$$`
]

Asimismo, si la esperanza de `$X$` es `$E[X] = \mu$`, se define el momento de orden `$k$` respecto a la
esperanza (o simplemente .red[ __momento central de orden k__]) como:

.resalta[
`$$\large{M_{k}=E\left[(X-\mu)^{k}\right]}$$`
]

La varianza se puede expresar alternativamente como:

`$$\textrm{var}\left(X\right)= M_2= \mu_{2}-\mu_{1}^{2}$$`
--
.resalta[

Los momentos de la distribución de una variable aleatoria dan información sobre la __forma__ de dicha distribución
]
---

### Momento central de orden 3: Asimetría

El momento `$M_3$` informa sobre la asimetría. Concretamente, se define el .red[ __coeficiente de asimetría__] de la variable aleatoria `$X$` como:

.resalta[

`$$\large{A=\frac{1}{\sigma^{3}}E\left[\left(X-\mu\right)^{3}\right]}$$`
]

<br>

* __A<0 (Asimetría negativa):__ la masa de probabilidad tiende a concentrarse a la derecha.

* __A>0 (Asimetría positiva):__ la masa de probabilidad tiende a concentrarse a la izquierda.

* __A=0 (Simetría):__ La masa de probabilidad se reparte simétricamente respecto a su centro (la esperanza).

---

### Momento central de orden 3: Asimetría

Funciones de densidad correspondientes a variables aleatorias con distintos grados de asimetría.

---

### Momento central de orden 4: Apuntamiento o curtosis

El momento `$M_4$` informa sobre el apuntamiento (kurtosis) de la distribución. Concretamente, se define el .red[ __coeficiente de curtosis__] como:

.resalta[

`$$\large{\kappa=\frac{1}{\sigma^{4}}E\left[\left(X-\mu\right)^{4}\right]-3}$$`
]

--
<br>

* `$\bf{\kappa<0}$` __(Curtosis negativa):__ corresponde a funciones de densidad más bien aplanadas y con colas cortas. Las curvas con esta forma reciben el nombre de _platicúrticas_.

* `$\bf{\kappa>0}$` __(Curtosis positiva):__ corresponde a funciones de densidad más bien “puntiagudas” y con colas largas. Las curvas con esta forma se llaman _leptocúrticas_.

* `$\bf{\kappa=0}$` __(Curtosis nula):__ corresponde al caso intermedio, con un pico redondeado y colas de tamaño intermedio, como ocurre con la curva en forma de campana. Las curvas de este tipo reciben el nombre de _mesocúrticas_.

---

### Momento central de orden 4: Apuntamiento o curtosis

Funciones de densidad de tres variables aleatorias con distintos grados de apuntamiento. Las tres variables tienen distribución simétrica y las mismas esperanza y varianza.

---
background-image: url(http://www.dma.ulpgc.es/profesores/personal/stat/webEyPE/imagenes/darkGaussianBlur.jpg)
background-size: cover
class: inverse, center, middle

# Posición: Cuantiles

---

## Cuantiles

El `$\large{\alpha}$`-ésimo cuantil de una variable aleatoria `$\large{X}$` es el valor `$\large{q_\alpha}$` que verifica:

.resalta[

`$$F(q_\alpha) =P(X\leq q_\alpha) =\alpha$$`
]

siempre y cuando esta ecuación tenga solución.

---

## Cuantiles

<br>

Algunos cuantiles de uso muy extendido son los siguientes:
<br>

* `$\large{q_{0.5}}$`: se denomina __mediana__ de la distribución de probabilidad.

* `$\large{q_{0.25}}$`: __Primer cuartil__

* `$\large{q_{0.75}}$`: __Tercer cuartil__

* `$\large{q_{0.01}, q_{0.02}, q_{0.03}, \dots, q_{0.98}, q_{0.99}}$` son los __percentiles__ de la distribución

---

### .blue[Ejemplo:]

En el ejemplo de los círculos de radio aleatorios generados por un programa informático de acuerdo con la función de densidad:

`$$f\left(x\right)=\begin{cases}
\frac{1}{32} x\left(1-x\right)\left(x-5\right) & 1\le x\le5\\
0 & \textrm{en otro caso}
\end{cases}$$`

determinar la mediana, y el primer y tercer cuartiles.

---

### .blue[Ejemplo:]

Para hallar el cuantil `$q_\alpha$` de esta distribución debemos resolver la ecuación:

`$$\int_{1}^{q_{\alpha}}f\left(x\right)dx=\alpha$$`
 
--

`$$\int_{1}^{q_{\alpha}}\frac{1}{32}x\left(1-x\right)\left(x-5\right)dx=\alpha$$`

`$$\frac{1}{32}\left[-\frac{x^{4}}{4}+\frac{6x^{3}}{3}-\frac{5x^{2}}{2}\right]_{1}^{q\alpha}=\alpha$$`

`$$\frac{1}{32}\left(\left[-\frac{q_{\alpha}^{4}}{4}+2q_{\alpha}^{3}-\frac{5q_{\alpha}^{2}}{2}\right]-
\left[-\frac{1}{4}+2-\frac{5}{2}\right]\right)=\alpha$$`

`$$\frac{1}{32}\left(\frac{1}{4}\left[-q_{\alpha}^{4}+8q_{\alpha}^{3}-10q_{\alpha}^{2}\right]-\frac{1}{4}\left[-1+8-10\right]\right)=\alpha$$`

`$$-q_{\alpha}^{4}+8q_{\alpha}^{3}-10q_{\alpha}^{2}-\left(-1+8-10\right)=128\alpha$$`

`$$-q_{\alpha}^{4}+8q_{\alpha}^{3}-10q_{\alpha}^{2}+3-128\alpha=0$$`

---
class:split-40

### .blue[Ejemplo:]

La mediana es el valor que deja a su izquierda una probabilidad `$\alpha=0.5$`. En este caso la ecuación anterior se convierte en:

`$$-q^{4}+8q^{3}-10q^{2}-61=0$$`

La mediana es la raíz de este polinomio entre 1 y 5. Utilizando .red[octave/matlab] la raíz es Me=3.31927 (la única en el intervalo [1,5]):

.column[

![](imagenes/octaveRoots1.png)

]

.column[

]

---

### .blue[Ejemplo:] Cuartiles 1 y 3

.pull-left[

.red[Cuartil 1:] `$\alpha=0.25$`

`$$-q^{4}+8q^{3}-10q^{2}-29=0$$`

<br>
 .red[Cuartil 3:] `$\alpha=0.75$`

`$$-q^{4}+8q^{3}-10q^{2}-93=0$$`

<img src="tema2-2_Caracteristicas_VA_files/figure-html/unnamed-chunk-27-1.png" style="display: block; margin: auto;" />
        
]

.pull-right[
.center[ ![](imagenes/octaveRoots2.png)]
]